The Creative Act in the Dialogue between Art and Mathematics

Abstract

This study was developed during 2018 and 2019, with 10th- and 11th-grade students from the Jose Maria Obando High School (Fredonia, Antioquia, Colombia) as the target population. Here, the “art as a method” was proposed, in which, after a diagnostic, three moments were developed to establish a dialogue between art and mathematics. The moments include Moment 1: introduction to art and mathematics as ways of doing art, Moment 2: collective experimentation, and Moment 3: re-signification of education as a model of experience. The methodology was derived from different mathematical-based theories, such as pendulum motion, centrifugal force, solar energy, and Chladni plates, allowing for the exploration of possibilities to new paths of knowledge from proposing the creative act. Likewise, the possibility of generating a broad vision of reality arose from the creative act, where understanding was reached from logical-emotional perspectives beyond the rational vision of science and its descriptions.

1. Introduction

There has always been a conception in the collective imagination concerning the intelligence of human beings. This conception has always been related to logical or rational thinking, thus encouraging contempt for that which does not have some logic or rationale. This philosophy empowers all disciplines that work on positivist methods to search for knowledge. We have worked to establish and naturalize this, leaving aside any viable alternative that does not conceive intelligence only from a rational perspective. For this reason, the school system has been responsible for generating a division between reason and emotion, where art has ended up being cataloged within the world of emotions, and science, in this case, mathematics, in the world of logic and reason. In this way, both art and mathematics have been harmed, excluding any rational conception in art and any kind of emotion in mathematics [1].

For Zalamea [2], the isolation of different branches of knowledge has resulted in losing sight of reality, the world, and the universe as a whole. In this sense, Max Neef [3] also states that knowledge is fragmented, which does not allow for a complete vision of reality. The socio-historical need to establish links between the different disciplines has led to a transition from the unidisciplinary paradigm. A plurality of worldviews has been revealed that seeks to give provide answers to reality from multiple perspectives. When establishing a dialogue between science and art, it is necessary to transcend traditional ideas about how knowledge is generated in both disciplines. The confluence of emotion and reason—art and science—encourages human beings to believe and express their most intimate thoughts and feelings. In addition, these forms of expression lead others to do so, or at least to understand and feel their thinking and affectivity [4].

The transition to a multidisciplinary paradigm reveals the need for research in which an expanded vision of education and knowledge is considered. This perspective values the cognitive and emotional capacities to exercise a genuinely transformative role in society, where the human being is conceived as a totality integrating reason and emotion, enabling various ways of reading the world. The present investigation explores the relationship between art and mathematics. The main objective is new forms of knowledge framed by the creative act through experiences generated in the dialogue between art and mathematics.

2. Art and Mathematics

Art has generally been associated with the domain of the aesthetic, the emotional, and the sensory. On the contrary, mathematics has, through the years, been associated in the domain of the logical–rational, precision, and truth [5]. It is necessary to understand that throughout history, the two disciplines have been more united than many might consider. Many characteristics believed to be antagonistic prove to be more convergent than divergent.

Oostra [4] suggests that this intimate and seductive relationship between the two disciplines has been full of nuances. When intermingled, math and art have given way to the creation of infinitely new ways of seeing, feeling, explaining, and thinking about the world, nature, the universe, and reality. The creative process, intuition, and emotions commonly related to art play a fundamental role in mathematical thinking. Conversely, structure, perspective, geometry, and arithmetic have been used by artists, consciously or unconsciously, when creating their works. Although Descartes proposed from his duality theory that the emotional and the rational are separate, the languages from art and mathematics are perfectly articulated.

Seen from many dimensions, as proposed by Bejarano-García [6], it is possible to approach art through mathematics and vice versa. In its infinite dimensions, both art and mathematics provide commonalities facilitating an internalization of concepts and abstractions. This approach can be found in music, painting, sculpture, dance, architecture (considered one of the fine arts), and literature.

In the dialogue between art and mathematics, Leonardo Da Vinci pioneered the use of perspective in his works. Later, the mathematician Desargues managed the first work on projective geometry for artists, which was considered as universal geometry until the arrival of topology. Many examples of this dialogue can be found from different characters throughout history, and it has been possible to observe a trend in which people dedicated to mathematics usually tend to be dedicated to art in one of its multiple expressions. For example, the mathematician Charles Lutwidge was also a writer and photographer. Felix Hausdorff, a founder of topology, was dedicated in youth to literature, and Colombian mathematician Otto de Greiff was a music lover. In art, people have used mathematical concepts consciously or unconsciously [4].

Mariño [7] mentions the mathematical concept of symmetry as one of the most obvious links between art and mathematics. In addition, symmetry emphasizes the aesthetic criteria as a fundamental point in the dialogue. Mariño highlights some of the renowned artists in whose works the relationship between art and mathematics is evident, such as Abbot, Dalí, and Escher. Carlos Vasco also focused his interest on the relationship between art and mathematics. In an article, Vasco expressed the relationship in four fundamental sections: art as mathematics, mathematics in art, the art in mathematics, mathematics as art. The central thesis in Vasco’s work is that one must be a mathematician to discover creativity [4].

3. Dialogue between Art and Mathematics at an Educational Level

The possibilities that art can offer at the educational level have recently gained increasing attention. One of the movements supporting this interest has been the science, technology, engineering, art, and mathematics (STEAM) movement, which has emerged as an initiative supporting the incorporation of art and design into the learning of traditional STEM disciplines [8]. One of the main objectives in integrating the arts with the other disciplines is the promotion of knowledge transfer between different fields to increase students’ academic performance [9,10].

Many studies have validated from various perspectives the advantages and possibilities offered by art in education. For instance, Palacios [1] offers multiple arguments that conceive in art a possibility to generate new ways of seeing the world. Luis de Tavira [11] also defends the possibilities of art at the educational level and how it can broaden views on diversity. As expressed by the author, art opens the conception of inclusion to a much broader meaning: diversity. Through art, it is possible to achieve education for and from diversity, where all the factors that generate heterogeneity are considered: each difference, each interest, and the singular motivation of each student in the classroom.

Parra [12] also proposes the advantages art offers in education. The author emphasizes that one can strive for critical training of school subjects through art, whose students then go out to play a transformative role in society. This benefit is one of the many possibilities that art offers. By attending to interiority and accounting for personal context, individuals might be able to question themselves, their world, and their reality. Parra considers that individuals can attend to the deepest part of their being, feeling, and thinking with art. Through art, this reflection offers possibilities to formulate critical subjects with a view toward a true social transformation, which is vital in these times of technological revolutions where human beings ultimately illuminate the path.

In the field of education, efforts have been made to establish a dialogue between art and mathematics. Various investigations have been carried out over the years that, in one way or another, have achieved an approach between both types of knowledge. Generally, this approach has been based on finding a method for independently enhancing one of the two disciplines, using one as an instrument of the other. In this way, the relationship cannot be understood as a dialogue between knowledge if one discipline is highlighted over the other.

At the Latin American level, there is currently a great concern because students are not acquiring the necessary knowledge in the areas of science and mathematics to be able to achieve productivity in their lives and ensure future work in the fields that have emerged from the development of the new technologies. When reviewing the results obtained by Latin American countries in international tests, it is evident that in most cases, the students are below the international average. For example, the PISA (Program for International Student Assessment) test assesses skills in mathematics, sciences, and reading. The particularity of this test is that instead of assessing the concepts that the students have learned from the school curriculum, it assesses how prepared students are for life after school [13].

In the results obtained by the Latin American countries in the PISA 2018 test [14], it can be seen that all obtained scores below the average in the areas of science and mathematics. On the other hand, Chile, which is the country that obtained the best Latin American results in the PISA 2018 test, was the only Latin American country in the TIMSS test (Trends in Mathematics and Sciences Study). This country was ranked among the countries with the worst results in the areas of science and mathematics, obtaining results similar to those obtained by countries such as Kosovo, Montenegro, Armenia, Morocco, Bosnia and Herzegovina, which have lower GDP per capita than Chile. If this situation is extended to the rest of Latin American countries, the situation found may be much more complex. These poor results obtained by countries such as Colombia, Mexico, Venezuela, Bolivia, etc., are due to a complex network of general situations in the region which are specific to each country, which would require a much more in-depth and detailed analysis. What can be evidenced is the need to seek alternatives to improve the results obtained, not only in terms of scores, but in terms of obtaining meaningful knowledge for life and to face the challenges that the future holds [13].

Regarding Latin America, several studies [15,16,17] have been carried out in Brazil in the field of education regarding new alternatives and methodologies establishing a relationship between art and mathematics. However, as mentioned earlier, this dialogue has not progressed from being an instrumentalization of art in favor of mathematics. In research conducted by Zago and Flores [18], the relationship between mathematical education and art was studied. In this case, the study focused on analyzing how one could contribute to the teaching of geometry from art. The authors examined the required mathematical knowledge and the development of aesthetic and visualization skills from an artistic perspective. As a result, it was concluded that the two areas could be mainstreamed through the exercise of thought, considering mathematics as an essential element in creating and contemplating art.

Santos-Luiz et al. [19] conducted a systematization of the connections between mathematics and musical content. Musical content was divided into music theory and analysis, acoustics, and musical composition. In the study, existing associations with mathematics were systematized in each of the themes. The methods considered the programs and achievements of mathematics in the population under study, namely elementary school students and students between 11 and 12 years old belonging to a secondary school. The results indicated that musical elements and concepts related to mathematics were distributed in arithmetic, algebra, trigonometry, and especially geometry.

At the Nove de Julho University in Sao Paulo, Brazil, an investigation was carried out, the main objective of which was to present the concept of a fractal pattern and its potential in the teaching and learning of mathematics [20]. The research was fundamental to the idea that both mathematics and the arts are linked to human activities, with expressions derived from intelligence, desires, ideas, and representational needs. The findings revealed that visual aspects relating art to mathematics can be contemplated from the exploration of fractal patterns.

In Colombia, Zuluaga-Arango and Pérez [21] applied a series of strategies designed to favor, through the arts, the teaching–learning processes of students from the San Carlos de La Salle Institute. The study sought to show the possibilities for mediating the teaching of mathematics through the plastic and performing arts. In this way, students can approach mathematical knowledge from less instrumental and operational positions, obtaining better results in the development of competencies.

Brooke and Nemirovsky [8] conducted a study reinforcing the arguments necessary to integrate the arts into math courses. The investigations that support these arguments are limited and complex, as it is difficult to find an instrument that can offer a measure of creativity. The study evidenced that additional perspectives were needed in favor of the integration of the arts into the teaching of mathematics. It was found that by creating works of art inspired by mathematics, students were able to combine mathematics into a wide range of life experiences, discovering situations in which mathematical research was encouraged, and changing attitudes toward a more artistic perspective.

Finally, Boruga [22] worked to reveal the impact origami can have in the educational process concerning behavior and learning. From a behavioral aspect, it was evidenced that students became friendlier and developed more patience and energy to carry out their activities. From a mathematical perspective, it could be demonstrated that logical thinking was enhanced in the students, consolidating in them some mathematical notions, especially geometric ideas. In addition, a better understanding of concepts such as fractions, shapes, and angles was reached by using mathematics in a different context, becoming a meaningful and pleasant experience for students. From an artistic perspective, it was found that students improved their aesthetic sense, creativity, and sensitivity to art, learning an appreciation for the work required to create something and, therefore, to value art.

Internationally, Sánchez [23] conducted a study based on geometric software, analyzing various paintings using dynamic geometry. Field [24] proposed some ideas on how mathematics can be seen from an artistic perspective, thus becoming a significant process in teaching math. In this way, Dietiker [25] proposed that challenges in the current educational model can be addressed from an art perspective. By considering assumptions, values, and visions of mathematical education, Dietiker sought to theorize mathematics as an art form, framing it in narrative terms to inspire a rewrite of mathematical experiences in students. Thus, the perception of mathematics was suggested as an art form where teachers and curriculum designers can renew views of math and avoid using the same methods.

4. Ways of Interpretation and Representations of Reality

4.1. The Senses and Experience

Through the senses, human beings appropriate experiences. From these experiences, mental processes arise where cognition and emotional dialogue begin to generate possibilities for knowledge [26]. Eisner [27] emphasizes the fundamental role that the senses have in conceptions of reality and how those conceptions are transformed into unique expressions of the experiences of each person. The senses provide the means to create symbols as forms representing reality. Experiences are acquired through the senses, and in turn, these experiences are transformed into symbols. Thus, with symbols, it is possible to transmit conceptions of reality and the particular experiences of each person [27]. Therefore, in the search for knowledge, the human being uses different rational and sensory instruments.

From a neuroscience view, the intersection between the right and left hemispheres (which are generally associated with the sensory and the rational, respectively) provides the interpretation of what is exact and overflowing from this reality. That is, a dialogue is established between the emotional–sensory and the logical–rational, revealing new ways of understanding and perceiving the world [26]. Thus, returning to the concept of cognition, Eisner [27] argues that cognition should be understood as a process inseparable from emotion, where “affectivity and cognition occur simultaneously” within human experience.

4.2. The Aesthetic Experience from Dewey

For Dewey [28], experience arises through the interaction between a person and his world, his reality. Emotional quality defines an experience as unique, and aesthetics is present when there is a particular emotion. Aesthetics is related to cognitive capacity and emotions and senses that form conscious or unconscious criteria to discern what is beautiful or not. Thus, if the experience possesses a quality called “aesthetic”, Dewey maintains it is possible to consider what he calls an “aesthetic experience”. Moreover, Dewey [28] suggests that the aesthetic experience arises from a feeling or emotion resulting from a process of complexity and maturation of that feeling, where a “something” occurs involving emotions and cognitive processes.

4.3. Art as a Form of Knowledge: The Logical and the Emotional

For Dewey [28], experience arises through the interaction between a being and their world, their reality. Emotional quality defines an experience as unique and aesthetics is present when there is a particular emotion. Aesthetics is related to emotions and senses with a conscious or unconscious criterion to discern what is beautiful or not and their cognitive ability. Thus, if the experience has that quality called aesthetics, it is possible to consider aesthetic experience. According to Dewey [28], the aesthetic experience arises from a feeling or emotion and results from a process of complexity and maturation of that feeling, where something happens where emotions and cognitive processes are involved.

The difference between the aesthetic and the intellectual is in the different points in which it is chosen to emphasize or the constant rhythm that marks the interaction between the being and its surroundings. The author proposes that a rational subject has his/her aesthetic moment when their ideas become the corporeal meaning of objects. Recognizing the aesthetic qualities of thought becomes a conception of cognitive processes as a dialogue between the rational and the aesthetic experience [28]. In this way, Best [29] declares that the confluence between emotion and reason, and art and science, makes human beings believe and express their most intimate thoughts and feelings. In addition, these forms of expression also lead to others to do so, or at least understand and feel their thinking and their affectivity.

Dewey [28] declared that, from this conception where art and science, the subjective and the objective, dialogue in a search to generate new possibilities of knowledge, art as a means of expression becomes a new experience of the world, where neither art and science have existed for themselves, but both planes cross generate a series of intersections that open up new possibilities to understand and apprehend the world.

The recognition of a worldview that establishes a dialogue between reason and emotion, science and art, will result in a range of possible responses, representations and interpretations of reality, where objectivity and subjectivity operate as a creativity generating circuit, triggering the creative act that allows a total understanding of the reality that is observed [4].

Eisner [5] thought that the arts are considered more affective than cognitive, being simpler rather than more complex. On the contrary, the possibilities and methods used in the arts for perceiving details and subtleties, imaginative possibilities, and representations and interpretations for abstracting reality demand complex forms of thought. The cognitive arises in parallel with the emotional, and both vectors add forces instead of having opposite meanings. Eisner considers complex forms of thought to be required from art, where the cognitive arises in parallel with the emotional. This process occurs from the perception of the details and subtleties of reality and its interpretation and representation. In this sense, Best [29] also proposes that the emotions generated from art involve cognitive processes, since these are identified and their character is determined by the conception, interpretation and understanding of the artistic object in question. In addition, this author maintains that the emotions involved in learning the arts become meaningful experiences for each person, with the artistic experience being completely emotional and rational.

5. Creativity and the Creative Act

Creativity is a concept that has been generally associated with artistic ability or searching for answers or solutions for a situation considered to be a problem. Creativity is influential as it draws from art and science to guarantee the emergence of ideas or solutions to problems at individual and societal levels [30].

Jaime Parra Rodríguez and Carlos González Quitián represent two of the most influential Colombian authors who have performed different creative processes focusing on how they relate to cognitive processes. For Parra [12], creative cognitive processes are operations of thought based on scientific achievement and the joy of the aesthetic. In this author’s conception, a framework can be observed that relates a creative process to the aesthetic and the scientific, finally demonstrating how that creative act can be a bridge establishing logics of articulation between the emotional, the logical, and the rational.

In contrast, González [31] maintained that creativity is how reason and emotion intervene in the generation of ideas. This intervention generates actions that spark transformation, which is framed by the formation of the person and their interaction with culture. In this way, talent, knowledge, culture, and emotions are homogeneously merged in the creative act, each one forming a mixture in perfect harmony so that social transformation is reached through creativity. Finally, González [31] incorporates some of Vigotsky’s conceptions regarding the creative act. Within these conceptions, it is considered that the imaginative function is the foundation of the creative act. In addition, experiences that have an emotional impact on the person are directly proportional to the richness of the creative act.

5.1. Max Neef’s Creative Act

Manfred Max Neef proposes from his perspective what the concept of a creative act reveals. For Neef [3], science can only describe, not understand: “We know a lot, but we understand little or almost nothing”, therefore, “science has separated us from the world to know more about it, taking an attitude of observers, of spectators of a reality that does not touch us”.

From Roger Bacon and René Descartes, the ability to act locally and fragment reality is consolidated. According to this conception, fragmenting reality helps to better comprehend the world. For Neef [3], the human being went from being someone who integrated everything to fragmenting each of the things that make up a person’s reality. To solve a specific problem, there is a specific form of knowledge. The fragmented reality is consolidated in the fragmented world, where perceptions are exclusively local and the ability to capture totalities is lost. This fragmentation leads to a refinement of language to describe situations and circumstances. In this process of describing and explaining, knowledge has been increasing and science has begun to be executed.

Analyzing the approaches of Bejarano-García [5], when viewed from the intention of understanding the world and reality, one begins to understand that rather than seeking solutions to problems, one must transcend towards transformations of which one must be a part. Only that which can be integrated can be understood.

For Max Neef [3]: “… a person may have studied everything that can be studied from a theological, sociological, psychological, biological and even biochemical view of a phenomenon that is known by the name of love. That is, the person is an expert on the subject of love who has written books and delivered lectures, knowing everything that can be known on the subject of love. However, that person will never understand love unless they fall in love. Understanding love is not something that can be learned; it is something that can only be lived. No one can understand pain if they do not suffer, even if it has been described in a thousand ways …”

Thus, you can only understand what you are part of, what you can integrate with, and what you can penetrate deeply. In this way, it is possible to begin to understand the creative act as understanding the world and the reality of which one is a part. This understanding is where the creative act begins. In this way, transcending, explaining, or describing reality allows you to enter it, enabling its integration and compression. The process is about moving from doing to being. This transition, according to Manfred, is the essence of the act of creation. In this sense, Max Neef [3] considers that the creative act begins when one is part of, when something is deeply penetrated, with love, that is, with the desire to want to be synergistically empowered with it.

5.2. The Act of Creation in Art and Mathematics

From the perspective of mathematics, creativity is commonly related to offering viable solutions to a problem. That is, the strengthening of creative abilities in mathematics is linked to confrontations with problems and their subsequent resolution. For creativity to flourish in mathematics, it is necessary beforehand to have a minimum amount of knowledge on how the awakening of creativity is being sought. The creative act in mathematics proposes that there must be a communion between logical thinking, intuition, deduction, and induction for creativity to arise. In this generation of creativity, it is imperative to keep in mind that creativity does not occur when the path to be followed is shown. If the path were known, one would reach something that was already expected.

The artist Marcel Duchamp proposed a definition of the creative act from the perspective of art. For Duchamp [32], the creative act is closely linked to the aesthetic level, where the artist goes from the intention of his work to the realization through subjective reactions of which he is not aware. With the symbol, the viewer can interpret the internal qualities, the essence of the work, which the artist has tried and managed to unconsciously express from an aesthetic level.

From the conception of Zalamea [2], when considering creativity, it is necessary to refer to the cahiers of Paul Valéry. The notebooks proposed multiple considerations about creativity not only in art but also in various fields of knowledge, mainly mathematics and the natural sciences. In scientific and artistic fields, reason, intuition, mind, body, reality and imagination are involved, becoming vital in the processes of creation [4]. In this sense, Piñón [33] argues that spaces are created and recreated in both art and science, building an oasis overnight. For this reason, they are interdependent. Both fields use creation, intuition, and imagination.

From the perspective of emerging inventiveness, the creative closeness between art and mathematics is endorsed from a formal, dual and reticular point of view within the general modes of knowledge [2]. Both artists and scientists experience creative acts in relation to aesthetic quality. In this way, both perform an artwork, each using the means and particular language the work requires [4].

6. Art as a Method to Reach Other Forms of Knowledge

When considering art as a method to generate new possibilities of knowledge, according to Alatriste et al. [34], it is necessary to transcend from the conception of knowledge biased by positivism towards an expanded conception of knowledge. Traditionally, knowledge has been related to science and this has been understood as the search for answers to questions that arise from the relationship of subjects to reality [4]. Taking a step toward an expanded knowledge paradigm results from instability in the search for answers that represent the discourse of knowledge. This lack of stability can be evidenced in concepts such as the second law of thermodynamics, which speaks of an always conflicting entropy, or in quantum physics, where chance plays a fundamental role in the theoretical foundations of its theories. Mathematics itself suffers from inadequacy by assigning truth to some statements for which it has to resort to internal principles that generate contradictions. For example, the Kurt Gödel theorem, which states that in first-order logic, every formula that is valid in a logical sense is demonstrable [35].

Following Alatriste et al. [34], the extended knowledge paradigm searches for something beyond a simple answer to a posed question. From the conceptions proposed by these authors, the expanded notion of knowledge arises from a systemic circuit confirmed by the possibility and the question together with the answer, where the important thing is not the search for knowledge as such, but rather its construction. If there is a conception of expanded knowledge, it is possible to unveil a method by which the knowledge is reached or constructed through art.

Art offers the possibility to consider sensualized knowledge; that is, it is possible to give sensuality to knowledge. More than answers, what is wanted is to achieve possibilities and questions by accommodating a new epistemic device [34]. As stated above, it is vital to clarify the need to cease considering art as an exclusive member of the emotional space and sensations, thus discarding any rational process in art or even thinking that rationality is harmful to the artistic exercise. From this viewpoint, art is given a value, both from emotion and reason, to consider new forms of knowledge that can be approached [5].

Although art is called upon to conceive knowledge framed within positivism, it is also possible through transdisciplinarity and post-disciplinarity measures to mutate the different ways of thinking and challenge society’s problems from different points of view. Breaking disciplinary barriers and eradicating limits between the disciplines reveals new forms of knowledge through diverse ways of creating art [36].

The misconception embedded in the collective imagination that emotion and reason are separate has been seen since the early 17th century in the Cartesian paradigm of duality, where reason and emotion cannot share the same path. It is here that reason is established in the field of knowledge and emotions in the field of art, which almost makes them appear to be contrary and opposite. This type of thinking has taken root in the collective imagination, becoming a powerful idea that, due to contemporary political and economic models, has permeated education. The emotional is seen as something of second-order importance compared to the rational. These types of ideas are improperly considered and perpetuated by social, political, educational, and cultural institutions [26].

In this research, a dialogue between art and mathematics is proposed. Through the creative act as a meeting point, new forms of knowledge can be established that entail, as Neef [3] maintains, an understanding of the world. In this dialogue of knowledge, it is not intended for art to be an instrument of mathematics or vice versa. In this sense, it is essential to clarify that the main objective of this work is linked to showing how, through this articulation, it is possible to give way to an expanded paradigm of knowledge [34]. In this manner, emotion and reason play a fundamental role in achieving the creative act, thus generating a complete vision of reality not fragmented by positivist or rational ideas. In this way, this research aims to analyze and interpret new forms of knowledge that arise from the creative act in the dialogue between art and mathematics. The subjects for analysis include 10th- and 11th-grade students in the José María Obando Rural Educational Institution of the municipality of Fredonia, Antioquia, Colombia.

7. Methodology

The present qualitative research aims to analyze and interpret experiences acquired during the proposed creation process from the dialogue between art and mathematics. The method occurred in three moments: Moment 1: introduction to art and mathematics as “ways of doing art”. Moment 2: collective experimentation, and Moment 3: re-signification of education as a model of experience. For this analysis, art emerged as a possible approach to the knowledge of how another discipline is generated, in this case, physics, mathematics, and art itself. From the present investigation, art as a method is the way each participant constructs meaning and approaches knowledge based on the subject’s particular experience.

Art is also the image of a way of thinking that can be understood as a record of thought. This means that art is a means of representation not only of ideas and philosophies but also of knowledge and ways of relating to the world. Art provides ways of thinking and imagining things, becoming an emergence of values, techniques, knowledge, and habits of thought still prevalent today [18].

In the first stage of the investigation, an initial diagnosis was made considering various characteristics that participate in the proposal about the population.

7.1. Participants

Sixteen students from the 10th grade and ten students from the 11th grade of the José María Obando Rural Educational Institution were selected for the project. The ages of the students in both grades ranged from 16 to 19 years old. This selection was made considering the hourly intensity in the area of physics and mathematics and previous knowledge in mathematics and physics.

Moments 1 and 2 were carried out with the 26 students of the 10th and 11th grades, and Moment 3 was carried out with six students who voluntarily decided to participate.

7.2. Initial Diagnosis

The José María Obando Rural Educational Institution shows from its academic guidelines and curricula a traditional educational model where mathematics and linguistics taught is prioritized, focusing on obtaining good results on the SABER 11 tests (similar to PISA tests). This emphasis shows evidence of a positivist model in science courses that prioritizes a rational perspective in science teaching. This focus leads to the exclusion of other types of expressions that can generate new possibilities in the teaching–learning process. Therefore, emotion, experience and the senses have come to play a secondary role in the educational teaching–learning process of this institution.

• An observation was made of the context of the institution and its educational community. It was found that both the institution and its students belong to a rural context, where coffee is the most important product of the local economy. The educational institution has based its educational model in a rural context, attempting to propose a multidisciplinary curricular approach framed in the learning of the different processes involved in the elaboration of roasted coffee beans and ground, and in different products derived from coffee.
• An analysis was made of the academic conditions of the students in the areas of science, specifically in physics and mathematics. This analysis sought quantitative data regarding the students’ academic performance. One of the researchers in this study was the mathematics and physics teacher of the students who participated in this study. In this way, through the quantitative and qualitative performance of the students throughout the classes and the different activities carried out in them, it was possible to determine that there was a heterogeneity in relation to the academic performance in these areas. In this way, it was possible to achieve the study characteristic that all participating students presented a diversity in terms of affinity to mathematics and art, and in terms of the level of academic performance in both areas as well.
• In addition, when selecting the group of students to conduct the different activities proposed, an analysis of the diversity present in this sample was carried out. The needs, differences, and potential of each student were considered. These data identified how it was possible to work on diversity from the arts and their multiple expressions.
• Finally, the institutional educational model and the institutional educational project (IEP) were reviewed. With this information, it was possible to identify that the institution operates a “humanist” educational model. From the theory, the model considers the formation of sensitive, critical and conscious citizens. In practice, however, this goal is not evident. For instance, science courses (mathematics, physics, natural sciences, chemistry, technology) are generally considered logical and rational. Therefore, the subjects are disconnected from the social, the sensible, and the “human”. This emphasis on the rational can also be observed in the place given to art within the IEP. Art, which people generally teach without knowledge or experience in the subject, is seen as an area with a secondary role in student development.

7.3. Moment 1: Introduction to Art and Mathematics as Ways of Doing Art

In the first moment, the students were contextualized regarding the ways of conducting art and mathematics. The objective of this contextualization was to show students different mathematical and physical concepts from a technical and theoretical point of view that would ultimately give rise to the articulation between art and mathematics. These “ways of doing” were made known through formulas, laws, or theories. In principle, the theories were framed in a logical-mathematical or technical language at an artistic level. These theories were transformed to show that art does not impose an absolute truth from a rational paradigm and from what is considered to be fine art.

The concepts developed to introduce ways of creating art were a simple pendulum, centrifugal force, symmetry, sequences, vibrations, proportions, electricity and renewable energies, plane and spatial geometry, addition and multiplication, and measurement. These concepts were presented from a theoretical perspective through a traditional masterclass. Some of the concepts used during the first moment are shown below.

7.3.1. Simple Pendulum

The pendulum is a physical system composed of a mass suspended from a fixed point by wire or rope, with which it is possible to measure time, the intensity of gravity, and more. Equation (1) governs a simple pendulum motion for small-amplitude oscillations, where $T$ is the period of oscillation, $l$ is the length from the fixed point to the suspended mass, and $g$ is the acceleration of gravity.

$$T\approx 2\pi \sqrt{\frac{l}{g}}$$

(1)

7.3.2. Centrifugal Force

In mechanical physics, when a body is in motion in a rotational system, it experiences a force that ejects it from the system in the opposite direction to the axis of rotation. This force is associated with a body of mass m, in a rotation system with angular speed ω, and in a position r concerning the axis of rotation. Equation (2) expresses the magnitude of the centrifugal force that a body experiences under these conditions.

$$F=m{\omega }^{2}r$$

(2)

7.3.3. Chladni Plate

With the Chladni plate, it is possible to study the standing waves generated by mechanical excitation on a square plate. The vibration modes of these plates can be visualized in two dimensions. Depending on the excitation frequency, the vibration modes of the plate will vary, creating pressure zones and acoustic shadow zones within the plate. According to Chladni’s Law, the vibration frequency of a circular plate is demonstrated by Equation (3), where m and n are the number of radial and non-radial nodal lines, respectively, and, C is a constant that depends on the properties of the plate.

$$f=C{\left(m+2n\right)}^2$$

(3)

In addition, for a square plate, the wave equation must be solved in two dimensions, where the boundary conditions imply an antinode. The resonance frequencies are obtained using Equation (4), where a is the dimension of one side of the plate, v is the speed of sound propagation on the plate, and m and n are the horizontal and vertical nodal lines, respectively.

$$\omega =\frac{v\pi }{a}{\left(m^2+n^2\right)}^{1/2}$$

(4)

7.3.4. Symmetry

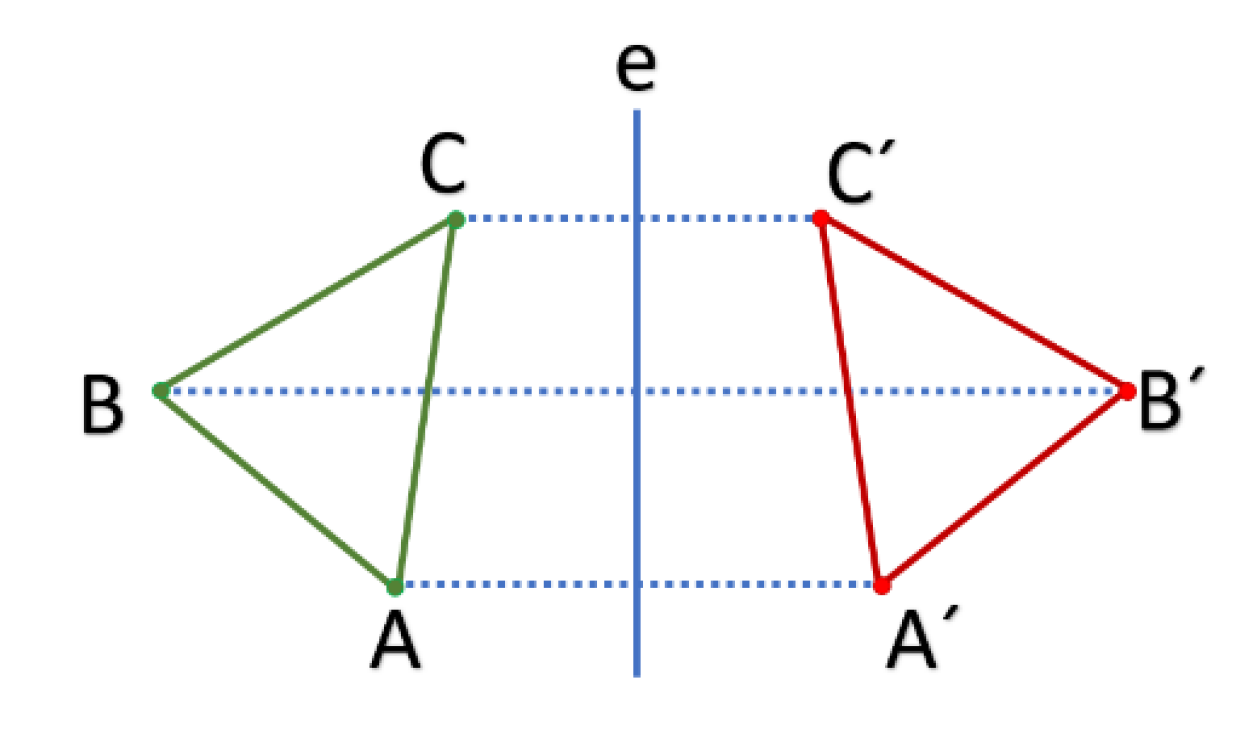
Symmetry can be defined as a feature of geometric figures, equations, systems, and material objects, among others, in which transformations or movements occur with no variation generated. The concept of symmetry can be found in the fields of geometry, physics, art, chemistry, and biology. For the present work, the concept of symmetry was taken from a geometric perspective in which, at each point of a figure, another point corresponds (Figure 1). This situation represents the concept of axial symmetry, where an internal or external axis can be provided to the figure, and the type of symmetry can be an injective or surjective function. This type of axial symmetry can be seen in the figure, where images A’, B’ and C’ correspond to points A, B and C, respectively, and e depicts the axis of symmetry.

7.3.5. Successions

Sequences are ordered sequences of numbers that respond to a general term, with which each of the terms in the sequence can be determined. In this way, there are an infinite number sequences that vary according to their general term. For example, to express the sequence of odd numbers, the following equation is used, where $a_n$ is the general term of the sequence, $a$ is positive integer, and $n$ is a natural number.

$$a_n=2n-1$$

(5)

7.4. Moment 2: Collective Experimentation

A review of background and information from various sources of literature and the internet reveals activities and approaches carried out to investigate and test different forms of articulation between art and mathematics. For this study, activities from the literature were transformed and adapted according to the students’ needs to provide feedback for each of the experiences during this stage of experimentation. From the experiences collected during the experimentation stage, a series of activities were designed in which the dialogue between art and mathematics was established through art as a method. Students had the opportunity to understand these methods of doing and were able to venture and be part of a construction and aesthetic experience from a logical and emotional perspective.

The activities were carried out for two weeks using the class hours of mathematics, physics, and art. This amounted to approximately 22 h of total work during the two weeks. For each of the proposed activities, the necessary materials were obtained beforehand and provided by the researchers in charge, the students, and the educational institution.

7.4.1. A Simple Pendulum as a Method of Doing Art

In this activity, the physical concepts that are part of the pendulum movement were worked on. The students built a device with a part of the body of a plastic bottle, which was drilled in the lower part for the exit of paint. The bottle was attached to a rope in the upper part in such a way that the weight of the pendulum (device and paint) would be evenly distributed. This device was attached to the ceiling of the place where the activity was conducted, seeking to make it remain in the geometric center of the space. In addition, the installation was made with an option to vary the height. Canvases were placed on the ground of the measurement site just below the pendulum position so that students could create different patterns by experimenting with the different proposed physical concepts.

During the activity, the students had the opportunity to vary the height, weight (mass of the volume of paint added), and the initial position from which the pendulum was thrown. Through the patterns achieved, students were able to observe and feel what happened when the different parameters of the experiment were modified. Students also achieved the creation of works of art and unique patterns through the experiences.

7.4.2. Chladni Plate as Art

For this activity, the physical concepts of sound waves and vibrations on rectangular plates were worked on. Students built a device that allowed the transmission of vibrations generated by a loudspeaker attached to a rectangular metal plate with a thickness of 0.5 mm. The loudspeaker was connected to a power amplifier, which, in turn, was connected to a mobile device serving as a frequency generator, either by playing music, or by playing pure tones at a specific frequency using Frequency Generator by KingZ Apps (available for free on Google Play). The amplifier’s power was adjusted so that the vibrations generated on the surface of the loudspeaker had the necessary energy to be transmitted to the plate using a cylindrical object connected both elements.

During the activity, students experimented with various electrical output powers of the amplifier and different wave frequencies emitted by the loudspeaker. With the help of fine sand on the metal plate, it was possible with different frequencies to check the patterns formed with the sand on top of the plate. In this way, the students showed areas in the patterns in which the sand did not accumulate and other areas in which it did. Thus, they were able to check the resonance modes of this particular plate for the different excitation frequencies and observe the artistic and physical significance of what they were experiencing.

7.4.3. Geometric Figures Built from Proportions as an Art Method

In this activity, a Tangram was built according to indications of the proportions and measurements that each of the seven figures that comprise the traditional Chinese game should have. The instructions were initially given so that students had to report the measurements of each of the figures according to an initial measurement established by themselves. This measurement corresponded to the sides of the square that can be built with the seven figures of the Tangram. The students were guided in the design of each figure based in the proportions of the total square. With these prompts, the students were finally able to build their own Tangram.

During the activity, the students experimented with different geometric constructions to create different figures and verify that regardless of the figure created, the proportions between the elements used and the total area of the figure were always preserved.

7.4.4. Centrifugal Force as an Art Method

In this activity, a device was built through which the concept of centrifugal force could be experienced. For this, an electric motor was used, which was configured through an external circuit to vary the input voltage, and thus, the RPM of the motor. In this case, a 9-volt motor was used, and a 3-, 6- and 9-volt selector circuit. A compact disc (CD) was anchored to the motor, which would rotate each time the motor was activated. The CD served as a base to position the canvas, which was experimented on with the help of paint.

During the activity, the students were able to experience how the centrifugal force acted on the mass of paint added to the canvas. By varying the angular velocity through voltage, the amount of paint added, and the position on the canvas on which the paint was being added, they demonstrated through their artistic creations the effect that all the variations made on the centrifugal force generated.

7.4.5. String Art

In this activity, the concepts of sequences, patterns and a solution of equations could be developed. Each student drew a circle on a rigid table that had a predefined number of points equally distributed. Students were listed in ascending order starting from zero to the amount of initially established numbers. For this, the students had to use different instruments such as the protractor, the compass, and the ruler to meet the established design criteria. After this, the students were instructed to decorate the circle with a design chosen by them, and to stick tacks in each of the equidistant points on the circumference. Having this part of the activity ready, each student was given a sequence using an equation and rope. Starting from a position established as zero, students had to find the next number holding the string in the tack corresponding to the number found.

Each student created a different pattern during this activity since each had an equation and several points on the circumference. In this way, different patterns could be created with the strings. By sharing their own experiences, students were able to mathematically demonstrate that their patterns were different from their peers.

7.4.6. Solar Vehicles

In this activity, concepts related to electricity and solar energy were worked on. Students learned about the construction of series and parallel circuits and the handling of different instruments to manufacture and measure the circuits. From art, concepts such as points, lines, surfaces, perspective, and geometry, served to aid in the design and construction of scale cars and elements related to the test track where they were used (planes, ramps, obstacles, etc.). From mechanical physics, the students were able to carry out different tests and put into practice concepts related to uniform rectilinear motion and uniformly accelerated rectilinear motion. The scale vehicles were built with homemade materials. The solar panels and elements such as resistors, capacitors, switches, among others, were delivered by the researchers.

In summary, art was used to approach the forms of knowledge that could be unveiled from the creative act in the dialogue between art and mathematics. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show some of the processes and results for each of the activities.

7.4.7. Experiences Achieved during the Activities

For Parra [12], the creative process is based on an aesthetic and scientific achievement, which would not have been possible without the students having notions of art and science before starting. In this same sense, Neef [3] proposed that to understand something, it is necessary to be able to integrate with it, which is impossible without prior knowledge of what one wants to understand.

Everything mentioned above in the creation process generated during each of the activities led to the emergence of this inventiveness. According to Zalamea [2], this inventiveness is where the creative act is experienced and where each student executed their work considering their own resources, languages, and experiences. In this way, the dialogue between science and art experienced during each activity evidenced how the reason, intuition, mind, body, reality, and imagination of each student intervened in each of their creations.

To consider art as a method for opening new forms of knowledge from the exercises, it is necessary to consider Alatriste et al. [34]. That is, the achievement of an expanded knowledge through art is related to systemic, relational logic in the constitution of the Lacanian Subject. This knowledge passes through three spaces in the process: the real, the imaginary, and the symbolic [37]. When traveling through these three spaces, namely ontological, mobile, and relative, it is possible to conceive of an expanded knowledge through art analogous to the constitution of the Lacanian Subject. Within these, Alatriste et al. [34] affirmed that the real is a qualitative experience mediated by the symbolic, while the imaginary is neither expressible nor communicable. The imaginary represents internal worlds with high doses of emotion, which is expressible but not communicable. Finally, the symbolic as the space of codes allows for the recognition of a stable world based on the context of knowledge as a communicable discourse.

It is now necessary to understand how these three spaces work when considering art as a method to approach the possibilities of an expanded knowledge when mobilizing for them. The space of the real is shown as a fissure space that generates the need to transform an experience into imaginary or symbolic events. In the space of the imaginary, a world emerges through the processes of creation that goes from a mental image to a material image in the abstraction of reality, shaping a possible construction of knowledge. In this space, which is strongly mediated by the emotional, “the original trauma of confrontation with the real is transformed into mythical worlds” [34]. Finally, a mediation is seen between the qualitative of the real, the affective of the imaginary, and the legal of the symbolic in the symbolic space. In this space, the other two spaces are transformed into thoughts that resignify a shared experience. This gives way to a new form of expression that comes from the most intimate knowledge of the subject reflected in the construction of new forms of knowledge.

Expanded knowledge through art as a method can then be outlined by a triadic systemic phenomenon that travels through three spaces: the real, as an invoicing quality that is also generating; the imaginary, as an intimate and internal affective experience, and the symbolic, as a representative and plot experience. This is the process of building knowledge from an expanded perspective through art as a method or vehicle that leads to its achievement. Note that, as proposed by Alatriste et al. [34], this construction of new forms of knowledge is neither definitive nor more real or true. These new forms of knowledge are simply different: experiential knowledge built in the creative act. Through art, it is possible to build an episteme generating its own knowledge grammars.

This type of knowledge should be understood not as the discovery of stabilized laws that demarcate and characterize reality with answers to fixed questions, but as a way of relating to the world from an understanding of what is finally obtained with the creative act. A knowledge of this type becomes something significant and representative in the context of the subjects, proving to be a range of possibilities rather than positivist realities. In addition, this knowledge cannot be proposed as absolute, definitive, or verifiable [34]. This is a crucial aspect to consider as what we propose in this research urges the recognition of new forms of knowledge from the multiple forms of interpretation and representation of reality that can occur when establishing a dialogue between art and mathematics. Through aesthetic experiences and events that involve reason and emotion in a recursive dynamic, the creative act is opened, reaching the possibility of understanding the world from a kaleidoscopic perspective where reason and emotion interact in a complex way toward a new vision of reality.

In general, knowledge relies on a corroboration given by its own validation instruments, which only shows verification of it based on its own beliefs. What it offers is an unfinished condition of knowledge, which implies that the conception of this expanded knowledge given by Alatriste et al. [34], and taken in the present work as sustenance and argument in the proposal of art, as a method in the dialogue of a diatopic type between art and mathematics framed in the creative act. This type of knowledge is a generator of creativity, where art is the space in which it develops (as a method). This call for expanding knowledge makes these new forms of knowledge conceive questions rather than answers, reveal possibilities rather than facts, curiosity, and searches rather than encounters. When considering the creativity generated from this type of knowledge, the category of the creative act or creative act considered in this investigation is considered as the main bridge in the dialogue between art and mathematics. In this way, the knowledge that is generated from art as a method and in which the creative act is given, transcends three spaces in which every form of relationship with the outside is a process of generation of meaning that occurs in the convergence of these spaces. Thus, the first space is defined by an affective experience that generates the creative process or act; the second space is defined as the production of an object that fulfills a representative purpose; the third space is defined as the thought that gives meaning and offers a symbolic discourse of it, where it is possible to share the experience and ideas that make sense.

8. Results

8.1. Moment 3: Re-Signification of Education as a Model of Experience

For the present investigation, at Moment Three, an interview was proposed as a conversation from which the stories and experiences of six of the students who were participants during this process were collected. This conversation was conducted under some trigger questions that could give rise to recounting all the meaning known and experienced during the two moments described above. This conversation was held for about an hour and in a space where students could feel comfortable. In this conversation, it was not intended to give a questionnaire to the students to answer it. We gave them some guiding questions such as: What do you think you learned from this experience? art? mathematics? How or what was your experience developing these activities? What have you felt? What have you experienced? These guiding questions were used in order to make a more natural conversation with the participants.

For the recording, the application of voice notes from a cell phone was used, and a notepad was also used to highlight important characteristics observed at the time of the conversation. The participation of the students in the conversation and in the other moments of the investigation was duly authorized by parents and by themselves by signing informed consent. Each story was configured with the reflections made by each student.

The reflections made during the interviews were transcribed. Through the transcription, different codes were identified in what was expressed by the students with which it was possible to establish a categorical matrix. This element was designed to identify emotions, strengthen ideas, and organize concepts to triangulate with the theoretical references of the present investigation. The structure used for the categorical matrix is shown in

Table 1. Categorical matrix decoding the information obtained from the experiences of the students.

Story (from the Transcription)	Situation	Emotion	Core/Main Idea	Fundamental Theory
					1	Juan Pablo: “… we’ve experienced new things … we’ve done things we didn’t know we had the talent to do …” “… I believe that we have approached knowledge in a different way, to the knowledge of science, to the knowledge of mathematics …”	Enthusiasm Desire Curiosity	We did not know we had the talent to do that. We have approached knowledge differently.	Experience Creativity Other forms of knowledge
2	Tiffany: “… to learn you need to see, feel, instead of just reading; That’s why practice is better …”	Impotence	To learn you need to see, you need to feel.	Senses
	“… art is something with which one can express many things … one does not realize that mathematics is also there, not always only numbers and formulas …”	Restlessness	Art is something with which you can express many things.	Emotions
	“… everything is based on feeling, if you don’t feel things, if you don’t feel what you do, nothing is going to turn out well for you; nothing is going to seem good, even if it is …”	Astonishment	If you do not feel things, nothing is going to work out for you.	Other forms of representation
	“… if you learn one way, they can’t tell you not to. We’re different. That is why emotion is very important. We are beings that feel. If we were machines, it would be very different …”	Passion	We are all different.	Diversity
	“… some are fearful. When we are going to experience something new, we feel fear. As always, they have taught us that things are like this and that’s it …”	Curiosity	As always, we have been taught that things are the way they are.	Traditional educational model
3	Victor D: “… It made me curious, because it is a subject that motivates one … it makes me really want to do something different … I don’t have to just be the one who likes to paint or the one who likes mathematics, and that I can learn of both. Also, I don’t have to know much to do these experiments (activities) either …” “… I think I learned a lot, mainly because I liked it … it makes us want to continue exploring this topic, keep moving forward more … explore and know what potential we have as students …” “… We are all different, but at a certain moment there is something that unites us, and that is creativity. Although we all like something different, we always have in common that we like to create, we like to explore and learn about many things …”	Curiosity Astonishment Excitement Enthusiasm Confidence	I do not have to just be the one who likes to paint or the one who likes mathematics. Explore and know what potential we have as students. There is something that unites us, and that is creativity.	Creativity Diversity Reason and Feelings
4	Valentina G: “… If you do not feel emotion in doing something, then things are not going to turn out well for you, because then you are going to say: I don’t like this. Then you close down and feel that you are not capable, that nothing is going to work for you. That’s not a good feeling …” “… For example, when you are conducting an experiment and you are failing no matter how hard you try, and finally, on the last attempt, you are succeeding; one feels super proud and wants to continue advancing and exploring new knowledge …”	Restlessness Curiosity Happiness Interest Satisfaction	If you are not excited to do something, then things are not going to turn out well for you. Advance and explore new knowledge.	Emotions Experience Creative Act
5	Lizeth: “… the fact of accepting and taking advantage of all the differences that we have, because, let’s say, in the working groups we were all very different. Then we were able to take advantage of all the skills of each one …” “… I have felt that teachers do not care if one learns or not. I do not agree that one is judged by a grade … it seems that the Colombian educational system is based on that: tell me what grade you have, and I’ll tell you how good a student you are …” “… not even creativity is rated in college courses. Only that knowledge that is learned as we have always been taught is valued …”	Solidarity Enthusiasm Curiosity Confidence Impotence Rage Rejection	Take advantage of all the differences we have. Tell me what grade you have, and I’ll tell you how good a student you are. You learn as we have always been taught.	Diversity Traditional educational model
6	Miguel: “… I believe that feelings are something main for one to learn … I did not believe that through mathematics you could create something. And. That is something new that we are learning …” “… art is a subject that should not be looked down upon at school and in society. With this activity, I was able to see many advantages that art offers. So, we have to take advantage of those new things that can serve us in the different areas of knowledge …” “… the school and the teachers only care that we get good grades, without worrying about what we are feeling and whether we are learning or not. Those notes say nothing …”	Interest Astonishment Desire Optimism Impotence Rage	I believe that feelings are something main for one to learn. Art is a subject that should not be looked down upon. Good grades say nothing.	Emotion Creative Act Art as a possibility

. First, the student’s story is established, then a particular situation within the story is identified. The emotions that characterize them are extracted from these situations later to establish a “force idea” of the story–situation–emotion. Finally, a triangulation is carried out with the theoretical foundations of the present study to frame the analyzed stories within a specific category. This process was conducted with the entire transcript of the interview, generating the proposed categories from Moment 3.

Based on the analysis of this matrix, the emerging categories for the construction of meaning were established where it was possible to show that experience and sensation play a fundamental role within the dialogue of knowledge proposed from the present investigation.

8.1.1. The Value of the Other Forms of Interpretation and Representations of Reality

Eisner [5] stated that not all experiences can be transmitted through traditional symbol systems, such as language or the logical–mathematical. Each form of representation suits what it wants to represent. In this case, art and its symbolic language can express different experiences and conceptions of the world through music, dance, painting, and poetry, among others.

“… I believe that we have approached knowledge differently, knowledge of science, knowledge of mathematics. We have always been accustomed to teachers arriving and filling the board with numbers, formulas, but we hardly understand …”.

Juan Pablo, 16 years old

“… Art is a subject that should not be given only by obligation and in a secondary place. For example, with this activity you can see many advantages that it offers, so we have to take advantage of those new things that can serve us in different areas …”.

Miguel, 16 years old

By analyzing what Juan Pablo has related, it can be interpreted that, by having the possibility of other forms of interpretation and representation of the world, new forms of knowledge generation will be accommodated. This is what the traditional educational model does not consider. The positivist paradigm and its model where the rational prevails, causes other expressions such as those present in art, to be relegated to cast-off roles where their true potential is wasted at the educational level. In this sense, what Miguel recounts shows how the students, with this work, could be aware of all the possibilities offered by art, not only in mathematics but in different areas in which teaching and learning processes are traditionally handled. For Best [29], with art, it is possible to experience reality rationally and emotionally. This is one of the great possibilities that art offers, that is, the ability to permeate any field of knowledge in such a way that an understanding of the world is promoted through an articulation of knowledge. This process allows for a complete vision of reality without the fragmentation that commonly occurs when you want to see the world from a single point of view.

“… with these activities, you can see another facet … if I do not feel comfortable with this, then I look for something that I feel comfortable with … teachers tell us that this should not be done. Well, of course, if you learn in a way … we are different …”.

Tiffany, 16 years old

Art shows other possibilities to students, with which it is possible to express multiple parallel realities. In contrast, the traditional educational model closes the possibilities of interpretation and representation of the world to the linguistic and the logical–mathematical. In this way, not only are students who do not find a place in these forms of representation excluded, but the possibility of exploring other realities through art will also be limited. Those who have felt excluded at some time by traditional forms of teaching may find in the artistic possibilities for learning, reaching those new forms of knowledge of which they can also be part.

All are different, as Tiffany says, and the diversity present in the classroom allows art to explore the cognitive and emotional abilities everyone has. As evidenced, art plays a fundamental role in recognizing diversity by enabling other forms of expression, where those who previously felt excluded can now find new possibilities. As commented by De Távira [11], art offers the potential to enhance the diversity present in the classroom, where work is carried out to promote respect for people and their culture, regardless of race, beliefs, and identities. With art and through it, heterogeneity can be significantly valued by ethnic, linguistic and cultural pluralism. With art, dialogic scenarios of tolerance and solidarity are evident, with a view to the development of transformative educational actions of society. With art, an experience of interculturality is generated, where the true work of art is society. In this work, the diversity present in the classroom was a point in favor that was taken when that exploration on the road traveled in the search for knowledge. Each difference and each skill led to finally representing something that carries their most intimate emotions experienced during the process and its reality. On the other hand, when analyzing the stories, a very explicit fragment was found in which diversity and the creative act are related:

“… we as people are different, but at one point, there is a theme that unites us, and it is the theme of creativity … we like to create, we like to explore and know …”.

Victor, 18 years old

8.1.2. Diversity as a Trigger of Creativity

In recent times, diversity has been “fashion” and on everyone’s lips, that in one way or another is related to the educational context. In this regard, López [38] proposes that“diversity is not a fashion slogan; it is an ideological discourse that invites the transformation of pedagogical practice that requires another mode of education, considering difference as value.” For this reason, from school, you must ensure each of the capacities or intelligence that Gardner [39] proposes from his theory of multiple intelligences, considering all the diversity present in the classroom, considering the differences in the true value that can lead to a social transformation.

Note that each student has different learning methods and motivations so that no one can be skewed within a type of intelligence. For this reason, as Palacios [1] proposes, education and school must value the entire universe of possibilities that make up each student. If this is not achieved, students who have different abilities and potentialities will be excluded, marginalizing individuals who do not find possibilities due to the limitations of the school.

Although diversity is present and everyone has particular ways of interpreting and representing the world, from creativity, common points can be identified, not only for this dialogue proposed from this work but also to reach new forms of knowledge. The creative act and creativity allow for exploration, without looking at tastes or particularities, as revealed in the desire to know and explore the world and the multiple realities that compose it. Our differences have always been seen as a problem. However, with creativity and the creative act, it is possible to use these differences as triggers in the exploration of the world from different perspectives, also reaching particular forms of knowledge, with which each person is integrated in a certain way to be able to understand their reality. This is the creative act.

With art, it is also possible to identify with the cultural, emotional, social, aesthetic, and rational level. This identification is one of the possibilities that should be potentialized in school. In art and mathematics, art emerges as a possibility for science to be seen from a perspective, where the rational and the emotional are in dialogue in the search for knowledge. An indissociable link between reason and emotion is established, which is a creativity enhancer and a true understanding of reality. In this way, the transformative objective from which the school has been separated can be fulfilled. From the perspective that is intended to be given in this work, art plays a leading role in establishing a front against traditional paradigms and models, becoming a possible turning point to change the educational, social, and cultural perspectives that institutions of power and education itself have been imposing.

8.1.3. Toward New Forms of Knowledge

“… The philosophers were also artists and mathematicians, but I didn’t understand how that related. That shows me that I don’t have to be just the one who likes to paint or the one who likes math, that I can know about both …”.

Victor, 18 years old

This reflection made by one of the students is vital to understand the dialogue that we tried to promote from the present investigation. Over the years, the search for knowledge has been linked to a scientific need to find the answers to everything that makes up reality. The more that knowledge increases, the more efficiently the world is approaching a state where, according to Max Neef [3], chaos and lack of control prevail. From the scientific perspective, efforts have been made to explain and describe the world, mistakenly believing that it will be possible to understand it in this way, when in fact, much is known, but little is understood.

Oostra [4] comments that a vision of the world from just one perspective, as proposed by the scientific or positivist paradigm, is a fragmented vision and practically null, where attempts are being made to respond to reality by observing it from a small hole that does not allow us to understand the universe from which it is composed. The recognition of a worldview that establishes a dialogue between reason and emotion, science and art, will result in a range of possible responses, representations and interpretations of reality, where objectivity and subjectivity operate as a circuit generating creativity, detonating the creative act that allows a total understanding of the reality that is observed.

The conception of duality must be discarded. Human beings should not be separated between emotional and rational, and this is the idea that students are being given from school. With this type of activity, it is being shown that art is for the sensitive, and mathematics for the “science guys”. It is possible to conceive an approach to knowledge where a dialogue between emotion and reason is established; where both the emotional and rational characteristics of art and mathematics are exploited in the search for that knowledge, as Victor proposes from his account.

8.1.4. The Senses and the Experience: The Emergency of the Creative Act

One of the authors with whom this research establishes the creative act as the main bridge in the dialogue between art and mathematics is Manfred Max Neef. From this proposal, you can see some ideas that become fundamental to establish this dialogue. Neef [3] proposes the creative act as the transcending of only explaining or describing reality to enter into it, thus enabling its integration and compression. It is about moving from doing to being.

“… Education really depends on this, not only the theoretical part but also the practice. This is a fundamental part, because in many occasions, to learn you need more to see, feel, than to be reading there; when one practices and goes more to practice, there has been the key, because I liked it a lot …”.

Tiffany, 16 years old

It is clear to see in Tiffany’s message the relevance of doing when generating learning. When you can experience what is being done and, in addition, good emotions are generated from this, reality will be penetrated. When this happens, the student is being part of what he is trying to understand, and that is when the creative act that Max Neef [3] proposes will begin to occur.

On the other hand, it is necessary to highlight the importance of the senses when generating those experiences that lead to the creative act. According to Parra [26], through the senses, the human being appropriates the experiences, and from these, mental processes arise where cognition and emotion are in dialogue to start generating possibilities of knowledge. Then, from those mentioned above, it can be interpreted that, having the possibility to smell, touch and listen to knowledge, these experiences will be given where, according to the generated emotions, internal processes will be generated that will eventually lead to interpretations of reality where you are part of this.

From the point of view of emotions, the stories can be interpreted as an interest in learning aroused through the emotions as well as a curiosity to explore the new ways of abstracting and representing the world that differ from traditional methods. This makes the desire to explore translate into a journey that is considered the way reality is really understood in the creative act. That trip undertaken with curiosity will lead to unknown paths, some pleasant and others perhaps not so much. In this unique experience, however, realities that were previously considered non-existent will be revealed.

“… everything is from feeling; if you don’t feel things, if you don’t feel what you are doing, nothing will work out for you …”.

Tiffany, 16 years old

“… those emotions that one feels are very important, because if one does not feel emotion in doing something, then things are not going to turn out well for you …”.

Valentina, 15 years old

The senses and emotions are not only important in the moment of wanting to understand the world, but also in what the disposition is before it. Good emotion is reflected in a willingness to continue traveling that path and come to an understanding of what you seek to understand. Best [29] stated that it is essential to understand the potential emotions have when generating more meaningful learning from experiences. These emotions generated in the activities carried out provide an account of how the initial perception of mathematics had changed. In the same way, plus a benefit for mathematics, it is an advantage that, in general, has to be able to enhance that approach to knowledge when considering the fundamental role of emotions. With these emotions, it is possible to integrate what one seeks to know, which will finally be seen as a truly creative act.

The students’ trip when the creative act is launched leads to good and not so good emotions. The emotions create lived experiences that lead students to continue exploring and delving deeper into knowledge. This process is what Neef [3] proposes as the penetration of reality. It is the creative act that will appear recursively to these emotions and experiences as they approach new ways of knowing the world, of understanding it. In this sense, experiences will dynamically involve reason and emotion through that exploration to understand reality.

“… Curiosity, because it is a topic that motivates you at the beginning, and when you start working, it makes you more and more want to do something different …”.

Victor, 18 years old

That experience is what Dewey [28] defines as “aesthetic experience”, where the interaction with reality, emotions and cognitive processes are involved. The experiences generated in that exploration trigger curiosity, which, seen from the creative act, is understood as a search for knowledge to achieve understanding of the world. However, that search, as Neef [3] proposes, is drifting, but in a state of alertness, acquiring experiences along the way and emotions that will leave traces on everyone’s realities. Navigating through mysterious worlds, each student can enter his reality and, finally, understand it, which is the true transformation process. The creative act is when curiosity is broken to reach discovery. In this way, which can be interpreted from Victor’s story, establishing a dialogue between art and mathematics generates positive emotions in students, which an awakening in motivation and curiosity in the search for knowledge is shown. It is here where the journey of the creative act begins.

9. Conclusions

The human being, in essence, abstracts and expresses his reality through the instruments he finds in reason and emotion. In this way, a complete vision of reality is generated that yields a true understanding of the world. Through art, diverse possibilities for teaching and learning emerge for spectators, students, and teachers. Moreover, teaching enables instructors to learn from their pupils, which is one of the great potentials of art at the educational level. The key is to bring students to aesthetic enjoyment and enjoy the experience of searching for knowledge. No real or transforming learning is possible without emotion.

If educators strive to strengthen the dialogue between emotion and reason as a generator of transformative knowledge that leads to a real understanding of the world, the possibility of aesthetics will be opened as a pedagogical tool. It is through this process that, for the present work, the relevance of using art is sustained as the same method by which new forms and possibilities of knowledge are reached. Art as a method escapes the conditions of time and space, providing students with the possibility to think, feel, and perceive reality and the world without prejudice or conditioning.

This research shows how students were able to experience this dialogue between art and mathematics. During the development of the activities, it was possible to observe how the students assimilated the different mathematical and physical concepts that underpinned each activity. This alternative approach to knowledge allowed students to know, experience, and transcend concepts by understanding, as proposed by Max Neef in his definition of the creative act [3]. Each student understands concepts from a unique experience; therefore, students cannot be evaluated from a traditional point of view. The same stories collected showed that the students could understand what each proposed activity concerned. In this way, the creative act allowed students not only to know but also to understand concepts. Beforehand, knowing the concepts of mathematics through the traditional method generated bad feelings and emotions. With an art-based articulation, students understand more, as evidenced by good feelings and emotions generated through the dialogue. Reaching forms of knowledge where emotion and reason meet and dynamically interact leads to knowledge that allows the description of the concepts from the particular form of abstraction experienced by each individual student. The result is a profound creative act with the possibility to integrate with the desired knowledge.

On the other hand, although it is necessary to continue with this type of long-term strategy in the teaching of mathematics and science to determine if the results obtained in national and international tests can improve, this does not mean that these alternatives should not be considered when seeking to give students tools to understand the world beyond school. Art has shown to be a way to approach in an alternative way to the knowledge of mathematical and scientific concepts, not in terms of solving a formula or a problem, but moving from a simple mathematical description to a true understanding of how concepts works. According to the above, although the present work was carried out in a very particular context, both art, science and mathematics are universal and fundamental disciplines, and therefore, this study can be applied in different contexts and situations in order to check if there is evidence of a better understanding of the proposed concepts. Currently, further opportunities are being developed where mathematics as a way of making art can be deployed, including different locations, contexts and the number of students involved. It is worth mentioning that, although the strategies considered here can be reproducible, results may vary from different socio-cultural scenarios in which the students usually find their place.