Waterlogging Resistance Evaluation Index and Photosynthesis Characteristics Selection: Using Machine Learning Methods to Judge Poplar’s Waterlogging Resistance

Abstract

Flood disasters are the major natural disaster that affects the growth of agriculture and forestry crops. Due to rapid growth and strong waterlogging resistance characteristics, many studies have explained the waterlogging resistance mechanism of poplar from different perspectives. However, there is no accurate method to define the evaluation index of waterlogging resistance. In addition, there is also a lack of research on predicting the waterlogging resistance of poplars. Based on the changes of poplar biomass and seedling height, the evaluation index of poplar resistance to waterlogging was well determined, and the characteristics of photosynthesis were used to predict the waterlogging resistance of poplars. First, four methods of hierarchical clustering, lasso, stepwise regression and all-subsets regression were used to extract the photosynthesis characteristics. After that, the support vector regression model of poplar resistance to waterlogging was established by using the characteristic parameters of photosynthesis. Finally, the results show that the SVR model based on Stepwise regression and Lasso method has high precision. On the test set, the coefficient of determination (R²) was 0.8581 and 0.8492, the mean square error (MSE) was 0.0104 and 0.0341, and the mean relative error (MRE) was 9.78% and 9.85%, respectively. Therefore, using the characteristic parameters of photosynthesis to predict the waterlogging resistance of poplars is feasible.

1. Introduction

Plant tolerance to environmental stress is a crucial part of vegetation geographic patterns, and it is also a core concept for understanding the structure of ecosystems. Environmental stress mainly includes flood, drought, high and low temperatures, insufficient light, etc. As a frequent environmental stress factor, waterlogging stress affects many plants and crops for a long time. Understanding the waterlogging tolerance mechanism of plants will help increase crop yields [1,2]. Flood disasters are the most common and direct factor that causes crop waterlogging stress, and the loss to agricultural finance is incalculable. Many countries are affected by flood disasters. With global warming, heavy rainfall and frequent floods have gradually increased. Therefore, there is an urgent need to study the mechanism of plant waterlogging tolerance [3,4].

Most crops cannot withstand the hazards of floods because the restricted underwater gas exchange will destroy their energy and carbohydrates [5,6]. Flood disasters have forced plants to evolve multiple resistance mechanisms, including plant morphological characteristics, metabolic response and molecular transcriptional regulation [7,8,9,10,11]. The metabolic response of plants to waterlogging mainly includes the stimulation of fermentation pathways and the increase of glycolytic flux, which is specifically manifested in the increase of transcript abundance, pyruvate decarboxylase and alcohol dehydrogenase (ADH) activity [12]. Among many plant populations, poplars have the characteristics of rapid growth and waterlogging resistance. To make full use of the soil that is susceptible to floods, it has become the main flood-resistant varieties in areas that are frequent and vulnerable to floods.

For the research on the resistance mechanism of poplars, from a macro perspective, the root system is the key organ of poplars to cope with waterlogging stress [13,14,15,16,17,18]. Waterlogging stress will slow down the growth of leaves and roots, change the content and composition of chlorophyll, accumulate toxic substances, destroy photosynthesis, and inhibit plant growth and biomass accumulation [19,20,21,22,23]. Many studies have shown that when plants are subjected to waterlogging stress, the contents of chlorophyll a, chlorophyll b and total chlorophyll in leaves will decrease. Waterlogging stress not only reduces the chlorophyll content, but also reduces the carotenoid content [24,25]. The survival and growth of poplars under flooded conditions are attributed to many factors, including the physiology and morphology of the roots. Kreuzwieser et al. [26] found that the leaves and roots of submerged poplars had metabolite changes. Du et al. [13] compared the ecophysiological and morphological adaption of two poplar clones to soil waterlogging stress. Their studies clarified the response of poplar growth and nutrient metabolism to floods. For poplars of the same varieties but different sexes, a large number of documents have confirmed that males are more resistant to waterlogging than females [27,28,29]. These results have increased people’s understanding of the gender factors and adaptability of poplars to waterlogging stress. In addition, genes and proteins related to poplar waterlogging resistance have also been extensively studied. Peng et al. [28] examined the different response mechanisms of two clones of poplar to waterlogging stress, and identified candidate genes related to flood tolerance. These candidate genes can be used in molecular breeding programs to improve the waterlogging stress of poplar trees. Hao et al. [30] discussed the role of the poplar expansin gene in cadmium enrichment and evaluated its potential role in phytoremediation. In short, these studies have greatly enriched the understanding of poplar’s anti-waterlogging mechanism. Even so, there is currently no work on analyzing the characteristics of poplar photosynthesis and chlorophyll fluorescence intrinsic characteristics related to the waterlogging resistance of poplars, and there is also a lack of research on predicting the waterlogging resistance of poplars. The past empirical judgments are mostly based on the ratio of changes in biomass and seedling height between the test group (shallow waterlogging) and the control group (normal growth) to reflect the flood tolerance of poplars. However, in actual treatment, waterlogging experiments are often complicated, expensive, and time-consuming. Consequently, it is necessary to adopt scientific methods to predict the waterlogging resistance of poplars.

Based on the previous work, this study determined the evaluation index of poplar waterlogging resistance, analyzed the relationship between the characteristics of poplar photosynthesis and poplar waterlogging resistance, and established a poplar waterlogging resistance prediction model. It is proposed for the first time to establish a prediction model of poplar waterlogging resistance by measuring the photosynthetic parameters of poplar seedlings. This method can be used to predict the flood tolerance of poplar seedlings. It is of great significance for precise flood control, scientific selection of seedlings, and cultivation of high-quality seedlings. Hence, it has considerable practical value. At the same time, it has also made important contributions to understanding the anti-waterlogging mechanism of poplars.

2. Materials and Methodology

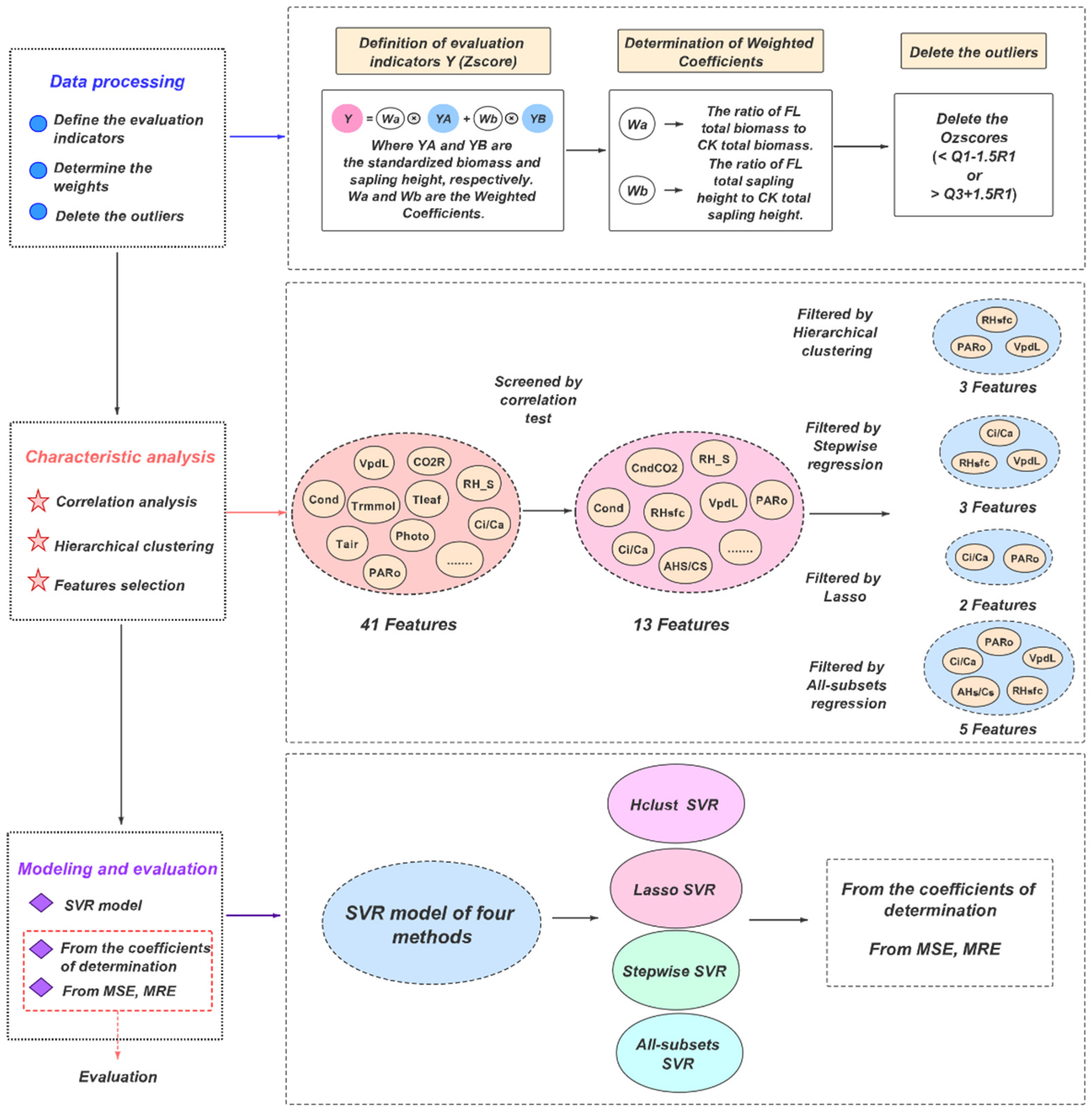
In this part, we will introduce the experimental materials and methodology. Firstly, the location of the experiment and the selected 20 poplar varieties are described. Meanwhile, the experiment process and parameter measuring instruments are introduced. Then, for methodology, four methods of feature selection are explained, namely, hierarchical clustering method, lasso method, stepwise regression method and all-subsets regression method. Finally, the parameters of four support vector regression (SVR) models are given, and the evaluation methods of these models are defined. The general process of the methodology is shown in Figure 1, and the specific implementation steps will be introduced separately below.

2.1. Experiment Location and Materials

This research was conducted at Huazhong Agricultural University in Wuhan, China (114°35′ E, 30°49′ E). This region has plenty of rainfall, plenty of sunshine, and four distinct seasons. The annual average temperature is 15.8–17.5 °C, rainfall of 1269 mm, frost-free period of 211 days to 272 days, and total sunshine hours of 1810 h to 2100 h. It belongs to the subtropical humid monsoon climate.

The conditions of container and soil used in the experiment are: nursery pots, $150\times 100\times 130$ mm; soil (matrix soil and peat soil 1:1), total organic matter of nutrient soil ≥28%, and total primary nutrient ≥2%.

The experimental materials of this study are divided into experimental group and control group. There are 20 poplar varieties, each of which has four experimental groups and four control groups, with a total of 160 experimental materials. The 20 poplar varieties are: 68, 81, 895, DD102-4, FLEVO, I-214, I-45-51, I-63, I-69, I-72, L04-13, L04-17, Lushan Poplar, P. Canadensis, P. Danhong, P. Juba, P. Ningshanica, Populus 2025, RASPCTE, TRIPLO, and the corresponding scientific names are shown in

Table 1. Scientific names of 20 poplar varieties.

Varieties	Scientific Names
68	Populus deltoides ‘Lux’ × Populus simonii (LS-68)
81	Populus deltoides ‘Lux’ × Populus simonii (LS-81)
895	Populus × euramericana ‘Nanlin 895’
RASPCTE	Populus deltoides ‘Raspalje’
I-63	Populus deltoides ‘Harvard’
I-214	Populus × euramericana ‘I-214’
I-45-51	Populus × euramaricana ‘I-45/51’
P. Ningshanica	Populus ningshanica
I-69	Populus deltoides ‘Lux’
I-72	Populus euramaricana ‘San Martino’
L04-13	Populus deltoides ‘Lux’ × Populus deltoides ‘Harvard’
L04-17	Populus deltoides ‘Lux’ × Populus deltoides ‘Harvard’
TRIPLO	Populus euramericana ‘Triplo’
P. Canadensis	Populus canadensis Moench.
P. Danhong	Populus deltoides ‘Danhong’
P. Juba	Populus deltoides 50 × P. deltoides 36
FLEVO	Populus euramericana ‘Flevo’
Populus 2025	Populus deltoides ‘Lux’ × P. deltoides ‘Shanhaiguan’
DD102-4	Populus deltoides ‘DD102-4’
Lushan Poplar	Populus × liaoningensis

.

2.2. Experimental Process and Parameter Measurement

Before the measurement of the parameters, the samples are divided into an experimental group and a control group, and the treatment of the experimental group and the control group are listed below.

• Experimental group (FL): Shallow flooded, the water surface is 10 cm above the soil surface;
• Control group (CK): Watered normally, and the soil moisture was kept at about 75% of the maximum water holding capacity in the field.

For the experimental group, the waterlogging test was started 5–6 weeks after the cuttings. The waterlogging test was 60 days in total, including the waterlogging time of 45 days and the drainage recovery time of 15 days. The data collected the photosynthesis parameters, ground diameter, seedling height and biomass of each poplar sample in the control group and the experimental group at 0, 15, 30, 45 and 60 days. The characteristic parameters of photosynthesis were measured with the LI-6400 photosynthesis analyzer (LI-COR Inc., Lincoln, NE, USA). The standard LI-COR leaf chamber, red and blue light source (6400-02 LED light source) was used for the measurement. The light intensity is set to 1000 μmol∙m⁻²∙s⁻¹, and the airflow rate is 500 μmol∙s⁻¹. Forty-one characteristic parameters such as photosynthesis rate (Photo), transpiration rate (Trmmol) and electrical conductivity (Cond) were measured, and their meanings will be given in

Table A1. The specific meanings and correlation coefficients of 41 features.

Features	Specific Meaning
Photo	Photosynthetic rate
Cond	Conductance to H2O
Ci	Intercellular CO2 concentration
Trmmol	Transpiration rate
VpdL	Vapor pressure deficit based on leaf temp
CTleaf	Computed leaf temp
Tair	Temperature in sample cell
Tleaf	Temperature of leaf thermocouple
TBlk	Temperature of cooler block
CO2R	Reference cell CO2
CO2S	Sample cell CO2
H2OR	Reference cell H2O
H2OS	Sample cell H2O
RH_R	Relative humidity in the reference cell
RH_S	Relative humidity in the sample cell
Flow	Flow rate to the sample cell
PARi	In-chamber PAR
PARo	External quantum sensor
Press	Atmospheric pressure
CsMch	Sample CO2 offset
HsMch	Sample H2O offset
fda	Flow/Area
Trans	Transpiration rate (mol H2O m−2 s−1)
Tair_K	Air temp in K
Twall_K	Twall temp K
R(W/m2)	Incoming radiation
Tl-Ta	Energy balance delta t
SVTleaf	SatVap (Tleaf)
H2O_i	Intercellular H2O
H2Odiff	Difference between Intercellular H2O and Sample cell H2O
CTair	The air temperature in the leaf chamber
SVTair	SatVap (Tair)
CndTotal	Total conductance
vp_kPa	Vapor pressure chamber air
VpdA	Vapor pressure deficit based on Air temp
CndCO2	Total conductance to CO2
Ci_Pa	Intercellular CO2
Ci/Ca	Intercellular CO2/AmbientCO2
RHsfc	Surface Humidity
C2sfc	Surface CO2
AHs/Cs	Ball-Berry parameter

of Appendix A.

2.3. Data Analysis and Processing

2.3.1. Definition of Evaluation Index

Biomass refers to the total amount of living organic matter (dry weight) in a unit area at a certain time, and the seedling height is the total height of plant growth. The increase in biomass and seedling height reflects the waterlogging resistance of plants to a certain extent. There are several empirical methods for evaluating poplar resistance to waterlogging, including direct changes in biomass and seedling height after waterlogging, and changes in the ratio of biomass and seedling height between experimental and control groups. However, previous studies did not accurately define the evaluation index of poplar waterlogging resistance. Here, we propose a method to characterize the waterlogging resistance of poplars. Based on the direct changes in poplar biomass and seedling height within 60 days, we take the standardized experimental group poplar biomass and seedling height as the dimensionless base, and the ratio of the total biomass and seedling height changes in the experimental group and the control group as weight coefficients. Then, a dimensionless evaluation index Zscore that considers both biomass and shoot height changes is well defined. Zscore represents the waterlogging resistance score of the poplar sample. Generally, the larger the value of Zscore, the stronger the waterlogging resistance of the poplar sample.

The calculation of $Zscore\left(x_i\right)$ of each poplar sample is shown in Formula (1):

$$Zscore\left(x_i\right)={\omega }_{bio}\times Zbio+{\omega }_{sap}\times Zsap$$

(1)

where $Zbio$ and $Zsap$ are the standardized seedling height and biomass of the experimental group. The calculation method is shown in Equation (2). ${\omega }_{bio}$ and ${\omega }_{sap}$ are the weight coefficients of biomass and seedling height, respectively, which satisfy the condition ${\omega }_{bio}+{\omega }_{sap}=1$. The definition and calculation method of the weight coefficients will be introduced in Section 2.3.2.

$$Zbio=\frac{bio\left(x_i\right)-E\left(bio\right)}{Std\left(bio\right)},Zsap=\frac{sap\left(x_i\right)-E\left(sap\right)}{Std\left(sap\right)}$$

(2)

where $bio\left(x_i\right)$ and $sap\left(x_i\right)$ are the biomass and seedling height of each poplar in the experimental group, respectively, $E\left(bio\right)$ and $E\left(sap\right)$ are means, and $Std\left(bio\right)$ and $Std\left(sap\right)$ are the standard deviations.

2.3.2. Definition of Weight Coefficients

Weight is the degree of importance of a factor or indicator relative to the research object, and it emphasizes the degree of importance. The stronger the waterlogging resistance of poplars is, the larger the ratio of seedling height to biomass between the experimental group and the control group, that is, the larger the value of FL/CK. Hence, the weight of the evaluation coefficient is defined according to the ratio of the total biomass and seedling height changes between FL and CK. The calculation equation is shown in Equation (3). This method can eliminate the influence of dimensions, and can better express the degree of reflection of poplar’s waterlogging resistance in the two evaluation indicators of biomass and seedling height. In other words, the indicators with large changes have higher weights, and vice versa.

$${\omega }_{bio}=\frac{TA}{TA+TB},{\omega }_{sap}=\frac{TB}{TA+TB}$$

(3)

where $TA=\frac{FL(Sum\left(bio\left(x_i\right)\right)}{CK(Sum\left(bio\left(x_i\right)\right)},TB=\frac{FL(Sum\left(sap\left(x_i\right)\right)}{CK(Sum\left(sap\left(x_i\right)\right)}$.

According to Equation (3), the ratio of the total amount of biomass and seedling height change between the experimental group and the control group is calculated, and finally the weight ${\omega }_{bio}=0.45$, ${\omega }_{sap}=0.55$.

2.3.3. Exclusion of Outliers

When analyzing actual problems, outliers may affect the accuracy of the final model. Therefore, before the analysis, two outliers are eliminated according to the Zscore values of the poplar sample. The process is as follows.

First, the outlier Ozscore is defined in Equation (4):

$$Ozscore\langle Q_1-1.5\times R_1 or Ozscore\rangle Q_3+1.5\times R_1$$

(4)

where $Q_3$ and $Q_1$ are the upper and lower quartiles, and $R_1$ is the quartile range, which satisfies the formula $R_1=Q_3-Q_1$.

Zscore statistics are shown in

Table 2. Statistics of Zscore.

$\mathbf{M}\mathbf{i}\mathbf{n}$	${\mathit{Q}}_{\mathbf{1}}$	$\mathbf{M}\mathbf{e}\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{n}$	${\mathit{Q}}_{\mathbf{3}}$	$\mathbf{M}\mathbf{a}\mathbf{x}$
−2.076712	−0.554362	−0.039611	0.466923	2.257776

, where $Max$ and $Min$ are the maximum and minimum values.

By calculation, the two outliers finally eliminated are P. DanhongFL2 and P. Dan-hongFL3, and 78 samples are left. After a series of operations, such as standardization, calculation of weights, and elimination of outliers, the final Zscore distribution is shown in Figure 2. The points on the right of the red dashed line in the figure are outliers. It can be observed that for all samples, the defined Zscore is roughly in the range of [–2, 2]. The larger the value of Zscore, the stronger the waterlogging resistance of the poplar samples. Then, the next step is to select the features related to the waterlogging resistance index Zscore.

2.4. Features Selection

There are many characteristics of poplar photosynthesis and chlorophyll fluorescence, but in fact, the characteristics significantly related to poplar waterlogging resistance may be only a few. Consequently, analysis and screening are required. Forty-one characteristics of photosynthesis, including photosynthetic rate (Photo), transpiration rate (Trmmol), and external light intensity (PARo), were selected for analysis. Firstly, 13 characteristics were selected from 41 characteristics according to the significance level of the correlation between each characteristic and the poplar Zscore, and these 13 characteristics all satisfy the significance test of $p\le 0.05$. The Pearson correlation coefficients were calculated, and the result was presented in the form of a heat map (Figure 3). Among them, Figure 3a is a heat map of 41 characteristics of poplar photosynthesis, the blank part is the case of $p>0.05$, that is, it is not significant. Figure 3b is a heat map of the Pearson correlation coefficients of 13 significant features, which satisfies the significance test $p\le 0.05$. The specific meanings and correlation coefficients of the 13 features after screening are shown in

Table 3. The specific meanings and correlation coefficients of 13 features.

Features	Specific Meaning	Coefficient
RHsfc	Surface Humidity	0.37
Cond	Conductance to H2O	0.34
CndTotal	Total conductance	0.34
CndCO2	Total conductance to CO2	0.34
PARo	External quantum sensor	0.32
Ci/Ca	Intercellular CO2/AmbientCO2	0.3
RH_S	Relative humidity in the sample cell	0.3
VpdL	Vapor pressure deficit based on leaf temp	−0.3
H2Odiff	Difference between Intercellular H2O and Sample cell H2O	−0.29
AHs/Cs	Ball-Berry parameter	0.26
Ci	Intercellular CO2 concentration	0.26
Ci_Pa	Intercellular CO2	0.25
VpdA	Vapor pressure deficit based on Air temp	−0.23

.

From Figure 3b, it can be found that the correlation between VpdA, VpdL, and H₂Odiff is particularly strong. At the same time, the correlation between Ci, Ci/Ca and Ci_Pa is also the same, the correlation coefficient between them exceeds 0.9, and some are even 1. The same conclusion appeared in CndTotal, CndCO₂, Cond, RHsfc, and RH_S. Therefore, we can select the features with the largest correlation coefficient from them, thereby excluding highly correlated features. After this operation, the final screened features were RHsfc, Ci/Ca, VpdL, PARo and AHs/Cs.

In regression analysis, a small number of suitable features can not only avoid overfitting, but also increase the interpretability of the model. The number of 5 features screened by the significance test is still relatively large, and there may be situations such as multicollinearity. To perform regression analysis more scientifically and accurately, four methods of hierarchical clustering, Lasso, stepwise regression, and all-subsets regression are used to further select features. The characteristic parameters and Zscore of 78 samples were calculated according to the means of each variety, and then the subsequent operations are carried out.

2.4.1. Hierarchical Clustering

Hierarchical clustering creates a hierarchical nested clustering tree by calculating the similarity between different types of data points. The basic idea is to calculate the similarity between nodes through a certain similarity measure, and press the metric value. The size is sorted from high to low, and each node is gradually reconnected. For research work on clustering, refer to [31,32]. A hierarchical clustering method is adopted to cluster the characteristics and varieties of poplars, and the measurement method is Euclidean distance. The clustering results are shown in Figure 4. Figure 4a is the total clustering heat map of features and poplar varieties, where Fcluster represents features, and Stype represents varieties. Figure 4b is the hierarchical clustering map of features, and Figure 4c is the hierarchical clustering map of poplar varieties. According to the clustering results, we can divide the features into 6 groups (F1–F6). At the same time, the poplar varieties are divided into 3 groups (A–C), as shown in

Table 4. The result of features grouping.

Groups	F1	F2	F3
Features	VpdL	PARo	AHS/CS Ci/Ca RHsfc

and

Table 5. The result of poplar varieties grouping.

Groups	A	B	C
	FLEVO
	P. Juba
	Populus 2025
	I-63		DD102-4
Varieties	P. Canadensis	68	I-214
	L04-13	P. Ningshanica	L04-17
	Lushan Poplar	RASPCTE	I-45-51
	81		TRIPLO
	I-69
	I-72

.

According to the correlation coefficient, one feature is selected for each group. Finally, the three selected features are VpdL, PARo, and RHsfc.

2.4.2. Lasso

Lasso method was proposed by Tibshirani in 1996 by combining the advantages of ridge regression and subset selection method [33]. This method achieves the purpose of feature selection by compressing the coefficients of insignificant variables to 0. After screening by Lasso regression, the final three variables are VpdL, PARo, and Ci/Ca.

2.4.3. Stepwise Regression

Stepwise regression uses collinearity and variance contribution tests to gradually find all the salient features and obtain the optimal model, which is mainly used to solve the multicollinearity problem [34]. The main idea is to adopt new variables one by one. When introducing a new variable, consider whether to eliminate the selected variable until the new variable is no longer used. In this work, 13 characteristics were screened, and the backward stepwise regression method was adopted. Finally, the 2 variables after screening are PARo, and Ci/Ca.

2.4.4. All-Subsets Regression

All-subsets regression performs regression on all feature combinations, and then selects the best model, which allows exploring all possible models produced by different predictor combinations [35]. The optimal model selected by this method generally satisfies the adjusted coefficient of determination (adjr2) to be the largest. Perform all-subsets regression on 13 features. The regression results are shown in Figure 5. It can be observed that when adjr2 is the maximum, the corresponding features at the top of Figure 5 are VpdL, PARo, Ci/Ca, RHsfc and AHs/Cs in order. Therefore, the three features finally screened out by the all-subsets regression are RHsfc, Ci/Ca, VpdL, PARo and AHs/Cs.

2.5. Support Vector Regression

2.5.1. Division of Test Set and Training Set

Linear regression is widely used as a small sample predictive model. However, the limitations of linear regression are particularly obvious. When the actual regression function is not a linear function, linear regression may not get the desired result. Machine learning algorithms are currently a hot topic. As a classic algorithm in machine learning, support vector machines (SVM) can be used for classification problems or regression problems. Vapnik et al. [36] proposed the concept of support vector machine (SVM) in the mid-1990s. This supervised machine learning method has received extensive attention from researchers since it was proposed. Support vector regression (SVR) is an application model of support vector machine (SVM) on regression problems. It is mainly used to solve the problem of function fitting and regression estimation [37]. The core idea of support vector regression is to find a separating hyperplane (or hypersurface) to minimize the expected risk. It is a classic regression model in the field of machine learning and can solve linear and nonlinear problems. By minimizing structural risks, SVR can effectively avoid the problems of overfitting and dimensionality disasters. It exhibits superior performance in dealing with small samples, non-linear, high-dimensional and other problems. Hence, it is widely used in various fields such as financial forecasting, data mining, and biomedicine [38,39,40,41,42,43]. When dealing with regression problems, SVR are suitable for small and medium-sized samples. We first used multiple linear regression (MLR) to perform regression analysis on the model, however, the accuracy of the results obtained was relatively low. The prediction results of the four methods on the training set and test set are shown in Figure A1 in the Appendix A. For this reason, support vector regression was chosen to build a predictive model.

Before establishing the regression model, to predict the flood resistance of poplar varieties, the characteristic parameters corresponding to the same varieties in the 80 samples of the shallow flooded group (FL) were averaged. Then, the varieties were divided into training set and test set according to the ratio of 4:1 (the training set has 16 varieties in total, and the test set is 4 varieties). According to the hierarchical clustering results of poplar varieties, 4 samples are randomly selected from the three groups A–C in proportion. The samples used and their corresponding Zscore, Stype and varieties are shown in

Table 6. Main information of varieties.

Varieties	Zscore	Stype
68	−0.66254	B
81	0.717527	A
895	−0.22744	A
Populus 2025	0.570264	A
I-63	0.244021	A
I-214	−1.0187	C
I-45-51	−0.70265	C
P. Ningshanica	−0.8433	B
I-69	0.356889	A
I-72	−0.12623	A
L04-13	0.845993	A
L04-17	0.348729	C
DD102-4	−0.65942	C
P. Canadensis	−0.31136	A
P. Danhong	0.714574	A
P. Juba	0.528128	A
FLEVO	−0.14908	A
Lushan Poplar	0.282405	A
RASPCTE	−0.10356	B
TRIPLO	−0.56122	C

.

2.5.2. Establishment of Regression Model

Use the features obtained by the four feature screening methods to conduct SVR prediction. The selection of model parameters uses a 3-fold cross-validation method. The four SVR models all use the ε-SVR model (the ε-SVR model is a model that minimizes the root mean square error RMSE), and the kernel function is the RBF kernel. The corresponding penalty coefficient c, gamma and kernel width p are shown in

Table 7. Parameters of SVR.

Methods	c	Gamma	p
Hclust	15	0.0015	0.001
Lasso	26	0.0015	0.01
Stepwise	2	0.005	0.001
All-subsets	12	0.001	0.001

.

2.6. Evaluation of Model Performance

Three evaluation indexes of coefficient of determination (R²), mean square error (MSE) and mean relative error (MRE) are used to evaluate the performance of the model, and their calculation formulas are shown in (5)–(7):

$$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(\widehat{y_i}-\overline{y_i}\right)}^2}$$

(5)

$$MSE=\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{n}$$

(6)

$$MRE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{\left|y_i-\widehat{y_i}\right|}{y_i}\times 100\%$$

(7)

where $n$ is the number of samples, $y_i$ is the actual value, $\widehat{y_i}$ is the predicted value, and $\overline{y_i}$ is the mean of $y_i$.

2.7. Programming Environment

In this article, the feature selection process is implemented with R 4.0.5, and the regression analysis is implemented with MATLAB R2018a.

3. Results

SVR prediction is performed on features selected through hierarchical clustering, Lasso, stepwise regression, and all-subsets regression, and the result is shown in Figure 6.

As shown in Figure 6a, on the training set, the predicted value of the hierarchical clustering SVR model is the closest to the true value, and the fitting effect is the best. The worst performance is the SVR model established by the stepwise regression method. However, from Figure 6b, on the test set, the stepwise regression SVR model has the best fitting effect and the smallest mean square error. Comparing the four SVR models, it can be seen from Figure 6c that although the predicted values deviate from the true values at some points, the overall prediction trends are consistent, and good prediction results have been achieved. Next, consider the determination coefficients $R^2$, MSE and MRE of the four methods on the training set and the test set. The results of the training set are shown in Figure 7, and the specific values are shown in

Table 8. The $R^2$, MSE and MRE of the four methods on the training set.

Methods	Hclust	Lasso	Stepwise	All-Subsets
$R^2$	0.8573	0.8596	0.8738	0.8541
MSE	0.0573	0.0550	0.0396	0.0609
MRE	8.85%	8.32%	5.85%	9.33%

. In addition, the results of the test set are shown in Figure 8, and the specific values are shown in

Table 9. The $R^2$, MSE and MRE of the four methods on the test set.

Methods	Hclust	Lasso	Stepwise	All-Subsets
$R^2$	0.8472	0.8492	0.8581	0.7844
MSE	0.0354	0.0341	0.0104	0.0668
MRE	10.49%	9.85%	9.78%	10.12%

.

Figure 7a–c are histograms of $R^2$, MSE, and MRE on the training set, respectively. It can be seen from Figure 7 and Table 8 that in the training set, the largest $R^2$ of the four methods is the stepwise regression SVR model, and the second is the Lasso SVR model. The corresponding $R^2$ is 0.8738 and 0.8596, respectively. The minimum MSE is the SVR method based on stepwise regression, with a value of 0.0396, and the second smallest is the SVR model of the Lasso method, with a MSE of 0.0550. The worst performer is the all-subsets regression SVR model, with a value of 0.0609. In addition, the smallest MRE is the SVR model of the stepwise regression method, and the second is the SVR model of the Lasso method, with values of 5.85% and 9.33%, respectively. The worst performer is the all-subsets regression SVR model, with a MRE of 9.33%.

Figure 8a–c are histograms of $R^2$, MSE, and MRE on the test set, respectively. It can be seen from Figure 8 and Table 9 that in the test set, the largest $R^2$ of the four methods is also the stepwise regression SVR model, and the second is the Lasso SVR model. The corresponding $R^2$ is 0.8581 and 0.8492, respectively. The minimum MSE is the SVR method based on stepwise regression, with a value of 0.0104, and the second smallest is the SVR model of the Lasso method, with a MSE of 0.0341. The worst performer is the all-subsets regression SVR model, with a value of 0.0668. Moreover, the smallest MRE is also the SVR model of stepwise regression and Lasso method, with values of 9.78% and 9.85%, respectively. The worst performer is the Hclust SVR model, with a MRE of 10.49%.

In short, the four SVR methods that perform well in both training and test are stepwise regression and Lasso, while all-subset and Hclust SVR perform generally. The method with the smallest MSE is the stepwise regression SVR, and the second is the Lasso SVR. It can be noticed that the results of the four methods of Hclust, Lasso, stepwise and all-subsets regression SVR have relatively close results on the training set and the test set. This shows that the four feature selection methods are very effective, and the variables after screening are reliable. However, when using SVR to predict the flood resistance of poplar, if the best fitting effect and the highest accuracy are pursued, the SVR model of stepwise regression can be used. At the same time, under lower accuracy requirements, the SVR model of the Lasso method can also be selected. Both methods have considerable high accuracy and are suitable for solving practical problems.

4. Discussion

Four methods of hierarchical clustering, Lasso, stepwise regression, and all-subsets regression are adopted for feature selection, and the selected features have a considerable amount of interpretability. Recently, support vector regression has been widely used in the field of agriculture and forestry sciences, and it is compared with classical linear methods and other methods of machine learning. Chen [44] discussed the effectiveness of three machine learning techniques, SVR, Gaussian Process Regression (GPR), and Random Forest (RF). He linked the forest reflectivity after the fire to the severity of burns, and evaluated the severity of burns before the forest fires in the framework of geographic object-based image analysis (GEOBIA). His results showed that the prediction accuracy of the SVR model is 29% higher than the traditional multiple regression model. This research has made a great contribution to better understand the relationship between forest reflectivity and fire interference. The yield of soybeans was predicted by Maitiniyazi using SVR, Deep Neural Network (DNN), partial least square regression (PLSR) and random forest regression (RFR) [45], and the results show that, compared with other methods, machine learning methods such as SVR and DNN have better fitting effects. Lu et al. [46] combined visible light and canopy height indicators, applied stepwise multiple linear regression (SMLR) and three machine learning algorithms (support vector regression, SVR; extreme learning machine; random forest, RF) to predict wheat aboveground biomass (AGB), which reduces the cost of accurate crop management decisions. In addition, a large number of studies have proved that compared with traditional linear regression, the use of SVR methods to predict crops and plants generally has higher accuracy [47,48,49,50]. Thus far, for poplars, no predictions have been made about the resistance to waterlogging. For the first time, the author proposed to use the photosynthesis parameters of poplar seedlings to predict the waterlogging resistance of poplars. This research is conducive to precise waterlogging resistance, scientific selection of seedlings and cultivation of high-quality saplings, and at the same time has made a great contribution to the research on the mechanism of poplar resistance to waterlogging.

This study shows that the SVR method exhibits high accuracy in predicting the waterlogging resistance of poplars, which can meet the actual engineering needs to a certain extent. We can choose a suitable SVR model to solve practical problems according to our needs. However, it must be mentioned that in the stage of feature selection and regression model establishment, we only considered the relationship between photosynthesis-related features and poplar waterlogging resistance, and did not consider parameters such as chlorophyll fluorescence. In addition, since the cost of the poplar flooding experiment is too high and the measured parameters are numerous, this article only considers 20 poplar varieties and 160 samples. Consequently, future research directions can increase the number of varieties studied or consider the impact of chlorophyll fluorescence-related characteristics and poplar waterlogging resistance. Meanwhile, the coupling of photosynthesis and chlorophyll fluorescence and poplar waterlogging resistance can be considered to screen out more representative predictors. Moreover, other machine learning algorithms can also be selected to improve the prediction accuracy of poplar waterlogging resistance.

5. Conclusions

Regarding the waterlogging resistance of poplars, the author first defines the evaluation index of waterlogging resistance and eliminates outliers based on the index. For the selection of related features, four methods are adopted: hierarchical clustering, Lasso, stepwise regression, and all-subsets regression. The selected features are interpretable and have a great role in promoting the understanding of poplar’s anti-waterlogging mechanism. Finally, the support vector regression (SVR) method was used to predict the waterlogging resistance of poplars. The results show that the predictions obtained by stepwise regression and Lasso method have higher accuracy. Therefore, the SVR model established by these two methods can be given priority in practical application. This study proposes for the first time to use the measurable parameters of poplars before waterlogging experiments to predict the waterlogging resistance of poplars. At the same time, in the feature selection part, a hierarchical clustering method was used to cluster the 13 characteristics and 20 poplar varieties that are significantly related to poplar waterlogging resistance according to Euclidean distance. The photosynthetic characteristics and varieties of poplars belonging to the same kind have high similarities.

This research has made a great contribution to precise anti-waterlogging, scientific seedling selection and understanding of poplar anti-waterlogging mechanism. In addition, it fills in the gaps in the current lack of poplar anti-waterlogging prediction. The analysis process in this paper is concrete and repeatable. When considering characteristics related to poplar waterlogging resistance, although only photosynthesis-related characteristics are considered, the final results can also be used in practice. The $R^2$ of the SVR model based on stepwise regression and Lasso method is 0.8581 and 0.8492, and the MSE of the two methods is 0.0104 and 0.0314, respectively. Moreover, the MRE of these two methods is 9.78% and 9.85%, respectively. In the end, this study shows that the measurable characteristic parameters of the poplar before the waterlogging experiment can be used to predict the waterlogging resistance of the poplar, and the SVR method can achieve a certain accuracy requirement, which is suitable for actual engineering problems.