Nonlinear Dynamics of the Introduction of a New SARS-CoV-2 Variant with Different Infectiousness
Abstract
:1. Introduction
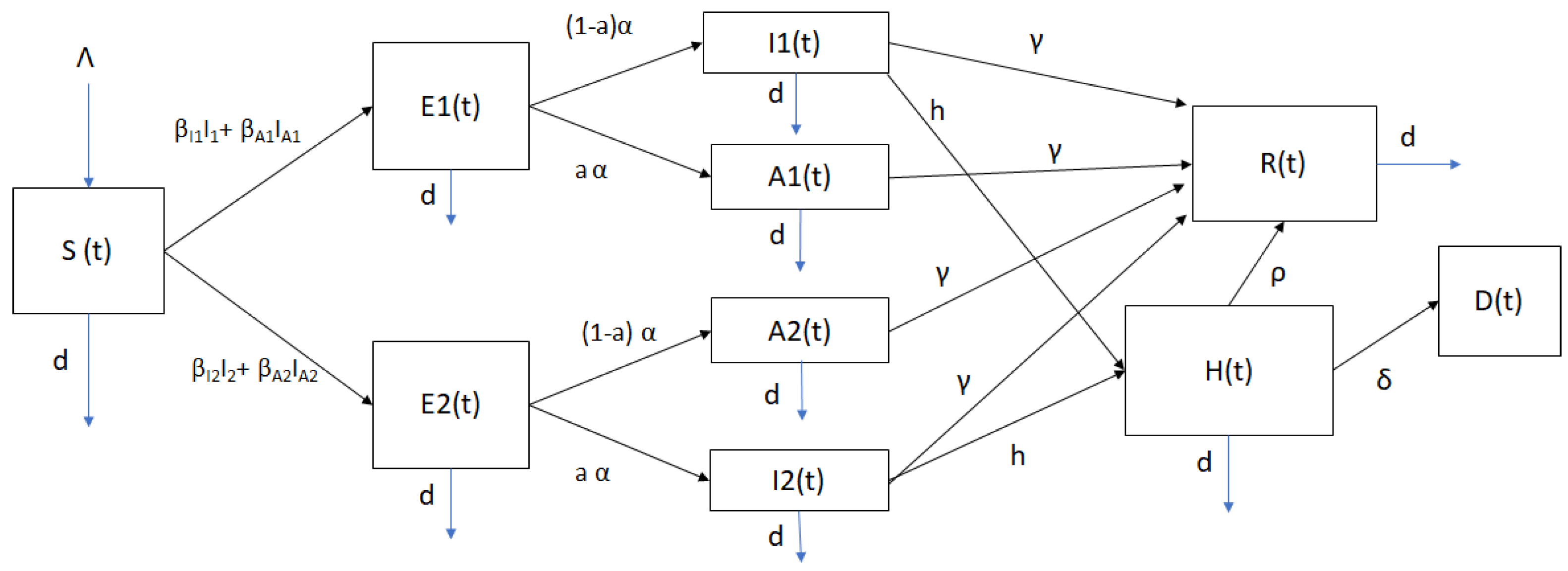
2. Mathematical Model of SARS-CoV-2 Spread
Positivity and Boundedness of Solutions
3. Mathematical Stability Analysis
3.1. Equilibrium Points and
- is the rate of appearance of new infections in compartment
- incorporates the remaining transitional terms, namely births, deaths, disease progression and recovery.
3.2. Local Stability of Disease-Free Equilibrium Point
3.3. Global Stability of Disease-Free Equilibrium Point
3.4. Global Stability of New SARS-CoV-2 Variant Endemic Point
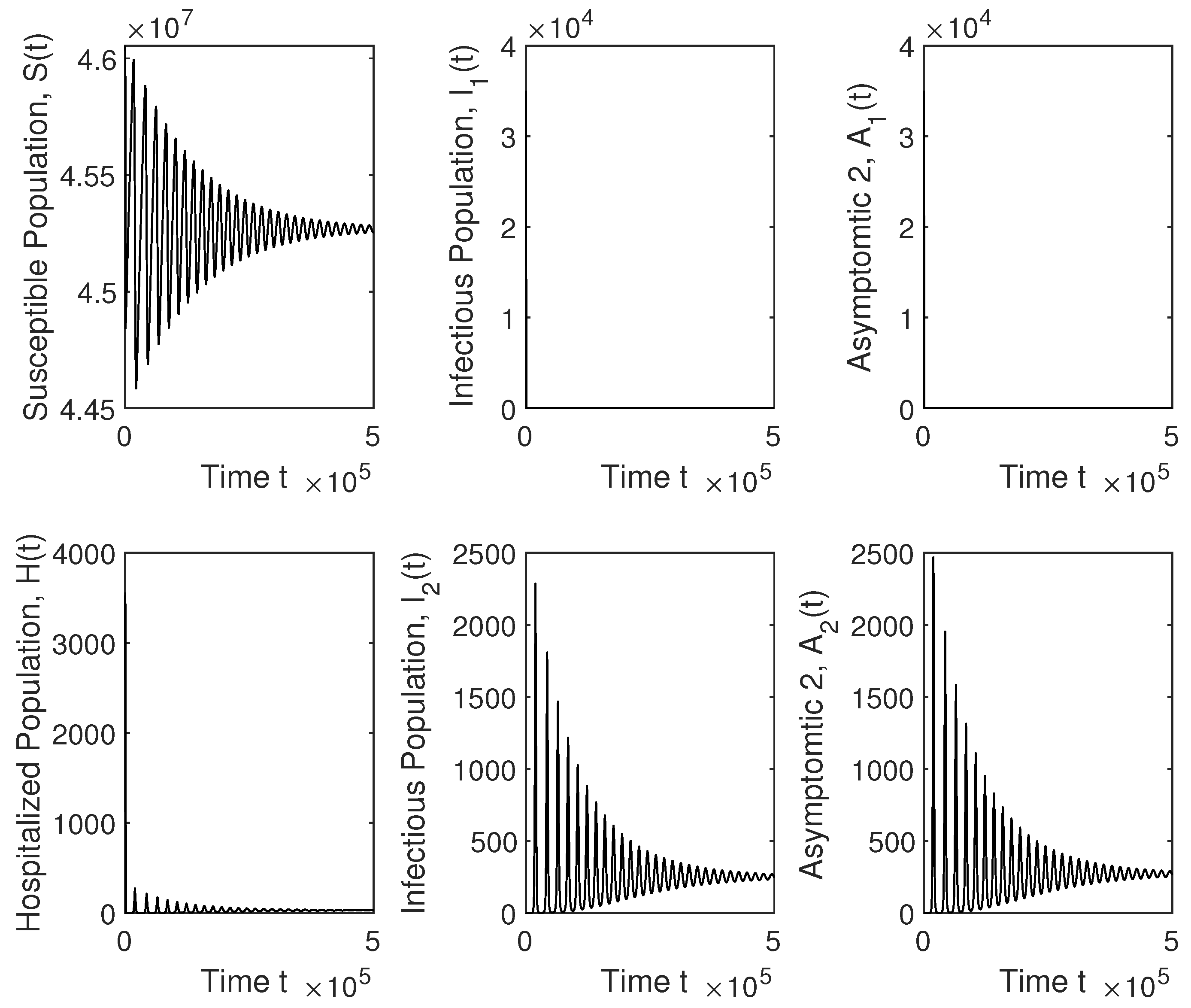
4. Numerical Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Centers for Disease Control and Prevention. 2020. Available online: https://www.cdc.gov/coronavirus/2019-nCoV/index.html (accessed on 1 January 2021).
- Johns Hopkins University and Medicine. 2020. Available online: https://coronavirus.jhu.edu (accessed on 1 January 2021).
- Alves, T.H.E.; de Souza, T.A.; de Almeida Silva, S.; Ramos, N.A.; de Oliveira, S.V. Underreporting of death by COVID-19 in Brazil’s second most populous state. Front. Public Health 2020, 8. in press. [Google Scholar] [CrossRef] [PubMed]
- Arvisais-Anhalt, S.; Lehmann, C.U.; Park, J.Y.; Araj, E.; Holcomb, M.; Jamieson, A.R.; McDonald, S.; Medford, R.J.; Perl, T.M.; Toomay, S.M.; et al. What the Coronavirus Disease 2019 (COVID-19) Pandemic Has Reinforced: The Need for Accurate Data. Clin. Infect. Dis. 2020, 72, 920–923. [Google Scholar] [CrossRef]
- Azmon, A.; Faes, C.; Hens, N. On the estimation of the reproduction number based on misreported epidemic data. Stat. Med. 2014, 33, 1176–1192. [Google Scholar] [CrossRef] [PubMed]
- Burki, T. COVID-19 in Latin America. Lancet Infect. Dis. 2020, 20, 547–548. [Google Scholar] [CrossRef]
- Do Prado, M.F.; de Paula Antunes, B.B.; Bastos, L.D.S.L.; Peres, I.T.; Da Silva, A.D.A.B.; Dantas, L.F.; Baião, F.A.; Maçaira, P.; Hamacher, S.; Bozza, F.A. Analysis of COVID-19 under-reporting in Brazil. Rev. Bras. Ter. Intensiv. 2020, 32, 224. [Google Scholar] [CrossRef] [PubMed]
- Lau, H.; Khosrawipour, T.; Kocbach, P.; Ichii, H.; Bania, J.; Khosrawipour, V. Evaluating the massive underreporting and undertesting of COVID-19 cases in multiple global epicenters. Pulmonology 2020, 27, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Rasjid, Z.E.; Setiawan, R.; Effendi, A. A Comparison: Prediction of Death and Infected COVID-19 Cases in Indonesia Using Time Series Smoothing and LSTM Neural Network. Procedia Comput. Sci. 2021, 179, 982–988. [Google Scholar] [CrossRef]
- Saberi, M.; Hamedmoghadam, H.; Madani, K.; Dolk, H.M.; Morgan, A.S.; Morris, J.K.; Khoshnood, K.; Khoshnood, B. Accounting for underreporting in mathematical modeling of transmission and control of COVID-19 in Iran. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Sarnaglia, A.J.; Zamprogno, B.; Molinares, F.A.F.; de Godoi, L.G.; Monroy, N.A.J. Correcting notification delay and forecasting of COVID-19 data. J. Math. Anal. Appl. 2021, 125202. [Google Scholar] [CrossRef]
- Altmann, D.M.; Boyton, R.J.; Beale, R. Immunity to SARS-CoV-2 variants of concern. Science 2021, 371, 1103–1104. [Google Scholar] [CrossRef]
- Grubaugh, N.D.; Hanage, W.P.; Rasmussen, A.L. Making sense of mutation: What D614G means for the COVID-19 pandemic remains unclear. Cell 2020, 182, 794–795. [Google Scholar] [CrossRef]
- Li, Q.; Wu, J.; Nie, J.; Zhang, L.; Hao, H.; Liu, S.; Zhao, C.; Zhang, Q.; Liu, H.; Nie, L.; et al. The impact of mutations in SARS-CoV-2 spike on viral infectivity and antigenicity. Cell 2020, 182, 1284–1294. [Google Scholar] [CrossRef]
- Lemieux, J.E.; Li, J.Z. Uncovering Ways that Emerging SARS-CoV-2 Lineages May Increase Transmissibility. J. Infect. Dis. 2021, 233, 1663–1665. [Google Scholar] [CrossRef]
- Plante, J.A.; Liu, Y.; Liu, J.; Xia, H.; Johnson, B.A.; Lokugamage, K.G.; Zhang, X.; Muruato, A.E.; Zou, J.; Fontes-Garfias, C.R.; et al. Spike mutation D614G alters SARS-CoV-2 fitness. Nature 2020, 592, 116–121. [Google Scholar] [CrossRef] [PubMed]
- Van Dorp, L.; Acman, M.; Richard, D.; Shaw, L.P.; Ford, C.E.; Ormond, L.; Owen, C.J.; Pang, J.; Tan, C.C.; Boshier, F.A.; et al. Emergence of genomic diversity and recurrent mutations in SARS-CoV-2. Infect. Genet. Evol. 2020, 83, 104351. [Google Scholar] [CrossRef] [PubMed]
- Walensky, R.P.; Walke, H.T.; Fauci, A.S. SARS-CoV-2 variants of concern in the United States—Challenges and opportunities. JAMA 2021, 325, 1037–1038. [Google Scholar] [CrossRef]
- Kupferschmidt, K. Vaccinemakers ponder how to adapt to virus variants. Science 2021, 371, 448–449. [Google Scholar] [CrossRef]
- Le Page, M. Threats from new variants. New Sci. 2021, 249, 8–9. [Google Scholar]
- Van Oosterhout, C.; Hall, N.; Ly, H.; Tyler, K.M. COVID-19 evolution during the pandemic–Implications of new SARS-CoV-2 variants on disease control and public health policies. Virulence 2021, 12, 507. [Google Scholar] [CrossRef]
- Korber, B.; Fischer, W.M.; Gnanakaran, S.; Yoon, H.; Theiler, J.; Abfalterer, W.; Hengartner, N.; Giorgi, E.E.; Bhattacharya, T.; Foley, B.; et al. Tracking changes in SARS-CoV-2 Spike: Evidence that D614G increases infectivity of the COVID-19 virus. Cell 2020, 182, 812–827. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, F.; Abadi, A.T.B. Implications of the Emergence of a New Variant of SARS-CoV-2, VUI-202012/01. Arch. Med. Res. 2021. [Google Scholar] [CrossRef]
- Leung, K.; Shum, M.H.; Leung, G.M.; Lam, T.T.; Wu, J.T. Early transmissibility assessment of the N501Y mutant strains of SARS-CoV-2 in the United Kingdom, October to November 2020. Eurosurveillance 2021, 26, 2002106. [Google Scholar] [CrossRef] [PubMed]
- Fiorentini, S.; Messali, S.; Zani, A.; Caccuri, F.; Giovanetti, M.; Ciccozzi, M.; Caruso, A. First detection of SARS-CoV-2 spike protein N501 mutation in Italy in August, 2020. Lancet Infect. Dis. 2021, 21, e147. [Google Scholar] [CrossRef]
- PublicHealthEngland. Investigation-of-Novel-SARS-CoV-2-Variant-Variant-of-Concern-20201201. 2021. Available online: https://www.gov.uk/government/publications/investigation-of-novel-sars-cov-2-variant-variant-of-concern-20201201 (accessed on 1 February 2021).
- Davies, N.G.; Abbott, S.; Barnard, R.C.; Jarvis, C.I.; Kucharski, A.J.; Munday, J.D.; Pearson, C.A.; Russell, T.W.; Tully, D.C.; Washburne, A.D.; et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B. 1.1.7 in England. Science 2021, 372, eabg3055. [Google Scholar] [CrossRef] [PubMed]
- Reuters. 2020. Available online: https://tinyurl.com/y5fe8q2u (accessed on 30 January 2021).
- Wang, Y.; Wu, J.; Zhang, L.; Zhang, Y.; Wang, H.; Ding, R.; Nie, J.; Li, Q.; Liu, S.; Yu, Y.; et al. The Infectivity and Antigenicity of Epidemic SARS-CoV-2 Variants in the United Kingdom. Res. Sq. 2021, 1–14. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin/Heidelberg, Germany, 2001; Volume 40. [Google Scholar]
- Hethcote, H.W. Mathematics of infectious diseases. SIAM Rev. 2005, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- Rios-Doria, D.; Chowell, G. Qualitative analysis of the level of cross-protection between epidemic waves of the 1918–1919 influenza pandemic. J. Theor. Biol. 2009, 261, 584–592. [Google Scholar] [CrossRef] [PubMed]
- González-Parra, G.; Arenas, A.; Diego, F.; Aranda, L.S. Modeling the epidemic waves of AH1N1/09 influenza around the world. Spat. Spatio Temporal Epidemiol. 2011, 2, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Andreasen, V.; Viboud, C.; Simonsen, L. Epidemiologic Characterization of the 1918 Influenza Pandemic Summer Wave in Copenhagen: Implications for Pandemic Control Strategies. J. Infect. Dis. 2008, 197, 270–278. [Google Scholar] [CrossRef] [Green Version]
- Roberts, M.; Tobias, M. Predicting and preventing measles epidemics in New Zealand: Application of a mathematical model. Epidemiol. Infect. 2000, 124, 279–287. [Google Scholar] [CrossRef]
- Legrand, J.; Grais, R.F.; Boelle, P.Y.; Valleron, A.J.; Flahault, A. Understanding the dynamics of Ebola epidemics. Epidemiol. Infect. 2007, 135, 610–621. [Google Scholar] [CrossRef] [PubMed]
- Thompson, K.M.; Duintjer Tebbens, R.J.; Pallansch, M.A. Evaluation of response scenarios to potential polio outbreaks using mathematical models. Risk Anal. 2006, 26, 1541–1556. [Google Scholar] [CrossRef]
- Kim, Y.; Barber, A.V.; Lee, S. Modeling influenza transmission dynamics with media coverage data of the 2009 H1N1 outbreak in Korea. PLoS ONE 2020, 15, e0232580. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Jung, E. Mathematical model of transmission dynamics and optimal control strategies for 2009 A/H1N1 influenza in the Republic of Korea. J. Theor. Biol. 2017, 412, 74–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delamater, P.L.; Street, E.J.; Leslie, T.F.; Yang, Y.T.; Jacobsen, K.H. Complexity of the basic reproduction number (R0). Emerg. Infect. Dis. 2019, 25, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zenk, L.; Steiner, G.; Pina e Cunha, M.; Laubichler, M.D.; Bertau, M.; Kainz, M.J.; Jäger, C.; Schernhammer, E.S. Fast Response to Superspreading: Uncertainty and Complexity in the Context of COVID-19. Int. J. Environ. Res. Public Health 2020, 17, 7884. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Bornaa, C.; Seidu, B.; Jin, Z. Mathematical analysis of the effects of controls on transmission dynamics of SARS-CoV-2. Alex. Eng. J. 2020, 59, 5069–5078. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Owusu, M.A.; Jin, Z.; Oduro, F.; Abidemi, A.; Gyasi, E.O. Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: Using data from Ghana. Chaos Solitons Fractals 2020, 140, 110103. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Doménech-Carbó, A.; Doménech-Casasús, C. The evolution of COVID-19: A discontinuous approach. Phys. Stat. Mech. Its Appl. 2021, 568, 125752. [Google Scholar] [CrossRef] [PubMed]
- Garrido, J.M.; Martínez-Rodríguez, D.; Rodríguez-Serrano, F.; Sferle, S.M.; Villanueva, R.J. Modeling COVID-19 with Uncertainty in Granada, Spain. Intra-Hospitalary Circuit and Expectations over the Next Months. Mathematics 2021, 9, 1132. [Google Scholar] [CrossRef]
- Rafiq, M.; Macías-Díaz, J.; Raza, A.; Ahmed, N. Design of a nonlinear model for the propagation of COVID-19 and its efficient nonstandard computational implementation. Appl. Math. Model. 2021, 89, 1835–1846. [Google Scholar] [CrossRef]
- Stutt, R.O.; Retkute, R.; Bradley, M.; Gilligan, C.A.; Colvin, J. A modelling framework to assess the likely effectiveness of facemasks in combination with lock-down in managing the COVID-19 pandemic. Proc. R. Soc. A 2020, 476, 20200376. [Google Scholar] [CrossRef]
- Triambak, S.; Mahapatra, D. A random walk Monte Carlo simulation study of COVID-19-like infection spread. Phys. A Stat. Mech. Its Appl. 2021, 574, 126014. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Cuomo-Dannenburg, G.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College: London, UK, 2020. [Google Scholar] [CrossRef]
- Kong, J.D.; Tchuendom, R.F.; Adeleye, S.A.; David, J.F.; Admasu, F.S.; Bakare, E.A.; Siewe, N. SARS-CoV-2 and self-medication in Cameroon: A mathematical model. J. Biol. Dyn. 2021, 15, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Rodríguez, D.; Gonzalez-Parra, G.; Villanueva, R.J. Analysis of key factors of a SARS-CoV-2 vaccination program: A mathematical modeling approach. Epidemiologia 2021, 2, 140–161. [Google Scholar] [CrossRef]
- Mbogo, R.W.; Orwa, T.O. SARS-CoV-2 outbreak and control in Kenya-Mathematical model analysis. Infect. Dis. Model. 2021, 6, 370–380. [Google Scholar]
- Kuniya, T. Prediction of the Epidemic Peak of Coronavirus Disease in Japan, 2020. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef] [Green Version]
- Péni, T.; Csutak, B.; Szederkényi, G.; Röst, G. Nonlinear model predictive control with logic constraints for COVID-19 management. Nonlinear Dyn. 2020, 102, 1965–1986. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Elbarkouky, R.A.; Omar, O.A.; Ragusa, M.A. Models for COVID-19 Daily Confirmed Cases in Different Countries. Mathematics 2021, 9, 659. [Google Scholar] [CrossRef]
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Szederkenyi, G.; Magyar, A.; Hangos, K.M. Analysis and Control of Polynomial Dynamic Models with Biological Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Amador Pacheco, J.; Armesto, D.; Gómez-Corral, A. Extreme values in SIR epidemic models with two strains and cross-immunity. Math. Biosci. Eng. 2019, 16, 1992–2022. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F. Mathematical epidemiology: Past, present, and future. Infect. Dis. Model. 2017, 2, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Meskaf, A.; Khyar, O.; Danane, J.; Allali, K. Global stability analysis of a two-strain epidemic model with non-monotone incidence rates. Chaos Solitons Fractals 2020, 133, 109647. [Google Scholar] [CrossRef]
- Shayak, B.; Sharma, M.M.; Gaur, M.; Mishra, A.K. Impact of reproduction number on multiwave spreading dynamics of COVID-19 with temporary immunity: A mathematical model. Int. J. Infect. Dis. 2021, 104, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Faes, C.; Abrams, S.; Van Beckhoven, D.; Meyfroidt, G.; Vlieghe, E.; Hens, N. Time between symptom onset, hospitalisation and recovery or death: Statistical analysis of belgian covid-19 patients. Int. J. Environ. Res. Public Health 2020, 17, 7560. [Google Scholar] [CrossRef] [PubMed]
- Faust, J.S.; Del Rio, C. Assessment of deaths from COVID-19 and from seasonal influenza. JAMA Intern. Med. 2020, 180, 1045–1046. [Google Scholar] [CrossRef] [PubMed]
- Paltiel, A.D.; Schwartz, J.L.; Zheng, A.; Walensky, R.P. Clinical Outcomes Of A COVID-19 Vaccine: Implementation Over Efficacy: Study examines how definitions and thresholds of vaccine efficacy, coupled with different levels of implementation effectiveness and background epidemic severity, translate into outcomes. Health Aff. 2020, 40, 42–52. [Google Scholar]
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar]
- Xia, S.; Duan, K.; Zhang, Y.; Zhao, D.; Zhang, H.; Xie, Z.; Li, X.; Peng, C.; Zhang, Y.; Zhang, W.; et al. Effect of an inactivated vaccine against SARS-CoV-2 on safety and immunogenicity outcomes: Interim analysis of 2 randomized clinical trials. JAMA 2020, 324, 951–960. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.; Lau, E.H.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus—Infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Team, I.C.F. Modeling COVID-19 scenarios for the United States. Nat. Med. 2020, 27, 94. [Google Scholar]
- Hoseinpour Dehkordi, A.; Alizadeh, M.; Derakhshan, P.; Babazadeh, P.; Jahandideh, A. Understanding epidemic data and statistics: A case study of COVID-19. J. Med. Virol. 2020, 92, 868–882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quah, P.; Li, A.; Phua, J. Mortality rates of patients with COVID-19 in the intensive care unit: A systematic review of the emerging literature. Crit. Care 2020, 24, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Oran, D.P.; Topol, E.J. Prevalence of Asymptomatic SARS-CoV-2 Infection: A Narrative Review. Ann. Intern. Med. 2020, 173, 362–367. [Google Scholar] [CrossRef] [PubMed]
- The World Bank. 2021. Available online: https://data.worldbank.org/ (accessed on 1 January 2021).
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Fred Brauer, J.A.N. The Qualitative Theory of Ordinary Differential Equations: An Introduction; Dover Publications: New York, NY, USA, 1989. [Google Scholar]
- Den Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Shaw, C.L.; Kennedy, D.A. What the reproductive number R0 can and cannot tell us about COVID-19 dynamics. Theor. Popul. Biol. 2021, 137, 2–9. [Google Scholar] [CrossRef]
- Gostic, K.M.; McGough, L.; Baskerville, E.B.; Abbott, S.; Joshi, K.; Tedijanto, C.; Kahn, R.; Niehus, R.; Hay, J.A.; De Salazar, P.M.; et al. Practical considerations for measuring the effective reproductive number, R t. PLoS Comput. Biol. 2020, 16, e1008409. [Google Scholar] [CrossRef] [PubMed]
- Yan, P.; Chowell, G. Beyond the Initial Phase: Compartment Models for Disease Transmission. In Quantitative Methods for Investigating Infectious Disease Outbreaks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 135–182. [Google Scholar]
- O’Regan, S.M.; Kelly, T.C.; Korobeinikov, A.; O’Callaghan, M.J.; Pokrovskii, A.V. Lyapunov functions for SIR and SIRS epidemic models. Appl. Math. Lett. 2010, 23, 446–448. [Google Scholar] [CrossRef] [Green Version]
- Arenas, A.J.; González-Parra, G.; De La Espriella, N. Nonlinear dynamics of a new seasonal epidemiological model with age-structure and nonlinear incidence rate. Comput. Appl. Math. 2021, 40, 1–27. [Google Scholar] [CrossRef]
- Khan, A.; Zarin, R.; Hussain, G.; Ahmad, N.A.; Mohd, M.H.; Yusuf, A. Stability analysis and optimal control of covid-19 with convex incidence rate in Khyber Pakhtunkhawa (Pakistan). Results Phys. 2021, 20, 103703. [Google Scholar] [CrossRef]
- Khyar, O.; Allali, K. Global dynamics of a multi-strain SEIR epidemic model with general incidence rates: Application to COVID-19 pandemic. Nonlinear Dyn. 2020, 102, 489–509. [Google Scholar] [CrossRef]
- González-Parra, G.C.; Aranda, D.F.; Chen-Charpentier, B.; Díaz-Rodríguez, M.; Castellanos, J.E. Mathematical modeling and characterization of the spread of chikungunya in Colombia. Math. Comput. Appl. 2019, 24, 6. [Google Scholar] [CrossRef] [Green Version]
- Taneco-Hernández, M.A.; Vargas-De-León, C. Stability and Lyapunov functions for systems with Atangana–Baleanu Caputo derivative: An HIV/AIDS epidemic model. Chaos Solitons Fractals 2020, 132, 109586. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Further Notes on the Basic Reproduction Number; Springer: Berlin/Heidelberg, Germany, 2008; pp. 159–178. [Google Scholar]
- Ma, J.; Earn, D.J. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol. 2006, 68, 679–702. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.C. A note on the derivation of epidemic final sizes. Bull. Math. Biol. 2012, 74, 2125–2141. [Google Scholar] [CrossRef]
- Jack, K.; Hale, S.M.V.L. Introduction to Functional Differential Equations, 1st ed.; Applied Mathematical Sciences 99; Springer: New York, NY, USA, 1993. [Google Scholar]
- Galloway, S.E.; Paul, P.; MacCannell, D.R.; Johansson, M.A.; Brooks, J.T.; MacNeil, A.; Slayton, R.B.; Tong, S.; Silk, B.J.; Armstrong, G.L.; et al. Emergence of SARS-CoV-2 b. 1.1. 7 lineage—United states, 29 December 2020–12 January 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 95. [Google Scholar] [CrossRef] [PubMed]
- Mahase, E. Covid-19: What new variants are emerging and how are they being investigated? BMJ (Clin. Res. Ed.) 2021, 372, n158. [Google Scholar]
- Kim, L.; Garg, S.; O’Halloran, A.; Whitaker, M.; Pham, H.; Anderson, E.J.; Armistead, I.; Bennett, N.M.; Billing, L.; Como-Sabetti, K.; et al. Risk factors for intensive care unit admission and in-hospital mortality among hospitalized adults identified through the US coronavirus disease 2019 (COVID-19)-associated hospitalization surveillance network (COVID-NET). Clin. Infect. Dis. 2020, 72, e206–e214. [Google Scholar] [CrossRef]
- Yehia, B.R.; Winegar, A.; Fogel, R.; Fakih, M.; Ottenbacher, A.; Jesser, C.; Bufalino, A.; Huang, R.H.; Cacchione, J. Association of race with mortality among patients hospitalized with coronavirus disease 2019 (COVID-19) at 92 US hospitals. JAMA Netw. Open 2020, 3, e2018039. [Google Scholar] [CrossRef]
- Mukandavire, Z.; Nyabadza, F.; Malunguza, N.J.; Cuadros, D.F.; Shiri, T.; Musuka, G. Quantifying early COVID-19 outbreak transmission in South Africa and exploring vaccine efficacy scenarios. PLoS ONE 2020, 15, e0236003. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, A.; Yi, B.; Ding, K.; Wang, H.; Wang, J.; Xu, G. The epidemiological characteristics of infection in close contacts of COVID-19 in Ningbo city. Chin. J. Epidemiol. 2020, 41, 668–672. [Google Scholar]
- Mc Evoy, D.; McAloon, C.G.; Collins, A.B.; Hunt, K.; Butler, F.; Byrne, A.W.; Casey, M.; Barber, A.; Griffin, J.M.; Lane, E.A.; et al. The relative infectiousness of asymptomatic SARS-CoV-2 infected persons compared with symptomatic individuals: A rapid scoping review. medRxiv 2020, 11, e042354. [Google Scholar]
- Kinoshita, R.; Anzai, A.; Jung, S.m.; Linton, N.M.; Miyama, T.; Kobayashi, T.; Hayashi, K.; Suzuki, A.; Yang, Y.; Akhmetzhanov, A.R.; et al. Containment, Contact Tracing and Asymptomatic Transmission of Novel Coronavirus Disease (COVID-19): A Modelling Study. J. Clin. Med. 2020, 9, 3125. [Google Scholar] [CrossRef] [PubMed]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orenes-Piñero, E.; Baño, F.; Navas-Carrillo, D.; Moreno-Docón, A.; Marín, J.M.; Misiego, R.; Ramírez, P. Evidences of SARS-CoV-2 virus air transmission indoors using several untouched surfaces: A pilot study. Sci. Total Environ. 2021, 751, 142317. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.j.; Lu, X.x.; Deng, Y.b.; Tang, Y.j.; Lu, J.c. COVID-19: Asymptomatic carrier transmission is an underestimated problem. Epidemiol. Infect. 2020, 148, 1–7. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value |
|---|---|---|
| Incubation period | [68,69] | |
| Infectious period | [68] | |
| Hospitalization rate | [50,68,70] | |
| Hospitalization period | [50,68,70] | |
| Death rate (hospitalized) | [65,71] | |
| Probability of being asymptomatic | a | [1,72] |
| Recruiting rate | [73] | |
| Death rate | d | [73] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Parra, G.; Arenas, A.J. Nonlinear Dynamics of the Introduction of a New SARS-CoV-2 Variant with Different Infectiousness. Mathematics 2021, 9, 1564. https://doi.org/10.3390/math9131564
Gonzalez-Parra G, Arenas AJ. Nonlinear Dynamics of the Introduction of a New SARS-CoV-2 Variant with Different Infectiousness. Mathematics. 2021; 9(13):1564. https://doi.org/10.3390/math9131564
Chicago/Turabian StyleGonzalez-Parra, Gilberto, and Abraham J. Arenas. 2021. "Nonlinear Dynamics of the Introduction of a New SARS-CoV-2 Variant with Different Infectiousness" Mathematics 9, no. 13: 1564. https://doi.org/10.3390/math9131564
APA StyleGonzalez-Parra, G., & Arenas, A. J. (2021). Nonlinear Dynamics of the Introduction of a New SARS-CoV-2 Variant with Different Infectiousness. Mathematics, 9(13), 1564. https://doi.org/10.3390/math9131564






