On-Off Intermittency in a Three-Species Food Chain
Abstract
:1. Introduction
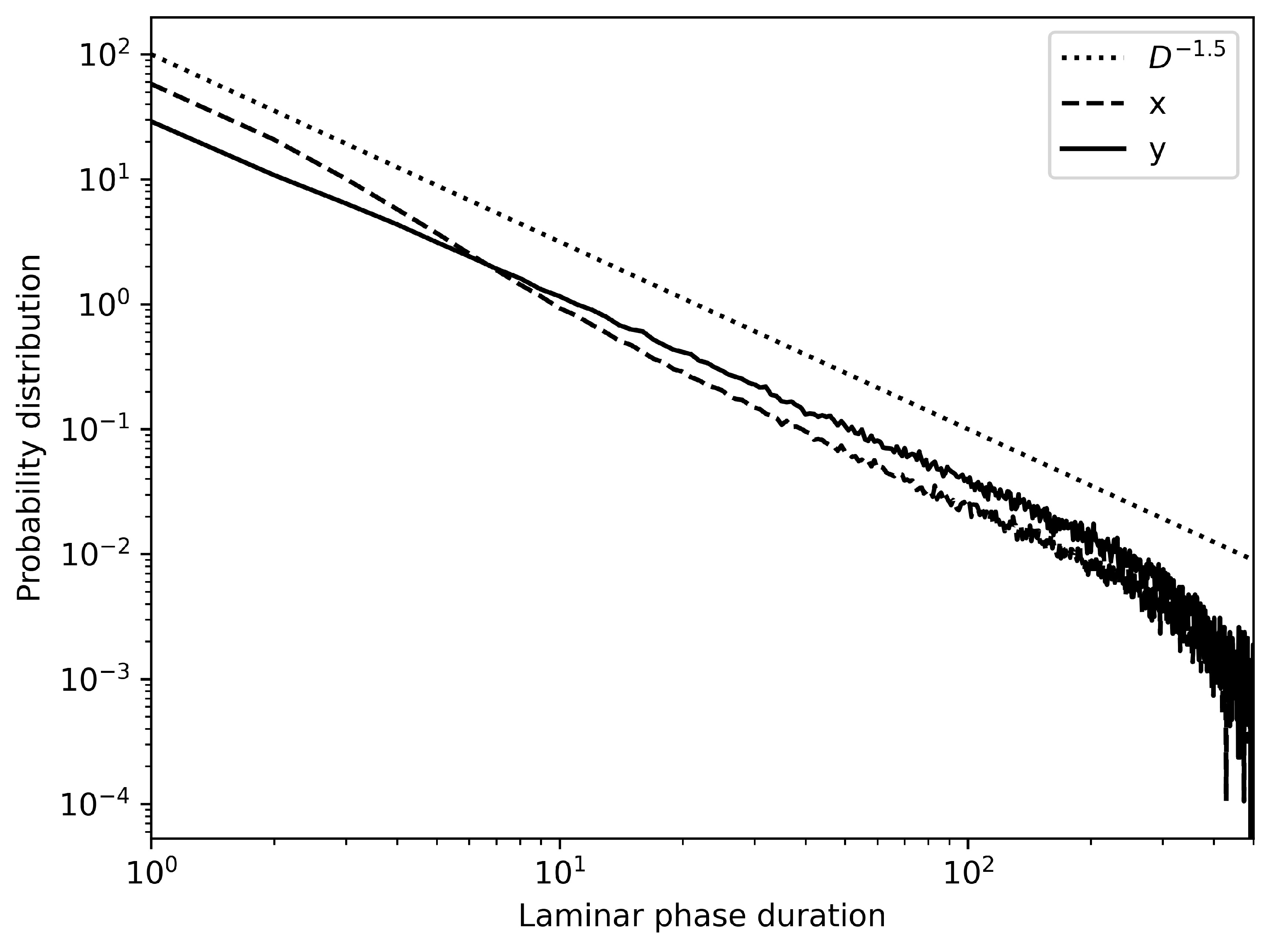
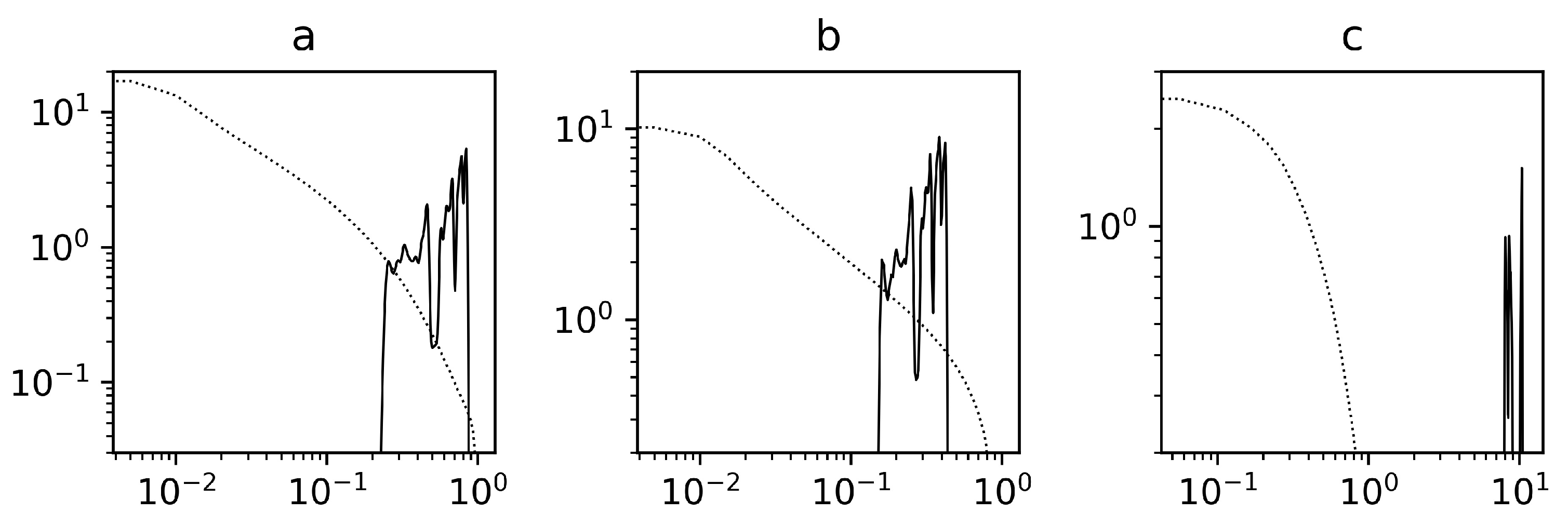
2. On-Off Intermittency
3. Hastings–Powell Model
Stochastic Parameters and Numerical Simulations
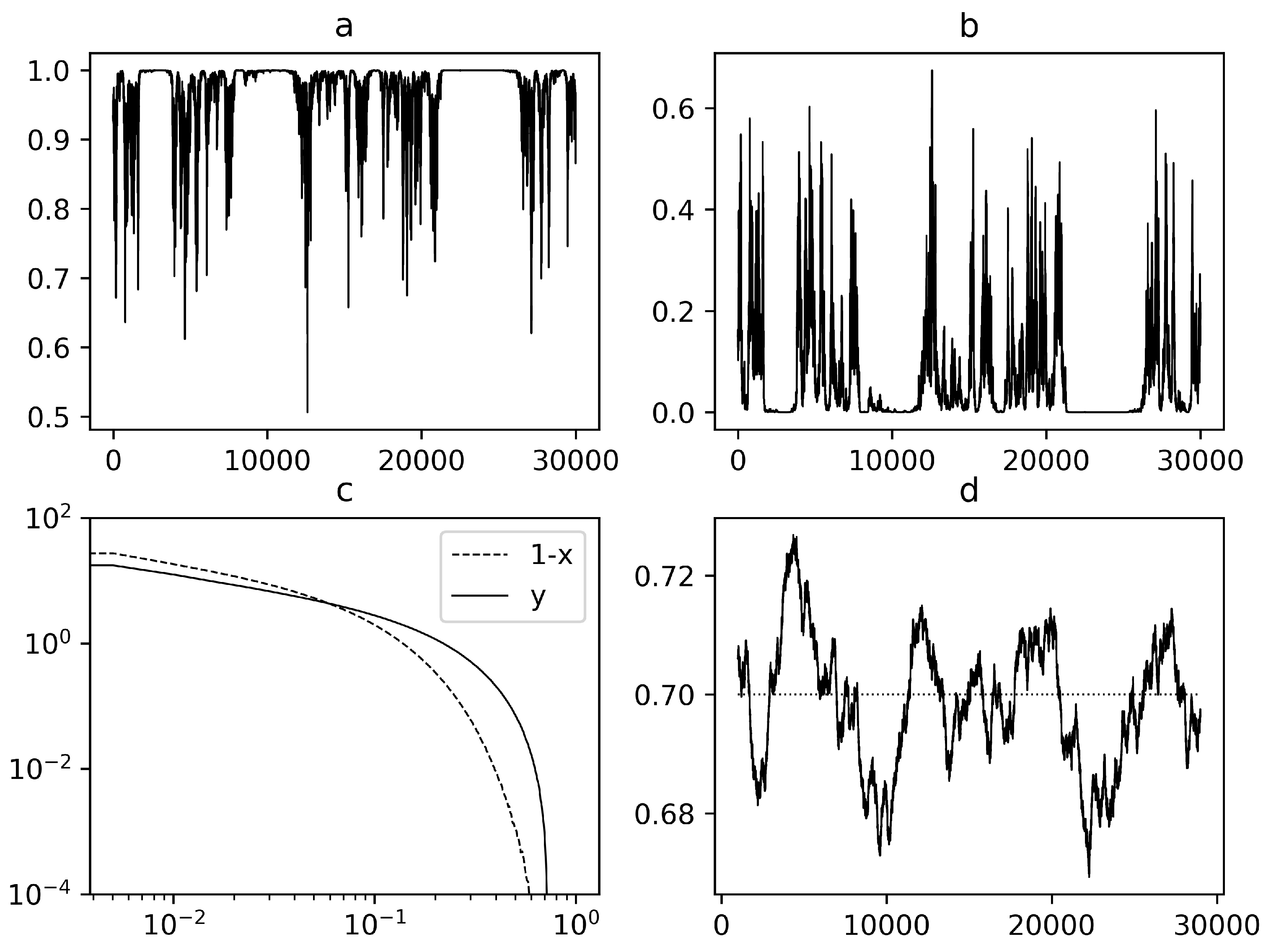
4. Results
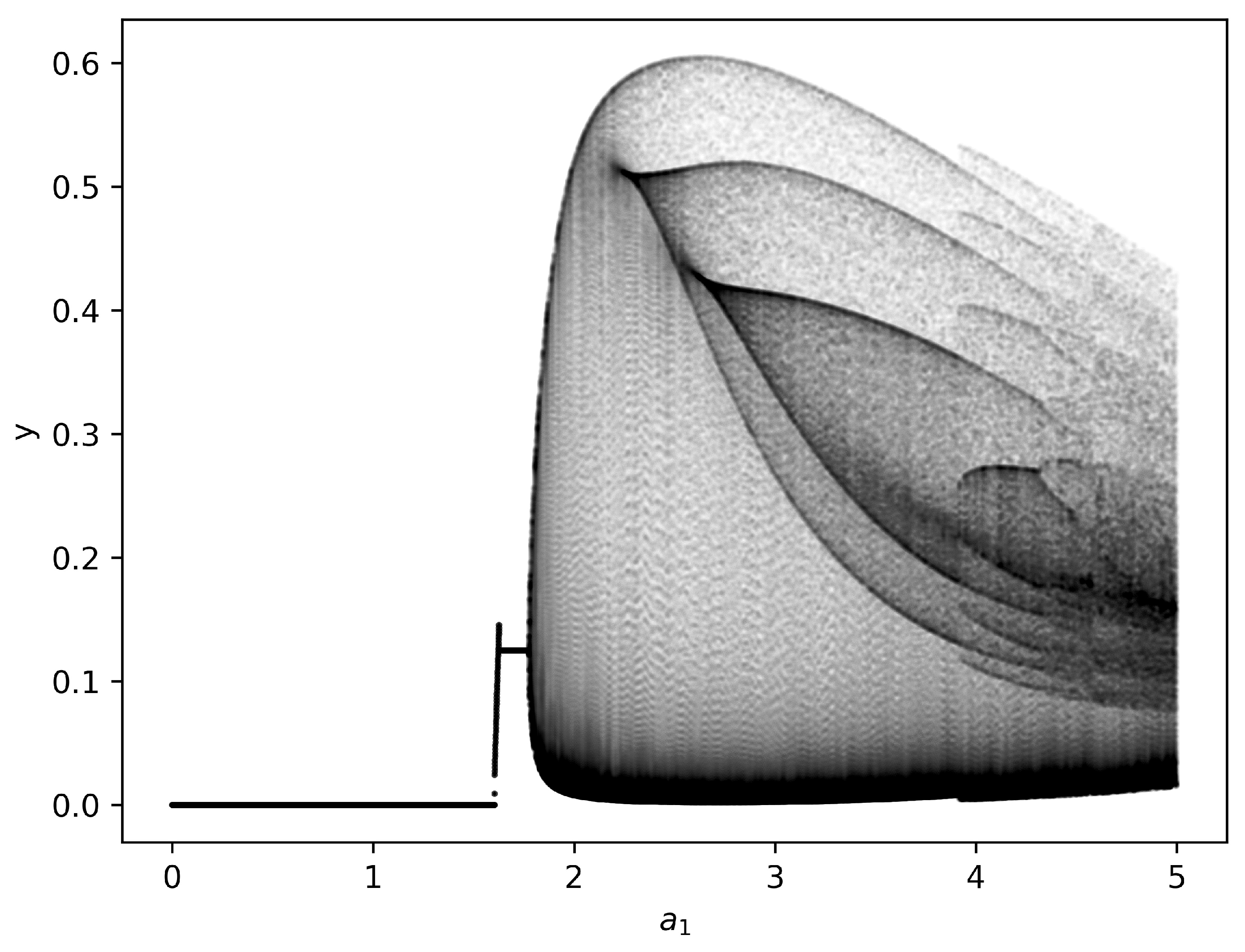
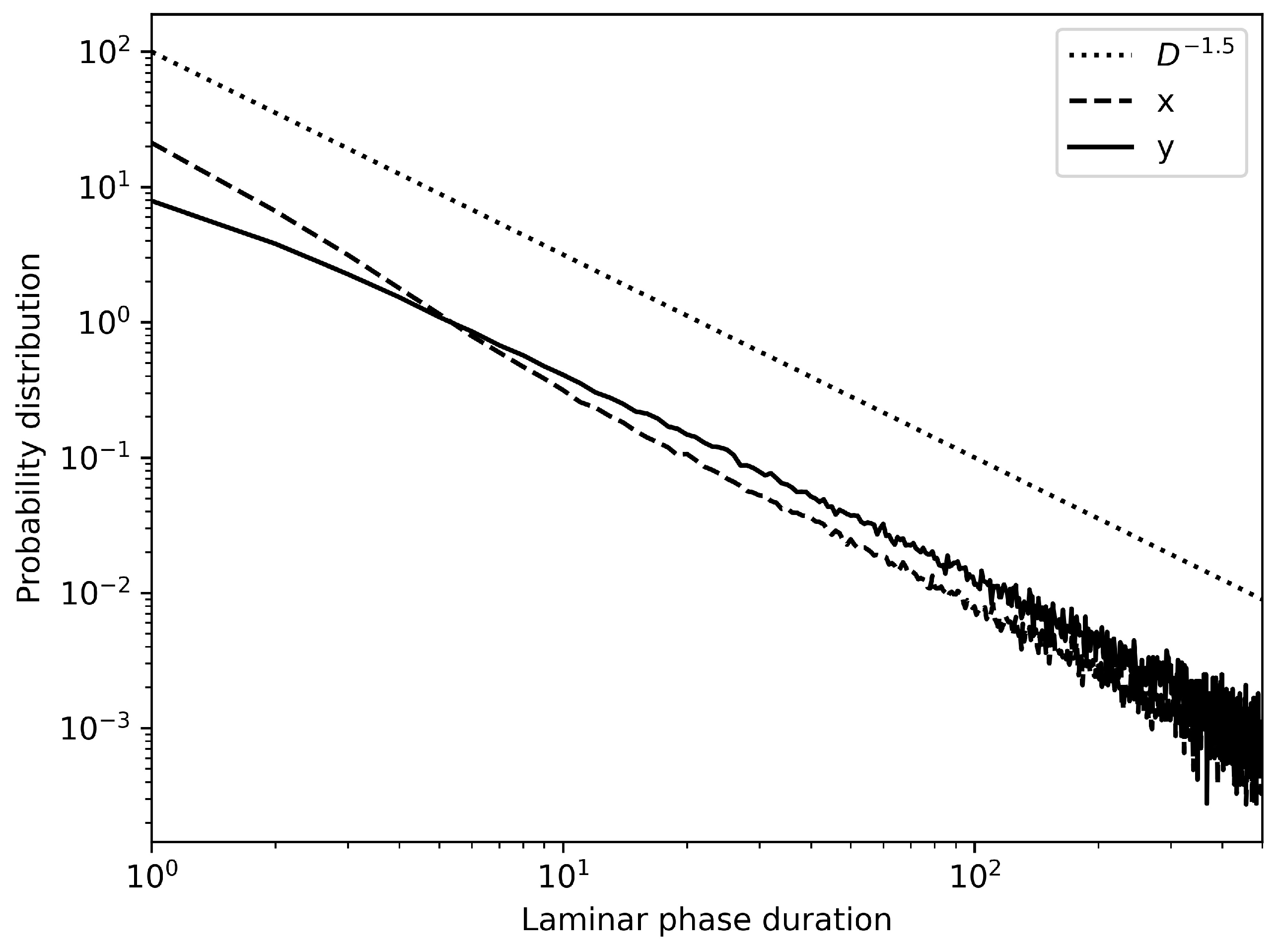
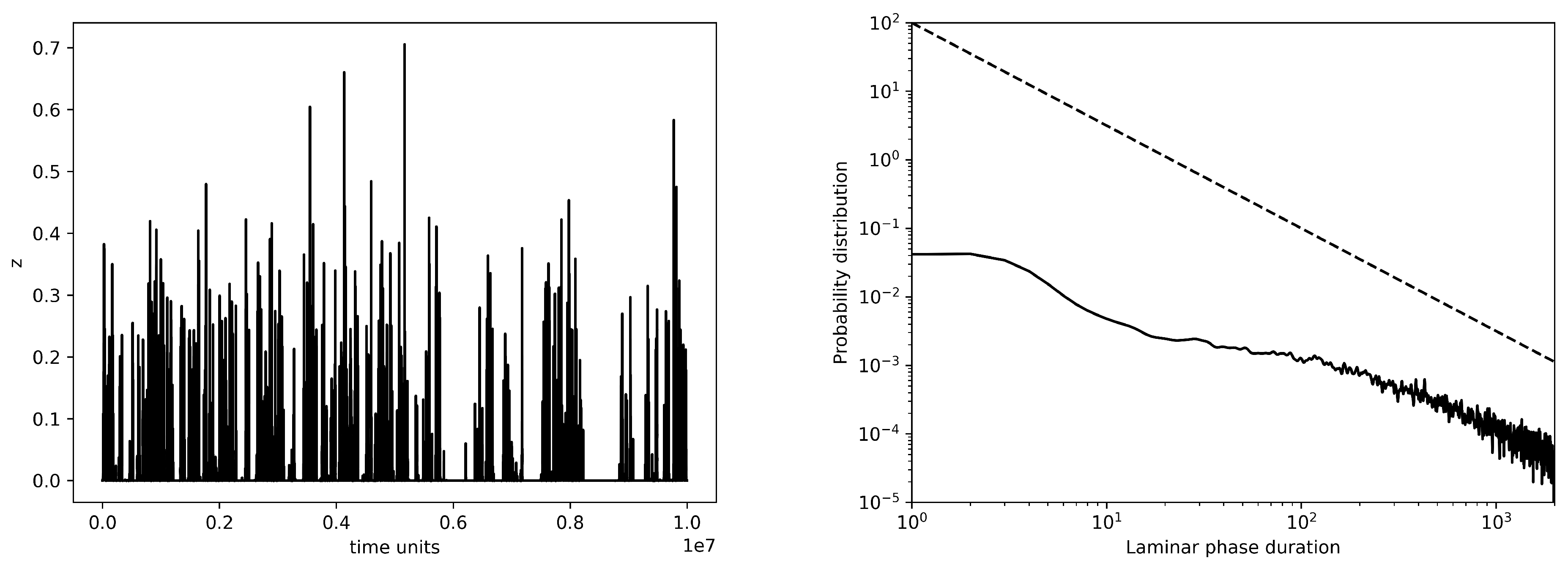
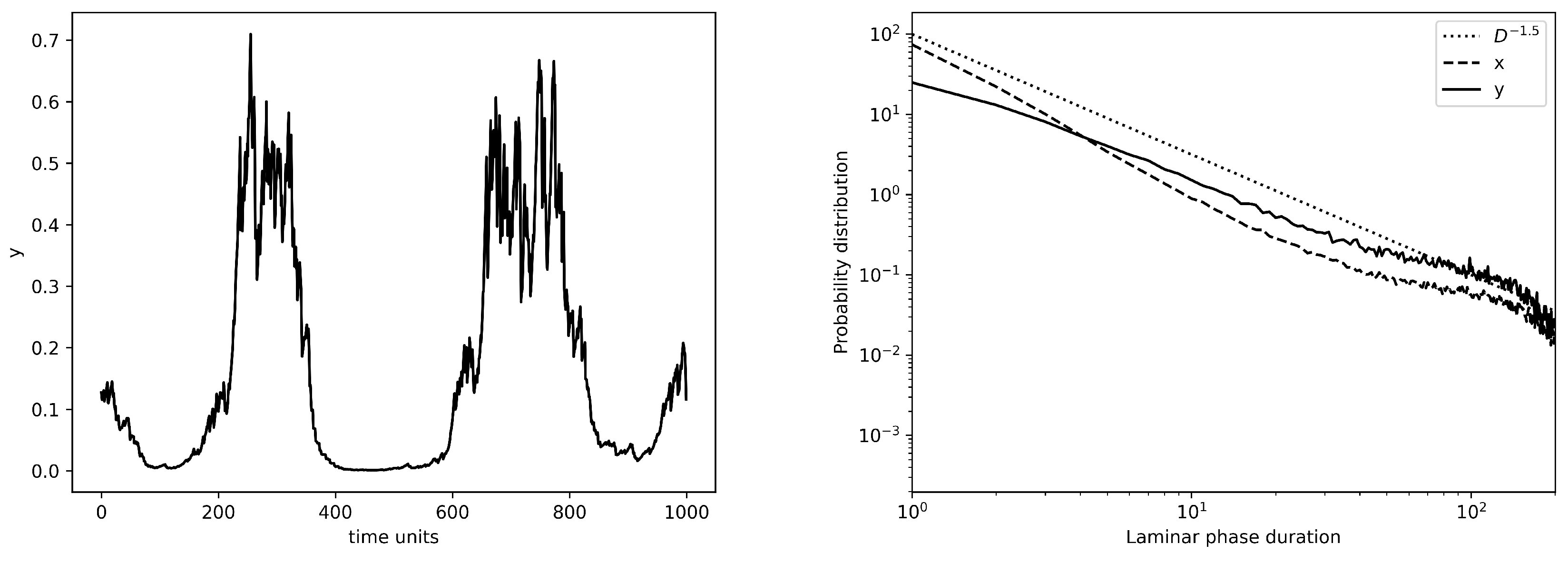
4.1. Intensity of Grazing
4.2. Carrying Capacity
5. Discussion and Conclusions
- For low maximum values of the carrying capacity, we observe only a stable fixed point for and z;
- Above a threshold of the maximum value of the carrying capacity, we observe on–off intermittency in x and y, while z goes extinct;
- For larger ranges of random variations, chaotic dynamics for x and y and intermittent behavior in z;
- For still larger fluctuations, we observe weak on–off intermittency in x and y and chaotic behavior of z.
- Would a deterministic, chaotic system representing the environment dynamics, in place of the stochastic process adopted here, allow for a more thoroughly mathematical analysis of the problem?
- How would spatial extension, with coupling across different location of the same species, affect our results?
- How would on–off intermittency manifest itself (if it does) in a food web rather than a simple food chain?
- Can we find intermittency when using real-world datasets or controlled laboratory experiments in microcosms?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Fixed Points in Hastings–Powell Model
- Computing the Jacobian and substituting these values leads to the eigenvalues 1, , . Note that the ecologically-relevant case has , so this fixed point is a saddle. If we numerically perturb the system along the x direction (e.g., adding a small perturbation to ), the system falls into the fixed point (see below) while, perturbing it along other directions, the null state is attractive.
- The three eigenvalues are , , . and are always negative, but the second eigenvalue depends on the values of the parameters . With the values used in the paper, the eigenvalue is positive and the system is therefore repulsive along one direction (it can be numerically checked perturbing ). If , then the fixed point becomes stable.
- From Equation (8), we obtain ; inserting it in Equation (6) leads to two (rather cumbersome) different solutions for and, consequently, two solutions for from Equation (7). With the parameter values adopted in this work, one solution for is negative and therefore not acceptable. The other solution is positive and, for the first case in Section 4.1 (with , as in Hastings–Powell’s paper), the fixed point is , , (numerically verified).
References
- Batchelor, G.; Townsend, A. The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1949, 199, 238–255. [Google Scholar]
- Platt, N.; Spiegel, E.A.; Tresser, C. On-off intermittency: A mechanism for bursting. Phys. Rev. Lett. 1993, 70, 279–282. [Google Scholar] [CrossRef] [PubMed]
- Hammer, P.; Platt, N.; Hammel, S.; Heagy, J.; Lee, B. Experimental Observation of On-Off Intermittency. Phys. Rev. Lett. 1994, 73, 1095–1098. [Google Scholar] [CrossRef] [PubMed]
- Bottiglieri, M.; Godano, C. On-off intermittency in earthquake occurrence. Phys. Rev. E 2007, 75, 026101. [Google Scholar] [CrossRef] [PubMed]
- Platt, N.; Spiegel, E.A.; Tresser, C. The intermittent solar cycle. Geophys. Astrophys. Fluid Dyn. 1993, 73, 147–161. [Google Scholar] [CrossRef]
- John, T.; Stannarius, R.; Behn, U. On-Off Intermittency in Stochastically Driven Electrohydrodynamic Convection in Nematics. Phys. Rev. Lett. 1999, 83, 749–752. [Google Scholar] [CrossRef] [Green Version]
- Heagy, J.; Platt, N.; Hammel, S.M. Characterization of on–off intermittency. Phys. Rev. E 1994, 49, 1140–1150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toniolo, C.; Provenzale, A.; Spiegel, E. Signature of on–off intermittency in measured signals. Phys. Rev. E 2002, 66, 066209. [Google Scholar] [CrossRef] [PubMed]
- Metta, S.; Provenzale, A.; Spiegel, E. On–off intermittency and coherent bursting in stochastically-driven coupled maps. Chaos Solitons Fractals 2010, 43, 8–14. [Google Scholar] [CrossRef]
- Moon, W. On-Off Intermittency in Locally Coupled Maps; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 2010. [Google Scholar]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd ed.; Westview Press: Boulder, CO, USA, 2014. [Google Scholar]
- Hastings, A.; Powell, T. Chaos in a Three–Species Food Chain. Ecology 1991, 72, 896–903. [Google Scholar] [CrossRef]
- Kot, M. Elements of Mathematical Ecology; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef] [Green Version]
- Ehrlich, P.; Hanski, I. On the Wings of Checkerspots: A Model System for Population Biology; Oxford University Press: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Schowalter, T. Insect Ecology—An Ecosystem Approach, 4th ed.; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar] [CrossRef]
- Murdoch, W.; Oaten, A. Predation and Population Stability. In Advances in Ecological Research; Academic Press: Cambridge, MA, USA, 1975; Volume 9, pp. 1–131. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vissio, G.; Provenzale, A. On-Off Intermittency in a Three-Species Food Chain. Mathematics 2021, 9, 1641. https://doi.org/10.3390/math9141641
Vissio G, Provenzale A. On-Off Intermittency in a Three-Species Food Chain. Mathematics. 2021; 9(14):1641. https://doi.org/10.3390/math9141641
Chicago/Turabian StyleVissio, Gabriele, and Antonello Provenzale. 2021. "On-Off Intermittency in a Three-Species Food Chain" Mathematics 9, no. 14: 1641. https://doi.org/10.3390/math9141641






