AutoNowP: An Approach Using Deep Autoencoders for Precipitation Nowcasting Based on Weather Radar Reflectivity Prediction

Abstract

Short-term quantitative precipitation forecast is a challenging topic in meteorology, as the number of severe meteorological phenomena is increasing in most regions of the world. Weather radar data is of utmost importance to meteorologists for issuing short-term weather forecast and warnings of severe weather phenomena. We are proposing $AutoNowP$, a binary classification model intended for precipitation nowcasting based on weather radar reflectivity prediction. Specifically, $AutoNowP$ uses two convolutional autoencoders, being trained on radar data collected on both stratiform and convective weather conditions for learning to predict whether the radar reflectivity values will be above or below a certain threshold. $AutoNowP$ is intended to be a proof of concept that autoencoders are useful in distinguishing between convective and stratiform precipitation. Real radar data provided by the Romanian National Meteorological Administration and the Norwegian Meteorological Institute is used for evaluating the effectiveness of $AutoNowP$. Results showed that $AutoNowP$ surpassed other binary classifiers used in the supervised learning literature in terms of probability of detection and negative predictive value, highlighting its predictive performance.

1. Introduction

Forecast of severe weather phenomena, including the quantitative precipitation forecast (QPF), represents a challenging topic in meteorology. Due to the increase in the number of heavy rainfall events in most regions of the world, population safety could be affected and significant damage may occur. The short-term weather forecasting is known as nowcasting and is of particular interest as it has an important role in risks management and crisis control. The problem of weather nowcasting is a complex and difficult one, due to its high dependence on numerous environmental conditions. Precipitation nowcasting represents a challenging and actual research topic, referring to producing predictions of rainfall intensities over a certain region in the near future, and playing an important role in daily life [1].

At global scale, flood threat is increasing because of climate change impact of heavy precipitation, as for instance the total urban area being exposed to flood has dramatically increased in Europe over the past century. Also, various socioeconomic sectors are impacted by climate change induced hazards, such as extreme rainfall, which amplify both the intensity and probability of floods [2]. Research on the exposure of flood hazard, using climate models simulations, showed that the climate change presents the potential to actively change the human, assets, and urban areas exposure to flood hazard, but nevertheless considerable uncertainty in the magnitude of the climate change impact in different regions around the globe exists [3].

Nowadays, integrating crowdsourced observations into research studies can contribute to reducing the risk and the costs related to extreme events. Citizens around the world have, currently, at their disposal a great number of sources of information and amazing possibilities to report and to study meteorological phenomena. Hence, these volunteers who collect, report and/or process the data they observe are citizen scientists. They are active not only in the field of meteorology, but also in sciences as astronomy, archeology, natural history and others [4]. Their contribution to science can have a practical effect, especially by increasing the awareness and perception on climate change related risks, thus helping in mitigating the effects.

Although significant progress has been made recently on nowcasting systems in general, and precipitation nowcasting in particular, the challenges remain as, for instance, severe convective storms are localized, occurring on a small spatial area (i.e., mesoscale) and having an overall short lifecycle. Due to its high spatiotemporal resolution, radar data is used both in the so-called expert nowcasting systems and in the less complex forms that involve processing the radar data solely [5,6]. These systems blend radar data and other observations with numerical weather prediction (NWP) models to generate forecasts up to 6 h [7]. Although NWP significantly improves the precipitation nowcasting, there are still issues to be resolved, like the predictability of precipitation systems, the improvement of rapid update NWP, and the need for improvement of mesoscale observation networks [8].

Some of the most used radar products in weather nowcasting are reflectivity (R) and Doppler radial velocity (V). For instance, operational meteorologists are mainly using the values of reflectivity and radial velocity to monitor the spatiotemporal evolution of precipitating clouds, while operational radar algorithms use the reflectivity for rainfall estimation and storm tracking and classification: R values above a certain threshold (e.g., 35 dBZ [5,9]) indicate possible convective storms occurrence associated with heavy rainfall. Estimating the values of the radar products based on their historical values is important for QPF. NWP models [10] represent the main techniques for QPF, but there are still errors in rainfall forecasting due to difficulties in modelling cloud dynamics and microphysics [11].

Deep learning methods [12,13,14] are believed to have the potential to overcome the limitations of NWP methods through modeling patterns in large amounts of historical meteorological data. Deep learning methods offer data-driven solutions for the nowcasting problem, by learning dependencies between radar measurements at consecutive time steps [15]. A central characteristic of deep neural networks is represented by their ability to learn abstract representations of the input data through stacking multiple layers and thus forming deep architectures. Autoencoders (AEs) are a type of neural network that can be trained to learn low dimensional representations that capture the relevant characteristics of the input data [16]. AEs are trained to learn data representations by reconstructing their inputs. They are built of two components, an encoder that maps the input to a latent representation and a decoder that uses this representation to reconstruct the input. Typically, the dimensionality of the latent representation is chosen to be smaller than the input space dimensionality, thus obtaining a so-called undercomplete autoencoder. Autoencoders can be trained using gradient descent methods to minimize the error between the input data and the predicted reconstruction [16]. Convolutional autoencoders (ConvAEs) are able to capture spatial patterns in the input data by using convolutions as their building blocks. Convolutional encoder-decoder architectures have been extensively used in various computer vision tasks and they are the typical choice for modeling the spatial characteristics of meteorological measurements gathered along geographical locations [15,17,18].

The contribution of the paper is threefold. First, we aim at introducing a supervised classifier $AutoNowP$ that uses two convolutional autoencoders for distinguishing between convective and stratiform rainfall based on radar reflectivity prediction. $AutoNowP$ is based on training two ConvAEs trained on radar data collected on both stratiform and convective weather conditions. After the training step, $AutoNowP$ will learn to predict whether the radar reflectivity values will be higher than a certain threshold, and thus indicating if a convective storm is likely to happen. $AutoNowP$ is intended to be a proof of concept that AEs applied on radar data are useful in distinguishing between convective and stratiform rainfall. Secondly, the effectiveness of $AutoNowP$ is empirically proven on two case studies consisting of real radar data collected from the Romanian National Meteorological Administration (NMA) and the Norwegian Meteorological Institute (MET). The obtained results are compared to the results of recent similar approaches in the field of precipitation nowcasting. As an additional goal we aim at analyzing the relevance of the obtained results from a meteorological perspective, as a proof of concept that autoencoders are able to capture relevant meteorological knowledge. To the best of our knowledge, an approach similar to $AutoNowP$ has not been proposed in the nowcasting literature so far.

To summarize, the research conducted in the paper is oriented toward answering the following research questions:

RQ1 

How to use an ensemble of ConvAEs to supervisedly discriminate between severe and normal rainfall conditions, considering the encoded relationships between radar products values corresponding to both normal and severe weather events?

RQ2 

What is the performance of $AutoNowP$ introduced for answering RQ1 on real radar data collected from Romania and Norway and how does it compare to similar related work?

The rest of the paper is organized as follows. A literature review on recent deep learning methods for precipitation nowcasting is presented in Section 2. Section 3 introduces our binary classification model $AutoNowP$ for predicting if the radar reflectivity values are above or below a specific threshold. The performed experiments and the obtained results are described in Section 4, while a discussion on the results and a comparison to related approaches is provided in Section 5. Section 6 presents the conclusions of our research and highlights directions for future work.

2. Literature Review on Machine-Learning-Based Precipitation Nowcasting

A lot of work has been carried out lately in the field of machine-learning-based precipitation nowcasting. We are reviewing, in the following, several recent approaches in the field.

Shi et al. [19] have approached precipitation nowcasting by introducing an extension of a long short-term memory (LSTM) network, named ConvLSTM, suitable for handling spatiotemporal data by preserving due to the convolutional structure of the spatiotemporal features. Their architecture is composed of two networks, a ConvLSTM encoder and a ConvLSTM decoder. As precipitation nowcasting performance indicators, a Rainfall Mean Squared Error (Rainfall-MSE) of 1.420, a Critical Success Index (CSI) of 0.577, a False Alarm Rate (FAR) of 0.195 and a Probability of Detection (POD) of 0.660 have been obtained.

Heye et al. [20] investigated a precipitation nowcasting approach based on a 3D ConvLSTM architecture. In their experiments, a vanilla sequence-to-sequence model achieved better performance than a model using attention layers. Overall, the CSI varied between 0.40 and 0.43, the FAR ranged from 0.28 to 0.31, and the POD fluctuated between 0.46 and 0.51.

A method for precipitation nowcasting, combining the advantages of convolutional gated recurrent networks (ConvGRU) and adversarial training was introduced by Tian et al. [21]. The method aimed at improving the sharpness of the predicted precipitation maps by means of adversarial training. The system is composed of a generator network, represented by the ConvGRU, which learns to generate realistically looking precipitation maps and a discriminator represented by a convolutional neural network that is trained to distinguish between predicted ground truth maps. Their method achieved better performance in terms of probability of detection than an optical flow algorithm and the original ConvGRU. Han et al. [22] used 3D convolutions to build a neural network for convective storm nowcasting. The task was formulated as a binary classification problem and their multisource approach achieved a CSI of 0.44, FAR of 0.45, and POD of 0.69 for 30 min forecasts, outperforming a Support-Vector Machine using hand-crafted features.

The MetNet model [15] has been introduced by Sønderby et al. using both radar and satellite data for precipitation forecasting with a lead time of up to 8 h. The model incorporates three components—a feature extractor formed of a succession of downsampling convolutional layers, a ConvLSTM component used for modeling dependencies on the past time steps and an attention module composed of several axial self-attention blocks that aim to capture relationships among geographic locations situated far away in the map. By including the forecasted time in the data given as input and thus conditioning the entire model on it, predictions for multiple time steps can be obtained in parallel. The loss function was computed only for points on good quality maps from the data set in order to account for possible noisy or incorrect labels. MetNet outperformed the persistence model, an optical flow-based algorithm, as well as the High-Resolution Rapid Refresh (HRRR) for forecasts up to 8 h in the future. By performing ablation studies, they pointed out that using a large spatial context leads to better performance than using a smaller context on long-term predictions. However, reducing the temporal context up to 30 min did not decrease the model’s performance. Moreover, the authors pointed out that radar data plays a more important role in the overall model performance for short-term predictions than for long-term ones. These results can be explained by the fact that long-term predictions need to take into account a larger spatial context that cannot be typically captured by radar, thus highlighting the importance of incorporating satellite data for this type of predictions.

The model proposed by Franch et al. [23] aimed to improve the performance of nowcasting systems on extreme events prediction by training an ensemble of Trajectory Gated Recurrent Units (TrajGRUs), each optimized by over-weighting the objective for a specific precipitation threshold. In addition to the ensemble components, a model stacking strategy that consists of training an additional model using the outputs of the ensemble components is employed. Moreover, their approach enhances the radar data with orographic features. The proposed model achieved overall better performance than several TrajGRU baselines and two models obtained by using only part of the components—an ensemble model without orographic features, and a single model trained with orographic features.

Chen et al. [1] improved upon the training of ConvLSTMs by introducing a multisigmoid loss function tailored for the precipitation nowcasting task and incorporating residual connections in the recurrent architecture. Additionally, the group normalization mechanism proved to be beneficial for the model’s performance. The model was trained on radar images and predictions were evaluated for lead times of up to one hour.

The Small Attention-Unet (SmaAt-Unet) [17] precipitation nowcasting model introduced by Trebing et al. is a modified U-Net architecture, in which traditional convolutions have been replaced by depthwise separable convolutions and convolutional block attention modules have been added to the encoder. The proposed approach achieved an overall comparable performance to the original U-Net, while using a quarter of the number of parameters. The nowcasting is done for up to 30 min in the future using 1 h of past radar data, sampled at a frequency of 5 min. Similarly to other U-Net-based methods, different time stamps are concatenated channelwise and given as input to the network. Patterns across the channel dimension are captured by the attention modules. As precipitation nowcasting performance indicators, a CSI of 0.647, a FAR of 0.270, and an F-$score$ of 0.768 have been obtained.

An approach for weather forecasting using ConvLSTMs and attention was introduced in [18]. Their proposed method was tested on the ECMWF (European Centre for Medium-Range Weather Forecasts) Reanalysis v5 (ERA5) data set, which contains several weather measurements such as temperature, geopotential, humidity and vertical velocity at a time resolution of one hour. The approach was shown to outperform other methods such as Simple Moving Average, U-Net, and ConvLSTM, achieving MSE values between 1.32 and 2.47.

Jeong et al. [24] alternatively proposed a weighted broadcasting strategy for ConvLSTMs, which is based on the idea of overweighting the last time stamp in the input sequence. Their approach reached generally better performance than the baseline ConvLSTM architecture, with CSI values ranging between 0.0108 and 0.5031, FAR between 0.2960 and 0.5653, POD values in the range 0.0110–0.6403 and Heidke skill score (HSS) between 0.01 and 0.3.

A deep learning approach for precipitation estimation from reflectivity values was introduced by Yo et al. [25]. The proposed approach was compared to an operational precipitation estimation method used by the Central Weather Bureau in Taiwan and was shown to slightly outperform it, especially in predicting extreme meteorological events. However, the improvement was not statistically significant, the proposed method obtaining an average POD of 0.8 and FAR of 0.0134.

3. Methodology

With the goal of answering research question RQ1, this section introduces our binary classification model proposal, $AutoNowP$, that consists of two ConvAEs, trained on radar data collected from rainfall conditions with different classes of severity, for recognizing severe phenomena. More specifically, $AutoNowP$ is trained for learning to predict whether the radar reflectivity values will be above or below a specific threshold. The ConvAE models are used due to their ability to preserve the structure of the input data and to detect underlying structural relationships within the data.

$AutoNowP$ is aimed to empirically demonstrate that autoencoders are able to learn, by self-supervision, features that are relevant for distinguishing structural relationships in radar data collected in both stratiform and convective weather conditions. The model is designed to classify if a radar product $Rp$ is below or above a threshold $\tau$. In the experiments we will use two radar products, the reflectivity at the first elevation level (R01) and the composite reflectivity, and different values for the threshold $\tau$ (e.g., 5, 20, 35 dBZ). $AutoNowP$ consists of three stages depicted in Figure 1: data representation and preprocessing, training, and testing (evaluation). These stages will be further detailed.

3.1. Data Representation and Preprocessing

The raw radar data used in our experiments is converted into two-dimensional arrays, with a grid cell representing a geographical location. A cell in the matrix stores the value of a specific radar product at a given time stamp. A sequence of such matrices is available for a given day, each matrix storing the values for a specific radar product p at a time moment t. We assume that $np$ radar products are available and thus, the radar data at a time moment t may be visualized as a data grid with $np$ channels.

In our previous works [11,26] we highlighted that similar values for the radar products in a specific location l at a time t are encoded in similar neighborhoods of the location l at time t−1. For a specific location l at time t, a $d^2$–dimensional vector containing the values of a radar product $Rp$ from the sub-grid of diameter d centered on l (at time t−1) will be assigned. The $d^2$—dimensional instance will be labeled with the of $Rp$ for the location l at time t [11]. A sample data grid containing the values for the product R01 at time t is shown in Figure 2a, while Figure 2b depicts the data grid at time t−1.

For the example from Figure 2, the instance corresponding to the location (3,3) at time t is the vector (15,10,20,10,15, 20,5,10,10) and is labeled with 10 (the value of R01 at location (3,3) and time t).

Consequently, considering a specific diameter d for the neighborhood, a data set R is built from the instances ($d^2$—dimensional points) associated to each location from the data grid and all available time moments [11]. The radar data set R will be divided in two classes: the positive class (denoted as “+”) composed by the instances having the label (i.e., values for the radar product $Rp$ at a certain time t) higher than a threshold $\tau$, while the negative class (denoted as “−”) contains the instances having the label lower or equal to the threshold $\tau$. The data set representing the positive class is denoted by $R_{+}$, while $R_{-}$ denotes the set of instances belonging to the negative class. We note that the dimensionality of $R_{-}$ is significantly larger than the cardinality of $R_{+}$, as the number of severe weather events is often small.

Both data sets are then normalized so that the value $Rp$ of a radar product is transformed to be in the $[0, 1]$ range. For normalization purposes, we use the classic min/max normalization formula:

$$R{p}^{\prime }(l,t)=\frac{Rp(l,t)-R{p}_{min}}{R{p}_{max}-R{p}_{min}},$$

where:

• $Rp(l,t)$ is the value of $Rp$ at time t and location l;
• $R{p}^{\prime }(l,t)$ is the normalized value of $Rp$ at time t and location l;
• $R{p}_{min}$ is the minimum value in the domain of $Rp$;
• $R{p}_{max}$ is the maximum value in the domain of $Rp$.

It should be noted that we are using the minimum and maximum values from a radar product’s domain to ensure that both $R_{+}$ and $R_{-}$ data sets are normalized in the same way (i.e., the same value in different data sets is mapped to the same normalized value), as the positive data set may have different minimum and maximums than the negative data set. $AutoNowP$ is trained and tested on the normalized data.

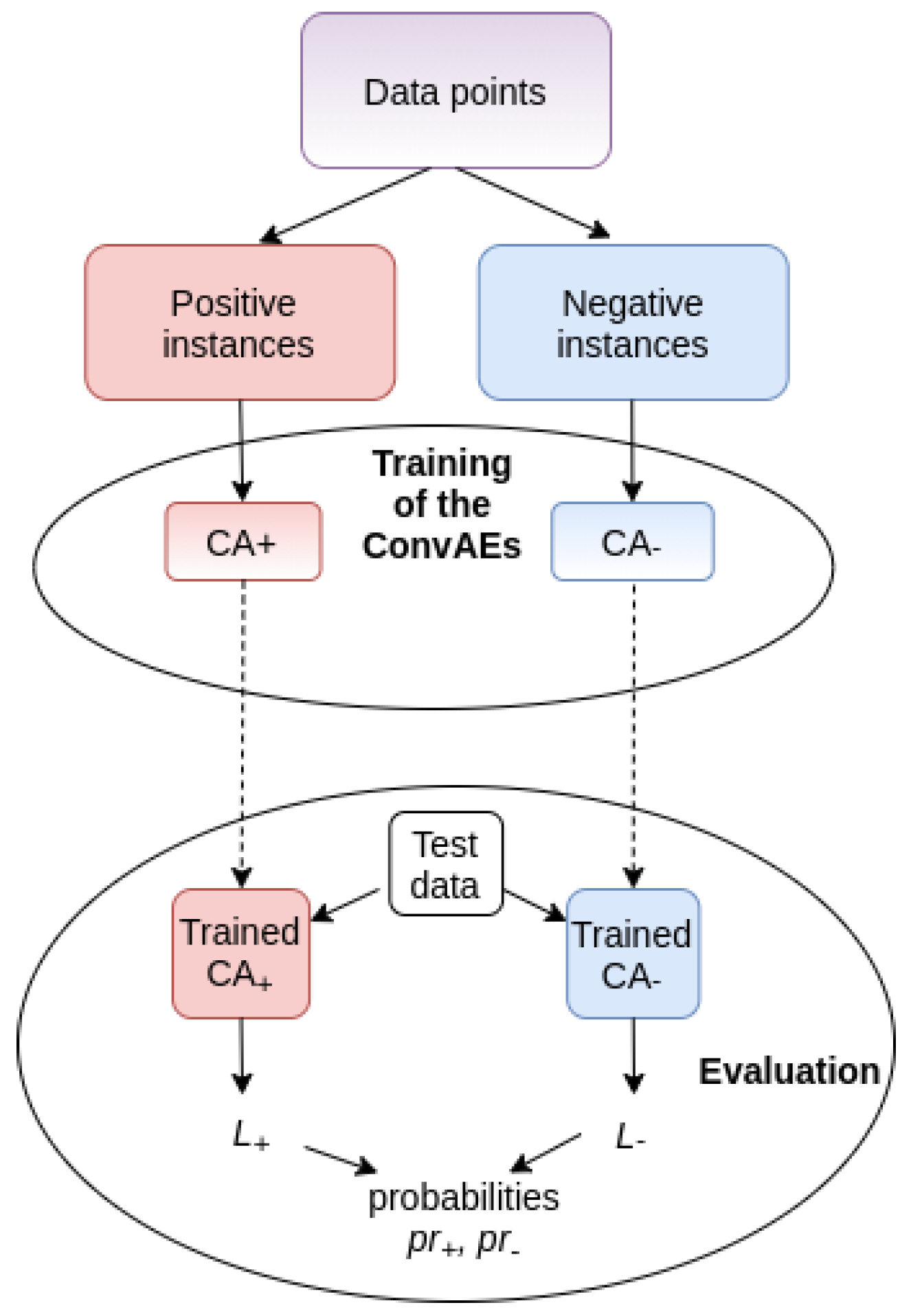
3.2. $AutoNowP$ Classification Model

Considering the notations from Section 3.1, the classification problem is formalized as the approximation of two target functions (i.e., one target function for each class) $t_c:{\mathcal{R}}_{+}\cup {\mathcal{R}}_{-}\to [0, 1]$ ($\forall c\in \{+,-\}$) that express the probability of instances from ${\mathcal{R}}_{+}\cup {\mathcal{R}}_{-}$ to belong to the “+” or “−” classes. Thus, the learning goal of $AutoNowP$ will be to approximate the functions $t_{+}$ and $t_{-}$. $AutoNowP$ consists of two ConvAEs, one for the “+” class ($C{A}_{+}$) and one for the “−” class ($C{A}_{-}$). For training an autoencoder $C{A}_c$ ($c\in \{+,-\}$ $47\%$ from the data set $R_c$ (i.e., $70\%$ from the data not used for testing) will be used for training, $20\%$ for the model validation and the rest of $33\%$ from $R_c$ will be further used for testing, using a 3-fold cross-validation testing methodology.

3.2.1. Training

As previously stated, $AutoNowP$ classifier will be trained to predict, based on the radar products values from the neighborhood of a geographical location at time $t-1$, whether the value of a radar product $Rp$ at time t will be higher than a threshold $\tau$. For instance, if $Rp$ is chosen as R01 and $\tau$ as 35 dBZ, then $AutoNowP$ will be trained to predict if, in a certain geographical location or area, a convective storm is likely to occur (i.e., if the value of R01 will be higher than 35 dBZ in that geographical location).

$AutoNowP$ is trained to recognize both normal and severe weather events, and thus it will learn to predict if a certain instance is likely to indicate stormy or normal weather. Each of the two autoencoders $C{A}_{+}$ and $C{A}_{-}$ will be self-supervisedly trained on the data set of positive and negative instances, respectively (${\mathcal{R}}_{+}$ and ${\mathcal{R}}_{-}$).

The prediction is based on estimating the probabilities (denoted by $p_{+}$ and $p_{-}$) that a high-dimensional instance corresponding to a particular geographic location (as described in Section 3.1) belongs to the positive and negative classes. The method for computing these probabilities will be detailed in Section 3.2.2.

Autoencoders Architecture

The current study uses convolutional undercomplete AEs to learn meaningful lower-dimensional representations for radar data. The autoencoders were implemented in Python, using the Keras framework with Tensorflow backend. Both autoencoders ($C{A}_{+}$ and $C{A}_{-}$) have the same architecture. The input data of the AEs is the 2D grid of the neighborhood of diameter d for one location (as exemplified in Figure 2b)—i.e., the 2D grid representing the values of an instance from ${\mathcal{R}}_{+}\cup {\mathcal{R}}_{-}$. As we have to choose a different diameter d for our experiments on different data sets (see Section 4.1), we made the architecture so that it minimally changes with d: while the number, type and hyper-parameters of each layer of the network remain the same, the number of neurons on each layer changes, proportionally, depending on d.

Even if the architecture of the autoencoder may be adapted to the diameter d of the neighborhood (i.e., the dimensionality $d^2$ of the input data), the value of d may influence the performance of $AutoNowP$ model. Intuitively, high values for d will make the AEs to harder distinguish between the positive and negative instances. This may happen since, hypothetically speaking, it would be possible that two neighboring points at time t (one positive and one negative) have a large number of identical neighbors at time $t-1$ (i.e., the data instances representing the two locations are similar) and thus the AEs are unable to distinguish between them. On the other hand, a small number of neighbors for a data point (i.e, small values for d) is not enough for $AutoNowP$ classifier to discriminate between the input instances. For determining the most appropriate value for the diameter d, a grid search was performed for selecting the value d that provides the best performance for $AutoNowP$.

In the following, we will present the architecture of the autoencoders and the hyper-parameters used, without mentioning the number of neurons, so that the following description is valid for the $AutoNowP$ model in general, regardless of the specific experiment. Figure 3 illustrates the architecture of the autoencoder (as mentioned above, both autoencoders, $C{A}_{-}$ and $C{A}_{+}$, have the same architecture). This is a Convolutional Autoencoder, thus the main layers are the Conv2D—2-dimensional convolution layers—represented in yellow in the figure. These layers reduce the data grid input in three steps, leading to an encoding layer (the blue layer in the figure). From the encoding, the autoencoder needs to recreate the input, thus the inverse of the Conv2D is needed: Conv2DTranspose (the orange layers). Using the Conv2DTranspose layers we apply the reverse transformation so that it recreates the data grid as it was before the convolutions. When using convolutions, we need to reduce the size of the image, and this works best if the size of the image is even. However, our input layer has always an odd size: since the input represents the neighborhood of one point, having that point in the center, for a given radius r, the size will be $(2r+1, 2r+1)$—i.e., we take r neighbors from all sides of the center; for example, r neighbors on the right with r neighbors on the left plus the center itself results in an $2r+1$ length. Since the input is always odd in size, we need to adjust it so that we can perform the convolutions. For this, we use a ZeroPadding2D layer: after the Input layer (first gray layer), we pad the margins of the data grid with zeros until it reaches the desired size, using the ZeroPadding2D layer (the red layer). Afterwards, the convolutions can occur. The transpose convolutions will recreate the data grid as it was before the convolutions—that is, after padding—so it is not the same size as the input. Since it is an autoencoder, we want to match the output to the input, thus, we need to adjust the transpose convolutions output so that the final size of the autoencoder output fits the size of its input. To readjust the size, we use a Cropping2D layer, which will also be the output layer of the autoencoder (the second gray layer represented in the figure).

As with other neural networks, while the architecture is the principal element of the network, there are other metaparameters that need to be tuned that change the network’s behavior. One of these is the number of neurons on each hidden layer, but as we mentioned above, this number may differ among the experiments if the input size changes; however, while the absolute number changes, the proportion of neurons on the hidden layers are preserved. Then, we have the activation used for the layers: for all convolutional layers, transpose convolutional layers and the dense layers, except for the last transpose convolutional layer, we use the SELU activation function (Scaled Exponential Linear Unit [27]). For the last transpose convolutional layer, we used the sigmoid activation function, so that the output of the autoencoder is between 0 and 1, as is the input. For all convolutional layers and transpose convolutional layers, we used a kernel size of 4 and 2 strides.

The training configuration was the following: we used a batch size of 1024 and we trained each autoencoder for 500 epochs in the case of the NMA data set and for 200 epochs for the MET data set; the Adam optimizer [28] was used with learning rates of 0.01 and 0.001 respectively for the NMA and MET data sets and $epsilon$ of 0.00001.

Loss Functions

As explained in Section 3.1, the high-dimensional input instance x may be visualized as a data grid, i.e., the neighborhood around the location of the value we want to predict. The autoencoders learn to encode and decode each instance, the output of the autoencoder being the reconstruction of the instance. The loss functions represent the difference between the original instances and their reconstruction; lower values for the loss indicate better reconstructions (i.e., closer to the input), with a loss equal to 0 meaning no difference. The loss is based on a modified mean squared error (MSE), to assign a priority to the values greater than the threshold $\tau$ relative to the other values. More specifically, we wanted to be able to make the autoencoders prioritize values in the neighborhood that are either greater or lower or equal to the given threshold $\tau$. We also wanted to be able to change this prioritization between $C{A}_{-}$ and $C{A}_{+}$ (i.e., $C{A}_{-}$ is trained to prioritize negative points, while $C{A}_{+}$ is trained by over-weighting positive points in the neighborhood) and between experiments, so we introduced a parameter, $\alpha$, that controls this prioritization. We split the computation of MSE in two parts: computing the MSE for values greater than $\tau$ (Formula (1)) and computing the MSE for values lesser or equal to $\tau$ (Formula (2)). The final loss value (Formula (3) is expressed as a linear combination between the two separately computed MSEs; we use the $\alpha$ parameter to decide how to prioritize the values greater than $\tau$ relative to the values less or equal to $\tau$. The exact way to compute the loss function $L(x,x^{\prime })$ for a given instance $x\in {\mathcal{R}}_{+}\cup {\mathcal{R}}_{-}$ is given by Formulae (1)–(3):

$$MS{E}_{greater}(x,x^{\prime })=\frac{1}{d^2}{\displaystyle \sum _{\begin{array}{c}1\le i\le d^2\\ x_i>\tau \end{array}}}{(x_i-x_i^{\prime })}^2$$

(1)

$$MS{E}_{lesser}(x,x^{\prime })=\frac{1}{d^2}{\displaystyle \sum _{\begin{array}{c}1\le i\le d^2\\ x_i\le \tau \end{array}}}{(x_i-x_i^{\prime })}^2$$

(2)

$$L(x,x^{\prime })=\alpha ·MS{E}_{greater}(x,x^{\prime })+(1-\alpha )·MS{E}_{lesser}(x,x^{\prime })$$

(3)

where:

• d is the diameter of the neighborhood used for characterizing the input instances x (see Section 4.1);
• $x\in {\mathcal{R}}_{+}\cup {\mathcal{R}}_{-}$ is the $d^2$-dimensional instance for which we compute the loss;
• $x^{\prime }$ is the autoencoder output for instance x (the reconstruction of x);
• $\tau$ is the chosen threshold that differentiates between positive and negative class;
• $\alpha$ is the parameter that we introduced for the loss;
• $x_i$ and $x_i^{\prime }$ denote the ith component from x and $x^{\prime }$ respectively.

3.2.2. Classification Using $AutoNowP$

After $AutoNowP$ has been trained as described in Section 3.2.1, when an unseen query instance q has to be classified, the probabilities $p_{+}\left(q\right)$ (that q belongs to the positive class) and $p_{-}\left(q\right)$ (that q belongs to the negative class) are computed. As shown above, a query instance q is a high-dimensional vector (Section 3.1) consisting of radar products values from the neighborhood of a specific geographical location l at time t. $AutoNowP$ will classify q as “+” (i.e., the value of the radar product $Rp$ at time t+1 is likely to be higher than the threshold $\tau$) iff $p_{+}\left(q\right)\ge p_{-}\left(q\right)$, i.e., $p_{+}\left(q\right)\ge 0.5$.

The underlying idea behind deciding that a query instance q is likely to belong to the “+” class (i.e., $p_{+}\left(q\right)\ge p_{-}\left(q\right)$) is the following. We started from the assumption that an AE is able to encode the structure of the class of instances it was trained on well and with the intention to further reconstruct data similar to the training data. In addition, the AE will be unable to reconstruct, through its learned latent space representation, the instances that are dissimilar to the training data (i.e., likely to belong to another class than the class on which the AE was trained on). Thus, if for a certain instance q the MSE between q and the reconstruction of q by $C{A}_{+}$ is less than the MSE between q and the reconstruction of q by $C{A}_{-}$, then it is likely that the query instance belongs to the “+” class, as it is more similar to the information encoded for the positive class.

Definition 1.

Let us denote by $MS{E}_c(\widehat{q},q)$ the MSE between q and the reconstruction ($\widehat{q}$) of q by the autoencoder $C{A}_c$ ($c\in \{+,-\}$) and by τ the threshold considered. The probabilities $p_{+}\left(q\right)$ and $p_{-}\left(q\right)$ are computed as given in Formulae (4) and (5).

$$p_{+}\left(q\right)=0.5+\frac{MS{E}_{-}(\widehat{q},q)-MS{E}_{+}(\widehat{q},q)}{2·(MS{E}_{-}(\widehat{q},q)+MS{E}_{+}(\widehat{q},q))}$$

(4)

$$p_{-}\left(q\right)=1-p_{+}\left(q\right).$$

(5)

From Formula (4) we observe that $0\le p_{+}\left(q\right)\le 1$ and that if $MS{E}_{+}(\widehat{q},q)\le MS{E}_{-}(\widehat{q},q)$, then $p{r}_{+}\left(q\right)\ge 0.5$, meaning that q is classified by $AutoNowP$ as being positive. Much more, we note that:

• if $MS{E}_{+}(\widehat{q},q)=0$ (and consequently $MS{E}_{-}(\widehat{q},q)\ne 0$) it follows that $p_{+}\left(q\right)=1$;
• $p_{+}\left(q\right)$ increases as $MS{E}_{+}(\widehat{q},q)$ decreases;
• if $MS{E}_{+}(\widehat{q},q)>MS{E}_{-}(\widehat{q},q)$, then $p{r}_{+}\left(q\right)<0.5$, meaning that q is classified by $AutoNowP$ as being negative.

After the probabilities $p_{+}\left(q\right)$ and $p_{-}\left(q\right)$ were computed from the training data, the classification $c\left(q\right)$ of q is computed as shown in Formula (6).

$$c\left(q\right)=\left\{\begin{array}{cc}+\hfill & if p{r}_{+}\left(q\right)\ge 0.5\hfill \\ -\hfill & otherwise.\hfill \end{array}\right.$$

(6)

3.3. Testing

After $AutoNowP$ was trained as described in Section 3.2.1, it is evaluated on $33\%$ of the instances from each data set $R_{+}$ and $R_{-}$ that were unseen during the training stage. The classification of a query instance q is made as described in Section 3.2.2.

For evaluating the performance of $AutoNowP$ on a testing data set, the confusion matrix is computed [29], composed by the number of true positives—TP, true negatives—TN, false positives—FP, and false negatives—FN. Then, based on the values from the confusion matrix, evaluation measures used for assessing the performance of supervised classifiers and weather predictors are employed:

1.

Critical success index ($CSI$) computed as $CSI=\frac{TP}{TP+FN+FP}$ is used for convective storms nowcasting based on radar data [30].

2.

True skill statistic ($TSS$), $TSS=\frac{TP·TN-FP·FN}{(TP+FN)·(FP+TN)}$.

3.

Probability of detection ($POD$), also known as sensitivity or recall, is the true positive rate (TPRate), $POD=\frac{TP}{TP+FN}$.

4.

Precision for the positive class, also known as positive predictive value ($PPV$), $PV=\frac{TP}{TP+FP}$.

5.

Precision for the negative class, also known as negative predictive value ($NPV$), $NPV=\frac{TN}{TN+FN}$.

6.

Specificity ($Spec$), also known as true negative rate (TNRate), $Spec=\frac{TN}{TN+FP}$.

7.

Area Under the ROC Curve ($AUC$). The $AUC$ measure is recommended in case of imbalanced data and is computed as the average between the true positive rate and the true negative rate, $AUC=\frac{Spec+POD}{2}$.

8.

Area Under the Precision–Recall Curve ($AUPRC$), computed as the average between the precision and recall values, $AUPRC=\frac{Precision+Recall}{2}$.

All these measures take values in the [0, 1] range, with higher values indicating better predictors, excepting $FAR$ that should be minimized for a better performance.

A three-fold cross-validation testing methodology is then applied. The value for each of the performance measures previously described are averaged over the three runs. The mean values are computed together with their $95\%$ confidence intervals (CI) [31].

4. Data and Experiments

In this section, we answer research question RQ2 by describing the experiments conducted for evaluating the performance of $AutoNowP$ and analyzing the obtained experimental results.

4.1. Data Sets

For assessing the performance of $AutoNowP$, experiments were conducted on real radar data provided by the Romanian National Meteorological Administration (NMA) and the Norwegian Meteorological Institute (MET).

4.1.1. NMA Radar Data Set

The NMA radar data set was collected over central Romania by a single polarization S-band Weather Surveillance Radar—98 Doppler (WSR-98D) located near the village of Bobohalma. The radar completes a full volume scan every 6 min, gathering data about the location, intensity and movement direction, and speed of atmospheric cloud systems. Volume scan data is collected by employing a scan strategy consisting in 9 elevation angles, the raw data being afterwards processed to compute a large variety of radar products. For $AutoNowP$ experiments, we used the base Reflectivity product (R) sampled at the lowest elevation angle (R01), being expressed in decibels relative to the reflectivity factor Z (dBZ). Using the so-called Z-R relationships, the base reflectivity is used to derive the rainfall rate, and further, the radar estimated precipitation accumulation over a given area and time interval.

The radar data set used herein contains the quality controlled (cleaned) values of the raw R01 product. The cleaning is needed, as during the radar scans, both meteorological and nonmeteorological targets can be detected. Various clutter sources (e.g., terrain, buildings), biological targets (e.g., insects, birds) and external electromagnetic sources (e.g., sun) can impact the data quality within the volume scan, and although the signal processing can effectively mitigate the effects of this data contamination, additional processing is required to identify and remove the residual nonmeteorological echoes. Herein, the quality control algorithm is applied in a two-way process, by firstly detecting and removing the contaminated radar data, and secondly tuning the key variables to mitigate the effects of the first step on good data. The method used to clean and filter the reflectivity data is based on the three-dimensional structure of the measured data, in terms of computing horizontal and vertical data quality parameters. The computation algorithm is executed on radar data projected on a polar grid to not alter the measurements and to remain at the level of data recording, and it is built considering various key quality issues like ground clutter echoes and external electromagnetic interferences. First, the radar data is passed through a noise filter to remove the isolated ground clutter reflectivity bins, and then the algorithm performs the identification and removal of echoes generated by external signals and calculates the horizontal texture and the vertical gradient of reflectivity. The outputs of these steps (i.e., sub-algorithms) are finally used to reconstruct the quality-controlled reflectivity field.

Within AutoNowP, the NMA radar data was processed by selecting a value of 7 for the diameter d of the neighborhood (introduced in Section 3.1), representing about 7 km on the physical map, and this distance commonly determines small gradients of the meteorological parameters [30]. The value 7 for d provided the best performance for $AutoNowP$.

4.1.2. MET Radar Data Set

The MET radar data set used in our experiments consists of composite reflectivity values gathered from the MET Norway Thredds Data Server [32].

The reflectivity product, available at [33] was derived from the raw reflectivity values by considering the best radar scan out of all considered elevations. Thus, it is a composite product, obtained by applying an interpolation scheme that weights radar volume sources differently based on their quality flags and various properties that may influence the measurement. The considered properties include ground or sea clutter, ships or airplanes, beam blockage, RLAN, sun flare, height above CAPPI level (typically 1000 m msl), range, and azimuth displacement. The measurements used in our experiments were collected by the radar at a time resolution of 7.5 min.

The dimension d of the neighborhood data grid was set to 15 for the MET experiment, since this dimensionality provided the best performance for $AutoNowP$.

Table 1. Description of the data sets.

Data Set	Product of Interest ($\mathit{Rp}$)	# Instances	% of “+” Instances	% of “−” Instances	Entropy
NMA	R01	9003688	3.44%	96.56%	0.216
MET	Composite reflectivity	6607836	31.97%	68.03%	0.904

describes the data sets used as our case studies. The second column in the table indicates the radar product $Rp$ of interest. The next three columns contain the number of instances from the data sets (both “+” and “−”) and the percentage of positive and negative instances obtained using a threshold of 10 dBZ. The last column illustrates the entropy of each data set. The entropy is used for measuring the imbalancement of each data set [34]: lower entropy values indicate a higher degree of imbalancement.

From Table 1 we can see that the NMA data set is severely imbalanced: only 3.44% of the instances belong to the positive class, leading to a negative to positive ratio of about 28:1. Another element that highlights the high degree of data imbalancement is the entropy; where an entropy value of 1 reflects a perfectly balanced data set, the NMA data set entropy of 0.216 reflects a data set with low diversity, heavily weighted in favor of one class to the detriment of the other. The MET data set, on the other hand, showed a higher proportion of positive samples for this choice of threshold, as reflected by a higher entropy. In this setting, the negative to positive ratio is approximately 2:1.

The two-dimensional PCA [35] projections of the instances from both NMA and MET data sets from Figure 4 highlight the difficulty of the classification task. For both data sets, there is a low degree of separation between the class of negative instances (blue colored) and the class of positive instances (red colored).

The NMA data sets used in our experiments are publicly available at [36], while the MET data is publicly available at [37].

4.2. Results

This section presents the experimental results obtained by applying $AutoNowP$ classifier on the data sets described in Section 4.1. For the ConvAEs, the implementation from the Keras deep learning API [38] using the Tensorflow framework was employed.

The experiments were performed on a workstation laptop, with an Intel i9-10980HK CPU, 32 GB RAM and Nvidia RTX 2080 Super for GPU acceleration; and on a Google cloud instance with 12 vCPUs, 64 GB RAM and access to a Nvidia Tesla V100 for GPU acceleration.

The evaluation measures and the testing methodology described in Section 3.3 were employed.

Table 2. Experimental results, using 95% CIs.

Data Set	$\mathit{\tau }$	$\mathit{CSI}$	$\mathit{TSS}$	$\mathit{POD}$	$\mathit{PPV}$	$\mathit{NPV}$	$\mathit{Spec}$	$\mathit{AUC}$	$\mathit{AUPRC}$
		0.615	0.861	0.876	0.674	0.996	0.985	0.931	0.775
	10	±	±	±	±	±	±	±	±
		0.018	0.012	0.012	0.017	0.001	0.002	0.006	0.013
		0.425	0.471	0.474	0.810	0.989	0.997	0.736	0.642
NMA	20	±	±	±	±	±	±	±	±
		0.072	0.091	0.092	0.015	0.001	0.001	0.046	0.039
		0.151	0.157	0.157	0.812	0.993	1.000	0.579	0.485
	30	±	±	±	±	±	±	±	±
		0.046	0.051	0.028	0.031	0.001	0.000	0.014	0.007
		0.681	0.740	0.872	0.757	0.936	0.867	0.870	0.814
	10	±	±	±	±	±	±	±	±
		0.014	0.009	0.019	0.027	0.005	0.026	0.005	0.008
		0.566	0.626	0.675	0.793	0.920	0.951	0.813	0.734
MET	15	±	±	±	±	±	±	±	±
		0.05	0.09	0.12	0.08	0.03	0.03	0.05	0.029
		0.401	0.500	0.536	0.710	0.947	0.963	0.750	0.623
	20	±	±	±	±	±	±	±	±
		0.090	0.223	0.269	0.173	0.026	0.046	0.111	0.048

depicts the obtained results for both data sets used in our case studies, for various values of the threshold $\tau$. The 95% confidence intervals (CIs) are used for the results.

The thresholds we decided to use were chosen considering both computational and meteorological factors. In the literature, there is no convention on thresholds for R. For example, Han et al. [9,39] chose to use the 35 dBZ threshold while Tran and Song [40] studied their prediction performance using the 5, 20 and 40 dBZ thresholds. Thus, the values 10, 20 and 30 were chosen for $\tau$ for the NMA data and 10, 15, 20 for the MET data set. Since the MET data contains few instances whose values are higher than 30 dBZ, $AutoNowP$ could not be applied for this threshold. The best values obtained for the evaluation measures are highlighted for both data sets.

As shown in Table 2, the values for most of the evaluation measures decrease as the threshold $\tau$ increases. This is normal behavior, as the prediction becomes more difficult for higher values. The precision values (both for the positive and negative classes—$PPV$ and $NPV$) and the true negative rate ($Spec$) increase for higher thresholds, denoting that the negative class is easier to predict for high values for $\tau$ and the number of false predictions decreases. However, the number of true positives significantly decreases for higher thresholds and this is reflected in the other performance metrics that decrease. High values (around 0.9) were obtained for sensitivity ($POD$), specificity, and $AUC$ for $\tau =10$ denoting a good enough performance of $AutoNowP$. In addition, the small values obtained for the 95% CI reveal the stability of the model.

5. Discussion

With the goal of better highlighting the performance of $AutoNowP$, this section discusses the obtained results and then provides a comparison between $AutoNowP$ and similar approaches from the nowcasting literature.

5.1. Analysis of $AutoNowP$ performance

As shown in Table 2, $AutoNowP$ succeeds in recognizing the negative class (high specificity) and detecting the positive class (probability of detection higher than 0.85 for $\tau =10$). This is a strength of $AutoNowP$, the ability to detect severe phenomena well. However, we observed false predictions, both for the positive and negative classes and these occur mostly close to the decision boundary. The performance of $AutoNowP$ is impacted mainly by a large enough amount of false positive predictions, but most of these errors appear near the edges of radar echoes. In these areas the difference between classes becomes blurred, as the neighborhood contains some high values, not enough to be similar enough to the center of the event, but not few enough to be outside the event. These kinds of neighborhoods are close to both classes, the dissimilarity between them and either class is small. For these kinds of instances, AutoNowP has the most prediction errors. In order to better understand the areas where these instances appear, we have created a visualization in Figure 5. This figure shows the actual R01 values read by the radar in two consecutive time steps, color-coded by the dBZ value at each location. In the figure, there are also white and black regions, which represent the regions where most of the errors made by AutoNowP appear. The aforementioned regions were found by studying the erroneous predictions of the model and discovering the common elements of the neighborhoods that are problematic, both for false negative errors and false positive errors. Then, in Figure 5, we changed a pixel to white or black if its neighborhood is problematic, if it belongs to the false negative problems or, respectively, false positive problems. In short, in the image are represented with black points the locations where the model is highly likely to erroneously predict them as positive and, similarly, with white points where it tends to wrongly predict them as negative. The black and white areas in the image account for more than 98% of AutoNowP’s errors.

In Figure 5, it can be observed that most errors appear either at the edges of meteorological events, mostly in case of false positives, or in areas where there are few positive values, in case of false negatives. In case of false positives (in black), the problem areas show a tendency of the model to smooth the predictions out, i.e., to create shapes that are much more uniform. This is not an effect typical for AutoNowP; it is a general problem affecting radar reflectivity prediction models (e.g., the RadRAR model [11]). In Figure 5, a region containing false positives is exemplified in the first highlighted region (the bigger one, around the pixel at (75,50)); it can be seen that the black region surrounds the actual meteorological event, smoothing it out, creating much more homogenous shapes. This tendency is kept from one time step to another, the smoothed shape following closely the real shape.

In case of false negatives (in white), the problems appear generally in areas where there are few positive values, i.e., the neighborhoods of locations contain many zero or close to zero values and few values higher than the threshold. For these kinds of neighborhoods, it is hard to differentiate between classes as they appear both at the start of meteorological events and at the end of meteorological events. The beginning of meteorological events is especially hard to predict, as there is no indication if and where a meteorological event will form; for this reason, the model generally predicts locations with these kinds of neighborhoods as being negative, introducing some false negative errors. In Figure 5, an example area containing a false negative region can be observed in the second highlight (the small one, around the pixel (125,50)). In that highlight, in the first time step (left side) it can be observed that the meteorological event is small, while in the next time step (right side), the region of the meteorological event has more than doubled in size. Since in the first time step the event region is so small, the model has problems predicting the relatively big changes that will happen until the next time step, thus introducing false negative errors, visualized as white regions.

Analyzing the false negative predictions of $AutoNowP$, we also noticed (in both NMA and MET experiments) situations as the one depicted in Figure 6. The figure presents the composite reflectivity for two consecutive radar acquisitions from MET data. The red rectangles highlight a region that illustrates a sample case where $AutoNowP$ provides false predictions.

From Figure 6 one observes that at time t (left side image) there are no values in the highlighted region for the composite reflectivity, but at $t+1$ (the next data received from the radar—right side image) high values for composite reflectivity are suddenly detected. Some of the data points inside the rectangle should be classified as positive instances (higher values are displayed in red), but the model fails to predict the correct class (i.e., the positive one) as the input for $AutoNowP$ (the data at t) contained mostly zero-valued data. While these situations are relatively infrequent in real life (the values are usually increasing slowly between consecutive time stamps), they still contribute to a lower prediction accuracy. However, even if $AutoNowP$ is unable to detect the positive instances at time step $t+1$, in the next step, at time $t+2$, the model will correctly classify the data points. This is not a limitation of $AutoNowP$, as such unexpected events cannot be detected by a learning model that was trained to predict time $t+1$ based on time t. A possible solution would be to include more previous time steps in the prediction ($t-1$, $t-2$, etc).

In order to assess how the cleaning of the raw radar data impacts the predictive performance of our model, $AutoNowP$ was trained on the uncleaned NMA data as well. A threshold $\tau =10$ and the methodology introduced in Section 3 were applied for building the $AutoNowP$ classification model on the uncleaned data.

Table 3. Experimental results obtained applying $AutoNowP$ on the uncleaned NMA data and the improvement achieved on the cleaned data, for all performance measures.

	$\mathit{CSI}$	$\mathit{TSS}$	$\mathit{POD}$	$\mathit{PPV}$	$\mathit{NPV}$	$\mathit{Spec}$	$\mathit{AUC}$	$\mathit{AUPRC}$
Value	0.364	0.439	0.463	0.641	0.953	0.976	0.719	0.552
	±	±	±	±	±	±	±	±
95% CI	0.035	0.072	0.084	0.050	0.003	0.012	0.036	0.018
Improvement	69%	96%	89%	5%	4%	1%	29%	40%

depicts the obtained results. One observes a significant performance improvement on the cleaned data. For a specific evaluation measure P, the performance improvement is computed as $\frac{P_{cleaned}-P_{uncleaned}}{P_{uncleaned}}$ being shown in the last row of the table.

Table 3 highlights an average improvement of $42\%$ on the performance measures when using the cleaned data. The highest improvements are observed on $TSS$ ($96\%$), $POD$ ($89\%$) and on $CSI$ ($69\%$), while the lowest improvements are on $PPV$, $NPV$ and $Spec$ (less than $5\%$). These variations in the measures occurs because the uncleaned data introduces many false negative errors while marginally introducing true positive errors, thus for measures reliant on false negatives, such as $POD$, the difference is great while for measures reliant on false positives, such as $Spec$, the difference is small. We can speculate why this happens by analyzing uncleaned data and how it might affect the model: as explained in Section 4.1, the cleaning of the NMA data removes noise and clutter introduced by the interference of nonmeteorological targets during the scan. Effectively, this means that in the uncleaned data there are many locations where there are wrong values, higher than zero instead of zero. Because of this, during training, the model receives many locations labeled as negative where the neighborhood still has a large number of high-valued locations (the erroneous values), thus leading the model to make a false negative prediction (i.e., it will predict “−” even where there were actual meteorological events with a similar pattern as the erroneous training instance).

5.2. Comparison to Related Work

As shown in Section 2, most of the approaches introduced in the literature are for precipitation nowcasting. The existing methods based on radar reflectivity nowcasting were applied to radar data collected from various geographical regions, using various parameters settings, testing methodologies and various thresholds for the radar reflectivity values. The analysis of the recent literature highlighted $CSI$ values ranging from 0.40 [20] to 0.647 [17]; $POD$ values ranging from 0.46 [20] to 0.71 [21]; F-$score$ values ranging from 0.58 [15] to 0.786 [15]. The performance of $AutoNowP$ on both data sets used in our experiments (Table 2) compares favorably with the literature results, considering the magnitude of the evaluation measures for a threshold of 10 ($CSI$ higher than 0.61, $POD$ higher than 0.87, F-$score$ higher than 0.8).

As the literature approaches for nowcasting do not use the same data model as our approach, an exact comparison with these methods cannot be made. For a more exact comparison, we decided to apply four well-known machine learning classifiers on the data sets described in Section 4.1, using $\tau =10$ and following the testing methodology used for evaluating the performance of $AutoNowP$ (the performance measures were computed as shown in Section 3.3 and the testing was repeated 3 times for each training–validation split): logistic regression (LR), linear support vector classifier (linear SVC), decison trees (DT), and nearest centroid classification (NCC). We have selected these classifiers as baseline methods so as to cover a diverse set of methods—linear classifiers, rule-based, and distance-based.

These classifiers were implemented in Python using the scikit-learn [41] machine learning library. The comparative results are depicted in

Table 4. Comparative results between $AutoNowP$ and other classifiers. 95% CIs are used for the results.

Data Set	Model	$\mathit{CSI}$	$\mathit{TSS}$	$\mathit{POD}$	$\mathit{PPV}$	$\mathit{NPV}$	$\mathit{Spec}$	$\mathit{AUC}$	$\mathit{AUPRC}$
		0.615	0.861	0.876	0.674	0.996	0.985	0.931	0.775
	AutoNowP	±	±	±	±	±	±	±	±
		0.018	0.012	0.012	0.017	0.001	0.002	0.006	0.013
		0.672	0.752	0.757	0.857	0.992	0.996	0.876	0.807
	LR	±	±	±	±	±	±	±	±
		0.012	0.013	0.013	0.005	0.001	0.000	0.007	0.008
		0.685	0.778	0.783	0.845	0.992	0.995	0.889	0.814
NMA	Linear SVC	±	±	±	±	±	±	±	±
		0.012	0.007	0.007	0.015	0.000	0.000	0.003	0.009
		0.574	0.725	0.734	0.724	0.991	0.990	0.862	0.729
	DT	±	±	±	±	±	±	±	±
		0.007	0.004	0.006	0.012	0.001	0.002	0.002	0.006
		0.571	0.793	0.807	0.662	0.993	0.986	0.896	0.735
	NCC	±	±	±	±	±	±	±	±
		0.006	0.013	0.013	0.015	0.001	0.001	0.006	0.003
		0.681	0.740	0.872	0.757	0.936	0.867	0.870	0.814
	AutoNowP	±	±	±	±	±	±	±	±
		0.014	0.009	0.019	0.027	0.005	0.026	0.005	0.008
		0.760	0.796	0.853	0.875	0.932	0.943	0.898	0.864
	LR	±	±	±	±	±	±	±	±
		0.006	0.002	0.001	0.007	0.003	0.002	0.001	0.004
		0.761	0.798	0.858	0.870	0.934	0.940	0.899	0.864
MET	Linear SVC	±	±	±	±	±	±	±	±
		0.006	0.002	0.001	0.007	0.003	0.003	0.001	0.004
		0.670	0.710	0.804	0.801	0.908	0.906	0.855	0.803
	DT	±	±	±	±	±	±	±	±
		0.010	0.004	0.005	0.009	0.003	0.002	0.002	0.007
		0.681	0.728	0.831	0.791	0.919	0.897	0.864	0.811
	NCC	±	±	±	±	±	±	±	±
		0.009	0.005	0.009	0.007	0.001	0.006	0.003	0.007

, with a 95% CIs for the values averaged over the three runs of the classifiers. The best values obtained for each performance metric are highlighted.

The comparative results from Table 4 reveal that $AutoNowP$ obtained the best results in terms of $POD$ and $NPV$ for both data sets. In addition, for the NMA data set, our classifier provided the highest $TSS$ and $AUC$ values. Figure 7 and Figure 8 illustrate the ROC curves for the classifiers from Table 4 on NMA and MET data sets.

Table 5. Summary of the comparison between $AutoNowP$ and existing classifiers.

	NMA Data	MET Data	Total
WIN	21	16	37
LOSE	11	16	27
% WIN	66%	50%	58%

summarizes the results of the comparison between $AutoNowP$ and the classifiers from Table 4. The table indicates, for both the NMA and MET data sets, the number of comparisons won (first row) and lost (second row) by $AutoNowP$ considering all the evaluation measures and the classifiers from Table 4. More specifically, a comparison between our approach and a classifier c, considering a specific performance measure p, is won by $AutoNowP$ if the value for p provided by $AutoNowP$ is greater than the one provided by the classifier c. Similarly, the comparison is lost by $AutoNowP$ if the value for p provided by $AutoNowP$ is lower than the one provided by the classifier c.

The results from Table 5 highlight that $AutoNowP$ outperforms similar classifiers in 66% of the cases for the NMA data set and in 50% of the cases for the MET data set out. Overall, out of 64 comparisons, our $AutoNowP$ approach wins in 37 cases, i.e in 58% of the cases.

One of the main current limitations of $AutoNowP$ is the training data: in order for the model to have a high performance it needs to be trained using large amounts of relevant data. While there are large amounts of historical meteorological data, finding a cohesive set of relevant, high-quality data is not trivial. Due to the large training data set needed, the training process of $AutoNowP$ tends to take quite some time, which may hamper the practicality of the model. The data model might be another drawback of the $AutoNowP$, as the way it is currently designed, it might lead to the confounding of the 2 classes in some special cases, as presented in Section 5.1. Nevertheless, these limitations can be addressed, which we plan to do in the future: the long training time can be improved by parallelizing the training process, while the data model can be improved, for example by extending it to contain more than one previous time step.

6. Conclusions and Future Work

The paper introduced $AutoNowP$, a new binary classification model for precipitation nowcasting based on radar reflectivity. $AutoNowP$ used two convolutional autoencoders that are trained on radar data collected on both stratiform and convective weather conditions for learning to predict if the value for the radar reflectivity on a specific location will be above or below a certain threshold. $AutoNowP$ was introduced in this paper as a proof a concept that autoencoders are helpful in distinguishing between convective and stratiform rainfall. Experiments performed on radar data provided by the Romanian National Meteorological Administration and the Norwegian Meteorological Institute highlighted that the ConvAEs used in $AutoNowP$ are able to learn structural characteristics from radar data and thus the lower-dimensional radar data encoded in the ConvAEs latent space is consistent with the meteorological evidence.

The generality of $AutoNowP$ classifier has to be noted. Even if it was introduced and evaluated in the context of precipitation nowcasting, it may be extended and applied for other meteorological data sources and binary classification tasks.

$AutoNowP$ is one step toward the end goal of our research: to create machine-learning-based prediction models to be integrated in existing national weather nowcasting systems. The integration of these models aims to improve the Early Warning System frameworks, as the predictions create the possibility of issuing more accurate early warnings. Better early warnings can lead to avoidance of loss and damage due to heavy precipitations, for example in events such as flash floods in densely populated areas [42].

Future work will be conducted in order to extend the data sets used in the experimental evaluation. In addition, we aim to apply $AutoNowP$ to other meteorological data sources (such as satellite data) and thus using the model for other nowcasting scenarios.