Multi-Time Generalized Nash Equilibria with Dynamic Flow Applications
Abstract
:1. Introduction
2. Preliminaries and Problem Formulations
- It is evident from the above definition that every open (respectively, closed) set is compactly open (respectively, compactly closed).
- The union or intersection of a finite number of compactly open (respectively, compactly closed) sets is compactly open (respectively, compactly closed).
- If and are compactly open (respectively, compactly closed) in and , respectively, then is compactly open (respectively, compactly closed) in .
- 1.
- 2.
- 3.
- is convex,
- 4.
- is compactly open,
- 5.
- there exists a nonempty, closed and compact subset D of K and such that .
3. An Equivalent Form of the Multi-Time Generalized Nash Equilibrium Problem
4. Existence of Equilibria
5. Applications
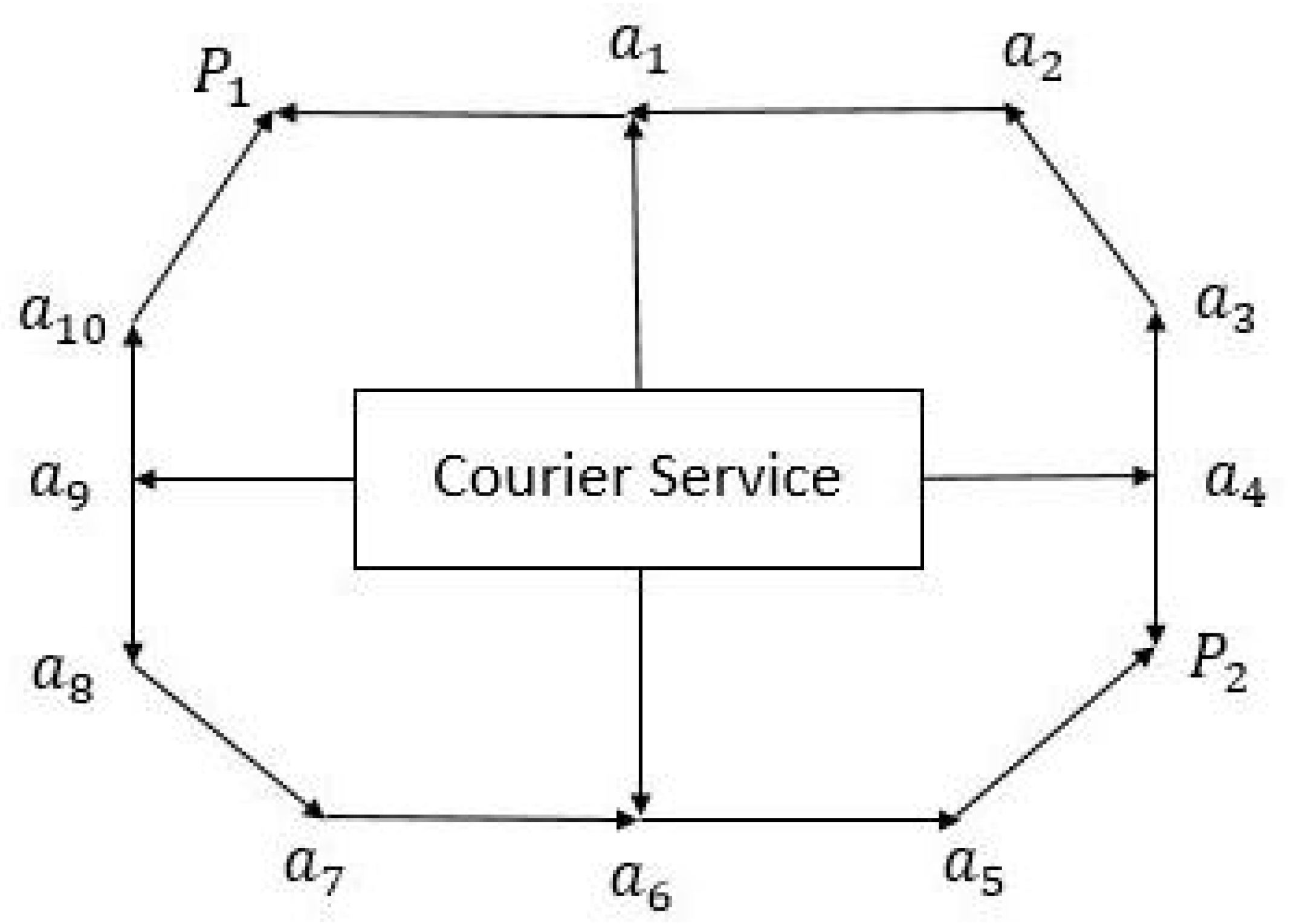
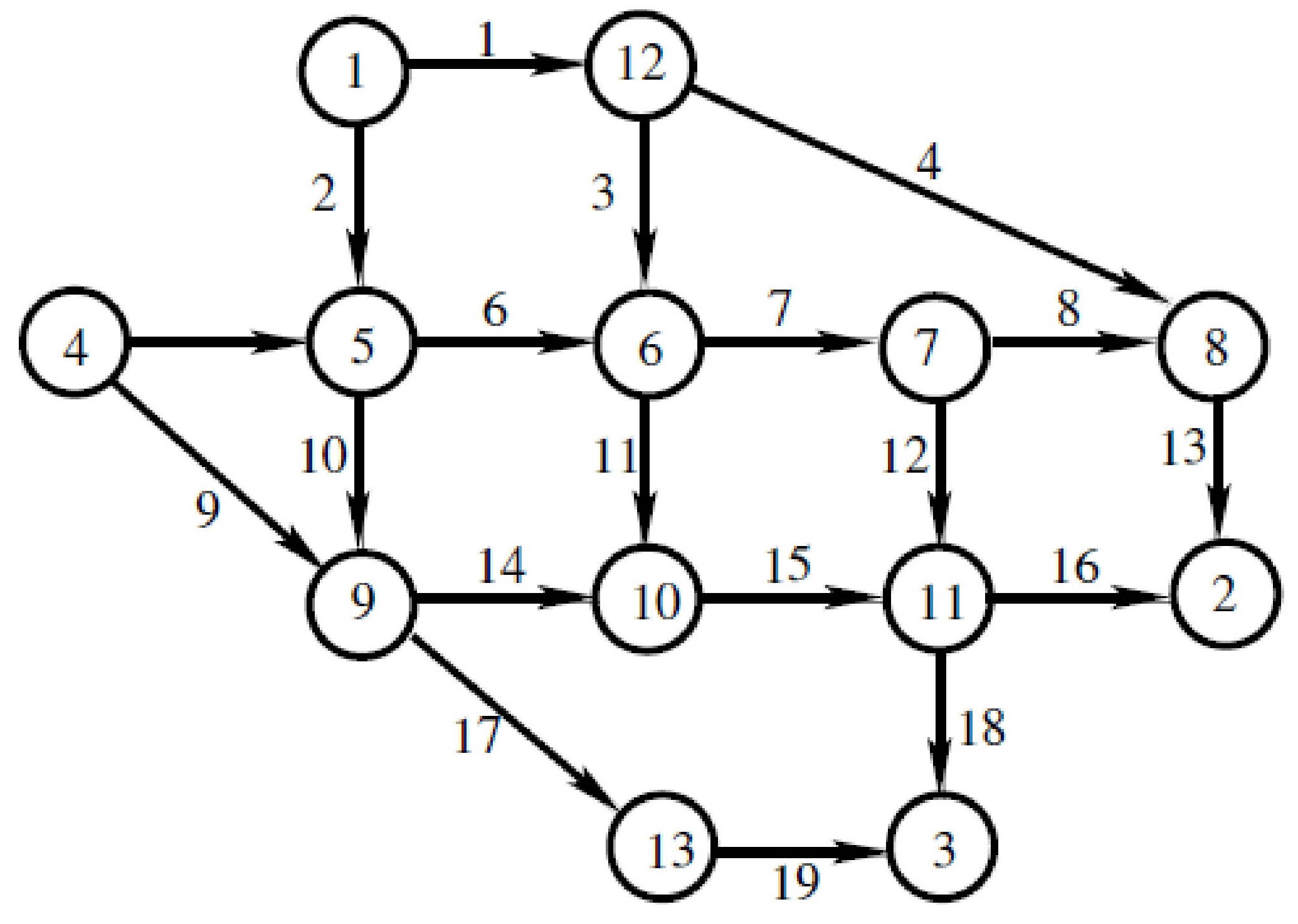
5.1. Traffic Network Problem
5.2. River Basin Pollution Problem
6. The Multi-Time Generalized Nash Equilibrium Problem as a Projected Dynamical System
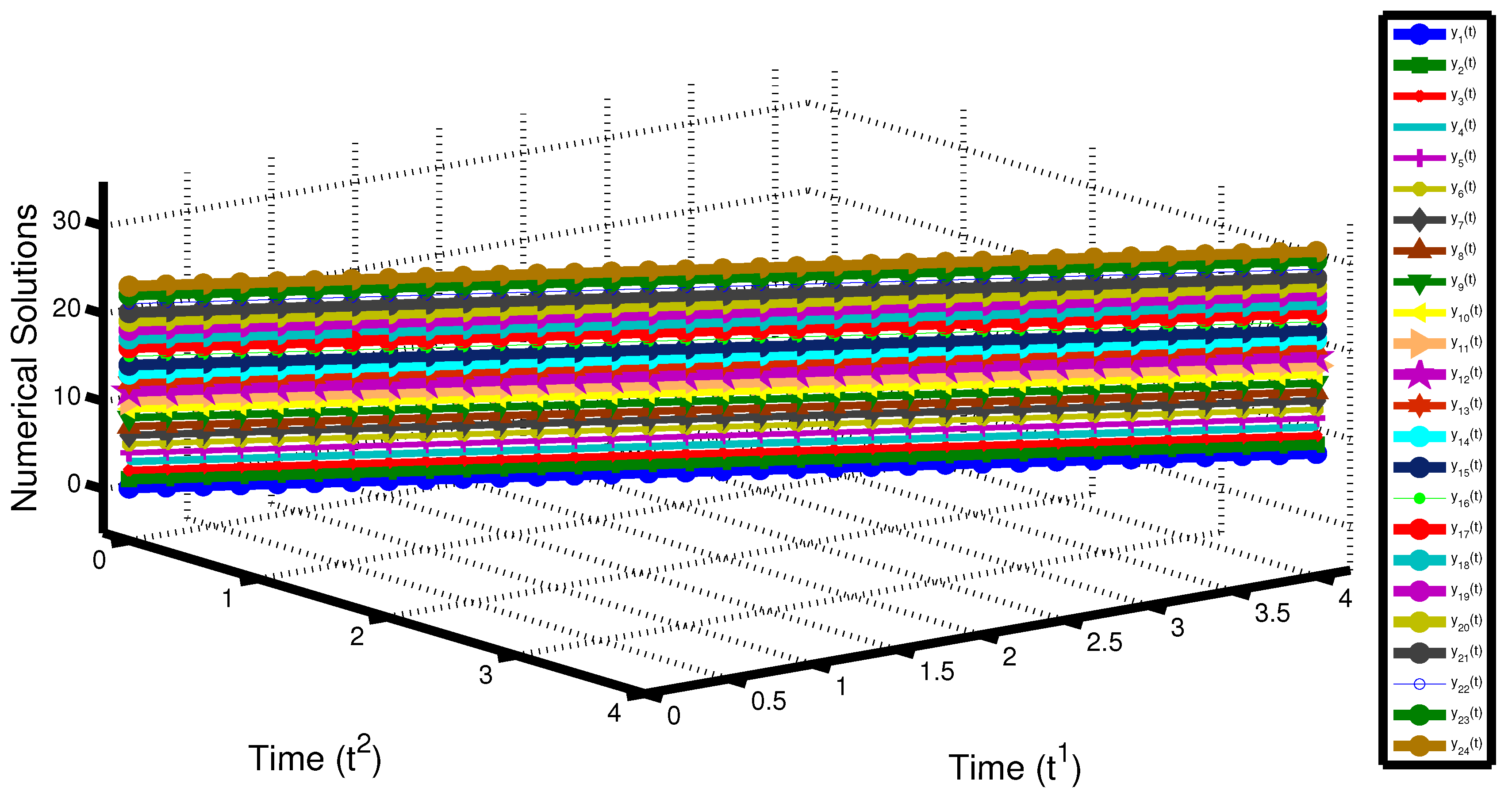
Numerical Illustrations
7. Conclusions and Further Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cournot, A.A. Recherches sur les Principes Mathématiques de la théorie des Richesses; Hachette: Paris, France, 1838. [Google Scholar]
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nash, J.F. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Arrow, K.J.; Debreu, G. Existence of an equilibrium for a competitive economy. Econometrica 1954, 22, 265–290. [Google Scholar] [CrossRef]
- Rosen, J.B. Existence and uniqueness of equilibrium points for concave n-person games. Econometrica 1965, 33, 520–534. [Google Scholar] [CrossRef] [Green Version]
- Kesselman, A.; Leonardi, S.; Bonifaci, V. Game-theoretic analysis of internet switching with selfish users. In Internet and Network Economics; Lecture Notes in Computer Science; Deng, X., Ye, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3828. [Google Scholar]
- Pang, J.-S.; Scutari, G.; Facchinei, F.; Wang, C. Distributed power allocation with rate constraints in Gaussian parallel interference channels. IEEE Trans. Inf. Theory 2008, 54, 3471–3489. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C. Generalized Nash equilibrium problems. Ann. Oper. Res. 2010, 175, 177–211. [Google Scholar] [CrossRef]
- Fischer, A.; Herrich, M.; Schönefeld, K. Generalized Nash equilibrium problems-recent advances and challenges. Pesqui. Oper. 2014, 34, 521–558. [Google Scholar] [CrossRef]
- Smith, M.J. The existence, uniqueness and stability of traffic equilibrium. Transp. Res. 1979, 13, 295–304. [Google Scholar] [CrossRef]
- Dafermos, S. Traffic equilibrium and variational inequalities. Transp. Sci. 1980, 14, 42–54. [Google Scholar] [CrossRef] [Green Version]
- Cojocaru, M.G.; Daniele, P.; Nagurney, A. Projected dynamical systems and evolutionary variational inequalities via Hilbert spaces with applications. J. Optim. Theory Appl. 2005, 127, 549–563. [Google Scholar] [CrossRef] [Green Version]
- Nagurney, A. Network Economics: A Variational Inequality Approach; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Barbagallo, A.; Cojocaru, M.G. Dynamic equilibrium formulation of the oligopolistic market problem. Math. Comput. Model. 2009, 49, 966–976. [Google Scholar] [CrossRef]
- Cojocaru, M.G.; Bauch, C.T.; Johnston, M.D. Dynamics of vaccination strategies via projected dynamical systems. Bull. Math. Biol. 2007, 69, 453–476. [Google Scholar] [CrossRef]
- Harker, P.T. Generalized Nash games and quasi-variational inequalities. Eur. J. Oper. Res. 1991, 54, 81–94. [Google Scholar] [CrossRef]
- Bensoussan, A. Points de Nash dans le cas de fontionnelles quadratiques et jeux differentiels linéaires a N personnes. SIAM J. Control 1974, 12, 460–499. [Google Scholar] [CrossRef]
- Aussel, D.; Gupta, R.; Mehra, A. Evolutionary variational inequality formulation of the generalized Nash equilibrium problem. J. Optim. Theory Appl. 2016, 169, 74–90. [Google Scholar] [CrossRef]
- Migot, T.; Cojocaru, M.-G. Nonsmooth dynamics of generalized Nash games. J. Nonlinear Var. Anal. 2020, 4, 27–44. [Google Scholar]
- Pang, J.-S.; Fukushima, M. Quasi-variational inequalities, generalized Nash equilibria, and multi-leader-follower games. Comput. Manag. Sci. 2005, 2, 21–56. [Google Scholar] [CrossRef]
- Shehu, Y.; Gibali, A.; Sagratella, S. Inertial projection-type methods for solving quasi-variational inequalities in real Hilbert spaces. J. Optim. Theory Appl. 2020, 184, 877–894. [Google Scholar] [CrossRef]
- Udrişte, C.; Ţevy, I. Multi-time Euler-Lagrange-Hamilton theory. WSEAS Trans. Math. 2007, 6, 701–709. [Google Scholar]
- Udrişte, C. Multitime controllability, observability and bang-bang principle. J. Optim. Theory Appl. 2008, 139, 141–157. [Google Scholar] [CrossRef]
- Udrişte, C. Simplified multitime maximum principle. Balkan J. Geom. Appl. 2009, 14, 102–119. [Google Scholar]
- Udrişte, C.; Dogaru, O.; Ţevy, I. Null Lagrangian forms and Euler-Lagrange PDEs. J. Math. Study 2008, 1, 143–156. [Google Scholar]
- Udrişte, C.; Ferrara, M. Multitime models of optimal growth. WSEAS Trans. Math. 2008, 7, 51–55. [Google Scholar]
- Singh, S.; Pitea, A.; Qin, X. An iterative method and weak sharp solutions for multitime-type variational inequalities. Appl. Anal. 2019. [Google Scholar] [CrossRef]
- Singh, S.; Reich, S. A multidimensional approach to traffic analysis. Pure Appl. Funct. Anal. 2021, 6, 383–397. [Google Scholar]
- Treanţă, S.; Singh, S. Weak sharp solutions associated with a multidimensional variational-type inequality. Positivity 2020. [Google Scholar] [CrossRef]
- Nguyen, S. Estimating Origin Destination Matrices from Observed Flows; Elsevier Science Publishers BV: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Jayswal, A.; Singh, S.; Kurdi, A. Multitime multiobjective variational problems and vector variational-like inequalities. Eur. J. Oper. Res. 2016, 254, 739–745. [Google Scholar] [CrossRef]
- Mititelu, Ş.; Treanţă, S. Efficiency conditions in vector control problems governed by multiple integrals. J. Appl. Math. Comput. 2018, 57, 647–665. [Google Scholar] [CrossRef]
- Ansari, Q.H.; Schaible, S.; Yao, J.C. Generalized vector quasi-variational inequality problems over product sets. J. Glob. Optim. 2005, 32, 437–449. [Google Scholar] [CrossRef]
- Ding, X.P. Existence of solutions for quasi-equilibrium problems in noncompact topological spaces. Comput. Math. Appl. 2000, 39, 13–21. [Google Scholar] [CrossRef] [Green Version]
- Nagurney, A.; Liu, Z.; Cojocaru, M.-G.; Daniele, P. Dynamic electric power supply chains and transportation networks: An evolutionary variational inequality formulation. Transp. Res. E Logist. Transp. Rev. 2007, 43, 624–646. [Google Scholar] [CrossRef]
- Daniele, P. Evolutionary variational inequalities and applications to complex dynamic multi-level models. Transp. Res. E Logist. Transp. Rev. 2010, 46, 855–880. [Google Scholar] [CrossRef]
- Haurie, A.; Krawczyk, J.B. Optimal charges on river effluent from lumped and distributed sources. Environ. Model. Assess. 1997, 2, 177–189. [Google Scholar] [CrossRef]
- Krawczyk, J.B. Coupled constraint Nash equilibria in environmental games. Resour. Energy Econ. 2005, 27, 157–181. [Google Scholar] [CrossRef]
- Krawczyk, J.B.; Uryasev, S. Relaxation algorithms to find Nash equilibria with economic applications. Environ. Model. Assess. 2000, 5, 63–73. [Google Scholar] [CrossRef]
- Kubota, K.; Fukushima, M. Gap function approach to the generalized Nash equilibrium problem. J. Optim. Theory Appl. 2010, 144, 511–531. [Google Scholar] [CrossRef] [Green Version]
- Cojocaru, M.G.; Jonker, L.B. Existence of solutions to projected differential equations in Hilbert spaces. Proc. Am. Math. Soc. 2003, 132, 183–193. [Google Scholar] [CrossRef]
- Cegielski, A. Iterative Methods for Fixed Point Problems in Hilbert Spaces; Springer: Heidelberg, Germany, 2012. [Google Scholar]
- Rockafellar, R.T.; Wets, R.J.-B. Variational Analysis; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1.25 | 2.25 | 3.25 | 4.25 | 5.25 | 6.25 | |
| 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | |
| 1.75 | 2.75 | 3.75 | 4.75 | 5.75 | 6.75 | |
| 2 | 3 | 4 | 5 | 6 | 7 | |
| 2.25 | 3.25 | 4.25 | 5.25 | 6.25 | 7.25 | |
| 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | |
| 2.75 | 3.75 | 4.75 | 5.75 | 6.75 | 7.75 | |
| 3 | 4 | 5 | 6 | 7 | 8 | |
| 3.25 | 4.25 | 5.25 | 6.25 | 7.25 | 8.25 | |
| 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | |
| 3.75 | 4.75 | 5.75 | 6.75 | 7.75 | 8.75 | |
| 4 | 5 | 6 | 7 | 8 | 9 | |
| 4.25 | 5.25 | 6.25 | 7.25 | 8.25 | 9.25 | |
| 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | |
| 4.75 | 5.75 | 6.75 | 7.75 | 8.75 | 9.75 | |
| 5 | 6 | 7 | 8 | 9 | 10 | |
| 5.25 | 6.25 | 7.25 | 8.25 | 9.25 | 10.25 | |
| 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | 10.5 | |
| 5.75 | 6.75 | 7.75 | 8.75 | 9.75 | 10.75 | |
| 6 | 7 | 8 | 9 | 10 | 11 | |
| 6.25 | 7.25 | 8.25 | 9.25 | 10.25 | 11.25 | |
| 6.5 | 7.5 | 8.5 | 9.5 | 10.5 | 11.5 | |
| 6.75 | 7.75 | 8.75 | 9.75 | 10.75 | 11.75 | |
| 7 | 8 | 9 | 10 | 11 | 12 | |
| 7.25 | 8.25 | 9.25 | 10.25 | 11.25 | 12.25 | |
| 7.5 | 8.5 | 9.5 | 10.5 | 11.5 | 12.5 | |
| 7.75 | 8.75 | 9.75 | 10.75 | 11.75 | 12.75 | |
| 8 | 9 | 10 | 11 | 12 | 13 | |
| 8.25 | 9.25 | 10.25 | 11.25 | 12.25 | 13.25 | |
| 8.5 | 9.5 | 10.5 | 11.5 | 12.5 | 13.5 | |
| 8.75 | 9.75 | 10.75 | 11.75 | 12.75 | 13.75 | |
| 9 | 10 | 11 | 12 | 13 | 14 |
| 7 | 8 | 9 | 10 | 11 | 12 | |
| 7.25 | 8.25 | 9.25 | 10.25 | 11.25 | 12.25 | |
| 7.5 | 8.5 | 9.5 | 10.5 | 11.5 | 12.5 | |
| 7.75 | 8.75 | 9.75 | 10.75 | 11.75 | 12.75 | |
| 8 | 9 | 10 | 11 | 12 | 13 | |
| 8.25 | 9.25 | 10.25 | 11.25 | 12.25 | 13.25 | |
| 8.5 | 9.5 | 10.5 | 11.5 | 12.5 | 13.5 | |
| 8.75 | 9.75 | 10.75 | 11.75 | 12.75 | 13.75 | |
| 9 | 10 | 11 | 12 | 13 | 14 | |
| 9.25 | 10.25 | 11.25 | 12.25 | 13.25 | 14.25 | |
| 9.5 | 10.5 | 11.5 | 12.5 | 13.5 | 14.5 | |
| 9.75 | 10.75 | 11.75 | 12.75 | 13.75 | 14.75 | |
| 10 | 11 | 12 | 13 | 14 | 15 | |
| 10.25 | 11.25 | 12.25 | 13.25 | 14.25 | 15.25 | |
| 10.5 | 11.5 | 12.5 | 13.5 | 14.5 | 15.5 | |
| 10.75 | 11.75 | 12.75 | 13.75 | 14.75 | 15.75 | |
| 11 | 12 | 13 | 14 | 15 | 16 | |
| 11.25 | 12.25 | 13.25 | 14.25 | 15.25 | 16.25 | |
| 11.5 | 12.5 | 13.5 | 14.5 | 15.5 | 16.5 | |
| 11.75 | 12.75 | 13.75 | 14.75 | 15.75 | 16.75 | |
| 12 | 13 | 14 | 15 | 16 | 17 | |
| 12.25 | 13.25 | 14.25 | 15.25 | 16.25 | 17.25 | |
| 12.5 | 13.5 | 14.5 | 15.5 | 16.5 | 17.5 | |
| 12.75 | 13.75 | 14.75 | 15.75 | 16.75 | 17.75 | |
| 13 | 14 | 15 | 16 | 17 | 18 | |
| 13.25 | 14.25 | 15.25 | 16.25 | 17.25 | 18.25 | |
| 13.5 | 14.5 | 15.5 | 16.5 | 17.5 | 18.5 | |
| 13.75 | 14.75 | 15.75 | 16.75 | 17.75 | 18.75 | |
| 14 | 15 | 16 | 17 | 18 | 19 | |
| 14.25 | 15.25 | 16.25 | 17.25 | 18.25 | 19.25 | |
| 14.5 | 15.5 | 16.5 | 17.5 | 18.5 | 19.5 | |
| 14.75 | 15.75 | 16.75 | 17.75 | 18.75 | 19.75 | |
| 15 | 16 | 17 | 18 | 19 | 20 |
| 13 | 14 | 15 | 16 | 17 | 18 | |
| 13.25 | 14.25 | 15.25 | 16.25 | 17.25 | 18.25 | |
| 13.5 | 14.5 | 15.5 | 16.5 | 17.5 | 18.5 | |
| 13.75 | 14.75 | 15.75 | 16.75 | 17.75 | 18.75 | |
| 14 | 15 | 16 | 17 | 18 | 19 | |
| 14.25 | 15.25 | 16.25 | 17.25 | 18.25 | 19.25 | |
| 14.5 | 15.5 | 16.5 | 17.5 | 18.5 | 19.5 | |
| 14.75 | 15.75 | 16.75 | 17.75 | 18.75 | 19.75 | |
| 15 | 16 | 17 | 18 | 19 | 20 | |
| 15.25 | 16.25 | 17.25 | 18.25 | 19.25 | 20.25 | |
| 15.5 | 16.5 | 17.5 | 18.5 | 19.5 | 20.5 | |
| 15.75 | 16.75 | 17.75 | 18.75 | 19.75 | 20.75 | |
| 16 | 17 | 18 | 19 | 20 | 21 | |
| 16.25 | 17.25 | 18.25 | 19.25 | 20.25 | 21.25 | |
| 16.5 | 17.5 | 18.5 | 19.5 | 20.5 | 21.5 | |
| 16.75 | 17.75 | 18.75 | 19.75 | 20.75 | 21.75 | |
| 17 | 18 | 19 | 20 | 21 | 22 | |
| 17.25 | 18.25 | 19.25 | 20.25 | 21.25 | 22.25 | |
| 17.5 | 18.5 | 19.5 | 20.5 | 21.5 | 22.5 | |
| 17.75 | 18.75 | 19.75 | 20.75 | 21.75 | 22.75 | |
| 18 | 19 | 20 | 21 | 22 | 23 | |
| 18.25 | 19.25 | 20.25 | 21.25 | 22.25 | 23.25 | |
| 18.5 | 19.5 | 20.5 | 21.5 | 22.5 | 23.5 | |
| 18.75 | 19.75 | 20.75 | 21.75 | 22.75 | 23.75 | |
| 19 | 20 | 21 | 22 | 23 | 24 | |
| 19.25 | 20.25 | 21.25 | 22.25 | 23.25 | 24.25 | |
| 19.5 | 20.5 | 21.5 | 22.5 | 23.5 | 24.5 | |
| 19.75 | 20.75 | 21.75 | 22.75 | 23.75 | 24.75 | |
| 20 | 21 | 22 | 23 | 24 | 25 | |
| 20.25 | 21.25 | 22.25 | 23.25 | 24.25 | 25.25 | |
| 20.5 | 21.5 | 22.5 | 23.5 | 24.5 | 25.5 | |
| 20.75 | 21.75 | 22.75 | 23.75 | 24.75 | 25.75 | |
| 21 | 22 | 23 | 24 | 25 | 26 |
| 19 | 20 | 21 | 22 | 23 | 24 | |
| 19.25 | 20.25 | 21.25 | 22.25 | 23.25 | 24.25 | |
| 19.5 | 20.5 | 21.5 | 22.5 | 23.5 | 24.5 | |
| 19.75 | 20.75 | 21.75 | 22.75 | 23.75 | 24.75 | |
| 20 | 21 | 22 | 23 | 24 | 25 | |
| 20.25 | 21.25 | 22.25 | 23.25 | 24.25 | 25.25 | |
| 20.5 | 21.5 | 22.5 | 23.5 | 24.5 | 25.5 | |
| 20.75 | 21.75 | 22.75 | 23.75 | 24.75 | 25.75 | |
| 21 | 22 | 23 | 24 | 25 | 26 | |
| 21.25 | 22.25 | 23.25 | 24.25 | 25.25 | 26.25 | |
| 21.5 | 22.5 | 23.5 | 24.5 | 25.5 | 26.5 | |
| 21.75 | 22.75 | 23.75 | 24.75 | 25.75 | 26.75 | |
| 22 | 23 | 24 | 25 | 26 | 27 | |
| 22.25 | 23.25 | 24.25 | 25.25 | 26.25 | 27.25 | |
| 22.5 | 23.5 | 24.5 | 25.5 | 26.5 | 27.5 | |
| 22.75 | 23.75 | 24.75 | 25.75 | 26.75 | 27.75 | |
| 23 | 24 | 25 | 26 | 27 | 28 | |
| 23.25 | 24.25 | 25.25 | 26.25 | 27.25 | 28.25 | |
| 23.5 | 24.5 | 25.5 | 26.5 | 27.5 | 28.5 | |
| 23.75 | 24.75 | 25.75 | 26.75 | 27.75 | 28.75 | |
| 24 | 25 | 26 | 27 | 28 | 29 | |
| 24.25 | 25.25 | 26.25 | 27.25 | 28.25 | 29.25 | |
| 24.5 | 25.5 | 26.5 | 27.5 | 28.5 | 29.5 | |
| 24.75 | 25.75 | 26.75 | 27.75 | 28.75 | 29.75 | |
| 25 | 26 | 27 | 28 | 29 | 30 | |
| 25.25 | 26.25 | 27.25 | 28.25 | 29.25 | 30.25 | |
| 25.5 | 26.5 | 27.5 | 28.5 | 29.5 | 30.5 | |
| 25.75 | 26.75 | 27.75 | 28.75 | 29.75 | 30.75 | |
| 26 | 27 | 28 | 29 | 30 | 31 | |
| 26.25 | 27.25 | 28.25 | 29.25 | 30.25 | 31.25 | |
| 26.5 | 27.5 | 28.5 | 29.5 | 30.5 | 31.5 | |
| 26.75 | 27.75 | 28.75 | 29.75 | 30.75 | 31.75 | |
| 27 | 28 | 29 | 30 | 31 | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Gibali, A.; Reich, S. Multi-Time Generalized Nash Equilibria with Dynamic Flow Applications. Mathematics 2021, 9, 1658. https://doi.org/10.3390/math9141658
Singh S, Gibali A, Reich S. Multi-Time Generalized Nash Equilibria with Dynamic Flow Applications. Mathematics. 2021; 9(14):1658. https://doi.org/10.3390/math9141658
Chicago/Turabian StyleSingh, Shipra, Aviv Gibali, and Simeon Reich. 2021. "Multi-Time Generalized Nash Equilibria with Dynamic Flow Applications" Mathematics 9, no. 14: 1658. https://doi.org/10.3390/math9141658
APA StyleSingh, S., Gibali, A., & Reich, S. (2021). Multi-Time Generalized Nash Equilibria with Dynamic Flow Applications. Mathematics, 9(14), 1658. https://doi.org/10.3390/math9141658







