Schistosomiasis Model Incorporating Snail Predator as Biological Control Agent
Abstract
1. Introduction
2. Mathematical Preliminaries
- A1:
- is the linearization matrix of (1) around equilibrium 0, and ω is evaluated at 0. Zero is a simple eigenvalue of , and the other eigenvalues of have a negative real part.
- A2:
- Matrix has a right eigenvector and a left eigenvector corresponding to the zero eigenvalue. Let be the component of f andThe dynamics of System (1) around 0 is totally determined by the signs of A and B.
- (i)
- . When with , 0 is asymptotically stable, and there is a positive unstable equilibrium. When with , 0 is unstable, and there is a negative asymptotically stable equilibrium;
- (ii)
- . When with , 0 is unstable. When with , 0 is asymptotically stable, and there is a positive unstable equilibrium;
- (iii)
- . When with , 0 is unstable, and there is a negative asymptotically stable equilibrium. When with , 0 is stable and a positive unstable equilibrium appears;
- (iv)
- . When ω changes from negative to positive, 0 changes its stability from stable to unstable. Correspondingly, a negative unstable equilibrium becomes positive and asymptotically stable.
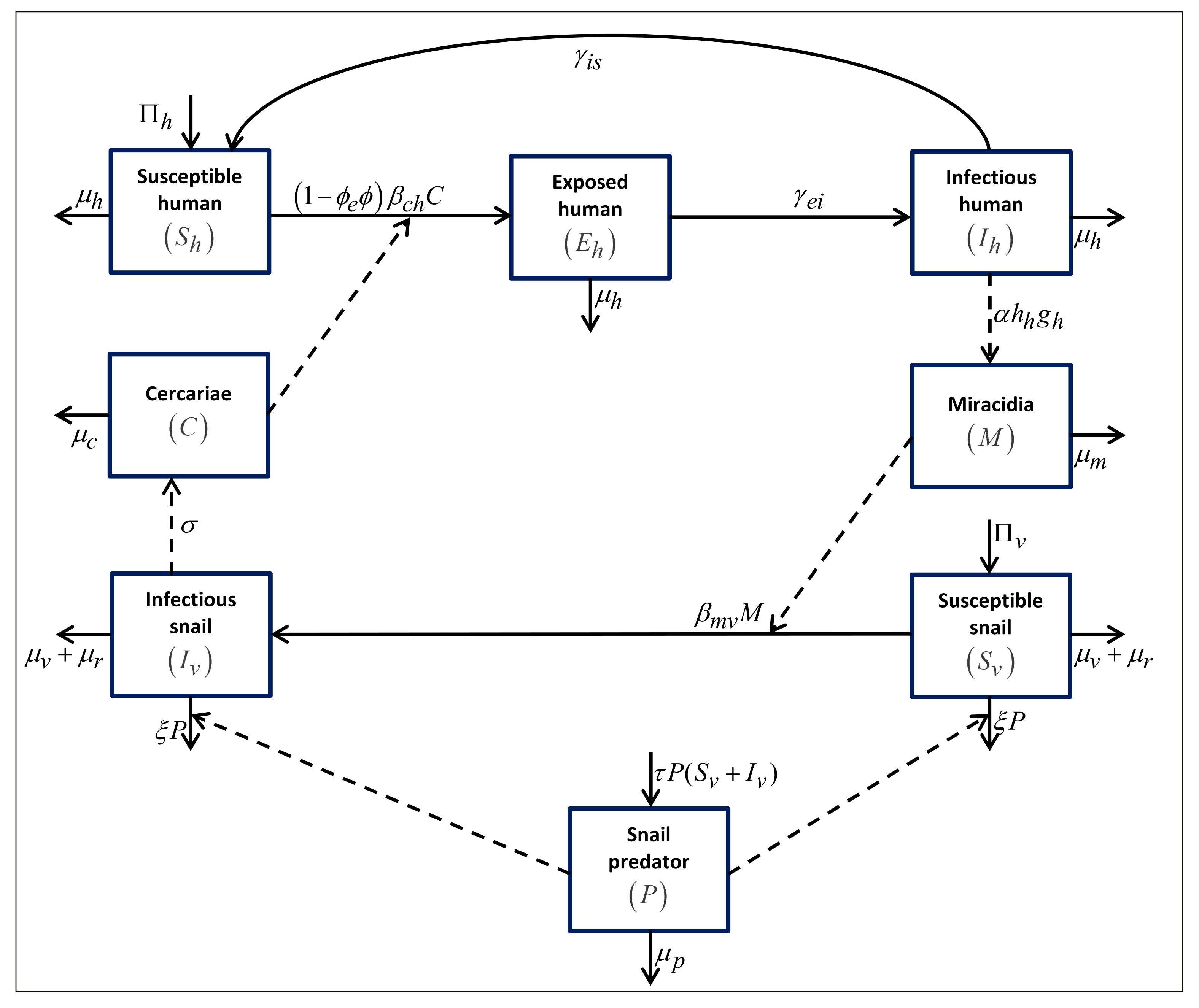
3. Model Formulation and Basic Properties
3.1. Model Formulation
3.2. Invariant Region
3.3. Equilibrium Points and Basic Reproduction Number
- Disease-free equilibrium point .always exists in .
- Endemic equilibrium point .whereIt is clear that exists in if .
- Disease-free equilibrium point .exists in if .
- Endemic equilibrium point .whereIt is clear that exists in if and .
4. Stability Analysis
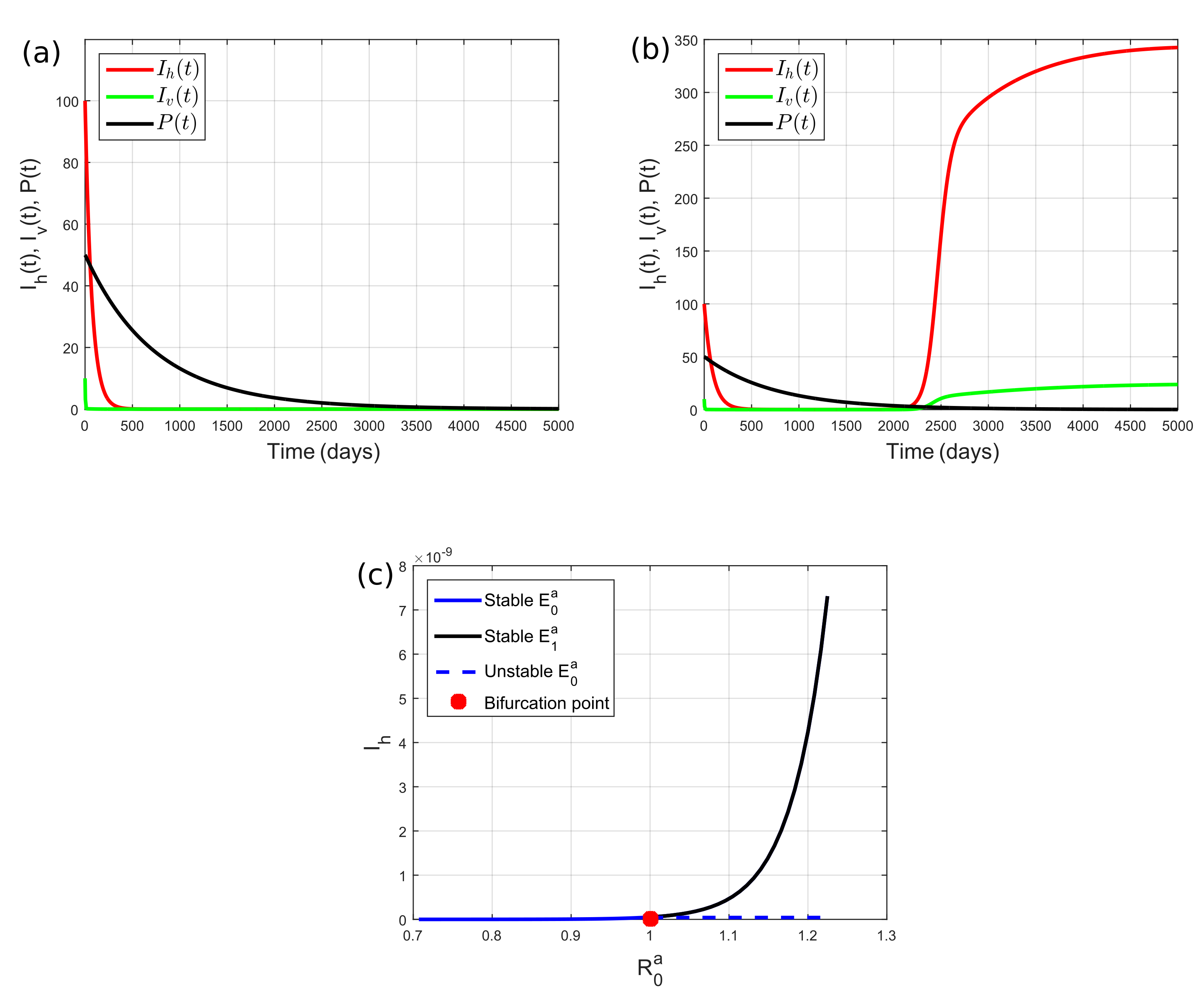
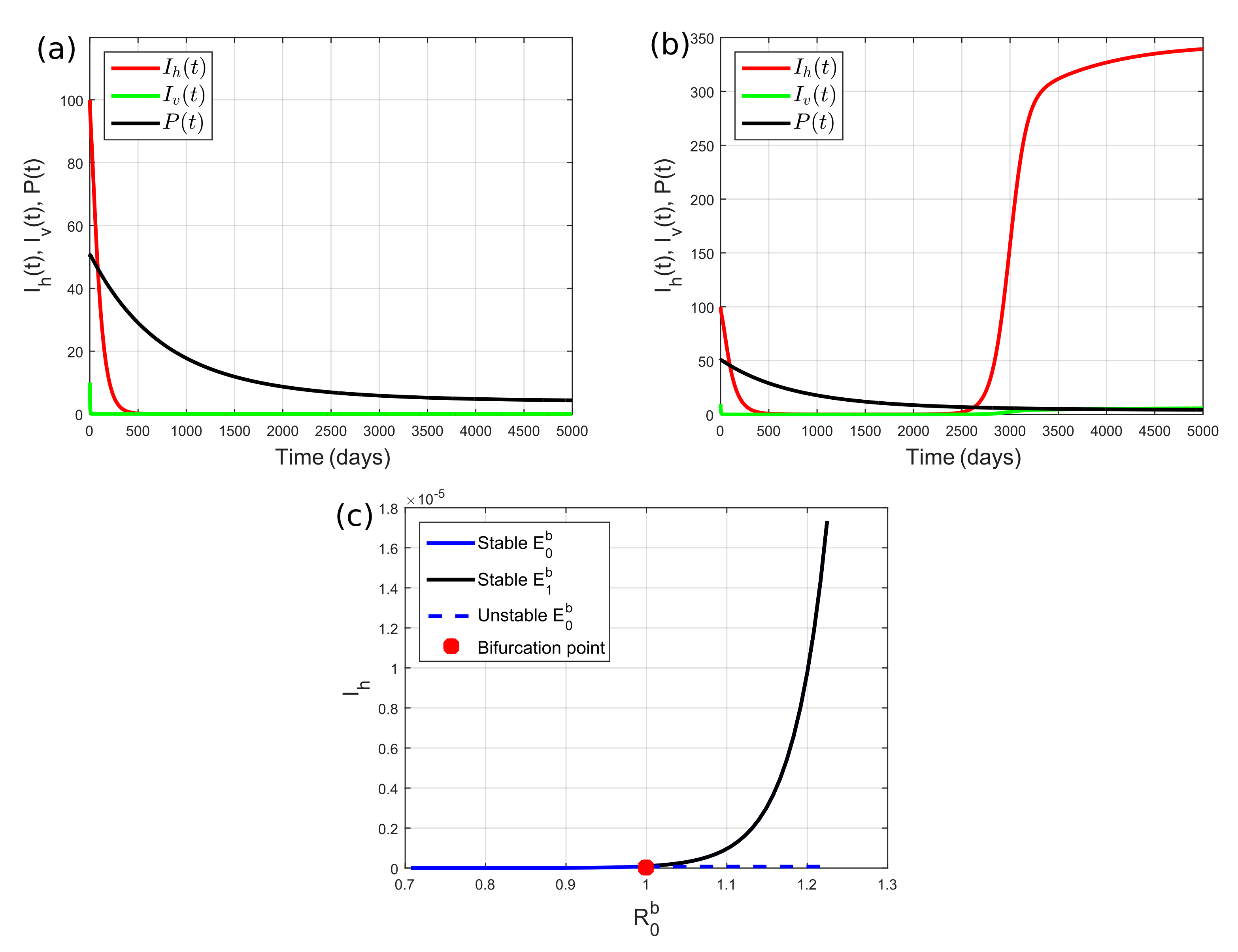
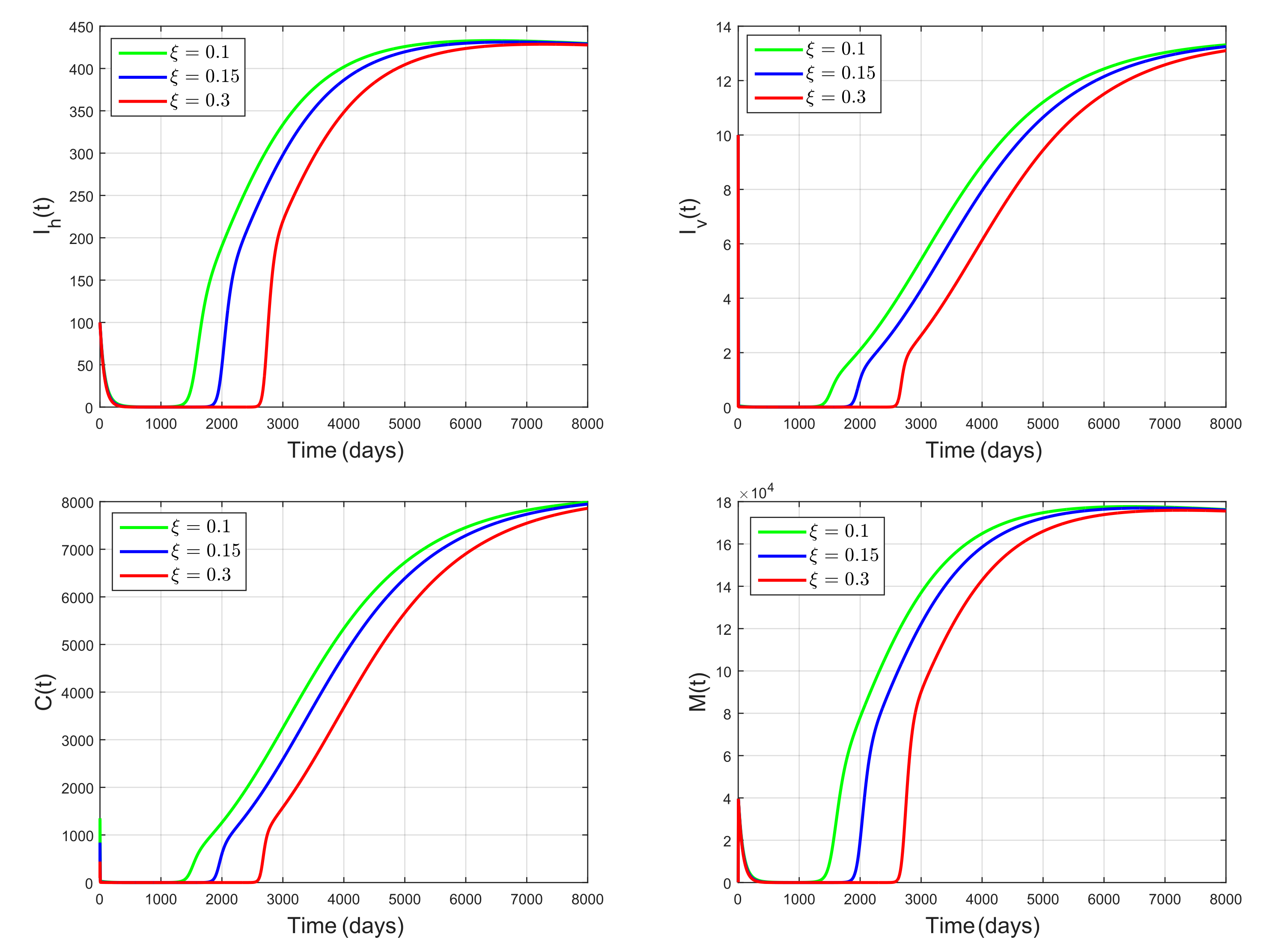
5. Numerical Simulations
5.1. Predator Becomes Extinct
5.2. Predator Survives
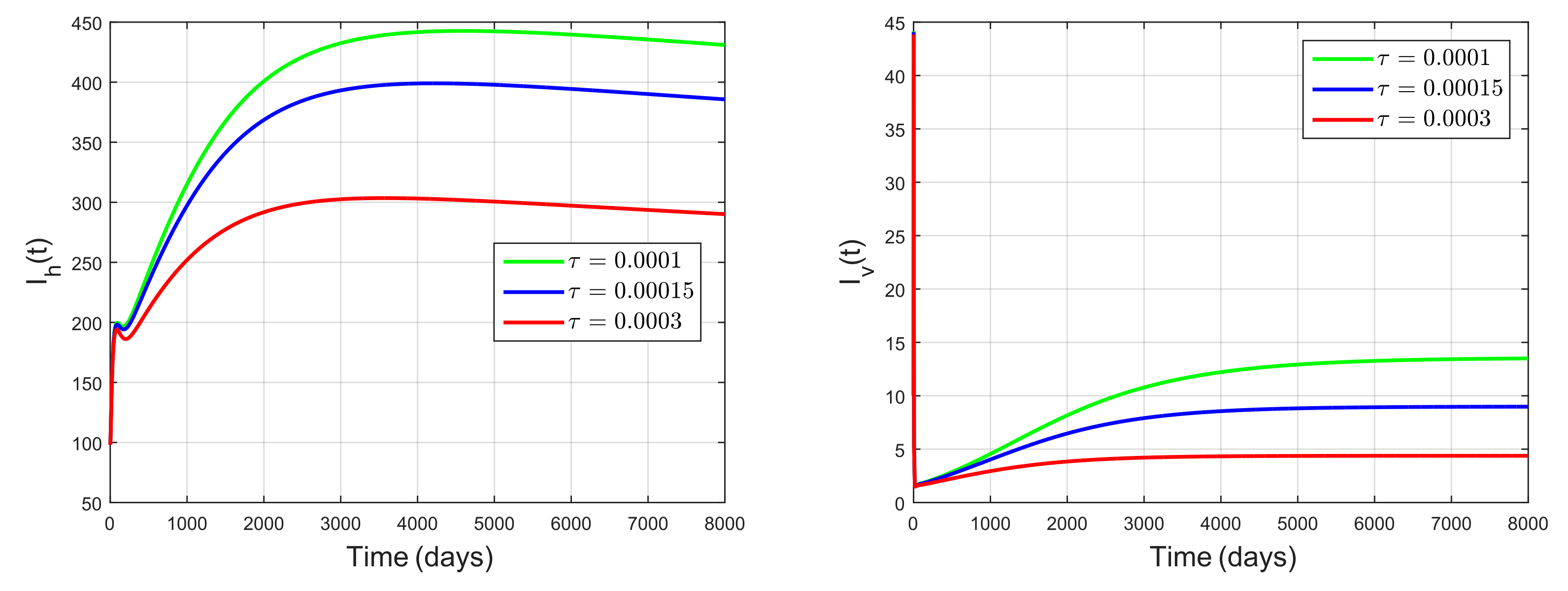
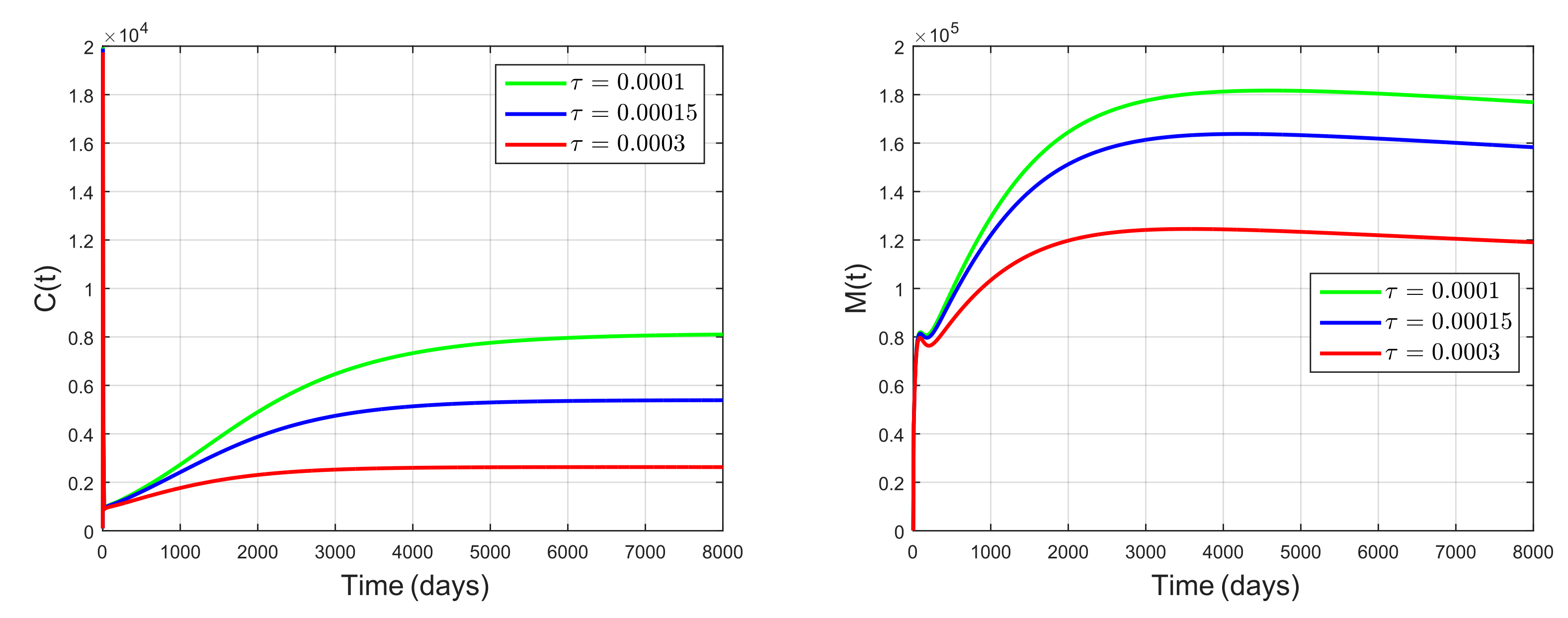
5.3. Impact of Snail Predator as Biological Control Agent
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Ross, A.G.; Chau, T.N.; Inobaya, M.T.; Olveda, R.M.; Li, Y.; Harn, D.A. A new global strategy for the elimination of schistosomiasis. Int. J. Infect. Dis. 2017, 54, 130–137. [Google Scholar] [CrossRef]
- WHO. Schistosomiasis: Progress Report 2001–2011, Strategic Plan 2012–2020; World Health Organization Press: Geneva, Switzerland, 2013; p. 74. [Google Scholar]
- Rollinson, D.; Knopp, S.; Levitz, S.; Stothard, J.R.; Tchuem Tchuenté, L.A.; Garba, A.; Mohammed, K.A.; Schur, N.; Person, B.; Colley, D.G.; et al. Time to set the agenda for schistosomiasis elimination. Acta Trop. 2013, 128, 423–440. [Google Scholar] [CrossRef]
- Arostegui, M.C.; Wood, C.L.; Jones, I.J.; Chamberlin, A.J.; Jouanard, N.; Faye, D.S.; Kuris, A.M.; Riveau, G.; De Leo, G.A.; Sokolow, S.H. Potential Biological Control of Schistosomiasis by Fishes in the Lower Senegal River Basin. Am. J. Trop. Med. Hyg. 2019, 100, 117–126. [Google Scholar] [CrossRef]
- Coelho, P.; Caldeira, R. Critical analysis of molluscicide application in schistosomiasis control programs in Brazil. Infect. Dis. Poverty 2016, 5, 57. [Google Scholar] [CrossRef]
- King, C.H.; Bertsch, D. Historical Perspective: Snail Control to Prevent Schistosomiasis. PLoS Negl. Trop. Dis. 2015, 9, e0003657. [Google Scholar] [CrossRef]
- Sokolow, S.H.; Huttinger, E.; Jouanard, N.; Hsieh, M.H.; Lafferty, K.D.; Kuris, A.M.; Riveau, G.; Senghor, S.; Thiam, C.; N’Diaye, A.; et al. Reduced transmission of human schistosomiasis after restoration of a native river prawn that preys on the snail intermediate host. Proc. Natl. Acad. Sci. USA 2015, 112, 9650–9655. [Google Scholar] [CrossRef]
- Sokolow, S.H.; Wood, C.L.; Jones, I.J.; Swartz, S.J.; Lopez, M.; Hsieh, M.H.; Lafferty, K.D.; Kuris, A.M.; Rickards, C.; De Leo, G.A. Global assessment of schistosomiasis control over the past century shows targeting the snail intermediate host works best. PLoS Negl. Trop. Dis. 2016, 10, e0004794. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, G. The dynamics of helminth infections, with special reference to schistosomes. Trans. R. Soc. Trop. Med. Hyg. 1965, 59, 489–506. [Google Scholar] [CrossRef]
- Chiyaka, E.T.; Garira, W. Mathematical Analysis of the Transmission Dynamics of Schistosomiasis in the Human-Snail Hosts. J. Biol. Syst. 2009, 17, 397–423. [Google Scholar] [CrossRef]
- Gao, S.; Liu, Y.; Luo, Y.; Xie, D. Control problems of a mathematical model for schistosomiasis transmission dynamics. Nonlinear Dyn. 2011, 63, 503–512. [Google Scholar] [CrossRef]
- Ding, C.; Sun, Y.; Zhu, Y. A schistosomiasis compartment model with incubation and its optimal control. Math. Methods Appl. Sci. 2017, 40, 5079–5094. [Google Scholar] [CrossRef]
- Nur, W.; Trisilowati; Suryanto, A.; Kusumawinahyu, W.M. Mathematical model of schistosomiasis with health education and molluscicide intervention. J. Phys. Conf. Ser. 2021, 1821, 012033. [Google Scholar] [CrossRef]
- Nur, W.; Trisilowati; Suryanto, A.; Kusumawinahyu, W.M. Mathematical Modelling of Schistosomiasis Transmission Dynamics in Traditional Cattle Farmer Communities. In Proceedings of the 1st International Conference on Mathematics and Mathematics Education (ICMMEd 2020), Ambon, Indonesia, 26 November 2020; Atlantis Press: Dordrecht, The Netherlands, 2021; pp. 462–470. [Google Scholar] [CrossRef]
- Diaby, M.; Iggidr, A.; Sy, M.; Sène, A. Global analysis of a schistosomiasis infection model with biological control. Appl. Math. Comput. 2014, 246, 731–742. [Google Scholar] [CrossRef][Green Version]
- Okamoto, K.W.; Amarasekare, P. The biological control of disease vectors. J. Theor. Biol. 2012, 309, 47–57. [Google Scholar] [CrossRef]
- Okamoto, K.W.; Gould, F.; Lloyd, A.L. Integrating Transgenic Vector Manipulation with Clinical Interventions to Manage Vector-Borne Diseases. PLoS Comput. Biol. 2016, 12, e1004695. [Google Scholar] [CrossRef][Green Version]
- Lemos-Paião, A.P.; Silva, C.J.; Torres, D.F. A cholera mathematical model with vaccination and the biggest outbreak of world’s history. AIMS Math. 2018, 3, 448–463. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Song, B. Dynamical Models of Tuberculosis and Their Applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef]
- Nelwan, M.L. Schistosomiasis: Life Cycle, Diagnosis, and Control. Curr. Ther. Res. 2019, 91, 5–9. [Google Scholar] [CrossRef]
- Gryseels, B.; Polman, K.; Clerinx, J.; Kestens, L. Human schistosomiasis. Lancet 2006, 368, 1106–1118. [Google Scholar] [CrossRef]
- Bergquist, R.; Zhou, X.N.; Rollinson, D.; Reinhard-Rupp, J.; Klohe, K. Elimination of schistosomiasis: The tools required. Infect. Dis. Poverty 2017, 6, 158. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Guo, S. Dynamics of A SIRC Epidemiological Model. Electron. J. Erential Equ. 2017, 2017, 1–18. [Google Scholar]
- Yang, X.; Chen, L.; Chen, J. Permanence and positive periodic solution for the single-species nonautonomous delay diffusive models. Comput. Math. Appl. 1996, 32, 109–116. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Mathematics for Engineers and Scientists; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Cook, M.Y. Flight Dynamics Principles, 2nd ed.; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Marghitu, D. Mechanical Enginer’s Handbook; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Liénard, A.; Chipart, M.H. Sur le signe de la partie réelle des racines d’une équation algébrique. J. Math. Pures Appl. 1914, 10, 291–346. [Google Scholar]
- Meiss, J.D. Differential Dynamical Systems; Society for Industrial and Applied Mathematics: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Lundström, N.L.P. How to find simple nonlocal stability and resilience measures. Nonlinear Dyn. 2018, 93, 887–908. [Google Scholar] [CrossRef]
- van Kan, A.; Jegminat, J.; Donges, J.F.; Kurths, J. Constrained basin stability for studying transient phenomena in dynamical systems. Phys. Rev. E 2016, 93, 042205. [Google Scholar] [CrossRef]
- Vucetich, J.A.; Hebblewhite, M.; Smith, D.W.; Peterson, R.O. Predicting prey population dynamics from kill rate, predation rate and predator-prey ratios in three wolf-ungulate systems. J. Anim. Ecol. 2011, 80, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Metz, J.A.J.; Sabelis, M.W.; Kuchlein, J.H. Sources of variation in predation rates at high prey densities: An analytic model and a mite example. Exp. Appl. Acarol. 1988, 5, 187–205. [Google Scholar] [CrossRef]
- Han, L.; Ma, Z.; Hethcote, H. Four predator prey models with infectious diseases. Math. Comput. Model. 2001, 34, 849–858. [Google Scholar] [CrossRef]
| Parameter | Description |
|---|---|
| Recruitment rate of humans | |
| Effectiveness of education in reducing contact between humans and cercariae | |
| Education coverage | |
| Cercaria infection rate on susceptible humans | |
| Recovery rate of infectious humans | |
| Natural death rate of humans | |
| Latent period | |
| Recruitment rate of snails | |
| Miracidia infection rate on susceptible snails | |
| Natural death rate of snails | |
| Molluscicide-related death rate of snails | |
| Predation rate | |
| Conversion rate | |
| Cercaria production rate | |
| Parasite-egg hatch rate | |
| Number of eggs per gram of stool | |
| Average weight of human stool per day | |
| Natural death rate of snail predators | |
| Natural death rate of cercariae | |
| Natural death rate of miracidiae |
| Column 1 | Column 2 | Column 3 | Column 4 | |
|---|---|---|---|---|
| 1 | 0 | |||
| 0 | ||||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 |
| Column 1 | Column 2 | Column 3 | Column 4 | |
|---|---|---|---|---|
| 1 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 |
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | |
|---|---|---|---|---|---|
| 1 | 0 | ||||
| 0 | |||||
| 0 | 0 | ||||
| 0 | 0 | ||||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
| Column 1 | Column 2 | Column 3 | Column 4 | Column 5 | |
|---|---|---|---|---|---|
| 1 | 0 | ||||
| 0 | 0 | ||||
| 0 | 0 | ||||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nur, W.; Trisilowati; Suryanto, A.; Kusumawinahyu, W.M. Schistosomiasis Model Incorporating Snail Predator as Biological Control Agent. Mathematics 2021, 9, 1858. https://doi.org/10.3390/math9161858
Nur W, Trisilowati, Suryanto A, Kusumawinahyu WM. Schistosomiasis Model Incorporating Snail Predator as Biological Control Agent. Mathematics. 2021; 9(16):1858. https://doi.org/10.3390/math9161858
Chicago/Turabian StyleNur, Wahyudin, Trisilowati, Agus Suryanto, and Wuryansari Muharini Kusumawinahyu. 2021. "Schistosomiasis Model Incorporating Snail Predator as Biological Control Agent" Mathematics 9, no. 16: 1858. https://doi.org/10.3390/math9161858
APA StyleNur, W., Trisilowati, Suryanto, A., & Kusumawinahyu, W. M. (2021). Schistosomiasis Model Incorporating Snail Predator as Biological Control Agent. Mathematics, 9(16), 1858. https://doi.org/10.3390/math9161858






