1. Introduction
Symmetry is a major organizational principle in different kinds of design [
1,
2]. The principle is present in living matter formed by evolutionary processes, as biological entities frequently possess a substantial degree of symmetry. The principle equally applies to man-made objects, whether it be in engineering, where symmetry is economical due to the use of identical components or parts, or in art, where playing with symmetry is a way of expressing aesthetic concepts.
Bio-inspired generative art is a field in evolutionary computation dealing with employing algorithmic ideas and templates observed in nature for creating artworks [
3,
4,
5]. As symmetry is both an important aesthetic concept in art and an organizational principle in biological entities, it follows rather naturally that different forms and meanings of symmetry matter to bio-inspired generative art, see e.g., [
6,
7,
8,
9] for explicitly addressing the topic. However, thus far in generative art, there is a certain lack of works dealing with symmetric color transformations.
Thus, in this paper, we focus on a special kind of symmetry: color symmetry. We assume that geometrical objects have symmetry properties that can be described by their symmetry group. If the objects can be colored, then color symmetry implies that the colors of the objects are derived consistently from the symmetry group [
8,
10,
11,
12,
13,
14]. A particularly straightforward method of obtaining symmetry properties frequently employed in visual art is to interpret the geometrical objects as motifs, which may repeat themselves. In this case, color symmetry means a symmetry-consistent coloring of each motif and its copies.
An illustrative example from the history of art for exploring the relationships between geometrical objects, motifs and colors is Vasily Kandinsky’s
Farbstudie-Quadrate mit konzentrischen Ringen (Color study. Squares with concentric rings), (1913) [
15].
Figure 1a shows the study, which consists of 12 squares filling a rectangle of three rows with each square containing a central circle surrounded by concentric rings. Some of the central circles are slightly off-center or almost squarish, and all are surrounded by concentric circles of different colors.
The colors are mainly the primary and the secondary colors of the RYB (red–yellow–blue) color wheel [
16,
17]; however, there are also various tertiary colors. Sometimes the circles’ colors repeat themselves, and other circles traverse a color space. For instance, we have the sequence (from the inside out) red–blue–red–yellow–blue–black in the upper square second to the right. The arrangement can be interpreted as 12 iterations (but also as more or less faithful copies) of a motif.
For a strict symmetry we might expect the geometrical form and/or the color of a constant element within the motif to differ each time, or to stay constant all the time; however, this was not Kandinsky’s intention. It is rather an exploration of the motifs taken from basic geometrical forms (squares and circles). In addition, we have variations in the form and color within individual copies and, throughout the study, experiments with different hues and brightness. Nevertheless, we may see Kandinsky’s color study as anticipating and preceding some elements of the conceptual framework of color symmetry.
In this paper, the motif generation preceding the actual experiments with color symmetry is performed using algorithms implementing a stigmergic design. Stigmergy is a principle of self-organization in nature, particularly in swarms, see e.g., [
7,
18,
19,
20,
21,
22] for applications in bio-inspired generative art. Similarly to previous works that used Kandinsky’s art as an inspiration of generative art [
5,
23,
24], some of the examples of color symmetry shown in this paper adopt some design elements from the color study shown in
Figure 1a.
The paper is structured as follows. After these prefatory remarks,
Section 2 briefly reviews the meanings and concepts of color, symmetry, and color symmetry in visual art. We also discuss how color symmetry can be imposed by color permutations. We additionally show how color symmetry can be applied to image distortions of pre-existing images.
Section 3 recalls the stigmergic generation of geometrical objects and, in particular, shows the motif design used in the paper. Numerical experiments and visual results are given in
Section 4, before concluding remarks close the paper with a summary and pointers to future work.
2. Color, Symmetry, and Color Symmetry
For describing the significance and meaning of color in art, there is the dictum of the Hungarian-French 20th century painter and graphic designer Victor Vasarely [
25]: “Every form is a base for color, every color is the attribute of a form.” Put differently, if we see visual art as composed of geometrical objects, then color can be viewed as a property of these objects. If the artistic content of the artwork relates to how and where the geometrical objects are arranged in the image, then different colors allow for distinguishing and contrasting the objects. Suppose there is a point
from a point set in a two-dimensional
-plane. Then, a color
is an attribute (or property) of the point
. In other words, a colored point is specified by
. Geometrical objects are built from a set of points. The objects are (monochromatically) colored for all points of the set with the same color.
A geometrical object may possess symmetry, which implies that the object is invariant under certain transformations [
1,
2,
26,
27]. The set of transformations under which the geometrical object is symmetric yields the symmetry group
of the object. On the one hand, we may focus on the symmetry properties of a single geometrical object. For creating or analyzing images, on the other hand, we may consider a geometrical object (which may or may not have symmetry properties itself) as a motif. In an image, such a motif may appear in several copies, and we can study the symmetry properties between these copies.
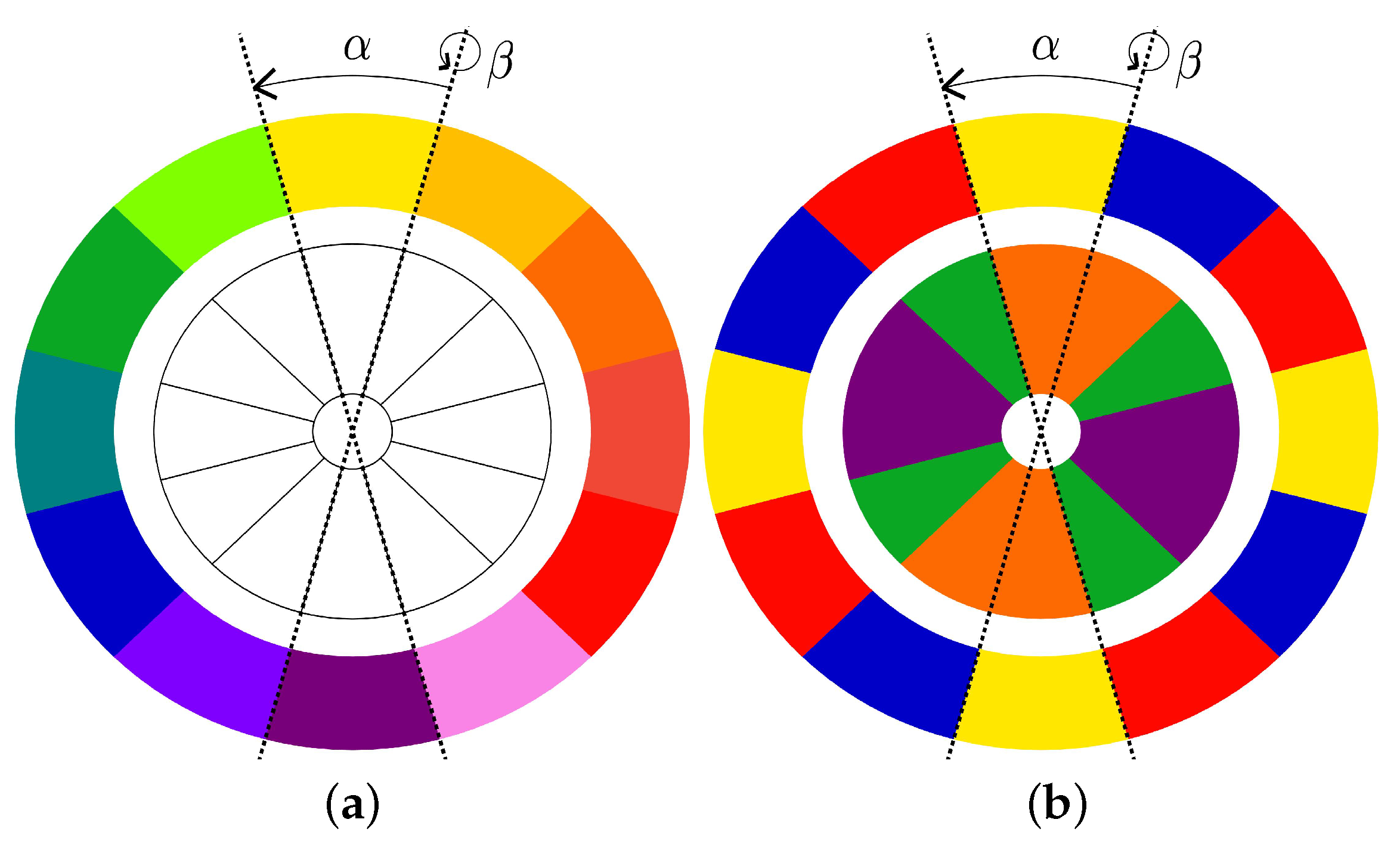
Suppose we have a circular structure (a wheel) with 12 slots as in
Figure 2. Each of the two wheels consists of an inner and an outer circle. Now, let us define a slot to be a motif attributable with a color. Thus, each circle consists of 12 copies of the motif, and we can discuss the symmetry properties. In this discussion, we may assign symmetry to the copies of the motif regardless of the color or taking into account the color. The former implies geometrical symmetry described by isometric transformations, and the latter leads us to color symmetry.
First, we assume the color of the slots is not taken into account or the color of all the slots is the same, see, for instance, the inner circle of
Figure 2a. We denote the slots according to the digits of a clock face with axes connecting slots on the right-hand side of the slot. Then, the symmetry group of the inner circle is the dihedral group
(or
in orbifold notation). Let
be a rotation counter-clockwise with 30
and
be a reflection in the axis connecting 12 and 6 o’clock, see
Figure 2a for illustration. We define that symmetries are composed from left to right. For instance,
is first a reflection
and then a rotation
.
Thus,
is a reflection in the axis connecting 11 and 5 o’clock. Likewise,
is a reflection in the axis connecting 10 and 4 o’clock, and so on. The symmetry group
is generated by
and
with
,
. We obtain
which is of the order 24.
We now add color as an attribute to the slots. The 12 slots can be colored with up to 12 different colors, see the outer circle of
Figure 2a and both circles of
Figure 2b. The colors of the outer circle of
Figure 2a match the RYB (red–yellow–blue) color wheel [
16,
17], which is also called the standard artistic color wheel. It defines three primary colors: red, yellow, and blue at 4, 12, and 8 o’clock, respectively, on the circle. Mixing two of these colors each gives the three secondary colors: orange (red and yellow), purple (red and blue), and green (yellow and blue) at 2, 6, and 10 o’clock. From these three primary and three secondary colors, we obtain another six tertiary colors by mixing: vermilion (red and orange), amber (orange and yellow), chartreuse (yellow and green), teal (green and blue), violet (blue and purple), and magenta (purple and red). The colors of the circles of
Figure 2b are also taken from the RYB color wheel.
Now, we consider the color symmetry of the colored slots. An element
is called a color symmetry if
g permutes the coloring of the slots’ colors consistently with the symmetry group
[
11,
13,
14]. In other words,
pre-defines the coloring of each copy of the motif. More specifically, some (or all) elements in
change colors, while the remaining elements in
preserve colors. Particularly from an artistic point of view, color symmetry becomes interesting if there is a mix between color-changing and color-preserving elements of
.
The color symmetry of the outer circle of
Figure 2a, which is the RYB circle with 12 colors, is trivial. Of the 24 elements of
, all non-trivial elements change colors, while only the identity
preserves colors. As more interesting color symmetries are obtained if the number of copies of the motif exceeds the number of colors, we next consider the color circles with three colors, see
Figure 2b, where the outer circle takes the primary colors and the inner circle takes the secondary colors. For such a threefold coloration, the color permutation has order 3. Recall that the symmetry group
of the 12-slot circle specifies counter-clockwise rotations about 30
and reflections along 12 axes. For the outer circle, all reflections
change colors (except the trivial
). Rotations
change or preserve the colors according to a color permutation. Using Cauchy’s two-line notation, the color permutation associated with the rotation
can be expressed by
The color permutation implies that the colors are preserved for the rotations , , and , which are the rotations about 90.
For the inner circle, almost all rotations
change color (except the trivial
and
). Reflections
change or preserve the colors according to the color permutation
which implies that the reflections
, and
preserve colors.
The color symmetry on a wheel with a finite number of slots such as in
Figure 2 implies a transitive color permutation, as shown with the examples
and
, see Equations (
1) and (
2). In other words, for any pair of colors on the wheel, there is an element
that maps one color of the pair to the other [
11]. Possible generalizations could mean that one color is “color-symmetric” to two or more colors, or that an element
is connected with more than one color mapping, for instance by applying to different sections of the motif differently. Another implication of the color symmetry discussed thus far is that it applies to motifs that are either pre-existing or designed in another way.
We next discuss color symmetry that applies to pre-existing images. Suppose we have a rectangular source images, for instance the Kandinsky study shown in
Figure 1a. The symmetry group of the rectangle is the dihedral group
. The rotation
is now counter-clockwise 180
, the reflections
and
are in the horizontal and vertical axis. The symmetry group is of order 4:
The reflection axes divide the image into four sections, north-east (
ne), north-west (
nw), south-east (
se), and south-west (
sw). Each section can be mapped into any other section by the elements of the symmetry group. The sections are separated in
Figure 1a by white lines (which are not present in the original Kandinsky study). We assume that the image is composed of
pixels and each pixel
has a color
in a HSV color space:
. In the following discussion (and also in the experiments reported later) the focus is on the hue
, while the saturation
and the value (brightness)
remain constant; however, of course the same method can be applied to the whole HSV color space.
We now define the color permutation associated with the symmetry group by a map
, which is a mapping of the hue component of the HSV color space onto itself. Thus, for rectangular source images, a color symmetry can be imposed by a color permutation as follows. We define a reference section, for instance north-east (
ne). The colors in this section remain unchanged. The colors of the pixels of the other sections are changed according to the rectangle’s symmetry group. For instance, the color permutation associated with the rotation is
which implies that the hue
of all pixels
in
sw is changed from
to
. For the remaining sections
nw and
se, we may, likewise, define for the reflections
Figure 1b shows an example using the Kandinsky study (
Figure 1a) as a source image. As color maps, the functions
,
, and
are used.
Such a design of color symmetry implies that the color permutations according to Equations (
4) and (
5) most likely still have finite order. Of course, any color described by the hue
could be mapped to another color
. However, most likely, the HSV color space used in computer graphics effectively imposes a finite number of different colors. Nevertheless, the number of different colors might be very large, which opens up a rich variety of color effects.
The visual result in
Figure 1b shows a substantial variety of color shifts in the sections affected by color symmetry, particularly for the color maps involving trigonometric functions. As the saturation and brightness of the pixels are preserved while the hue is changed, the “color symmetric” sections of the image resembles the original image; however, we also have a kind of alienation effect (or distancing effect) in terms of color.
In
Section 4, generative art, which is the result of experiments with color, symmetry, and color symmetry, is presented and discussed. This is done in connection with stigmergic generation algorithms, which are discussed next.
3. Stigmergy and Generative Art
Stigmergy is a bio-inspired paradigm of self-organization in swarms. The members of the swarm coordinate themselves by indirect communication, for instance by deposing and collecting visual, olfactory or tactile markers. This paradigm has been used as a computational framework for generating swarm art, see for example [
3,
4,
5,
7,
18,
19,
28,
29].
In the experiments with designing color symmetry presented in this paper, we used a model of stigmergic nest construction. The model describes the nest building by the ant species
T. albipennis and was proposed by Urbano [
22]. The nests are constructed by the ants collecting sand grains from a foraging ground and deposing them to build a closed curved outer boundary wall around the nest. Different colonies of ants may be sensitive to sand with different colors, thus, making it possible to construct polychromatic swarm paintings.
The nest construction modelling
T. albipennis behavior builds toroidal walls [
7,
22]. However, it was suggested by Greenfield [
19] that the boundary walls could also follow other types of curves, which would make them more interesting than circles from a geometrical point of view. In such an interpretation of boundary walls, different colonies would be sensitive to different types of walls. In the following, this idea is adopted and the stigmergic art discussed In this paper is constructed from the following algorithmic framework. Each nest has a center point
in a 2D plane. The nest is further characterized by a boundary wall with radius
, which describes the distance to the center point in polar coordinates with
,
. For instance, by setting
, circles can be constructed by
, and
ℓ-leaf roses are obtained for
and
. Archimedean spirals are described by
, with
and
k specifying the desired length of the spiral.
The nest’s boundary wall is built by ants collecting grain with the nest’s boundary type from the foraging ground. An ant has a certain distance from the nest’s center point and can either carry a grain or not. If it carries a grain it moves randomly toward the center point and deposes the sand grain with a certain probability within the vicinity of the radius . Using parameters, we can control the speed of nest formation and also the wall thickness. If the ant does not carry a grain, it moves randomly away from the center point and collects a sand grain with a second probability.
Again, we can control, by parameters, the collecting speed and foraging range. The visual effect is that boundary walls are built that have a grain density resembling realizations of a random variable with the center
—for instance, a Gaussian distribution with
. Contrary to previous works [
7,
19,
22], we assume that the foraging ground is completely emptied in the nest building activity. Therefore, we can describe the
i-th nest by its center point, its color, and its radius:
. We consider these nests as motifs.
4. Experiments and Visual Results
In the sections above, a framework was set out for the stigmergic generation of motifs. In addition, the motifs may be the object of experiments designing color symmetries. In the following, we present and discuss artistic experiments generating visual art using this framework.
A first set of experiments takes the nests generated by stigmergic design, colors the grains according to color-symmetric principles, and places them on a black canvas. The examples in
Figure 3 are directly inspired by Kandinsky’s color study shown in
Figure 1a. The images seize the idea of 12 squares filling a rectangle in three rows. The squares contain circles as well as Archimedean spirals and
ℓ-leaf roses. The nests are colored with elements from the RYB color wheel (
Figure 2a). The 12 squares fit exactly the whole set of primary, secondary, and tertiary colors of the RYB wheel.
Accordingly, the upper left image (
Figure 3a), for instance, has six squares and six inner circles on the left hand side with primary and secondary colors, while the outer circles are the complementary colors (which are exactly opposite on the RYB color wheel). The six remaining squares on the right hand side of the image do the same with the tertiary colors.
Thus, a vertical reflection imposes a color symmetry from primary and secondary colors to tertiary colors. Based on the symmetry group (
3), the image is generated by the color permutation
for the inner circle and the outer square, while there is
for the circle in the middle.
The other images similarly play with squares, circles, Archimedean spirals, and
ℓ-leaf roses and the color symmetries between the RYB colors. Of particular note, in the lower left image, the primary colors are preserved by vertical reflection, while the secondary colors may change. The images in
Figure 4 leave behind the rows-and-columns arrangement and place the nests at any prescribed locations on the canvas. Again, isometric symmetry induces color symmetry.
In the upper right image (
Figure 4b), the geometrical aspect of symmetry is almost invisible; however, we have color symmetry insofar as any circle with an Archimedean spiral has an color-symmetric counterpart, which is obtained by a rotation about a random center point. The radii of the smallest seven circles in the lower left image (
Figure 4d) follow a Fibonacci series with the circles on the left-hand side of the image following a Fibonacci circle curve as proposed by Happersett [
30]. The Fibonacci circle curve places subsequent circles according to the Golden Angle 180
.
A second set of experiments uses the framework of stigmergic art and color symmetry to generate images based on source images. Modifying the source images with the aim of creating visual art that resembles known pictures or paintings but also provides a reinterpretation has also been a topic in bio-inspired generative art. For example, see the modification of source images from the history of art by stochastic hillclimbers, plant propagation algorithms, simulated annealing, or particle swarms [
31,
32], as well as image transitions by random walks [
5,
23,
33]. In the experiments reported here, two well-known painting by Johannes Vermeer were used:
Girl with a Pearl Earring (1665) and
View of Delft (1661). (
Figure 5a,b).
In a first step, the colors in these images were modified using color permutations similar to Equations (
4) and (
5). In addition to the functions given above, the color maps
,
, and
were used, see the examples of a triangular pattern and a chess board pattern with 16 elements in
Figure 5c,d.
An initial experiment shows color symmetry imposed by triangular section of the rectangular source image, see
Figure 6. In the left image, all reflections change colors, while, in the right image, up-down reflection preserves colors. Thus, the images are generated by color permutations as defined by Equation (
5). For further examples, see also [
9].
Subsequently, patterns of nests are generated where the grains take the colors of the source image while the grains of the symmetric nest patterns take the color-symmetric hues.
Figure 7 and
Figure 8 show the results, which can be seen as a quotation and homage to Vermeer’s famous paintings. Again, the original art works remain recognizable, while, at the same time, an alienation or distancing effect occurs.