Approximation of Fixed Points of Multivalued Generalized (α,β)-Nonexpansive Mappings in an Ordered CAT(0) Space
Abstract
:1. Introduction and Preliminaries
- (1)
- is nonexpansive if
- (2)
- is quasi-nonexpansive if is nonempty and for any
- (i)
- (ii)
- (i)
- Define a mapping byFor each the value is called asymptotic radius of at v [1].
- (ii)
- Denote asymptotic radius of relative to M by
- (iii)
- (1)
- the Mann iterative process is defined by ,where satisfiesand ,
- (2)
- the Ishikawa iterative process is defined aswith and satisfying and , and .
- (i)
- monotone nonexpansive if is monotone and such that for any comparable ,
- (ii)
- monotone quasi-nonexpansive if is monotone with and such that whenever are comparable,holds.
2. Multivalued Generalized -Nonexpansive Mapping
- (a)
- is monotone,
- (b)
- satisfies (9) for all and either or .
- (1)
- Multivalued generalized (α,β)-nonexpansive mappings extend and generalize the class of mappings introduced by [31]. Indeed, if then the mapping is reduced to multivalued generalized α-nonexpansive mapping.
- (2)
- Multivalued generalized (α,β)-nonexpansive mappings contain the class of mappings satisfying the Condition (C). Clearly, substituting we get our desired mapping.
- (3)
- Every nonexpansive mapping is generalized -nonexpansive mapping.
- (1)
- The mapping does not satisfy the Condition (C) on M and therefore is not nonexpansive. Indeed, for and we haveandThus, . Note thatIf then we haveAlso,If then we haveThusimplies that .
- (2)
- Now, we show that is multivalued generalized ()-nonexpansive mapping, where and . We consider the following cases.CASE-IIf and Observe thatandFor and , we obtain thatCASE-IIIf thenNow gives thatSimilarly,Now givesThusAlso,For and , we obtain thatHence is -nonexpansive multivalued mapping.
- (1)
- If satisfies the Condition (C) as defined in then satisfies the Condition .
- (2)
- If satisfies the Condition with , then is quasi-nonexpansive.
- (1)
- If satisfies the Condition (C) then it trivial that satisfies the Condition for
- (2)
- Let then,As satisfies the Condition (), there exists such thatholds. Then,impliesSince , it follows that . Hence is quasi-nonexpansive multivalued mapping.
- (1)
- (2)
- Either or
- (3)
- Either or
- (1)
- As, we havewhich implies thatand hencewe havewhich implies thatand hence
- (2)
- Suppose that and From (i), we getThus,implies thatAlso, we haveThus,Combining the inequalities and we obtain a contradiction. Hence (ii) holds.
- (3)
- The condition (iii) directly follow from the condition (ii).
3. Convergence Results
- (1)
- or for any and .
- (2)
- provided that -converges to a point
- (1)
- If then by convexity of order interval and we have,Thus, there exists such thatAs, is monotone there exists such that . Again by convexity of order interval and we haveThus,From and we havewhich implies thatHence the statement is true forAssuming the statement is true for n, that is, for we haveNow, we show is true forBy the convexity of order interval and we haveThus, we haveBy monotonicity of there exists such that . Again by convexity of order interval and we havewhich implies thatIt follows from and thatand thereforeFrom we haveBy the convexity of order interval and we obtain thatand henceThe monotonicity of yields that there exists such that Now the convexity of order interval and gives thatwhich implies thatSo, from and we obtainHence, (21) is true for all
- (2)
- Suppose that x is Δ-limit of From (i), we have for all Since the order interval is closed and convex and the sequence is is increasing we deduce that for a fixed , if not, that is, if then a subsequence of may be constructed by leaving the first terms of the sequence and then the asymptotic center of would not be x, which contradicts that x is the Δ-limit of the sequence . This completes the proof.
- (1)
- exists for all
- (2)
- where
- (1)
- Let . If then Lemma 7 and the transitivity of the order imply . Applying mathematical induction, we obtain for all . On the other hand, assume that . Since there exists we have as . Further, (21) yieldsAgain, there exists which implies that as . Finally, we haveContinuing in this manner, we obtain , and . Therefore, in both cases and p are comparable. Now, from (21) we haveAs ,Also,andFrom and we obtain thatNow using and in , we haveThus, for all that is, is decreasing and consequently, exists.
- (2)
- We now prove thatFrom (1), we know that for each , exists. For some letFrom and on taking the limit superior as , we havethat is,Similarly, from and on taking limit superior as , we getand henceNow, by applying Lemma 4, we getFrom we haveOn taking limit superior as we obtain thatNote thatCombining and , we haveAlso,By taking limit inferior as on both sides, we haveEmploying and , yieldsFrom , , and applying Lemma 5, we get
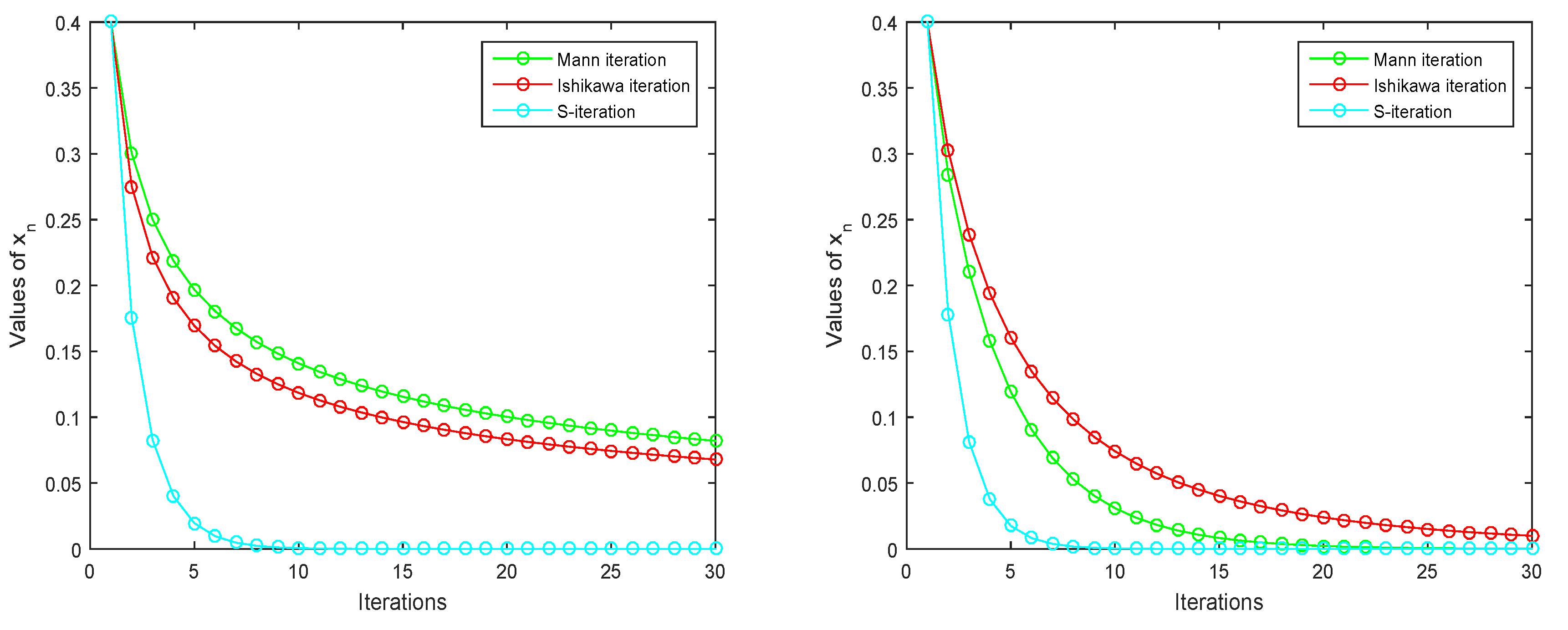
4. Numerical Experiments
5. Application to Integral Equations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agarwal, R.P.; O’Regan, D.; Sahu, D.R. Fixed Point Theory for Lipschitzian-Type Mappings with Applications; Springer: New York, NY, USA, 2009; Volume 6. [Google Scholar]
- Bridson, M.R.; Haefliger, A. Metric Spaces of Non-Positive Curvature; Springer Science & Business Media: Berlin, Germany, 2013; Volume 319. [Google Scholar]
- Niculescu, C.P.; Rovenţa, I. Fan’s inequality in geodesic spaces. Appl. Math. Lett. 2009, 22, 1529–1533. [Google Scholar] [CrossRef] [Green Version]
- Shabanian, S.; Vaezpour, S.M. A minimax inequality and its applications to fixed point theorems in cat (0) spaces. Fixed Point Theory Appl. 2011, 2011, 61. [Google Scholar] [CrossRef] [Green Version]
- Haeiger, A.; Bridson, M.R. Metric Spaces of Non-Positive Curvature, Fundamental Principle of Mathematical Sciences; Springer: Berlin, Germany, 1999; Volume 319. [Google Scholar]
- Kirk, W.A. Fixed point theorems in CAT(0) spaces and R-trees. Fixed Point Theory Appl. 2004, 2004, 309–316. [Google Scholar] [CrossRef] [Green Version]
- Shafrir, I.; Reich, S. Nonexpansive iterations in hyperbolic spaces. Nonlinear Anal. 1990, 15, 537. [Google Scholar]
- Brown, K.S. Buildings; Springer: New York, NY, USA, 1998; Volume 319. [Google Scholar]
- Markin, J.T. A fixed point theorem for set valued mappings. Bull. Am. Math. Soc. 1968, 74, 639–640. [Google Scholar] [CrossRef] [Green Version]
- Nadler, S.B., Jr. Multi-valued contraction mappings. Pac. J. Math. 1969, 30, 475–488. [Google Scholar] [CrossRef]
- Altun, I.; Simsek, H. Some fixed point theorems on dualistic partial metric spaces. J. Adv. Math. Stud. 2008, 1, 1–9. [Google Scholar]
- Mlaiki, N.; Abodayeh, K.; Aydi, H.; Abdeljawad, T.; Abuloha, M. Rectangular metric-like type spaces and related fixed points. J. Math. 2018, 2018, 3581768. [Google Scholar] [CrossRef]
- Oltra, S.; Valero, O. Banach’s Fixed Point Theorem for Partial Metric Spaces; Università degli Studi di Trieste. Dipartimento di Matematica e Informatica: Trieste, Italy, 2004. [Google Scholar]
- Shukla, S. Partial b-metric spaces and fixed point theorems. Mediter. J. Math. 2014, 11, 703–711. [Google Scholar]
- Aydi, H.; Abbas, M.; Vetro, C. Partial hausdorff metric and nadler’s fixed point theorem on partial metric spaces. Topol. Appl. 2012, 159, 3234–3242. [Google Scholar] [CrossRef] [Green Version]
- Lim, T. A fixed point theorem for multivalued nonexpansive mappings in a uniformly convex banach space. Bull. Am. Math. Soc. 1974, 80, 1123–1126. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, T.; Takahashi, W. Fixed points of multivalued mappings in certain convex metric spaces. Topol. Methods Nonlinear Anal. 1996, 8, 197–203. [Google Scholar] [CrossRef] [Green Version]
- Dhompongsa, S.; Kaewkhao, A.; Panyanak, B. Lim’s theorems for multivalued mappings in cat (0) spaces. J. Math. Anal. Appl. 2005, 312, 478–487. [Google Scholar] [CrossRef] [Green Version]
- Razani, A.; Shabani, S. Approximating fixed points for nonself mappings in cat (0) spaces. Fixed Point Theory Appl. 2011, 2011, 65. [Google Scholar] [CrossRef] [Green Version]
- Uddin, I.; Nieto, J.J.; Ali, J. One-step iteration scheme for multivalued nonexpansive mappings in CAT (0) spaces. Mediter. J. Math. 2016, 13, 1211–1225. [Google Scholar] [CrossRef]
- Lu, H.; Lan, D.; Hu, Q.; Yuan, G. Fixed point theorems in CAT(0) spaces with applications. J. Inequal. Appl. 2014, 2014, 320. [Google Scholar] [CrossRef] [Green Version]
- Bartolini, M.P.I.; Ciaccia, P. String Matching with Trees Using an Approximate Distance. In Spir Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef] [Green Version]
- Kirk, W.A.; Espinola, R. Fixed point theorems in r-trees with applications to graph theory. Topol. Appl. 2006, 153, 1046–1055. [Google Scholar]
- La Sen, M.D. About fixed points in CAT(0) spaces under a combined structure of two self-mappings. J. Math. 2017, 2017, 13. [Google Scholar] [CrossRef] [Green Version]
- Uddin, I.; Ali, J.; Nieto, J.J. An iteration scheme for a family of multivalued mappings in CAT (0) spaces with an application to image recovery. Rev. Real Acad. Cienc. Exactas Físicas Nat. Ser. A Matemáticas 2018, 112, 373–384. [Google Scholar] [CrossRef]
- Suzuki, T. Fixed point theorems and convergence theorems for some generalized nonexpansive mappings. J. Math. Anal. Appl. 2008, 340, 1088–1095. [Google Scholar] [CrossRef] [Green Version]
- Abkar, A.; Eslamian, M. Fixed point theorems for suzuki generalized nonexpansive multivalued mappings in banach spaces. Fixed Point Theory Appl. 2010, 2010, 457935. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.; Wen, C.; Yao, J. Proximal point algorithms involving cesaro type mean of asymptotically nonexpansive mappings in cat (0) spaces. J. Nonlinear Sci. Appl. 2016, 9, 4317–4328. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.H.; Abbas, M. Common fixed points of two multivalued nonexpansive maps in Kohlenbach hyperbolic spaces. Fixed Point Theory Appl. 2014, 2014, 181. [Google Scholar] [CrossRef] [Green Version]
- Aoyama, K.; Kohsaka, F. Fixed point theorem for α-nonexpansive mappings in Banach spaces. Nonlinear Anal. Theory Methods Appl. 2011, 74, 4387–4391. [Google Scholar] [CrossRef]
- Iqbal, H.; Abbas, M.; Husnine, S.M. Existence and approximation of fixed points of multivalued generalized α-nonexpansive mappings in banach spaces. Numer. Algor. 2020, 85, 1029–1049. [Google Scholar] [CrossRef]
- Amini-Harandi, A.; Fakhar, M.; Hajisharifi, H.R. Approximate fixed points of α-nonexpansive mappings. J. Math. Anal. Appl. 2018, 467, 1168–1173. [Google Scholar] [CrossRef]
- Laowang, W.; Panyanak, B. Strong and convergence theorems for multivalued mappings in CAT(0) spaces. J. Inequal. Appl. 2009, 2009, 730132. [Google Scholar] [CrossRef] [Green Version]
- Panyanak, B. Mann and Ishikawa iterative processes for multivalued mappings in Banach spaces. Comput. Math. Appl. 2007, 54, 872–877. [Google Scholar] [CrossRef] [Green Version]
- Dhompongsa, S.; Panyanak, B. On Δ-convergence theorems in CAT (0) spaces. Comput. Math. Appl. 2008, 56, 2572–2579. [Google Scholar] [CrossRef] [Green Version]
- Laowang, W.; Panyanak, B. Approximating fixed points of nonexpansive nonself mappings in cat (0) spaces. Fixed Point Theory Appl. 2009, 2010, 367274. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, R.P.; Regan, D.O.; Sahu, D.R. Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 2007, 8, 61–79. [Google Scholar]
- Pandey, R.; Pant, R.; Al-Rawashdeh, A. Fixed point results for a class of monotone nonexpansive type mappings in hyperbolic spaces. J. Funct. Spaces 2018, 2018, 5850181. [Google Scholar] [CrossRef]
- Khan, S.H. Convergence of iterates with errors of asymptotically quasi-nonexpansive mappings and applications. J. Math. Anal. Appl. 2007, 328, 821–829. [Google Scholar]
- Pant, R.; Shukla, R. Approximating fixed points of generalized α-nonexpansive mappings in banach spaces. Numer. Funct. Anal. Optimiz. 2017, 38, 248–266. [Google Scholar] [CrossRef]

| Initial Points | Iteration Processes | ||
|---|---|---|---|
| Mann | Ishikawa | S-iteration | |
| 183 | 79 | 13 | |
| 239 | 104 | 14 | |
| 234 | 108 | 14 | |
| 241 | 111 | 14 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, M.; Iqbal, H.; De la Sen, M.; Ahmad, K. Approximation of Fixed Points of Multivalued Generalized (α,β)-Nonexpansive Mappings in an Ordered CAT(0) Space. Mathematics 2021, 9, 1945. https://doi.org/10.3390/math9161945
Abbas M, Iqbal H, De la Sen M, Ahmad K. Approximation of Fixed Points of Multivalued Generalized (α,β)-Nonexpansive Mappings in an Ordered CAT(0) Space. Mathematics. 2021; 9(16):1945. https://doi.org/10.3390/math9161945
Chicago/Turabian StyleAbbas, Mujahid, Hira Iqbal, Manuel De la Sen, and Khushdil Ahmad. 2021. "Approximation of Fixed Points of Multivalued Generalized (α,β)-Nonexpansive Mappings in an Ordered CAT(0) Space" Mathematics 9, no. 16: 1945. https://doi.org/10.3390/math9161945








