Validity and Reliability of the Portuguese Version of Mathematics Academic Motivation Scale (MATAMS) among Third Cycle of Basic School Students
Abstract
:1. Introduction
2. Literature Review
2.1. Brief Overview of Self-Determination Theory (SDT)
2.2. Academic Motivation Scale (AMS)
3. Materials and Methods
3.1. Methodology
3.1.1. Adaptation of AMS to MATAMS
3.1.2. Pilot Study Using ALIPT
3.2. Data
4. Results
4.1. Exploratory Factor Analysis (EFA)
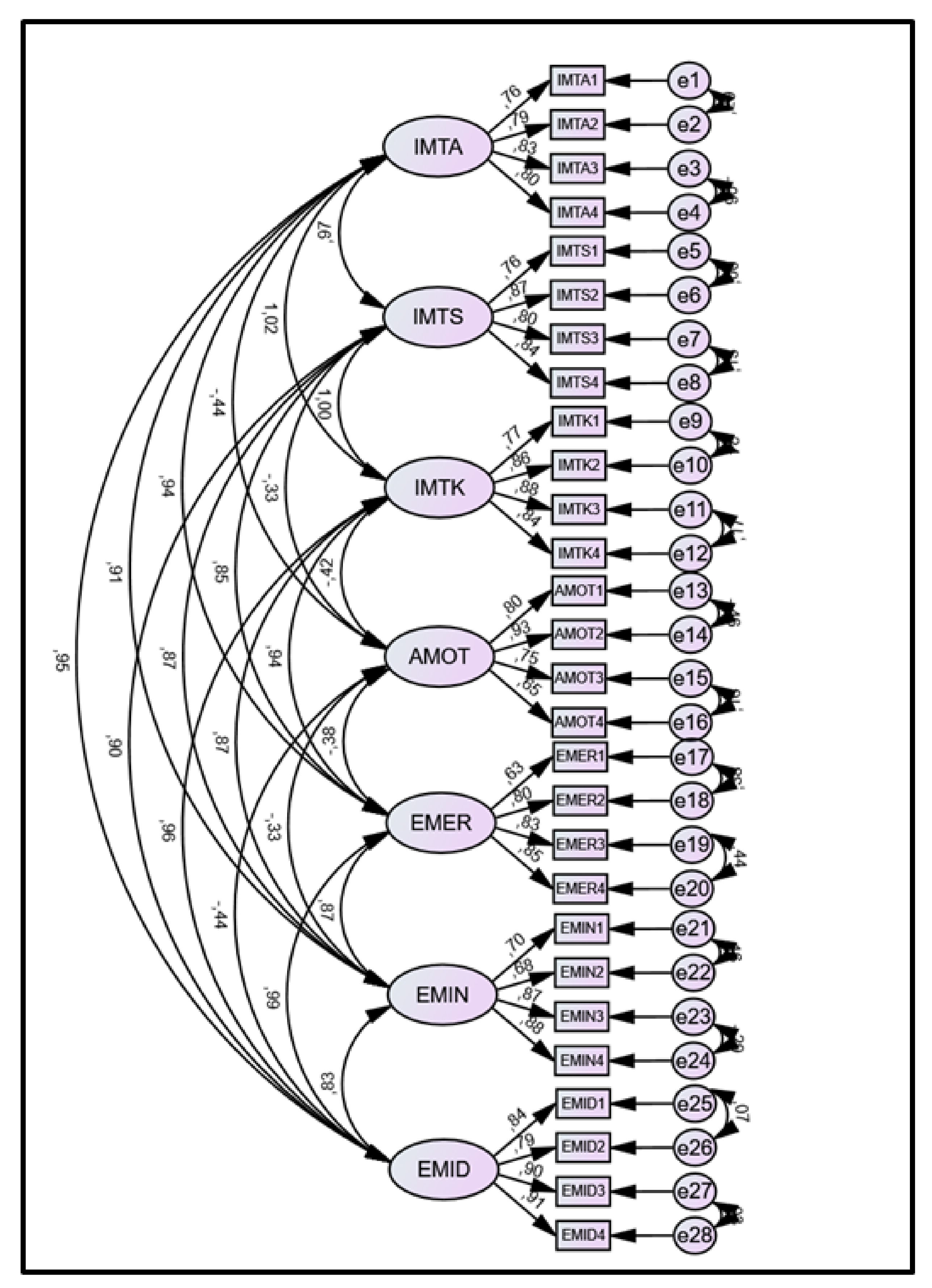
4.2. Confirmatory Factor Analysis (CFA)
4.3. Explanation of the Validated Scale
5. Discussion of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hanushek, E.A.; Woessmann, L. The economics of international differences in educational achievement. In Handbook of the Economics of Education; Elsevier: Amsterdam, The Netherlands, 2011; Volume 3, pp. 89–200. [Google Scholar]
- Grosskopf, S.; Hayes, K.J.; Taylor, L.L. Applied efficiency analysis in education. Econ. Bus. Lett. 2014, 3, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Sousa, S.P. Factors that Influence Student Achievement Gains and Performance Assessment of the Portuguese Public Schools. Ph.D. Thesis, University of Minho, Braga, Portugal, 2016. Chapter 5. pp. 121–168. [Google Scholar]
- Sousa, S.P. Teacher Characterístics and Student Progress. Ph.D. Thesis, University of Minho, Braga, Portugal, 2016. Chapter 6. pp. 170–196. [Google Scholar]
- Amrai, K.; Motlagh, S.E.; Zalani, H.A.; Parhon, H. The relationship between academic motivation and academic achievement students. Procedia-Soc. Behav. Sci. 2011, 15, 399–402. [Google Scholar] [CrossRef] [Green Version]
- Scheerens, J. The use of theory in school effectiveness research revisited. Sch. Eff. Sch. Improv. 2013, 24, 1–38. [Google Scholar] [CrossRef]
- Reynolds, D.; Sammons, P.; De Fraine, B.; Van Damme, J.; Townsend, T.; Teddlie, C.; Stringfield, S. Educational effectiveness research (EER): A state-of-the-art review. Sch. Eff. Sch. Improv. 2014, 25, 197–230. [Google Scholar] [CrossRef] [Green Version]
- Güvendir, M.A. Students’ extrinsic and intrinsic motivation level and its relationship with their mathematics achievement. Int. J. Math. Teach. Learn. 2016, 17, 1–21. [Google Scholar]
- Gupta, P.; Mili, R. Impact of academic motivation on academic achievement: A study on high schools students. Eur. J. Educ. Stud. 2017, 2, 10. [Google Scholar]
- Pintrich, P.R. A motivational science perspective on the role of student motivation in learning and teaching contexts. J. Educ. Psychol. 2003, 95, 667. [Google Scholar] [CrossRef] [Green Version]
- Alivernini, F.; Lucidi, F. Relationship between social context, self-efficacy, motivation, academic achievement, and intention to drop out of high school: A longitudinal study. J. Educ. Res. 2011, 104, 241–252. [Google Scholar] [CrossRef]
- Barkoukis, V.; Tsorbatzoudis, H.; Grouios, G.; Sideridis, G. The assessment of intrinsic and extrinsic motivation and amotivation: Validity and reliability of the Greek version of the Academic Motivation Scale. Assess. Educ. Princ. Policy Pract. 2008, 15, 39–55. [Google Scholar] [CrossRef]
- Lim, S.Y.; Chapman, E. Adapting the academic motivation scale for use in pre-tertiary mathematics classrooms. Math. Educ. Res. J. 2015, 27, 331–357. [Google Scholar] [CrossRef]
- Hannula, M.S.; Di Martino, P.; Pantziara, M.; Zhang, Q.; Morselli, F.; Heyd-Metzuyanim, E.; Lutovac, S.; Kaasila, R.; Middleton, J.A.; Jansen, A.; et al. Attitudes, Beliefs, Motivation and Identity in Mathematics Education; Springer: Cham, Switzerland, 2016; pp. 1–35. [Google Scholar]
- Fortier, M.S.; Vallerand, R.J.; Guay, F. Academic motivation and school performance: Toward a structural model. Contemp. Educ. Psychol. 1995, 20, 257–274. [Google Scholar] [CrossRef]
- Gottfried, A.E.; Marcoulides, G.A.; Gottfried, A.W.; Oliver, P.H.; Guerin, D.W. Multivariate latent change modeling of developmental decline in academic intrinsic math motivation and achievement: Childhood through adolescence. Int. J. Behav. Dev. 2007, 31, 317–327. [Google Scholar] [CrossRef]
- Özen, S.O. The effect of motivation on student achievement. In The Factors Effecting Student Achievement; Springer: Berlin/Heidelberg, Germany, 2017; pp. 35–56. [Google Scholar]
- Sivrikaya, A.H. The Relationship between Academic Motivation and Academic Achievement of the Students. Asian J. Educ. Train. 2019, 5, 309–315. [Google Scholar] [CrossRef]
- Tus, J. Academic Stress, Academic Motivation, and Its Relationship on the Academic Performance of the Senior High School Students. Asian J. Multidiscip. Stud. 2020, 8. [Google Scholar] [CrossRef]
- Stage, F.K. Motivation, academic and social integration, and the early dropout. Am. Educ. Res. J. 1989, 26, 385–402. [Google Scholar] [CrossRef]
- Alivernini, F.; Lucidi, F. The Academic Motivation Scale (AMS): Factorial structure, invariance and validity in the Italian context. Test. Psychom. Methodol. Appl. Psychol. 2008, 15, 211–220. [Google Scholar]
- Rump, M.; Esdar, W.; Wild, E. Individual differences in the effects of academic motivation on higher education students’ intention to drop out. Eur. J. High. Educ. 2017, 7, 341–355. [Google Scholar] [CrossRef]
- Rajiah, K.; Coumaravelou, S.; Ying, O.W. Relationship of test anxiety, psychological distress and academic motivation among first year undergraduate pharmacy students. Int. J. Appl. Psychol. 2014, 4, 68–72. [Google Scholar]
- Elmelid, A.; Stickley, A.; Lindblad, F.; Schwab-Stone, M.; Henrich, C.C.; Ruchkin, V. Depressive symptoms, anxiety and academic motivation in youth: Do schools and families make a difference? J. Adolesc. 2015, 45, 174–182. [Google Scholar] [CrossRef] [Green Version]
- Fairchild, A.J.; Horst, S.J.; Finney, S.J.; Barron, K.E. Evaluating existing and new validity evidence for the Academic Motivation Scale. Contemp. Educ. Psychol. 2005, 30, 331–358. [Google Scholar] [CrossRef]
- Cokley, K.O.; Bernard, N.; Cunningham, D.; Motoike, J. A psychometric investigation of the academic motivation scale using a United States sample. Meas. Eval. Couns. Dev. 2001, 34, 109–119. [Google Scholar] [CrossRef]
- Cokley, K. A confirmatory factor analysis of the Academic Motivation Scale with black college students. Meas. Eval. Couns. Dev. 2015, 48, 124–139. [Google Scholar] [CrossRef]
- Smith, K.J.; Davy, J.A.; Rosenberg, D.L. An examination of the validity of the Academic Motivation Scale with a United States business student sample. Psychol. Rep. 2010, 106, 323–341. [Google Scholar] [CrossRef]
- Smith, K.J.; Davy, J.A.; Rosenberg, D.L. An empirical analysis of an alternative configuration of the Academic Motivation Scale. Assess. Educ. Princ. Policy Pract. 2012, 19, 231–250. [Google Scholar] [CrossRef]
- Maurer, T.; Allen, D.; Gatch, D.B.; Shankar, P.; Sturges, D. Students’ academic motivations in allied health classes. Internet J. Allied Health Sci. Pract. 2012, 10, 6. [Google Scholar]
- Maurer, T.W.; Allen, D.; Gatch, D.B.; Shankar, P.; Sturges, D. Students’ academic motivations in three disciplines. J. Scholarsh. Teach. Learn. 2013, 13, 77. [Google Scholar]
- Liu, Y.; Ferrell, B.; Barbera, J.; Lewis, J.E. Development and evaluation of a chemistry-specific version of the academic motivation scale (AMS-Chemistry). Chem. Educ. Res. Pract. 2017, 18, 191–213. [Google Scholar] [CrossRef]
- Scifres, E.L.; Cox, M.; Crocker, R.M.; Mishra, R.; Scott, G.W. Academic motivation and the undergraduate business major. J. Educ. Bus. 2021, 1–10. [Google Scholar] [CrossRef]
- Vallerand, R.J.; Pelletier, L.G.; Blais, M.R.; Briere, N.M.; Senecal, C.; Vallieres, E.F. The Academic Motivation Scale: A measure of intrinsic, extrinsic, and amotivation in education. Educ. Psychol. Meas. 1992, 52, 1003–1017. [Google Scholar] [CrossRef]
- Vallerant, R.; Pelletier, L.G.; Blais, M.R.; Briere, N.M.; Senecal, C.; Vallieres, E.F. On the assessment of intrinsic, extrinsic, and amotivation in education: Evidence on the concurrent and construct validity of the Academic Motivation Scale. Educ. Psychol. Meas. 1993, 53, 159–172. [Google Scholar] [CrossRef]
- Ratelle, C.F.; Guay, F.; Vallerand, R.J.; Larose, S.; Senécal, C. Autonomous, controlled, and amotivated types of academic motivation: A person-oriented analysis. J. Educ. Psychol. 2007, 99, 734. [Google Scholar] [CrossRef] [Green Version]
- Areepattamannil, S.; Freeman, J.G. Academic achievement, academic self-concept, and academic motivation of immigrant adolescents in the greater Toronto area secondary schools. J. Adv. Acad. 2008, 19, 700–743. [Google Scholar] [CrossRef] [Green Version]
- Guay, F.; Morin, A.J.; Litalien, D.; Valois, P.; Vallerand, R.J. Application of exploratory structural equation modeling to evaluate the academic motivation scale. J. Exp. Educ. 2015, 83, 51–82. [Google Scholar] [CrossRef] [Green Version]
- Tóth-Király, I.; Orosz, G.; Dombi, E.; Jagodics, B.; Farkas, D.; Amoura, C. Cross-cultural comparative examination of the Academic Motivation Scale using exploratory structural equation modeling. Personal. Individ. Differ. 2017, 106, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Ntoumanis, N. Motivational clusters in a sample of British physical education classes. Psychol. Sport Exerc. 2002, 3, 177–194. [Google Scholar] [CrossRef]
- Blanchard, S.; Vrignaud, P.; Lallemand, N.; Dosnon, O. Validation de léchelle de motivation en éducation aupres de lycéens francais. Orientat. Sc. Prof. 1997, 26, 33–56. [Google Scholar]
- Martín-Albo, J.; Núñez, J.L.; Navarro, J.G. Validation of the Spanish version of the Situational Motivation Scale (EMSI) in the educational context. Span. J. Psychol. 2009, 12, 799. [Google Scholar] [CrossRef] [Green Version]
- Núñez, J.L.; Martín-Albo, J.; Navarro, J.G.; Suárez, Z. Adaptación y validación de la versión española de la Escala de Motivación Educativa en estudiantes de educación secundaria postobligatoria. Estud. Psicol. 2010, 31, 89–100. [Google Scholar] [CrossRef]
- Karaguven, M. The Adaptation of Academic Motivation Scale to Turkish. Educ. Sci. Theory Pract. 2012, 12, 2611–2618. [Google Scholar]
- Can, G. Turkish version of the academic motivation scale. Psychol. Rep. 2015, 116, 388–408. [Google Scholar] [CrossRef]
- Aydın, S.; Yerdelen, S.; Yalmancı, S.G.; Göksu, V. Academic Motivation Scale for Learning Biology: A Scale Development Study. Educ. Sci./Egit. Bilim 2014, 39, 425–435. [Google Scholar] [CrossRef] [Green Version]
- Melike, F.A.I.Z.; AVCI, E.K. Academic Motivation Levels of Secondary School Students and Their Attitudes towards a Social Studies Course. Rev. Int. Geogr. Educ. Online 2020, 10, 156–185. [Google Scholar]
- Stover, J.B.; de la Iglesia, G.; Boubeta, A.R.; Liporace, M.F. Academic Motivation Scale: Adaptation and psychometric analyses for high school and college students. Psychol. Res. Behav. Manag. 2012, 5, 71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caleon, I.S.; Wui, M.G.L.; Tan, J.P.L.; Chiam, C.L.; Soon, T.C.; King, R.B. Cross-cultural validation of the Academic Motivation Scale: A Singapore investigation. Child Indic. Res. 2015, 8, 925–942. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y.M.; Li, J.; Li, Y.; Zhang, H. The revision and validation of the Academic Motivation Scale in China. J. Psychoeduc. Assess. 2016, 34, 15–27. [Google Scholar] [CrossRef]
- Staribratov, I.; Babakova, L. Development and Validation of a Math-specific Version of the Academic Motivation Scale (AMS-Mathematics) Among First-year University Students in Bulgaria. TEM J. 2019, 8, 317. [Google Scholar]
- Ardeńska, M.; Ardeńska, A.; Tomik, R. Validity and reliability of the Polish version of the Academic Motivation Scale: A measure of intrinsic and extrinsic motivation and amotivation. Health Psychol. Rep. 2019, 7, 254–266. [Google Scholar] [CrossRef]
- Orsini, C.; Binnie, V.; Evans, P.; Ledezma, P.; Fuentes, F.; Villegas, M.J. Psychometric validation of the academic motivation scale in a dental student sample. J. Dent. Educ. 2015, 79, 971–981. [Google Scholar] [CrossRef]
- Sturges, D.; Maurer, T.W.; Allen, D.; Gatch, D.B.; Shankar, P. Academic performance in human anatomy and physiology classes: A 2-yr study of academic motivation and grade expectation. Adv. Physiol. Educ. 2016, 40, 26–31. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M.; Cardoso, A.P.; Abrantes, J.L. Motivation and relationship of the student with the school as factors involved in the perceived learning. Procedia-Soc. Behav. Sci. 2011, 29, 1707–1714. [Google Scholar] [CrossRef] [Green Version]
- Lemos, M.S.; Veríssimo, L. The relationships between intrinsic motivation, extrinsic motivation, and achievement, along elementary school. Procedia-Soc. Behav. Sci. 2014, 112, 930–938. [Google Scholar] [CrossRef] [Green Version]
- Imaginário, S.; de Jesus, S.N.; Morais, F.; Fernandes, C.; Santos, R.; Santos, J.; Azevedo, I. Motivação para a aprendizagem escolar: Adaptação de um instrumento de avaliação para o contexto português. Rev. Lusófona Educ. 2014, 28, 28. [Google Scholar]
- Silva, R.; Rodrigues, R.; Leal, C. Academic Motivation Scale: Development, Application and Validation for Portuguese Accounting and Marketing Undergraduate Students. Int. J. Bus. Manag. 2018, 13, 11. [Google Scholar] [CrossRef] [Green Version]
- Lopes, P.; Silva, R.; Oliveira, J.; Ambrósio, I.; Ferreira, D.; Crespo, C.; Feiteira, F.; Rosa, P.J. Rasch analysis on the academic motivation scale in Portuguese university students. NeuroQuantology 2018, 16, 41–46. [Google Scholar] [CrossRef] [Green Version]
- Gomes, M.; Monteiro, V.; Mata, L.; Peixoto, F.; Santos, N.; Sanches, C. The Academic Self-Regulation Questionnaire: A study with Portuguese elementary school children. Psicol. Reflex. Crít. 2019, 32, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ribeiro, M.F.; Saraiva, V.; Pereira, P.; Ribeiro, C. Academic Motivation Scale: Validity in Portuguese Public Higher Education/Escala de Motivacao Academica: Validacao no Ensino Superior Publico Portugues. RAC-Rev. Adm. Contemp. 2019, 23, 288–311. [Google Scholar] [CrossRef]
- Deci, E.L.; Ryan, R.M. Self-determination theory: A macrotheory of human motivation, development, and health. Can. Psychol./Psychol. Can. 2008, 49, 182. [Google Scholar] [CrossRef] [Green Version]
- Deci, E.L.; Vallerand, R.J.; Pelletier, L.G.; Ryan, R.M. Motivation and education: The self-determination perspective. Educ. Psychol. 1991, 26, 325–346. [Google Scholar] [CrossRef]
- Ryan, R.M.; Deci, E.L. Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemp. Educ. Psychol. 2000, 25, 54–67. [Google Scholar] [CrossRef]
- Ryan, R.M.; Deci, E.L. Self-determination theory and the facilitation of intrinsic motivation, social development, and well-being. Am. Psychol. 2000, 55, 68–78. [Google Scholar] [CrossRef]
- Deci, E.L.; Ryan, R.M. The general causality orientations scale: Self-determination in personality. J. Res. Personal. 1985, 19, 109–134. [Google Scholar] [CrossRef]
- Deci, E.L.; Ryan, R.M. Facilitating optimal motivation and psychological well-being across life’s domains. Can. Psychol./Psychol. Can. 2008, 49, 14. [Google Scholar] [CrossRef] [Green Version]
- Deci, E.L.; Ryan, R.M. The“ what” and“ why” of goal pursuits: Human needs and the self-determination of behavior. Psychol. Inq. 2000, 11, 227–268. [Google Scholar] [CrossRef]
- Vallerand, R.J.; Blais, M.R.; Briere, N.M.; Pelletier, L.G. Construction et validation de l’échelle de motivation en éducation (EME). Can. J. Behav. Sci./Rev. Can. Sci. Comport. 1989, 21, 323. [Google Scholar] [CrossRef] [Green Version]
- Barbera, J.; VandenPlas, J.R. All assessment materials are not created equal: The myths about instrument development, validity, and reliability. In Investigating Classroom Myths through Research on Teaching and Learning; ACS Publications: Washington, DC, USA, 2011; pp. 177–193. [Google Scholar]
- Netemeyer, R.G.; Bearden, W.O.; Sharma, S. Scaling Procedures: Issues and Applications; Sage Publications: Southend Oaks, CA, USA, 2003. [Google Scholar]
- Pestana, H.; Gageiro, N. Análise de Dados para as ciências Sociais: A Complementaridade do SPSS, 3rd ed.; Edições Silabo: Lisbon, Portugal, 2003. [Google Scholar]
- Costello, A.B.; Osborne, J. Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Pract. Assess. Res. Eval. 2005, 10, 7. [Google Scholar]
- Raykov, T.; Marcoulides, G.A. Estimation of generalizability coefficients via a structural equation modeling approach to scale reliability evaluation. Int. J. Test. 2006, 6, 81–95. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis; Pearson: London, UK, 2010. [Google Scholar]
- Thompson, B. Exploratory and Confirmatory Factor Analysis; American Psychological Association: Washington, DC, USA, 2004. [Google Scholar]
- Brown, T.A. Confirmatory Factor Analysis for Applied Research; Guilford Publications: New York, NY, USA, 2015. [Google Scholar]
- Hair, J.F., Jr.; Sarstedt, M.; Hopkins, L.; Kuppelwieser, V.G. Partial least squares structural equation modeling (PLS-SEM): An emerging tool in business research. Eur. Bus. Rev. 2014, 26, 106–121. [Google Scholar] [CrossRef]
| Article | Country | Sample | Cronbach’s Alpha | CFA | Subject |
|---|---|---|---|---|---|
| Ntoumanis [40] | England | 428 | >0.6 | GFI: 0.940 | Physical Education |
| Aydin et al. [46] | Turkey | 472 | >0.7 | GFI: 0.88 | Biology |
| Lim and Chapman [13] | Singapore | 1610 | >0.8 | GFI: 0.890 | Mathematics |
| Itens | Original Scale (AMS) | Adapted Scale (MATAMS) |
|---|---|---|
| Question | Why Do You Go to College? | Why Do You Spend your Time Studying mathematics? |
| AMOT1 | Honestly, I don’t know; I really feel that I am wasting my time in school. | Honestly, I don’t know; I really feel that I am wasting my time studying mathematics. |
| AMOT2 | I can’t see why I go to college and frankly, I couldn’t care less. | I can’t see why I study mathematics and frankly, I couldn’t care less. |
| AMOT3 | I don’t know; I can’t understand what I am doing in school. | I don’t know; I can’t understand what I am doing studying mathematics. |
| AMOT4 | I once had good reasons for going to college; however, now I wonder whether I should continue. | I’m not sure. I do not see how mathematics could be important to me. |
| EMER1 | Because with only a high-school degree I would not find a high paying job later on. | Because only with a good grade in mathematics, will I find a high paying job later on. |
| EMER2 | In order to obtain a more prestigious job later on. | In order to be able to get a job later on. |
| EMER3 | Because I want to have “the good life” later on. | Because I want to have a “good life” later on. |
| EMER4 | In order to have a better salary later on. | In order to have a better salary later on. |
| EMIN1 | Because of the fact that when I succeed in college I feel important. | Because of the fact that when I succeed in everything that is related to mathematics I feel important. |
| EMIN2 | To prove to myself that I am capable of completing my college degree. | To prove the others (teachers, relatives, friends) that I can be good at mathematics. |
| EMIN3 | To show myself that I am an intelligent person. | To show myself that I am an intelligent person. |
| EMIN4 | Because I want to show myself that I can succeed in my studies. | Because I want to show myself that I can succeed in everything that has to do with mathematics. |
| EMID1 | Because I think that a college education will help me better prepare for the career I have chosen. | Because I think that mathematics will help me better prepare for the career I have chosen. |
| EMID2 | Because eventually it will enable me to enter the job market in a field that I like. | Because studying mathematics will prove useful for me later on. |
| EMID3 | Because I believe that a few additional years of education will improve my competence as a worker. | Because I believe that mathematics will improve my competence as a worker. |
| EMID4 | Because this will help me make a better choice regarding my career orientation. | Because what I learn in mathematics will be very useful throughout my course. |
| IMTA1 | For the pleasure I experience while surpassing myself in my studies. | For the pleasure I experience while surpassing myself in mathematics. |
| IMTA2 | For the satisfaction I feel when I am in the process of accomplishing difficult academic activities. | For the satisfaction I feel when I am in the process of accomplishing difficult academic activities related to mathematics. |
| IMTA3 | For the pleasure that I experience while I am surpassing myself in one of my personal accomplishments. | Because I want to know about mathematics. |
| IMTA4 | Because college allows me to experience a personal satisfaction in my quest for excellence in my studies. | Because I experience personal satisfaction if I am knowledgeable about mathematics. |
| IMTK1 | Because I experience pleasure and satisfaction while learning new things. | Because I experience pleasure and satisfaction while learning new things about mathematics. |
| IMTK2 | For the pleasure I experience when I discover new things never seen before. | For the pleasure I experience when I discover new things about mathematics that I had never learned before. |
| IMTK3 | For the pleasure that I experience in broadening my knowledge about subjects which appeal to me. | For the pleasure that I experience in broadening my knowledge about mathematics. |
| IMTK4 | Because my studies allow me to continue to learn about many things that interest me. | Because studying mathematics allows me to learn about many things in this area. |
| IMTS1 | For the intense feelings I experience when I am communicating my own ideas to others. | For the intense feelings I experience when I am communicating my own ideas about mathematics to others. |
| IMTS2 | For the pleasure that I experience when I read interesting authors. | For the pleasure that I experience when I learn how things work due to the agency of mathematics. |
| IMTS3 | For the pleasure that I experience when I feel completely absorbed by what certain authors have written. | For the pleasure that I experience when I feel completely absorbed by what the main researchers on mathematics have written. |
| IMTS4 | For the “high” feeling that I experience while reading about various interesting subjects. | For the “high” feeling that I experienced when I read several interesting studies on mathematics. |
| Rotated Component Matrix | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Constructs | Variables | Factors | Model Validity | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | AVE | CR | |||
| Intrinsic Motivation to Accomplish | IMTA1 | 0.760 | |||||||||
| IMTA2 | 0.788 | 0.633 | 0.873 | 0.880 | |||||||
| IMTA3 | 0.828 | ||||||||||
| IMTA4 | 0.805 | ||||||||||
| Intrinsic Motivation to Stimulate | IMTS1 | 0.759 | |||||||||
| IMTS2 | 0.866 | 0.668 | 0.889 | 0.893 | |||||||
| IMTS3 | 0.804 | ||||||||||
| IMTS4 | 0.838 | ||||||||||
| Intrinsic Motivation to Know | IMTK1 | 0.773 | |||||||||
| IMTK2 | 0.862 | 0.704 | 0.904 | 0.911 | |||||||
| IMTK3 | 0.876 | ||||||||||
| IMTK4 | 0.843 | ||||||||||
| Amotivation | AMOT1 | 0.800 | |||||||||
| AMOT2 | 0.927 | 0.618 | 0.864 | 0.857 | |||||||
| AMOT3 | 0.747 | ||||||||||
| AMOT4 | 0.647 | ||||||||||
| EMER1 | 0.634 | ||||||||||
| Extrinsic Motivation | EMER2 | 0.800 | 0.615 | 0.863 | 0.880 | ||||||
| External Regulation | EMER3 | 0.831 | |||||||||
| EMER4 | 0.855 | ||||||||||
| EMIN1 | 0.704 | ||||||||||
| Extrinsic Motivation | EMIN2 | 0.682 | 0.823 | 0.867 | 0.863 | ||||||
| Introjection | EMIN3 | 0.870 | |||||||||
| EMIN4 | 0.880 | ||||||||||
| EMID1 | 0.845 | ||||||||||
| Extrinsic Motivation | EMID2 | 0.845 | 0.743 | 0.920 | 0.920 | ||||||
| Identification | EMID3 | 0.896 | |||||||||
| EMID4 | 0.911 | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sousa, S.P.; Silva, R. Validity and Reliability of the Portuguese Version of Mathematics Academic Motivation Scale (MATAMS) among Third Cycle of Basic School Students. Mathematics 2021, 9, 2049. https://doi.org/10.3390/math9172049
Sousa SP, Silva R. Validity and Reliability of the Portuguese Version of Mathematics Academic Motivation Scale (MATAMS) among Third Cycle of Basic School Students. Mathematics. 2021; 9(17):2049. https://doi.org/10.3390/math9172049
Chicago/Turabian StyleSousa, Sandra P., and Rui Silva. 2021. "Validity and Reliability of the Portuguese Version of Mathematics Academic Motivation Scale (MATAMS) among Third Cycle of Basic School Students" Mathematics 9, no. 17: 2049. https://doi.org/10.3390/math9172049
APA StyleSousa, S. P., & Silva, R. (2021). Validity and Reliability of the Portuguese Version of Mathematics Academic Motivation Scale (MATAMS) among Third Cycle of Basic School Students. Mathematics, 9(17), 2049. https://doi.org/10.3390/math9172049








