Adaptive Secure Control for Leader-Follower Formation of Nonholonomic Mobile Robots in the Presence of Uncertainty and Deception Attacks
Abstract
:1. Introduction
- (i)
- To the best of the authors’ knowledge, an adaptive secure control problem for leader-follower formation of nonholonomic mobile robots in the presence of deception attacks is the first trial of the formation control field of nonholonomic mobile robots. The secure formation control design and stability strategies using the adaptive technique are firstly established in this paper.
- (ii)
- Compared with the related works in the literature, a robust, resilient control design with adaptive attack compensation mechanisms is firstly developed to compensate for time-varying velocity attacks of the leader. It is proven that all closed-loop signals are uniformly ultimately bounded in the Lyapunov stability sense, and the formation errors are ensured for converging to an adjustable neighborhood of the origin.
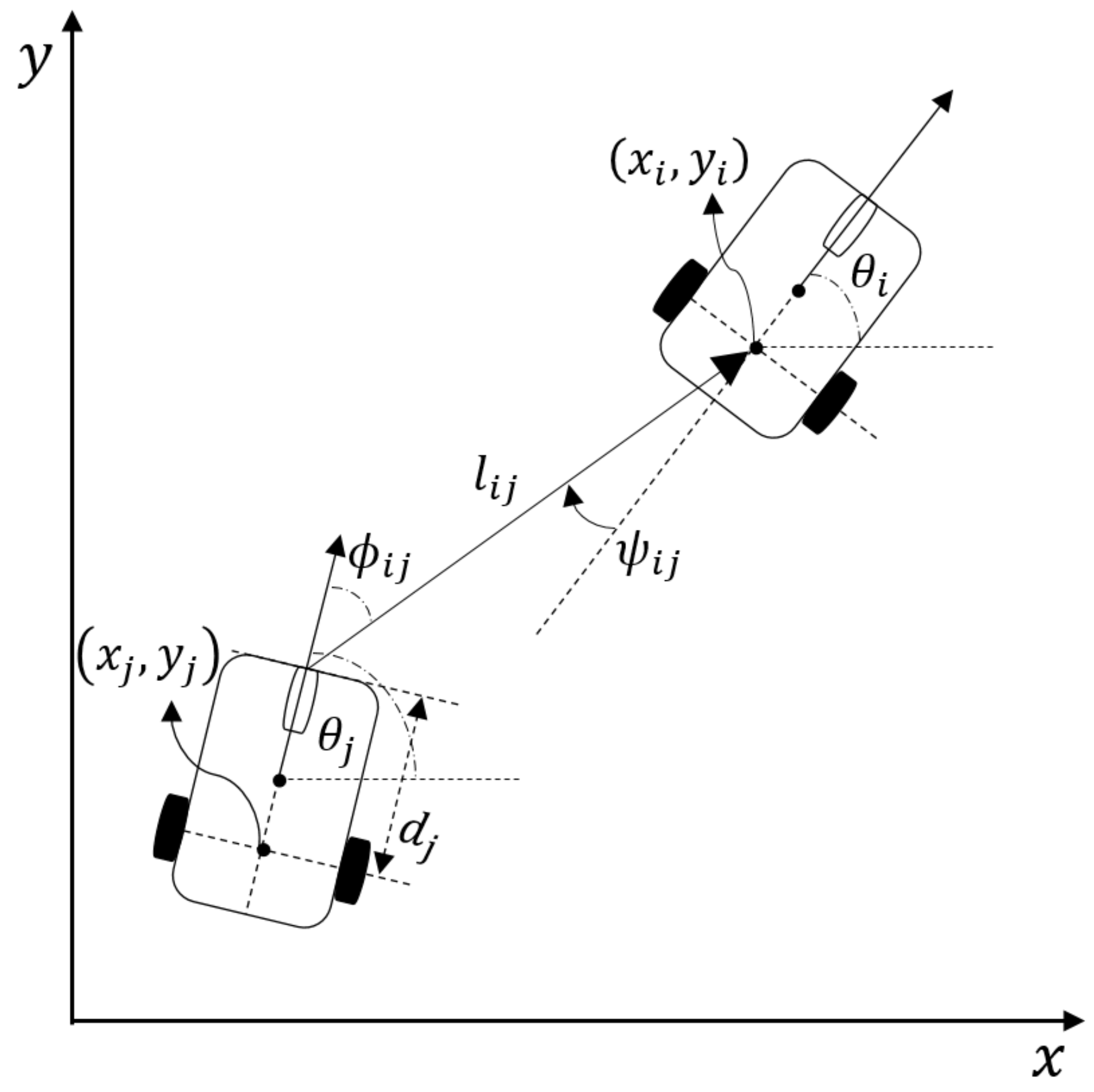
2. System Description and Problem Statement
2.1. Leader-Follower Model
2.2. Radial Basis Function Network
2.3. Problem Statement
- (i)
- The leader’s velocities and accelerations are bounded.
- (ii)
- The external disturbance is bounded, such that , where is an unknown positive constant.
- (iii)
- The time-varying attack signals and are unknown and bounded, such that and , where and are unknown positive constants.
- (iv)
- The optimal weight vector W and reconstruction error ε are bounded, such that and , where and are unknown positive constants.
- (v)
- The first derivatives of the desired distance and angle exist and are bounded.
- (i)
- The follower j cannot follow the leader i unless the leader’s velocity and acceleration are bounded. The unbounded leader’s velocity and acceleration lead to the unstable operation of the leader i. Therefore, the leader’s velocity and acceleration must be bounded for the leader-follower formation.
- (ii)
- In a real environment, external disturbances, such as friction and wind, are bounded. If external disturbances are unbounded (i.e., infinite), the control problem cannot be formulated.
- (iii)
- In real applications, since the defender can obtain some statistical information of the attack signal (e.g., extreme values) by monitoring the target online for some time, the bounded attack signals can ensure the concealment of the attacker [32]. Thus, Assumption 1-(iii) is reasonable in the secure control field.
- (iv)
- (v)
- and are the desired values chosen by the control designer for achieving the formation control objective. That is, they are the reference signals for the leader-follower control. Thus, they should be bounded. If they are infinite, the formation control problem cannot be formulated. In addition, for the continuous formation operation, and should be continuous and differentiable signals. Thus, Assumption 1-(v) is reasonable.
3. Controller Design
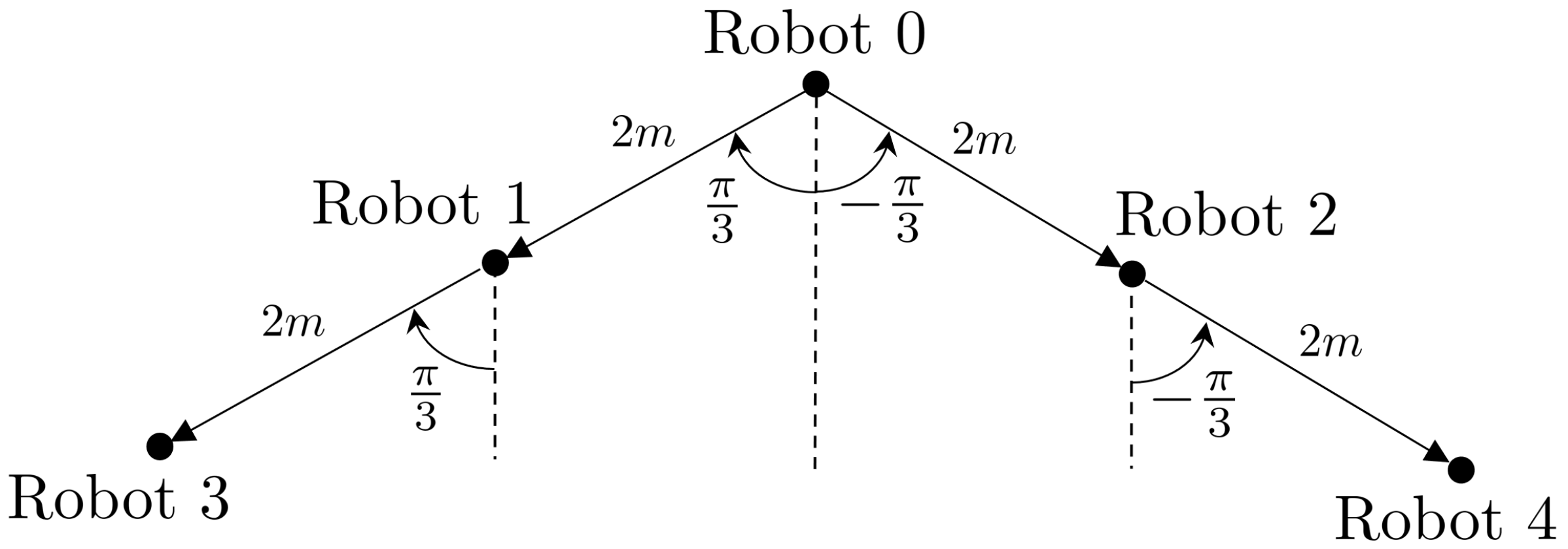
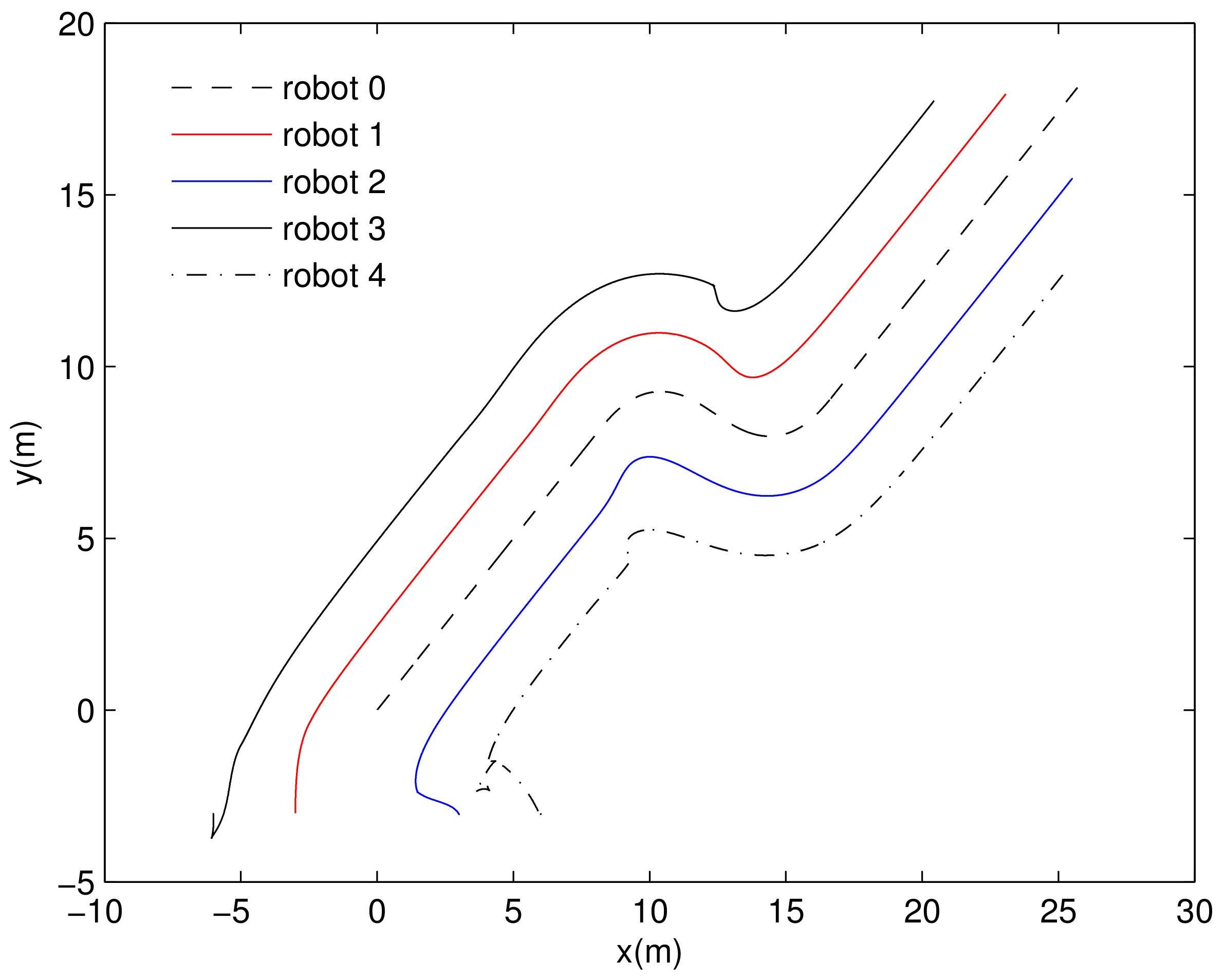
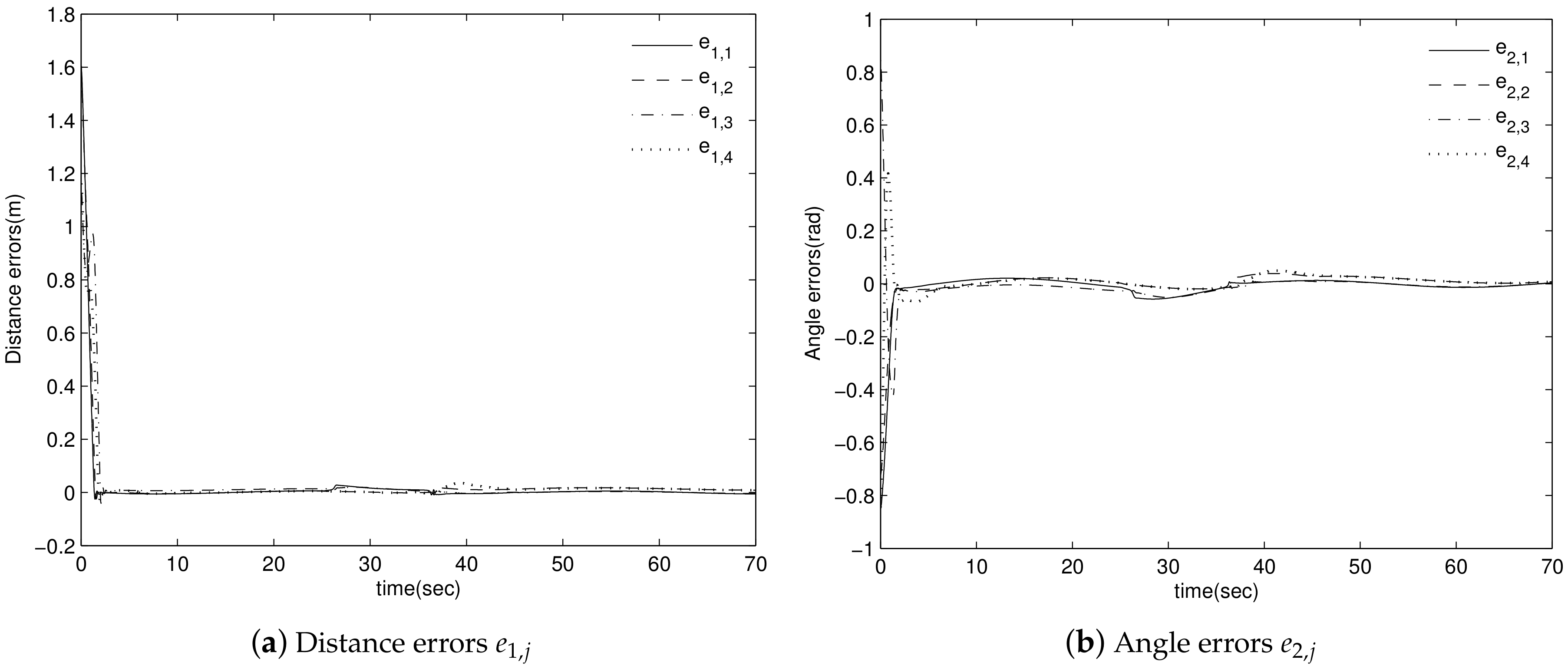
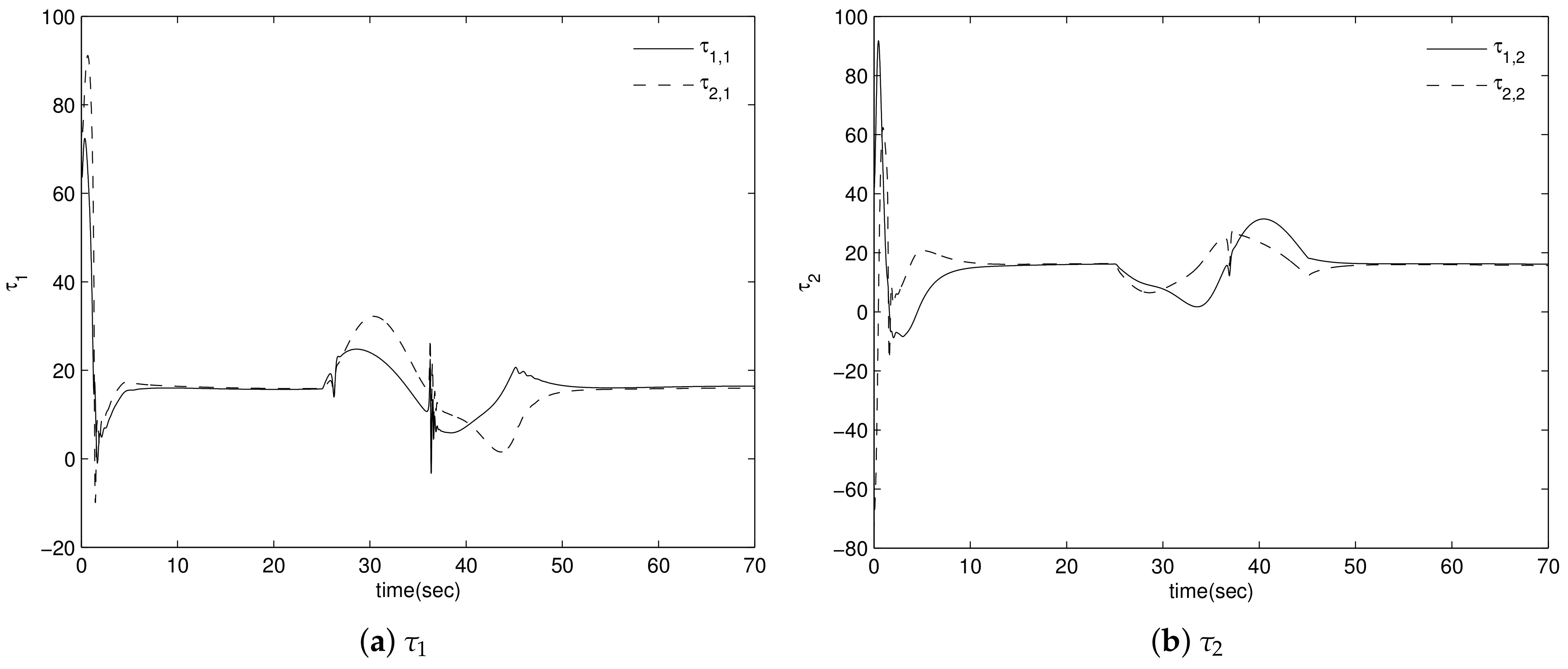
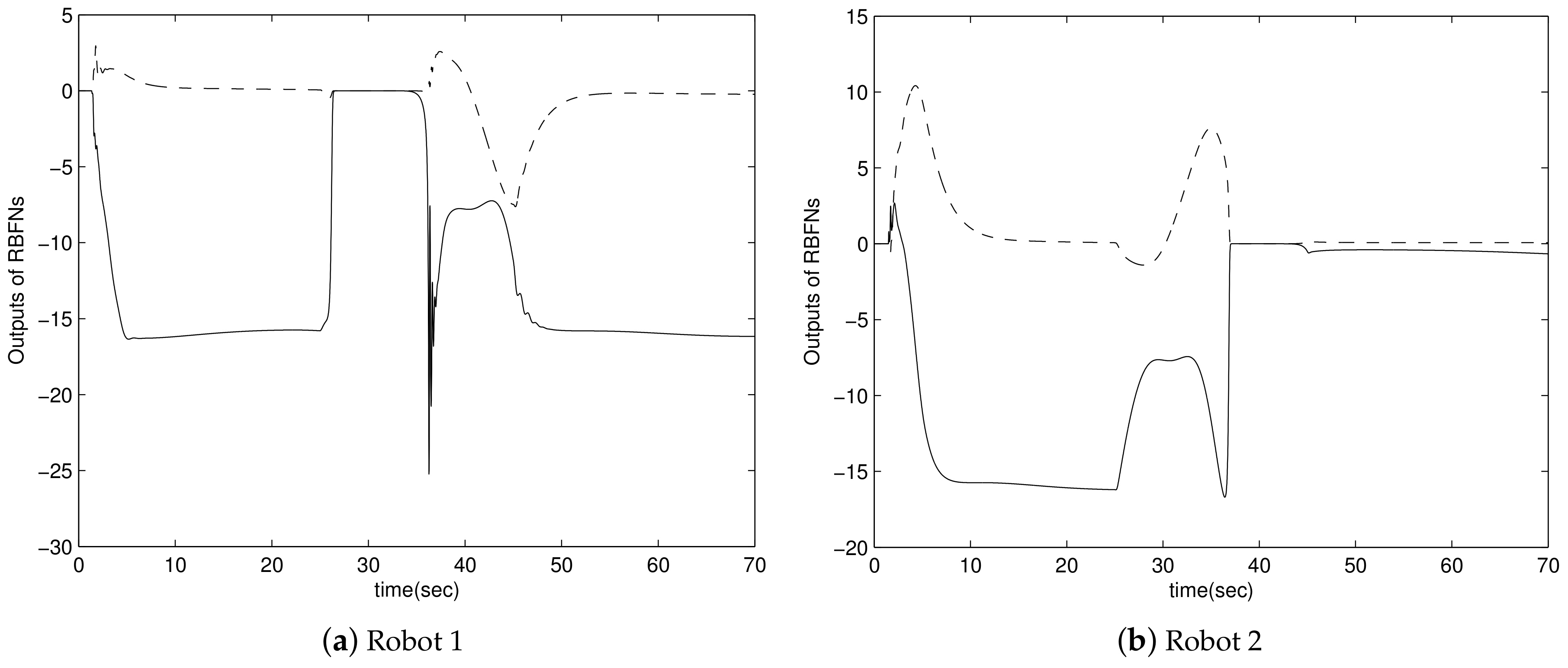
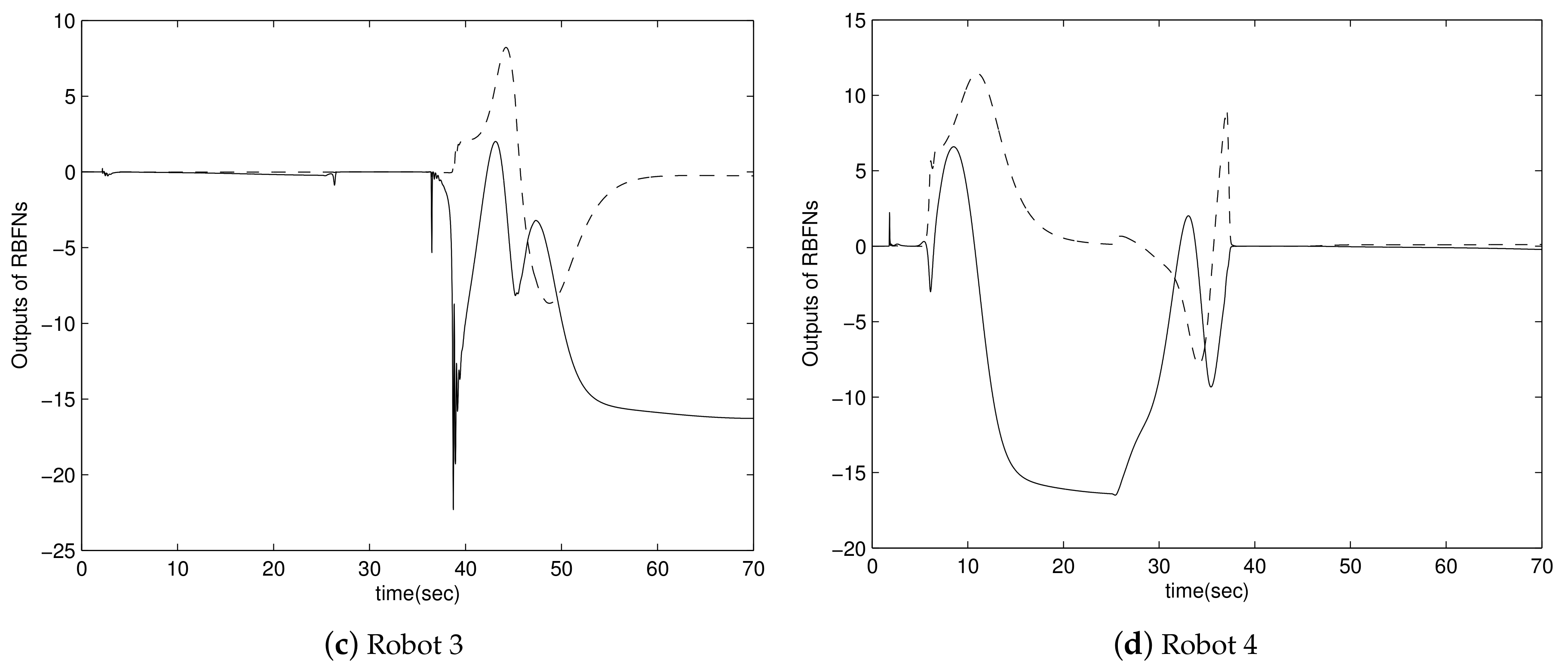
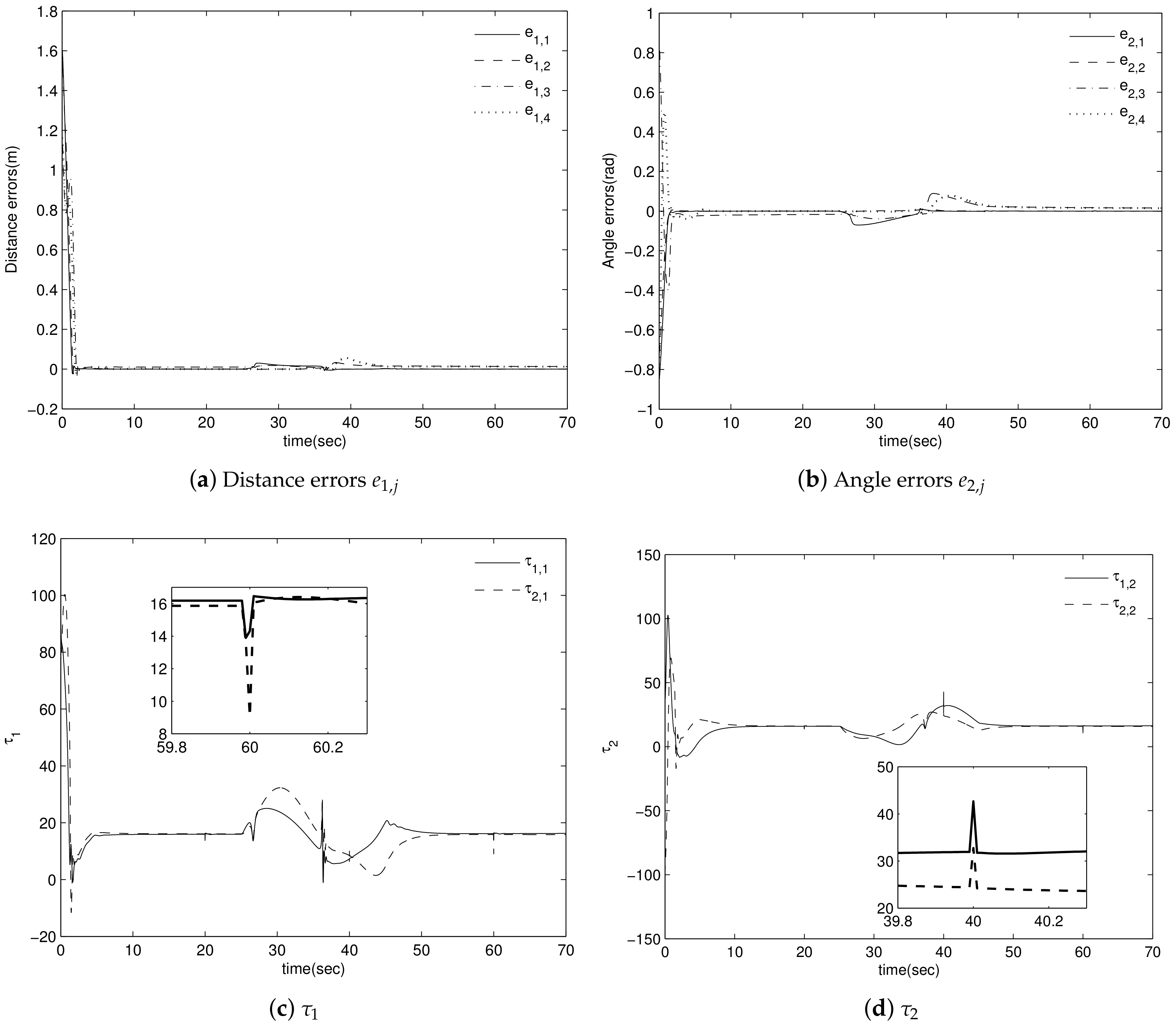
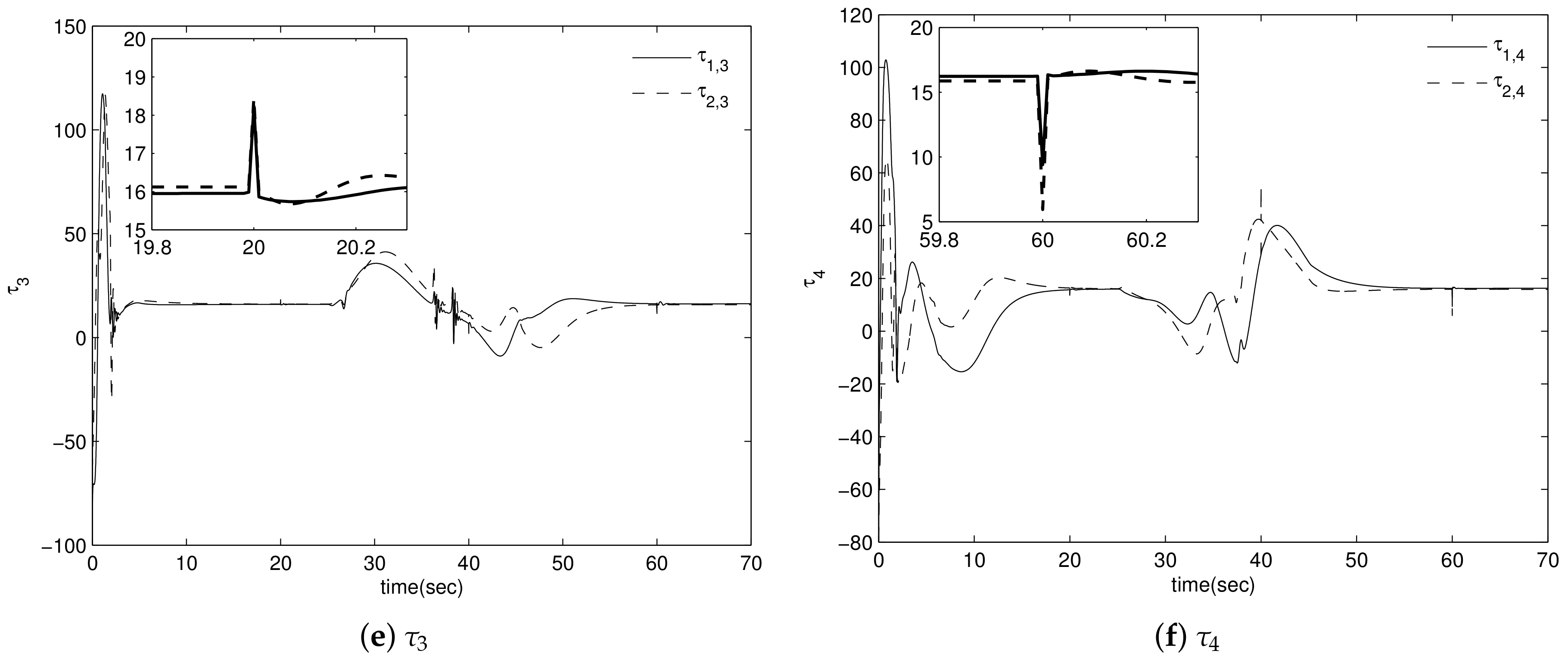
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amin, S.; Crdenas, A.A.; Sastry, S.S. Safe and secure networked control systems under denial-of-service attacks. In Hybrid Systems: Computation and Control; Springer: Berlin, Germany, 2009; pp. 31–45. [Google Scholar]
- Corona, I.; Giacinto, G.; Roli, F. Adversarial attacks against intrusion detection systems: Taxonomy, solutions and open issues. Inf. Sci. 2013, 239, 201–225. [Google Scholar] [CrossRef]
- Dolk, V.S.; Tesi, P.; Persis, C.; Heemels, W.P.M.H. Event-triggered control systems under denial-of-service attacks. IEEE Trans. Control Netw. Syst. 2017, 4, 93–105. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.X.; Liu, Z.X.; Zhang, S.G.; Zhang, X. Defending collaborative false data injection attacks in wireless sensor networks. Inf. Sci. 2014, 254, 39–53. [Google Scholar] [CrossRef]
- He, W.; Gao, X.; Zhong, W.; Qian, F. Secure impulsive synchronization control of multi-agent systems under deception attacks. Inf. Sci. 2018, 459, 354–368. [Google Scholar] [CrossRef]
- Ding, D.; Wang, Z.; Han, Q.L.; Wei, G. Security control for discrete-time stochastic nonlinear systems subject to deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 779–789. [Google Scholar] [CrossRef]
- Zhu, M.H.; Martnez, S. On the performance analysis of resilient networked control systems under replay attacks. IEEE Trans. Autom. Control 2014, 59, 804–808. [Google Scholar] [CrossRef] [Green Version]
- Ye, D.; Zhang, T.Y.; Guo, G. Stochastic coding detection scheme in cyber-physical systems against replay attack. Inf. Sci. 2019, 481, 432–444. [Google Scholar] [CrossRef]
- Huang, J.S.; Zhao, L.; Wang, Q.G. Adaptive control of a class of strict nonlinear systems under replay attacks. ISA Trans. 2020, 107, 134–142. [Google Scholar] [CrossRef]
- Yucelen, T.; Haddad, W.M.; Feron, E.M. Adaptive control architecture for mitigating sensor attacks in cyber-physical systems. Cyber-Phys. Syst. 2016, 2, 24–52. [Google Scholar] [CrossRef]
- Jin, X.; Haddad, W.M.; Yucelen, T. An adaptive control architecture for mitigating sensor and actuator attacks in cyber-physical systems. IEEE Trans. Autom. Control 2017, 62, 6058–6064. [Google Scholar] [CrossRef]
- An, L.; Yang, G.H. Improved adaptive resilient control against sensor and actuator attacks. Inf. Sci. 2018, 423, 145–156. [Google Scholar] [CrossRef]
- Yin, T.; Gu, A. Z. Security control for adaptive event-triggered networked control systems under deception attacks. IEEE Access 2020, 9, 10789–10796. [Google Scholar]
- Mousavinejad, E.; Ge, X.; Han, Q.; Yang, F.; Vlacic, L. Resilient tracking control of networked control systems under cyber attacks. IEEE Trans. Cybern. 2021, 51, 2107–2119. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Xu, H.; Wei, X.; Hu, X. Security correction control of stochastic cyber-physical systems subject to false data injection attacks with heterogeneous effects. ISA Trans. 2021, in press. [Google Scholar] [CrossRef]
- Yoo, S.J. Neural-network-based adaptive resilient dynamic surface control against unknown deception attack of uncertain nonlinear time-delay cyberphysical systems. IEEE Tran. Neural Netw. Learn. Syst. 2019, 31, 4341–4353. [Google Scholar] [CrossRef]
- Yoo, S.J. Approximation-based event-triggered control against unknown injection data in full states and actuator of uncertain lower-triangular nonlinear systems. IEEE Access 2020, 8, 101747–101757. [Google Scholar] [CrossRef]
- Yang, Y.; Huang, J.; Su, X.; Wang, K.; Li, G. Adaptive control of second-order nonlinear systems with injection and deception attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Zhang, K.; Su, R.; Zhang, H.; Tian, Y. Adaptive resilient event-triggered control design of autonomous vehicles with an iterative single critic learning framework. IEEE Trans. Neural Netw. Learn. Syst. 2021, in press. [Google Scholar]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multi-robot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef] [Green Version]
- Lewis, M.A.; Tan, K.H. High precision formation control of mobile robots using virtual structures. Auton. Robot. 1997, 14, 387–403. [Google Scholar] [CrossRef]
- Desai, J.P.; Ostrowski, J.; Kumar, V. Modeling and control of formations of nonholonomic mobile robots. IEEE Trans. Robot. Autom. 2001, 17, 905–908. [Google Scholar] [CrossRef] [Green Version]
- Consolini, L.; Morbidi, F.; Prattichizzo, D.; Tosques, M. Leader-follower formation control of nonholonomic mobile robots with input constraints. Automatica 2008, 44, 1343–1349. [Google Scholar] [CrossRef]
- Defoort, M.; Floquet, T.; Kokosy, A.; Perruquetti, W. Sliding-mode formation control for cooperative autonomous mobile robots. IEEE Trans. Ind. 2008, 55, 3944–3953. [Google Scholar] [CrossRef] [Green Version]
- Dierks, T.; Jagannathan, S. Neural network control of mobile robot formations using RISE feedback. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 332–347. [Google Scholar] [CrossRef]
- Poonawala, H.A.; Satici, A.C.; Exkert, H.; Spong, M.W. Collision-free formation control with decentralized connectivity preservation for nonholonomic wheeled mobile robots. IEEE Trans. Control. Syst. Technol. 2015, 2, 122–130. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Yang, S.; Shan, M. A practical leader-follower tracking control scheme for multiple nonholonomic mobile robots in unknown obstacle environments. IEEE Trans. Control Syst. Technol. 2019, 27, 1685–1693. [Google Scholar] [CrossRef]
- Kan, Z.; Klotz, J.R.; Shea, J.M.; Doucette, E.A.; Dixon, W.E. Decentralized rendezvous of nonholonomic robots with sensing and connectivity constraints. J. Dyn. Syst. Meas. Control 2017, 39, 024501. [Google Scholar] [CrossRef] [Green Version]
- Park, B.S.; Yoo, S.J. Connectivity-maintaining obstacle avoidance approach for leader-follower formation tracking of uncertain multiple nonholonomic mobile robots. Expert Syst. Appl. 2021, 171, 114589. [Google Scholar] [CrossRef]
- Fukao, T.; Nakagawa, H.; Adachi, N. Adaptive tracking control of a nonholonomic mobile robot. IEEE Trans. Robot. Autom. 2000, 16, 609–615. [Google Scholar] [CrossRef]
- Fawzi, H.; Tabuada, P.; Diggavi, S. Secure estimation and control for cyber-physical systems under adversarial attacks. IEEE Trans. Autom. Control 2014, 59, 1454–1467. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yang, H.; Xia, Y.; Zhu, C. Attack detection and distributed filtering for state-saturated systems under deception attack. IEEE Trans. Control Netw. Syst. 2021, in press. [Google Scholar] [CrossRef]
- Ge, S.S.; Wang, C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Trans. Neural Netw. 2004, 15, 674–692. [Google Scholar] [CrossRef] [PubMed]
- Polycarpou, M.M. Stable adaptive neural control scheme for nonlinear systems. IEEE Trans. Autom. Control 1996, 41, 447–451. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef] [Green Version]
- Tanner, H.G.; Pappas, G.J.; Kumar, V. Leader-to-formation stability. IEEE Trans. Robot. Autom. 2004, 20, 443–455. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, B.-S.; Yoo, S.-J. Adaptive Secure Control for Leader-Follower Formation of Nonholonomic Mobile Robots in the Presence of Uncertainty and Deception Attacks. Mathematics 2021, 9, 2190. https://doi.org/10.3390/math9182190
Park B-S, Yoo S-J. Adaptive Secure Control for Leader-Follower Formation of Nonholonomic Mobile Robots in the Presence of Uncertainty and Deception Attacks. Mathematics. 2021; 9(18):2190. https://doi.org/10.3390/math9182190
Chicago/Turabian StylePark, Bong-Seok, and Sung-Jin Yoo. 2021. "Adaptive Secure Control for Leader-Follower Formation of Nonholonomic Mobile Robots in the Presence of Uncertainty and Deception Attacks" Mathematics 9, no. 18: 2190. https://doi.org/10.3390/math9182190
APA StylePark, B.-S., & Yoo, S.-J. (2021). Adaptive Secure Control for Leader-Follower Formation of Nonholonomic Mobile Robots in the Presence of Uncertainty and Deception Attacks. Mathematics, 9(18), 2190. https://doi.org/10.3390/math9182190






