1. Introduction
Owing to its outstanding ductility, thermal conductivity, and electrical conductivity, copper is widely used in various fields such as electric power, construction, home appliances, transportation, and other industries. However, there is a worldwide shortage of copper. According to the latest data from the World Bureau of Metals Statistics, the global copper market was short by 1.39 million tons in 2020. Since the beginning of 2018, the supply and demand dilemma of copper resources has been aggravated by a drop in explicit global copper inventories, difficulties in wage negotiations among copper miners, and the closure of Smelters owned by India’s Vedanta. The high degree of absolute international dependence will inevitably lead to a bad situation for Chinese enterprises in the world economy and trade. As the world’s largest copper consumer, China faces a shortage of mineral resources in the development process, and smelting capacity is greater than the support capability of structural problems in mines. Additionally, China’s copper dispersion and resources are heavily dependent on imports; that is, the external dependency on copper of up to 80% is bound to cause adverse situations for Chinese enterprises in the global economy and trade. Copper prices have been climbing as the central environmental watchdog has carried out “look back” measures. On 15 June 2018, the U.S. announced a 25% tariff on roughly USD $50 billion of imported goods, and China retaliated. The escalation of friction regarding trade has led to a temporary slowdown in the process of global economic growth, and risks are also increasing.
Given the closer international metal trade relationships, metal futures, metal options, and other financial instruments are gradually being promoted, and the Shanghai futures trading market is gradually opening and has an increasingly obvious relationship with the international futures market. Copper futures are futures contracts whose subject matter is non-ferrous metal copper. Copper futures began trading on the London Metal Exchange (LME) in 1877, being the first metal futures traded on the LME. Currently, the New York Mercantile Exchange (COMEX), the LME, and the Shanghai Futures Exchange (SHFE) are the main international copper futures trading venues. Among them, The London Stock Exchange is the most well-known and the most widely referenced and researched non-ferrous metal futures circulation venue, and has become the universally recognized place for international copper prices to be set. China’s copper futures trading appeared relatively late and has developed rapidly in recent years. The futures market is more and more legalized, and its international influence is constantly increasing. The price of Copper futures in Shanghai has formed a high-level linkage with other international markets, and the prices between the markets continue to spread among them. The launch of London and New York copper futures contracts will help Chinese spot traders better manage the risk of renminbi-denominated commodity contracts and establish a pricing mechanism for metals in Asia.
Therefore, from the two perspectives of diffusion and jumping, this paper precisely analyzes the price of copper futures contracts to correlation effect and compares the copper futures market strain capacity of the international market price information to promptly provide a solid operational foundation for the relevant regulatory authorities and traders and supply accurate pricing and hedging. Our data is comprised of data from 2 June 2006 to 30 June 2020 for three futures markets, including the closing prices of futures on the Shanghai Futures Exchange, The New York Futures Exchange, and the London Futures Exchange.
With the rise and development of futures markets worldwide, analysis of the price correlation effect between futures markets in various countries (or regions) has become a research focus. The theory of the linkage of commodity futures markets mainly includes the convenience theory, the inventory theory, the herd effect, and the market contagion theory. Commodity, storage loss, the opportunity cost of spot purchase, and convenience income act together in the pricing process of futures contracts. Convenience income and commodity price are positively correlated, where a higher commodity price brings higher convenience income. Spot copper, as an important industrial raw material, has a high degree of openness in the copper trade among countries, while the futures price tends to converge on the spot price, which makes the copper futures price in each market maintain its equilibrium. The study of herd behavior belongs to behavioral finance, that is, investors will adopt the same decision-making means as others when they have no way to choose their investment modes [
1,
2]. The International Monetary Fund believes that one of the causes of the recent financial crisis was the transmission and spread of volatility risks among countries, that is, when a country’s economy fluctuates, it will trigger the re-judgment and evaluation of information by investors in other markets. This would change the prices of various financial products to a certain extent and cause the transmission of volatility between countries [
3]. The forms of futures market linkages mainly include co-integration and spillover effects between market prices, and the co-integration relationship, spillover effect, and price discovery are interrelated rather than completely independent. Guangxi C. et al. proposed a correlation analysis method to measure and calculate the price relationships in different regional markets, utilizing a simple regression coefficient to calculate the correlation coefficient for measuring the degree of fusion [
4]. However, the instability of the price series resulted in inaccurate model statistics, which led to significant errors. Engle R.F. and Granger C.W.J. found that the combined variance residuals of non-stationary sequences were stable and thus proposed the concept of “co-integration,” which indicated a stable long-term equilibrium relationship between sequences [
5]. The two-step E–G method is widely used in economics, including futures markets. The co-integration relationship between the grain futures market and the spot market, the grain futures markets of different countries, special dollar futures, and the United States bond futures have been verified [
6,
7,
8].
On this basis, scholars began to apply combinations of various models for market linkage analysis. For example, Zhou B. and Wu C. used the VAR-DCC-MGARCH to comprehensively explore the idea that the index futures market dominates the price discovery process between the CSI 300 index futures and spot markets [
9]. Chiao-Yi Chang et al. used energy futures as a research object by building the ECM-MD model, ECM-BEKK model, and six other models [
10]. It was found that there is, consistently, asymmetric hedging performance between upward and downward price trends. Based on the DCC method, some researchers have developed the trend consistency of futures price fluctuations for the London and Shanghai copper markets [
11,
12]. Gulley and Tilton found that when the market is in a state of strong premium, investors’ demand for the futures market will affect spot and futures prices, and its influence is greater than that of a weak market [
13]. Yue identified that the impact of London metal pricing was more prominent based on the DCC model, while the impact of the Shanghai metal market was less prominent [
14]. Mayer et al. used a bidirectional Granger causality test and EGARCH volatility analysis to find that, in the long run, trading activities have almost no impact on metal spot prices, only promoting volatility to a certain extent [
15]. Song and Xing used the VECM, BEKK-GARCH, and CCC-GARCH models to find that copper futures in Shanghai, London, and New York had a co-integration correlation [
16]. Moreover, the pricing mechanism of Shanghai copper is more significant, but the exchange of information between Shanghai copper futures and the outside world is insufficient. More and more researchers have built DCC-GARCH-T, VAR-DCC-GARCH, and VAR-BEKK-GARCH models to explore the relationship between the volatility spillover effect and price discovery in futures markets [
17,
18]. From a short-term perspective, price discovery shows that markets remain closely related. When one market is disturbed, price changes will spread to other markets, and different markets will show a consistent trend under this interaction. A volatility spillover is an outcome of linkage analysis, that is, market risks communicate. That is, due to the co-integration effect between different price series, various markets have volatility spillover effects, and volatility risks are transmitted between markets.
In different market environments, most investors will be affected by external factors and show irrational characteristics, thus causing the phenomenon of the market jump. Hull illustrated that the introduction of this phenomenon can improve some non-normal characteristics, that is, the form of jump diffusion perfectly describes the price changes of commodities [
19]. Duffie et al. proved that affine classes in the multi-factor jump diffusion process are flexible [
20]. Maosen Zhong et al. found that the Mexican futures market had a certain price discovery function, but had a negative impact on its spot market [
21]. Jacod and Todorov took the conversion rate between pound sterling, mark, and U.S. dollar as the research object, and found a certain correlation between them, as well as pair jumping [
22]. Gilde identified a significant correlation between the U.S. stock market and the number of joint jumps between stocks showing a relatively stable trend in the number and range of jumps [
23]. Some researchers have explored the manifestation of the jump process and behavior of stock prices in various stages [
24,
25,
26]. Liu and Xu compared and analyzed the detection level and efficacy of eight different jump test methods using the Monte Carlo analysis method, and found that BN-S non-parametric test methods have more advantages than the TMPV methods when there is a large fluctuation in the sample data [
27]. Cao and Guernsey found that the fluctuation of crude oil and natural gas futures prices could be decomposed into an infinite active fluctuation diffusion process and a lower, but larger fluctuation process [
28]. Gong et al. constructed a generalized double-exponential distribution jump-diffusion model based on a Markov chain Monte Carlo simulation and found that it could better capture the peak and thick tail characteristics of the rate of return distribution and that the probability of the rise and fall of stock index futures returns and stock index spot returns presented asymmetry [
29]. Yaoqi Guo et al. applied the nonlinear Granger causality and multifractal methods to test market efficiency, which found that there is a significant high-order nonlinear correlation between futures and spot markets [
30]. Hui Yu et al. proposed an integrated research framework combining the grey correlation and wavelet analysis and indicated that the correlations of copper prices are dynamic and uncertain [
31]. Some researchers have considered price jump behaviors such as macroscopic to microcosmic exploration and combined the introduction of the financial asset price jump component with the test of a leap in the related literature, pointing out that future jump tests should focus on high-frequency financial derivatives pricing and the trading of jumping phenomenon research to improve the jumping test’s noise control [
32,
33].
Based on a comprehensive analysis of the literature, this study determines that domestic and foreign scholars usually study futures market correlation from three perspectives:
- (1)
A co-integration test and an error correction mechanism to verify the long-term and short-term equilibrium relationships between variables;
- (2)
The GARCH model to explore the relationship between market volatility spillover;
- (3)
The Granger causality test or information model to study the intensity of price discovery between markets.
However, currently, few studies combine the non-parametric test method with the futures market correlation effect analysis method from the perspectives of diffusion and jumping.
From the perspective of diffusion and jump, to clarify the reasons and paths of the interaction effect of Shanghai, New York, and London copper futures markets, and put forward feasible measures for the development of the current Chinese copper futures market, this article is organized as follows.
Section 1 continues the literature review of the futures market linkage effect research.
Section 2 introduces the spillover effect models from the perspectives of diffusion and jump.
Section 3 presents the data and test, followed by
Section 4, which shows the results of the price relationship of copper futures on three futures exchanges.
Section 5 presents the most important conclusions.
The innovation of this paper includes:
- (1)
This paper extends other scholars’ work based on the copper futures contract price before the diffusion angle of empirical research and the diffusion angle using the cointegration test, the Granger causality test, and BEKK model research, based on the future jump, from the perspective of the use of the BN-S nonparametric test method and the linkage of the copper futures price in particular market environment characteristics.
- (2)
This paper selects the daily closing data of copper futures from three domestic and foreign markets in the past 14 years as the research sample. The sample size is large, and the sample interval is divided into three sections from the diffusion perspective to better discuss the linkage characteristics between markets with special events as time nodes.
- (3)
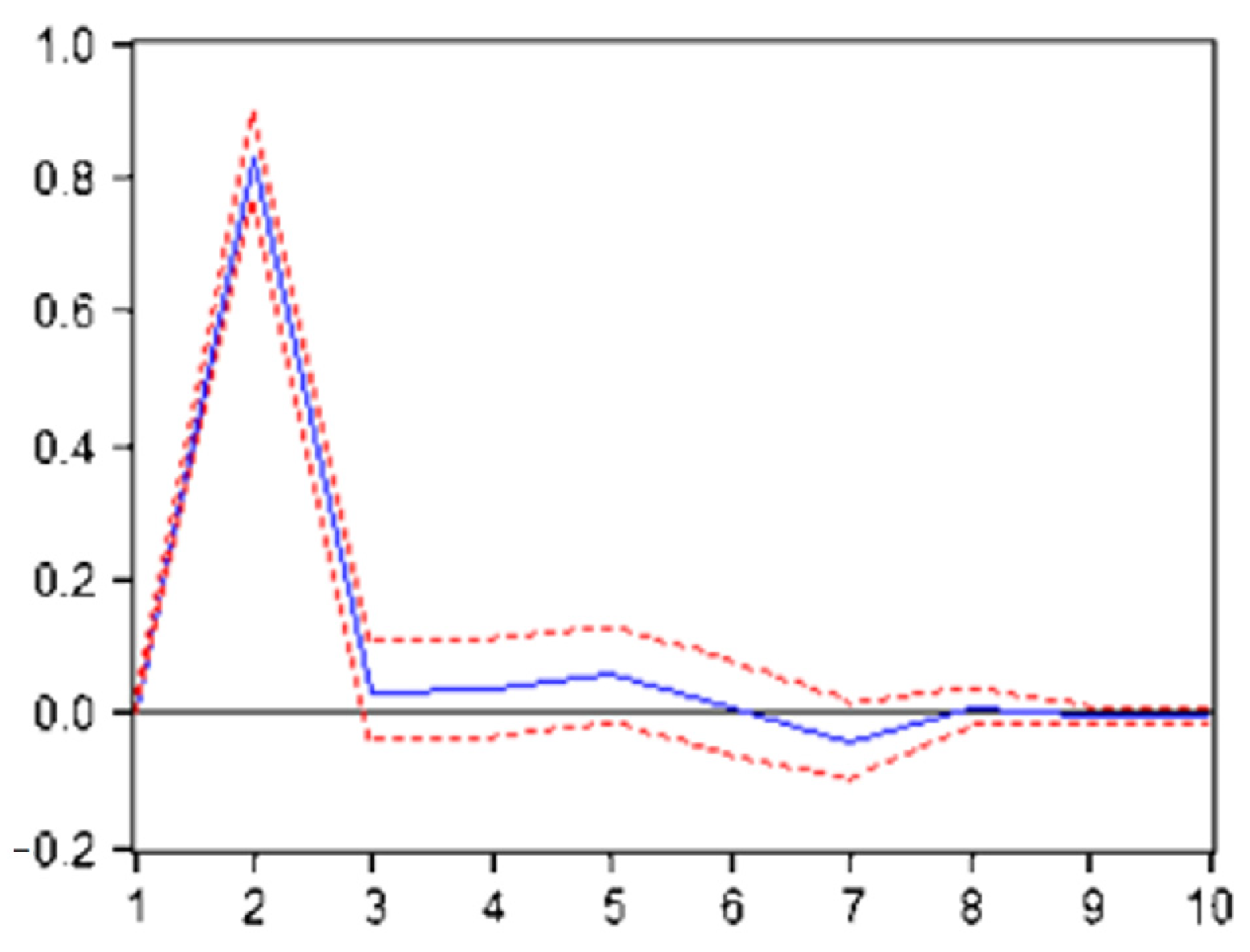
This paper takes the interaction between the three markets as the research topic. In this paper, the Shanghai copper futures market price is taken as the benchmark, the New York copper futures price and the London copper futures price are taken as the independent variables, and empirical analysis is carried out using the ECM model and impulse response and variance decomposition, enriching the research on the linkage phenomenon between the domestic and foreign copper futures markets from the perspective of diffusion.