A Dynamic Model of Cytosolic Calcium Concentration Oscillations in Mast Cells
Abstract
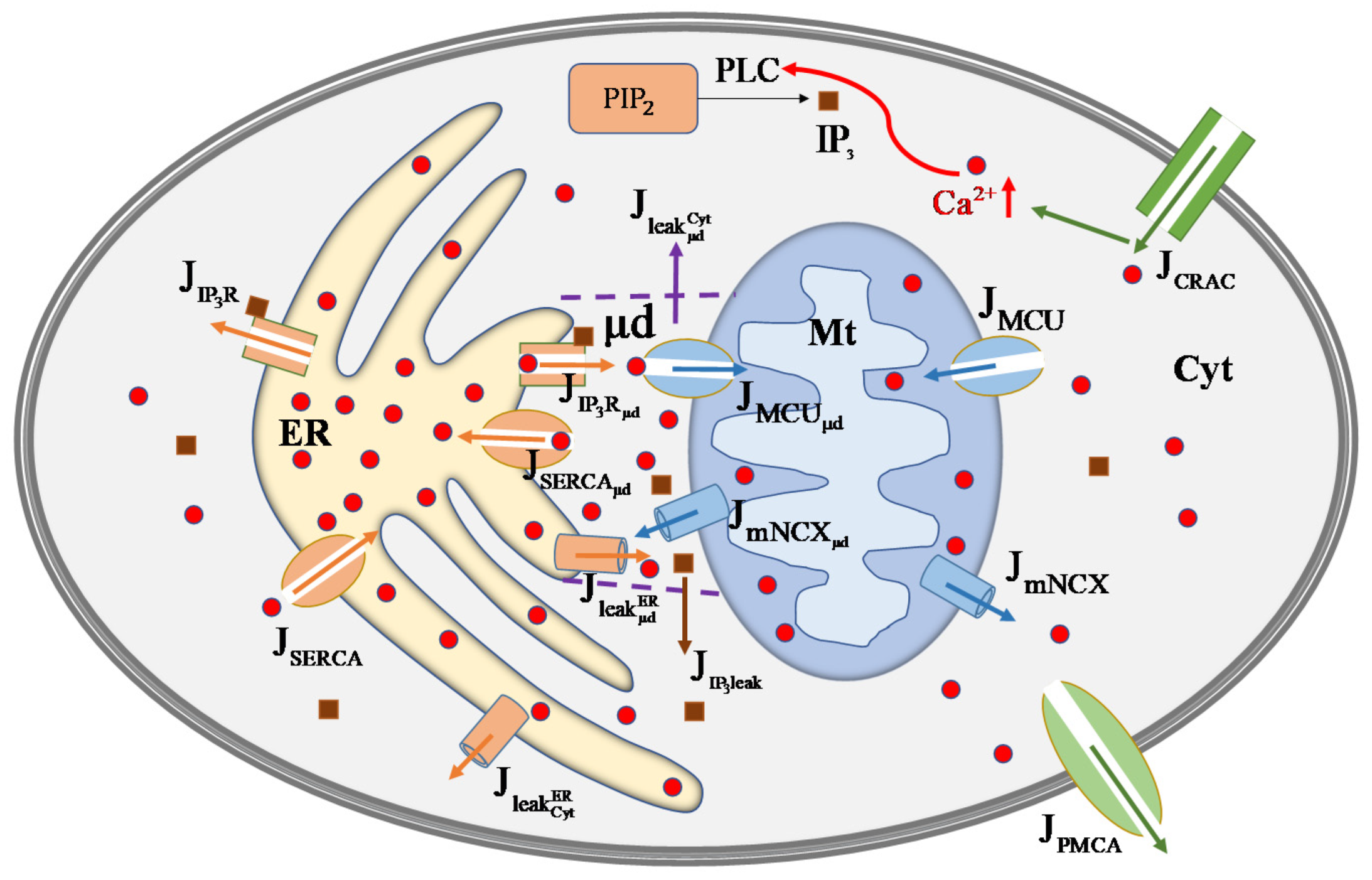
:1. Introduction
2. Mathematical Model
2.1. Cross-Membrane Current
2.2. Outflows from ER
2.3. Outflows from Mt
2.4. Effective Cytosol
2.5. μd Volume
2.6. Temporal Changes in in Each Compartment
3. Results
3.1. Effect of the Degradation and Production of on Oscillations
3.2. Effect of the ER–Mt Distance (D) on Oscillations
3.3. Effect of the on Oscillations
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, N.; Jiang, J.; Qin, P.; Wang, Q.; Hu, J.; Li, Z. Mast cells are important regulator of acupoint sensitization via the secretion of tryptase, 5-hydroxytryptamine, and histamine. PLoS ONE 2018, 13, e0194022. [Google Scholar] [CrossRef] [PubMed]
- Berridge, M.J.; Bootman, M.D.; Roderick, H.L. Calcium signalling: Dynamics, homeostasis and remodelling. Nat. Rev. Mol. Cell Biol. 2003, 4, 517–529. [Google Scholar] [CrossRef] [Green Version]
- Parekh, A.B. Decoding cytosolic Ca2+ oscillations. Trends Biochem. Sci. 2011, 36, 78–87. [Google Scholar] [CrossRef]
- Zhu, L.; Luo, Y.; Chen, T.; Chen, F.; Wang, T.; Hu, Q. Ca2+ oscillation frequency regulates agonist-stimulated gene expression in vascular endothelial cells. J. Cell Sci. 2008, 121, 2511–2518. [Google Scholar] [CrossRef] [Green Version]
- Smedler, E.; Uhlén, P. Frequency decoding of calcium oscillations. Biochim. Biophys. Acta 2013, 1840, 964–969. [Google Scholar] [CrossRef] [Green Version]
- Capite, J.D.; Parekh, A.B. CRAC channels and Ca2+ signaling in mast cells. Immunol. Rev. 2010, 231, 45–58. [Google Scholar] [CrossRef]
- Hoth, M.; Penner, R. Depletion of intracellular calcium stores activates a calcium current in mast cells. Nature 1992, 355, 353–356. [Google Scholar] [CrossRef]
- Baker, H.L.; Errington, R.J.; Davies, S.C.; Campbell, A.K. A mathematical model predicts that calreticulin interacts with the endoplasmic recticulum Ca. Biophys. J. 2002, 82, 582–590. [Google Scholar] [CrossRef] [Green Version]
- Contreras, L.; Drago, I.; Zampese, E.; Pozzan, T. Mitochondria: The calcium connection. BBA Bioenerg. 2010, 1797, 607–618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hajno’czky, G.; Robb-Gaspers, L.D.; Seitz, M.B.; Thomas, A.P. Decoding of cytosolic calcium oscillations in the mitochondria. Cell 1995, 82, 415–424. [Google Scholar] [CrossRef] [Green Version]
- Samanta, K.; Douglas, S.; Parekh, A.B. Mitochondrial Calcium Uniporter MCU Supports Cytoplasmic Ca2+ Oscillations, Store-Operated Ca2+ Entry and Ca2+-Dependent Gene Expression in Response to Receptor Stimulation. PLoS ONE 2014, 9, e101188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishii, K.; Hirose, K.; Iino, M. Ca2+ shuttling between endoplasmic reticulum and mitochondria underlying Ca2+ oscillations. EMBO J. 2006, 7, 390–396. [Google Scholar] [CrossRef] [Green Version]
- Rizzuto, R.; De Stefani, D.; Raffaello, A.; Mammucari, C. Mitochondria as sensors and regulators of calcium signalling. Nat. Rev. Mol. Cell Biol. 2012, 13, 566–578. [Google Scholar] [CrossRef] [PubMed]
- De Stefani, D.; Rizzuto, R.; Pozzan, T. Calcium in Mitochondria Back and Forth. Annu. Rev. Biochem. 2016, 85, 161–192. [Google Scholar] [CrossRef] [PubMed]
- Csordás, G.; Renken, C.; Várnai, P.; Walter, L.; Weaver, D.; Buttle, K.F.; Balla, T.; Mannella, C.A.; Hajnóczky, G. Structural and functional features and significance of the physical linkage between ER and mitochondria. J. Cell Biol. 2006, 174, 915–921. [Google Scholar] [CrossRef] [Green Version]
- Raturi, A.; Simmen, T. Where the endoplasmic reticulum and the mitochondrion tie the knot: The mitochondria-associated membrane (MAM). Biochim. Biophys. Acta 2013, 1833, 213–224. [Google Scholar] [CrossRef] [Green Version]
- Patergnani, S.; Suski, J.M.; Agnoletto, C.; Bononi, A.; Bonora, M.; De Marchi, E.; Giorgi, C.; Marchi, S.; Missiroli, S.; Poletti, F.; et al. Calcium signaling around Mitochondria Associated Membranes (MAMs). Cell Commun. Signal. 2011, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- de Brito, O.M.; Scorrano, L. An intimate liaison: Spatial organization of the endoplasmic reticulum–mitochondria relationship. EMBO J. 2010, 29, 2715–2723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Y.; Huang, H.; Ding, G. A dynamic model of calcium signaling in mast cells and LTC4 release induced by mechanical stimuli. Chin. Sci. Bull. 2014, 59, 956–963. [Google Scholar]
- Miyakawa, T.; Mizushima, A.; Hirose, K.; Yamazawa, T.; Bezprozvanny, I.; Kurosaki, T.; Iino, M. Ca2+-sensor region of IP3 receptor controls intracellular Ca2+ signaling. EMBO J. 2001, 20, 1674–1680. [Google Scholar] [CrossRef] [Green Version]
- Berridge, M.J. Inositol trisphosphate and calcium signalling mechanisms. Biochim. Biophys. Acta 2009, 1793, 933–940. [Google Scholar] [CrossRef] [Green Version]
- Bezprozvanny, I.; Watras, J.; Ehrlich, B.E. Bell-shaped calcium-response curves of Ins (1,4,5) P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature 1991, 351, 751–754. [Google Scholar] [CrossRef]
- Csordás, G.; Várnai, P.; Golenár, T.; Roy, S.; Purkins, G.; Schneider, T.G.; Balla, T.; Hajnóczky, G. Imaging interorganelle contacts and local calcium dynamics at the ER-mitochondrial interface. Mol. Cell 2010, 39, 121–132. [Google Scholar] [CrossRef]
- Giacomello, M.; Drago, I.; Bortolozzi, M.; Scorzeto, M.; Gianelle, A.; Pizzo, P.; Pozzan, T. Ca2+ hot spots on the mitochondrial surface are generated by Ca2+ mobilization from stores, but not by activation of store-operated Ca2+ channels. Mol. Cell 2010, 38, 280–290. [Google Scholar] [CrossRef]
- Williams, G.S.; Boyman, L.; Chikando, A.C.; Khairallah, R.J.; Lederer, W.J. Mitochondrial calcium uptake. Proc. Natl. Acad. Sci. USA 2013, 110, 10479–10486. [Google Scholar] [CrossRef] [Green Version]
- Di Capite, J.; Shirley, A.; Nelson, C.; Bates, G.; Parekh, A.B. Intercellular Ca2+ wave propagation involving positive feedback between CRAC channels and cysteinyl leukotrienes. FASEB J. 2009, 23, 894–905. [Google Scholar] [CrossRef] [PubMed]
- Osipchuk, Y.; Cahalan, M. Cell-to-cell spread of calcium signals mediated by ATP receptors in mast cells. Nature 1992, 359, 241–244. [Google Scholar] [CrossRef] [PubMed]
- Dupont, G.; Berridge, M.J. Minimal model for signal-induced Ca2+ oscillations and for their frequency encoding through protein phosphorylation. Proc. Natl. Acad. Sci. USA 1990, 87, 1461–1465. [Google Scholar]
- Hufer, T. Model of Intercellular Calcium Oscillations in Hepatocytes: Synchronization of Heterogeneous Cells. Biophys. J. 1999, 77, 1244–1256. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.X.; Rinzel, J. Equations for InsP3 Receptor-mediated [Ca2+]i Oscillations Derived from a Detailed Kinetic Model: A Hodgkin-Huxley Like Formalism. J. Theor. Biol. 1994, 166, 461–473. [Google Scholar] [CrossRef] [PubMed]
- Falcke, M.; Hudson, J.; Camacho, P.; Lechleiter, J. Impact of Mitochondrial Ca2+ Cycling on Pattern Formation and Stability. Biophys. J. 1999, 77, 37–44. [Google Scholar] [CrossRef] [Green Version]
- Xiao-Min, S.; Zeng-Rong, L. An Intracellular Calcium Oscillations Model Including Mitochondrial Calcium Cycling. Chin. Phys. Lett. 2005, 22, 3206. [Google Scholar] [CrossRef]
- Qi, H.; Li, L.; Shuai, J. Optimal microdomain crosstalk between endoplasmic reticulum and mitochondria for Ca2+ oscillations. Sci. Rep. 2015, 5, 7984. [Google Scholar] [CrossRef] [Green Version]
- Moshkforoush, A.; Ashenagar, B.; Tsoukias, N.M.; Alevriadou, B.R. Modeling the role of endoplasmic reticulum-mitochondria microdomains in calcium dynamics. Sci. Rep. 2019, 9, 17072. [Google Scholar] [CrossRef] [PubMed]
- Kapela, A.; Bezerianos, A.; Tsoukias, N.M. A mathematical model of Ca2+ dynamics in rat mesenteric smooth muscle cell: Agonist and NO stimulation. J. Theor. Biol. 2008, 253, 238–260. [Google Scholar] [CrossRef] [PubMed]
- Silva, H.S.; Kapela, A.; Tsoukias, N.M. A mathematical modelof plasma membrane electro physiology and calcium dynamics in vascular endothelial cells. Am. J. Physiol. Cell Physiol. 2007, 293, 277–293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Csordas, G.; Hajnoczky, G. Plasticity of Mitochondrial Calcium Signaling. J. Biol. Chem. 2003, 278, 42273–42282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chalmers, S.; Mccarron, J.G. The mitochondrial membrane potential and Ca2+ oscillations in smooth muscle. J. Cell Sci. 2008, 121 Pt 1, 75–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mccarron, J.G.; Olson, M.L.; Chalmers, S. Mitochondrial regulation of cytosolic Ca2+ signals in smooth muscle. Pflug. Arch. 2012, 464, 51–62. [Google Scholar] [CrossRef]
- Rizzuto, R.; Pinton, P.; Carrington, W.; Fay, F.S.; Fogarty, K.E.; Lifshitz, L.M.; Tuft, R.A.; Pozzan, T. Close contacts with the endoplasmic reticulum as determinants of mitochondrial Ca2+ responses. Science 1998, 280, 1763–1766. [Google Scholar] [CrossRef]
- Giedt, R.J.; Pfeiffer, D.R.; Matzavinos, A.; Kao CYAlevriadou, B.R. Mitochondrial dynamics and motility inside living vascular endothelial cells: Role of bioenergetics. Ann. Biomed. Eng. 2012, 52, 348–356. [Google Scholar] [CrossRef] [Green Version]
- Higgins, E.R.; Cannell, M.B.; Sneyd, J. A buffering SERCA pump in models of calcium dynamics. Biophys. J. 2006, 91, 151–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kummer, U.; Olsen, L.F.; Dixon, C.J.; Green, A.K.; Bornberg-Bauer, E.; Baier, G. Switching from simple to complex oscillations in calcium signaling. Biphys. J. 2000, 79, 1188–1195. [Google Scholar] [CrossRef] [Green Version]
- Nash, M.S.; Young, K.W.; Challiss, R.A.J.; Nahorski, S.R. Intracellular signalling: Receptor-specific messenger oscillations. Nature 2011, 413, 381–382. [Google Scholar] [CrossRef] [PubMed]
- Politi, A.; Gaspers, L.D.; Thomas, A.P.; Höfer, T. Models of IP3 and Ca2+ oscillations: Frequency encoding and identification of underlying feedbacks. Biophys. J. 2006, 90, 3120–3133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michalak, M.; Parker, J.R.; Opas, M. Ca2+ signaling and calcium binding chaperones of the endoplasmic reticulum. Cell Calcium 2002, 32, 269–278. [Google Scholar] [CrossRef]








| Parameter | Value | Description |
|---|---|---|
| 0.3 | the conductance [19] | |
| the membrane potential [19] | ||
| the universal gas constant [19] | ||
| the absolute temperature [19] | ||
| Faraday constant [19] | ||
| the Ca2+ concentration for half activation of SOC [19] | ||
| the maximum PMCA current [36] | ||
| the Ca2+ concentration for half activation of PMCA channels [36] | ||
| the extracellular Ca2+ concentration [19] | ||
| volume of ER [41] | ||
| volume of Mt [41] | ||
| volume of Cyt [34] | ||
| cell surface [34] | ||
| max flux of IP3R [34] | ||
| max flux of SERCA pump [34] | ||
| activation constant for SERCA pump [34] | ||
| IP3R binding rate at Ca2+ inhibition sites [34] | ||
| IP3R dissociation constant for IP3 sites [34] | ||
| IP3R dissociation constant for Ca2+ inhibition sites [34] | ||
| IP3R dissociation constant for IP3 sites [34] | ||
| IP3R dissociation constant for Ca2+ activation sites [34] | ||
| max rate of Ca2+ uptake by MCU [34] | ||
| half-max rate of Ca2+ pumping from Cyt to Mt [34] | ||
| max rate of Ca2+ release through NCX [34] | ||
| activation constant for NCX [34] | ||
| Na+ activation constant for MCU [34] | ||
| Na+ in Cyt [34] | ||
| Na+ in μd [34] | ||
| leak constant from ER to μd [34] | ||
| leak constant from ER to Cyt [34] | ||
| leak constant from μd to Cyt [34] | ||
| 0.486 | fraction of IP3R facing microdomain [34] | |
| 0.603 | fraction of SERCA facing microdomain [34] | |
| 0.894 | fraction of MCU facing microdomain [34] | |
| 0.569 | fraction of mNCX facing microdomain [34] | |
| total buffer concentration in Cyt [42] | ||
| 11.1 | buffer rate constant ratio [42] | |
| total buffer concentration in ER [42] | ||
| 967 | buffer rate constant ratio [42] | |
| total buffer concentration in Mt [42] | ||
| 698 | buffer rate constant ratio [42] | |
| total buffer concentration in μd [42] | ||
| 12 | buffer rate constant ratio [42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Li, Y.; Yao, W. A Dynamic Model of Cytosolic Calcium Concentration Oscillations in Mast Cells. Mathematics 2021, 9, 2322. https://doi.org/10.3390/math9182322
Sun M, Li Y, Yao W. A Dynamic Model of Cytosolic Calcium Concentration Oscillations in Mast Cells. Mathematics. 2021; 9(18):2322. https://doi.org/10.3390/math9182322
Chicago/Turabian StyleSun, Mingzhu, Yingchen Li, and Wei Yao. 2021. "A Dynamic Model of Cytosolic Calcium Concentration Oscillations in Mast Cells" Mathematics 9, no. 18: 2322. https://doi.org/10.3390/math9182322
APA StyleSun, M., Li, Y., & Yao, W. (2021). A Dynamic Model of Cytosolic Calcium Concentration Oscillations in Mast Cells. Mathematics, 9(18), 2322. https://doi.org/10.3390/math9182322






