Adaptive Robust Motion Control of Quadrotor Systems Using Artificial Neural Networks and Particle Swarm Optimization
Abstract
:1. Introduction
- Only position measurements are required for feedback control;
- High-gain feedback is reduced by using B-spline artificial neural networks;
- Reduced amount of control parameters needs to be tuned;
- The use of disturbance observers is unnecessary;
- The use of the tracking error derivatives is avoided in the controller design;
- Offline training of B-spline artificial neural networks is performed by particle swarm optimization;
- Low dependency of the quadrotor non-linear mathematical model;
- Robustness against a class of external disturbances, including undesirable vibrating forces and torques.
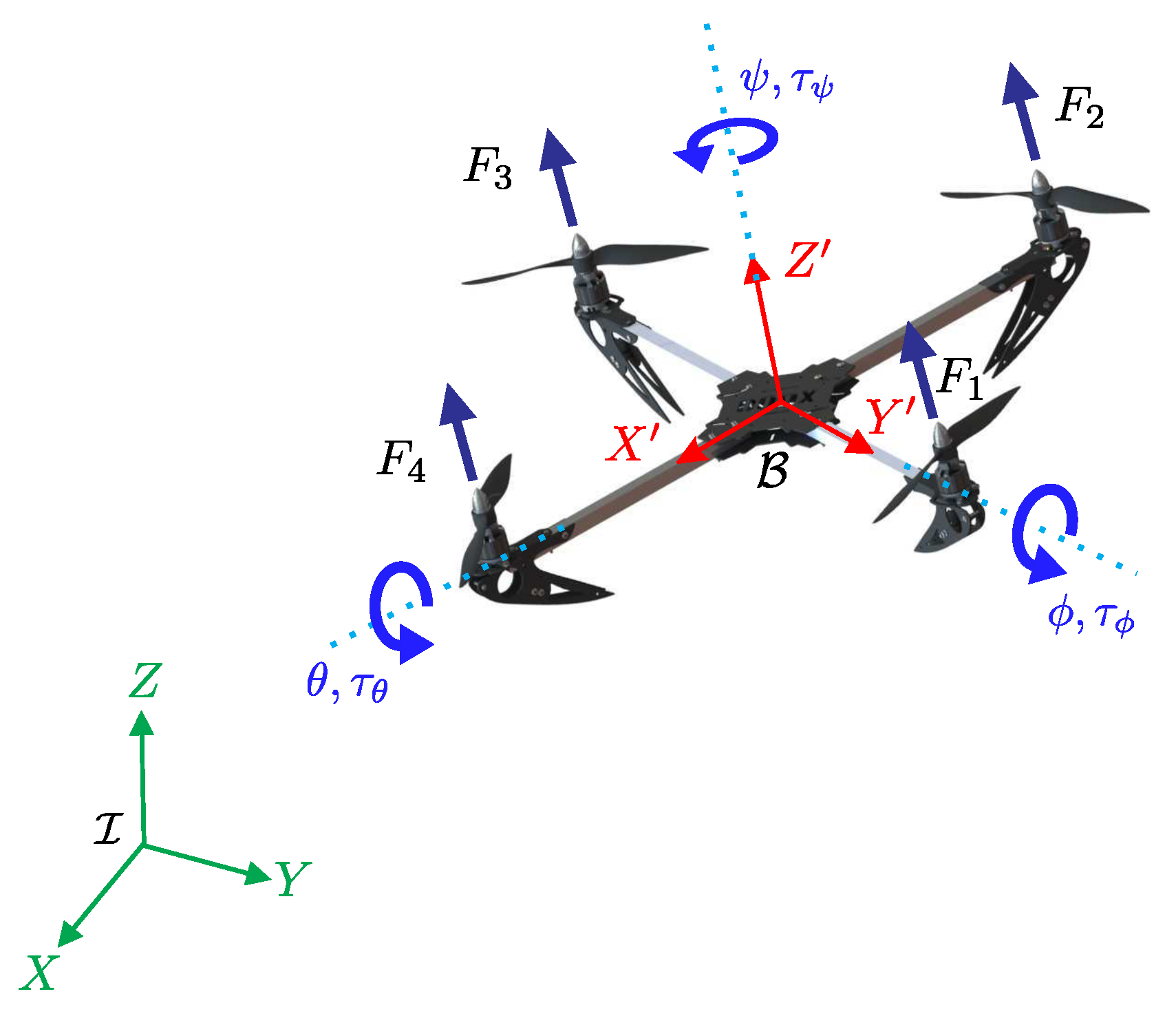
2. Mathematical Quadrotor Model
3. Syntheses of an Adaptive Robust Motion Controller
3.1. Dynamic Compensators for Robust Control Design
3.2. Adaptive Outline for Control Purposes
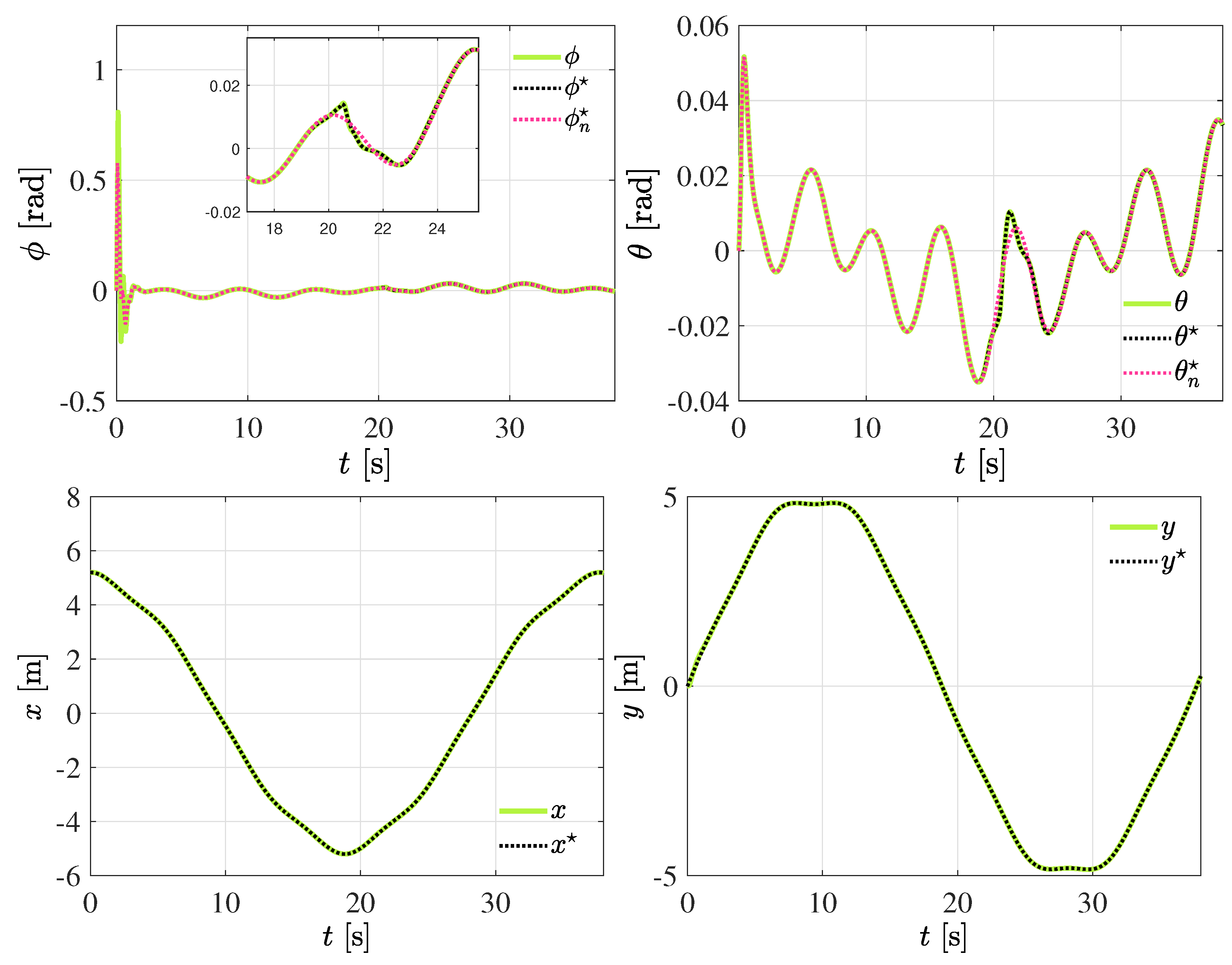
4. Validation through Simulation Experiments
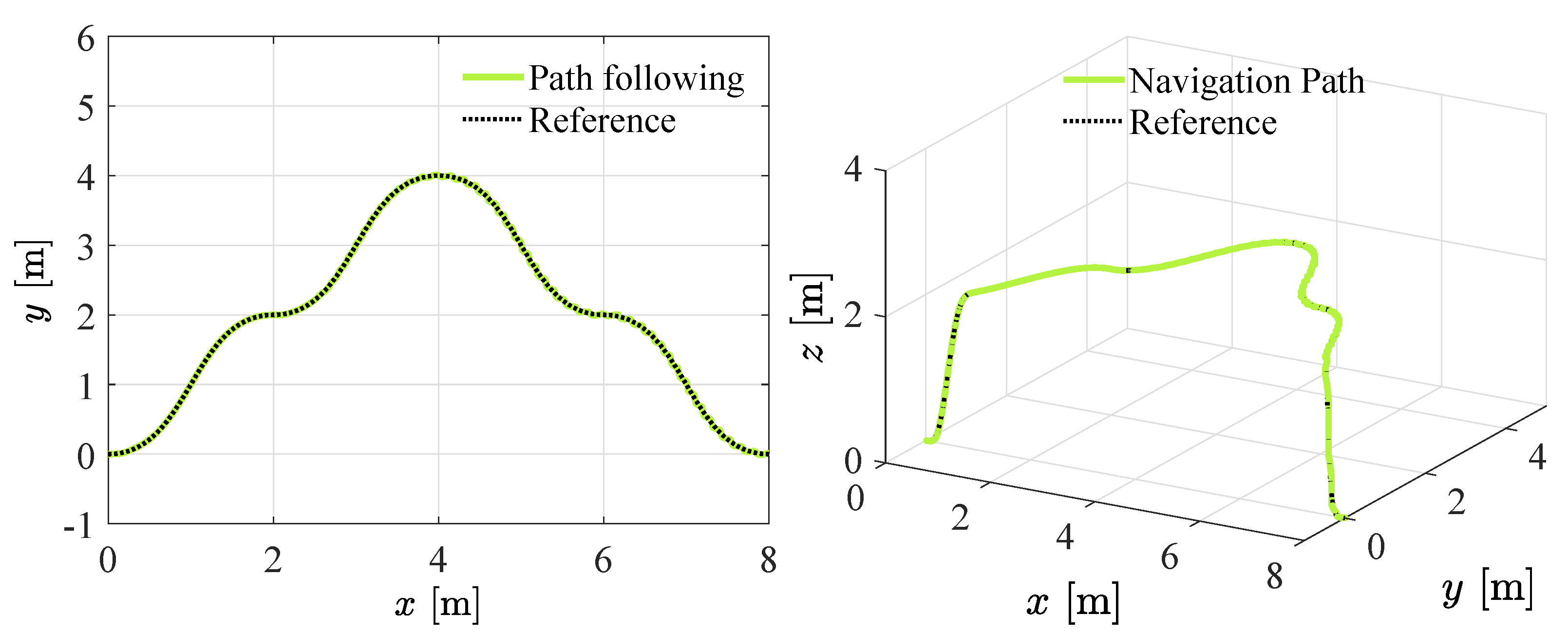
4.1. Polynomial Interpolation for Quadrotor Navigation
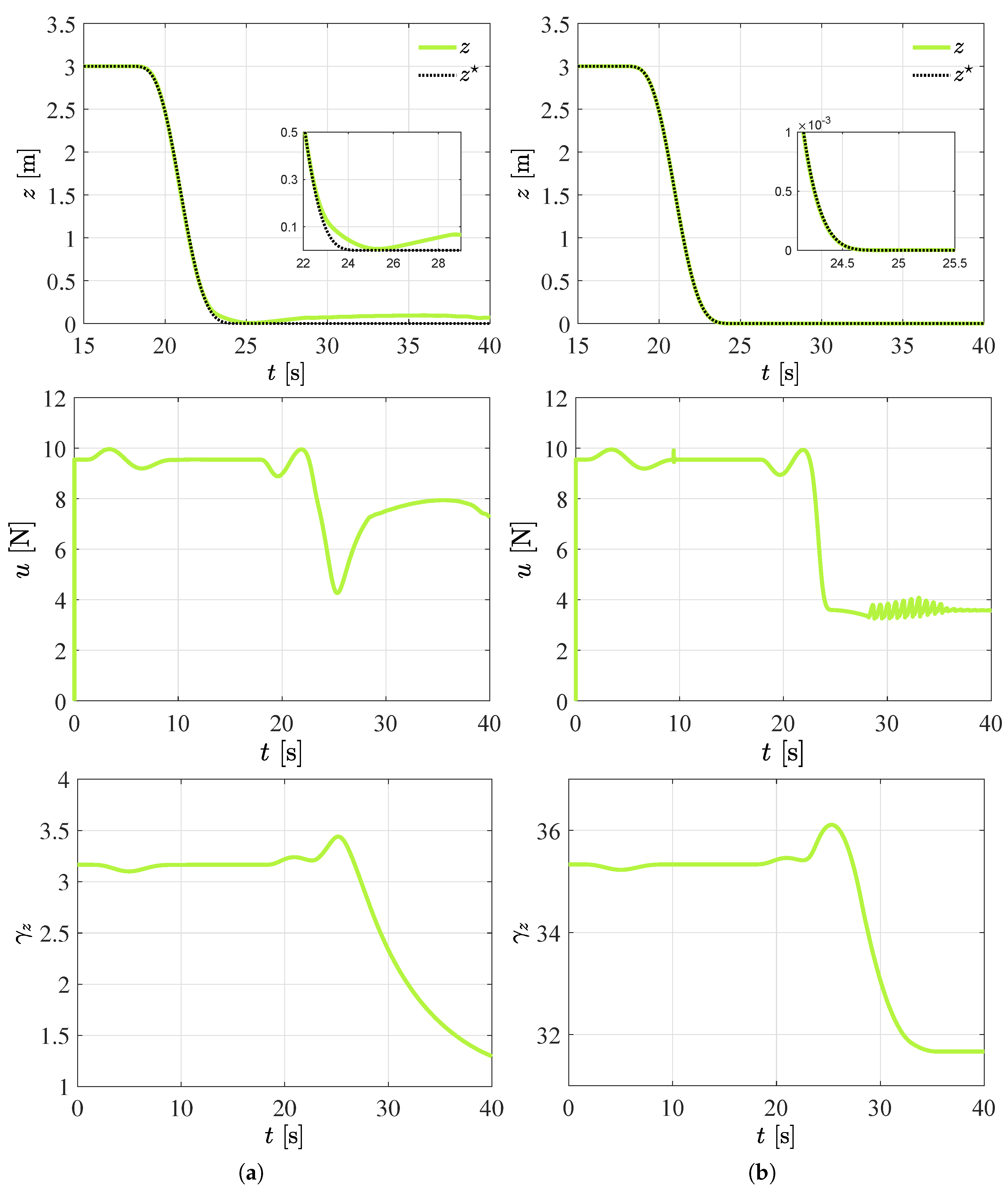
4.2. Improved Robust Quadrotor Autonomous Landing
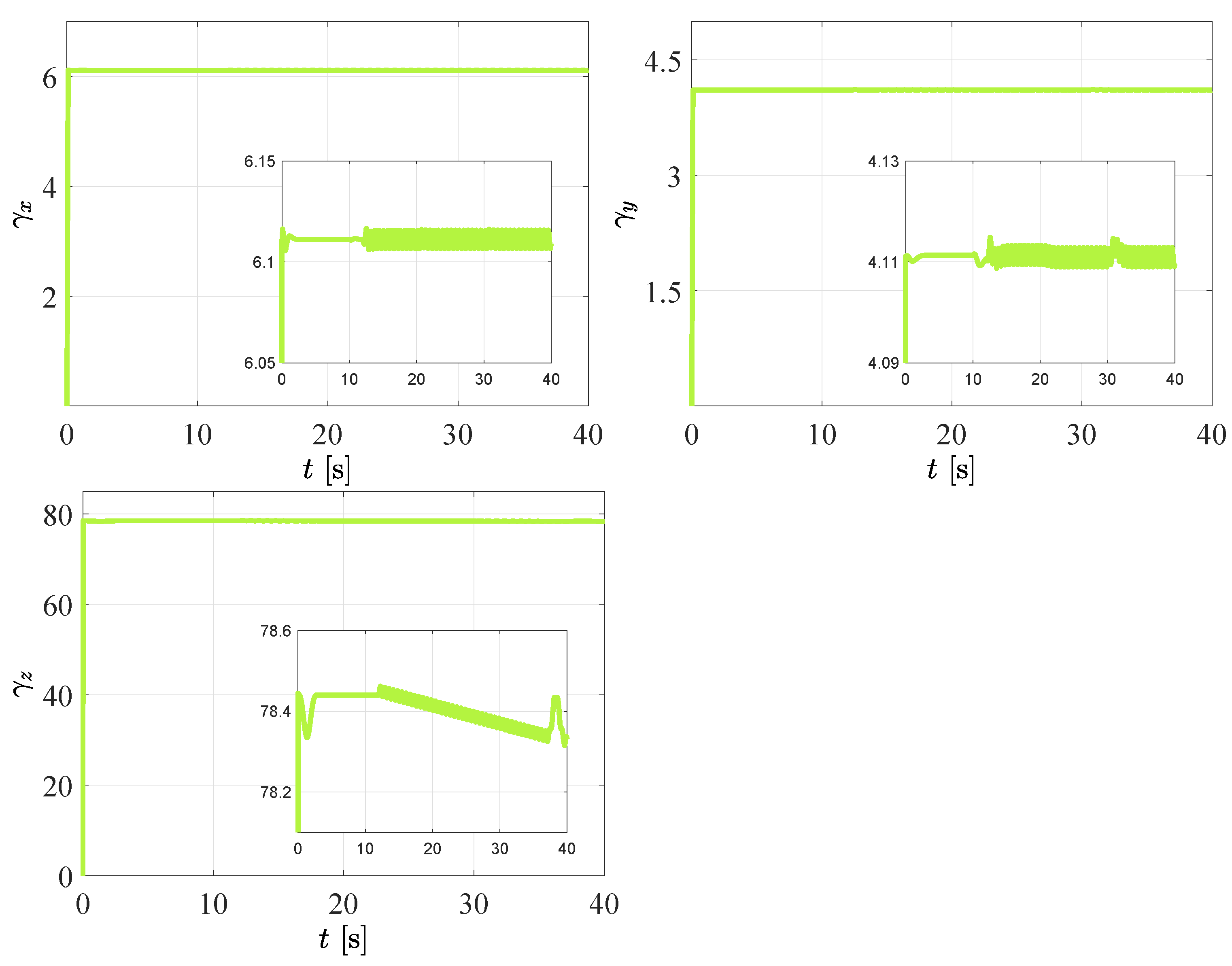
4.3. Bs-ANN Offline Training by Particle Swarm Optimization
| Algorithm 1: Evaluation of the objective function . |
 |
4.4. Quadrotor Subjected to Wind Gust Disturbances
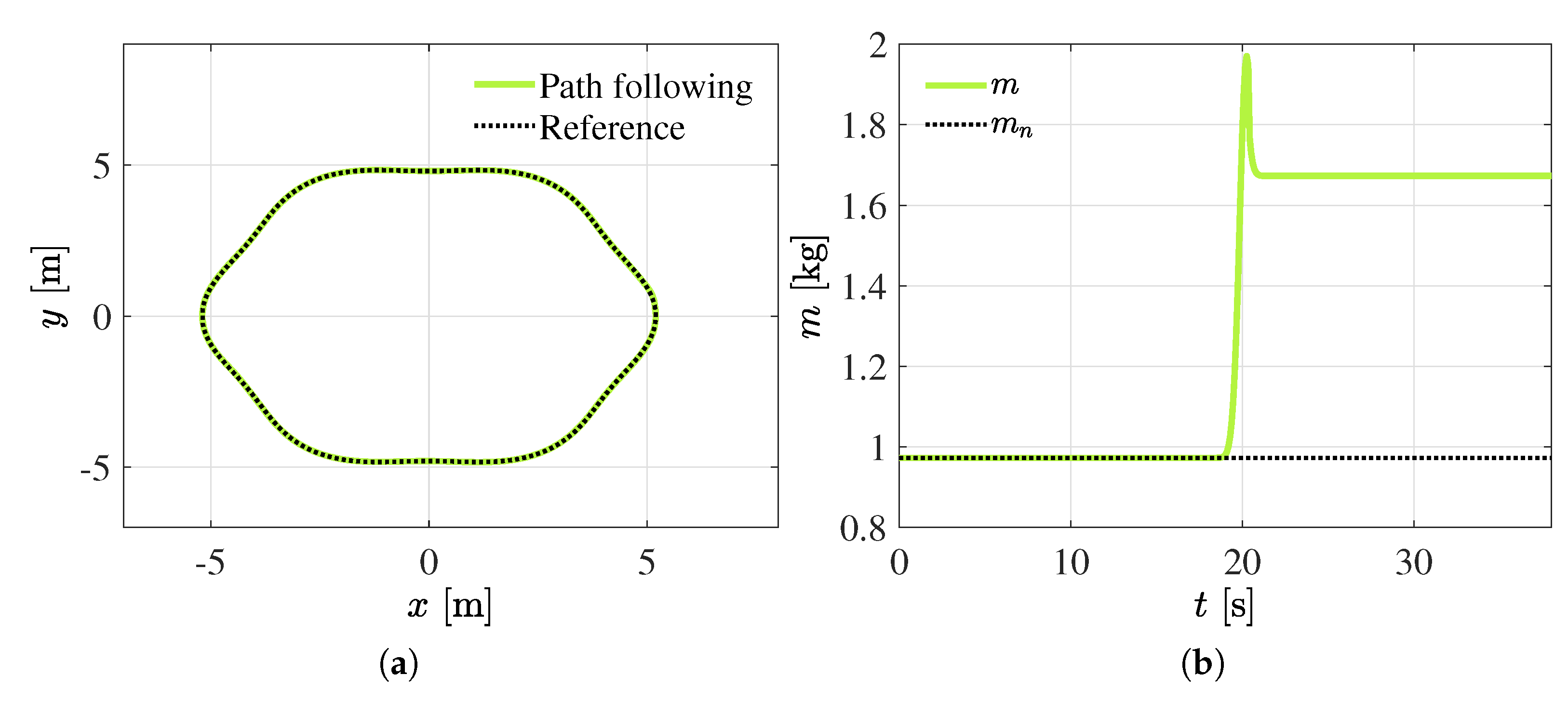
4.5. Robustness against Uncertainty of Quadrotor Mass
4.6. Discussion of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Castillo, P.; Dzul, A. Aerodynamic Configurations and Dynamic Models. In Unmanned Aerial Vehicles; Lozano, R., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 1–20. [Google Scholar]
- Leutenegger, S.; Hürzeler, C.; Stowers, A.K.; Alexis, K.; Achtelik, M.W.; Lentink, D.; Oh, P.Y.; Siegwart, R. Flying Robots. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 623–670. [Google Scholar]
- Fahimi, F. Autonomous Helicopters. In Autonomous Robots: Modeling, Path Planning, and Control; Springer: Boston, MA, USA, 2009; pp. 263–317. [Google Scholar]
- Gerdes, J.; Holness, A.; Perez-Rosado, A.; Roberts, L.; Greisinger, A.; Barnett, E.; Kempny, J.; Lingam, D.; Yeh, C.H.; Bruck, H.A.; et al. Robo Raven: A Flapping-Wing Air Vehicle with Highly Compliant and Independently Controlled Wings. Soft Robot. 2014, 1, 275–288. [Google Scholar] [CrossRef]
- Burri, M.; Gasser, L.; Käch, M.; Krebs, M.; Laube, S.; Ledergerber, A.; Meier, D.; Michaud, R.; Mosimann, L.; Müri, L.; et al. Design and Control of a Spherical Omnidirectional Blimp. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 1873–1879. [Google Scholar]
- Luque-Vega, L.; Castillo-Toledo, B.; Loukianov, A.G. Robust block second order sliding mode control for a quadrotor. J. Frankl. Inst. 2012, 349, 719–739. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, H.; Li, X. Active disturbance rejection switching control of quadrotor based on robust differentiator. Syst. Sci. Control Eng. 2020, 8, 605–617. [Google Scholar] [CrossRef]
- Glida, H.E.; Abdou, L.; Chelihi, A.; Sentouh, C.; Hasseni, S.E.I. Optimal model-free backstepping control for a quadrotor helicopter. Nonlinear Dyn. 2020, 100, 3449–3468. [Google Scholar] [CrossRef]
- Pérez-Alcocer, R.; Moreno-Valenzuela, J. A novel Lyapunov-based trajectory tracking controller for a quadrotor: Experimental analysis by using two motion tasks. Mechatronics 2019, 61, 58–68. [Google Scholar] [CrossRef]
- Noormohammadi-Asl, A.; Esrafilian, O.; Ahangar Arzati, M.; Taghirad, H.D. System identification and H∞-based control of quadrotor attitude. Mech. Syst. Signal Process. 2020, 135, 106358. [Google Scholar] [CrossRef]
- Huynh, M.Q.; Zhao, W.; Xie, L. 1 adaptive control for quadcopter: Design and implementation. In Proceedings of the 2014 13th International Conference on Control Automation Robotics Vision (ICARCV), Singapore, 10–12 December 2014; pp. 1496–1501. [Google Scholar]
- Jafarnejadsani, H.; Sun, D.; Lee, H.; Hovakimyan, N. Optimized L1 Adaptive Controller for Trajectory Tracking of an Indoor Quadrotor. J. Guid. Control Dyn. 2017, 40, 1415–1427. [Google Scholar] [CrossRef]
- Erginer, B.; Altuğ, E. Design and implementation of a hybrid fuzzy logic controller for a quadrotor VTOL vehicle. Int. J. Control. Autom. Syst. 2012, 10, 61–70. [Google Scholar] [CrossRef]
- Boudjedir, H.; Bouhali, O.; Rizoug, N. Adaptive neural network control based on neural observer for quadrotor unmanned aerial vehicle. Adv. Robot. 2014, 28, 1151–1164. [Google Scholar] [CrossRef]
- Eskandarpour, A.; Sharf, I. A constrained error-based MPC for path following of quadrotor with stability analysis. Nonlinear Dyn. 2020, 99, 899–918. [Google Scholar] [CrossRef]
- Liu, J. Introduction to Intelligent Control. In Intelligent Control Design and MATLAB Simulation; Springer: Singapore, 2018; pp. 1–5. [Google Scholar]
- Dydek, Z.T.; Annaswamy, A.M.; Lavretsky, E. Adaptive Control of Quadrotor UAVs: A Design Trade Study With Flight Evaluations. IEEE Trans. Control Syst. Technol. 2013, 21, 1400–1406. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.N.; Roy, S. Introducing switched adaptive control for quadrotors for vertical operations. Optim. Control Appl. Methods 2020, 41, 1875–1888. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.N.; Roy, S.; Baldi, S. Aerial Transportation of Unknown Payloads: Adaptive Path Tracking for Quadrotors. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 7710–7715. [Google Scholar]
- Tian, B.; Cui, J.; Lu, H.; Zuo, Z.; Zong, Q. Adaptive Finite-Time Attitude Tracking of Quadrotors With Experiments and Comparisons. IEEE Trans. Ind. Electron. 2019, 66, 9428–9438. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Mung, N.X.; Thanh, H.L.N.N.; Huynh, T.T.; Lam, N.T.; Hong, S.K. Adaptive Sliding Mode Control for Attitude and Altitude System of a Quadcopter UAV via Neural Network. IEEE Access 2021, 9, 40076–40085. [Google Scholar] [CrossRef]
- Mehmood, Y.; Aslam, J.; Ullah, N.; Chowdhury, M.S.; Techato, K.; Alzaed, A.N. Adaptive Robust Trajectory Tracking Control of Multiple Quad-Rotor UAVs with Parametric Uncertainties and Disturbances. Sensors 2021, 21, 2401. [Google Scholar] [CrossRef]
- Sun, C.; Liu, M.; Liu, C.; Feng, X.; Wu, H. An Industrial Quadrotor UAV Control Method Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Electronics 2021, 10, 376. [Google Scholar] [CrossRef]
- Yañez-Badillo, H.; Beltran-Carbajal, F.; Tapia-Olvera, R.; Valderrabano-Gonzalez, A.; Favela-Contreras, A.; Rosas-Caro, J.C. A Dynamic Motion Tracking Control Approach for a Quadrotor Aerial Mechanical System. Shock Vib. 2020, 2020, 6635011. [Google Scholar]
- Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control, 2nd ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Fliess, M.; Marquez, R.; Delaleau, E.; Sira-Ramirez, H. Correcteurs proportionnels-intégraux généralisés. ESAIM Control Optim. Calc. Var. 2002, 7, 23–41. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Deng, W. Active disturbance rejection adaptive control of uncertain nonlinear systems: Theory and application. Nonlinear Dyn. 2017, 89, 1611–1624. [Google Scholar] [CrossRef]
- Yañez-Badillo, H.; Tapia-Olvera, R.; Beltran-Carbajal, F. Adaptive Neural Motion Control of a Quadrotor UAV. Vehicles 2020, 2, 468–490. [Google Scholar] [CrossRef]
- Brown, M.; Harris, C. Neurofuzzy Adaptive Modelling and Control; Prentice Hall International (UK) Ltd.: Hertfordshire, UK, 1994. [Google Scholar]
- Saad, D. (Ed.) On-Line Learning in Neural Networks; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C. Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beltran-Carbajal, F.; Tapia-Olvera, R.; Valderrabano-Gonzalez, A.; Yanez-Badillo, H.; Rosas-Caro, J.; Mayo-Maldonado, J. Closed-loop online harmonic vibration estimation in DC electric motor systems. Appl. Math. Model. 2021, 94, 460–481. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Silva-Navarro, G. On the algebraic parameter identification of vibrating mechanical systems. Int. J. Mech. Sci. 2015, 92, 178–186. [Google Scholar] [CrossRef]
- Conyers, S.A.; Rutherford, M.J.; Valavanis, K.P. An Empirical Evaluation of Ground Effect for Small-Scale Rotorcraft. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–26 May 2018; pp. 1244–1250. [Google Scholar]
- Li, D.; Zhou, Y.; Shi, Z.; Lu, G. Autonomous landing of quadrotor based on ground effect modelling. In Proceedings of the 2015 34th Chinese Control Conference, Hangzhou, China, 28–30 July 2015; pp. 5647–5652. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Zhao, J.; Li, T.; Qian, J. Application of Particle Swarm Optimization Algorithm on Robust PID Controller Tuning. In Advances in Natural Computation; Wang, L., Chen, K., Ong, Y.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 948–957. [Google Scholar]
- Kaminski, M. Neural Network Training Using Particle Swarm Optimization—A Case Study. In Proceedings of the 2019 24th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 26–29 August 2019; pp. 115–120. [Google Scholar]
- Shi, D.; Wu, Z.; Chou, W. Generalized Extended State Observer Based High Precision Attitude Control of Quadrotor Vehicles Subject to Wind Disturbance. IEEE Access 2018, 6, 32349–32359. [Google Scholar] [CrossRef]
- Sreenath, K.; Michael, N.; Kumar, V. Trajectory generation and control of a quadrotor with a cable-suspended load—A differentially-flat hybrid system. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4888–4895. [Google Scholar]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Beltran-Carbajal, F.; Silva-Navarro, G. A fast parametric estimation approach of signals with multiple frequency harmonics. Electr. Power Syst. Res. 2017, 144, 157–162. [Google Scholar] [CrossRef]






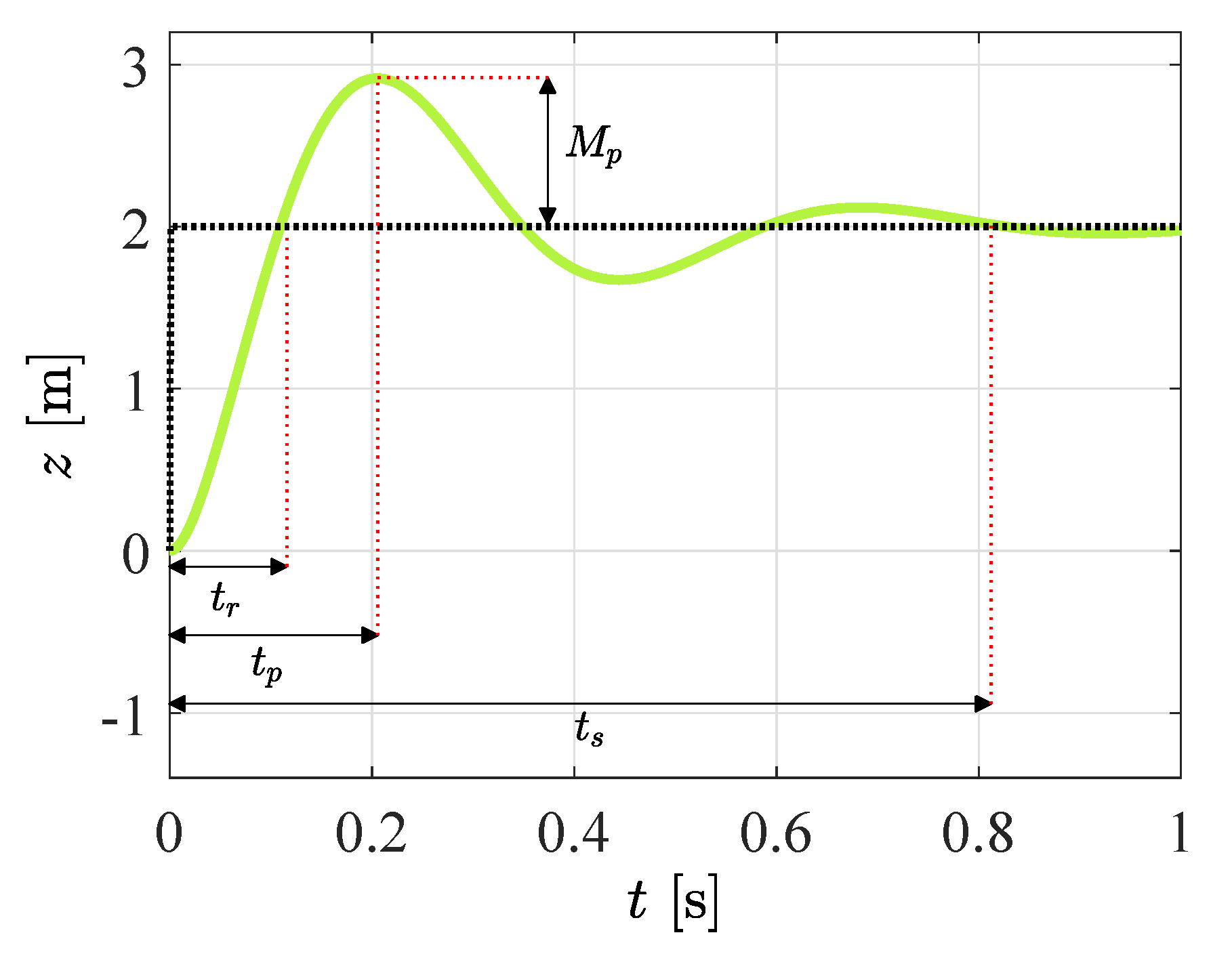
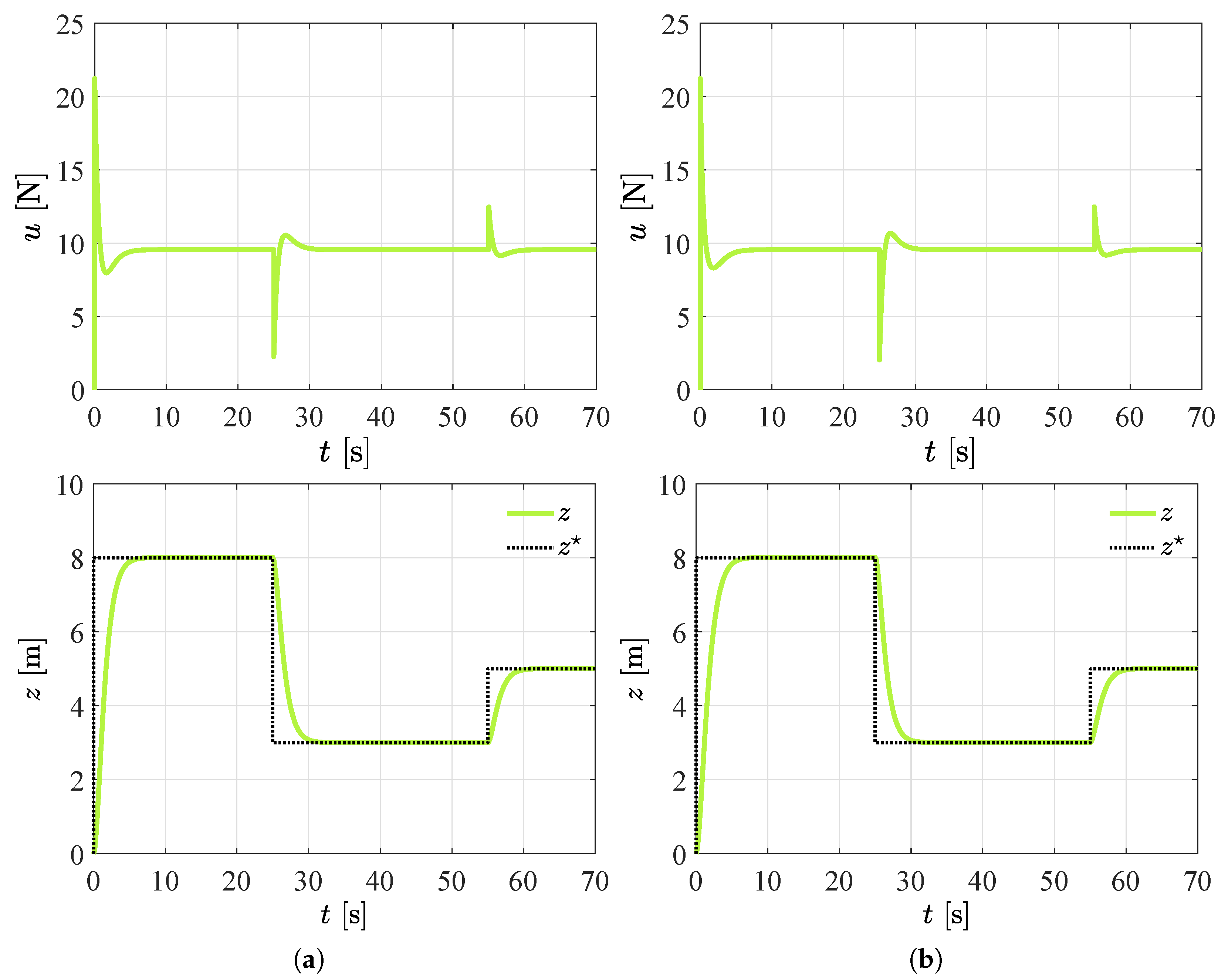

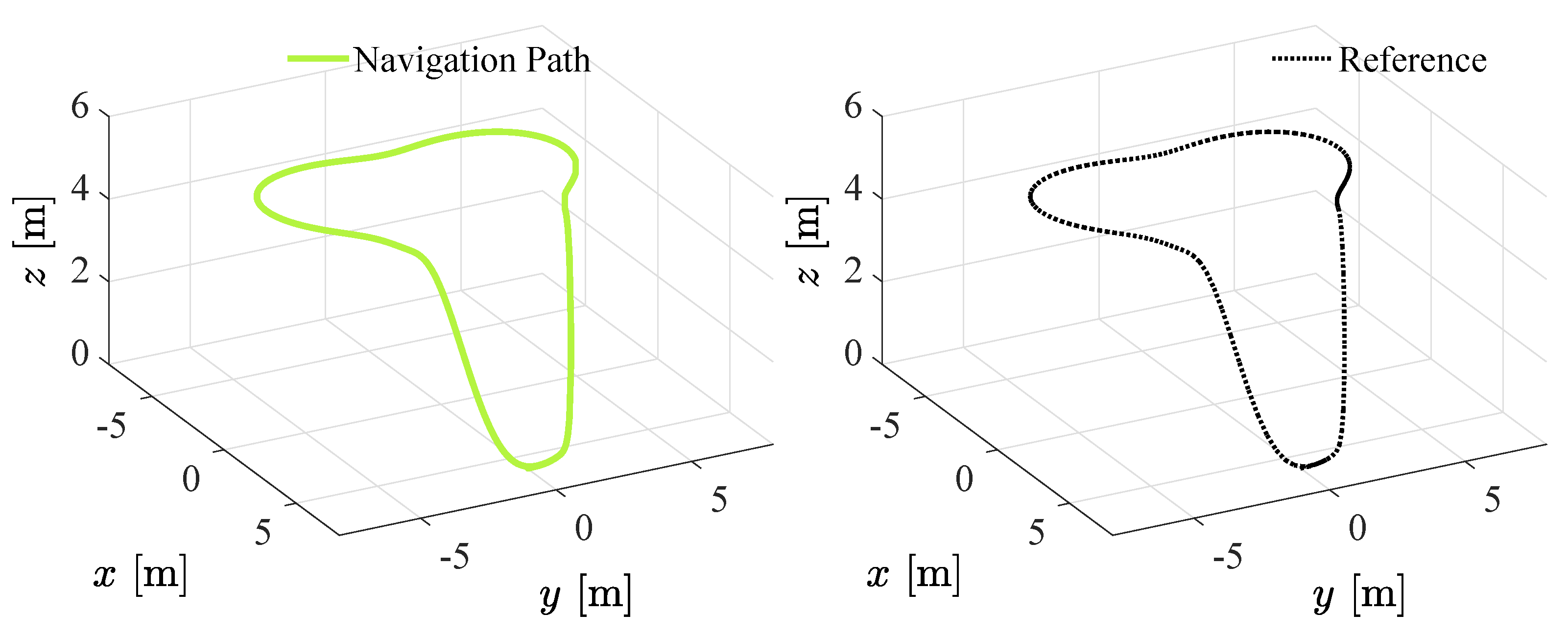


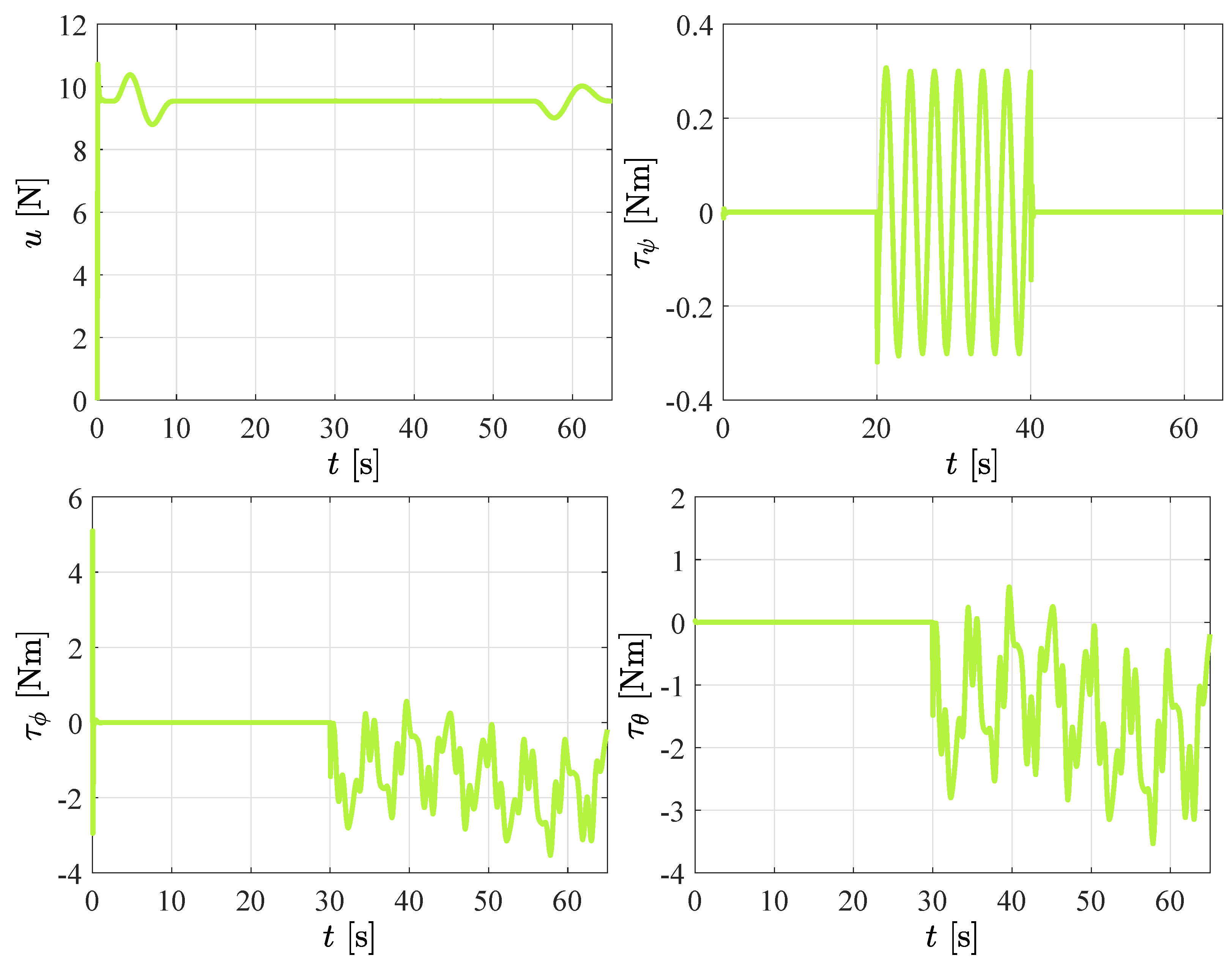


| Parameter | Units | Values |
|---|---|---|
| m | kg | 0.98 |
| g | m/s2 | 9.81 |
| l | m | 0.25 |
| kg m2 | 0.012450 | |
| kg m2 | 0.012450 | |
| kg m2 | 0.024752 |
| Segment | Time Lapse [s] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 | 2 | 2 | 2 | ||
| 2 | 2 | 2 | 3 | 2 | 3 | 4 | 4 | 4 | ||
| 3 | 4 | 4 | 5 | 4 | 5 | 2 | 6 | 2 | ||
| 4 | 6 | 2 | 7 | 2 | 7 | 0 | 8 | 0 |
| Case | |||||
|---|---|---|---|---|---|
| First | 5 | 1 | 1 | 2 | 1 |
| Second | 5 | 30 | 20 | 3 | 3 |
| Gain Case | ISCI | ITAE |
|---|---|---|
| Fixed | 6.4181 | 423.9004 |
| Adaptive | 6.4140 | 422.9049 |
| 0.3 | ||||
| 0.6 | ||||
| 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yañez-Badillo, H.; Beltran-Carbajal, F.; Tapia-Olvera, R.; Favela-Contreras, A.; Sotelo, C.; Sotelo, D. Adaptive Robust Motion Control of Quadrotor Systems Using Artificial Neural Networks and Particle Swarm Optimization. Mathematics 2021, 9, 2367. https://doi.org/10.3390/math9192367
Yañez-Badillo H, Beltran-Carbajal F, Tapia-Olvera R, Favela-Contreras A, Sotelo C, Sotelo D. Adaptive Robust Motion Control of Quadrotor Systems Using Artificial Neural Networks and Particle Swarm Optimization. Mathematics. 2021; 9(19):2367. https://doi.org/10.3390/math9192367
Chicago/Turabian StyleYañez-Badillo, Hugo, Francisco Beltran-Carbajal, Ruben Tapia-Olvera, Antonio Favela-Contreras, Carlos Sotelo, and David Sotelo. 2021. "Adaptive Robust Motion Control of Quadrotor Systems Using Artificial Neural Networks and Particle Swarm Optimization" Mathematics 9, no. 19: 2367. https://doi.org/10.3390/math9192367
APA StyleYañez-Badillo, H., Beltran-Carbajal, F., Tapia-Olvera, R., Favela-Contreras, A., Sotelo, C., & Sotelo, D. (2021). Adaptive Robust Motion Control of Quadrotor Systems Using Artificial Neural Networks and Particle Swarm Optimization. Mathematics, 9(19), 2367. https://doi.org/10.3390/math9192367








