A Goal Programming-Based Methodology for Machine Learning Model Selection Decisions: A Predictive Maintenance Application
Abstract
:1. Introduction
2. Literature Review
- To our knowledge there seems to be a small number of research efforts that provide a multi-criteria decision-making methodology for ML algorithm selection.
- The aforementioned research efforts provide time consuming multicriteria methodologies, are theoretical in nature and cannot be easily adapted to multiple scenarios as the weights assigned to ML selection criterions are a result of a time-consuming statistical process. Moreover, they do not relate to any focus areas or case studies, and their applicability in PdM is not demonstrated.
- Development of a multi-criteria decision-making methodology for ML model selection that utilizes the method of Goal Programming. The methodology allows for undertaking a time-efficient sensitivity analysis process of the weights assigned to the criteria, and of the criteria threshold values, thus providing the decision maker with a wide range of alternatives for optimal ML model selection that make the model suitable for multiple PdM scenarios where the weights on time and accuracy efficiency maybe different.
- Assessment of the model’s applicability on the real-world dataset of NASA Turbofans time to failures and the generation of practical managerial insights for predicting the remaining lifetimes of machines and equipment.
3. Materials and Methods
3.1. Support Vector Regression (SVR)
3.2. Decision Tree Regression (DTR)
3.3. Random Forest Regression (RFR)
3.4. Artificial Neural Networks (ANNs)
4. Numerical Analysis
5. Results
6. Discussion and Conclusions
- ○
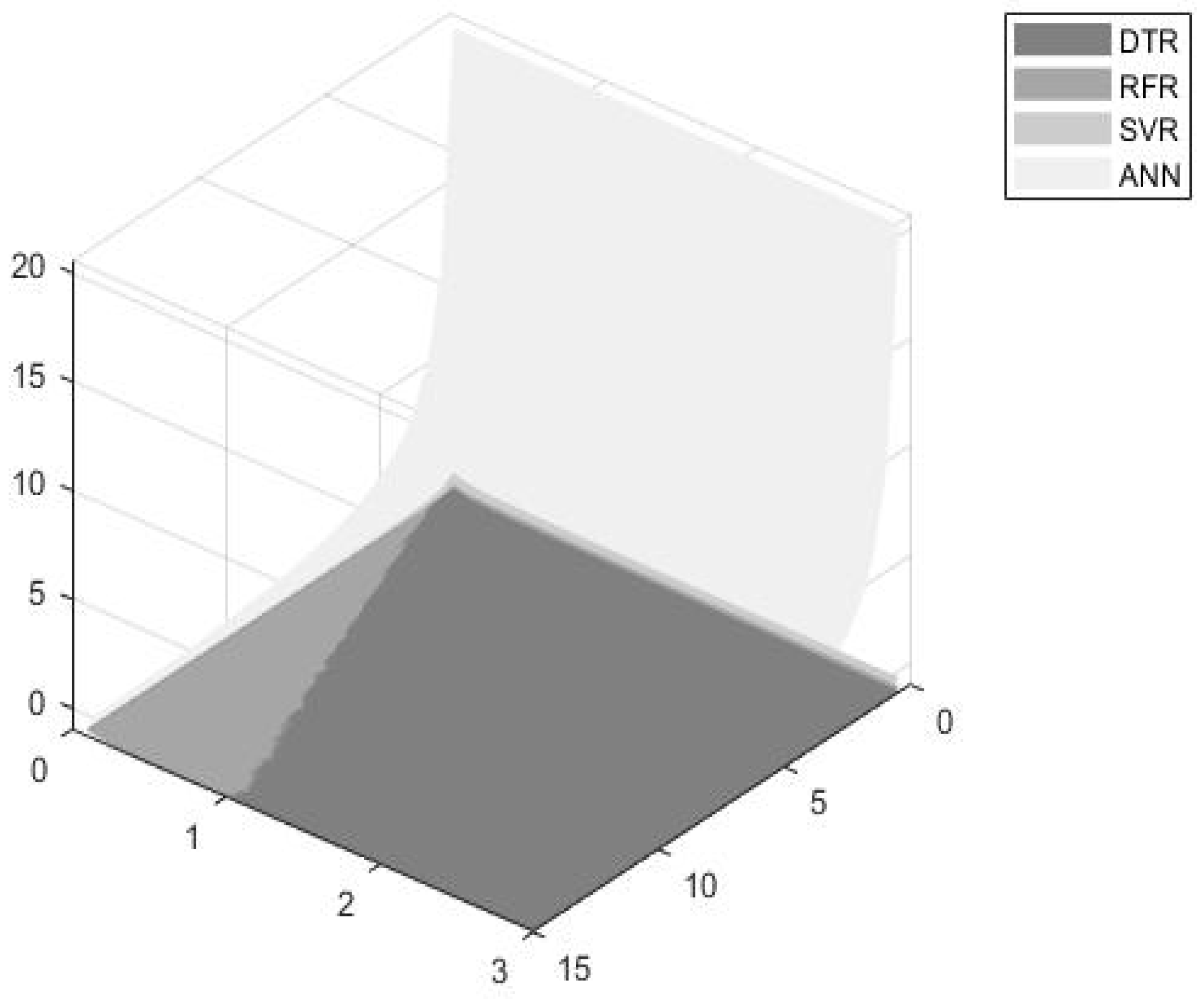
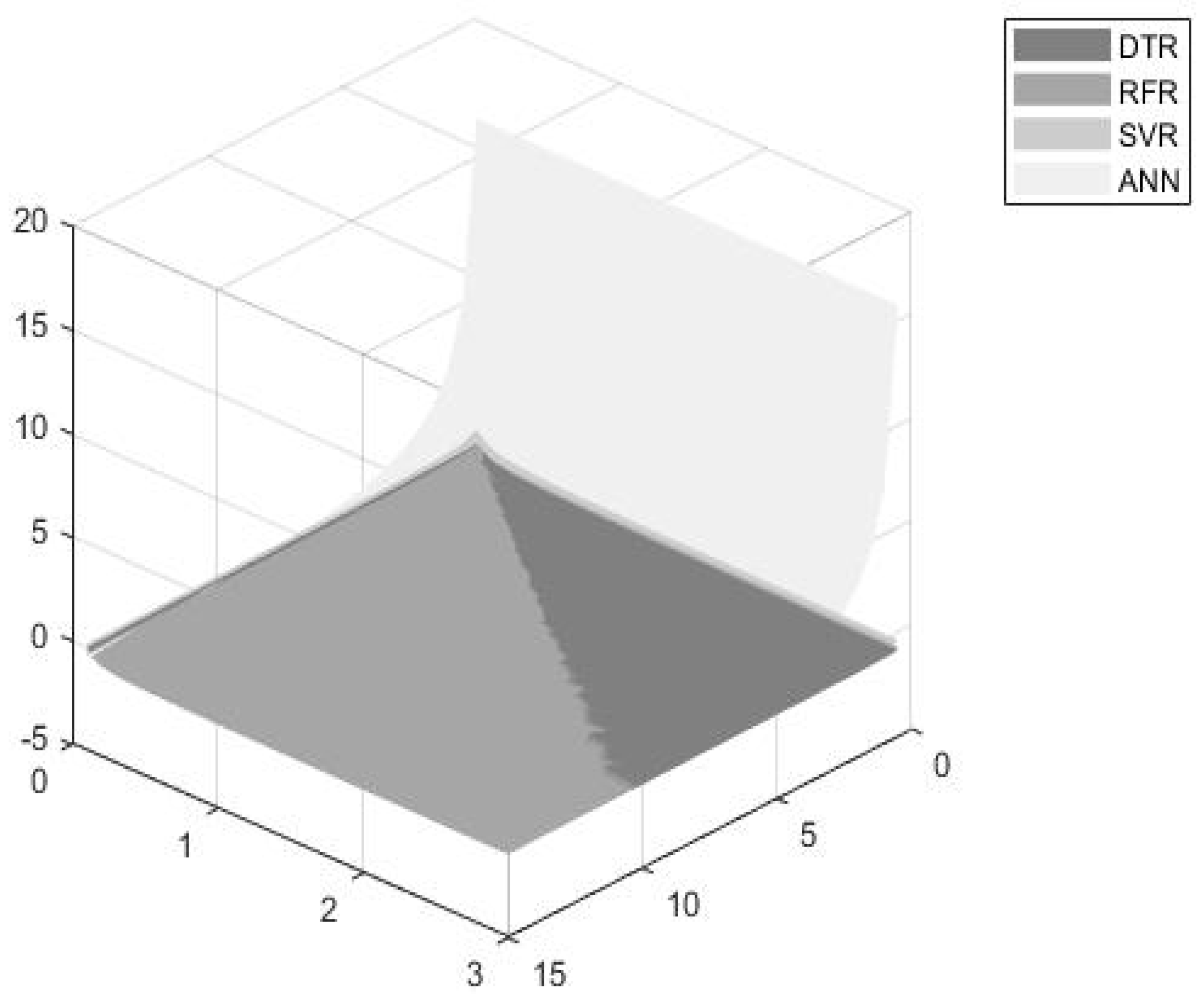
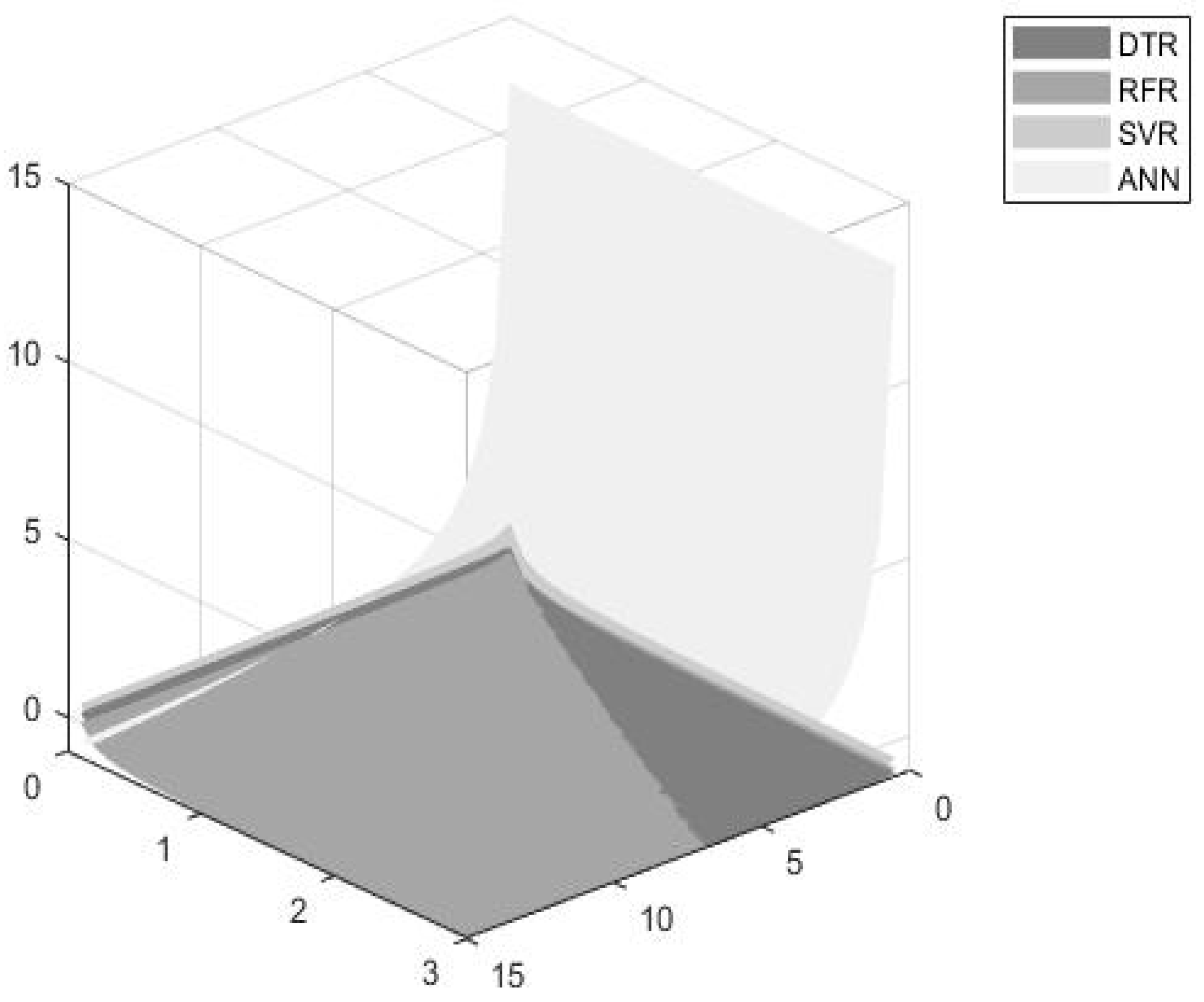
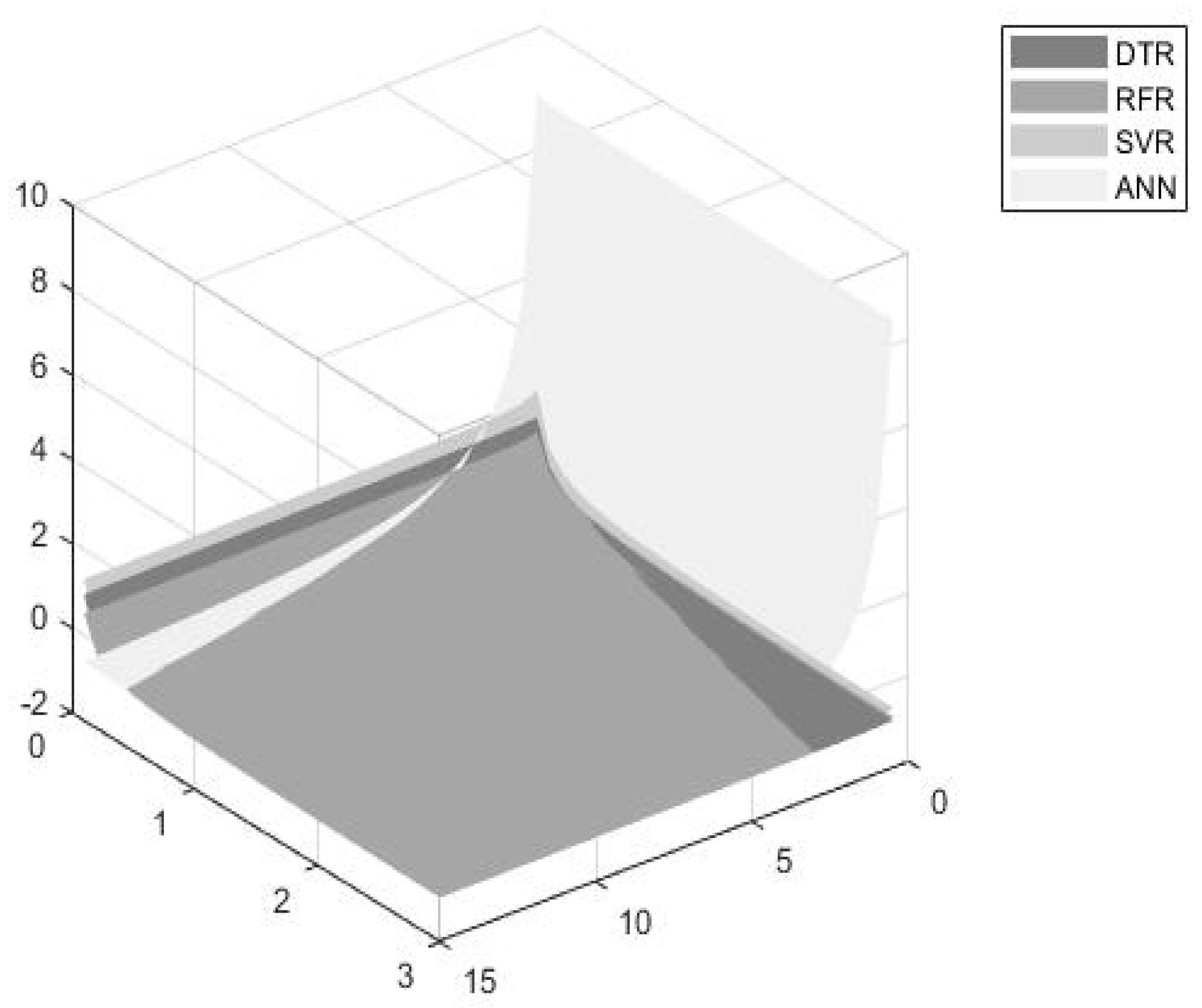
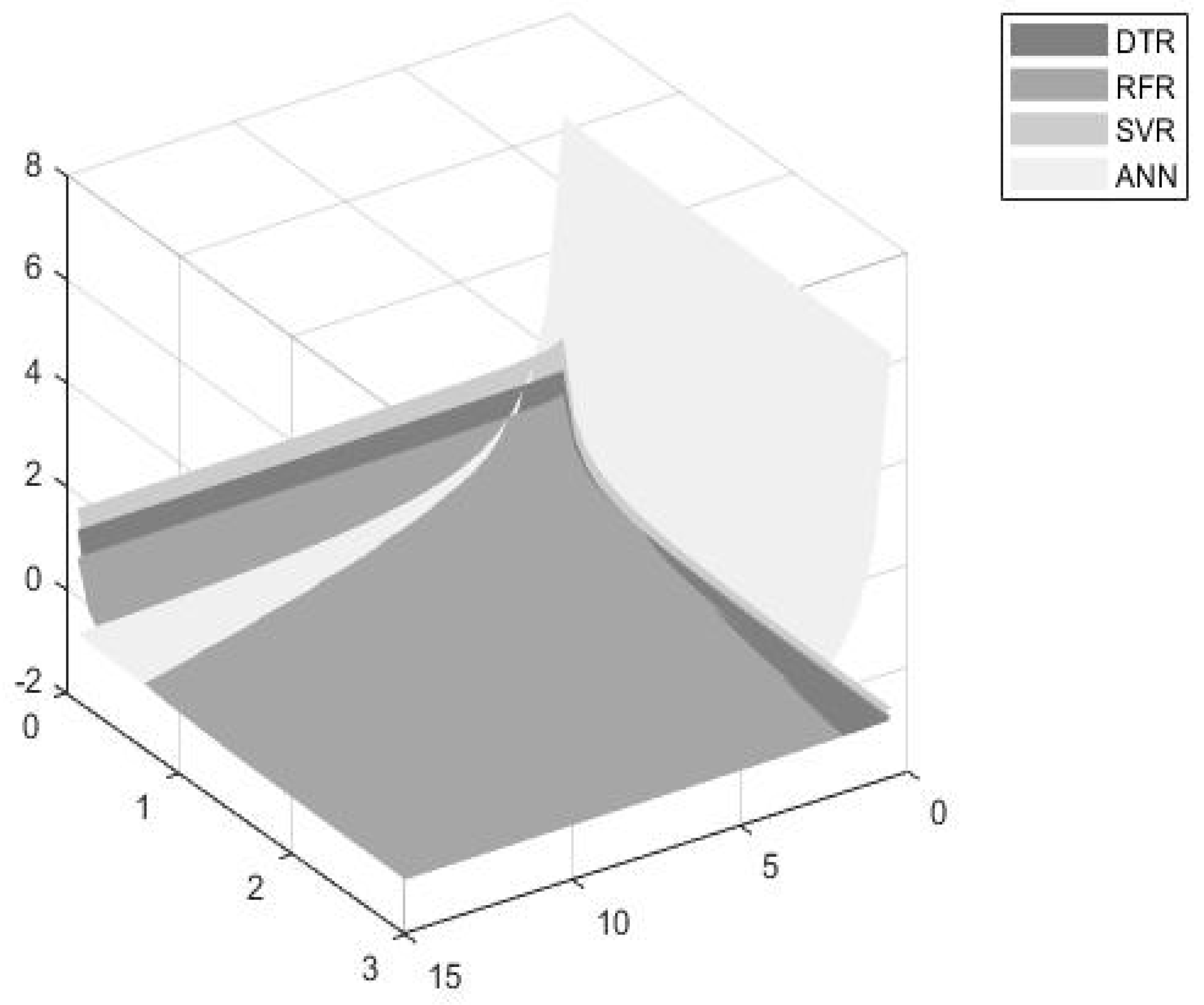
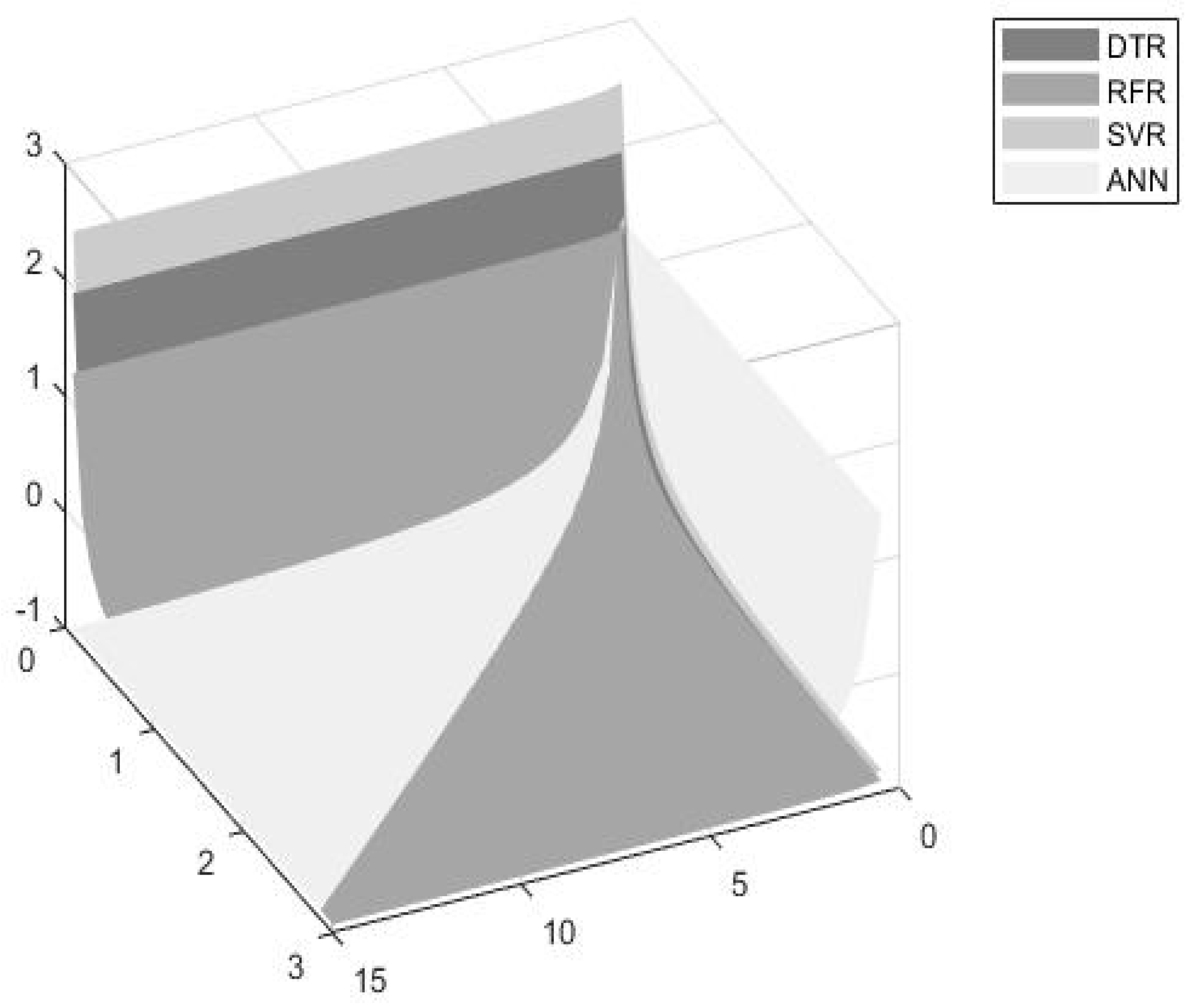
- The DTR model seems to be the most efficient model for dynamically estimating turbofan time to failures when considering an accuracy significance weight up to 30%. However, the model’s efficiency seems to decrease as the accuracy and time thresholds increase.
- ○
- The RFR seems to be more efficient for accuracy weights ranging from 30% to 90%, and for higher accuracy and time threshold values.
- ○
- The ANN model exhibits significantly high accuracy values and thus, seems to be more preferable for accuracy weights ranging from 90% to 100%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| ML | Machine Learning |
| PdM | Predictive Maintenance |
| ANNs | Artificial Neural networks |
| RF | Random Forest |
| RFR | Random Forest Regression |
| DT | Decision Tree |
| DTR | Decision Tree Regression |
| SVM | Support Vector Machine (SVM) |
| KNN | k-Nearest Neighbor |
| LDA | Linear Discriminant Analysis |
| RNN | Recurrent Neural Networks |
| FAHP | Fuzzy Analytical Hierarchical Process |
| SVR | Support Vector Regression |
| MAPE | Mean Absolute Percentage error |
References
- Zonta, T.; da Costa, C.A.; da Rosa Righi, R.; de Lima, M.J.; da Trindade, E.S.; Li, G.P. Predictive Maintenance in the Industry 4.0: A Systematic Literature Review. Comput. Ind. Eng. 2020, 150, 106889. [Google Scholar] [CrossRef]
- Patel, J. The democratization of machine learning features. In Proceedings of the 2020 IEEE 21st International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 11–13 August 2020; pp. 136–141. [Google Scholar]
- Samsonov, V.; Enslin, C.; Lütkehoff, B.; Steinlein, F.; Lütticke, D.; Stich, V. Managing disruptions in production with machine learning. In Proceedings of the 1st Conference on Production Systems and Logistics (CPSL 2020), Stellenbosch, South Africa; pp. 360–368.
- Cavallaro, L.; Bagdasar, O.; De Meo, P.; Fiumara, G.; Liotta, A. Artificial Neural Networks Training Acceleration through Network Science Strategies. Soft Comput. 2020, 24, 17787–17795. [Google Scholar] [CrossRef]
- Gęca, J. Performance comparison of machine learning algorithms for predictive maintenance. Inform. Autom. Pomiary Gospod. Ochr. Środowiska 2020, 10, 32–35. [Google Scholar] [CrossRef]
- Mobley, R.K. Plant Engineer’s Handbook; Elsevier Science & Technology: Oxford, UK, 2001; ISBN 978-0-7506-7328-0. [Google Scholar]
- Einabadi, B.; Baboli, A.; Ebrahimi, M. Dynamic Predictive Maintenance in Industry 4.0 Based on Real Time Information: Case Study in Automotive Industries. IFAC-PapersOnLine 2019, 52, 1069–1074. [Google Scholar] [CrossRef]
- Dalzochio, J.; Kunst, R.; Pignaton, E.; Binotto, A.; Sanyal, S.; Favilla, J.; Barbosa, J. Machine Learning and Reasoning for Predictive Maintenance in Industry 4.0: Current Status and Challenges. Comput. Ind. 2020, 123, 103298. [Google Scholar] [CrossRef]
- Girdhar, P.; Scheffer, C. Predictive maintenance techniques. In Practical Machinery Vibration Analysis and Predictive Maintenance; Elsevier: Amsterdam, The Netherlands, 2004; pp. 1–10. [Google Scholar]
- Thomas, E.; Levrat, E.; Iung, B.; Monnin, M. ‘ODDS Algorithm’-based ipportunity-triggered preventive maintenance with production policy. In Fault Detection, Supervision and Safety of Technical Processes 2006; Elsevier: Amsterdam, The Netherlands, 2007; pp. 783–788. [Google Scholar]
- Wang, J.; Liu, C.; Zhu, M.; Guo, P.; Hu, Y. Sensor data based system-level anomaly prediction for smart manufacturing. In Proceedings of the 2018 IEEE International Congress on Big Data (BigData Congress), San Francisco, CA, USA, 2–7 July 2018; pp. 158–165. [Google Scholar]
- Carvalho, T.P.; Soares, F.A.A.M.N.; Vita, R.; da Francisco, R.P.; Basto, J.P.; Alcalá, S.G.S. A Systematic Literature Review of Machine Learning Methods Applied to Predictive Maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Strobl, C.; Malley, J.; Tutz, G. An Introduction to Recursive Partitioning: Rationale, Application, and Characteristics of Classification and Regression Trees, Bagging, and Random Forests. Psychol. Methods 2009, 14, 323–348. [Google Scholar] [CrossRef] [Green Version]
- Salin, E.D.; Winston, P.H. Machine Learning and Artificial Intelligence An Introduction. Anal. Chem. 1992, 64, 49A–60A. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbas, A.K.; Al-haideri, N.A.; Bashikh, A.A. Implementing Artificial Neural Networks and Support Vector Machines to Predict Lost Circulation. Egypt. J. Pet. 2019, 28, 339–347. [Google Scholar] [CrossRef]
- Blömer, J.; Lammersen, C.; Schmidt, M.; Sohler, C. Theoretical analysis of the k-means algorithm—A survey. In Algorithm Engineering: Selected Results and Surveys; Springer: Cham, Switzerland, 2016; Volume 9220, pp. 81–116. [Google Scholar]
- McLachlan, G.J. Discriminant Analysis and Statistical Pattern Recognition; A John Wiley & Sons, Inc. Publication: Hoboken, NJ, USA, 2004; ISBN 978-0-471-69115-0. [Google Scholar]
- Ansari, F.; Glawar, R.; Sihn, W. Prescriptive Maintenance of CPPS by Integrating Multimodal Data with Dynamic Bayesian Networks. Mach. Learn. Cyber Phys. Syst. Technol. Intell. Autom. 2020, 11, 1–8. [Google Scholar]
- Cakir, M.; Guvenc, M.A.; Mistikoglu, S. The Experimental Application of Popular Machine Learning Algorithms on Predictive Maintenance and the Design of IIoT Based Condition Monitoring System. Comput. Ind. Eng. 2021, 151, 106948. [Google Scholar] [CrossRef]
- Syafrudin, M.; Alfian, G.; Fitriyani, N.; Rhee, J. Performance Analysis of IoT-Based Sensor, Big Data Processing, and Machine Learning Model for Real-Time Monitoring System in Automotive Manufacturing. Sensors 2018, 18, 2946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, M.I.; Patel, P.; Breslin, J.G. Middleware for real-time event detection andpredictive analytics in smart manufacturing. In Proceedings of the 15th International Confer-ence on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 29–31 May 2019; pp. 370–376. [Google Scholar]
- Liu, Z.; Jin, C.; Jin, W.; Lee, J.; Zhang, Z.; Peng, C.; Xu, G. Industrial AI enabled prognostics for high-speed railway systems. In Proceedings of the 2018 IEEE International Conference on Prognostics and Health Management (ICPHM), Seattle, WA, USA, 11–13 June 2018; pp. 1–8. [Google Scholar]
- Li, Z.; Wang, Y.; Wang, K.-S. Intelligent Predictive Maintenance for Fault Diagnosis and Prognosis in Machine Centers: Industry 4.0 Scenario. Adv. Manuf. 2017, 5, 377–387. [Google Scholar] [CrossRef]
- Crespo Márquez, A.; de la Fuente Carmona, A.; Antomarioni, S. A Process to Implement an Artificial Neural Network and Association Rules Techniques to Improve Asset Performance and Energy Efficiency. Energies 2019, 12, 3454. [Google Scholar] [CrossRef] [Green Version]
- Daniyan, I.; Mpofu, K.; Oyesola, M.; Ramatsetse, B.; Adeodu, A. Artificial Intelligence for Predictive Maintenance in the Railcar Learning Factories. Procedia Manuf. 2020, 45, 13–18. [Google Scholar] [CrossRef]
- Lee, W.J.; Wu, H.; Yun, H.; Kim, H.; Jun, M.B.G.; Sutherland, J.W. Predictive Maintenance of Machine Tool Systems Using Artificial Intelligence Techniques Applied to Machine Condition Data. Procedia CIRP 2019, 80, 506–511. [Google Scholar] [CrossRef]
- Rivas, A.; Fraile, J.M.; Chamoso, P.; González-Briones, A.; Sittón, I.; Corchado, J.M. A predictive maintenance model using recurrent neural networks. In International Workshop on Soft Computing Models in Industrial and Environmental Applications; Springer: Cham, Switzerland, 2020; Volume 950, pp. 261–270. [Google Scholar]
- Bogojeski, M.; Sauer, S.; Horn, F.; Müller, K.-R. Forecasting Industrial Aging Processes with Machine Learning Methods. Comput. Chem. Eng. 2021, 144, 107123. [Google Scholar] [CrossRef]
- Huang, M.; Liu, Z.; Tao, Y. Mechanical Fault Diagnosis and Prediction in IoT Based on Multi-Source Sensing Data Fusion. Simul. Model. Pract. Theory 2020, 102, 101981. [Google Scholar] [CrossRef]
- Cheng, J.C.P.; Chen, W.; Chen, K.; Wang, Q. Data-Driven Predictive Maintenance Planning Framework for MEP Components Based on BIM and IoT Using Machine Learning Algorithms. Autom. Constr. 2020, 112, 103087. [Google Scholar] [CrossRef]
- Kimera, D.; Nangolo, F.N. Predictive Maintenance for Ballast Pumps on Ship Repair Yards via Machine Learning. Transp. Eng. 2020, 2, 100020. [Google Scholar] [CrossRef]
- Gohel, H.A.; Upadhyay, H.; Lagos, L.; Cooper, K.; Sanzetenea, A. Predictive Maintenance Architecture Development for Nuclear Infrastructure Using Machine Learning. Nucl. Eng. Technol. 2020, 52, 1436–1442. [Google Scholar] [CrossRef]
- Çınar, Z.M.; Abdussalam Nuhu, A.; Zeeshan, Q.; Korhan, O.; Asmael, M.; Safaei, B. Machine Learning in Predictive Maintenance towards Sustainable Smart Manufacturing in Industry 4.0. Sustainability 2020, 12, 8211. [Google Scholar] [CrossRef]
- Ali, R.; Lee, S.; Chung, T.C. Accurate Multi-Criteria Decision Making Methodology for Recommending Machine Learning Algorithm. Expert Syst. Appl. 2017, 71, 257–278. [Google Scholar] [CrossRef]
- Akinsola, J.E.T.; Awodele, O.; Kuyoro, S.O.; Kasali, F.A. Performance evaluation of supervised machine learning slgorithms using multi-criteria decision making techniques. In Proceedings of the International Conference on Information Technology in Education and Development (ITED); 2019; pp. 17–34. Available online: https://ir.tech-u.edu.ng/416/1/Performance%20Evaluation%20of%20Supervised%20Machine%20Learning%20Algorithms%20Using%20Multi-Criteria%20Decision%20Making%20%28MCDM%29%20Techniques%20ITED.pdf (accessed on 23 June 2021).
- Zhang, J.; Nazir, S.; Huang, A.; Alharbi, A. Multicriteria Decision and Machine Learning Algorithms for Component Security Evaluation: Library-Based Overview. Secur. Commun. Netw. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Shen, D.; Zhang, J.; Su, J.; Zhou, G.; Tan, C.-L. Multi-criteria-based active learning for named entity recognition. In Proceedings of the 42nd Annual Meeting on Association for Computational Linguistics—ACL ’04, Association for Computational Linguistics, Barcelona, Spain, 21–26 July 2004; pp. 589–596. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning. Data Mining, Inference and Prediction. Springer Series in Statistics, 2nd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Loh, W. Classification and Regression Trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer Texts in Statistics; Springer: New York, NY, USA, 2013; Volume 103, ISBN 978-1-4614-7137-0. [Google Scholar]
- Chen, J.; Li, M.; Wang, W. Statistical Uncertainty Estimation Using Random Forests and Its Application to Drought Forecast. Math. Probl. Eng. 2012, 2012, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Braspenning, P.J.; Thuijsman, F.; Weijters, A.J.M. Artificial Neural Networks; Braspenning, P.J., Thuijsman, F., Weijters, A.J.M.M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1995; Volume 931, ISBN 978-3-540-59488-8. [Google Scholar]
- NASA. (Bearing Data Set). Available online: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repository/ (accessed on 23 June 2021).




| References | Focus Area/ Case Study | ML Model | Optimization Criteria | Methodology Used | Decisions |
|---|---|---|---|---|---|
| [20] | PdM for the detection of the faulty bearing | SVM, LDA, RF, DT, and KNN | Accuracy, precision, TPR, TNR, FPR, FNR, F1 score and, Kappa metrics | Statistical (resampling) methods, cross-validation approach | ML models performance evaluation |
| [21] | Real-Time Monitoring System/ automotive manufacturing assembly line | Hybrid prediction model: Density-Based Spatial Clustering of Applications with Noise-based outlier detection RF classification | Fault prediction accuracy | Comparison of the hybrid prediction model with other classification models (NB, LR, MLP, RF) | Fault detection |
| [22] | Production forecasting/ Biomedical devices manufacturing | Regression-based approaches (MLR, SVR, DTR and RFR) | Scrap, Rework, Lead Time and Output | Semantically interoperable framework, Root Mean Square Error mechanism | Predictions about future production goals, abnormal events detection |
| [23] | PdM/High-speed railway transportation system | Auto-Associative Neural Network (AANN) | Vibration and speed relationship | Training of ML models at the edge of the networks | Potential faults prediction |
| [24] | PdM/Machine Centers | ANNs | Backlash error | Training and prediction process | Fault prediction |
| [25] | Asset performance monitoring/energy plants and facilities | ANNs with Data Mining tools (Association Rule Mining) | Behavior abnormalities | Combination of ANNs and Association Rule mining approaches | Prediction of any loss of energy consumption efficiency |
| [26] | PdM/railcar wheel bearing | ANN with dynamic time series model | Wheel-bearing temperature | Levenberg Marquardt algorithm | Failure prediction |
| [27] | PdM/machine tool systems | SVM, ANN (RNN and CNN) | Prediction accuracy | Confusion matrix | Failure prediction |
| [29] | Industrial aging process/chemical plant | Linear and kernel ridge regression (LRR and KRR), feed-forward neural networks, RNN (echo state networks and long short term memory networks) | Degradation KPIs | Training of ML models and model comparison | Predicting a KPI |
| [31] | PdM/building maintenance management | ANNs, SVM | The condition index of MEP components in buildings, triggers and alarms for the required maintenance actions | Training of ML models and algorithms comparison | Future condition of MEP components |
| [32] | PdM/floating dock ballast pumps | SVM | Principle components, e.g., PC1–flow rate and PC2–suction pressure | Principal component analysis (PCA) | Maintenance/failure prediction |
| [33] | PdM/Nuclear infrastructure | SVM, logistic regression algorithms | State of an engine, scoring | Confusion matrix | Failure prediction |
| [35] | - | Multi-class classification algorithms | Accuracy, computational complexity, and consistency | AMD methodology, Wgt.Avg.F-score, CPUTimeTesting, CPUTimeTraining, and Consistency measures, TOPSIS method | - |
| [36] | - | Bayes Network, Naive Bayes, LR, Sequential Minimal Optimization, Multilayer Perceptron, Tree and Lazy (Instance Based Learner) | Performance Metrics, Criteria weights | Multi-criteria–approach, FAHP and TOPSIS model | - |
| [38] | Named entity recognition | SVM | Informativeness representativeness and diversity | Multi-criteria -based active learning approach | To minimize the human annotation efforts |
| This paper | PdM/prediction of the lifetime of aircraft engines | ANNs and Regression models (SVR, the DTR and the RFR) | Forecasting accuracy, time accuracy | Multi-criteria–approach, Goal programming | ML model selection |
| Significance weights assigned to the models forecasting accuracy and time efficiency respectively | |
| (0–100%) | |
| (time units) | |
| Fixed target accuracy and time value thresholds (0–100%) set by the planner |
| Model | ||
|---|---|---|
| DTR | 0.329 | 0.07 |
| RFR | 0.253 | 0.19 |
| SVR | 0.388 | 0.42 |
| ANN | 0.011 | 10.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallidis, I.; Yakavenka, V.; Konstantinidis, A.; Sariannidis, N. A Goal Programming-Based Methodology for Machine Learning Model Selection Decisions: A Predictive Maintenance Application. Mathematics 2021, 9, 2405. https://doi.org/10.3390/math9192405
Mallidis I, Yakavenka V, Konstantinidis A, Sariannidis N. A Goal Programming-Based Methodology for Machine Learning Model Selection Decisions: A Predictive Maintenance Application. Mathematics. 2021; 9(19):2405. https://doi.org/10.3390/math9192405
Chicago/Turabian StyleMallidis, Ioannis, Volha Yakavenka, Anastasios Konstantinidis, and Nikolaos Sariannidis. 2021. "A Goal Programming-Based Methodology for Machine Learning Model Selection Decisions: A Predictive Maintenance Application" Mathematics 9, no. 19: 2405. https://doi.org/10.3390/math9192405
APA StyleMallidis, I., Yakavenka, V., Konstantinidis, A., & Sariannidis, N. (2021). A Goal Programming-Based Methodology for Machine Learning Model Selection Decisions: A Predictive Maintenance Application. Mathematics, 9(19), 2405. https://doi.org/10.3390/math9192405





