Mathematical Modeling of Immune Responses against SARS-CoV-2 Using an Ensemble Kalman Filter
Abstract
:1. Introduction
2. Model and Assimilation Scheme
2.1. Mathematical Model
2.2. Ensemble Kalman Filter (EnKF)
3. Mathematical Analysis of the Immune Response Model
3.1. Disease-Free Equilibrium and Basic Reproduction Number of the Model
3.2. Analysis of the Steady States
- The disease-free equilibrium .
- The virus persistence equilibrium in the absence of immune responses given bywhere:
- 3.
- The virus persistence equilibrium in the absence of the adaptive immune response given bywhere:and is the root of the quadratic equation:with:
- 4.
- The all cells and virus co-existence equilibrium is given bywhere:
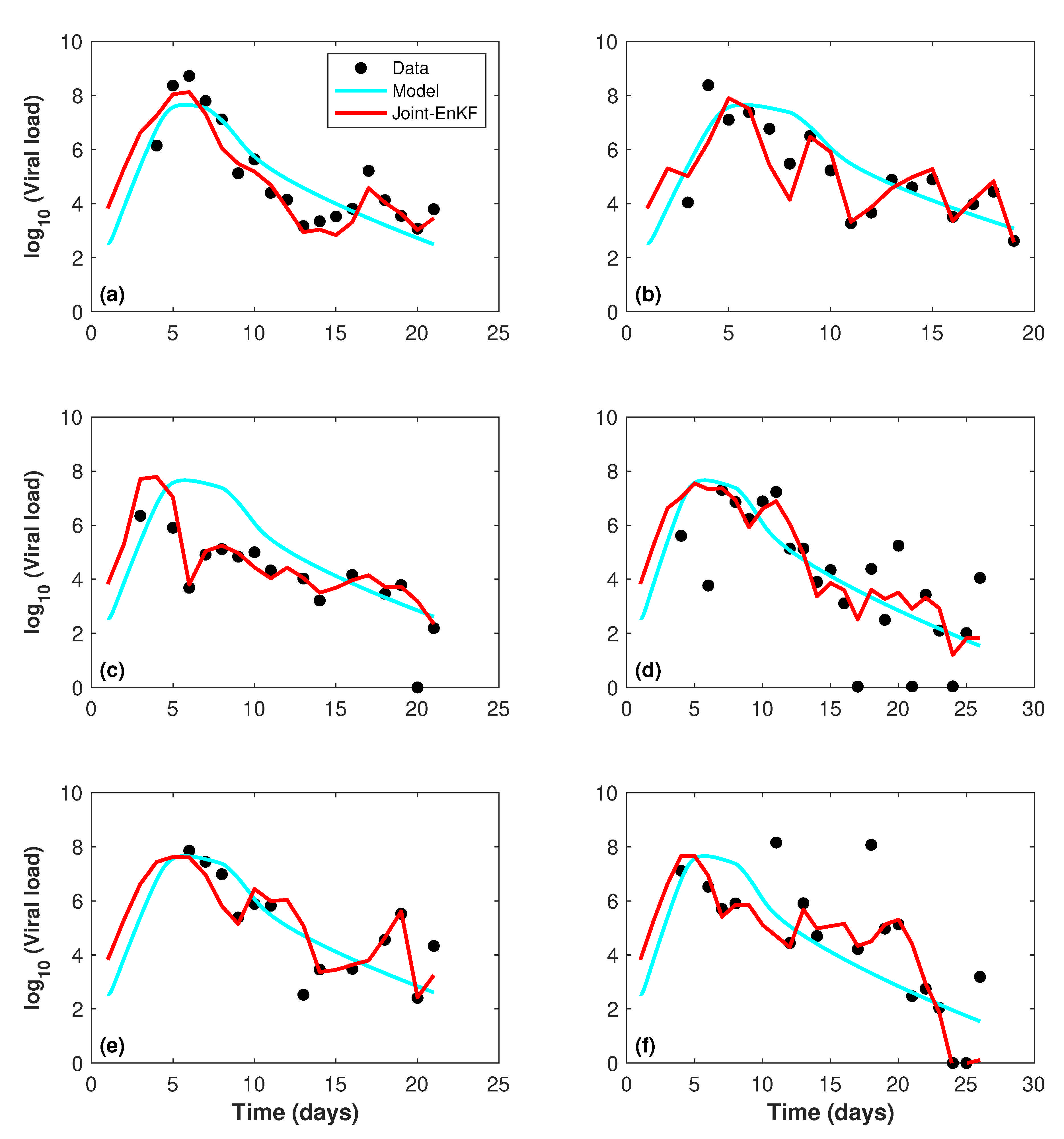
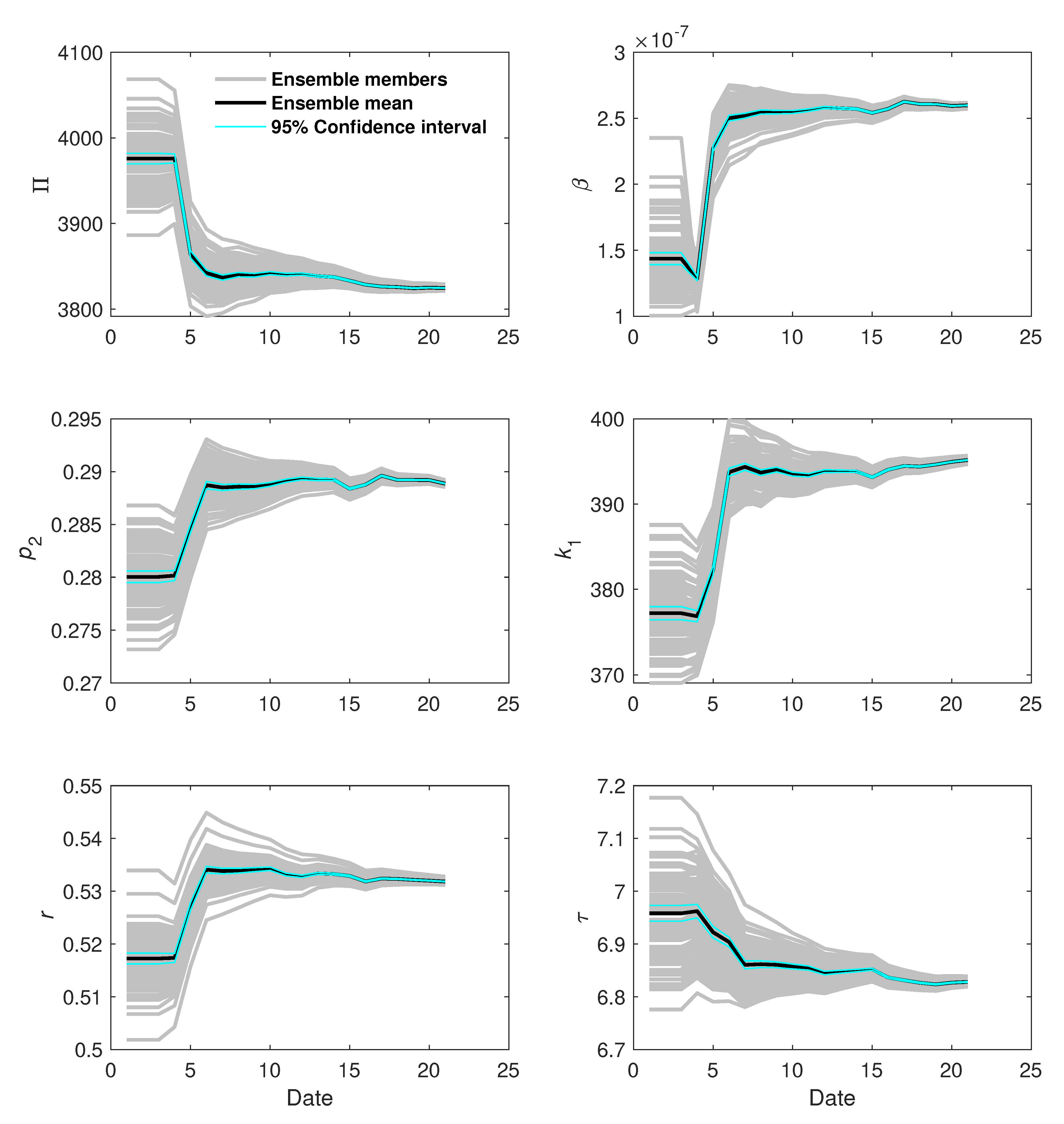
4. Results and Discussion
4.1. Assimilation Settings
4.2. Sensitivity to Ensemble Size
4.3. Assimilation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, W.J.; Ni, Z.Y.; Hu, Y.; Liang, W.H.; Ou, C.Q.; He, J.X.; Liu, L.; Shan, H.; Lei, C.l.; Hui, D.S.; et al. Clinical characteristics of coronavirus disease 2019 in China. N. Engl. J. Med. 2020, 382, 1708–1720. [Google Scholar] [CrossRef]
- Sohrabi, C.; Alsafi, Z.; O’Neill, N.; Khan, M.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, R. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19). Int. J. Surg. 2020, 76, 71–76. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2019; Volume 32. [Google Scholar]
- Choi, W.; Shim, E. Optimal strategies for vaccination and social distancing in a game-theoretic epidemiologic model. J. Theor. Biol. 2020, 505, 110422. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Ahmadian, A.; Kumar, R.; Kumar, D.; Singh, J.; Baleanu, D.; Salimi, M. An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics 2020, 8, 558. [Google Scholar] [CrossRef] [Green Version]
- Mahajan, A.; Sivadas, N.A.; Solanki, R. An epidemic model SIPHERD and its application for prediction of the spread of COVID-19 infection in India. Chaos Soliton Fractals 2020, 140, 110156. [Google Scholar] [CrossRef] [PubMed]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Torres, D.F. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Soliton Fractals 2020, 135, 109846. [Google Scholar] [CrossRef] [PubMed]
- Nkwayep, C.H.; Bowong, S.; Tewa, J.; Kurths, J. Short-term forecasts of the COVID-19 pandemic: Study case of Cameroon. Chaos Soliton Fractals 2020, 140, 110106. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G. Modelling the role of optimal social distancing on disease prevalence of COVID-19 epidemic. Int. J. Dyn. Control 2020, 9, 1053–1077. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Soliton Fractals 2020, 139, 110049. [Google Scholar] [CrossRef]
- Van Wees, J.D.; Osinga, S.; Van Der Kuip, M.; Tanck, M.W.; Tutu-van Furth, A. Forecasting hospitalization and ICU rates of the COVID-19 outbreak: An efficient SEIR model. Bull. World Health Organ. 2020. [Google Scholar] [CrossRef]
- Yang, Q.; Yi, C.; Vajdi, A.; Cohnstaedt, L.W.; Wu, H.; Guo, X.; Scoglio, C.M. Short-term forecasts and long-term mitigation evaluations for the COVID-19 epidemic in Hubei Province, China. Infect. Dis. Model 2020, 5, 563–574. [Google Scholar]
- Choi, W.; Shim, E. Optimal strategies for social distancing and testing to control COVID-19. J. Theor. Biol. 2021, 512, 110568. [Google Scholar] [CrossRef] [PubMed]
- Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. An extended SEIR model with vaccination for forecasting the COVID-19 pandemic in Saudi Arabia using an ensemble Kalman filter. Mathematics 2021, 9, 636. [Google Scholar] [CrossRef]
- Du, S.Q.; Yuan, W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. J. Med. Virol. 2020, 92, 1615–1628. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, I. Within host dynamics of SARS-CoV-2 in humans: Modeling immune responses and antiviral treatments. arXiv 2020, arXiv:2006.02936. [Google Scholar]
- Hernandez-Vargas, E.A.; Velasco-Hernandez, J.X. In-host mathematical modelling of COVID-19 in humans. Annu. Rev. Control 2020, 50, 448–456. [Google Scholar] [CrossRef] [PubMed]
- Chimal-Eguia, J.C. Mathematical Model of Antiviral Immune Response against the COVID-19 Virus. Mathematics 2021, 9, 1356. [Google Scholar] [CrossRef]
- Edwards, C.A.; Moore, A.M.; Hoteit, I.; Cornuelle, B.D. Regional ocean data assimilation. Ann. Rev. Mar. Sci. 2015, 7, 21–42. [Google Scholar] [CrossRef] [Green Version]
- Hoteit, I.; Luo, X.; Bocquet, M.; Kohl, A.; Ait-El-Fquih, B. Data assimilation in oceanography: Current status and new directions. New Front. Oper. Oceanogr. 2018, 2018, 465–512. [Google Scholar]
- Hoteit, I.; Luo, X.; Pham, D.T. Particle Kalman filtering: A nonlinear Bayesian framework for ensemble Kalman filters. Mon. Weather Rev. 2012, 140, 528–542. [Google Scholar] [CrossRef] [Green Version]
- Hoteit, I.; Pham, D.T.; Blum, J. A simplified reduced order Kalman filtering and application to altimetric data assimilation in Tropical Pacific. J. Mar. Syst. 2002, 36, 101–127. [Google Scholar] [CrossRef]
- Hoteit, I.; Hoar, T.; Gopalakrishnan, G.; Collins, N.; Anderson, J.; Cornuelle, B.; Köhl, A.; Heimbach, P. A MITgcm/DART ensemble analysis and prediction system with application to the Gulf of Mexico. Dynam. Atmos. Ocean 2013, 63, 1–23. [Google Scholar] [CrossRef]
- Buehner, M.; McTaggart-Cowan, R.; Heilliette, S. An ensemble Kalman filter for numerical weather prediction based on variational data assimilation: VarEnKF. Mon. Weather Rev. 2017, 145, 617–635. [Google Scholar] [CrossRef]
- Gharamti, M.; Tjiputra, J.; Bethke, I.; Samuelsen, A.; Skjelvan, I.; Bentsen, M.; Bertino, L. Ensemble data assimilation for ocean biogeochemical state and parameter estimation at different sites. Ocean Model. 2017, 112, 65–89. [Google Scholar] [CrossRef]
- Yu, L.; Fennel, K.; Bertino, L.; El Gharamti, M.; Thompson, K.R. Insights on multivariate updates of physical and biogeochemical ocean variables using an Ensemble Kalman Filter and an idealized model of upwelling. Ocean Model. 2018, 126, 13–28. [Google Scholar] [CrossRef]
- Raboudi, N.F.; Ait-El-Fquih, B.; Dawson, C.; Hoteit, I. Combining Hybrid and One-Step-Ahead Smoothing for Efficient Short-Range Storm Surge Forecasting with an Ensemble Kalman Filter. Mon. Weather Rev. 2019, 147, 3283–3300. [Google Scholar] [CrossRef]
- Gharamti, M.; Kadoura, A.; Valstar, J.; Sun, S.; Hoteit, I. Constraining a compositional flow model with flow-chemical data using an ensemble-based Kalman filter. Water Resour. Res. 2014, 50, 2444–2467. [Google Scholar] [CrossRef] [Green Version]
- Gharamti, M.; Ait-El-Fquih, B.; Hoteit, I. An iterative ensemble Kalman filter with one-step-ahead smoothing for state-parameters estimation of contaminant transport models. J. Hydrol. 2015, 527, 442–457. [Google Scholar] [CrossRef] [Green Version]
- Ait-El-Fquih, B.; Gharamti, M.E.; Hoteit, I. A Bayesian consistent dual ensemble Kalman filter for state-parameter estimation in subsurface hydrology. Hydrol. Earth Syst. Sci. 2016, 20, 3289–3307. [Google Scholar] [CrossRef] [Green Version]
- Khaki, M.; Ait-El-Fquih, B.; Hoteit, I. Calibrating land hydrological models and enhancing their forecasting skills using an ensemble Kalman filter with one-step-ahead smoothing. J. Hydrol. 2020, 584, 124708. [Google Scholar] [CrossRef]
- Kimura, N.; Hsu, M.H.; Tsai, M.Y.; Tsao, M.C.; Yu, S.L.; Tai, A. A river flash flood forecasting model coupled with ensemble Kalman filter. J. Flood Risk Manag. 2016, 9, 178–192. [Google Scholar] [CrossRef]
- Ziliani, M.G.; Ghostine, R.; Ait-El-Fquih, B.; McCabe, M.F.; Hoteit, I. Enhanced flood forecasting through ensemble data assimilation and joint state-parameter estimation. J. Hydrol. 2019, 577, 123924. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Mar. Syst. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Nikin-Beers, R.; Ciupe, S.M. The role of antibody in enhancing dengue virus infection. Math. Biosci. 2015, 263, 83–92. [Google Scholar] [CrossRef]
- Duffin, R.P.; Tullis, R.H. Mathematical models of the complete course of HIV infection and AIDS. J. Theor. Biol. 2002, 4, 215–221. [Google Scholar] [CrossRef] [Green Version]
- Clapham, H.E.; Tricou, V.; Van Vinh Chau, N.; Simmons, C.P.; Ferguson, N.M. Within-host viral dynamics of dengue serotype 1 infection. J. R. Soc. Interface 2014, 11, 20140094. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ben-Shachar, R.; Koelle, K. Minimal within-host dengue models highlight the specific roles of the immune response in primary and secondary dengue infections. J. R. Soc. Interface 2015, 12, 20140886. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, S.K.; Dong, Y.; Takeuchi, Y. Mathematical modeling on T-cell mediated adaptive immunity in primary dengue infections. J. Theor. Biol. 2017, 429, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Gujarati, T.P.; Ambika, G. Virus antibody dynamics in primary and secondary dengue infections. J. Math. Biol. 2014, 69, 1773–1800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2015; Volume 61. [Google Scholar]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Variable | InitialValue | Description | Reference |
| H | cells per mL | Healthy cells | [36] |
| I | cells per mL | Infected cells | [36] |
| V | 357 RNA per mL | Viral load | [36] |
| C | 0 cells per mL | Cytokines | [16] |
| N | 100 cells per mL | Natural killer cells | [16] |
| T | 500 cells per mL | T-cells | [16] |
| B | 100 cells per mL | B-cells | [16] |
| P | 0 cells per mL | Plasma cells | [36] |
| A | 0 molecules per ml | Antibodies level | [36] |
| Parameter | Initial value | Description | Reference |
| cells mL day | Production rate of healthy cells | [37] | |
| mL (RNA copies) day | Rate at which healthy cells are infected | [17] | |
| mL cells day | Rate at which T-cells destroy infected cells | [38] | |
| (0–1) mL cells day | Rate at which viral particles are neutralized by cytokines | [16] | |
| (0–1) mL molecules day | Rate at which viral particles are neutralized by antibodies | [16] | |
| mL (RNA copies) day | Rate at which virus neutralizes antibodies | [36] | |
| mL cells day | Rate at which infected cells are diminished by NK cells | [39] | |
| k | mL (RNA copies) day | Plasma cells recruitment | [36] |
| (8.2–525) day | Production rate of virus from infected cells | [17] | |
| (0–10) day | Production rate of cytokines | [16] | |
| r | day | Activation rate of NK cells | [39] |
| mL cells day | Activation rate of T cells | [40] | |
| mL cells day | Activation rate of B cells | [40] | |
| (0–1) day | Antibodies production rate | [41] | |
| day | Natural death rate of healthy cells and protected cells | [40] | |
| (0–1) day | Natural death rate of infected cells | [16] | |
| (0–1) day | Clearance rate of virus | [16] | |
| day | Natural death rate of cytokines | [16] | |
| day | Natural death rate of NK cells | [39] | |
| 1 day | Natural death rate of T cells | [40] | |
| day | Natural death rate of B cells | [36] | |
| 4 day | Natural death rate of plasma cells | [18] | |
| day | Natural death rate of antibodies | [40] | |
| 7–14 days | Time delay for antibody production | [16] |
| Patient | Model | Joint-EnKF | Improvement % |
|---|---|---|---|
| 1 | 0.1496 | 0.0792 | 47.06 |
| 2 | 0.1646 | 0.1110 | 32.56 |
| 3 | 0.3566 | 0.1297 | 63.63 |
| 4 | 0.3131 | 0.2498 | 20.22 |
| 5 | 0.1853 | 0.1078 | 41.82 |
| 6 | 0.3255 | 0.1953 | 40.00 |
| Patient | r | |||||
|---|---|---|---|---|---|---|
| 1 | 3824.63 | 0.2889 | 395.17 | 0.5318 | 6.83 | |
| 2 | 3948.25 | 0.2943 | 376.06 | 0.5291 | 7.22 | |
| 3 | 4036.26 | 0.2746 | 383.67 | 0.5157 | 9.52 | |
| 4 | 3941.78 | 0.2840 | 369.57 | 0.5180 | 11.96 | |
| 5 | 3916.61 | 0.2789 | 383.86 | 0.5190 | 7.43 | |
| 6 | 3990.69 | 0.2835 | 372.31 | 0.5127 | 10.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. Mathematical Modeling of Immune Responses against SARS-CoV-2 Using an Ensemble Kalman Filter. Mathematics 2021, 9, 2427. https://doi.org/10.3390/math9192427
Ghostine R, Gharamti M, Hassrouny S, Hoteit I. Mathematical Modeling of Immune Responses against SARS-CoV-2 Using an Ensemble Kalman Filter. Mathematics. 2021; 9(19):2427. https://doi.org/10.3390/math9192427
Chicago/Turabian StyleGhostine, Rabih, Mohamad Gharamti, Sally Hassrouny, and Ibrahim Hoteit. 2021. "Mathematical Modeling of Immune Responses against SARS-CoV-2 Using an Ensemble Kalman Filter" Mathematics 9, no. 19: 2427. https://doi.org/10.3390/math9192427
APA StyleGhostine, R., Gharamti, M., Hassrouny, S., & Hoteit, I. (2021). Mathematical Modeling of Immune Responses against SARS-CoV-2 Using an Ensemble Kalman Filter. Mathematics, 9(19), 2427. https://doi.org/10.3390/math9192427








