1. Random Variable as a Fundamental Idea
The advances in science and technology, the exponential growth in data collection systems, and a globalised world that bombards its citizens with information through figures and graphs daily have generated the need for new analytic tools that could help people with the interpretation of the information surrounding them. A key tool in this process is so-called statistical literacy. Batanero [
1] explains that statistics have played a fundamental role in the development of modern society, because they have provided a battery of methodological tools to analyse variability, the relationships among variables, the design of studies and experiments, and to improve the predictions that are needed to make decisions in situations of uncertainty. Due to the foregoing points, the need for statistically literate citizens has become an objective for the leaders of diverse nations, who have promoted the incorporation of statistics and probability in formal education. In this sense, researchers and teachers have contributed to defining the curricular lines that allow these topics to be addressed. The teaching of stochastic ideas throughout the education process began to be conceived by Bruner (1959; cited in [
2]), who, in September 1959, at the Woods Hole Conference, proposed the idea of a spiral curriculum consisting of a series of possibly fundamental ideas to teach at different levels of complexity, from preschool to university. Years later, Heitele [
3] boldly proposed 10 fundamental stochastic ideas, based on psychological and epistemological reflections. These were expressions of belief, the probability field, independence, the addition rule, equidistribution and symmetry, combinatorics, urn model and simulation, the stochastic variable, the law of large numbers, and the sample.
Heitele established the random variable as a fundamental idea from three perspectives: the epistemological perspective, which plays a basic role in the mathematisation of probability throughout history; the psychological perspective, in which the intuition of magnitudes when chance is involved arises earlier than that of the random experiment; as an explanatory model, which plays a key role in three aspects—its distribution, expectancy and the operations between random variables.
Kachapova and Kachapov [
4] identified some of the misconceptions of students about the random variable. For example, the ideas that a random variable X is any real-valued function in the sample space, any random variable is discrete or continuous, and thinking of a continuous random variable as a variable with a continuous distribution function, because the condition of continuity of the distribution function is necessary but not sufficient.
Some studies on the random variable have focused on showing examples of activities that promote the idea of the discrete random variable [
5,
6], whereas others deal with the conceptual understanding of the idea of the random variable and the connections or links with other concepts, such as estimators, parameters, probability distribution, sampling distribution, unbiased estimators, and expected values [
7]. There are also studies that propose activities in which it is necessary for students to have prior knowledge about the random variable for the study of probability distributions (such as binomial, normal and exponential), and framed within them the characteristics of the binomial random variable [
8,
9,
10]. Likewise, in the task of constructing double-entry tables, Gea, Gossa, Batanero and Pallauta [
11] identified that prospective teachers had problems in identifying the variables. Gea, Batanero, Arteaga and Estepa [
12] indicate that students often confuse independent and dependent variables when performing regression analyses.
Nevertheless, even when the importance of the random variable is well-known, how do the mathematics curriculums and textbooks address the study of this notion? The aim of this article is to present the results of a research project that had the objective of characterising the meanings of the random variable that are expected and promoted by the Chilean mathematics curriculum (understood as the duo <Plans of study, textbooks>), as well as the representativeness of those meanings regarding the reference meaning of the random variable.
2. Theoretical Framework
The present work uses some of the theoretical–methodological notions from the onto-semiotic approach (OSA) of mathematical cognition and instruction. To study a mathematical concept, it is necessary to comprehend its characteristics, scopes and fields of action, among other elements which it might comprise, in order to gain a deeper understanding of that which is intended to be observed. It is necessary to know the meaning of such mathematical objects. It is possible to determine the meaning or meanings of a given mathematical object by its historical development through time [
13]. In this sense, Pino-Fan, Godino and Font [
14] propose that the reference meaning is understood as the systems of practices that are used as a reference to elaborate the meanings that are intended to be included in a process of study. For a concrete educational institution, the reference meaning will be a part of the holistic meaning of the mathematical object.
In the OSA, the notion of mathematical practice is of great relevance and refers to any performance or manifestation (verbal, graphic, etc.) that is carried out by someone in order to solve mathematical problems, to communicate the solution to others, to validate the solution, and to generalise it to other contexts and problems [
15] (p. 334). The practices can be idiosyncratic of a person (personal practices) or shared within an institution (institutional practices). Furthermore, from the systems of practices (operational and discursive), at least six primary mathematical objects emerge [
16,
17]. In the OSA, the anthropological premise of the socio-epistemic relativity of the system of practices (the emergent objects and the meaning) is assumed. Thus, the meaning of a mathematical object is understood as the system of practices that a person performs (personal meaning) or that is shared in the heart of an institution (institutional meaning) to solve a type of situation or problem.
Pino-Fan, Godino and Font [
14] indicate that the holistic meaning of reference is defined on the basis of two notions. The first is global meaning, comprising several partial meanings of the mathematical object that have associated epistemic configurations (situations/problems, linguistic elements, concepts/definitions, properties/propositions, procedures and arguments) that are mobilised when solving certain problem situations, in given historical problems, and that gave rise to the emergence, evolution, formalisation and generalisation of a given mathematical object. The second notion is the reference meaning, which is understood as the systems of practices that are used as a reference for the meanings that are intended to be included in a process of a study; in this sense, the reference meaning will be part of the global meaning of the mathematical object—in this case, the random variable.
In mathematics education, the importance and complexity of representations in teaching and learning processes is well known [
18,
19,
20]. The importance and complexity lie in the mathematical objects to be represented and their meanings. Then, if the representations attend to the complexity of the mathematical object and its diverse meanings, the same mathematical object can admit different representations (geometric, algebraic, graphic, and so on). Furthermore, it is recognised that it is possible to change the representation by substituting it for another in the same semiotic register, and move between different representations; this is implied by a change in the semiotic register [
18].
2.1. Reference Meaning of the Random Variable
According to the study of diverse historical stages of the random variable evolution carried out by different authors [
2,
3,
21,
22], the mathematical object variable is the result of numerous generalisations made over a development of more than 800 years. Based on this, it is possible to identify four meanings of the random variable, which are described below.
2.1.1. Meaning 1: The Random Variable as a Variable of Interest
One of the first problem areas in which the idea of random variable is observed is the one linked with games of chance. The more formal mathematical analysis of them has appeared in relatively recent times [
23]. The ideas depicted in these works are not very formal, as the existence of variables or distributions in a general form is not mentioned. Nevertheless, variables are defined for cases, and in certain cases, their distributions are considered. Different mathematicians were attracted by the problem of estimating the equitable wager in the game of chance, which led them to implicitly consider random variables and distribution. In modern terms, their main interest was the mathematical expectation of the variable. Such was the case of Fournival, Cardano or Galileo, who, motivated by their interest to find the best wager in games of chance, were devoted to study the possible outcomes for rolling three dice [
24]. At a later stage, Pascal and Fermat started with the probability theory in search of the solution for the equitable wager. Further on, Huygens manifested the need to think about a variable of study, that is to say, a
variable of interest in consideration of the context. In the analysis of his solution, Huygens makes the needed variable to analyse explicit: “In the first place we must consider the number of Games still wanting to (win) either Party” [
25] (p. 4), which he situates in the context of the problem.
2.1.2. Meaning 2: Random Variable as Magnitude
De Moivre [
26] established a change regarding previous books of probability. Latin began to be replaced by writing in or simultaneously translating into English or the native language of the author, which meant that a specialised vocabulary would develop faster by working with a living language. Furthermore, he presented a different conceptual approach, in which he clearly separated the probability of an outcome from its value or the expectation. In his third edition, the author [
26] established the paradigm of mathematical probability, leaving behind the philosophical problems and forming the theoretical basis to all his propositions [
27]. This paradigm can also be observed in the work of Jacob Bernoulli from 1713 [
28].
According to Pearson [
29], De Moivre wrote the first treatment of the probability integral and the essence of the normal curve, contributing with diverse tools for the field of probability. In that age, scientists used the idea of variables connected with the study of mathematical analysis. It was commonly called quantity or variable magnitude, which evidenced its character linked with measurement, a process in which the quality could take different values.
2.1.3. Meaning 3: Random Variable as Statistical Variable
In parallel to the evolution of the probability theory through the resolution of game problems, the birth of statistics emerged through the gathering and description of social or economic data. From the beginning of time, humanity has had a need to perform counts and representations that may be classified as simple statistical recounts. The need to know and plan, in the sense of understanding what is at hand and making that information accessible and manageable to make decisions, has prompted politicians, traders, and militaries to conduct increasingly complex censuses and counting.
Thus, the statistical variable is associated with the observation and description of a sample from a dataset. Following this idea, Ríos [
30] proposed that the statistical variable describes the set of values obtained in the data by performing an experiment a concrete
n number of times; then, if we consider a random experiment
S and make a certain
n number of tests relative to the same, we obtain a set of observations called the
random sample of extension n. This set of results will provide a statistical table in which certain values of the variable correspond to certain frequencies. As such “variable, that only represents the
n results of
n executions of the
S random experiment will be referred as statistical variable” [
30] (p. 70).
2.1.4. Meaning 4: Random Variable as a Function
Hawkins, Jolliffe and Glickman [
31] consider the concept of random variable as a function with numerical values of which the domain is a sample space. Borovcnik, Bentz and Kapadia [
32] indicate that a variable is random when its value is determined as a result of a random experiment; they also establish that to characterise a random variable, we need to know the set of all its possible results and the probabilities associated with each of them.
Then, a random variable is defined as a function of the sample space E in the set of real numbers R. Not any function can be a random variable. It is necessary that for each interval I, the set should be an event of the sample space, and thus, should have a well-defined probability. This guarantees that the random variable would carry the P probability that is defined over the E sample space to the real line.
On the basis of that, Ortiz [
22] identified the following elements of the meaning of the random variable (RV) as a function:
RV 1: The random variable takes its values depending on the results of a random experiment;
RV 2: It is a function of the sample space in R;
RV 3: It is characterised through the distribution of probability, along with the values that it takes with its probability;
RV 4: It is required that for each I interval of R, the original set would be the event of the sample space;
RV 5: A random variable defines a measurement of probability over the set of real numbers;
RV 6: For each random variable Xi, we can define a function of distribution in the following way: (1) R: [0,1] and (2) x: F(x) = P(𝜉 ≤ x);
RV 7: The function of distribution of a random variable is a real function of real variable, monotonous non-decrescent;
RV 8: The function of distribution of a random variable determines on a biunivocal form of the distribution of probability;
RV 9: Let (xi, pi) i ∈ I be the distribution of probability of a discrete random variable. The mean or mathematical expectation is defined as E[𝜉] = ∑i ∈ I xi, pi. This concept expands the idea of median in a random variable;
RV 10: The mode is the most likely value of the variable;
RV 11: The median is the value of the variable by which the function of distribution takes the 1/2 value. Then, the probability that one random variable would take a value lower than or equal to the median is exactly 1/2.
3. Methodological Aspects of the Study
The sample selected corresponded to a secondary school mathematics textbook in Chile. Secondary education in Chile considers four levels, from 7th Grade (12 years old) to 10th Grade (15 years old). Each year, the Chilean Ministry of Education (MINEDUC) provides textbooks for free to all the students from public institutions. The elaboration of such textbooks is awarded on a tender basis; thus, throughout secondary education, it is observed that different editorials oversee the elaboration of them, as we can see in
Figure 1.
For the purposes of the present work, textbooks from secondary education were selected. Particularly, the mathematics textbooks of 7th, 8th, 9th, and 10th Grade, and 8th and 11th grade history textbooks were analysed because of the relationship between the axis of statistics and probability with the objectives set by the history subject around the development of skills such as critical thinking.
The mathematics included in the curriculum for grades 7–10 is cross-curricular in secondary education, whereas the mathematics declared for grades 11 and 12 are differentiated according to the specialisation selected by the student. These specialisations mean that some students will take mathematics subjects in greater depth, which is why we considered it appropriate to analyse grades 11 and 12 in a second stage.
Each of the tasks present in the texts and programmes of study was extracted and subjected to a thorough analysis. First, we identified general elements such as the source document, educational level, and page number, among others. Consequently, we moved towards the identification of the primary elements present in them (and in their solutions), such as the working context, the type of variable used, and the types of representations that are put into play. Lastly, we completed the analysis by associating the problem/task and the practice used to solve it with a reference meaning of the random variable and a typology of problems (only for those tasks linked to meaning M4, random variable as a function). A summary of this process is given in
Figure 2.
Support Interface for Analysis
To facilitate the process of recording information and subsequent analysis, for this research, we created an interface that allowed us to visualise the images of the tasks, assign categories of analysis in a predefined way, and assign observations at the same time, in an orderly way, and which record was automatically stored in a database that we could easily link to statistical software.
Figure 3 shows the interface created. In this case, FVA stands for
Función Variable Aleatoria (random variable as a function, in Spanish).
The input fields considered both in the user interface and in the database were elaborated on the basis of the flow chart presented above in
Figure 2. The records entered through the interface were stored in a database, which can be seen in
Figure 4.
4. Analysis and Results
Based on the plans of study and the mathematics and history textbook suggested by the curriculum framework, we conducted an analysis of how the random variable is approached in the Chilean secondary school mathematics curriculum. We have divided the analysis and results into four sections. In the first section, we present the analysis of the meanings that are promoted in the tasks proposed in the textbooks. These meanings are as follows: (M1) as a variable of interest; (M2) as a magnitude; (M3) as a statistical variable; and (M4) as a function. In the second section, we detail the types of representations activated or expected to be activated by the task/problem proposed in the textbook, which may be verbal, graphic, symbolic, tabular, or iconic. In the third section, the types of variables intended to be promoted are shown. Finally, in the fourth section, we categorise the context (areas of application): (a) gambling, (b) census and registration, (c) natural and biological sciences, (d) physics and astronomy, (e) observation and interpretation from surveys, (f) intramathematical–formal, and (g) intramathematical.
In particular, due to space constraints, we will provide the results relating to 10th Grade. Regarding the structure of the documents analysed, the programme of study (PS) for secondary school mathematics proposed by the Chilean Ministry of Education [
33] is divided into four Units, each one associated with a thematic axes: Numbers, Algebra and Functions, Geometry, and Probability and Statistics. The random variable notion is addressed in Unit 4, which is related to the thematic axis of Probability and Statistics. In this unit, there are three expected learning outcomes, and for each expected learning outcome, there are a set of assessment indicators. For its part, the text for the students presents the study of elements related to the random variable in Unit 4 entitled “Statistics and Probability”. This unit is divided into three sections, and in turn, each section is divided into lessons, highlighting among them
Section 2 called “random variable”. On the other hand, the history book presents five units, which are, in turn, divided into sections. The numbers of tasks extracted from each of the documents were 175, 24 and 24, respectively, making a total of 225 tasks analysed for the school level mentioned above.
4.1. Meanings
Figure 5 shows the distribution of meanings across the documents studied.
As mentioned, the tasks linked to the meaning
M1 random variable as a variable of interest are ranked first in both the textbook and the programme of study with 54.24% (96) and 75% (18), respectively. An example of that type of task can be seen in
Figure 6.
The tendency presented in the mathematics textbooks is not replicated in the tasks analysed in the history texts, in which it was possible to appreciate tasks linked to the meaning M3, random variable as a statistical variable, in 75% (18) of the tasks analysed. An example of this type of task is shown in
Figure 7, where it is requested to establish links between the data observed in the graphs and historical processes.
One aspect that was observed at this level, in contrast to the other levels analysed (7th to 9th Grade), is the appearance of the meaning
M4 variable as a function, in the student’s mathematics text with 17.51% (31) and in the programme of study with a presence of 13% (3). An example of this type of task is presented in
Figure 8, where explicit use is made of the random variable concept.
This activity can be classified as problem type SVA2 (Determine the probability that a random variable takes a certain value), according to the problem typology proposed by Ortiz [
18].
Table 1 shows the classification by type of problem of the tasks in the textbooks analysed.
4.1.1. Meaning Development by Educational Level
The trend observed in 10th grade mathematics textbooks and programmes of study is repeated at the other educational levels where the presentation of tasks corresponding to the meaning M1 as a variable of interest, and M3 as a statistical variable, are prioritised, as shown in
Figure 9. At a general level among the textbooks and curriculum, it was possible to determine that the M1 meaning of the random variable as a variable of interest, was present in 55.7% (463) of the tasks analysed, followed by the M3 meaning as a statistical variable with 24.9% (207), whereas the M4 meaning of the random variable as a function was present in only 4.09% (34) of the tasks, and with respect to the M2 meaning of the random variable as a magnitude, it was not possible to identify tasks that mobilised it, an aspect that is important to study in greater depth.
The observed results represent an advance in relation to the findings of Ortiz [
22], which showed a scarce presence of vocabulary related to random variables, with the use of it rather implicit or of low depth; however, in the documents observed in our study, explicit use of the concept of random variable in definitions as well as in tasks can be discerned. However, some considerations must be added to these advances: (1) there is a tendency towards the use of tasks of meaning 1 (M1), random variable as variable of interest, over other meanings, which could limit the development of a more holistic meaning by students, which could allow them a better transition towards concepts such as the central limit theorem; (2) the type of task presented in the history texts in relation to the type of meaning and context could represent a contribution to the axis of probability and statistics, and in particular to the work with random variables, which opens an interesting field of study; (3) it was not possible to appreciate tasks related to meaning 2 (M2), random variable as a magnitude, which is linked to the idea of statistical error from a more intuitive idea of measurement; this could cause some difficulties in students considering that the new curricular bases proposed in the 10th and 11th level concepts such as hypothesis testing and confidence intervals, in which the understanding of the idea of error could facilitate the interpretation of results.
4.2. Representations
We identify the types of representations (verbal, graphic, symbolic, tabular or iconic) activated or expected to be activated by each task/problem. Furthermore, a distinction is made between initial representation, which we understand as the representations that the learner (or a subject) must initially interpret and decode in order to understand and approach the task; emergent representation is understood as that which emerges as part of the subjects’ responses (or responses that are expected to emerge, if viewed from an institutional point of view). Depending on the type of task, it is possible that in addition to a prior and an emergent representation, a transient one may emerge. The transitional representation is the one through which the learner needs to pass before sketching the emergent representation.
We found 19 kinds of tasks which arise from the various possible combinations of initial, transient and emergent representation types; however, it is possible to classify them into three groups in relation to their structure, as shown in
Figure 10:
An example of a group 1 task is shown in
Figure 11, where a symbolic representation is provided in the initial statement, and the student is asked to provide a response that activates a symbolic representation.
Figure 12 shows an example of a group 2 task where symbolic representation is provided in the initial statement, and the learner is asked to provide a response that activates a verbal representation.
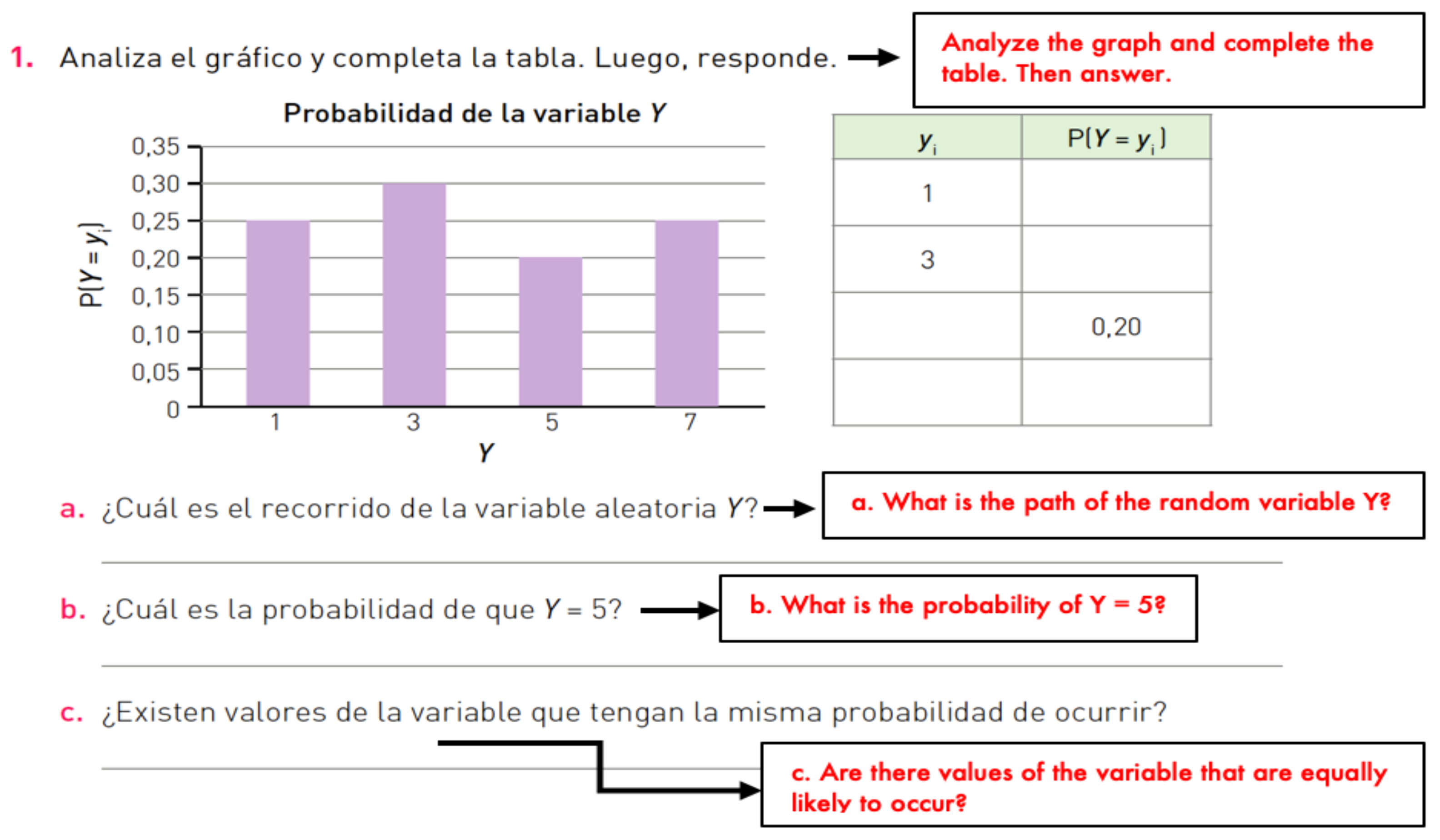
Figure 13 shows an example of a group 3 task where a graphical representation is provided in the initial statement and the student is asked to provide a response that prompts a verbal representation; however, to do so, the student must transition from the graphical to the tabular and from the tabular to a response in the verbal register, as indicated in the task instruction.
Table 2 shows the frequencies of initial, transitional, and emergent representations mobilised in the 10th grade mathematics and history curriculum and textbooks.
Some aspects to highlight, regarding the type of representations, are that the tasks belonging to group 3, i.e., those that require some type of transitory representation, opt-for symbolic representation in 89% (29) of the cases because the instruction given to the students usually includes the performance of some type of calculation. These findings coincide with the study conducted by Alvarado and Segura [
36], which mentions that the most used representations for presenting sampling distributions in classic and modern textbooks for engineering are notations and symbols. In mathematics textbooks, the graphical and tabular component is worked on to a low extent, whereas in history texts, this type of representation is prioritised both individually and in a mixed way, i.e., both types at the same time. An example of a task with mixed representation can be seen in
Figure 14.
4.2.1. Presence of Representations by Educational Level
At the general level in the textbooks and curriculum, the possible combinations between initial, emergent, and transient types of representations gave rise to 38 types of tasks which were possible to categorise into the three groups mentioned and exemplified previously. Nevertheless, it seems relevant to us to show the presence of the types of initial, emerging, and transitory representations mobilised throughout the levels analysed, which is why, in
Table 3, it is possible to observe the initial and emerging representations for each educational level as well as the existing transitory representations, identified by the colours indicated on the labels. It is observed that throughout the four educational levels, the initial and transitory representations are mostly of the verbal type, whereas the initial representations of the graphical type only reach 11.6% (97) of the cases analysed, and 10.83% (90) of the tabular type. If we observe the emerging representations of the graphical type, they were only requested in 4.5% (38) and tabular representations in 0.8% (7). As for transitory representations, these are requested in 27.67% (230) of the cases analysed, and of these cases, 15.21% (35) correspond to graphical type, 14.75% (34) correspond to tabular, whereas 66.95% correspond to symbolic.
In addition to the low representativeness of tasks related to the graphic area, worrying aspects were observed in the 7th, and 8th grade levels, such as the poor use of labels on graphs indicating frequencies or percentages, which results in students not really enhancing their work with graphs, because displaying the information symbolically on them makes it unnecessary to work with the axes and therefore with the graph itself; examples of this can be seen in
Figure 15.
Regarding the representations, a positive aspect to highlight in the history texts is that even though the number of tasks extracted is not so significant in terms of quantity, they are significant in terms of their richness regarding the types of representations used in the graphical tabular area and the combination of these with other types, as in the case shown in
Figure 16. In this figure, a graphical representation is explicitly linked to other verbal representations, and the student is asked to establish connections between the two in order to draw conclusions. These results could be similar to those obtained by Alvarado and Segura [
36] in textbooks related to administration and economics, in which symbolic language was promoted alongside graphical language.
All the aspects mentioned in this section are of great importance because interpreting the information presented in the different types of representations (verbal, graphic, symbolic, tabular or iconic) and ‘converting’ it to another type of representation to solve the activity accounts for statistical reasoning [
40]. According to Wild and Pfannkuch [
41], one of the foundations for statistical reasoning is transnumeration, the general idea of which is to form and change representations of data to generate system understanding. This requires: (a) capturing measurements from the original system, (b) changing data representations, and (c) communicating messages with the data. In other words, what these authors propose is that through a process of transnumeration, we can reinterpret or obtain new information through various representations in the hope that these will convey a new meaning of the data.
4.3. Types of Variables
Given the discrete or continuous character that the random variable can take and the role of these variables in the type of treatment to be given to solve each problem/task, it is essential to identify the types of variables present in the proposed tasks and their relationship with the meanings of reference.
It was observed that both the textbook and the mathematics programme of study most frequently use discrete variables in the tasks they propose. This was reflected in 63.28% (112) and 87.50% (21) of the cases, respectively, whereas the history text opted for the use of continuous variables in 62.50% (15) of the cases, a percentage far removed from the 8.33% and 1.69% observed in the mathematics curriculum and textbook, respectively.
Table 4 presents a summary of the types of variables that were identified in the tasks proposed in each learning objective, section and lesson.
It should be noted that in 14.69% of the tasks analysed in the mathematics text, the type of variable was classified as
undefined since the type of variable to be used is not made explicit because it is subject to the students’ choice.
Figure 17 presents an example of a task where the variable is not specified and is classified as
undefined.
Presence of Variable Types by Educational Level
Again, the trend observed in the 10th Grade was replicated throughout the four levels analysed, as can be seen in
Figure 18. In general, in the texts and curriculum analysed, 44.64% (371) of the tasks work with discrete variables, whereas only 16.12% of the tasks work with continuous variables.
These findings could be a warning in consideration of research such as that of Hawkins, Joliffe and Glickman [
31], who describe that among the errors made by university students in their first statistics courses is the approximation of a binomial distribution by the normal distribution, which is due to the failure to differentiate between the discrete and the continuous. On the other hand, Kachapova and Kachapov [
4] strengthen this idea by commenting that some students’ misconceptions about probability relate to continuous random variables, which constitute a more difficult subject than discrete random variables. One of the misconceptions is to define a continuous random variable as a variable with a set of countable values.
4.4. Contexts
The random variable has been present in almost all the history of probability and statistics; however, it is only in relatively recent years that it has explicitly come to the fore. Its development has been linked to various areas of knowledge such as physics, astronomy, gambling, and others.
The following contexts (areas of application) arise from the documentary analyses, carried out for our research, on the historical development of the random variable, and we use them to analyse and categorise the tasks/problems: (a) games of chance, considering any task related to dice, cards, coins, bag drawing and others; (b) censuses and records, considering any task related to counting a population and its characteristics; (c) natural and biological sciences, considering any task related to the environment, health, flora and fauna; (d) physics and astronomy, with which all tasks related to stars and physical processes such as sound, speed, among others, are considered; (e) observation and interpretation from surveys, which considers all tasks related to the interpretation of data from non-determined surveys of a particular population and whose size is smaller than that of a census—also considered here are the recording of data in matches of different types of sport; (f) economics, which considers all tasks related to economic and political aspects; (g) formal, considering a task whose context is the use of axioms and formal definitions of the variable; (h) intramathematical, considering those tasks in which the use of previously seen notions is presented through a pseudo-application, in the sense that it is applied but to a fictitious situation, only to mobilise mathematical knowledge; and (i) without context.
Table 5 shows a summary of the historical contexts of the random variable observed in the tasks proposed throughout each section and lesson of Unit 4, which corresponds to the thematic axis of Probability and Statistics.
From this analysis, the presence of the physics and astronomy context in the curriculum at this level stands out; however, this corresponds to only one case. On the other hand, the student’s mathematics text shows a clear tendency towards the context of observation and interpretation from surveys, present in 48.59% (86) of the tasks, as opposed to contexts such as economics and physics and astronomy, which were not possible to observe in this text, but this is compensated in the student’s history text in which 58.22% (14) of the cases correspond to the context of economics. The mathematics curriculum for its part promotes tasks linked to contexts related to observation and interpretation based on surveys in 58.33% (14), followed by data and chance with 29.17% (7); at the other extreme are the formal and intramathematical contexts, which were not possible to observe in this document.
Presence of Contexts by Educational Level
Similarly, the distribution of contexts observed for Grade 10 tends to be replicated at the other levels analysed. It is possible to comment that at a general level, the most used contexts in the mathematics text and curriculum are
observation and interpretation from surveys, with 44.52% (370), and
games of chance, with 25.27% (210). The rest of the contexts had a presence of less than 10%, the least used contexts being
Economics with 1.32% (11),
Formal with 1.08% (9), and
Physics and Astronomy with 0.12% (1), as can be seen in
Figure 19.
Again, history texts emerge as an interesting alternative in the diversification of contexts, because it was possible to observe tasks linked to economics and censuses and records with a national stamp. For example, in
Figure 20, we observe a task in which a historical context of Chile is presented linked to the change in fiscal spending in sectors such as education, health, defence and public administration, which could be more attractive to students.
5. Final Reflections
The present study has shown that, regarding the types of variables, there is a clear tendency to use discrete-type variables. It was also possible to observe that the definitions of the concept of variable, their classifications, and differences are barely present in textbooks. These results could imply an exacerbation of students’ issues, such as those mentioned by Arteaga, Batanero, Contreras and Cañadas [
42], from which we can highlight problems in differentiating continuous from discrete variables, the erroneous selection of graphs, poor elaboration of intervals, mixing of values or statistics from different variables in a single graph, and not understanding that each distribution is associated with a single variable. These errors are also consistent with those described by Wu [
43] in students and by Bruno and Espinel [
44] in prospective teachers. Another difficulty that the lack of attention to the types of variables and their relationships might cause is that related to the identification of independent and dependent variables in linear regression, as observed by Terán and Ciminarí [
45], where the most significant error made by the students in solving simple linear regression problems was the interchange of the variables X and Y.
In relation to the meanings, there is a tendency in the Chilean mathematics curriculum for secondary education (7th to 10th Grade) to promote the meaning M1, random variable as a variable of interest, at all the educational levels reviewed. These findings are linked to the conclusions obtained by Andrade, Fernández and Méndez-Reina [
46], where the interpretation of frequency as a variable of interest by students is a fact that is regularly detected by teachers. Although the authors propose that this could be used as a first approach to the idea of distribution, the presence of this type of task in more than 50% of the cases analysed, both in the curriculum and in the textbooks, could imply that this first approach could be overextended, perhaps limiting the elaboration of more robust observations and conclusions by students; this could hinder the development of other meanings of the random variable. Examples of these limitations are presented in the work of Andrade, Fernández and Méndez-Reina [
46], in which students focus on the individual behaviour of the data and not on the collective behaviour of the data, focusing on a value or range of values of the variable. According to Bakker and Gravemeijer [
47], this perception is more related to working with frequency distributions, whereas dealing with data as a whole or aggregate is closer to dealing with probability distributions with their models. We consider that promoting tasks linked to the meanings M3, random variable as a statistical variable, and M4 as a function, could help students to visualise the random variable in a more holistic and integral way, making the step from the analysis of isolated data to the behaviour of distributions. In addition, it seems relevant to us to work in studies to include tasks linked to the meaning M2, random variable as a magnitude, which is linked to the work with the theory of error and measurements whose use would also enhance the use of continuous type variables that are currently worked on to a lesser extent in the curriculum as discussed in these conclusions, and more specifically in
Section 4.1.1. Another aspect that seems relevant to study in future research is the representativeness of meanings for 11th and 12th grade levels that were not included in this study, for which we would expect a greater presence of meanings M3, as statistical variables, and M4, as a function.
The results regarding the types of representations show a tendency towards verbal representation both initially and emergently. Although it was expected that student responses would be mostly verbal in a subject that expects students to draw conclusions and interpret data, the low presence of other types of representations such as graphical or tabular in the initial or transitory moment is a worrying aspect since not diversifying the types of representations and the transitions between them, limits the development of statistical reasoning [
40], as well as amplifies difficulties such as those raised by Gea, Batanero, Artega and Estepa [
12], where future teachers only consider as representation tasks those in which the student is asked to make or interpret a graph, not visualising the diversity of representations of the same object. Our results also coincide with those of Pallauta and Gea [
48], who already pointed out that tabular representations were not receiving due attention in curriculum and textbooks, of which the presence was practically non-existent, and the same could be seen in Brazil, according to Giordano [
49]. As we could observe and as we have commented in these same conclusions, there are representations that are not enhanced and could promote better reasoning and approximation on the notions on the part of the students, for example, those of graphical type. That is the reason why further investigation is necessary to promote teachers’ analyses of tasks, in which aspects such as the types of representations that they enhance in their classes or how to identify tasks that request greater transit between representations could be explored. These aspects could help teachers to identify the appropriate information to be delivered, so they can effectively exploit the potential of the work with a given representation and avoid the misuses of them such as the ones discussed in
Section 4.2.1, in which the inappropriate use of labels could negatively affect the work with a graphic by hindering its richness.
Finally, after analysing the mathematics and history textbooks and curriculum in terms of contexts, it can be observed that the history textbooks are more diverse and linked to topics relevant to the students’ lives, such as the history of their country, global economy and demographics, whereas the mathematics textbooks continue to work mainly with contexts related to games of chance and the interpretation of surveys. Furthermore, the use of the random variable presented in history textbooks was also much richer and more comprehensive in terms of the types of representations, including mixing and enhancing inferences. Little evidence of this had already been commented on by Giordano [
50], who highlighted the presence of tabular representations in textbooks in other disciplines, such as geography. This leads us to wonder how other subject areas could contribute to providing rich contexts for students to use the random variable in meaningful and understandable ways, because, as noted in the analysis from 7th to 10th Grade, work with the random variable was much richer in the history textbook than in the mathematics textbook. This is an issue that is not conclusive in our study, but that should be investigated through future research to reflect on how the relationship between the random variable and other subject areas could contribute to the study of the random variable, and how we can work in an interdisciplinary way within the school to better promote the understanding of the study of the notions of the random variable.