Connecting Mathematics and Science in Primary School STEM Education: Modeling the Population Growth of Species

Abstract

In this research, we explored the potential of using a research-based teaching and learning sequence to promote pupils’ engagement in practices that are coherent with those of real world mathematical and scientific activity. This STEM (Science, Technology, Engineering and Mathematis) sequence was designed and implemented by pre-service teachers and science and mathematics education researchers with the aim of modeling the growth of a real population of rabbits. Results show explicit evidence of pupils’ engagement in relevant mathematical and scientific practices, as well as detailed descriptions of mathematical connections that emerged from those practices. We discuss how these practices and connections allowed the progressive construction of models, and the implications that this proposal may have for STEM task design and for the analysis of extra-mathematical connections.

1. Introduction

STEM activities are characterised by dealing with complex problems using, in an integrated manner, two or more of the disciplines which form the acronym STEM. Real-world situations and problems can bring STEM fields alive for pupils and foster the integration of fields. In particular, the integration of mathematics and science can be nurtured by creating mathematical models of natural systems in the classroom (Dickes and Sengupta [1]; Wilensky and Reisman [2]). Some studies indicate that the nature of the mathematical tools and systems of representation available to pupils determine the depth of learning about science ideas, since mathematical forms correspond to forms of understanding natural systems (Sherin [3]; DiSessa [4]). Lehrer and Schauble [5] found that some challenging scientific concepts in elementary grades can be enhanced by the use of mathematics as a resource for representing and modeling natural systems.

However, the analysis of complex real-world situations is challenging for pupils, and many of them can face difficulties in integrating mathematics and science. Although some studies signal a positive effect of integration on both science and mathematics learning (Czerniak et al. [6]), others report that such an effect is greater for scientific than for mathematical learning, indicating a difficulty in enhancing mathematics achievement in integrated contexts (Hurley [7]). This could be related to the fact that, by holding the concept of mathematics as a product, in many STEM education proposals mathematics is not integrated or connected with other STEM disciplines, and it is commonly portrayed as a set of aiding tools for science and engineering (Couso, Mora and Simarro [8]; Li and Shoenfeld [9]; English [10]). This is because integrative STEM (I-STEM) proposals quite often hide the singularity of each of the disciplines, and pupils cannot benefit from the richness of understanding their epistemic complementarity (Couso Mora and Simarro [8]). For instance, in I-STEM school proposals, it is common that the problem to be solved requires the construction of an engineering solution, which usually requires a very limited set of mathematical practices to be developed. As such, the complementarity of the different practices of the STEM disciplines are not usually emphasised. Research findings suggest (National Research Council [11]) that activities aimed at supporting the integration of mathematics and science for the analysis of natural systems should promote pupils’ knowledge and practices in both disciplines, and make the integration of mathematics and science explicit.

The practice of modeling, which is one of the overlapping practices between mathematics and science, is an interesting case of this common lack of connection between the STEM disciplines. On the one hand, modeling is rarely incorporated into the educational experiences of elementary school pupils (Schwarz et al. [12]). This is, in part, because models, as abstract entities, are often considered inadequate for young children (Archer, Arcà, Sanmartí [13]) and thus usually neglected in the early years of schooling. On the other hand, when modeling is introduced, it is either from the mathematical or the scientific perspective, but rarely from a combination of both. This paper argues that modeling a phenomenon from a both mathematical and scientific perspective is possible in the primary classroom, and can be done in such a way that children engage in core practices of both disciplines in a connected way.

A teaching and learning sequence (TLS) was, therefore, designed around the natural phenomenon of population growth of a species. To understand and act upon this topic in real contexts, pupils were expected to model the ideal and real situation using both mathematical and scientific ideas, such as the Fibonacci series or the effect of resource scarcity on population growth. Following Li and Shoenfeld [9], we focused on the pupil’s experience of both disciplines and on the opportunities the teaching environment provides the pupils in making sense in both mathematics and science. The goal was to show how the designed TLS could serve as an example of how to give an authentic role to mathematics in STEM education. To serve this goal, we posed two research questions:

• In which mathematical and scientific practices do pupils engage within the context of a STEM TLS specifically addressed to promote the overlapping practice of modeling in both mathematics and science?
• What is the role of the connections that can be identified between mathematical and scientific knowledge in the pupils’ modeling of a real world phenomenon?

2. Theoretical Framework

2.1. Mathematical and Scientific Practices

Viewing mathematical and scientific learning as participation in the practices of both disciplines is a framework gaining momentum in the mathematics and science education research literature and recent policy documents (NGACPB [14], NRC [15]). Teaching science and mathematics within the practices framework is proposed as an alternative to traditional schooling in which pupils participate in ‘school mathematics’ and ‘school science’ activities that are socially embedded (both discursive and cognitive in nature) and which are coherent with those of real/professional mathematics and science (analogous to but not the same as those done by mathematicians and scientists).

We conceive mathematics as a human activity focused on the solution of problem situations by implementing systems of practices. These practices are actions or expressions that are produced during the solution of a problematic situation in mathematics (Font, Planas and Godino [16]). In mathematical practices, different mathematical objects intervene (any material or immaterial entity such as representations), and can play an instrumental, representational, regulatory, explanatory or justifying role (Godino, Batanero, and Font [17]). Therefore, some key practices in school mathematics are related to dealing with representations, procedures, explanations and justifications.

In our view, promoting pupils’ participation in scientific practices allows them to experience what makes science different from other ways of knowing in a genuine manner that facilitates their learning (Couso and Garrido-Espeja, [18]). Within this framework, both science and school science are viewed as discursive, cognitive and social activities consisting of developing explanations, carrying out investigations and evaluating and arguing with evidence (Osborne [19]). This signals the key role of the scientific practices of modeling, inquiry and argument in the context of school science.

In order to identify and analyse the mathematical and scientific practices activated throughout the intervention, we used the frameworks proposed by the most recent standards for mathematics and science education, the Common Core State Standards for Mathematics (CCSSM; NGACPB [14]) and the Next Generation Science Standards (NGSS; NRC 2013a [20]). The CCSSM [20] provide a framework that presents eight Standards for Mathematical Practice (SMP) to describe the diversity of relevant mathematical practices: (M1) make sense of problems and persevere in solving them; (M2) reason abstractly and quantitatively; (M3) construct viable arguments and critique the reasoning of others; (M4) model with mathematics; (M5) use appropriate tools strategically; (M6) attend to precision; (M7) look for and make use of structure, and (M8) look for and express regularity in repeated reasoning. The standards define rigorous skills that aim to be clear, specific, internationally benchmarked and research and evidence-based (NGACPB [14]). The NGSS framework is also organised around eight scientific and engineering practices, from which only six are specifically for science: (S1) asking scientific questions; (S2) developing and using models; (S3) planning and carrying out investigations; (S4) analyzing and interpreting data; (S5) using mathematics and computational thinking, and (S6) constructing scientific explanations.

These two frameworks propose a description of mathematical and scientific practices which emphasise the overlap between the two fields. These overlapping practices are mostly related to two overarching practices: modeling and argumentation. The practice of modeling in the mathematics classroom involves solving a real problem using mathematical concepts, methods, and results (Blum and Niss [21]). Models include a conceptual system for describing and explaining the relevant mathematical objects involved, and procedures for generating useful constructions or predictions for achieving clearly recognized goals (Lesh and Harel [22]). In science, modeling has been largely described as entailing the construction, evaluation and revision of scientific models that help pupils to describe, predict and explain the natural phenomena that surround them (Gilbert and Justi [23]).

Li and Shoenfeld [9] claim that emphasising sense-making and making sense in mathematics education “opens opportunities for connections with similar practices in other STEM disciplines”. The same can be said the other way round, with sense-making and making sense in science as opening opportunities to connect with mathematics. As such, relating the practices of mathematical and scientific modeling in a way that is epistemically adequate and pedagogically useful in the classroom requires new frameworks for STEM teaching that specifically focus on the connections between the two disciplines, and which focus on making sense of the studied natural phenomena.

2.2. Connections within Mathematics and between Mathematic and Scientific Practices

In STEM education, the integration of mathematics with other disciplines, such as science, may entail the emergence of several types of connections both within mathematical ideas and between mathematics and scientific ideas.

The notion of mathematical connection is associated with a deep and lasting understanding of mathematics (Smith, M., Bill, V., and Raith, M. L. [24]; Hiebert and Carpenter [25]). The consensus in the mathematics education community on the importance of making connections for the learning of mathematics led to their explicit incorporation by the National Council of Teachers of Mathematics in the curricular standards of the U.S. (NCTM [26]) and also to the appearance of a line of research devoted to the characterisation of mathematical connections (e.g., Businskas [27]; Duval [28]; Evitts [29]; Eli [30]; De Gamboa and Figueiras [31]; De Gamboa et al. [32]; Rodríguez-Nieto et al. [33]).

The definition of a connection, and the types of connections described in the research literature differ, among different research studies. However, some particular types of connections are particularly relevant in this research study. An initial division of mathematical connections into the intra and extra-mathematical is proposed by the connection standard (NCTM, 2000) and many research studies (e.g., De Gamboa and Figueiras [31]; Dolores-Flores and García-García [34]). Extra-mathematical connections occur when mathematics is related to contexts outside mathematics, as is the case of the incorporation of mathematics into STEM activities. Intra-mathematical connections occur when there is an explicit relationship between representations, definitions, concepts, procedures and propositions within the context of mathematics. Although this first division is clearly described, most research studies focus on a fine-grained characterisation of intra-mathematical connections, describing a single category of extra-mathematical connections related to the idea of modeling.

Among the many types of intra-mathematical connections analysed in previous research studies, connections between representations appear consistently in most analyses (e.g., Businskas [27]; Duval [28]; De Gamboa and Figueiras [31]; Rodríguez-Nieto et al. [33]; Adu-Gyamfi, Bossé and Chandler [35]; Dreher, Kuntze and Lerman [36]). One of the most relevant contributions to the analysis of connections related to changes in representation is that carried out by Duval [28]. In his work, two kinds of transformation between representations are described. First, transformations that entail changes in the register of representations (e.g., numerical, geometric or algebraic), called conversions and, second, those where no change of register is carried out, called treatments. A second, more complex type of intra-mathematical connection can also play a relevant role in the context of the analysis of natural systems: mathematical connections that explicitly highlight processes that transverse the mathematical activity. This type of connection is described in De Gamboa and Figueiras [31] and refers to connections that emphasise transverse processes in mathematics, such as argumentation, justification, or heuristics for problem-solving.

Despite the consensus on the benefits of making connections in mathematics, the making of such connections can be problematic for many pupils, since the practices that are to be connected and the symbolic register and discursive patterns may differ (Walkerdine [37]; Jackson, Johnson and Blanksby [38]; Berland, Steingut and Ko [39]). Therefore, the integrated use of mathematical and scientific practices, in particular the overlapping practice of modeling, needs to take into account potential difficulties for pupils and to provide guidance for pupils to overcome such potential difficulties (National Research Council [11]). As such, STEM education designs are needed that provide explicit evidence of connections between both mathematic and scientific practices and ideas in such a way that supports pupils’ understanding of real-world phenomena.

3. Methods

3.1. Context of the Research

The context of this research is the practicum of preservice teachers (PTs) on the Primary Education degree in Catalonia, Spain. Within the modeling-based instruction approach (Windschitl, Thompson and Braaten [40]) that we follow on this training course, one of the professional tasks is to design and implement a sequence of activities (TLS) using the Modeling Cycle shown in Figure 1 (Couso and Garrido-Espeja [18]).

The design team was formed by two PTs, two mentors from the Primary Education degree who are experts in Mathematics Education and Science Education, and the mathematics teacher of the primary school class in which the TLS was implemented. The practicum took place in a school in the Barcelona area, with a group of 22 pupils (12–13 years old) who enrolled in an optional class on problem-solving during their last year in primary school.

3.2. The Teaching and Learning Sequence “A Problem of Rabbits”

The teaching and learning sequence (TLS) designed consisted of seven activities. The aim of the sequence was the construction of a model based on both mathematical and scientific ideas to interpret the growth of a population of rabbits. The TLS was designed considering the phases defined by the modeling cycle (Couso and Garrido-Espeja [18]). The modeling cycle divides the teaching sequence into six instructional phases according to the modeling practice in which the pupils are expected to engage (Figure 1). The cycle organises teaching and learning starting with an activity that helps pupils recognize the need of a model (1). It is followed by different activities that require subsequent mini-cycles of expression/use (1), evaluation (2) and revision (3) of the progressively more sophisticated models of the pupils (Hernández, Couso and Pintó [41]; Schwarz et al. [12]), and ends with activities that promote the explicit expression of a final consensus model and the application, or use, of this model to describe, predict or explain new phenomena (6).

The TLS was initially contextualised using the children’s storybook The rabbit problem (Gravett [42]). The selection of this context with historical connections serves both a mathematical and scientific aim. From a mathematical point of view, it focuses on the importance of the concept of a mathematical sequence by using the paradigmatic example of the Fibonacci sequence, which historically is also contextualised in an ideal example of the growth of rabbits. From a scientific point of view, it connects with a very relevant scientific phenomenon (the growth of populations) that historically was also first addressed, by Darwin himself, by analysing the impossibility of an ideal quantitative growth of populations if no other factors than offspring birth rates are considered.

In the first activity (A1), pupils were asked to justify whether the growth of the population of rabbits shown in the storybook, which is portrayed as unlimited, is possible in a real context. The storybook was contextualised within the same historical problem about the growth of a rabbit population used by Fibonacci to illustrate his famous sequence of numbers: 1, 1, 2, 3, 5, 8, 13… The aim of this activity was to trigger the need to construct a model for the growth of the population of rabbits through the discussion of the real and fictional elements of the book. The key idea stressed in the final discussion of the activity was that the ideal growth of rabbits presented in Fibonacci’s historical problem could be analysed using mathematics.

The second activity (A2) consisted of solving Fibonacci’s historical problem implicitly introduced in The rabbit problem storybook (Gravett [42]). Pupils were asked to calculate the number of couples of rabbits after eight months, one year and four years, justifying in detail the strategies used. Pupils were provided with laminated images of couples of both adult and young rabbits. To perform this task, a scaffolding tool based on the sequence of steps inspired by the work of Polya [43] was available for pupils to use to help them to regulate the problem-solving process. The tool included the following steps: understand the problem and identify the relevant data; devise a plan; implement the plan, and check and interpret the solution in relation to the conditions of the problem. The aim of this activity was to express an initial model that could be used to describe the ideal growth of a rabbit population, fulfilling the restrictions of Fibonacci’s historical problem. The key idea stressed in the final discussion of the activity was that the Fibonacci sequence was useful to model the ideal growth of a rabbit population.

In the third activity (A3), pupils were provided with a table with the numbers of couples of rabbits from 1 to 48 months. In a whole group discussion, pupils were shown an Excel table and graph that represented the population for the first year, the first two years, and the first four years. Next, pupils were asked if the data (numerical values displayed in the table along with their graphical representation) surprised them and if they believed that these data represented the growth of a real population of rabbits. Pupils were also asked to justify what factors could affect the growth of a real population of rabbits. The aim of this activity was to evaluate the model expressed in the previous activity (A2) in a real context and to trigger the necessity to revise it by considering other aspects, such as habitat resources (food and shelter availability or diseases, climatic incidents such as drought or fire, human alterations such as construction and changes in crops, among others). The key idea stressed in the final discussion of the activity was that the Fibonacci sequence was not a good-enough model to describe and explain the growth of a real population of rabbits.

In the fourth activity (A4), a simulation was carried out to explore the equilibrium between the population of rabbits and the habitat where they live (Figure 2). The simulation was performed by pupils themselves through a game. Pupils were divided into two groups of the same size. Each group of pupils stood back to back with the other group. All the pupils in the first group represented rabbits, while the ones in the second group represented resources of the habitat. Each pupil in the first group decided which resource they needed and made a predefined gesture representing it: hand on the belly if they need food; hands on the mouth if they were thirsty; and hand on the head if they needed shelter. Each pupil in the second group decided which resource they offered and made the corresponding gesture. Before starting the game, pupils were asked to represent graphically a prediction of the growth of the population during the simulation. When the teacher said “now” all pupils turned around. The elements of the habitat stood still and the rabbits searched for the resources they needed among those available. If a rabbit found what it needed, the habitat resource that it used became new rabbit, indicating that the rabbits’ needs had been met and it could reproduce. Pupils in the rabbit group who could not find the resource they had to leave the game, indicating that the real rabbit would die. The pupils in the resources group who could not find a couple remained in the game (the resource had not been used). Eight rounds were played and after each round the number of surviving rabbits was represented on a graph (Figure 3). At the end of the game, the resulting graph was compared with the one obtained in A3 (ideal rabbit growth) and the one predicted by each pupil at the beginning of A4. The aim of the activity was to express a final consensus model (the final graph) using some of the variables introduced in A3. The key idea stressed in the final discussion of the activity was that the population of a species fluctuates according to the habitat conditions, but maintains a dynamic equilibrium.

In Activity 5 (A5), pupils played a card game which allowed them to visualise that some rabbits had better possibilities of surviving than others in a particular environment. The cards displayed images of rabbits with different physical characteristics, of resources of the environment where rabbits lived and of other species that interacted with them. The aim of the activity was to revise the model expressed in A4, adding the scientific concept of competition. The key idea was that resources in the environment are limited and rabbits may compete with other rabbits and with other species, and that not all rabbits survive to be able to reproduce.

In Activity 6 (A6), pupils had to agree on how to address the answer to the question “How can we analyse the real growth of any population?” To do so, they developed a scaffolding tool known in our context as the General Actions Self-Guiding Scheme (GASS), based on the work of Sanmartí [44]. This GASS tool was organised in the six aspects shown in Figure 4. At the beginning of the activity each group of pupils received one of the six aspects of the GASS tool. Each group discussed the impact of the aspect given on analysing the growth of a population, and then explained such an impact to the rest of the class, using their experience in the previous activities to justify their claims. Finally, a whole group discussion was carried out to organise the six aspects in order of importance for the analysis. The aim of this activity was to generalise, in abstract form (applicable to contexts other than that studied), the final model they had learned in a particular context. As such, the GASS tool helped pupils to identify the aspects that should be taken into account when analysing the growth of any population by abstracting what they had learned with the rabbit problem. The key idea was that there were conditions of the environment that affected the survival probability and the growth of any population, not only rabbits.

In Activity 7 (A7), the final model built in A4, A5 and A6 was applied to a new context: a real problematic situation of species growth that took place on Marion Island (South Africa). The situation was introduced by reading a newspaper article that explained a programme for the eradication of mice that resulted in an overpopulation of cats and the extinction of three species of autochthonous birds. In groups, pupils read the first part of the article that just explained the problem of the plague of mice. The pupils were then asked, “What actions would you carry out to reduce the population of mice?” Afterwards, pupils read the second part of the article that explained human intervention and its consequences. In groups, pupils used the GASS tool to analyse which aspects were not considered in the eradication programme. Pupils’ answers were discussed by the whole group. The aim of this activity was to use scientific ideas, previously structured in the GASS, to analyse real cases of population growth. The key idea was the same as A6, incorporating the impact of human interventions on the growth of a population. A summary of the phases, and key ideas of the sequence is presented below in

Table 1. Summary of the phases, activities and key ideas developed throughout the sequence. In activities A2 to A5 the initial model of the students was engaged (expression/use), put to test (evaluated) and reformulated to include new aspects (revised).

Activity	Phase of the Modeling Cycle	Key Idea
A1: Reading of the illustrated book The Rabbit Problem (Gravett, 2009)	Recognize the need for a model	The ideal growth of rabbits presented in Fibonacci’s historical problem can be analysed using mathematics.
A2: Resolution of Fibonacci’s classical problem for 8 months, 1 year and 4 years.		The Fibonacci sequence is useful to model the ideal growth of a rabbit population.
A3: Interpretation of the numerical results and their graphic representation in a real context		The Fibonacci sequence is not a good-enough model to describe and explain the growth of a real population of rabbits
A4: Simulation of the growth of a population in a real habitat according to the availability of resources.		The population of a species fluctuates according to the habitat conditions, but maintaining a dynamic equilibrium.
A5: Card game about survival expectancy of rabbits depending on their different individual characteristics and the presence of other species		Resources of the environment are limited and rabbits may compete with other rabbits and with other species, and not all rabbits survive to be able to reproduce
A6: Reconstruction of a scaffolding tool (GASS) to answer the question “How can we analyse the real growth of any population?”	Express a final consensus model	There are conditions of the environment that affect the survival probability and the growth of any population, not only rabbits.
A7: Applying the constructed ideas, the understanding, critical analysis and informed decision-making regarding a real case: the mice eradication programme on Marion Island, South Africa	Use the model to predict or explain new phenomena	Conditions of the environment and the effect of human interventions affect the survival probability and the growth of any population.

.

3.3. Method of Analysis

With the aim of gaining insights into what sort of mathematical and scientific modeling practices and connections took place in the implementation of the above-described TLS, we present an exploratory study based on a purposeful selection of examples of pupils’ productions as well as robust descriptions of classroom practice (Merriam [45]). The aim of the analysis is to evidence how, in this STEM TLS, (a) pupils productively engage in both mathematical and scientific practices and (b) mathematic and scientific ideas contribute to the construction of more sophisticated models of the studied phenomena. Our goal is not to offer causal relations by performing an exhaustive analysis of a complete set of pupils’ productions in the context of the presented STEM TLS. Consequently, this study is inspired by richly qualitative methodologies typical of case study research, evaluation research and developmental research (DBR [46]).

In line with this methodological focus, the data gathering strategy was the purposeful selection of idiosyncratic pupils’ productions performed in the natural context of the implementation of all the activities of the TLS “A Problem with Rabbits” in a real classroom. In addition to pupils’ multimodal written and graphical productions, data also included pupils’ oral comments contained in researchers’ and preservice teachers’ field notes (Phillippi and Lauderdale [47]). To select the pupils’ productions, the four authors grouped them by similarity, in an individual manner, following the constant comparative method of Miles and Huberman [48], and classified them according to the evidenced use of mathematical or scientific practices. This analysis was undertaken in two steps. First, experts in maths education identified the evidenced mathematical practices and subpractices the pupils engaged in during the activities. Second, another pair of science education experts did the same regarding the scientific practices involved. Finally, the group of four researchers triangulated their analysis, identifying those moments in which there were connections between mathematic and scientific practices.

The sequence that we are presenting fosters the sophisticated use of mathematics and science from several perspectives. In order to analyse how pupils engaged in these practices (research question 1), we used a system of categories based on The Standards for Mathematical Practice (NGACBP [14]) and the Next Generation Science Standards (NRC [20]). We focused on standards for practice because we aim to show how pupils mobilised explicit mathematical and scientific practices during the resolution of the activities. Each of the standards is multidimensional and addresses multiple contexts (Harel [49]). Therefore, we focus on the ones that keep a direct relation with the activities designed and implemented in the sequence.

To evidence that a certain mathematical or scientific practice was mobilised by pupils, we elaborated a set of indicators. The specification of the indicators for each practice were adapted to our purposes from the descriptions provided in the above-mentioned standards (NGACBP [14]; NRC [20]). In the case of mathematical practices, they entail the diversity of those practices that emerged in our analysis. In the case of the scientific practices, the selection and adaptation were performed regarding the modeling practice, due to the fact that this is the overlapping practice with mathematics on which both the TLS and the research are focused. The coding of these indicators is shown in

Table 2. Indicators for the analysis of mathematical practices adapted from NGACBP [14].

Make Sense of Problems and Persevere in Solving them MP1

- Recognize data and understand the questions (MP1a) - Make conjectures about the form and meaning of the solution (MP1b) - Devise a plan (MP1c) - Use different representations in a strategic way (MP1d) - Carry out a plan (MP1e)

Reason Abstractly and Quantitatively MP2

- Translate a problem into mathematical symbols (MP2a) - Interpret the results obtained through symbolic transformations in relation to the problem’s context (MP2b)

Construct Viable Arguments and Critique the Reasoning of Others MP3

- Make conjectures (MP3a) - Analyse particular cases (MP3b) - Look for counter-examples (MP3c) - Justify their conclusions (MP3d)

Model with Mathematics MP4

- Use graphics to interpret real phenomena (MP4a) - Express a mathematical pattern (MP4b) - Extract and interpret information from diagrams, tables, graphs or formulas (MP4c) - Interpret the mathematical results in the context of the situation (MP4d) - Modify the model when it has not worked (MP4e)

Use Appropriate Tools Strategically MP5

- Use tools strategically (MP5a)

and

Table 3. Indicators for the analysis of scientific practices adapted from NRC [20].

Developing and Using Models (SP2) for Primary School

- Use and express models through different communicative tools (diagrams, simple physical prototypes, simulations and graphs) to describe, predict and/or explain phenomena (SP2b) - Identify the merits and limitations of models to describe, predict and/or explain phenomena (evaluate the model) (SP2c) - Develop simple models based on evidence to represent the phenomena under study (develop and revise the model) (SP2d)

.

To identify both intra and extra-mathematical connections (research question 2), we used the four types of connections proposed by De Gamboa and Figueiras [31], since they emerged from the analysis of classroom practice. These four types of connections have been described in a theoretical framework and are: extra-mathematical connections, intra-mathematical connections related to processes, intra-mathematical connections with conversion and intra-mathematical connections with treatment. Extra-mathematical connections are identified when an explicit relation is made between mathematical objects and relevant characteristics of the real growth of a population of rabbits. Intra-mathematical connections with treatment and conversion are identified when an explicit relation is made between two particular mathematical representations in the sense of Duval [28]. Intra-mathematical connections related to processes are identified when an explicit relation is made between a particular result of the mathematical analysis and a transverse mathematical process such as the validation of mathematical results in relation to the problem’s context. In Section 4 we provide a robust description (Merriam [45]), based on both pupils’ productions and field notes (Phillippi and Lauderdale [47]), of the particular fragment of the classroom activity in which such relations are made explicit to define connections.

4. Results

4.1. Mathematical and Scientific Practices Mobilised by Pupils

The STEM sequence we analysed is intended to foster the sophisticated use of mathematics and science to construct a progressively more adequate model of the real growth of a rabbit population. Consequently, the sequence of teaching and learning activities was intended to construct a selection of progressively more sophisticated mathematical and/or scientific key ideas (See Table 1). Below we describe in detail how the pupils engaged in different mathematical and scientific practices, as shown by the mathematical and scientific indicators of Table 2 and Table 3, in order to progressively construct these ideas (Table 1).

4.1.1. Pupils’ Construction of the Key Idea that the Fibonacci Sequence Is Useful to Model the Ideal Growth of a Rabbit Population

In A1, pupils discussed the situation presented in the storybook and reached the conclusion that the ideal growth of rabbits in the Fibonacci meadow could be analysed using mathematics. In A2, pupils solved the classical problem of Fibonacci for eight months, one year and four years. Pupils’ answers showed evidence of the use of the scaffolding tool provided (GASS, Figure 4), as they recognized data and understood the questions (MP1a), devised and carried out a plan (MP1c; MP1e) and gave explicit arguments justifying how they reached the final solution. In the introduction of A2, a discussion was carried out in each group to decide on the best strategy to tackle the problem and to reach its numerical solutions. In this discussion, pupils made conjectures about different pathways to solve the problem (MP1b). To do this, pupils used concrete representations of the rabbits in an iconic form (cards showing images of adult and young rabbits), drawings and symbols (MP1d). The use of concrete iconic representations of the rabbits allowed pupils to explore the number of couples for a small number of months, as Figure 5 shows. However, the use of this type of representation was problematic, as both the number of pictures and the space on the table were limited. Pupils thus faced the need to change the register of representation to be able to calculate the number of couples after one and four years. This entailed having to choose a new representation that allowed them to perform the calculation for more than 12 months, which meant a strategic use of representations during the resolution (MP1d). The use of abstract representations of quantities helped pupils to recognize the pattern of growth of the whole population of rabbits.

As pupils analysed the particular cases (MP3b) of the number of rabbits at eight months, one year and four years, a mathematical pattern emerged. About half of the pupils (10 out of 22) provided an explanation for the pattern (MP4b) they used to perform the calculations. The three different patterns used by pupils are presented and explained in Figure 6.

When calculating the number of couples for four years, pupils also used different representations strategically (MP1d). Approximately one third of the pupils continued to calculate the number of adult and young rabbits separately after each month, without showing recognition of the pattern. Most of the pupils who followed this strategy could not provide an answer for the number of couples after four years, as they lost the track of the calculations, made a mistake or just abandoned the task. The rest of the pupils evidenced the understanding of the pattern underlying the growth in the number of couples. However, the way of representing the results varied. Approximately half of these pupils provided the number of couples for every month from 1 to 48, while the other half provided only the results required, asserting use of the calculator.

All these pupils’ practices in A2 are indicators of pupils’ engagement in the mathematical practices of “Make sense of problems and persevere in solving them (M1)” and of “Reasoning abstractly and quantitatively (M2).” The involvement of pupils in these mathematical practices in A2 also served to trigger their involvement in the scientific practice of modeling phenomena (SP2), as pupils were engaging in the expression of their initial model (SP2a) of the ideal phenomena of the Fibonacci meadow:

“I never thought that the number of rabbits would be so many!”

(Pupil 4)

4.1.2. Pupils’ Construction of the Key Idea that “The Fibonacci Sequence Is Not a Good-Enough Model to Describe and Explain the Growth of a Real Population of Rabbits”

To achieve this idea, at the beginning of A3,pupils were provided with a table showing the number of couples for each month between 1 and 48 and then asked to justify, interpreting the results in the context of the problem, whether or not they believed this growth to be possible and why (MP2b; MP4d). Pupils extracted and interpreted information from tables (MP4c) when they had to decide whether the growth of the population was possible, using a table that showed the number of couples from 1 to 48 months in A3. The use of graphs had also been introduced as a complementary representation of the number of rabbits from 1 to 48 months, fostering the translation of the problem into different registers of representation (MP2a).

From this quantitative reasoning, all groups of pupils reached the same conclusion: the ideal growth of the population calculated using the Fibonacci Sequence did not accurately describe what would happen with a real population of rabbits. Such a conclusion shows an interpretation of the results obtained through symbolic transformations in relation to the problem’s context (MP2b; MP4d). While only three out of 22 pupils gave an explicit answer identifying an impossible rate of growth in A1, all of them identified this impossibility after solving A2. Therefore, the sequence of activities, along with the classroom management, fostered a reflection on numerical results based on the problem’s context. The arguments provided by pupils in A3 to justify the impossibility of the growth of the population (shown below) constitute counter-examples (MP3c) to the results obtained in A2 and constitute justifications of the partial conclusions reached in A3.

The numerical results obtained when quantitatively analysing the Fibonacci problem highly surprised the pupils. The obtained numbers were in contradiction with the expected behaviour of the phenomena in reality. This contradiction between the ideal model and reality triggered the scientific practice of model evaluation. In particular, pupils started to identify some limitations of the model presented in the storybook to describe the growth of rabbits (SP2c). Pupils realised that this ideal, purely mathematical model did not fit in accurately with real phenomena.

When doing this, they started to mention limiting factors that could have an impact on the growth of the rabbit population, such as time needed to reproduce, lack of food resources, natural death and others (i.e., each couple can’t have exactly one female and one male in each birth; food resources would be exhausted sometime; rabbits would need more space to live; some rabbits would die from illnesses; not every month is breeding season.). Interestingly, at this initial stage pupils mostly referred to rabbits as homogeneous individuals without relations with other species in the same environment, not taking into account either intra-species or inter-species factors that could limit the growth of the number of rabbits. They also ignored the possibility of extinction due to plagues or other causes of population variation over time.

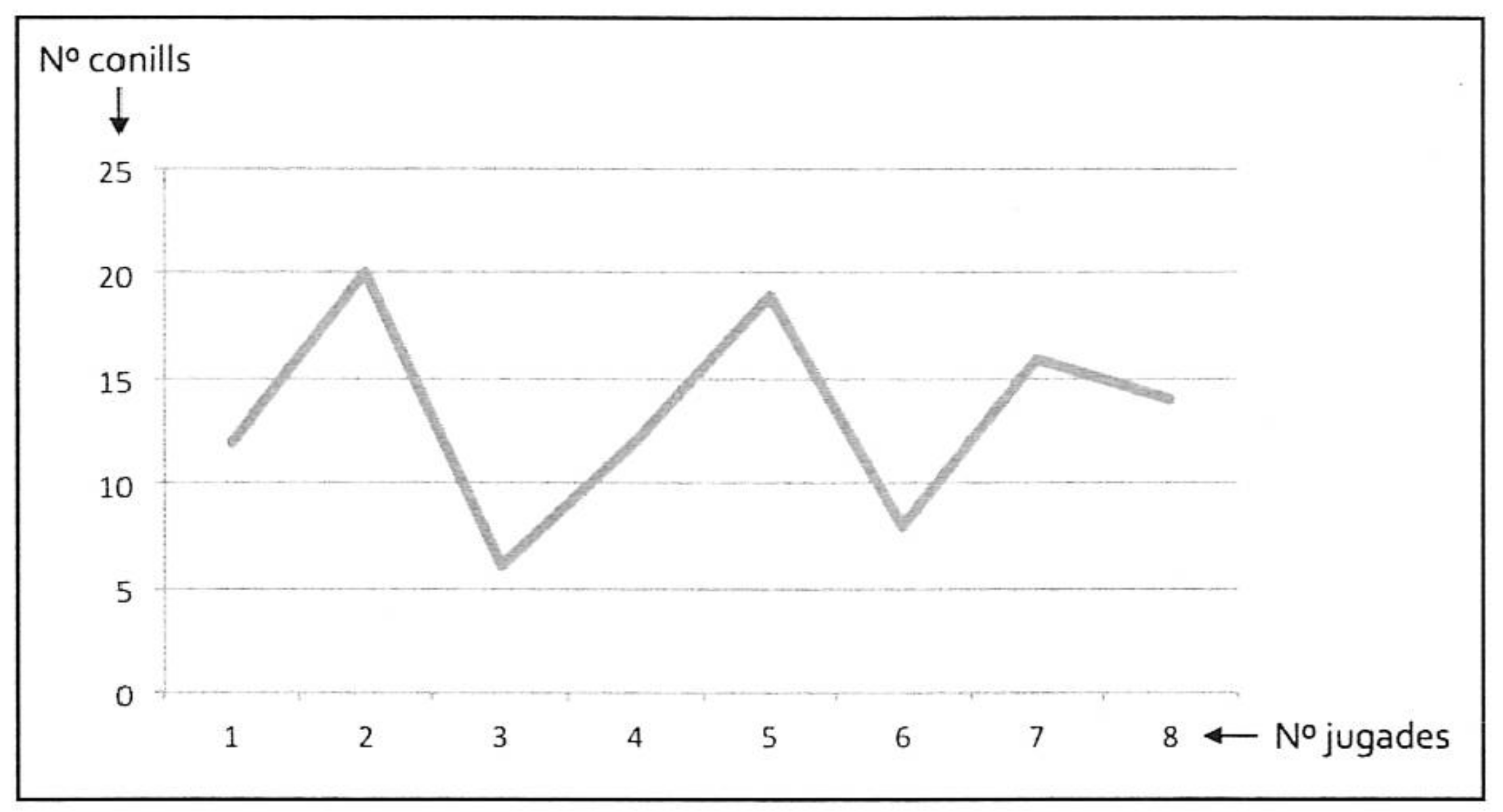
4.1.3. Pupils’ Construction of the Key Idea that “The Population of a Species Fluctuates According to the Habitat Conditions, but Maintaining a Dynamic Equilibrium.”

At the beginning of A4 pupils were asked to predict, by drawing a graph, how the growth of the population would be after eight rounds of the game. This entailed the expression of their initial scientific model of the new phenomena presented to them: rabbit growth when resources are limited and there was competition among individuals. As such, pupils were involved in the scientific practice of expressing models through different communicative tools (diagrams, simple physical prototypes, simulations, graphs) to describe, predict and/or explain phenomena (SP2b) (Figure 7).

Pupils’ predictions showed three different initial models for real rabbit growth. Some pupils represented populations of rabbits growing in some form but stating that they did not actually have a clear model of what would happen (Figure 7, Model a.). Most pupils used an initial model that had both a growth and a decrease phase. However, for some of them, this happened once (the population increased up to a maximum and then decreased abruptly, as in Figure 7, Model b.), while for others the growth showed a continuous oscillation (as in Figure 7, Model c.).

To allow the scientific modeling practices mentioned above, the pupils had to engage in certain mathematical practices. The three examples of predictions shown in Figure 7 illustrate different levels in the use of graphs from the perspective of translating a problem into mathematical symbols. Model a. shows different growth rates during the simulation, but no decrease at all. Model b. shows a pronounced growth during the first rounds, followed by a rapid decrease caused by an exhaustion of resources. In the case of Model c.), the pupil used the axis scales adequately to represent an oscillatory growth of the population.

The simulation/game performed by pupils in A4 evidenced the need for a different rabbit population model. The pupils’ arguments, that arose from the comparison between the actual graph made during the simulation (Figure 2) and the graph proposed by the pupils as a prediction (Figure 7), signal important differences between the graphs. This helped pupils revise their initial models by engaging in the practice of “identifying the merits and limitations of models to describe, predict and/or explain phenomena (evaluate the model) (SP2c).” As such, the pupils’ model of the phenomena started to take into account the complex idea that the number of rabbits fluctuates, going up and down, in a sort of dynamic equilibrium. Mathematically, this comparison also fostered pupils’ skill in using graphics to interpret real phenomena. Pupils extracted information from graphs (MP4c) as they had to interpret the graph provided by the teacher and compare it with the one that they proposed (Figure 7).

4.1.4. Pupils’ Construction of the Key Ideas that “Resources of the Environment Are Limited, and Rabbits May Compete with Other Rabbits and with Other Species”

The qualitative and graphic model of rabbit growth discussed and agreed in A4 was not accurate enough in considering that all rabbits had the same survival capacities and did not compete with other animals. To help pupils to expand this scientific model, new variables were introduced in A5, such as different physical characteristics among rabbits (for instance, rabbits of different colour) and the existence of other species (such as foxes). By discussing the effect of these new variables on population growth, pupils engaged in the scientific practice of revising their model to develop a new, more sophisticated one (SP2d). Some quotes by pupils that show the emergence of these new ideas of intraspecies competition (according to different characteristics) and competition with other species (predators) are:

“Even if they have no predators, other animals that are stronger than her [reference to a weak rabbit] will eat her food”

(Pupil 7)

“In this ecosystem the fox has arrived, a rabbit predator. I think that the white rabbits will decrease before [the brown ones] because they are easier to see [in this particular ecosystem in which there is no snow] and the fox will be able to hunt them more easily”

(Pupil 22)

In the context of this activity, we observed evidence of pupils’ combined use of mathematical and scientific practices, for instance combining a variety of mathematical registers to support their scientific argumentation. An example of this is Pupil 6′s argumentation: “If it (the growth pattern) continues the same, as there are too many rabbits, they would have food, but not enough to feed the whole population since there would be a smaller percentage of food for each rabbit”. Figure 8 shows how Pupil 6 used the inverse relationship between the number of rabbits and the quantity of food available for each rabbit, to interpret the growth of the rabbit population if no other competing factor was considered.

The ideas of the sophisticated model of rabbit population growth that developed during activities A1, A2, A3, A4 and A5 had to be expressed in an abstract way that allows generalisation and transferability to apply this knowledge in other contexts. This was done in activity A6, as explained above, by co-constructing a scaffolding tool able to be applied to any situation.

4.1.5. Pupils’ Construction of the Key Idea that “Conditions of the Environment and the Effect of Human Interventions Affect the Survival Probability and the Growth of any Population”

In Activity 7, the model for the growth of any population that was developed in activities A1 to A5, and explicitly stated in A6, was applied to a new situation: the real case of the introduction of cats on Marion Island to control the growth of mice. In this activity, pupils had to apply the ideas/model of real growth of any population to a new context in which there was human intervention. Below we show examples of pupils using their model to describe the situation, particularly ideas on rate of reproduction, limit of resources and inter-species competition.

“[the problem is] that cats eat mice, but they didn’t take into account that they also eat other animals such as birds and they also reproduce very quickly, and without any predator [for cats]”

(Pupil 23)

“The cats started to hunt other animals easier to catch. This meant that there were too many cats and mice, an overpopulation of them and the extinction of birds”

(Pupil 2)

“They wanted the extinction of mice and they didn’t take into account that cats eat other animals and there were no competitors for cats”

(Pupil 22)

The interesting aspect introduced by this application activity is the requirement of a critical use of the biological concepts acquired. Pupils were asked to argue whether or not they agreed with the decisions made on Marion Island and what knowledge was or was not considered in deciding upon these actions. By doing this, pupils applied their population growth model to judge other people’s actions, and enriched it with the idea of human intervention as one of the aspects to consider when analysing the growth of any animal population in interaction with humans. Only a few of pupils’ productions included references to the increase in quantity.

“The solution has been negative due to the fact that their initial problem was to [eliminate] the mice and they didn’t take into account the [other] problems that appeared later”

(Pupil 11)

“They didn’t take into account that cats will eat birds and not mice. And they didn’t create an ecosystem or some competition [for the cats], to avoid overpopulation”

(Pupil 4)

4.2. Connections between Mathematical Ideas and between Mathematics and Science

The mathematical practices described above were not activated disjointedly. Some of them entailed several relevant mathematical connections. In this section we present a robust description (Merriam [45]) of the mathematical connections that stemmed from the scientific and mathematical practices in which pupils engaged during the TLS. Several mathematical connections of all four types of connections described in our theoretical framework were observed. First, the three types of intramathematical connections are described and discussed in terms of the progressive complexity of the different types of intramathematical connections. Second, extra-mathematical connections are described and discussed in terms of the level of complexity of each connection in relation to the expression, evaluation and revision of the model.

4.2.1. Intramathematical Connections

Pupils made intramathematical connections with treatment (in the sense of Duval [28]) at two different moments: when they discussed the pattern that arose in A2 and when they discussed the relationship between the three different graphs plotted in A3. The discussion about the equivalence of the different patterns identified by the pupils in A2 (Figure 6) brought to the fore the connections between three equivalent numerical patterns. This connection was important because the simpler the formulation of the pattern, the clearer the pattern of increases after each month (the increase for the month n + 1 is the number of rabbits in n − 1). In the case of A3, the fact of comparing the graphs of three periods (one year, two years and four years) allowed pupils to visualise the scale of the population growth for large terms of the Fibonacci sequence (n > 48). By comparing the three graphs, pupils could identify that increasing by one year implied an increase in the slope (inclination) of the curve, which helped them to realise that such an increase was not possible in real life.

Intramathematical connections with conversion were made when pupils used changes of registers of representation in A2. The first change of register was made when they translated the problem into mathematical symbols, as they explored different ways to represent the rabbits that included the use of materials, drawings, symbols such as dots and lines, and numbers. The second change of register was made when pupils used tables and graphs to extract and interpret information in A3. This connection in A3 allowed them to express changes in the population growth in a visual way in A4.

An intramathematical connection related to processes emerged at the end of A3 when pupils were asked if they believed that the data represented in the table and the graphs could correspond with the growth of a real population of rabbits. The connection was made between the growth of a population of rabbits and the role that mathematics plays in the modeling of complex situations. During the whole class discussion, pupils gave several arguments about the impossibility for a population of rabbits growing at the speed of the Fibonacci sequence. These ideas were used by the teacher to emphasise that even if the mathematical analysis performed in A2 provided a model for an ideal population that fulfilled the restrictions of the problem, in the case of a real population of rabbits such a mathematical analysis had some limitations. Therefore, it was necessary to explore other approaches that included habitat resources, such as the design of simulations, in the analysis of the growth of the populations, and to use both mathematics and science in an integrated way.

4.2.2. Extra-Mathematical Connections

The main goal of the first four activities was to understand the growth of a population of rabbits in two cases: a population that fulfilled the restrictions of the classical Fibonacci problem (A2 and A3) and a real population of rabbits in which different factors were progressively taken into account (A4, A5 and A6). Throughout the two cases, different extra-mathematical connections took place, particularly between mathematics and the actual phenomenon of the growth of a population of rabbits.

The first extra-mathematical connection (EMC1) was made in A3, as a result of the comparison between pupils’ previous ideas about the studied phenomenon and the mathematical ideas of the Fibonacci series. The comparison between ideal mathematical descriptions and the world was mediated by their initial scientific knowledge of the phenomenon, mainly centred on the individual factors of species’ growth. This connection was superficial due to the fact that no real data of the phenomena were offered. By connecting with their initial scientific knowledge, centred on their knowledge about living beings, pupils only provided descriptions of rabbits’ characteristics that may limit the growth of the population.

A second extra-mathematical connection (EMC2) was made in A4 between mathematical representations (graphs) and the hypothetical growth of a population subject to resources’ restrictions. In this case, mathematics played a semiotic role that allowed pupils to express a modification of their initial model. The three examples of predictions shown in Figure 7 illustrate different levels in the use of graphs from the perspective of translating a problem into mathematical symbols. Graph 1 shows different growth rates during the simulation, but no decrease at all. Graph 2 shows a pronounced growth during the first rounds, followed by a rapid decrease caused by an exhaustion of resources. In the case of Graph 3, the pupil used the graph adequately to represent an oscillatory growth of the population due to changes in resources, but it is not clear what concrete scientific knowledge they were considering.

A third extra-mathematical connection (EMC3) was made in A5 between mathematics and the particular case in which the population was subject to both intraspecies and interspecies competition. In this case, mathematics played an argumentative role, since the initial mathematical model was used to discuss the hypothetical implications of changes between individuals’ phenotype and the presence of predators.

Finally, in A7 we identified a sign of an extra-mathematical connection between the real problem of Marion Island and quantitative reasoning. We did not explicitly classify it as an extra-mathematical connection since it was made through the use of the scientific concept of overpopulation or a general reference to an increase in the population of rabbits. Although there was no evidence of a critical use of the mathematical concepts acquired, it is interesting to note the emergence of quantitative reasoning in some of the pupils’ productions in spite of the fact that the question posed to pupils (what actions were considered on Marion Island) did not require this sort of reasoning.

5. Discussion

The results of the implementation of the TLS show that the analysis of complex natural systems can favour the integration of mathematics and science, which coincides with the conclusions of various studies (Dickes and Sengupta [1]; Wilensky and Reisman [2]). The use of different representation registers (numbers, formulas, tables and graphs) in the mathematical analysis of the data showed the need to take into account environmental factors (limited resources and competition) that conditioned the growth of a population, favouring a deeper approach to the problem, in line with the results of other studies (Lehrer and Schauble [5]; Sherin [3]; DiSessa [4]).

In addition, the results show that mathematical and scientific core ideas were worked on, both separately and in an integrated manner, throughout the implementation of the TLS, following the recommendations proposed by the National Research Council [11]. In the case of mathematics, pupils explicitly analysed number sequences in the context of the problem; identified and expressed numerical patterns; and identified, represented and interpreted functional relationships. In the case of science, pupils explicitly dealt with relevant scientific concepts, such as the effect of the environment on the survival of a species and inter and extra-species competition. These are the ideas that all livings beings need food, space and suitable surroundings to live. The resources of the environment are limited and have an implication on the possible growth of a population. Living beings may compete with one another for what they need, both inter and intra-species, some individuals having a better chance to survive and reproduce. Although some of these relevant ideas were traditionally addressed at higher levels (e.g., the Fibonacci sequence, Monsoriu et al. [50]), this research provides explicit examples of how primary school pupils may benefit from such ideas.

However, we consider that the mobilisation of mathematical and scientific ideas and practices does not occur spontaneously, but rather requires an intentional design in which these ideas and practices are promoted in a both particular and integrated way, as occurred in the modeling cycle that articulated the TLS analysed in this article. This cycle, which was a concrete operational proposal of based instruction (Windschitl, Thompson and Braaten [40]), focused on the pupils’ knowledge construction and making sense of phenomena in a progressive way, step by step, incorporating new aspects of the studied phenomena in each modeling cycle. The results suggest that the use of subsequent modeling mini-cycles constitutes a methodological tool that favours the mobilisation of mathematical and scientific core practices and their integration for the construction of progressively complex models. Specifically, the sub-cycles aimed at evaluating, expressing and revising the model (Table 1) explicitly promoted diverse mathematical practices, not exclusive to modeling, which underpinned the construction of the model and its successive refinements.

One of the most interesting results of this research, which has relevant consequences for STEM education, is the evidenced complementarity of the overlapping practices of mathematical modeling and scientific modeling in the pupils’ knowledge construction process. We observed how, in this TLS, both mathematical and scientific modeling were a necessary condition for pupils’ comprehension of real phenomena. The isolated use of mathematical modeling resulted in an exponential model that did not correspond with real growth when ecological restrictions appeared. On the other hand, the isolated use of scientific modeling would not have contemplated the initial stages of population growth when restrictions were negligible, nor would it have allowed the pupils to explore the quantitative magnitude of the problem without these restrictions. As such, we consider this proposal to be an example of a STEM TLS that does not trivialise the integration of the STEM disciplines involved, as it was through participation in the practices of the different STEM disciplines that pupils were able to make real sense of the phenomenon.

The analysis of intra-mathematical and extra-mathematical connections shows that the establishment of intra-mathematical connections serves as the basis for the establishment of complex extra-mathematical connections, in agreement with (De Gamboa et al. [32]). While the EMC1 connection was mediated by the pupils’ previous ideas about the phenomenon in a superficial way, in the EMC2 connection the mathematical contents played a semiotic role, based on intra-mathematical connections with treatment in a graphic register and with conversion between tables and graphs. At a more complex level, in the EMC3 connection, mathematics was used to argue about the impact of the idea of competition. This argument was based on previous intra-mathematical connections, which dealt with the conditions in which the initial mathematical model was fulfilled. The fact that, in the application activity (A7), an explicit connection between the phenomenon and mathematics was not observed, may be because the formulation of the questions in A7 did not refer explicitly to the initial mathematical model.

The relationship between the complexity of intra-mathematical connections and that of extra-mathematical connections shows that when mathematics is used in STEM activities in a superficial way, the possibility of establishing complex extra-mathematical connections that allow a deep analysis of phenomena is hindered. This could explain why the use of mathematics restricted to a calculation tool is accompanied by a mostly isolated use of science and mathematics in STEM activities (Couso, Mora and Simarro [8]). This may explain, in turn, the limited presence of mathematical and scientific modeling processes in primary education (Schwarz et al. [12]) and the negligible prominence given to the process of argumentation of scientific and mathematical ideas in the primary classroom (Archer, Arcà and Sanmartí [13]).

6. Conclusions

This research shows how the use of modeling cycles for the analysis of the phenomenon of the growth of a population of rabbits allowed a progressively more complex construction of models that integrated mathematical and scientific ideas. Specifically, the progressive construction of the model was based on a design of separate cycles that first made it possible to identify the relevant mathematical ideas for the analysis of the phenomenon, and later to build new versions of the model, more adapted to reality, incorporating some scientific ideas relevant to the study of the phenomenon. This progressive modification of the initial model is considered to be epistemically adequate since it reflects how scientific models are built.

The incorporation of mathematical and scientific ideas was evident in the participation of pupils in mathematical and scientific practices, the activation of which depended on the tasks that pupils had to solve. The use of tasks that explicitly required the application of concepts and language typical of mathematics and science allowed pupils to argue the construction of the model and justify its subsequent refinements. In this respect, we consider that the explicit demands of the proposed tasks conditioned the use of mathematical and scientific ideas and the depth with which they are integrated.

The integration of science and mathematics is made explicit by establishing connections between the two disciplines. These types of connections are often characterised in mathematics education research in a broad way, as relationships between mathematical ideas and nonmathematical contexts. The three extra-mathematical connections are good examples of how extra-mathematical connections can play different roles (descriptive, semiotic or argumentative), which in turn carry a different complexity. In this respect, we consider that a deep integration of mathematics with science requires the establishment of connections that are not limited to describing mathematical or scientific elements, but rather use them to represent complex relationships and to construct arguments that allow a better understanding of the phenomenon that occurs. The identification of these three roles of extra-mathematical connections may contribute to research focused on the characterisation of mathematical connections (e.g., Businskas [27]; Evitts [29]; Eli [30]; De Gamboa and Figueiras [31]; Rodríguez-Nieto et al. [33]).

However, the construction of these extra-mathematical connections can be problematic for pupils (Jackson, Johnson, Blanksby [38]; Berland, Steingut and Ko [39]) and does not occur spontaneously. When the request made to pupils does not explicitly ask for connections, most pupils avoid making complex connections, as shown by the limited presence of mathematical arguments in the last application activity. Therefore, for complex extra-mathematical connections to emerge, the tasks must require the incorporation of relevant mathematical practices and their coordination with scientific ideas, strategically selecting the aspects of the studied phenomenon, which may be richer from a mathematical and scientific perspective.

The TLS was designed by a team of both science and mathematics education researchers, which is not a trivial contextual factor. As many research studies in STEM education have pointed out, it is necessary to work in interdisciplinary teams to produce real interdisciplinary STEM work (Johnson, Mohr-Schroeder, Moore, English [51]; Margot, Kettler [52]). For us, the idea of establishing connections between disciplines that make sense in each of them can be an interesting way of rethinking this interdisciplinarity in a form that respects the idiosyncrasy and epistemic value of each of the STEM disciplines (Couso, Mora and Garrido [8]), contributing to the array of ways that STEM integration can take place (Moore, Johnston, Glancy [53]).