1. Outline
Interest rate contracts constitute the largest chunk of the global over-the-counter derivatives market, with an estimated total notional outstanding of just over $480 trillion, of which roughly $350 trillion is traded in swaps and almost $50 trillion is traded in interest rate options. The total market value of interest rate swaps and options tallied together exceeds $8 trillion—or about 10% of world GDP.
Anticipating a more formal discussion, an interest rate swap is simply a contract in which two parties exchange two flows of payments (“legs”)—one calculated on the basis of a fixed, pre-determined rate (coupon), and one calculated on the basis of a floating interest rate (typically the interbank market benchmark, often referred to as- London Interbank Offered Rate (LIBOR). Swap options, or swaptions, give the owner the right—but not the obligation—to enter into an interest rate swap with a given final maturity and a pre-determined strike rate at a certain, specific time in the future called option expiration and corresponding to the fixing date of the swap. Swaptions come in many shapes and forms, some more complex (“exotic”) than others. A prototypical example of an exotic interest rate derivative is a Bermudan swaption. Somewhat, the name has nothing to do with geography, but rather with the option exercise profile, as Bermudans, unlike their simpler—so-called European—counterparts, can be exercised not just on a single date, but on any one of a given set of dates prior to the final maturity of the swap (an option that can be exercised at any time is called American).
While we do not know exactly how much of the total market value of interest rate derivatives is made up by Bermudan swaptions, such a breakdown would not do full justice to their importance anyway, as the numbers cited do not account for options and option-like features of Bermudan nature built into simpler fixed income instruments, like callable bonds and mortgage backed securities. Consider that roughly 60% of bonds included in the Bloomberg Barclays Global Aggregate Credit Index—a widely followed benchmark for the corporate bond universe—are issued with call provisions giving issuers the right to repurchase them at par at certain dates in the future. The call provision may be added to increase the coupon, and hence the perceived attractiveness of the issue, but it rarely stays with the issuer, who will instead typically seek to strip the call option and sell it—e.g., in the form of a cancelable swap—to an exotic dealer desk to lower the effective cost of the issuance. For example, Goldman Sachs analysts estimate that Bermudans embedded in 70% of the so-called Formosa bonds (bonds that are denominated in a foreign currency, but registered and listed on the Taipei Exchange) acquire a new life being passed on to exotic dealer desks who tend to actively manage this risk by selling European swaptions with risks most closely mimicking that of the Bermudan (effectively providing “Vega supply” to the market) (“Formosa issuance and USD rate vol supply”, Global Rates Insight, Goldman Sachs, 13 February 2020). Other notable natural buyers of such stripped Bermudan swaptions are mortgage originators or issuers of mortgage-backed securities (such as, e.g., Fannie Mae and Freddie Mac in the US), who seek to offset the risk of prepayment options inherent in typical fixed rate mortgage products.
What is special about Bermudan swaptions, and what explains their important role in the financial system, is the complex risk profile stemming from the multiple exercise feature. It turns out that accounting properly for this exotic feature poses a considerable challenge and has been a major driver of the (r)evolution in interest rate modeling—a story that we intend to tell below.
From a mathematical standpoint, the early exercise property gives rise to a free boundary problem not unlike the so-called Stefan problem encountered when analyzing the temperature of water bordering a melting block of ice: if there are
N exercise dates
, then at each
,
, the Bermudan holder must decide whether to retain the option or exercise by entering into the
i-th co-terminal swap. Naturally, for each
there will be some critical value of the underlying instrument below which it no longer makes sense to exercise. This reduces the problem of valuing the Bermudan to determining the optimal exercise boundary that separates the “region” where exercise is optimal from the “region” where it is optimal to continue holding the swaption—with obvious analogies to Stefan problems for the location of the interface between water and melting ice (see, e.g., [
1]). Such parallels have been known for decades and fruitfully exploited, at least in the case of early exercise boundaries for American-style equity options. And while an early exercise boundary as such cannot be solved for in closed form, it can be represented using an integral equation to be solved iteratively [
2] and its upper and lower bounds can be rigorously determined. Barles, Burdeau, Romano, and Samsoen [
3] even show that near expiration these upper and lower bounds approach each other, which leads them to postulate an approximation for the value of the option.
Unfortunately, those results do not carry through to interest rate options in a straightforward way. For one, the partial differential equation governing the evolution of the stock option price (the Black–Scholes Partial Differential Equation(PDE)) has been derived under the assumption that the underlying instrument, a share of common stock, is a tradable asset. After all, as shown by Black and Scholes [
4], the self-financing dynamic trading strategy replicating the final payoff of the option is implemented by taking positions in, i.e., buying and selling, units of the underlying instrument. That underlying instrument may be—as initially considered—a stock or a commodity futures contract, but not an interest rate that is
not tradable—one cannot “buy” or “sell” a yield on, say, a 10-year bond, a swap rate or the LIBOR. As it turns out, this obstacle can be overcome by a judicious application of the change-of-measure technique ([
5]; more on this below). But even if one can come up with an equivalent probability measure under which a given underlying interest rate is a martingale, and thus price the option by simply taking expectation of the terminal payoff, a more profound problem arises: how to ensure consistency between options on different interest rate underlyings? The crucial difference between interest rates and, say, stocks—other than tradability—is that individual interest rates are simply pieces of a greater whole called the term structure, bound together by no-arbitrage relations and complex correlation patterns. This becomes immediately clear when we consider a swaption where the underlying is a (stochastic) average of a number of forward LIBOR rates. As explained above, a Bermudan can even be viewed as a “best of” chooser option to optimally select and enter into one of potentially many co-terminal swaps spanned by the contract. As such, it is by definition an instrument driven by complex dependence patterns among interest rate underlyings—a phenomenon we shall have more to say on later. All this implies that handling interest rate derivatives, and Bermudans especially, requires a consistent model of the term structure. And since different approaches have been proposed to the modeling of interest rates, so too there have been—and still are—different ideas about pricing and risk-managing Bermudan swaptions.
Although it is impossible within the confines of this essay to do justice to the large and still growing literature in the area of interest rate modeling ([
6,
7] and vol. II are very good general references), we may, at least at this stage, identify two broad schools of thought: low-factor short-rate models and multi-factor market models. The first camp, drawing inspiration from Vasicek [
8], starts from a fundamental assumption that the dynamics of the whole yield curve is driven by the “instantaneous spot rate”, or short rate,
, at which interest accrues continuously in a locally risk-free way. This definition leads to the so-called money market account,
, which evolves according to:
and induces the risk-neutral measure
making all discounted asset prices martingales. Although the short rate is a purely artificial mathematical construct (all be it with an intuitive interpretation), it determines prices of all discount bond that are simply
-expectations of the future path of
,
. And since all interest rates are derived from bond prices, it follows that the entire discount curve can in principle be parameterized by stipulating a suitable stochastic process for
—a point supported by a large body of empirical evidence suggesting that the first principal component typically accounts for about 90% of the variation in the entire term structure. With two factors—two state variables feeding through to the evolution of
—one would expect to cover well over 95% of yield curve variation. Apart from parsimony and consistency, short rate models have another considerable virtue that came to explain their initial success as tools-of-choice for the valuation of path-dependent interest rate instruments such as Bermudan swaptions: they are relatively easy to implement numerically in
lattices, i.e., finite differences or trees, which can efficiently handle the early exercise boundary through backward induction.
However, these virtues do not come without vices to match. With only one or two factors, it might be difficult to generate all practically relevant yield curve shapes (two Principal Components Analysis PCAs would still leave about 5% of variation unexplained) and match a large set of market prices—especially with intuitive and economically justifiable parameter values (using a large set of calibration instruments is necessary if one wishes to consistently apply a single calibrated model to many kinds of exotic interest rate derivatives). More importantly, a low number of factors (one or two) may limit the degree of de-correlation achievable among interest rates, artificially lowering prices of Bermudan swaptions (when correlation among rates is high, the right to choose among different swaptions is lower than in the case when interest rates are decorrelated and subsequent payoffs are unpredictable). Longstaff, Santa-Clara, and Schwartz [
9] even thought that the errors and pitfalls of using single-factor models amounted to “throwing away a billion dollars” and in their influential paper argued for a move towards a multi-factor setting. In fact, the stage in that respect had already been set in the form of so-called LIBOR/swap market models [
10,
11,
12] and their later extensions. Models in this class are generally expressed in terms of discretely compounded market rates (hence the term “market models”), each of which can be shown to be a martingale under an appropriate forward measure. This perspective naturally allows for multiple sources of randomness (often there are more than 50 state variables), with almost arbitrarily complex dependence structure, and offers many degrees of freedom to fit observed market patterns, even including the so-called implied volatility smiles (e.g., [
13,
14] or [
15]; cf. also [
16,
17,
18,
19,
20,
21,
22]). Whether the number of factors, in and of itself, is enough to improve the pricing of Bermudans has been persuasively contested [
23] and we shall review the main arguments presented in this debate. It is clear, however, that while increasing dimensionality improves calibration, it does so at the cost of efficiency and numerical accuracy: with a high number of state variables, lattice techniques are no longer viable, and even if viable (cf. e.g., [
24])—not really practicable. One therefore is left with Monte Carlo simulations (with some variance reduction technique to reduce bias). This presents an obvious problem: by evolving the underlying state variables
forward in time, the simulation cannot easily determine the optimal time to exercise. And while efficient techniques of circumventing that problem have since been proposed (cf. especially the classic approach of [
25,
26] for a very good general reference), the exercise region and corresponding Bermudan swaption prices will necessarily be
estimated—not exact.
The two approaches sketched broadly above, the single- and multi-factor ones, are like Scylla and Charybdis, the mythical sea monsters, lurking for the Bermudan swaption modeler: pass too close to Scylla, and your model shall crash against the rocks of computational challenges and estimation biases of the multidimensional setting; move towards Charybdis and risk getting sucked by a whirlpool of artificial parameter values and unachievable calibration targets. And yet, unlike in the classical Greek tragedy, we believe there is safe passage between the two hazards, and one that does not involve losing six strongest and bravest companions—a cost tragically borne by Odysseus. Thus, in what follows we try to tell the story—the odyssey—behind the evolution of Bermudan swaption pricing in greater detail, reviewing in a much more formal way the main ideas and solutions underlying both single- and multi-factor models. We discuss their relative merits and drawbacks, presenting especially the crux of the consensus-shattering debate between Longstaff, Santa-Clara, and Schwartz [
9] and Andersen and Andreasen [
23]. Finally, building on Gatarek and Jabłecki [
27], we show our dimension reduction approach based on the concept of Markovian projection pioneered by Gyöngy [
28] and independently adapted to the financial landscape by Dupire [
29] under the guise of “local volatility”. Our idea consists essentially in showing that for purposes of pricing Bermudan swaptions, a potentially complex and multidimensional process for the swap rate can—using the tools of Markovian projection—be collapsed to a one-dimensional one. Naturally, the diffusions of the two processes will differ, but it turns out the early exercise boundaries will approximately agree, with pricing errors within normal bid–ask spreads.
The rest of the essay proceeds as follows.
Section 2 presents notation and formally introduces the relevant interest rate instruments.
Section 3 presents the evolution of term structure modeling, from single- to multi-factor approaches, zooming in on implementation and calibration aspects.
Section 4 then discusses the specific challenges related to applying the models in the context of pricing Bermudan swaptions, and revisits the issue of their factor dependence with some numerical tests. Finally,
Section 5 presents a novel argument in the factor-sensitivity debate, demonstrating an elegant extension of the classic result due to Gyöngy [
28] on Markovian projection and dimension reduction.
Section 6 draws conclusions.
2. Notation, Modeling Setting and
Instruments
Consider a continuous-time economy together with a probability space
with a frictionless and arbitrage-free market for zero coupon bonds, i.e., contracts that guarantee holders the payment of one unit of currency at maturity, with no intermediate payments. Let
be the time
t price of a zero coupon bond maturing at time
T such that
for every
t. We assume that such a
exists for every
and for a given
t,
is differentiable with respect to maturity time
T. The instantaneous forward rate
with maturity
T contracted at
t is defined by:
The instantaneous spot rate
—i.e., the short rate—has already been loosely defined above and can now be formalized as:
As discussed,
can be thought of as capturing the locally risk-free return from a continuously compounded money market account
with dynamics
. The significance of the money market account in modern finance stems from the fact that it establishes a connection between the economic concept of absence of arbitrage and the mathematical property of existence of the equivalent martingale measure (risk-neutral measure). Specifically, as shown by Harrison and Kreps (1979) and Harrison and Pliska (1981, 1983), postulating that our market is arbitrage-free is equivalent to stating that there exists a measure
on
, equivalent to
, such that all asset prices discounted by
are
-martingales. In other words, in our economy, for any
T we have:
so that time-zero bond (asset) prices are
-expectations of their terminal values (payoffs). We will explore (
4) in
Section 3 in greater detail as it gives rise to an important class of term structure models, but for now let us simply observe that when we allow for stochastic interest rates—as we naturally should when dealing with interest rate derivatives—the martingale measure
may not be the most convenient or natural to work with. Thus, Geman et al. (1995) prove that for any positive non-dividend-paying asset
N (so-called
numeraire) there exists a measure
, which is equivalent to the original martingale measure
, making the prices of all claims normalized by
N -martingales. Furthermore, the Radon–Nikodym derivative defining
is given simply by
.
We now move on to introducing other instruments. For this we define a uniformly spaced tenor structure:
and set
for
. A spot
LIBOR rate over the interval
is given by the formula:
whereas its forward counterpart,
forward LIBOR, is given by:
A
fixed-for-floating interest rate swap (IRS) with unit notional, fixed rate (coupon)
K, and a specified tenor structure
is a contract whereby two parties exchange differently indexed cashflows over a pre-agreed time span. Specifically, on each date
, the fixed leg pays
, whereas the floating leg pays the floating LIBOR rate given by (
6). When the fixed leg is paid, the IRS is called a “payer”, and conversely the swap is called a “receiver.”
An
interest rate cap/floor is a payer (receiver) IRS in which each payment is executed only if it has positive value. It has become market practice to quote prices of caps in terms of Black’s implied volatilities, i.e., parameters
, which plugged into the formula:
give the market price. The Black model itself is inconsistent with market quotes, which tend to exhibit a pronounced implied volatility smile/skew.
The
forward swap rate corresponding to the tenor structure
is the rate in the fixed leg that sets it equal to the floating leg and hence makes the net present value of the transaction equal zero:
The portfolio of zero-coupon bonds in the denominator of Equation (
9) is the so-called annuity factor, for which we will sometimes use a continuous-time definition, writing
along with:
Note, in passing, that since is positive and is a tradable asset (a portfolio of “long” the bond and “short” the one), it follows that is a martingale under induced by .
A
European payer (receiver) swaption with strike
K, maturity
and tenor
(henceforth referred to also as
, or
-into-
) is simply an option that gives the holder the right to enter at
into a payer (receiver) swap that matures at
and entitles to pay (receive) a fixed rate
K in exchange for a floating LIBOR rate on the tenor dates
. Thus, the time zero price of a European payer swaption with unit notional is given by:
Analogously, as with caps/floors, market practice is to quote swaption prices in terms of Black (or more recently—Bachelier) implied volatilities; i.e., parameters
, which plugged into the Black formula retrieve the market price, e.g., for a payer swaption:
Again, from a theoretical point of view, applying the Black model to price swaptions would be inconsistent as the swaptions market exhibits a pronounced implied volatility smile.
Finally, a
Bermudan receiver (payer) swaption is an option to enter at any time
,
into a swap that terminates at
and gives the holder the right to receive (pay) a pre-determined fixed rate
K in exchange for floating LIBOR. The period up to
is called the lockout or no-call period, and hence a Bermudan swaption with final exercise date
and first exercise
is often called “
no-call
”, or “
nc
.” For example, a 11nc1 swaption with annually spaced exercise dates can be exercised at the beginning of any year, starting from year 1. By exercising the option, the holder enters a swap starting at the time of exercise (i.e., years 1, 2, 3,..., 10) and ending at year 11. Accordingly, the price of the “
no-call
” Bermudan receiver is given by:
4. Bermudan Swaption Pricing
Before we turn to pricing Bermudan swaptions more formally, it is useful first to consider some stylized facts related to the economic risk profile of the instrument. As is evident from the preceding discussion, each Bermudan swaption spans a basket of European co-terminal options, all struck at the same rate K, of which only one can be exercised. This basket nature of Bermudan swaptions has two implications.
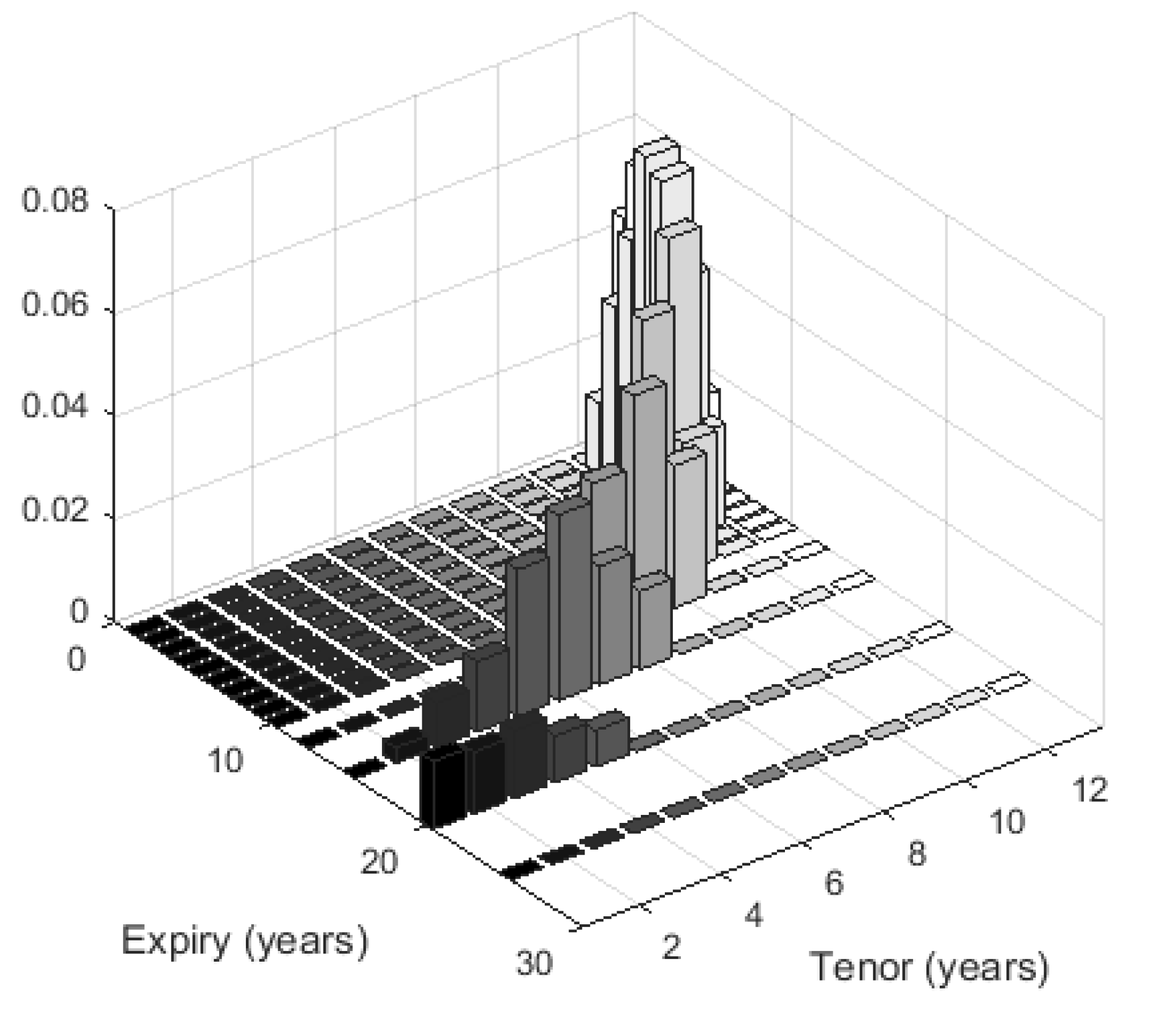
First, compared to European counterparts, Bermudans typically have much higher sensitivity to changes in implied volatility, i.e., Vega, and their volatility risk profile is also more distributed along the whole term/tenor structure, rather than concentrated at a single point. On the one hand this underscores the attractiveness of Bermudan swaptions as a hedging instrument for investors in callable products, but on the other it suggests that hedging or replicating the risk profile of a Bermudan requires multiple European swaptions to match the former’s Vega buckets. For example, the 11nc1 Bermudan receiver swaption priced using current data and a calibrated HW1F model has 1 bp Vega (defined as the change in market value for a 1 bp shift in volatilities of the co-terminal swaptions) of 0.06% of notional, while Vegas of its co-terminal Europeans range from 0.009% (10Y × 1Y) to 0.048% (3Y × 8Y). More importantly, as shown in
Figure 1 for a 20Y Bermudan receiver swaption, the volatility risk profile is distributed along the spectrum of term/tenor buckets.
Second, to preclude straightforward arbitrage, a Bermudan swaption must be at least as valuable as any European swaption spanned by it. Consequently, the price of the most expensive European swaption spanned by a given Bermudan tenor structure must be the lower bound on the price of the Bermudan swaption itself. This valuation difference between a Bermudan and its Most Expensive European (MEE) swaption—called the Bermudan-MEE gap, or B/E basis—is a useful simple handle for the economic value of the Bermudan exercise right, i.e., the privilege of having all other exercise possibilities available. Indeed, Qu [
41] suggests analyzing the MEE basis in historical perspective as an indication of potential pricing anomalies and a handle for the model risk inherent in the chosen Bermudan pricer (see also [
47]).
Figure 2 shows the price of the 10Y Bermudan receiver plotted against the prices of its co-terminal European swaptions, all struck at the same rate,
. Evidently, the Bermudan price is higher than each of the Europeans in the “basket” and the gap is tightest for the 3Y-into-8Y swaption, which is therefore the MEE. Both the size of the MEE gap and the MEE swaption itself are likely to depend on a combination of market factors, most importantly yield curve level and steepness, as well as forward swap rate volatilities and correlations. For example, while the 3 × 8 swaption is the MEE for the 1 × 10 Bermudan at current prices, under a significant fall in market interest rates, a 1 × 10 swaption would become the MEE, and should rates rise a 6 × 5 European would become the MEE. The MEE basis in these scenarios would fluctuate from 30 to 200 bp (
Figure 3).
4.1. Numerical Methods for Pricing Models
Consider now a tenor structure
and a “
no-call
” Bermudan receiver swaption introduced above with time
t value
. Assuming no prior exercise, at any time point
the swaption holder has the right to receive the exercise value
of the swaption, i.e., present value of the underlying swap:
The exercise value has to be compared to the so-called continuation value,
, of holding the option beyond
:
The value of the Bermudan swaption can now be given in terms of (
45) and (
46) via a dynamic programming recursion:
for
. The evaluation of (
47) proceeds backward in time: at
the value of the Bermudan is known and determined by the standard swaption payoff. This allows us to update the continuation value at
by discounting and comparing it to the exercise value prevailing at the time. The procedure of comparing “backwardly-cumulated” continuation value with the immediate exercise value and deciding upon a swaption exercise is repeated until the initial valuation date is reached, at which point the algorithm yields a price estimate for the Bermudan swaption. The calculation of the continuation value is clearly model-dependent and the choice of modeling framework itself often determines the scope of available numerical techniques. Again without pretense of being exhaustive, we shall consider and briefly discuss three main approaches—binomial/trinomial trees, finite difference schemes based on the derivative PDE and Monte Carlo simulation—traditionally applied in the context of the model categories described above. Our focus will not be on the technical details—for which we refer readers to Glasserman [
26], Tavella and Randall [
48] as well as Mitchell and Griffiths [
49]—but rather on the connection between the modeling framework and numerical implementation techniques.
4.1.1. Tree-Based Methods
Perhaps the most classic approach for pricing derivatives with early exercise features, including Bermudan swaptions, is by building a binomial/trinomial tree for the underlying variable using its discretized SDE (forward induction method). Such methods are only feasible for low-dimensional processes (ideally one- or two-dimensional), which is why they have been extensively used in modeling one-factor short rate models, all of which can be approximated with lattices. Specifically, when approximating a one-factor interest rate diffusion on a trinomial tree, it is assumed that at each time
from a discretized domain of time points
(note that the time points in general do not need to be uniformly spaced) there is a finite number of equispaced interest rate states
(
i corresponds to the time point and
j to the space index), and at each node
the short rate can move to
, with probability
with probability
, or
, with probability
, whereby the branching parameters are determined in such a way as to ensure that the conditional mean and variance match as closely as possible their model values. For example, in a simple brute-force implementation of the Hull–White model (
17), the probabilities associated with the node
are:
where
is the drift and we have omitted the dependence of transition probabilities on nodes to ease notation. Clearly, building a tree requires as an input the values for short rate volatility
and mean reversion speed
, while for numerical stability and convergence considerations
(in fact, this procedure can be improved upon as explained, e.g., in Hull and White [
50]).
The Hull–White model is particularly convenient for pricing Bermudans because knowledge of the short rate is tantamount to the knowledge of all bond prices through the closed reconstitution Formula (
20), and thus once an interest rate tree is built along the lines sketched above, we can immediately value all relevant payoffs. Thus, starting from
, i.e., the last time the swaption can be exercised, and using the readily available bond prices, we calculate for all nodes
j in the current column the value
as:
We then propagate these continuation values backward in time through the interval
using the Formula (
46) and the transition probabilities, obtaining “backwardly cumulated” continuation values for each node:
Once the exercise point
is reached we check the exercise opportunity by comparing
with the exercise value:
and update the option value accordingly. Proceeding in this way we finally reach the first exercise date
and subsequently the initial node of the tree with the time 0 swaption price.
While the method sketched in general terms above can be optimized and/or generalized along various dimensions (e.g., varying the discretization step, or including backward propagation of bond prices where no analytical reconstitution formulas are available as in the Black–Karasiński model) it should come as no surprise that the tree can only efficiently handle low-factor short rate rate models. Building a binomial tree for the Hull–White two-factor model is still relatively straightforward; however the added layers of computational complexity seem to defeat the purpose of using a simple (simplistic?) model of the term structure in the first place.
4.1.2. Finite Difference Schemes
The trinomial trees discussed above are in fact a special kind of the so-called explicit finite difference scheme and as such are only conditionally stable. A more efficient method of handling Bermudans in low-factor models, by directly discretizing the partial differential equation for the swaption price, can be deployed as follows. Recall first that if
is the state variable of the model—driving the discount curve and all its derivables—then by no-arbitrage arguments, the swaption price
can be expressed as the risk-neutral expectation of the terminal payoff
. Now, since
is a martingale, its drift must be zero (in the appropriate measure), and hence applying Ito’s lemma and writing down the dynamics
, we find that
must satisfy the following parabolic partial differential equation (PDE):
where
is the infinitesimal operator for the SDE describing the dynamics of the state variable. For example, in the special case of the Hull–White model, the European swaption price solves the following parabolic PDE:
Analogously, in the Cheyette model, i.e., Equations (
38) and (
39), the pricing PDE takes the following form:
Associated with both equations is of course the known terminal swaption payoff condition.
To solve Equation (
51) numerically, we discretize it on some finite rectangular domain
, where the grid boundaries
and
are either determined a priori as some multiples of the variance of
or within the PDE itself. The partial derivatives are then replaced by corresponding finite difference operators, with schemes differing i.a. in the nature of approximation. The central difference approximation of
, known as the Crank–Nicolson scheme, is often the method of choice (second-order convergent in
), whereas the backward approximation—given the explicit scheme—should be avoided for stability and convergence considerations. Specifically, for the Crank–Nicolson scheme,
where I is the identity matrix,
and
stands for the approximation to the true solution
, and
is a tri-diagonal matrix of coefficients derived from approximating PDE terms. For a known
, (
53) is simply a linear system of equations to be solved by standard methods. Thus, starting from the terminal condition
—where the swaption payoff is known—we use Equation (
53) to iterate backwards in time until we get to
. Of course, since we are dealing with Bermudan swaptions, at each time step corresponding to exercise time, we additionally need to compare the rollback value with the exercise value—just as has been done on the trinomial tree.
Multi-dimensional PDEs for pricing within the two-factor Hull–White or Cheyette models can still be handled efficiently using the so-called alternating direction implicit method (ADI), introduced by Craig and Sneyd [
51]. However, it should be borne in mind that the computational complexity of such problems grows exponentially in the dimension, making it prohibitively inefficient to use finite difference schemes for pricing Bermudans in truly multi-factor models of the term structure.
4.1.3. Monte Carlo
An obvious conclusion would therefore be to switch to Monte Carlo simulation, where the computational cost grows only linearly in dimension. Unfortunately, by design, Monte Carlo simulation works forward in time and therefore dynamic programming of the kind we used above to value Bermudans is not straightforward to implement. A brute-force approach to computing the conditional expectation underlying the continuation value at
, as per Equation (
46), would consist in nesting a new simulation— within the original one—with an initial condition
, for every
and each simulation path, and then calculating the expectation directly. Thus, if the simulation consistently uses
M paths, then at time 0 we have
M paths, at
we generate additional
paths, and so on until at the penultimate exercise date
we produce another
simulation paths (this time spanning just the final fixing period
). Clearly, even for a modest choice of
M and
N the computational burden of such an embedded scheme becomes prohibitive.
This subtle yet crucial point had arguably been one of the key hindrances holding back the financial industry’s embrace of multi-factor market models. Whether many factors per se are desirable for accurate valuation of Bermudans or not—we shall see below that the question is in general not trivial—if they are not amenable to efficient numerical implementation, then they are of little practical significance. A breakthrough came with Longstaff and Schwartz [
25], who adapted earlier ideas found in Tilley [
52] and Carriere [
53], suggesting that the continuation value (
46) can be interpreted as a regression of the one-step-ahead payout on the state variables. Indeed, recall that
Since the conditional expectation of the swaption payoff is an element of the space of square-integrable functions, it has a countable orthonormal basis and can be represented as a linear function of the elements of the basis. Moreover, in a Markovian model, only current values of the state variables are necessary, so we can write:
for some unknown function
and
d Markov state variables
. Longstaff and Schwartz [
25] suggest estimating
—and hence the continuation value—by a linear combination of a finite set of
J basis functions
where the weights
are determined by least-squares regression on the Monte Carlo paths (typically, to improve quality of fit and run-time performance, only in-the-money paths may be considered, which limits the region on which the conditional expectation is to be estimated). Since the values of the basis functions are independently and identically distributed, it can be shown that the fitted value
converges in mean-square and in probability to
as the number of paths goes to infinity, which justifies the method.
Once the basis functions and their loadings are determined, valuation follows the dynamic programing method applied above in the context of finite difference schemes and lattices. Thus the algorithm to perform least-squares Monte Carlo (LSMC) to value a Bermudan might look as follows (for concreteness we assume the pricing model is LMM):
- 1.
Start by specifying and calibrating a desired form of the LMM (number of factors, correlation etc.) as well as the numeraire for the simulation;
- 2.
Simulate the desired number of paths for the underlying LIBOR rates;
- 3.
Calculate the numeraire, the value of the underlying swap, the values of the basis functions and the exercise values along each path and on all relevant exercise dates;
- 4.
Set and ;
- 5.
Going backward in time, i.e., for
, calculate the weights on the basis functions
along all paths
through standard error minimization:
and use the resulting estimates to update the swaption values
;
- 6.
Return .
Several remarks are in order at this point. First, as should be clear from the discussion above, the robustness of our valuation scheme is critically affected by the choice of the explanatory variables in the regression, i.e., the form and number of the basis functions. In their formulation, Longstaff and Schwartz [
25] recommend using a polynomial basis, i.e., monomials of the state variables. While sound in principle, this approach might be impractical in the context of LMM due to the possibly high dimension of the vector of state variables (core LIBOR rates). Note also that with too many regressors, the quality of the parameter estimates is likely to deteriorate, given a fixed number of Monte Carlo paths. For example, Glasserman and Yu [
54] show that the number of regression variables for which accurate estimation is possible from
M paths is
. Thus with, say, 50,000 paths we should not use more than four variables. A popular choice is to choose i.a. the front LIBOR rate (fixing on the exercise date), and several swap rates capturing the overall level and shape of the yield curve.
Second, unlike in lattices or finite difference schemes, in LSMC, exercise decisions will be sub-optimal by design as they rest on estimates of continuations values. At the same time, to the extent that the same set of paths is used to determine both the parameters
and continuation values, the price estimate might be biased upwards. To reduce bias and make sure that the regression generates a lower bound on the option price, we could use two independent Monte Carlo simulations: the first pilot run to fit the coefficients and then a second run to estimate continuation values for a newly seeded set of paths based on the previously determined decision rule. To gauge the quantitative effect of sub-optimal exercise decisions we conducted a simple experiment in which we priced the same 20-non-call-10 Bermudan swaption with a one-factor Hull–White model using a standard Crank–Nicolson finite-difference grid and LSMC. The model was calibrated to ATM European swaptions with final 20Y maturity, and the mean reversion rate was in each case set at 0.03. The results are shown in
Figure 4 and clearly demonstrate the downward bias of the Monte Carlo with spreads relative to the exact finite-difference scheme in the order of 40–50 bps.
4.2. Factor Dependence of Bermudan Swaptions
Having presented the main categories of models and implementation techniques that can be used to price Bermudan swaptions we now turn to the issue of their factor dependence. In particular, using a set of numerical experiments we revisit the debate between Longstaff, Santa-Clara, and Schwartz [
9] and Andersen and Andreasen [
23], and the threats posed by the modeling equivalents of Scylla and Charybdis mentioned in the introduction.
Consider once again a “
no-call
” Bermudan receiver swaption, which, as we know, can be exercised into one of the so-called core swap rates:
at either one of the designated exercise times
, at the same strike rate
K. In an important paper Longstaff, Santa-Clara, and Schwartz [
9] made a point that this “chooser-option” character of a Bermudan makes is critically sensitive to the correlation among the core rates. Drastically simplifying their argument, we can imagine that when the individual
are perfectly correlated, so too should be the respective exercise values. Hence, there is likely to be little value added provided by the option to postpone the exercise. By contrast, the argument goes, when correlation between
is low or even negative, a Bermudan’s right to choose the exercise date will have more value. Indeed, if the exercise value of the first swaption happens to be positive, it is worth exercising sooner, as payoffs further down the line are likely to turn negative. A straightforward conclusion follows that since single-factor models by design imply perfect correlation between core swap rates, they should artificially under-price Bermudan swaptions, making traders “throw away billions of dollars.” From a theoretical point of view, the result—coupled with advances in numerical techniques under the guise of LSMC— provided a powerful argument in favor of switching from short-rate to multi-factor market models.
And yet, Andersen and Andreasen [
23] pointed out a subtle flaw in the above reasoning: to the extent that our Bermudan is viewed as a chooser option, one has to bear in mind that the choice we refer to is made at different points in time:
. Consequently, what matters for pricing is not the instantaneous correlation
between the Brownian motions driving the dynamics of the core swap rates, but rather the forward or serial correlation between the rates setting at different dates
and
, which can be very roughly approximated as:
and depend not just on
but also on the volatilities of
- and
-maturity rates. This shows that while single-factor models do indeed imply perfect instantaneous correlation, they can de-correlate core rates setting at different times (through the time-dependent volatilities), with non-trivial consequences for Bermudan swaptions prices.
To appreciate this last point, we conducted our own set of numerical experiments using the modeling tools described above. Specifically, we priced Bermudan swaptions on a 5Y and 10Y swap with quarterly payment frequency and time to first exercise set at 1, 5 and 10 years. The strikes in each case were set to ATM levels based on the USD interest rate curve as of 11 September 2020. We used the Hull–White one-factor model (HW1F) implemented on a finite-difference grid as a benchmark and considered its two-factor extension (HW2F), and four versions of the LIBOR market model assuming 2-, 3-, 4- and full-factor parameterization. In line with standard practice, we used a piece-wise constant volatility function and Rebonato’s two-parameter correlation structure of the form , for the full-factor model. We used 25,000 pre-simulation paths to fit the coefficients and then another 25,000 with antithetic variates (a total of 50,000 paths) to estimate continuation values based on the previously determined decision rule.
The results of our numerical experiments, shown in
Figure 5, are generally in line with those reported in a much more comprehensive study by Andersen and Andreasen [
23] and seem to confirm the de-correlation possibilities of low-factor models. Indeed, prices produced by the HW1F model are consistently higher than those derived from the two-, three- and very high-factor market models. For longer-maturity products this pattern can be quite pronounced with the relative error for the 20-nc-10 swaption reaching almost 15%. Whereas a part of this pattern may be due to different numerical procedures employed (grid solution for HW1F and LSMC for other models), our earlier tests, reported in
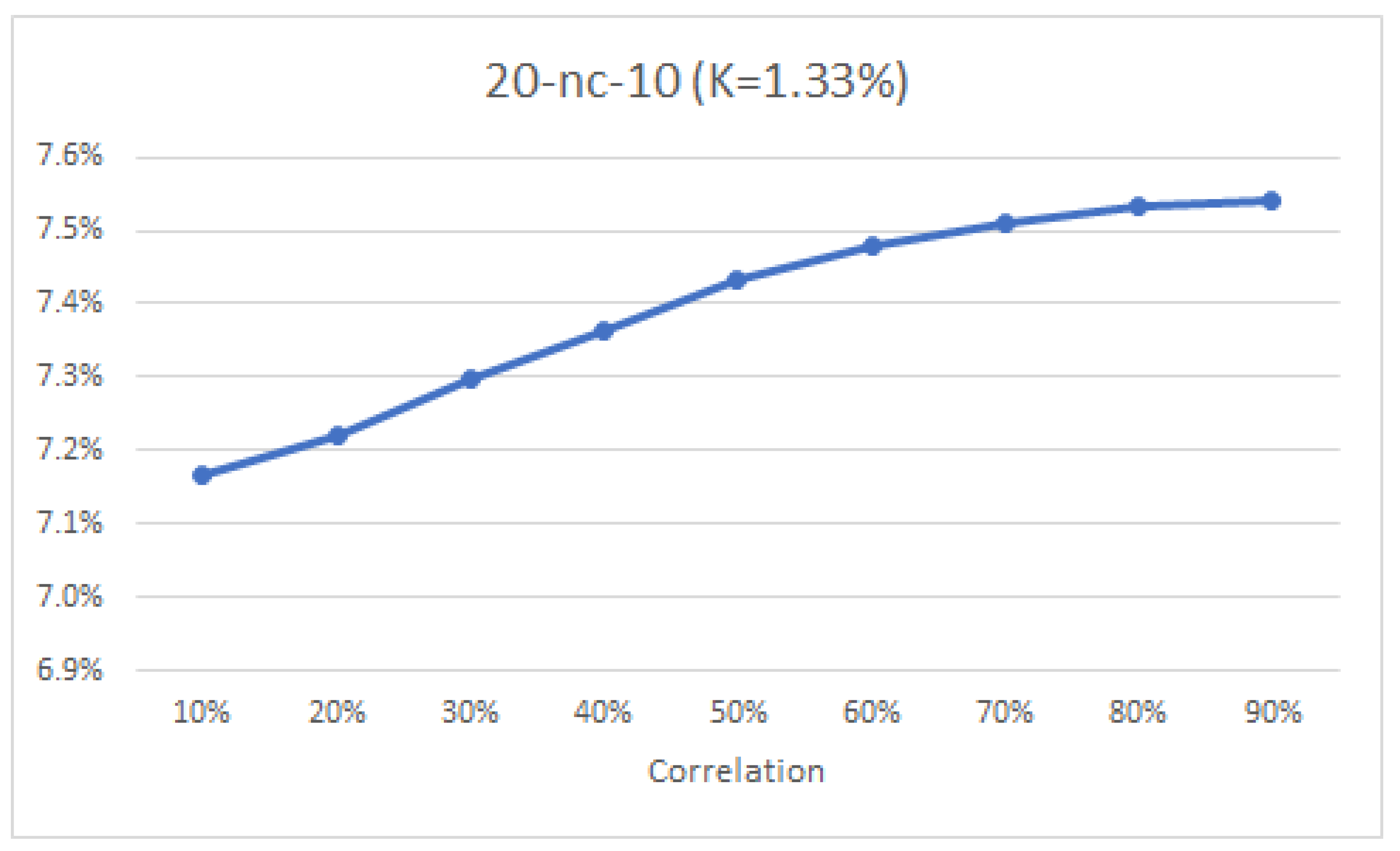
Figure 4, show that this cannot be the entire explanation. Indeed, to assess the dependence of swaption prices on rate correlation, we used our calibrated full-factor LMM to reprice the same 10 × 10 Bermudan receiver (struck at 1.33%) varying base correlation
from 0.1% to 0.9% (
Figure 6). Again, the results show that increasing correlation increases, not decreases, Bermudan swaption prices.
To provide some intuition for these results, we recall that a forward swap rate is a complex average of underlying forward rates, so we can write:
where the weights are given by:
If we now freeze the weights at their time-zero values—as originally proposed by Jackel and Rebonato [
55], Rebonato [
56] and justified by the fact that the variability of
s is significantly smaller than the variability of the LIBOR rates—we can differentiate (
61) to obtain:
Calculating the quadratic variation and approximating it further by freezing all rates at their time-zero values, we obtain the following approximate expression for integrated percentage variance, or (squared) swap rate volatility:
which must be plugged into the Black Formula (
12) to recover the market price of a European swaption on the swap fixing in
and maturing in
. Now, if the volatilities of the forward rates spanning the swap are held fixed (e.g., through thorough calibration), then decreasing
by moving to a lower-factor model or by adjusting the base correlation parameter
will necessarily also reduce the swap rate volatility—and hence ultimately the price of the Bermudan.
Although other subtle effects can also play a role, justifying more extensive tests than allowed by the scope of this essay (see, e.g., [
57,
58] and as usual [
7] for a general reference), we can nevertheless safely conclude at this point that factor dependency does seem to be an issue in pricing Bermudan swaptions. This empirical conclusion validates our perspective on the evolution of Bermudan swaption pricing as driven by a difficult choice between a more cumbersome and difficult to sensibly calibrate low-factor model that can be more efficiently implemented (Charybdis) and a multi-factor model that allows much more calibration freedom, but raises problems on the numerical implementation front and produces sub-optimal exercise decisions.