The Variational Iteration Transform Method for Solving the Time-Fractional Fornberg–Whitham Equation and Comparison with Decomposition Transform Method
Abstract
:1. Introduction
2. Preliminaries Concepts
3. The Conceptualization of VITM
4. The Conceptualization of SDM
5. Implementation of Techniques
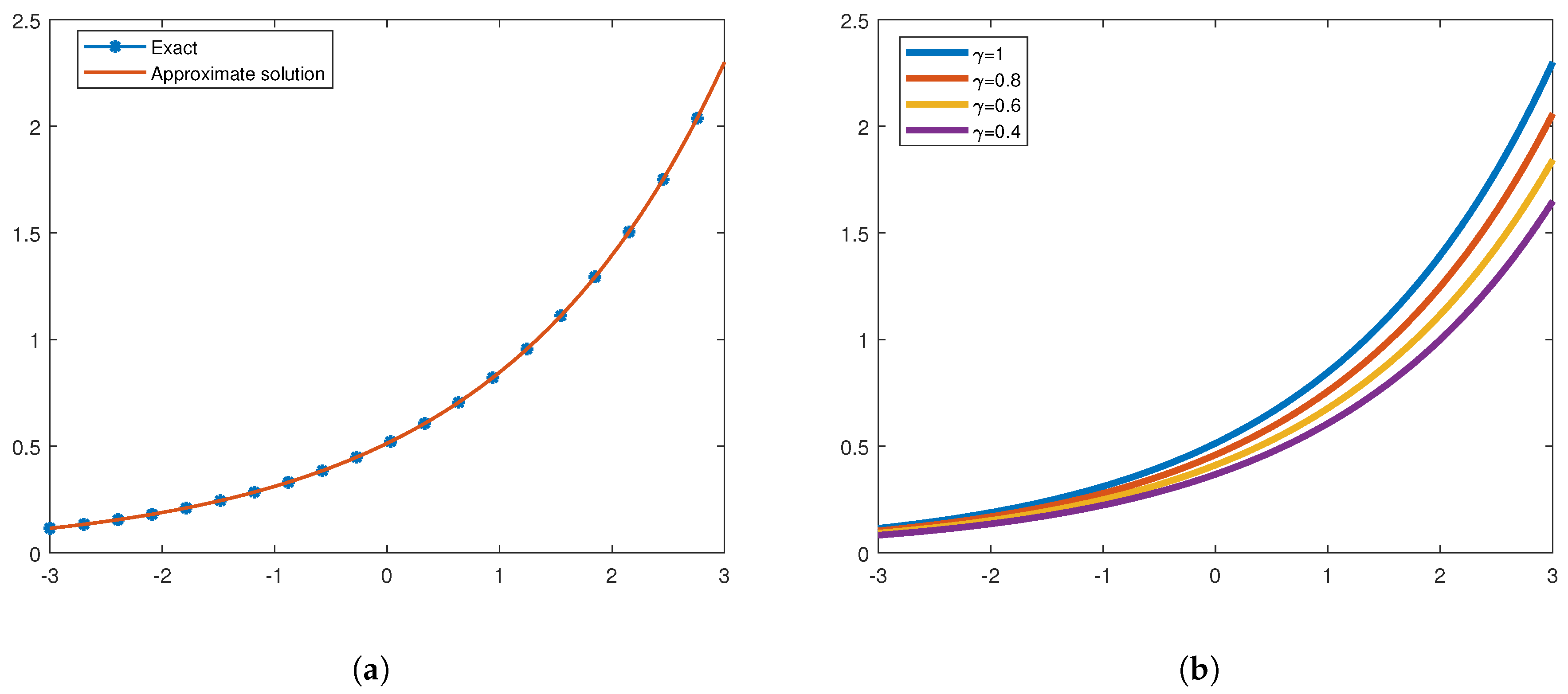
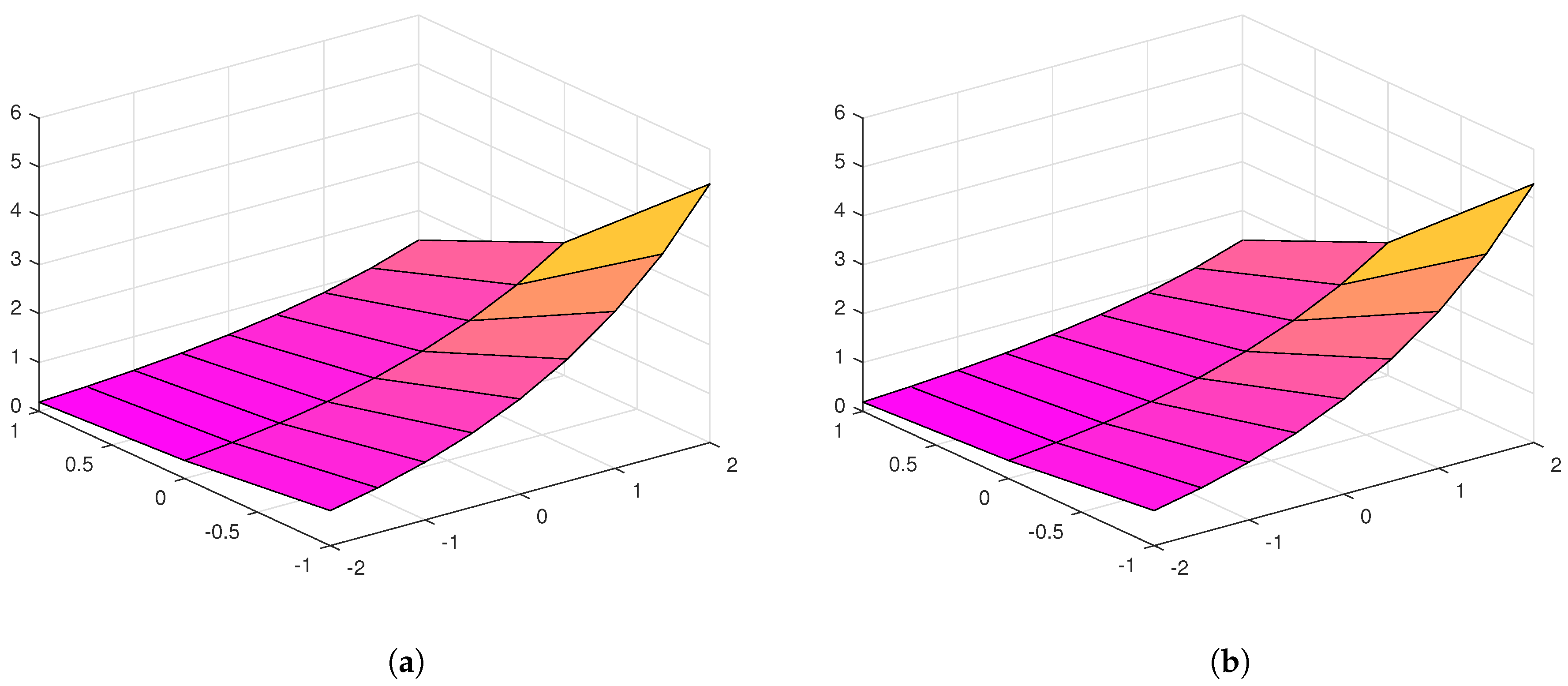
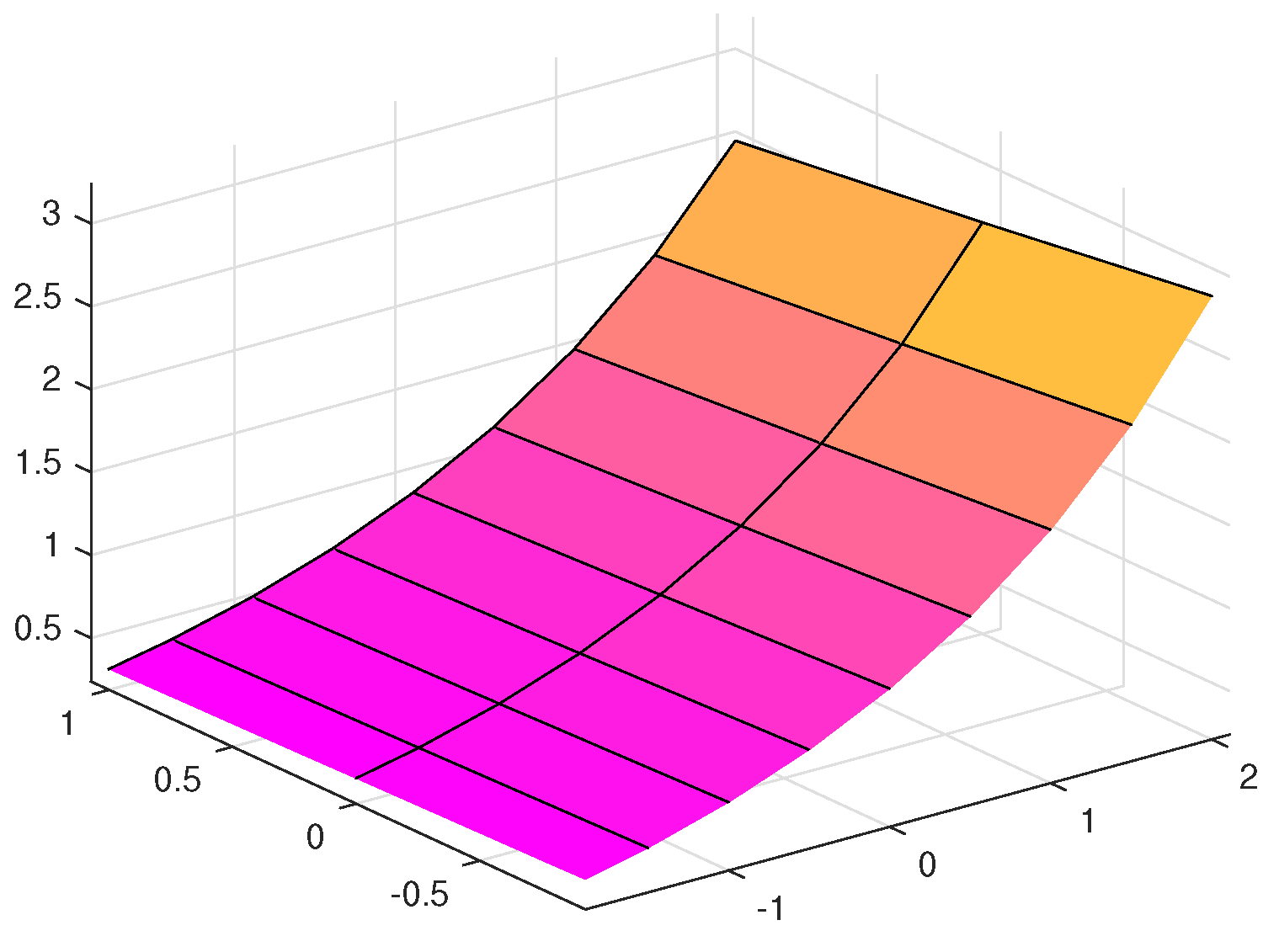
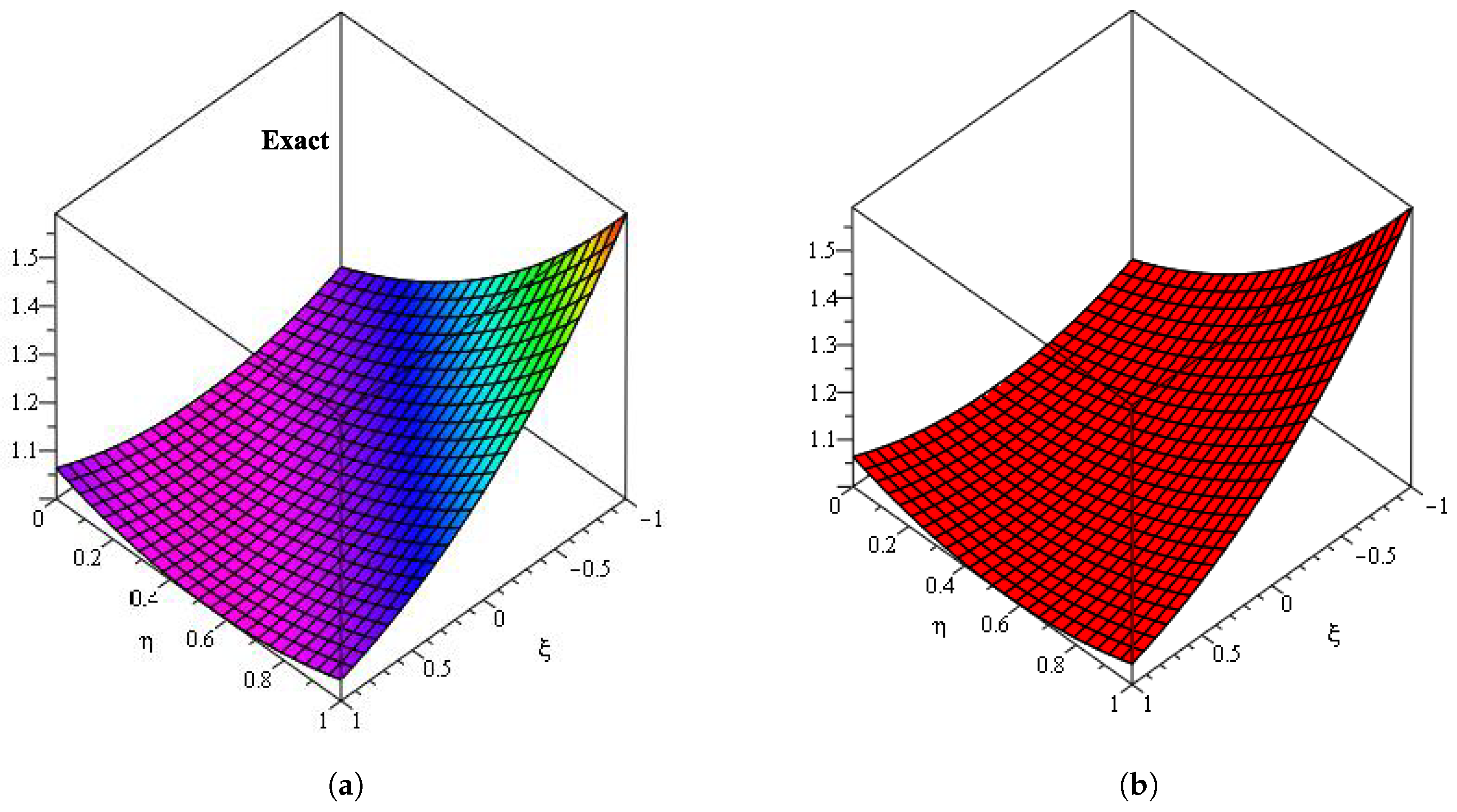
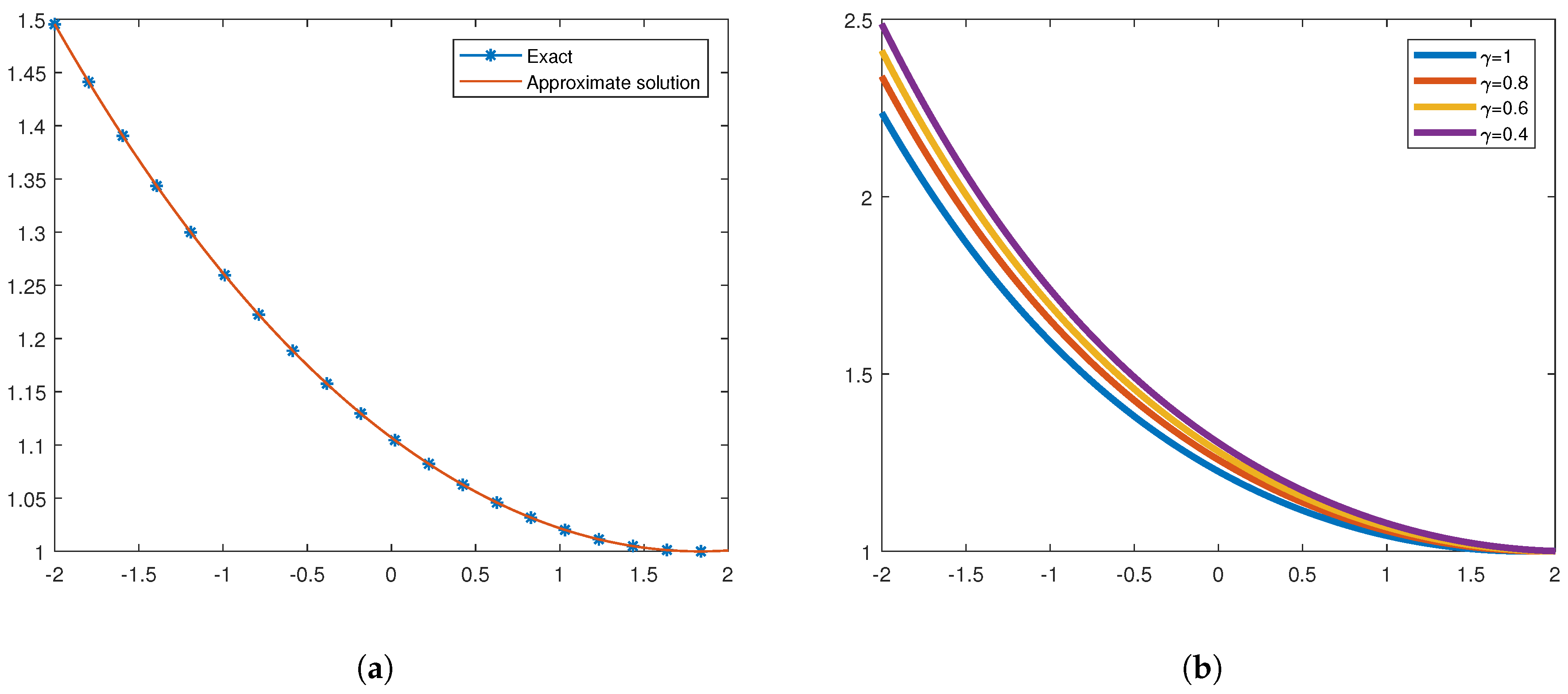
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000; Volume 35, pp. 87–130. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House: Redding, CA, USA, 2006; Volume 2. [Google Scholar]
- Sabatier, J.A.T.M.J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007; Volume 4. [Google Scholar]
- Al-luhaibi, M.S. An analytical treatment to fractional Fornberg–Whitham equation. Math. Sci. 2017, 11, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Camacho, J.C.; Rosa, M.; Gandarias, M.L.; Bruzon, M.S. Classical symmetries, travelling wave solutions and conservation laws of a generalized Fornberg–Whitham equation. J. Comput. Appl. Math. 2017, 318, 149–155. [Google Scholar] [CrossRef]
- Bruzon, M.S.; Marquez, A.P.; Garrido, T.M.; Recio, E.; de la Rosa, R. Conservation laws for a generalized seventh order KdV equation. J. Comput. Appl. Math. 2019, 354, 682–688. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Proceedings of the Royal Society of London. Series A. Math. Phys. Sci. 1967, 299, 6–25. [Google Scholar]
- Fornberg, B.; Whitham, G.B. A numerical and theoretical study of certain nonlinear wave phenomena. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1978, 289, 373–404. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. A new analysis of the Fornberg–Whitham equation pertaining to a fractional derivative with Mittag-Leffler-type kernel. Eur. Phys. J. Plus 2018, 133, 1–10. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Haji-Badali, A.; Vafadar, P. Group invariant solutions and conservation laws of the Fornberg–Whitham equation. Z. Naturforschung A 2014, 69, 489–496. [Google Scholar] [CrossRef]
- Lu, J. An analytical approach to the Fornberg–Whitham type equations by using the variational iteration method. Comput. Math. Appl. 2011, 61, 2010–2013. [Google Scholar] [CrossRef] [Green Version]
- Merdan, M.; Gokdogan, A.; Yildirim, A.; Mohyud-Din, S.T. Numerical simulation of fractional Fornberg–Whitham equation by differential transformation method. Abstr. Appl. Anal. 2012, 2012, 965367. [Google Scholar] [CrossRef]
- Ramadan, M. New Iterative Method for Solving the Fornberg-Whitham Equation and Comparison with Homotopy Perturbation Transform Method. Br. J. Math. Comput. Sci. 2014, 4, 1213–1227. [Google Scholar] [CrossRef]
- Abidi, F.; Omrani, K. Numerical solutions for the nonlinear Fornberg–Whitham equation by He’s methods. Int. J. Mod. Phys. B 2011, 25, 4721–4732. [Google Scholar] [CrossRef]
- Wang, K.; Liu, S. Application of new iterative transform method and modified fractional homotopy analysis transform method for fractional Fornberg–Whitham equation. J. Nonlinear Sci. Appl. 2016, 9, 2419–2433. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. Approximate solution of nonlinear differential equations with convolution product nonlinearities. Comput. Methods Appl. Mech. Eng. 1998, 167, 69–73. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Variational iteration method for fractional calculus-a universal approach by Laplace transform. Adv. Differ. Equ. 2013, 2013, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Anjum, N.; He, J.H. Laplace transform: Making the variational iteration method easier. Appl. Math. Lett. 2019, 92, 134–138. [Google Scholar] [CrossRef]
- Dehghan, M. Finite difference procedures for solving a problem arising in modeling and design of certain optoelectronic devices. Math. Comput. Simul. 2006, 71, 16–30. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Boston, MA, USA, 1994. [Google Scholar]
- Khalouta, A.; Kadem, A. A New Method to Solve Fractional Differential Equations: Inverse Fractional Shehu Transform Method. Appl. Appl. Math. 2019, 14, 926–941. [Google Scholar]
- Bokhari, A.; Baleanu, D.; Belgacem, R. Application of Shehu transform to Atangana-Baleanu derivatives. J. Math. Comput. Sci. 2019, 20, 101–107. [Google Scholar] [CrossRef] [Green Version]
- Belgacem, R.; Baleanu, D.; Bokhari, A. Shehu Transform and Applications to Caputo-Fractional Differential Equations. Int. J. Anal. Appl. 2019, 17, 917–927. [Google Scholar]
- Machado, J.; Baleanu, D.; Chen, W.; Sabatier, J. New trends in fractional dynamics. J. Vib. Control. SAGE Publ. 2014, 20, 963. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Guvenc, Z.; Machado, J. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Maitama, S.; Zhao, W. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. arXiv 2019, arXiv:1904.11370. [Google Scholar]

| η | ξ | ||||
|---|---|---|---|---|---|
| 0.5 | 2.0515098570 × 10−4 | 4.0570000000 × 10−8 | 3.4157500000 × 10−6 | 4.0570000000 × 10−8 | |
| 1 | 8.4542014000 × 10−4 | 5.3500000000 × 10−9 | 1.4746800000 × 10−7 | 5.3500000000 × 10−9 | |
| 1.5 | 6.8110913000 × 10−5 | 7.5600000000 × 10−10 | 2.3936000000 × 10−7 | 7.5600000000 × 10−10 | |
| 2 | 7.4324428000 × 10−4 | 5.7400000000 × 10−9 | 1.3258200000 × 10−6 | 5.7400000000 × 10−9 | |
| 2.5 | 5.3344053000 × 10−4 | 8.5560000000 × 10−9 | 1.3236200000 × 10−6 | 8.5560000000 × 10−9 | |
| 0.1 | 3 | 7.4491757000 × 10−3 | 6.3450000000 × 10−8 | 3.6455200000 × 10−6 | 6.3450000000 × 10−8 |
| 3.5 | 2.0565077000 × 10−4 | 6.4160000000 × 10−8 | 5.2393400000 × 10−6 | 6.4160000000 × 10−8 | |
| 4 | 4.4514678000 × 10−4 | 5.6400000000 × 10−9 | 4.5667200000 × 10−6 | 5.6400000000 × 10−9 | |
| 4.5 | 6.0056729000 × 10−4 | 4.4300000000 × 10−9 | 3.5344000000 × 10−7 | 4.4300000000 × 10−9 | |
| 5 | 7.4339041000 × 10−4 | 3.3700000000 × 10−9 | 2.3356500000 × 10−7 | 3.3700000000 × 10−9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, N.A.; Dassios, I.; El-Zahar, E.R.; Chung, J.D.; Taherifar, S. The Variational Iteration Transform Method for Solving the Time-Fractional Fornberg–Whitham Equation and Comparison with Decomposition Transform Method. Mathematics 2021, 9, 141. https://doi.org/10.3390/math9020141
Shah NA, Dassios I, El-Zahar ER, Chung JD, Taherifar S. The Variational Iteration Transform Method for Solving the Time-Fractional Fornberg–Whitham Equation and Comparison with Decomposition Transform Method. Mathematics. 2021; 9(2):141. https://doi.org/10.3390/math9020141
Chicago/Turabian StyleShah, Nehad Ali, Ioannis Dassios, Essam R. El-Zahar, Jae Dong Chung, and Somaye Taherifar. 2021. "The Variational Iteration Transform Method for Solving the Time-Fractional Fornberg–Whitham Equation and Comparison with Decomposition Transform Method" Mathematics 9, no. 2: 141. https://doi.org/10.3390/math9020141
APA StyleShah, N. A., Dassios, I., El-Zahar, E. R., Chung, J. D., & Taherifar, S. (2021). The Variational Iteration Transform Method for Solving the Time-Fractional Fornberg–Whitham Equation and Comparison with Decomposition Transform Method. Mathematics, 9(2), 141. https://doi.org/10.3390/math9020141






