An Information-Theoretic Approach for Multivariate Skew-t Distributions and Applications †
Abstract
:1. Introduction
2. Multivariate Skew- Distribution
2.1. Entropies
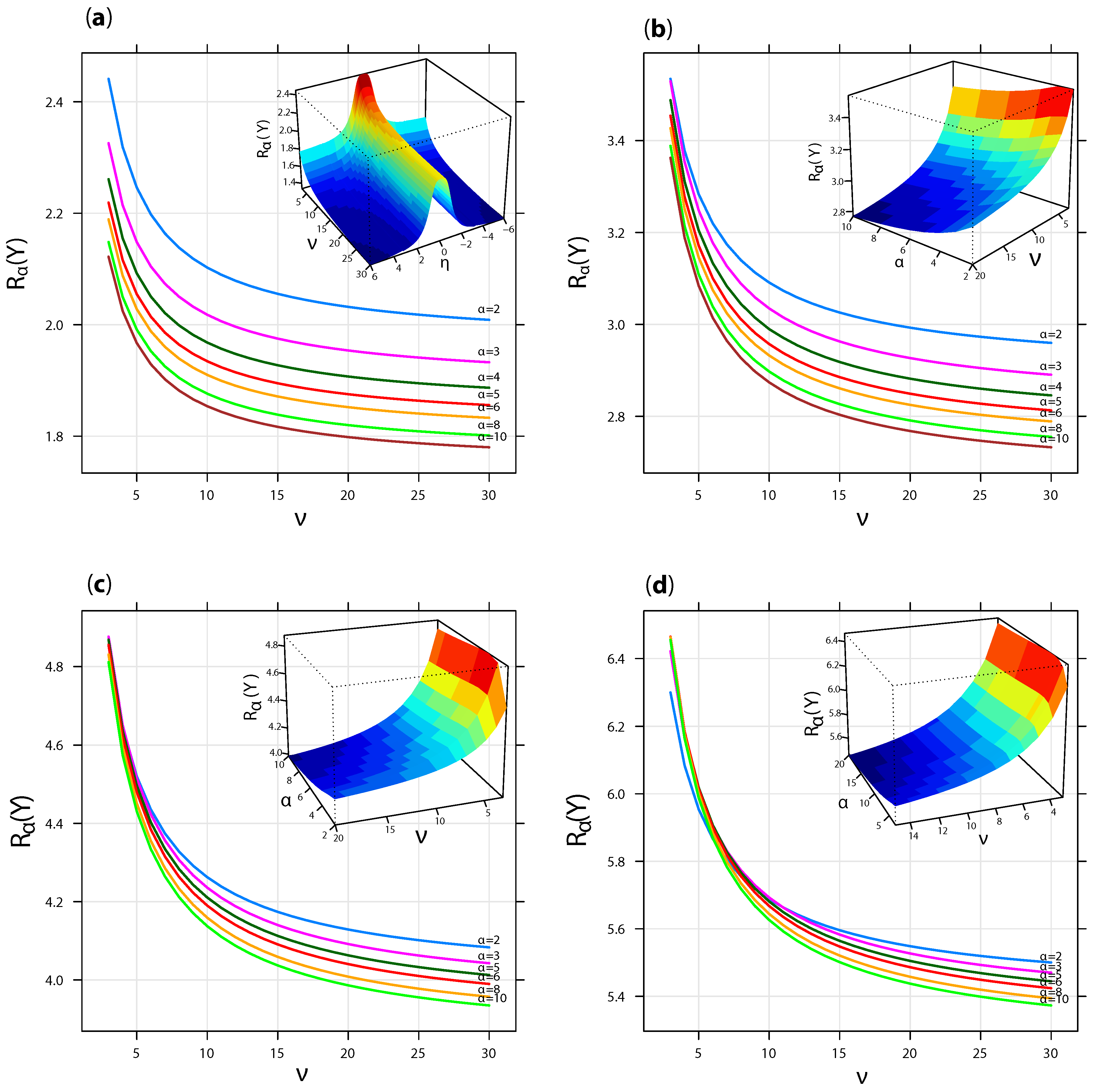
2.2. Computational Implementation and Numerical Simulations
- (a)
- , , , and .
- (b)
- , , , and .
- (c)
- , , , and .
- (d)
- , , , and .
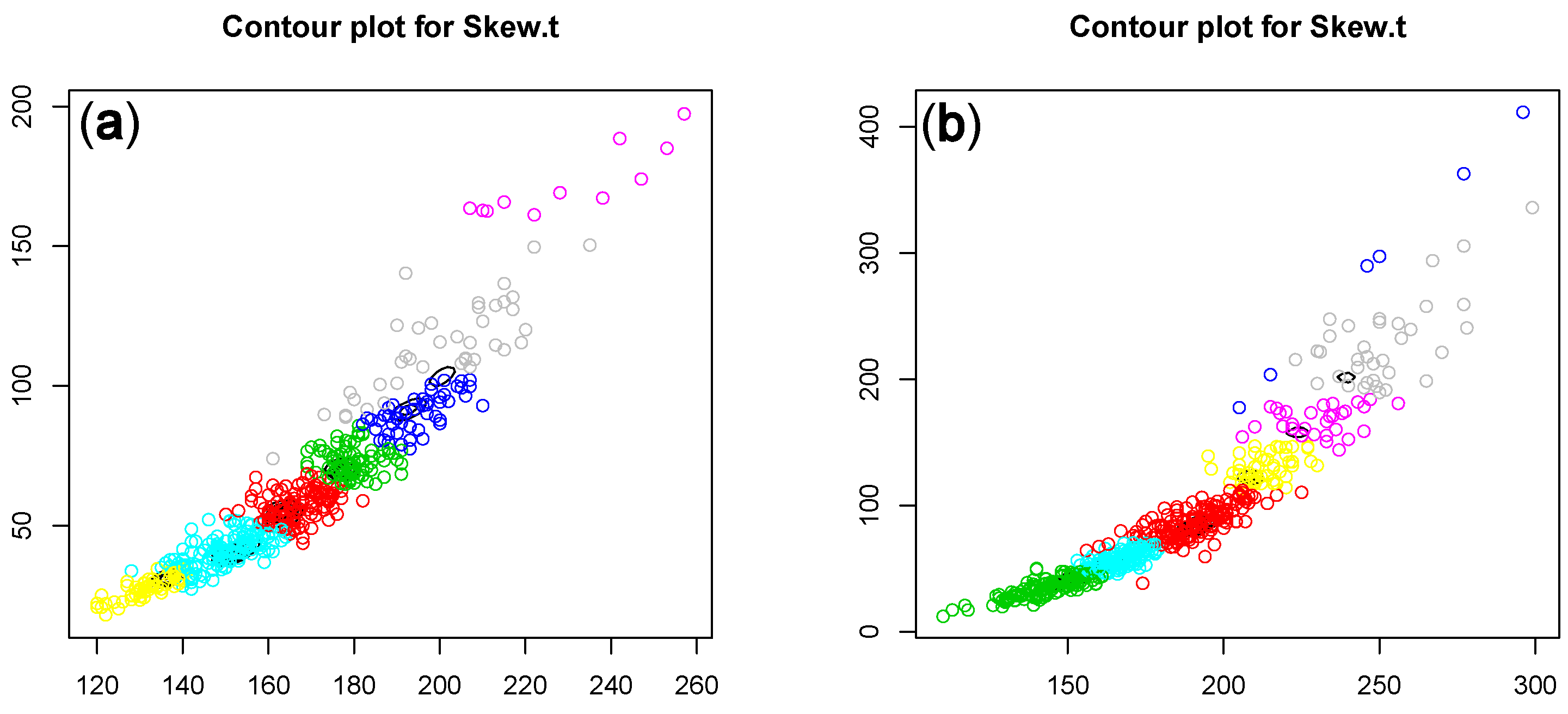
3. Application to Finite Mixtures of Multivariate Skew- Distributions
Swordfish Data Analysis
4. Conclusions and Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McLachlan, G.; Peel, D. Finite Mixture Models; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Carreira-Perpiñán, M.A. Mode-Finding for Mixtures of Gaussian Distributions. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1318–1323. [Google Scholar] [CrossRef] [Green Version]
- Celeux, G.; Soromenho, G. An entropy criterion for assessing the number of clusters in a mixture model. J. Classif. 1996, 13, 195–212. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.X.; McLachlan, G.J. Finite mixtures of multivariate skew t-distributions: Some recent and new results. Stat. Comput. 2014, 24, 181–202. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, S.; Pyne, S. Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 2010, 11, 317–336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Contreras-Reyes, J.E.; Cortés, D.D. Bounds on Rényi and Shannon entropies for finite mixtures of multivariate skew-normal distributions: Application to swordfish (Xiphias gladius linnaeus). Entropy 2016, 18, 382. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Quintero, F.O.L.; Yáñez, A. Towards age determination of Southern King crab (Lithodes Santolla) off Southern Chile using flexible mixture modeling. J. Mar. Sci. Eng. 2018, 6, 157. [Google Scholar] [CrossRef] [Green Version]
- Huber, M.F.; Bailey, T.; Durrant-Whyte, H.; Hanebeck, U.D. On entropy approximation for Gaussian mixture random vectors. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Korea, 20–22 August 2008; pp. 181–188. [Google Scholar]
- Azzalini, A.; Dalla-Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. Roy. Stat. Soc. B 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Lin, T.I.; Lee, J.C.; Hsieh, W.J. Robust mixture modeling using the skew t distribution. Stat. Comput. 2007, 17, 81–92. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Contreras-Reyes, J.E.; Genton, M.G. Shannon entropy and mutual information for multivariate skew-elliptical distributions. Scand. J. Stat. 2013, 40, 42–62. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Asymptotic form of the Kullback–Leibler divergence for multivariate asymmetric heavy-tailed distributions. Phys. A 2014, 395, 200–208. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Rényi entropy and complexity measure for skew-gaussian distributions and related families. Phys. A 2015, 433, 84–91. [Google Scholar] [CrossRef] [Green Version]
- Abid, S.H.; Quaez, U.J. Rényi Entropy for Mixture Model of Ultivariate Skew Normal-Cauchy distributions. J. Theor. Appl. Inf. Technol. 2019, 97, 3526–3539. [Google Scholar]
- Abid, S.H.; Quaez, U.J. Rényi Entropy for Mixture Model of Multivariate Skew Laplace distributions. J. Phys. Conf. Ser. 2020, 1591, 012037. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Coêlho, H.; Nascimento, A.D. A family of divergence-based classifiers for Polarimetric Synthetic Aperture Radar (PolSAR) imagery vector and matrix features. Int. J. Remote Sens. 2021, 42, 1201–1229. [Google Scholar] [CrossRef]
- Lin, P.E. Some Characterization of the Multivariate t Distribution. J. Multivar. Anal. 1972, 2, 339–344. [Google Scholar] [CrossRef] [Green Version]
- Branco, M.; Dey, D. A general class of multivariate skew-elliptical distribution. J. Multivar. Anal. 2001, 79, 93–113. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Sys. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley & Son, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Guerrero-Cusumano, J.L. A measure of total variability for the multivariate t distribution with applications to finance. Inf. Sci. 1996, 92, 47–63. [Google Scholar]
- Dehesa, J.S.; Gálvez, F.J.; Porras, I. Bounds to density-dependent quantities of D-dimensional many-particle systems in position and momentum spaces: Applications to atomic systems. Phys. Rev. A 1989, 40, 35. [Google Scholar] [CrossRef]
- Azzalini, A.; Regoli, G. Some Properties of Skew-symmetric Distributions. Ann. Inst. Stat. Math. 2012, 64, 857–879. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Piessens, R.; de Doncker-Kapenga, E.; Uberhuber, C.; Kahaner, D. Quadpack: A Subroutine Package for Automatic Integration; Springer: Berlin, Germany, 1983. [Google Scholar]
- Cabral, C.R.B.; Lachos, V.H.; Prates, M.O. Multivariate mixture modeling using skew-normal independent distributions. Comput. Stat. Data Anal. 2012, 56, 126–142. [Google Scholar] [CrossRef]
- Bennett, G. Lower bounds for matrices. Linear Algebra Appl. 1986, 82, 81–98. [Google Scholar] [CrossRef] [Green Version]
- Arellano-Valle, R.B.; Contreras-Reyes, J.E.; Stehlík, M. Generalized skew-normal negentropy and its application to fish condition factor time series. Entropy 2017, 19, 528. [Google Scholar] [CrossRef] [Green Version]
- Prates, M.O.; Lachos, V.H.; Cabral, C. mixsmsn: Fitting finite mixture of scale mixture of skew-normal distributions. J. Stat. Soft. 2013, 54, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Contreras-Reyes, J.E.; Maleki, M.; Cortés, D.D. Skew-Reflected-Gompertz information quantifiers with application to sea surface temperature records. Mathematics 2019, 7, 403. [Google Scholar] [CrossRef] [Green Version]
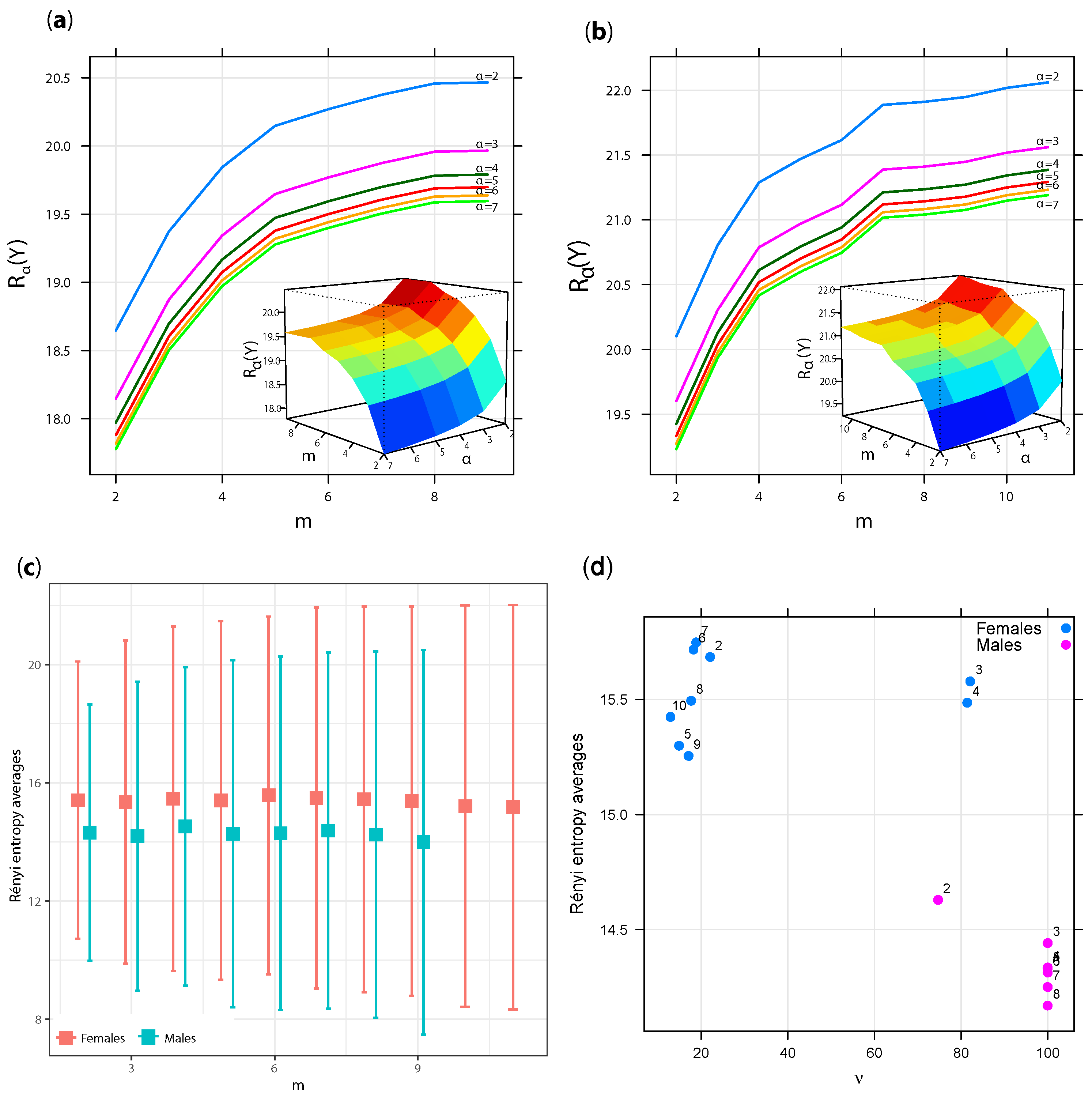
| Gender | m | Upper | Lower | Average | AIC | BIC | |
|---|---|---|---|---|---|---|---|
| Males | 2 | 26.43 | 18.65 | 9.98 | 14.31 | 7747.17 | 7809.96 |
| 3 | 100 | 19.39 | 9.05 | 14.22 | 7747.83 | 7844.11 | |
| 4 | 100 | 19.81 | 9.27 | 14.54 | 7747.76 | 7877.53 | |
| 5 | 100 | 20.07 | 8.44 | 14.26 | 7753.50 | 7916.77 | |
| 6 | 100 | 20.32 | 8.87 | 14.60 | 7756.28 | 7953.03 | |
| 7 | 100 | 20.43 | 8.38 | 14.41 | 7770.71 | 8000.95 | |
| 8 | 100 | 20.43 | 8.01 | 14.22 | 7775.86 | 8039.59 | |
| 9 | 100 | 20.52 | 7.82 | 14.17 | 7778.41 | 8075.64 | |
| Females | 2 | 20.09 | 20.10 | 10.72 | 15.41 | 8835.20 | 8898.62 |
| 3 | 70.62 | 20.82 | 9.88 | 15.35 | 8842.99 | 8940.25 | |
| 4 | 85.97 | 21.30 | 9.60 | 15.45 | 8838.54 | 8969.62 | |
| 5 | 16.35 | 21.45 | 9.53 | 15.49 | 8847.64 | 9012.55 | |
| 6 | 17.68 | 21.76 | 9.25 | 15.51 | 8846.07 | 9044.81 | |
| 7 | 15.99 | 21.87 | 9.32 | 15.60 | 8850.85 | 9083.42 | |
| 8 | 17.23 | 21.91 | 8.82 | 15.36 | 8864.95 | 9131.34 | |
| 9 | 16.83 | 21.96 | 8.72 | 15.34 | 8874.23 | 9174.45 | |
| 10 | 20.02 | 22.04 | 8.68 | 15.36 | 8892.39 | 9226.44 | |
| 11 | 11.91 | 22.08 | 8.41 | 15.24 | 8902.36 | 9270.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abid, S.H.; Quaez, U.J.; Contreras-Reyes, J.E. An Information-Theoretic Approach for Multivariate Skew-t Distributions and Applications. Mathematics 2021, 9, 146. https://doi.org/10.3390/math9020146
Abid SH, Quaez UJ, Contreras-Reyes JE. An Information-Theoretic Approach for Multivariate Skew-t Distributions and Applications. Mathematics. 2021; 9(2):146. https://doi.org/10.3390/math9020146
Chicago/Turabian StyleAbid, Salah H., Uday J. Quaez, and Javier E. Contreras-Reyes. 2021. "An Information-Theoretic Approach for Multivariate Skew-t Distributions and Applications" Mathematics 9, no. 2: 146. https://doi.org/10.3390/math9020146
APA StyleAbid, S. H., Quaez, U. J., & Contreras-Reyes, J. E. (2021). An Information-Theoretic Approach for Multivariate Skew-t Distributions and Applications. Mathematics, 9(2), 146. https://doi.org/10.3390/math9020146







