Nonlinear Position Control with Augmented Observer in Brushless DC Motor
Abstract
:1. Introduction
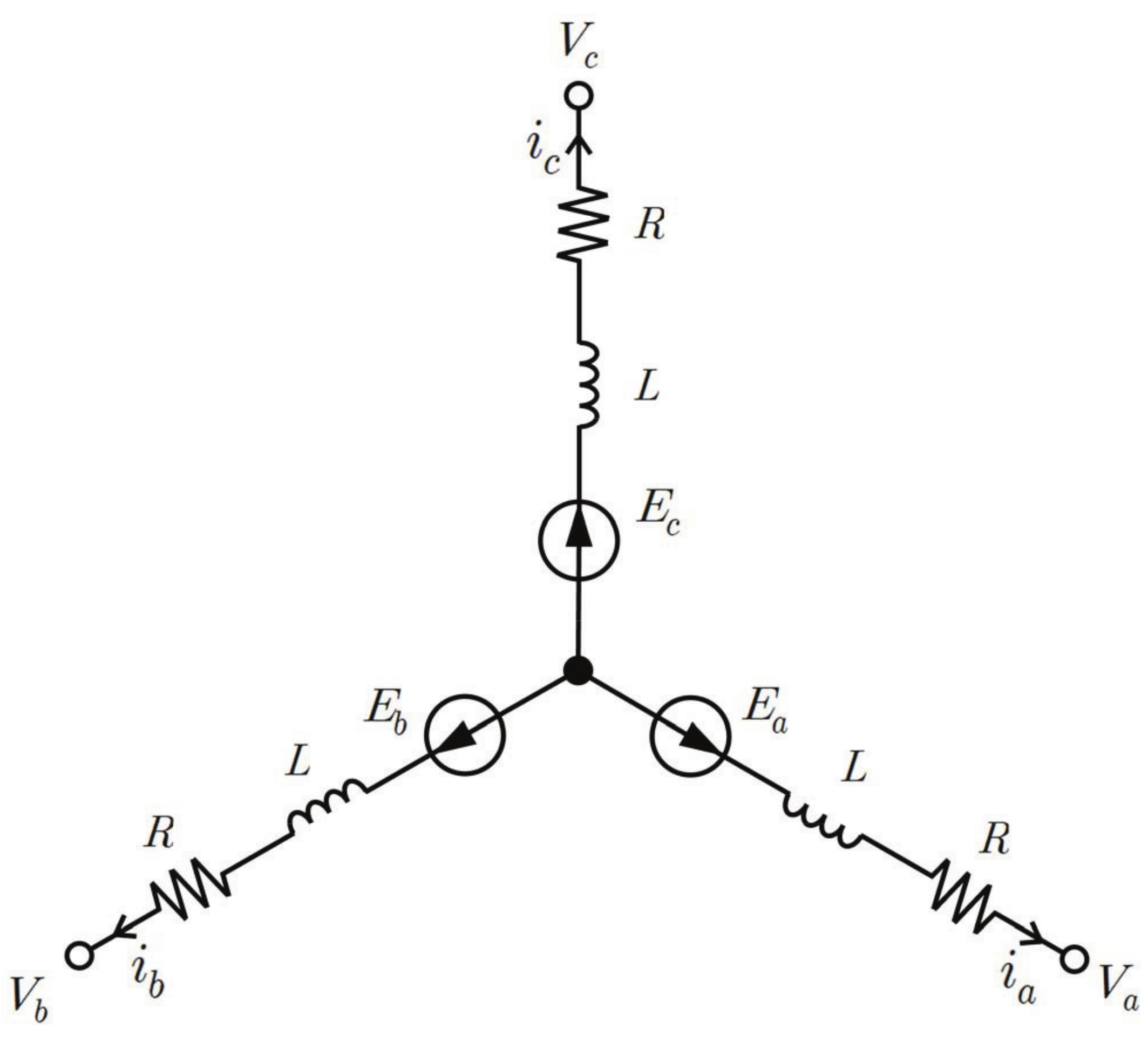
2. BLDCM Mathematical Model
2.1. Mechanical and Electrical Dynamics
2.2. Back-EMF Modeling
2.3. Error Dynamics
3. Controller Design
3.1. Nonlinear Position Controller via Backstepping Approach
3.2. Current Controller
4. Augmented Observer Design and Closed-Loop Stability
4.1. Augmented Observer Design

4.2. Closed-Loop Stability
5. Simulation Results
- Case 1: conventional PI controller.
- Case 2: proposed controller.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maharajan, M.P.; Xavier, S.A.E. Design of speed control and reduction of torque ripple factor in BLdc motor using spider based controller. IEEE Trans. Power Electron. 2019, 34, 7826–7837. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, X.; Liu, G. Instantaneous torque control of small inductance brushless DC motor. IEEE Trans. Power Electron. 2012, 27, 4952–4964. [Google Scholar] [CrossRef]
- Low, T.-S.; Lee, T.-H.; Tseng, K.-J.; Lock, K.-S. Servo performance of a BLDC drive with instantaneous torque control. IEEE Trans. Ind. Appl. 1992, 28, 455–462. [Google Scholar] [CrossRef]
- Bae, J.; Lee, D.-H. Position control of a rail guided mover using a low-cost BLDC motor. IEEE Trans. Ind. Appl. 2018, 54, 2392–2399. [Google Scholar] [CrossRef]
- Dat, N.T.; Kien, C.V.; Anh, H.P.H. Optimal FOC-PID parameters of BLDC motor system control using parallel PM-PSO optimization technique. Int. J. Comput. Intell. Syst. 2021, 1, 1141–1154. [Google Scholar]
- Ozturk, S.B.; Toliyat, H.A. Direct torque and indirect flux control of brushless DC motor. IEEE/ASME Trans. Mechatron. 2011, 16, 351–360. [Google Scholar] [CrossRef]
- Krishnamurthy, P.; Khorrami, F. An analysis of the effects of closed-loop commutation delay on stepper motor control and application to parameter estimation. IEEE Trans. Control Syst. Technol. 2008, 16, 70–77. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, Z.; Wang, X.; Ling, X.; Cao, X. Position sensorless control based on coordinate transformation for brushless DC motor drives. IEEE Trans. Power Electron. 2010, 25, 2365–2371. [Google Scholar] [CrossRef]
- Hernández-Guzmán, V.M.; Orrante-Sakanassi, J. PID control of robot manipulators actuated by BLDC motors. Int. J. Control 2021, 94, 267–276. [Google Scholar] [CrossRef]
- Immaneni, H. Mathematical modelling and position control of brushless Dc (Bldc) motor. Int. J. Eng. Res. Appl. 2013, 3, 1050–1057. [Google Scholar]
- Stirban, A.; Boldea, I.; Andreescu, G.-D. Motion-sensorless control of BLDC-PM motor with offline FEM-information-assisted position and speed observer. IEEE Trans. Ind. Appl. 2012, 48, 1950–1958. [Google Scholar] [CrossRef]
- Ba, D.X.; Yeom, H.; Kim, J.; Bae, J. Gain-adaptive robust backstepping position control of a BLDC motor system. IEEE/ASME Trans. Mechatron. 2018, 23, 2470–2481. [Google Scholar]
- Ko, J.S.; Youn, S.K.; Bose, B.K. A study on adaptive load torque observer for robust precision position control of BLDC motor. In Proceedings of the IECON’99, Conference Proceedings, 25th Annual Conference of the IEEE Industrial Electronics Society (Cat. No. 99CH37029), San Jose, CA, USA, 29 November–3 December 1999; pp. 1091–1096. [Google Scholar]
- Darba, A.; D’haese, P.; De Belie, F.; Melkebeek, J.A. Improving the dynamic stiffness in a self-sensing BLDC machine drive using estimated load torque feedforward. IEEE Trans. Ind. Appl. 2015, 51, 3101–3114. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Chen, W.-H.; Mei, K.; Murray-Smith, D.J. Disturbance observer design for nonlinear systems represented by input output models. IEEE Trans. Ind. Electron. 2020, 67, 1222–1232. [Google Scholar] [CrossRef] [Green Version]
- Delibas, B.; Koc, B. A method to realize low velocity movability and eliminate friction induced noise in piezoelectric ultrasonic motors. IEEE/ASME Trans. Mechatron. 2020, 25, 2677–2687. [Google Scholar] [CrossRef]
- Lin, C.; Yau, H.; Tian, Y. Identification and compensation of nonlinear friction characteristics and precision control for a linear motor stage. IEEE/ASME Trans. Mechatron. 2013, 18, 1385–1396. [Google Scholar] [CrossRef]
- Slotine, J.; Weiping, L.W. Applied Nonlinear Control; Prentice-Hall: London, UK, 1991; pp. 331, 365. [Google Scholar]
- Conte, G.; Moog, C.; Perdon, A. Algebraic Methods for Nonlinear Control Systems; Springer: London, UK, 2007. [Google Scholar]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineers guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]






| BLDCM Plant Parameters and Control Gains | ||
|---|---|---|
| BLDCM Plant parameters | [Nm/rad/s] | |
| [Kg·m2] | ||
| L | 55 [Ω] | |
| R | 0.215 [mH] | |
| 2 [V/rad/s] | ||
| Nonlinear position controller gains | 0.25 | |
| 2 | ||
| Current controller gains | 80 | |
| 80 | ||
| 80 | ||
| Conventional PI controller gains (outer-loop) | 0.5 | |
| 8 | ||
| Conventional PI controller gains (inner-loop) | 1 | |
| Augmented observer gains | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Kim, W. Nonlinear Position Control with Augmented Observer in Brushless DC Motor. Mathematics 2021, 9, 2553. https://doi.org/10.3390/math9202553
Lee Y, Kim W. Nonlinear Position Control with Augmented Observer in Brushless DC Motor. Mathematics. 2021; 9(20):2553. https://doi.org/10.3390/math9202553
Chicago/Turabian StyleLee, Youngwoo, and Wonhee Kim. 2021. "Nonlinear Position Control with Augmented Observer in Brushless DC Motor" Mathematics 9, no. 20: 2553. https://doi.org/10.3390/math9202553







