Development of a Magnetic Fluid Heating FEM Simulation Model with Coupled Steady State Magnetic and Transient Thermal Calculation
Abstract
:1. Introduction
- Development of a magnetic fluid FEM model with consideration of electromagnetic and thermal soft coupling.
- Adjustment of the mathematical model in such a way that it enables a link between the magnetic and thermal calculations in commercial software (Altair Flux3D).
- Analysis of an effective anisotropy’s influence on the calculation results, and suggestions for correct setting of an effective anisotropy.
- The correctness of the model and the correctness of the used parameters are confirmed with measurements.
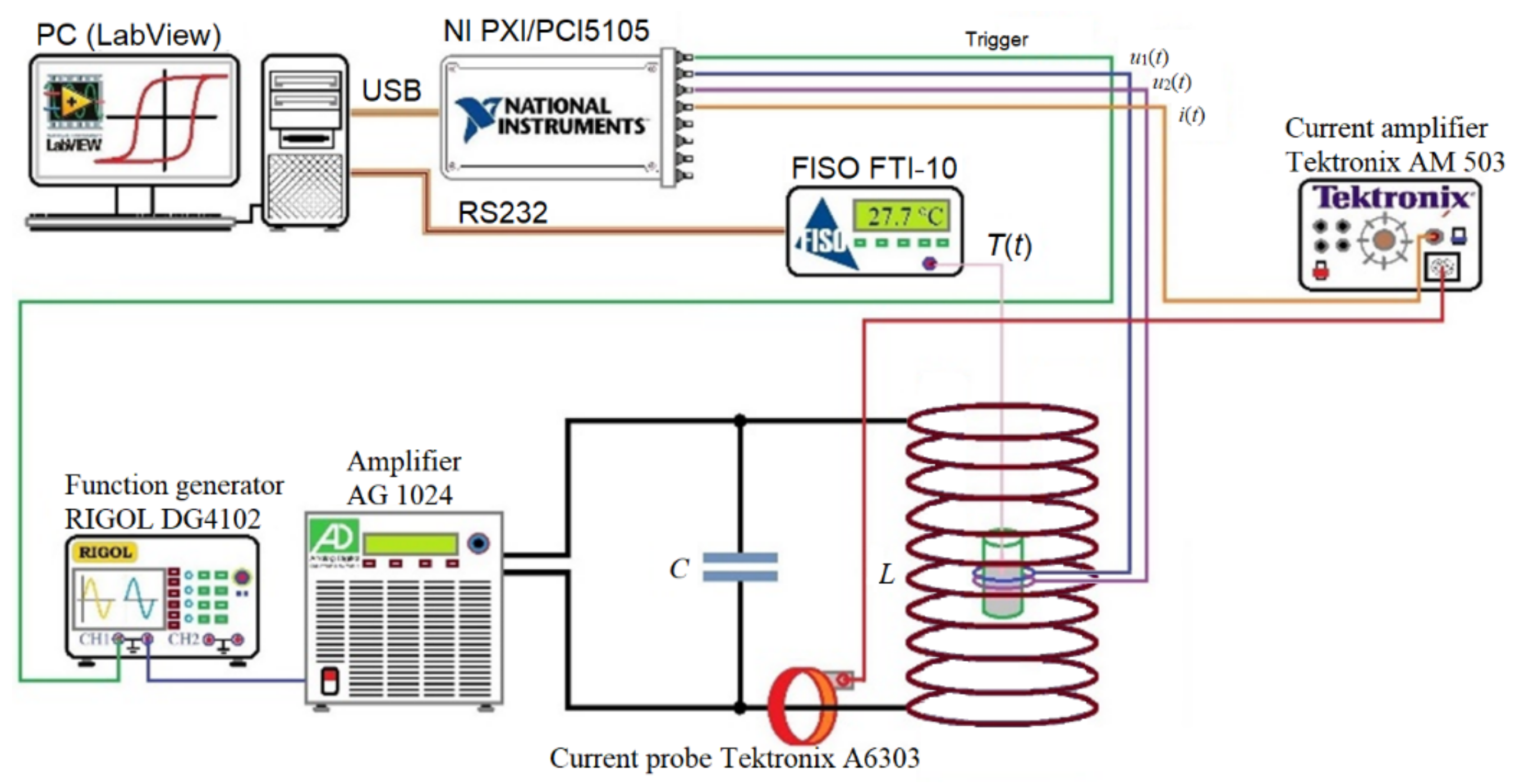
2. Measurement System
3. Mathematical Model
- Volume fraction ϕj,
- Particle diameter dj,
- Particle volume Vpj and hydrodynamic volume Vhj,
- Brown and Néel relaxation times τBj and τNj,
- Langevin parameter αj.
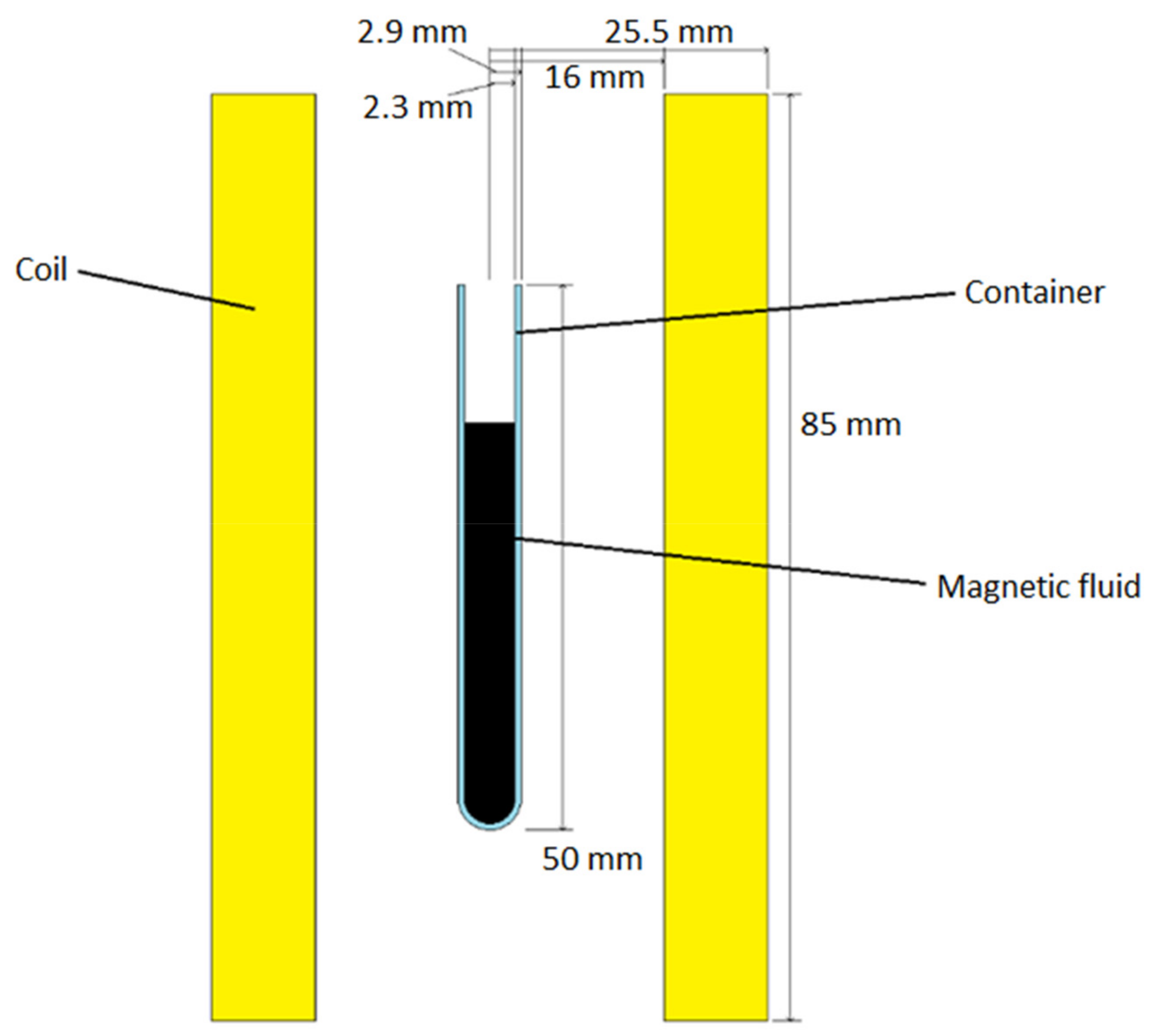
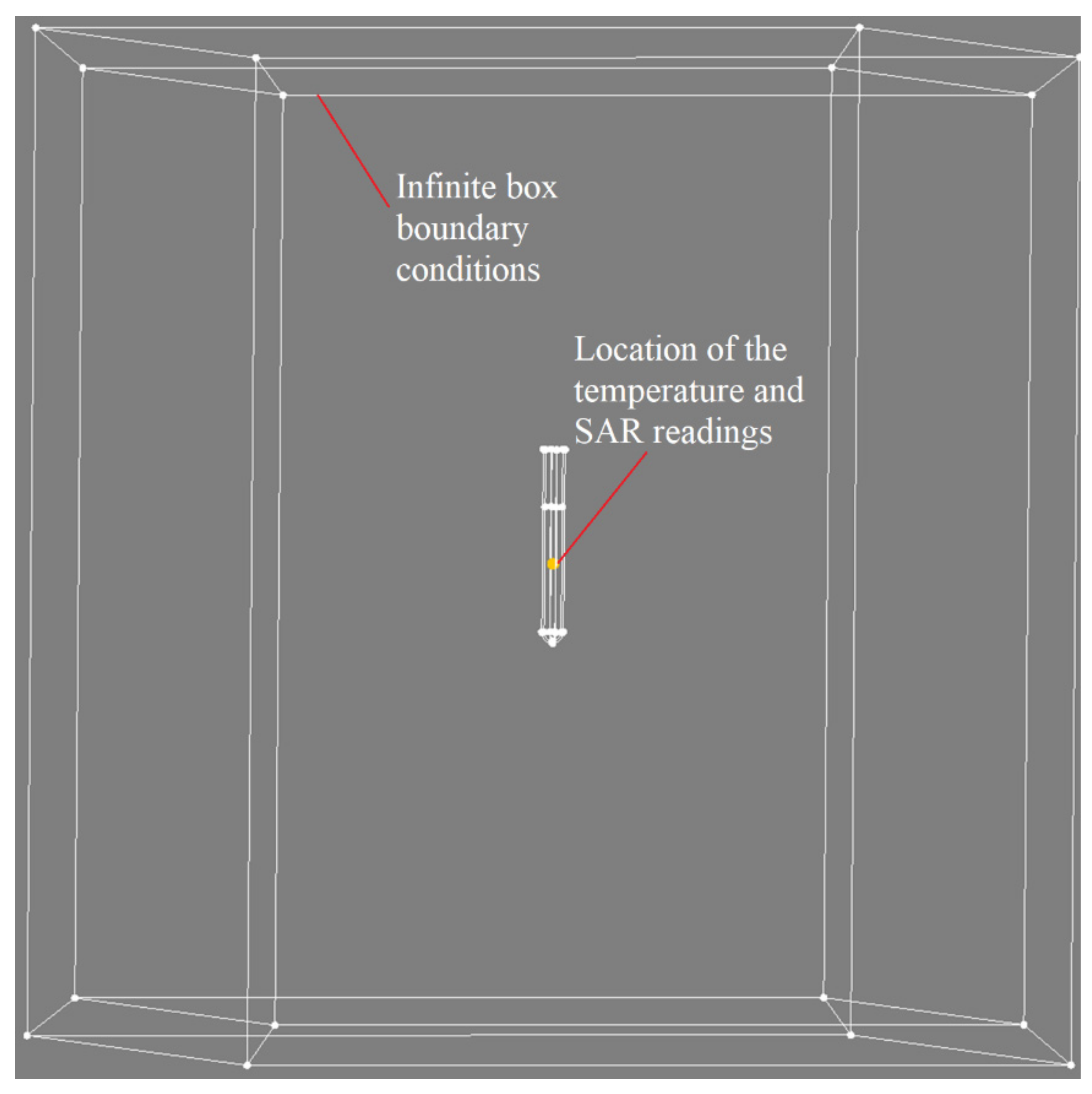
4. Simulation
- Length: l = 85 mm,
- Inner diameter: di = 32 mm,
- Outer diameter: do = 51 mm,
- Number of turns: N = 36.
- Length: le = 50 mm,
- Outer diameter: de = 5.8 mm,
- Glass thickness: dg = 0.6 mm.
5. Selection of Parameters
5.1. Parameters Used for the Determination of the Software’s Spatial Quantities Determined with the Equations
5.1.1. Volume Fraction ϕ
5.1.2. Volumes Vp and Vh
5.1.3. Viscosity η
5.1.4. Attempt Time τ0
5.1.5. Effective Anisotropy Keff
5.1.6. Saturation Magnetization of the Bulk Material Ms
5.2. Basic Parameters Used in the Simulation Model for Material’s Properties’ Determination
- Density [34]: ρ = 1.204 kg/m3,
- Relative magnetic permeability: μr = 1,
- Density: ρ = 1314.3 kg/m3,
- Specific heat capacity: c = 1214.9 J/kgK,
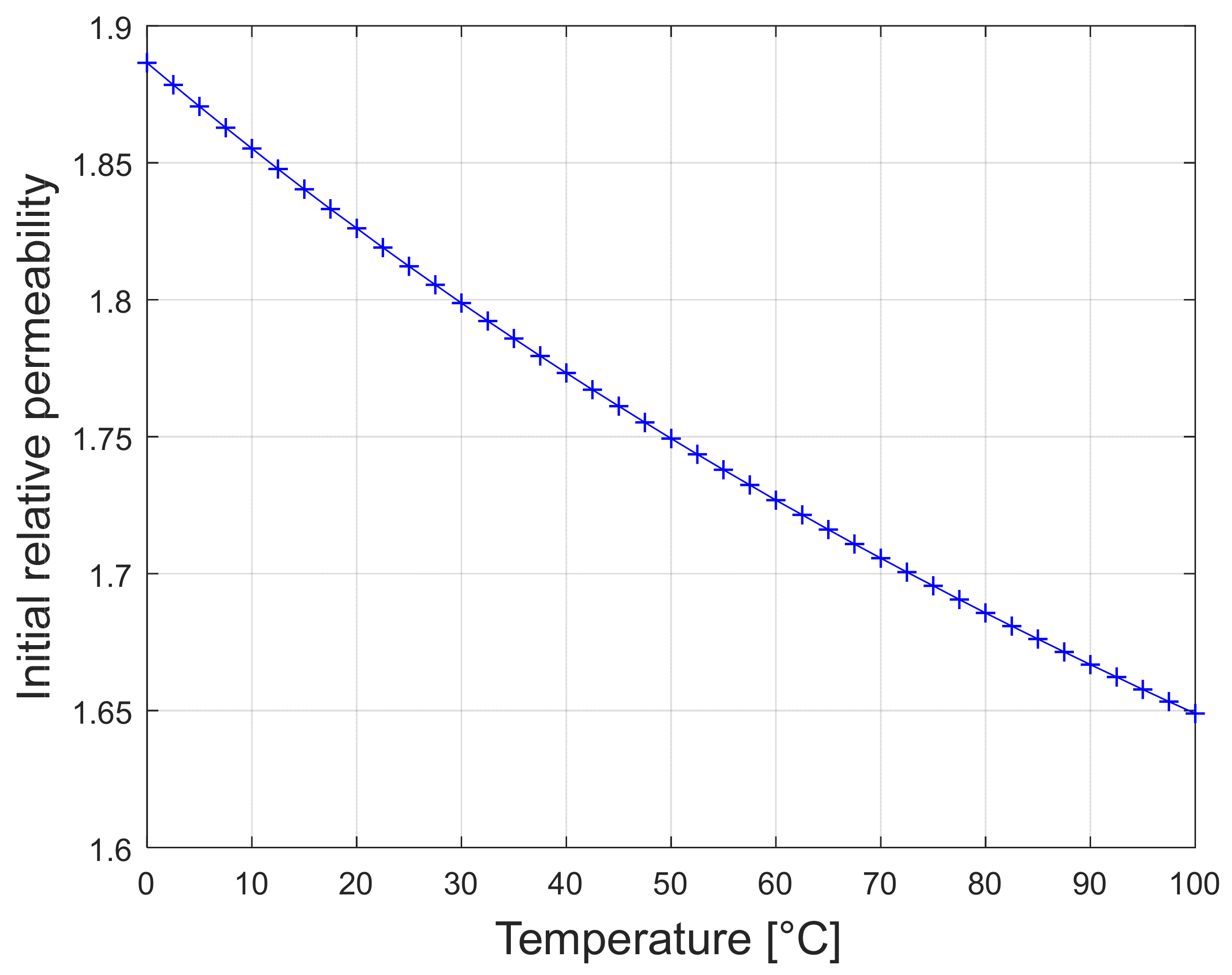
- For the magnetic permeability, the initial susceptibility was calculated using Equation (8) and converted into permeability using the equation:
- Initial magnetic permeability was then (Figure 9):
- Saturation magnetization of the magnetic fluid: Mf = ϕMs = 42.3 kA/m,
- The thermal conductivity was calculated with equation [38]:where λf is the thermal conductivity of the magnetic fluid, and β = (λp − λf)/(λp + 2λf), with λp being the thermal conductivity of the MNP. For the thermal conductivity of the carrier fluid, the value of λf = 0.15 W/mK was estimated for mineral oil, taking literature [39] as a guide. For maghemite, the thermal conductivity falls in the range of 0.86–1.30 W/mK, according to [40]. For the value λp = 0.92 W/mK, using Equation (17), the magnetic fluid thermal conductivity was λ = 0.187 W/mK.
6. Results
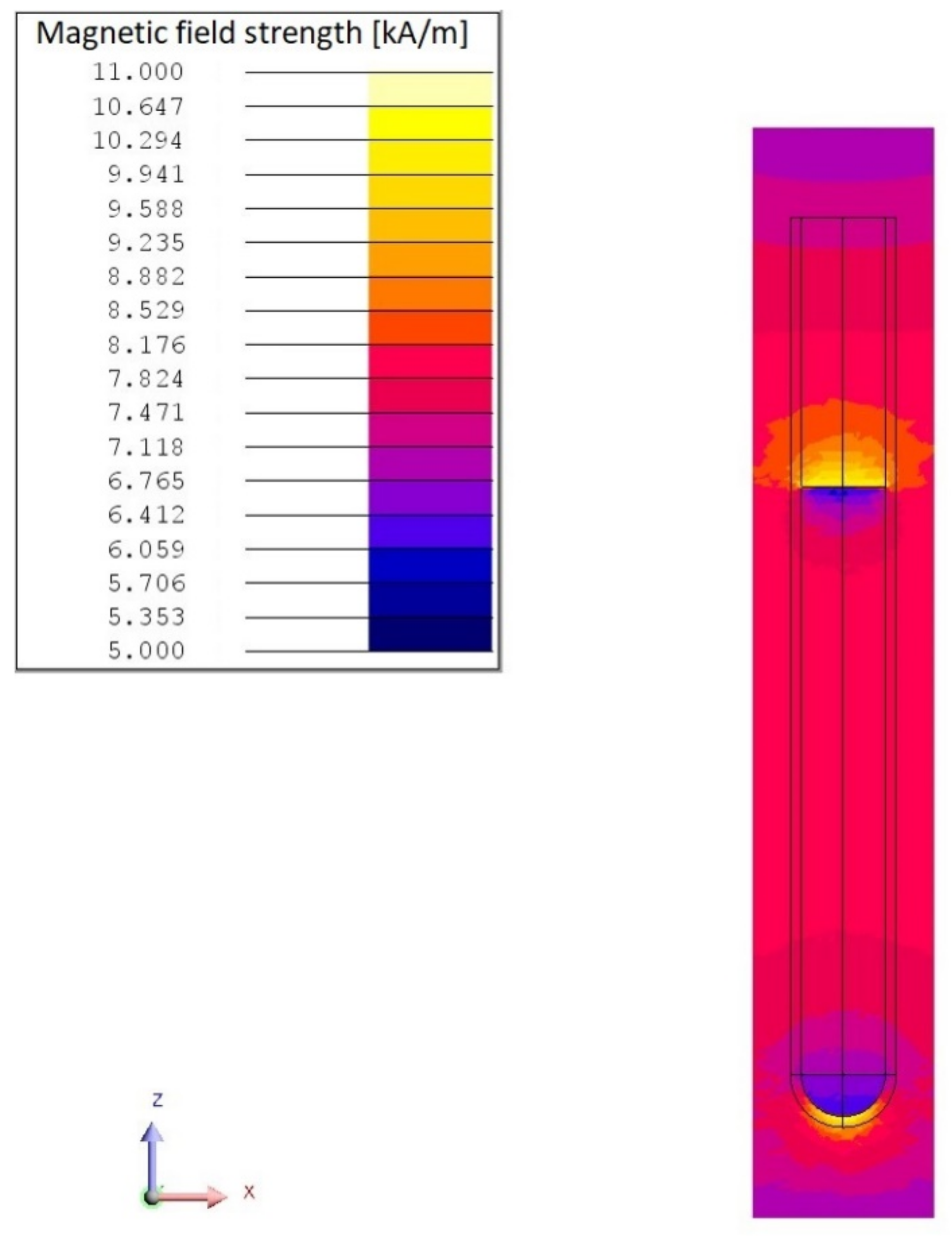
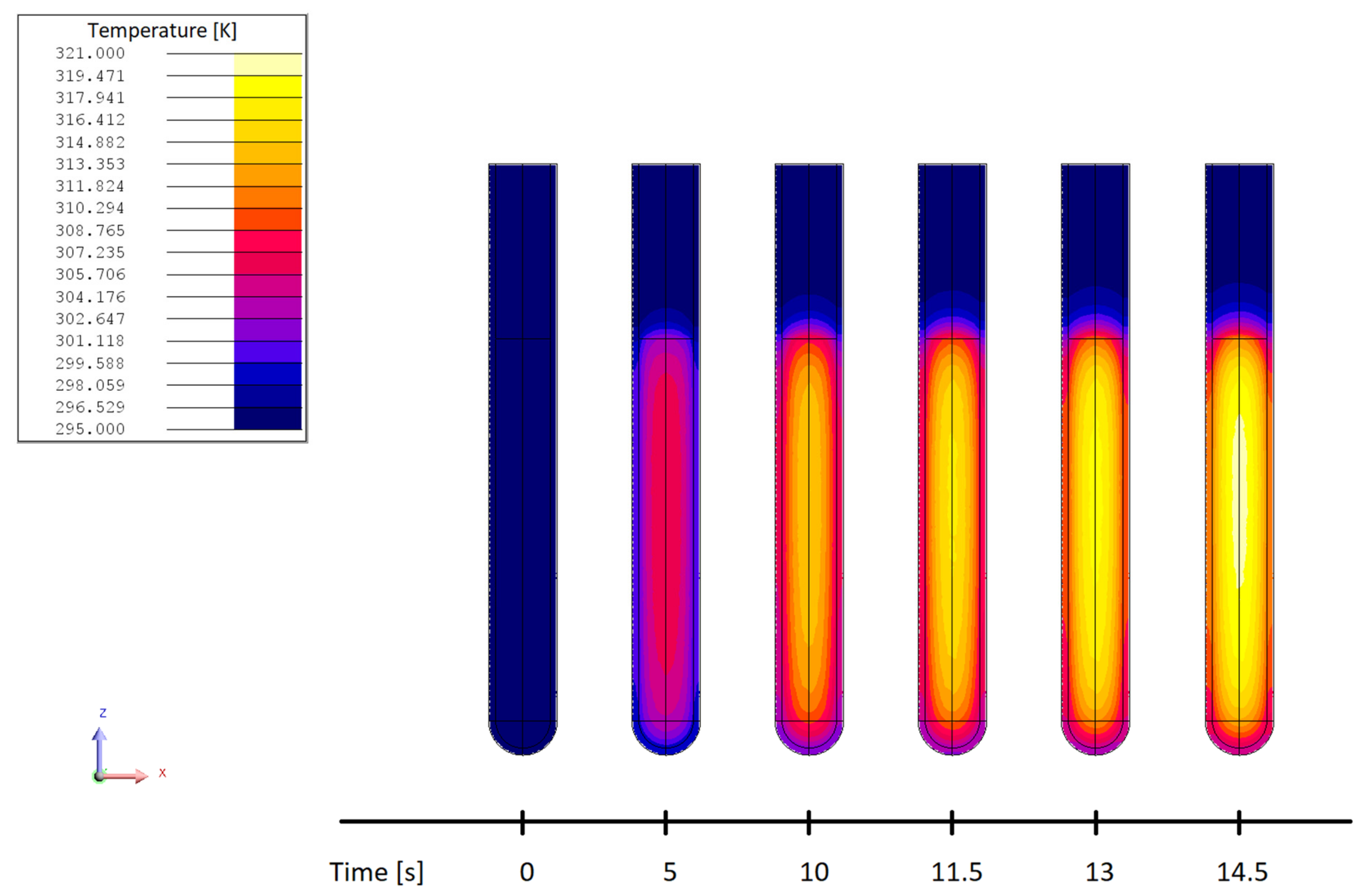
6.1. Magnetic Field and Temperature Distribution
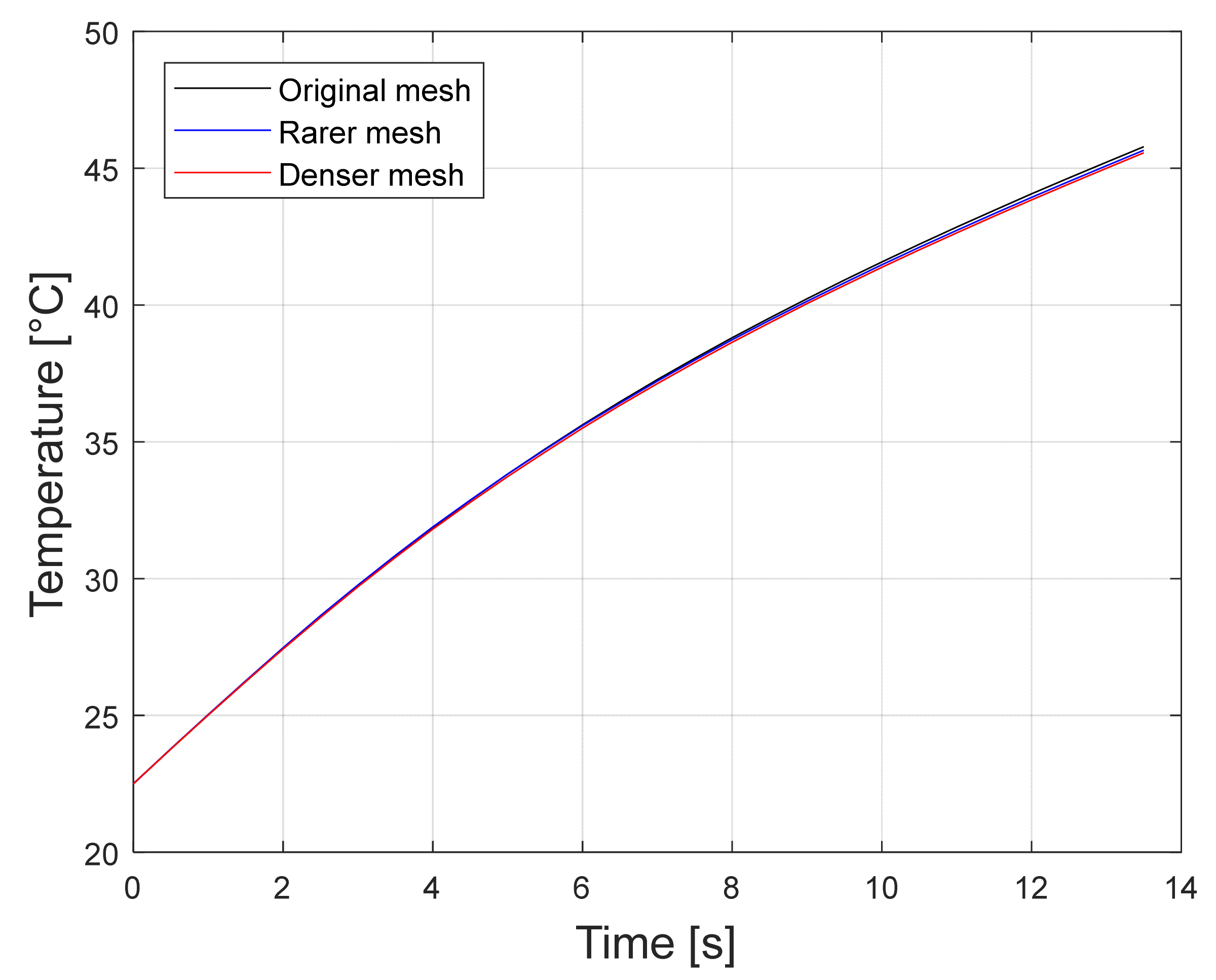
6.2. Mesh Dependency Test
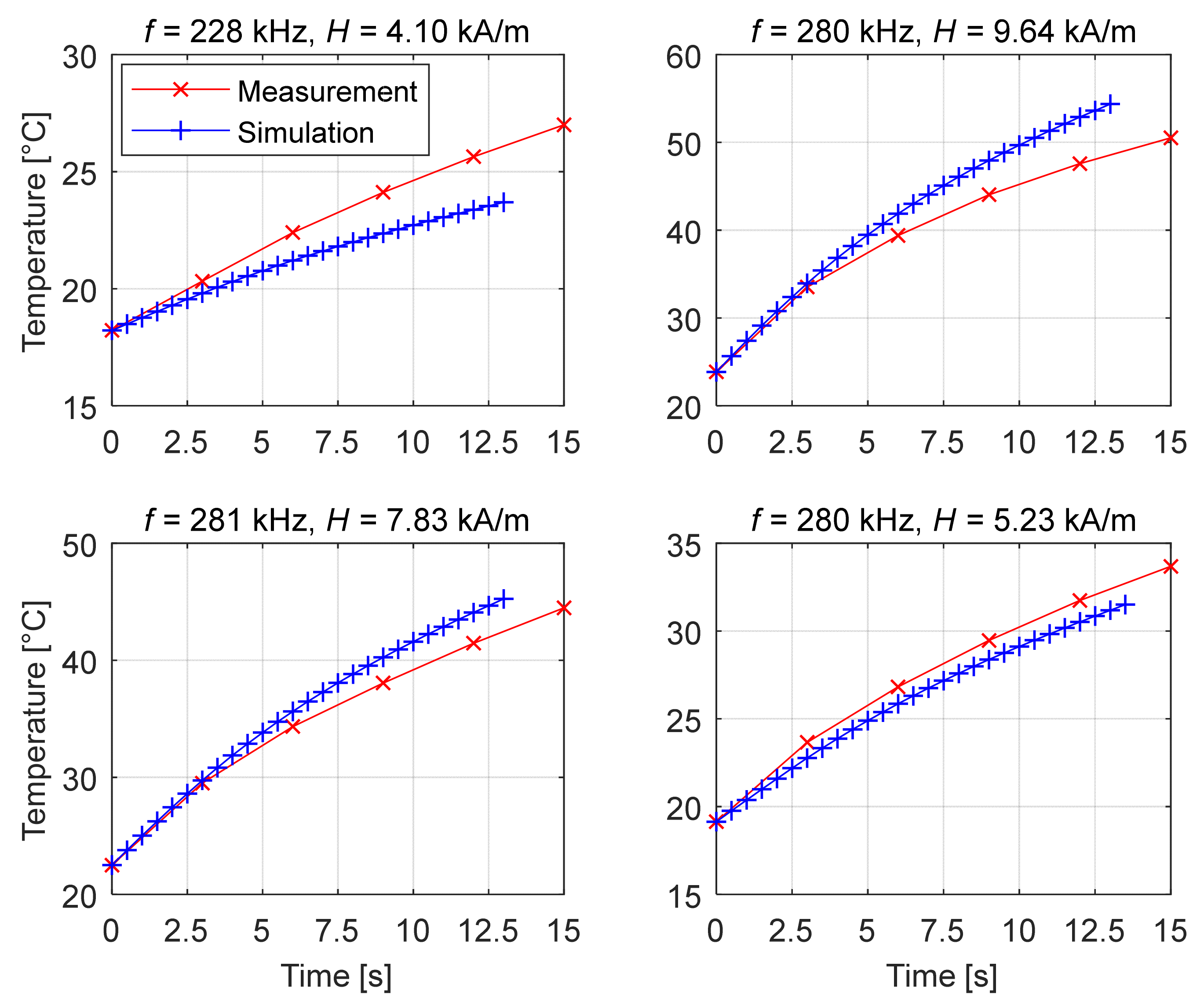
6.3. Comparison with the Measurements
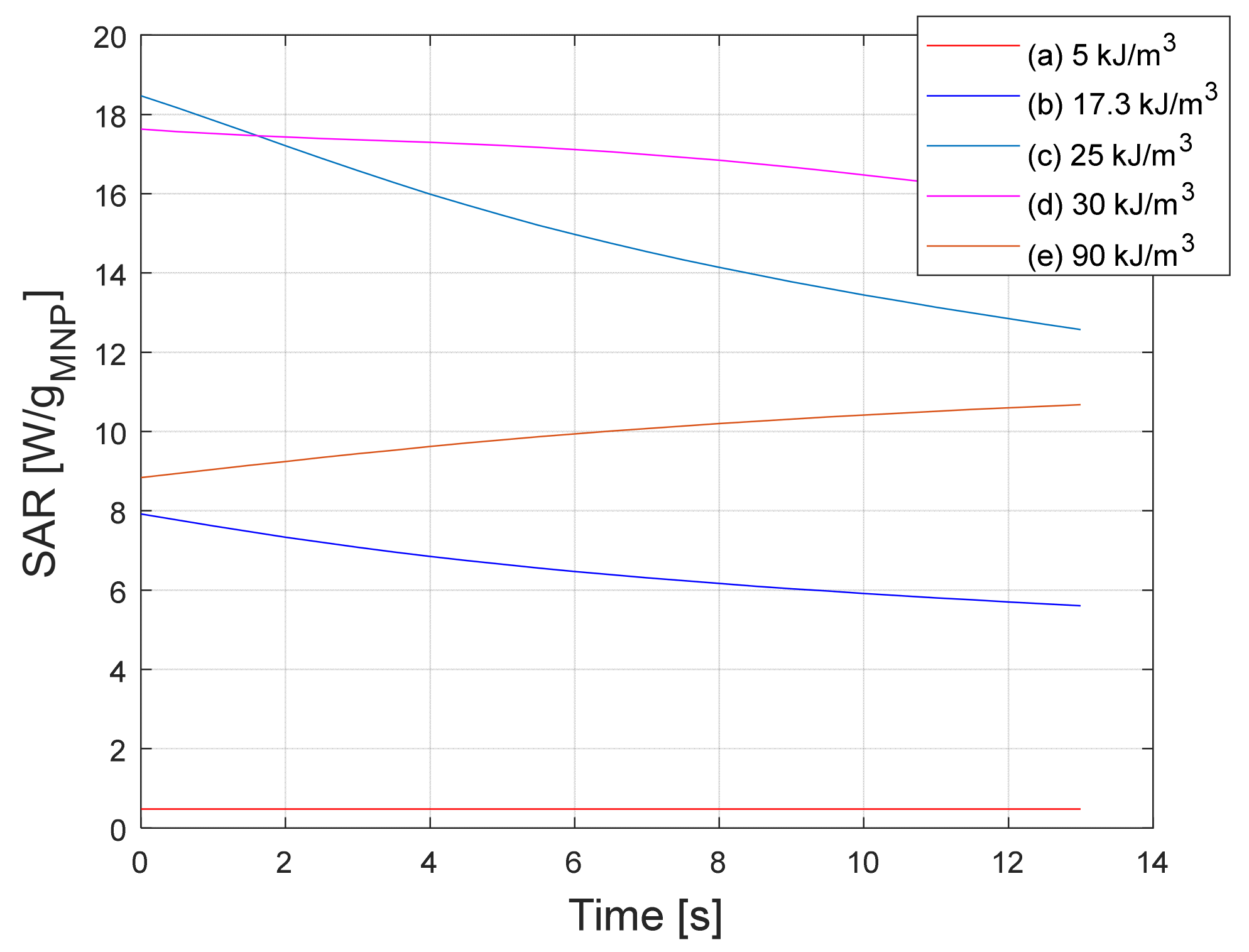
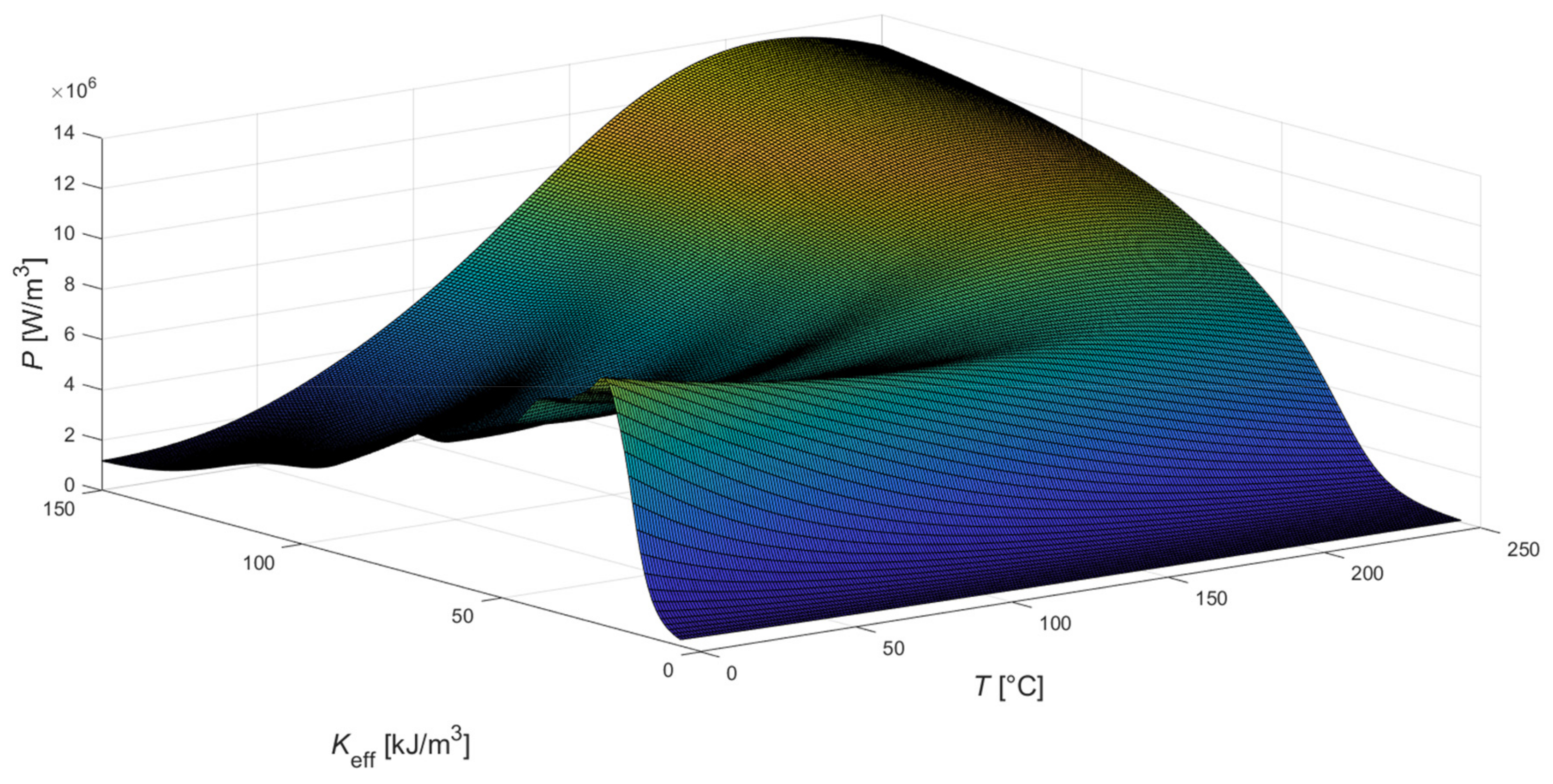
6.4. Effective Anisotropy’s Influence on the Simulation Results
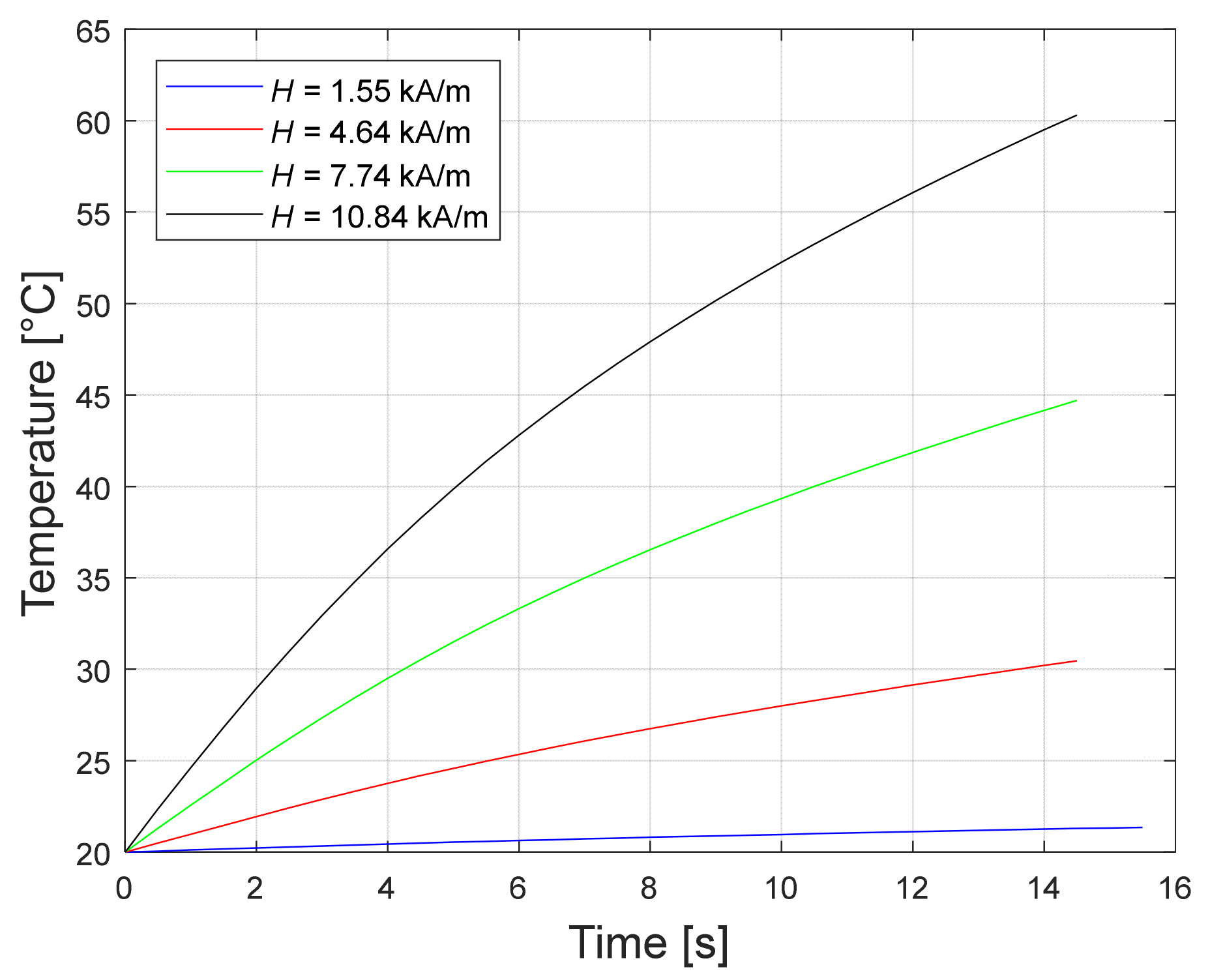
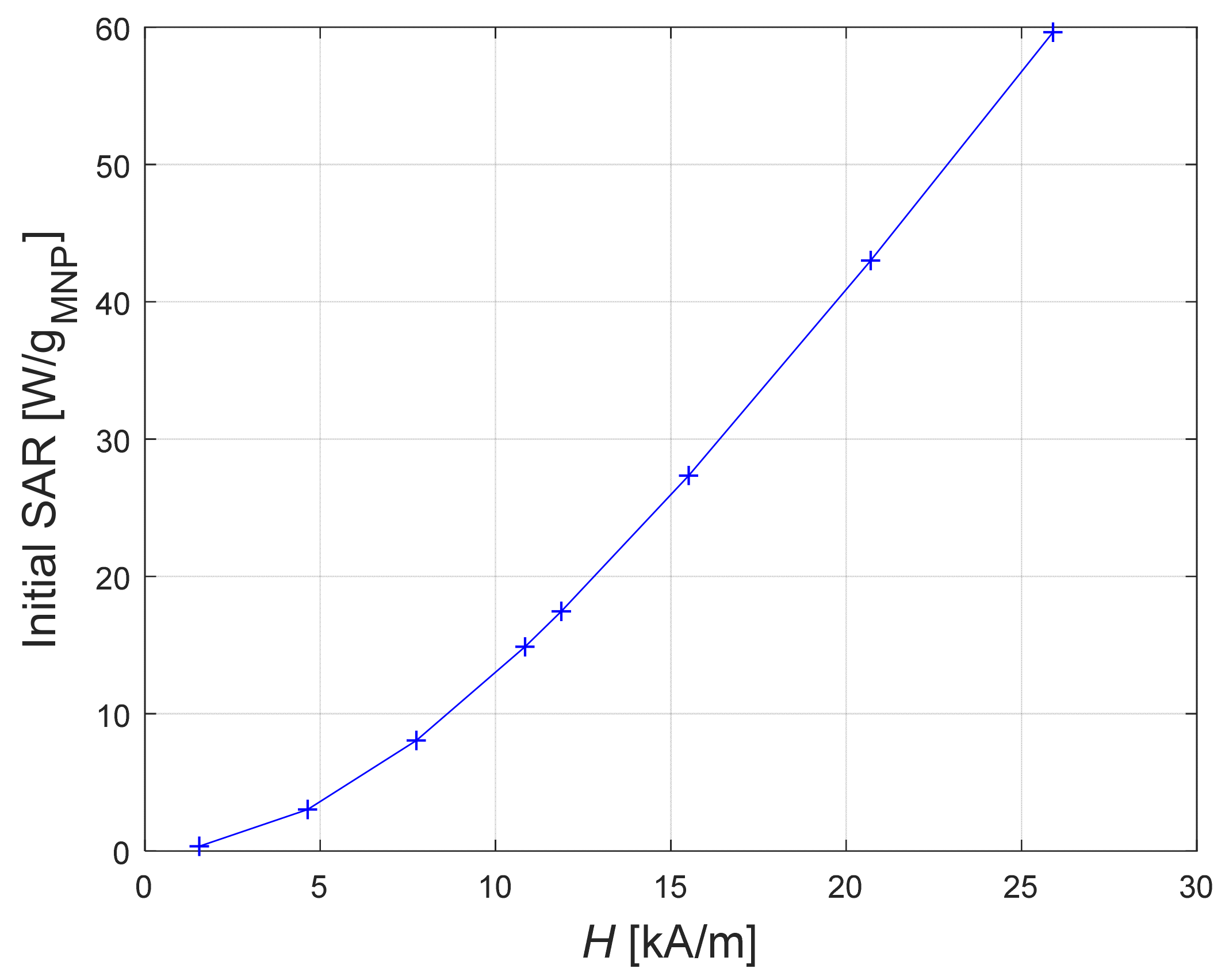
6.5. Magnetic Field Strength Amplitude’s Influence on the Simulation Results
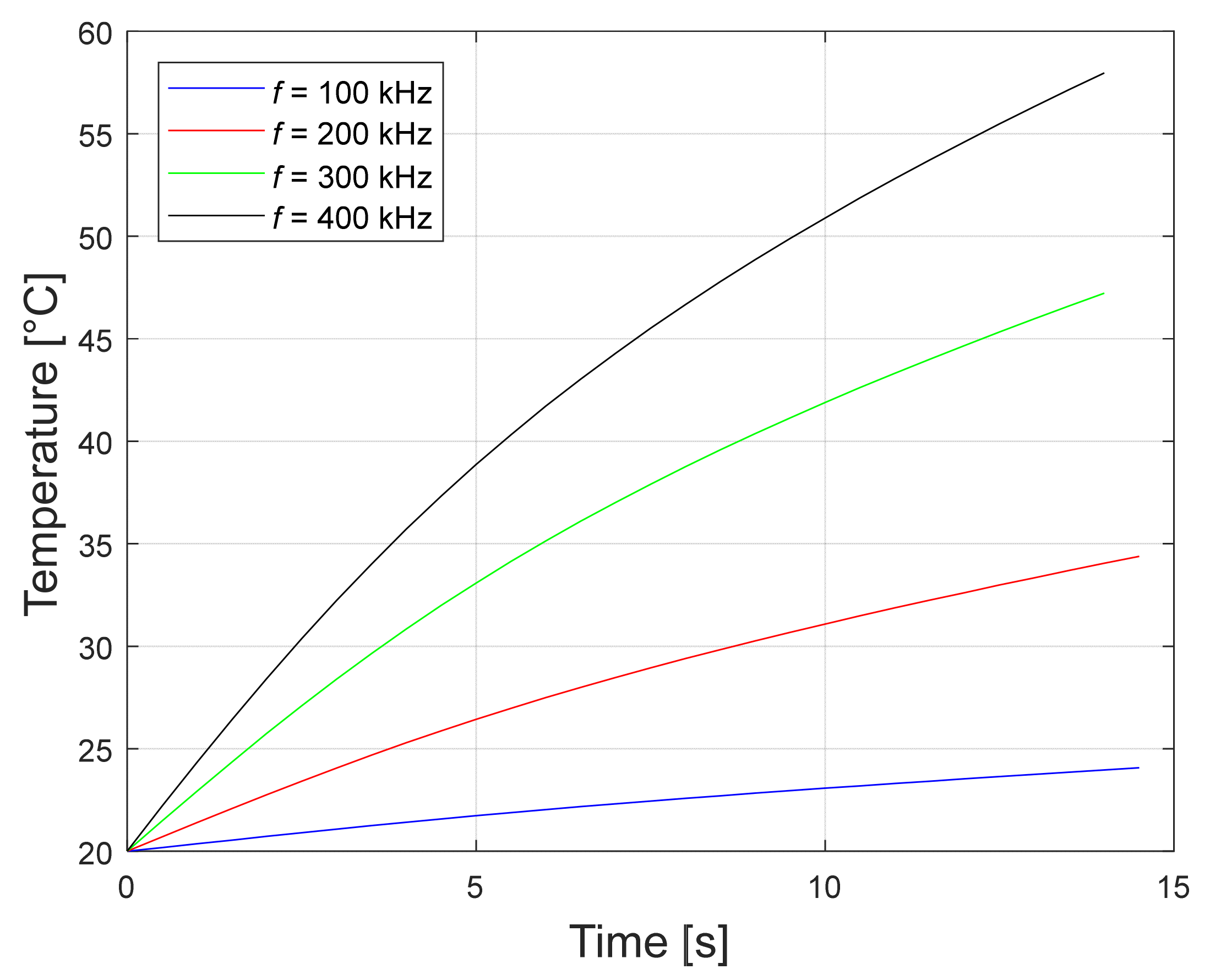
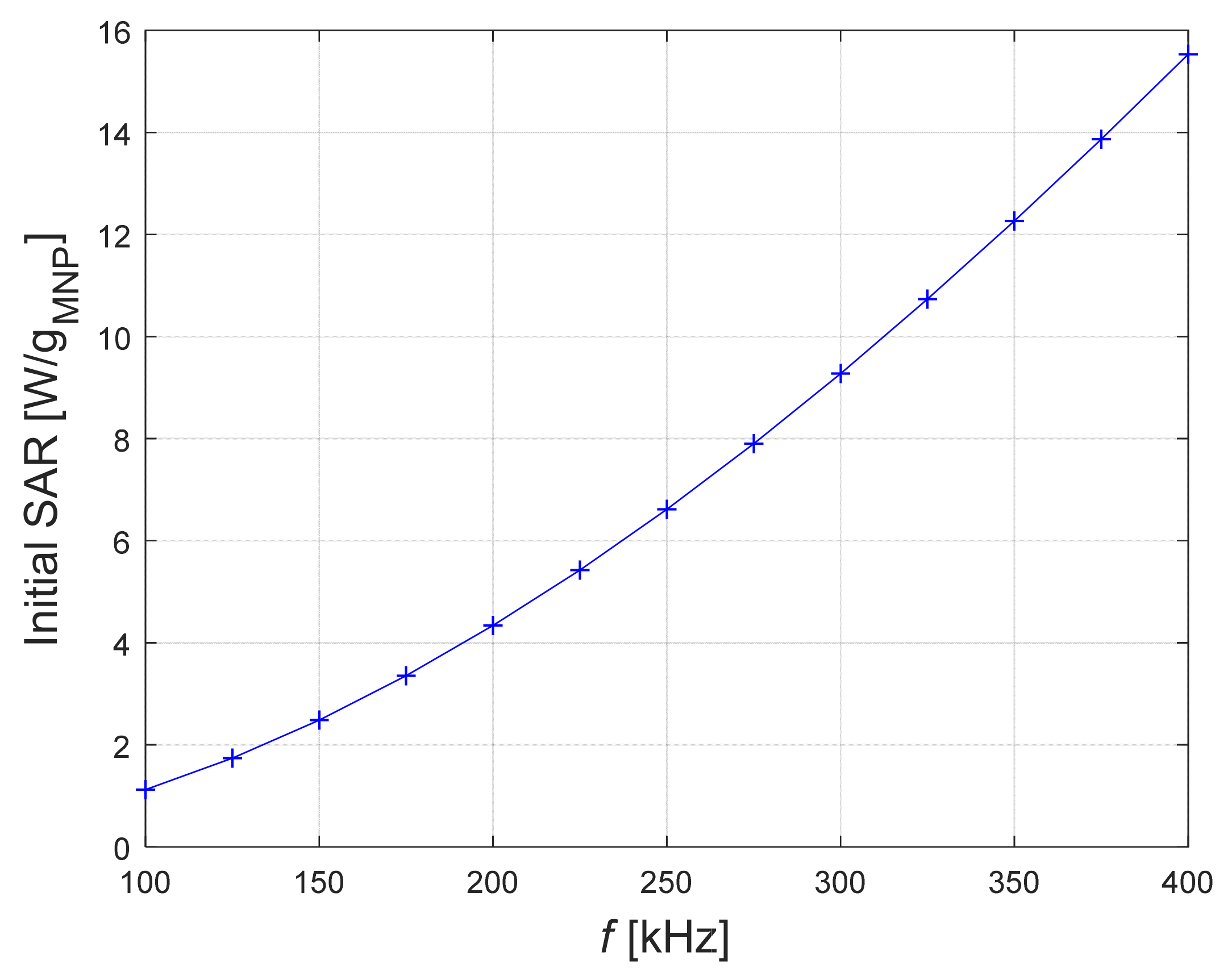
6.6. Frequency’s Influence on the Simulation Results
6.7. Discussion of the Results’ Accuracy
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lanier, O.; Korotych, O.I.; Monsalve, A.G.; Wable, D.; Savliwala, S.; Grooms, N.W.F.; Nacea, C.; Tuitt, O.R.; Dobson, J. Evaluation of magnetic nanoparticles for magnetic fluid hyperthermia. Int. J. Hyperth. 2019, 36, 687–701. [Google Scholar] [CrossRef]
- Smakulski, P.; Pietrowicz, S.; Ishimoto, J. The numerical modeling of cell freezing in binary solution under subcooling conditions. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 3005–3025. [Google Scholar] [CrossRef]
- Beković, M.; Hamler, A. Determination of the Heating Effect of Magnetic Fluid in Alternating Magnetic Field. IEEE Trans. Magn. 2010, 46, 552–555. [Google Scholar] [CrossRef]
- Kandasamy, G.; Sudame, A.; Bhati, P.; Chakrabarty, A.; Maity, D. Systematic investigations on heating effects of carboxyl-amine functionalized superparamagnetic iron oxide nanoparticles (SPIONs) based ferrofluids for in vitro cancer hyperthermia therapy. J. Mol. Liq. 2018, 256, 224–237. [Google Scholar] [CrossRef]
- Kandasamy, G.; Sudame, A.; Bhati, P.; Chakrabarty, A.; Kale, S.N.; Maity, D. Systematic magnetic fluid hyperthermia studies of carboxyl functionalized hydrophilic superparamagnetic iron oxide nanoparticles based ferrofluids. J. Colloid Interface Sci. 2018, 514, 534–543. [Google Scholar] [CrossRef]
- Khoramian, S.; Saeidifar, M.; Zamanian, A.; Saboury, A. Synthesis and characterization of biocompatible ferrofluid based on magnetite nanoparticles and its effect on immunoglobulin G as an immune protein. J. Mol. Liq. 2019, 273, 326–338. [Google Scholar] [CrossRef]
- Rosensweig, R. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Beković, M.; Trbušić, M.; Gyergyek, S.; Trlep, M.; Jesenik, M.; Szabo, P.S.B.; Hamler, A. Numerical Model for Determining the Magnetic Loss of Magnetic Fluids. Materials 2019, 12, 591. [Google Scholar] [CrossRef] [Green Version]
- Bekovic, M. FEM Thermal Calculation of the Warming of Magnetic Fluid Exposed to Alternating Magnetic Field. 2010. Available online: https://www.semanticscholar.org/paper/FEM-Thermal-Calculation-of-the-Warming-of-Magnetic-Bekovic/1097570d4e8b04dacbe9b66601653609970788d3 (accessed on 31 August 2021).
- Raouf, I.; Lee, J.; Kim, H.S.; Kim, M.-H. Parametric investigations of magnetic nanoparticles hyperthermia in ferrofluid using finite element analysis. Int. J. Therm. Sci. 2021, 159, 106604. [Google Scholar] [CrossRef]
- Rast, L.; Harrison, J.G. Computational Modeling of Electromagnetically Induced Heating of Magnetic Nanoparticle Materials for Hyperthermic Cancer Treatment. PIERS Online 2010, 6, 690–694. [Google Scholar] [CrossRef] [Green Version]
- Miaskowski, A.; Sawicki, B. Magnetic Fluid Hyperthermia Modeling Based on Phantom Measurements and Realistic Breast Model. IEEE Trans. Biomed. Eng. 2013, 60, 1806–1813. [Google Scholar] [CrossRef]
- Adhikary, K.; Banerjee, M. A Thermofluid Analysis of the Magnetic Nanoparticles Enhanced Heating Effects in Tissues Embedded with Large Blood Vessel during Magnetic Fluid Hyperthermia. J. Nanoparticles 2016, 2016, 6309231. [Google Scholar] [CrossRef] [Green Version]
- Candeo, A.; Dughiero, F. Numerical FEM Models for the Planning of Magnetic Induction Hyperthermia Treatments with Nanoparticles. IEEE Trans. Magn. 2009, 45, 1658–1661. [Google Scholar] [CrossRef]
- Li, J.; Yao, H.; Lei, Y.; Huang, W.; Wang, Z.; Yan, L. Numerical simulation of magnetic fluid hyperthermia based on multiphysics coupling and recommendation on preferable treatment conditions. Curr. Appl. Phys. 2019, 19, 1031–1039. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Hou, H.; Shao, J. Simulation analysis of coupled magnetic-temperature fields in magnetic fluid hyperthermia. AIP Adv. 2019, 9, 105317. [Google Scholar] [CrossRef]
- Reis, R.F.; Loureiro, F.; Lobosco, M. 3D numerical simulations on GPUs of hyperthermia with nanoparticles by a nonlinear bioheat model. J. Comput. Appl. Math. 2016, 295, 35–47. [Google Scholar] [CrossRef]
- Salloum, M.; Ma, R.; Zhu, L. Anin-vivoexperimental study of temperature elevations in animal tissue during magnetic nanoparticle hyperthermia. Int. J. Hyperth. 2008, 24, 589–601. [Google Scholar] [CrossRef]
- Engelmann, U.M.; Shasha, C.; Teeman, E.; Slabu, I.; Krishnan, K.M. Predicting size-dependent heating efficiency of magnetic nanoparticles from experiment and stochastic Néel-Brown Langevin simulation. J. Magn. Magn. Mater. 2019, 471, 450–456. [Google Scholar] [CrossRef]
- Papadopoulos, C.; Efthimiadou, E.K.; Pissas, M.; Fuentes, D.; Boukos, N.; Psycharis, V.; Kordas, G.; Loukopoulos, V.C.; Kagadis, G.C. Magnetic fluid hyperthermia simulations in evaluation of SAR calculation methods. Phys. Med. 2020, 71, 39–52. [Google Scholar] [CrossRef]
- Deatsch, A.E.; Evans, B.A. Heating efficiency in magnetic nanoparticle hyperthermia. J. Magn. Magn. Mater. 2014, 354, 163–172. [Google Scholar] [CrossRef]
- Karvelas, E.; Lampropoulos, N.; Sarris, I. A numerical model for aggregations formation and magnetic driving of spherical particles based on OpenFOAM®. Comput. Methods Programs Biomed. 2017, 142, 21–30. [Google Scholar] [CrossRef]
- Vartholomeos, P.; Mavroidis, C. In Silico Studies of Magnetic Microparticle Aggregations in Fluid Environments for MRI-Guided Drug Delivery. IEEE Trans. Biomed. Eng. 2012, 59, 3028–3038. [Google Scholar] [CrossRef]
- Mathieu, J.-B.; Martel, S. Aggregation of magnetic microparticles in the context of targeted therapies actuated by a magnetic resonance imaging system. J. Appl. Phys. 2009, 106, 044904. [Google Scholar] [CrossRef]
- Beković, M.; Goričan, V.; Hamler, A. Materiali s Posebnimi Lastnostmi in Pojavi—Laboratorijske Vaje. 2019. Available online: https://www.um.si/studij/podiplomski-studij/Lists/Studijski%20progami%202stopnja/Attachments/3/U%C4%8Dni%20na%C4%8Drti.pdf (accessed on 31 August 2021).
- Viswanath, D.S.; Ghosh, T.K.; Prasad, D.H.L.; Dutt, N.V.K.; Rani, K.Y. (Eds.) Correlations and estimation of pure liquid viscosity. In Viscosity of Liquids: Theory, Estimation, Experiment, and Data; Springer: Dordrecht, The Netherland, 2007; pp. 135–405. ISBN 978-1-4020-5482-2. [Google Scholar]
- Berndt, T.; Muxworthy, A.R.; Paterson, G.A. Determining the magnetic attempt time τ 0, its temperature dependence, and the grain size distribution from magnetic viscosity measurements. J. Geophys. Res. Solid Earth 2015, 120, 7322–7336. [Google Scholar] [CrossRef] [Green Version]
- Cullity, B.D.; Graham, C.D. Magnetic Anisotropy. In Introduction to Magnetic Materials; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 197–239. ISBN 978-0-470-38632-3. [Google Scholar]
- Carrey, J.; Mehdaoui, B.; Respaud, M. Simple models for dynamic hysteresis loop calculations of magnetic single-domain nanoparticles: Application to magnetic hyperthermia optimization. J. Appl. Phys. 2011, 109, 083921. [Google Scholar] [CrossRef]
- Komorida, Y.; Mito, M.; Deguchi, H.; Takagi, S.; Millán, A.; Silva, N.J.O.; Palacio, F. Surface and core magnetic anisotropy in maghemite nanoparticles determined by pressure experiments. Appl. Phys. Lett. 2009, 94, 202503. [Google Scholar] [CrossRef] [Green Version]
- Figueroa, A.; Bartolomé, J.; García, L.; Arauzo, A.; Millán, A.; Palacio, F. Magnetic Anisotropy of Maghemite Nanoparticles Probed by RF Transverse Susceptibility. Phys. Procedia 2015, 75, 1050–1057. [Google Scholar] [CrossRef] [Green Version]
- Pisane, K.L.; Singh, S.; Seehra, M.S. Unusual enhancement of effective magnetic anisotropy with decreasing particle size in maghemite nanoparticles. Appl. Phys. Lett. 2017, 110, 222409. [Google Scholar] [CrossRef] [Green Version]
- Usov, N.; Barandiarán, J.M. Magnetic nanoparticles with combined anisotropy. J. Appl. Phys. 2012, 112, 53915. [Google Scholar] [CrossRef]
- Engineering ToolBox. Air—Density, Specific Weight and Thermal Expansion Coefficient at Varying Temperature and Constant Pressures. Available online: https://www.engineeringtoolbox.com/air-density-specific-weight-d_600.html (accessed on 13 April 2021).
- Engineering ToolBox. Air—Specific Heat at Constant Pressure and Varying Temperature. Available online: https://www.engineeringtoolbox.com/air-specific-heat-capacity-d_705.html (accessed on 13 April 2021).
- Engineering ToolBox. Air—Thermal Conductivity. Available online: https://www.engineeringtoolbox.com/air-properties-viscosity-conductivity-heat-capacity-d_1509.html (accessed on 13 April 2021).
- Saint-Gobain Sekurit Glass Properties. Available online: https://www.saint-gobain-sekurit.com/global-excellence/our-production-processes/glossary (accessed on 3 May 2021).
- Genc, S. Heat Transfer of Ferrofluids. In Nanofluid Heat and Mass Transfer in Engineering Problems; Kandelousi, M.S., Ed.; InTechOpen: Rijeka, Croatia, 2017. [Google Scholar]
- Nadolny, Z.; Dombek, G.; Przybylek, P. Thermal Properties of a Mixture of Mineral Oil and Synthetic Ester in Terms of Its Application in the Transformer. In Proceedings of the 2016 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Toronto, ON, Canada, 16–19 October 2016; pp. 857–860. [Google Scholar]
- Spencer, M.P.; Lee, W.; Alsaati, A.; Breznak, C.M.; Branco, R.B.N.; Dai, J.; Gomez, E.D.; Marconnet, A.; von Lockette, P.; Yamamoto, N. Cold sintering to form bulk maghemite for characterization beyond magnetic properties. Int. J. Ceram. Eng. Sci. 2019, 1, 119–124. [Google Scholar] [CrossRef] [Green Version]

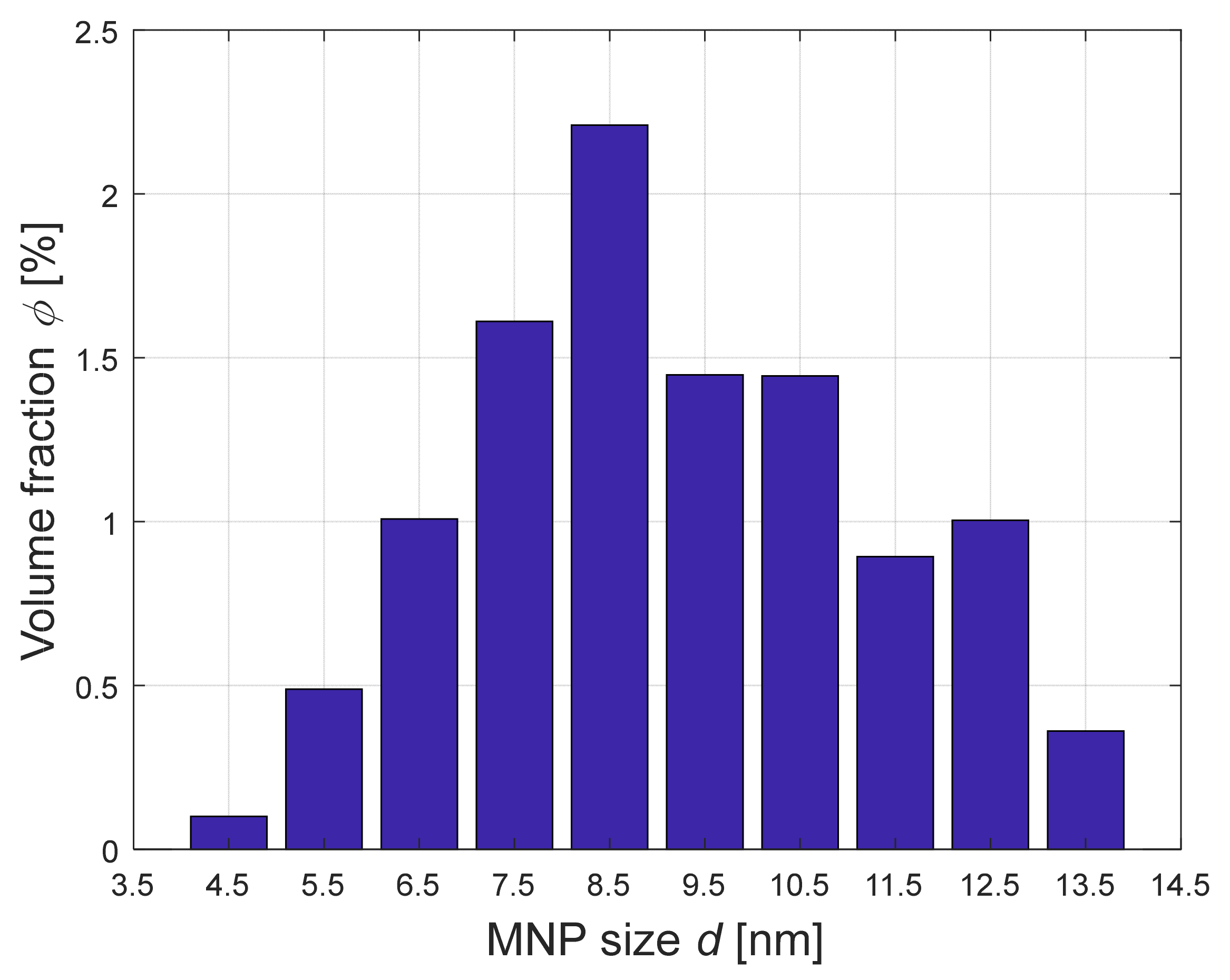





| MNP Size [nm] | Volume Fraction ϕ [%] |
|---|---|
| 4.5 | 0.1004 |
| 5.5 | 0.4887 |
| 6.5 | 1.0080 |
| 7.5 | 1.6110 |
| 8.5 | 2.2100 |
| 9.5 | 1.4480 |
| 10.5 | 1.4450 |
| 11.5 | 0.8935 |
| 12.5 | 1.0040 |
| 13.5 | 0.3613 |
| Parameter | Value |
|---|---|
| Attempt time τ0 | 10−9 s |
| Effective anisotropy Keff | 17.3 kJ/m3 |
| Saturation magnetization of the bulk material Ms | 400 kA/m |
| Type of Element | Number of Elements (Original Mesh) | Number of Elements (Rarer Mesh) | Number of Elements (Denser Mesh) |
|---|---|---|---|
| Node | 29,839 | 16,718 | 34,921 |
| Line element | 2126 | 1065 | 2646 |
| Surface element | 30,408 | 15,794 | 36,674 |
| Volume element | 168,537 | 95,482 | 195,612 |
| Field Frequency f [kHz] | Field Strength Amplitude H [kA/m] | Measured SAR [W/gFe] | Calculated SAR [W/gFe] | Deviation from Measurement [%] |
|---|---|---|---|---|
| 101 | 13.50 | 3.330 | 3.062 | 8.05 |
| 100 | 11.68 | 2.692 | 2.295 | 14.75 |
| 100 | 9.75 | 2.240 | 1.683 | 24.87 |
| 229 | 7.80 | 4.296 | 4.908 | 14.25 |
| 228 | 4.10 | 2.158 | 1.659 | 23.12 |
| 280 | 9.64 | 9.927 | 11.288 | 13.71 |
| 281 | 7.83 | 7.194 | 7.920 | 10.09 |
| 280 | 5.23 | 4.645 | 3.849 | 17.14 |
| 279 | 3.05 | 1.788 | 1.346 | 24.72 |
| 279 | 1.55 | 0.370 | 0.350 | 5.41 |
| 397 | 6.48 | 10.646 | 10.197 | 4.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vizjak, J.; Beković, M.; Jesenik, M.; Hamler, A. Development of a Magnetic Fluid Heating FEM Simulation Model with Coupled Steady State Magnetic and Transient Thermal Calculation. Mathematics 2021, 9, 2561. https://doi.org/10.3390/math9202561
Vizjak J, Beković M, Jesenik M, Hamler A. Development of a Magnetic Fluid Heating FEM Simulation Model with Coupled Steady State Magnetic and Transient Thermal Calculation. Mathematics. 2021; 9(20):2561. https://doi.org/10.3390/math9202561
Chicago/Turabian StyleVizjak, Jakob, Miloš Beković, Marko Jesenik, and Anton Hamler. 2021. "Development of a Magnetic Fluid Heating FEM Simulation Model with Coupled Steady State Magnetic and Transient Thermal Calculation" Mathematics 9, no. 20: 2561. https://doi.org/10.3390/math9202561
APA StyleVizjak, J., Beković, M., Jesenik, M., & Hamler, A. (2021). Development of a Magnetic Fluid Heating FEM Simulation Model with Coupled Steady State Magnetic and Transient Thermal Calculation. Mathematics, 9(20), 2561. https://doi.org/10.3390/math9202561








