On Invariant Operations on a Manifold with a Linear Connection and an Orientation
Abstract
:1. Introduction
2. The Category of Ringed Spaces
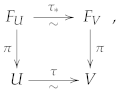
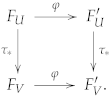
2.1. Limits of Ringed Spaces
- -
- The underlying topological space is the inverse limit of the topological spaces , i.e., the setis endowed with the minimum topology for which the canonical projections are continuous.
- -
- Its sheaf of smooth functions is the direct limit .
2.2. Quotients by the Action of Groups
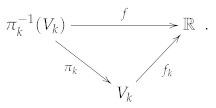
2.3. Differential Operators
- 1.
- is an open set of .
- 2.
- The map , defined as , is smooth.
3. Natural Operations in the Presence of an Orientation
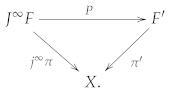
3.1. Natural Bundles
- 1.
- Functorial character: and .
- 2.
- Local character: For any diffeomorphism and any open subset ,
- 3.
- Regularity: If is a smooth family of diffeomorphisms between open sets on X, then the family is also smooth.
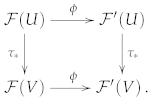
3.2. Natural Operations in the Presence of an Orientation
4. Invariants of Linear Connections and an Orientation
- 1.
- They are symmetric in the last m covariant indices:
- 2.
- The symmetrization of the covariant indices is zero:
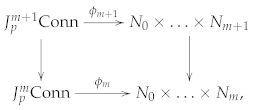
5. An Application
5.1. Invariant Theory of the Special Linear Group
- There exists a linear isomorphism .
- If is a sub-representation, then any equivariant linear map is the restriction of an equivariant linear map .
5.2. Uniqueness of the Torsion and Curvature Operators
5.3. Vector-Valued Natural Forms
5.4. Endomorphism-Valued Natural Forms
- (a)
- ,
- (b)
- ,
- (c)
- ,
- (d)
- .
Author Contributions
Funding
Conflicts of Interest
References
- Mehra, J. Einstein, Hilbert, and the Theory of Gravitation. Historical Origins of General Relativity Theory; Reidel: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Atiyah, M.; Bott, R.; Patodi, V.K. On the heat equation and the index theorem. Invent. Math. 1973, 19, 279–330. [Google Scholar] [CrossRef]
- Gilkey, P.B. Curvature and the eigenvalues of the Dolbeault complex for Kaehler manifolds. Adv. Math. 1973, 11, 311–325. [Google Scholar] [CrossRef] [Green Version]
- Gilkey, P. Local invariants of an embedded Riemannian manifold. Ann. Math. 1975, 102, 187–203. [Google Scholar] [CrossRef]
- Kolář, I.; Michor, P.W.; Slovák, J. Natural Operations in Differential Geometry; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Bernig, A. Natural operations on differential forms on contact manifolds. Differ. Geom. Appl. 2017, 50, 34–51. [Google Scholar] [CrossRef] [Green Version]
- Freed, D.S.; Hopkins, M.J. Chern-Weil forms and abstract homotopy theory. Bull. Am. Math. Soc. 2013, 50, 431–468. [Google Scholar] [CrossRef] [Green Version]
- Navarro, J.; Sancho, J.B. Natural operations on differential forms. Differ. Geom. Appl. 2015, 38, 159–174. [Google Scholar] [CrossRef]
- Gilkey, P.; Park, J.H.; Sekigawa, K. Universal curvature identities. Differ. Geom. Appl. 2011, 62, 814–825. [Google Scholar] [CrossRef] [Green Version]
- Gilkey, P.; Park, J.H.; Sekigawa, K. Universal curvature identities and Euler Lagrange Formulas for Kaehler manifolds. J. Math. Soc. Jpn. 2016, 68, 459–487. [Google Scholar] [CrossRef]
- Navarro, A.; Navarro, J. Uniqueness of the Gauss-Bonnet-Chern formula (after Gilkey-Park-Sekigawa). J. Geom. Phys. 2016, 101, 65–70. [Google Scholar] [CrossRef]
- Timashev, D.A. On differential characteristic classes of metrics and connections. J. Math. Sci. 2017, 223, 763–774. [Google Scholar] [CrossRef]
- Navarro, J. On second-order, divergence-free tensors. J. Math. Phys. 2014, 55, 062501. [Google Scholar] [CrossRef] [Green Version]
- Khavkine, I.; Moretti, V. Analytic Dependence is an Unnecessary Requirement in Renormalization of Locally Covariant QFT. Commun. Math. Phys. 2016, 344, 581–620. [Google Scholar] [CrossRef] [Green Version]
- Khavkine, I.; Melati, A.; Moretti, V. On Wick Polynomials of Boson Fields in Locally Covariant Algebraic QFT. Ann. Henri Poincaré 2019, 20, 929–1002. [Google Scholar] [CrossRef] [Green Version]
- Gordillo-Merino, A.; Martínez-Bohórquez, R.; Navarro, J. On the uniqueness of the torsion and curvature operators. Revista de la Real Academia de Ciencias Exactas Físicas y Naturales Serie A Matemáticas 2020, 114, 1–13. [Google Scholar] [CrossRef]
- Slovák, J. On invariant operations on a manifold with connection or metric. J. Differ. Geom. 1992, 36, 633–650. [Google Scholar] [CrossRef]
- Navarro, A.; Navarro, J.; Tejero-Prieto, C. Natural operations on holomorphic forms. Arch. Math. (Brno) 2018, 54, 239–254. [Google Scholar] [CrossRef] [Green Version]
- Navarro, J.; Sancho, J.B. Peetre-Slovák theorem revisited. arXiv 2014, arXiv:1411.7499. [Google Scholar]
- Gordillo, A.; Navarro, J. On moduli spaces for finite-order jets of linear connections. Filomat 2017, 31, 2035–2044. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gordillo-Merino, A.; Martínez-Bohórquez, R.; Navarro-Garmendia, J. On Invariant Operations on a Manifold with a Linear Connection and an Orientation. Mathematics 2021, 9, 2577. https://doi.org/10.3390/math9202577
Gordillo-Merino A, Martínez-Bohórquez R, Navarro-Garmendia J. On Invariant Operations on a Manifold with a Linear Connection and an Orientation. Mathematics. 2021; 9(20):2577. https://doi.org/10.3390/math9202577
Chicago/Turabian StyleGordillo-Merino, Adrián, Raúl Martínez-Bohórquez, and José Navarro-Garmendia. 2021. "On Invariant Operations on a Manifold with a Linear Connection and an Orientation" Mathematics 9, no. 20: 2577. https://doi.org/10.3390/math9202577






