Spectral Properties of Clipping Noise

Abstract

One serious disadvantage of any multicarrier-modulation technique such as orthogonal frequency division multiplexing (OFDM) is its high peak-to-average-power ratio (PAPR) which might lead to signal clipping in several scenarios. To maximize the transmit data rate, it is important to take this non-linear distortion into account. The most common approach is based on the Bussgang theorem, which splits the distortion in a correlated part, represented by a linear damping factor, and uncorrelated additive noise. However, there are two aspects that are not correctly considered by the Bussgang theorem. Firstly, clipping noise shows a frequency-dependent power spectrum which depends on the clipping probability. Secondly, some of the clipping noise power is located outside of the transmission bandwidth, so that it does not influence the transmission quality. In this work, the Bussgang theorem is reviewed in detail and the exact power spectral density of the uncorrelated clipping noise is approximated to determine the signal-to-noise power ratio on every subcarrier separately. Although it is shown that the frequency dependence within the transmission bandwidth is relatively small, at least 36% of the uncorrelated noise power, depending on the clipping level, lays outside of the transmission band. Monte Carlo simulations validate that a simple expression for the power spectral density allows to calculate the symbol error probability of an OFDM transmission system that suffers from clipping. Furthermore, the newly found result can be used to optimize bit allocation tables in bit loading algorithms or to calculate the channel capacity.

1. Introduction

Today’s world is becoming more and more connected. The number of devices that use radio communication rises exponentially. This will—sooner or later—result in a network overload. One idea to combat this effect is utilizing the optical spectrum, not only in fiber networks but in wireless scenarios as well. There are multiple advantages doing this, such as nearly unlimited and license-free bandwidth, higher security and most important no interference between multiple spatially separated rooms [1]. However, the signal-to-noise power ratio at the output of an optical receiver decays with the factor $1/f^2$ [2]. To combat this strong frequency dependence, the modulation technique orthogonal frequency division multiplexing (OFDM) can be utilized. Since optical wireless communication systems are highly divergent, a coherent detection is not possible. Thus, intensity modulation (IM) and direct detection (DD) have to be used [3]. This results in the conditions that the modulating time signal has to be purely real-valued and unipolar. Although a real-valued signal can be constructed by applying Hermitian symmetry on the subcarriers, there are several methods to accomplish unipolarity. The two most prominent ones are direct current-biased optical (DCO)-OFDM and asymmetrical clipped optical (ACO)-OFDM [4]. In this work, only DCO-OFDM is investigated so far. It follows the principle to add a bias signal to the time-domain signal that shifts it to positive values only. In optical transmission systems, this is usually realized by the direct current that is added to adjust the operating point of the transmitting diode. According to the central limit theorem, OFDM signals tend to be Gaussian distributed in time domain when at least 64 subcarriers are used, resulting in a high peak-to-average-power-ratio (PAPR). There are various methods to reduce the PAPR, such as selective mapping (SLM) [5] or pilot-assisted techniques [6]. However, these typically reduce the data rate of the system. Therefore, PAPR reduction techniques are not considered in this work. This implies that unipolarity can not be guaranteed, especially because it is of interest to keep the quotient between DC power and signal variance low, in order to modulate as much of the linear range of the transmit diode’s characteristic as possible. However, since the optical power can not become negative, the transmit signal is hard-limited (clipped) at zero. Furthermore, an extremely high peak in positive direction could destroy the transmitting diode in the worst case. To prevent this scenario and to achieve an optimal utilization of the digital-to-analog converter, the signal is symmetrically clipped. This clipping is a non-linear process that distorts the signal. A lot of research has been performed on this topic in the past years [7,8]. Tsonev et al. model the complete non-linear distortion in an optical wireless communication system in [9] and Mazahir et al. calculate the achievable data rate for multi-carrier modulation in bandlimited IM/DD systems in [10]. Furthermore, in [11] the optimal power allocation among the subcarriers in an optical wireless communication OFDM-system is formulated and in [12] a receiver, based on decision aided reconstruction, is proposed to mitigate the clipping noise. All these works utilize the Bussgang theorem [13] to analytically describe the non-linear clipping distortion. However, the Bussgang theorem does not take into account the power spectral density of clipping noise. The asymptotic distortion spectrum of one-sided clipped Gaussian noise is calculated by Mazo et al. in [14], based on approximations made by Rice [15]. Similar approximations are used by one of the authors in order to calculate the error probability due to clipping in subcarrier-multiplexed fiber-optic systems [16].

In this work, the approximations are adapted to the case of symmetrical clipping and the power spectral density of clipping noise is calculated. The results are verified by Monte Carlo simulations. Additionally, the frequency dependence of the clipping distortion is investigated and the amount of noise power being located in the transmission bandwidth is determined.

In Section 2, the system model is explained. In Section 3, the Bussgang theorem is reviewed. This includes a detailed and comprehensive derivation, an evaluation by Monte Carlo simulations and a discussion of the results. In Section 4, the power spectral density of clipping noise is calculated, resulting in a well-fitting approximation that is verified by simulations. It is shown that the Bussgang theorem overestimates the clipping noise power in a practical system by at least 1.9 dB. Finally, in Section 5 conclusions of this work are presented.

2. System Model

The aim of this work is to find an analytical expression that describes the nonlinear distortion caused by hard-limiting (clipping) Gaussian distributed signals. As practical scenario a Free-Space Optical (FSO)-OFDM-transmission system is considered. Nevertheless, the results can be applied to other scenarios, such as clipping in analog-to-digital converters or nonlinear amplifiers, too. Since the DC offset required in intensity modulated optical transmission systems does not carry any information, it is not considered in this work. The system model is represented in Figure 1.

At first, an OFDM signal is generated based on a random bitstream. Note that hermitian symmetry is applied during the modulation to maintain a signal that is purely real-valued in time domain. Thus, for the modulated symbol $s_n$ on the n-th subcarrier, it holds:

$$s_n=\left\{\begin{array}{cc}{s}_{N-n+2}^{*}\in \mathcal{M}\hfill & \mathrm{for}2\le n\le \frac{N}{2}\hfill \\ 0\hfill & \mathrm{for}n=1,\frac{N}{2}+1,\hfill \end{array}\right.$$

(1)

where ${(·)}^{*}$ is the complex conjugate operator, N the total number of subcarriers (FFT-size) and $\mathcal{M}$ is the symbol alphabet of the respective modulation. No guard interval is added since a frequency-dependent channel is not considered in this work. Additionally, the benefits of a guard interval for optical OFDM-transmissions are neglectable anyway, since line-of-sight dominates [17]. After the inverse Fourier transform (IFFT), the OFDM signal is digital-to-analog converted and low-pass filtered. The converters and filters are assumed to be ideal in this work. Thus, no quantization noise occurs and the low-pass filters have an infinitely sharp slope at the corner frequency which is equal to the one-sided signal bandwidth. Nevertheless, the results can be applied on a real system very well, if the resolution of the converters is high enough. To compensate for the non-ideal filters, methods such as oversampling in the receiver can be utilized. The analog transmit signal is denoted as x. In terms of simplicity, the dependency of the time t is not noted in the following. Nevertheless, all signals are considered as random processes.

Next, the signal is transmitted over a nonlinear memoryless characteristic that represents a two-sided hard limiter. If the input signal rises above or below a certain threshold $\pm A$, it is limited to this value. For the clipped output signal, denoted as $x_{\mathrm{c}}$, it holds:

$$x_{\mathrm{c}}=\left\{\begin{array}{cc}x\hfill & \mathrm{for}\left|x\right|\le A,\hfill \\ A\hfill & \mathrm{for}x>A,\hfill \\ -A\hfill & \mathrm{for}x<-A.\hfill \end{array}\right.$$

(2)

Furthermore, the clipping level A and the standard deviation ${\sigma }_x$ of the transmit signal x, which are known to the receiver, are used to calculate a linear damping factor K, that will be introduced in Section 3.1.1. This factor is later on used for zero forcing equalization in the receiver. The optical channel, including the frequency response of the photoreceiver, is assumed to be ideal and thermal noise is neglected since the focus of this work is laid on the clipping distortion exclusively.

At the receiver, the clipped signal $x_{\mathrm{c}}$ is low-pass filtered to prevent out-of-band-noise to fall into the signal band during analog-to-digital conversion due to aliasing. This low-pass filter can be switched on and off and is a crucial aspect in this work as will be shown later. Afterwards, conventional signal processing of an OFDM-receiver with respect to Hermitian symmetry is performed.

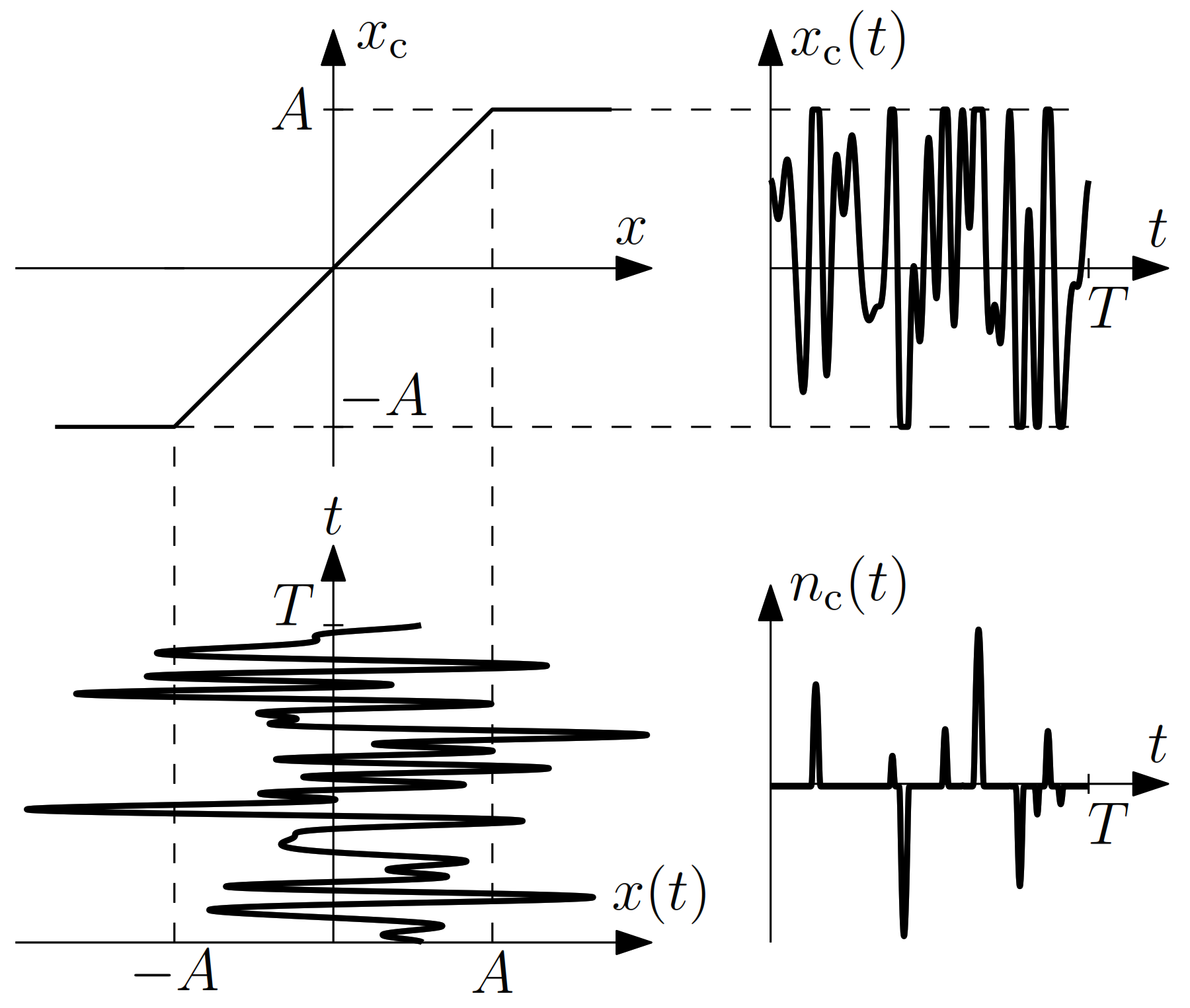
3. Review of the Bussgang Theorem

In this section, the representation of clipping distortion using the Bussgang theorem is considered. In the first subsection, the mathematical derivation is shown in detail for easy comprehension. Afterwards, the signal-to-noise power ratio and the resulting symbol error probability are calculated based on the previous results. This is verified by Monte Carlo simulations. It is shown that the analytical result only fits for the case of not low-pass filtering the clipped signal $x_{\mathrm{c}}$, leading to the conclusion that a part of the clipping distortion power is located outside of the transmission bandwidth.

3.1. Mathematical Derivation of the Bussgang Theorem

The main idea of the Bussgang theorem is to divide the non-linear distortion in two parts. Firstly, the transmit signal x becomes damped by a linear factor K, which represents the correlated distortion. Secondly, uncorrelated noise is added to the damped signal. Thus, the clipped signal $x_{\mathrm{c}}$ is stated to be [7,8]:

$$x_{\mathrm{c}}=K·x+u.$$

(3)

Based on the non-linear characteristic of a hard limiter shown in (2), the clipped signal $x_{\mathrm{c}}$ can also be described using the following equation:

$$x_{\mathrm{c}}=x-n_{\mathrm{c}}.$$

(4)

where $n_{\mathrm{c}}$ is the part of x rising above or below the thresholds $\pm A$. The damping factor K and the variance ${\sigma }_u^2$ of the uncorrelated additive noise u are calculated in the following. Note that x is Gaussian distributed and all random processes in (3) and (4) are zero-mean.

3.1.1. Calculation of the Linear Damping Factor K

The linear damping factor K in (3) can be expressed as follows:

$$\begin{array}{cc}\hfill K& =\frac{K·\mathrm{E}\left\{x^2\right\}}{\mathrm{E}\left\{x^2\right\}}\hfill \\ \hfill & =\frac{K·\mathrm{E}\left\{x^2\right\}+\mathrm{E}\{u·x\}-\mathrm{E}\{u·x\}}{\mathrm{E}\left\{x^2\right\}}\hfill \\ \hfill & =\frac{\mathrm{E}\left\{\right(K·x+u)·x\}-\mathrm{E}\{u·x\}}{\mathrm{E}\left\{x^2\right\}}\hfill \\ \hfill & =\frac{\mathrm{E}\{x_{\mathrm{c}}·x\}-\mathrm{E}\{u·x\}}{\mathrm{E}\left\{x^2\right\}}\hfill \\ \hfill & =\frac{\mathrm{Cov}\{x_{\mathrm{c}},x\}-\mathrm{Cov}\{u,x\}}{{\sigma }_x^2}\hfill \end{array}$$

(5)

with $\mathrm{E}\{·\}$ being the expectation operator, $\mathrm{Cov}\{a,b\}$ representing the covariance of the random processes a and b and ${\sigma }_x^2$ being the variance of the transmit signal x.

Following the assumption that x and u are uncorrelated and zero-mean, $\mathrm{Cov}\{u,x\}$ equals zero. Thus, only $\mathrm{Cov}\{x_{\mathrm{c}},x\}$ has to be calculated (see Appendix A.1):

$$\mathrm{Cov}\{x_{\mathrm{c}},x\}={\sigma }_x^2·\mathrm{erf}\left(\frac{A}{\sqrt{2}{\sigma }_x}\right),$$

(6)

with $\mathrm{erf}(·)$ being the Gaussian error function. Inserting the results in (5), the final expression for K is given by:

$$K=\mathrm{erf}\left(\frac{A}{\sqrt{2}{\sigma }_x}\right)$$

(7)

and matches the results in [7,8]. Note that $1-K$ is equal to the probability of the process x being symmetrically clipped at the levels $\pm A$ (see (28)).

3.1.2. Calculation of the Noise Variance ${\sigma }_u^2$

To calculate the variance ${\sigma }_u^2$ of the uncorrelated additive noise u, the law of power conservation is used. Thus, the first step is to calculate the power difference $\Delta {\sigma }^2$ between the information signal x and its clipped version $x_{\mathrm{c}}$. Since they are correlated to each other, this does not simply result in the variance of $n_{\mathrm{c}}$, what is shown below:

$$\begin{array}{cc}\hfill \Delta {\sigma }^2& ={\sigma }_x^2-{\sigma }_{x_{\mathrm{c}}}^2\hfill \\ \hfill & =\mathrm{E}\left\{x^2\right\}-\mathrm{E}\left\{x_{\mathrm{c}}^2\right\}\hfill \\ \hfill & =\mathrm{E}\left\{{(x_{\mathrm{c}}+n_{\mathrm{c}})}^2\right\}-\mathrm{E}\left\{x_{\mathrm{c}}^2\right\}\hfill \\ \hfill & =\mathrm{E}\left\{n_{\mathrm{c}}^2\right\}+2·\mathrm{E}\{x_{\mathrm{c}}·n_{\mathrm{c}}\}\hfill \\ \hfill & ={\sigma }_{n_{\mathrm{c}}}^2+2·\mathrm{Cov}(x_{\mathrm{c}},n_{\mathrm{c}}).\hfill \end{array}$$

(8)

The probability density function of x and $n_{\mathrm{c}}$ are shown in Figure 2 and used to calculate the variance ${\sigma }_{n_{\mathrm{c}}}^2$ as a first part of the power difference $\Delta {\sigma }^2$.

The weight of the delta function, which describes its area, is equal to the probability of the signal x not being clipped, which equals the damping factor K (see (7) and (28)). Thus, the clipping noise $n_{\mathrm{c}}$ becomes zero with the probability K. Nevertheless, since the delta function is located at $n_{\mathrm{c}}=0$, it does not contribute to the variance and can be neglected. It follows:

$$\begin{array}{cc}\hfill {\sigma }_{n_{\mathrm{c}}}^2& ={\int }_{-\infty }^{\infty }{n}_{\mathrm{c}}^2·f_{n_{\mathrm{c}}}\left(n_{\mathrm{c}}\right)\mathrm{d}{n}_{\mathrm{c}}\hfill \\ \hfill & =2·{\int }_0^{\infty }{n}_{\mathrm{c}}^2·f_{n_{\mathrm{c}}}\left(n_{\mathrm{c}}\right)\mathrm{d}{n}_{\mathrm{c}}\hfill \\ \hfill & =2·{\int }_0^{\infty }{n}_{\mathrm{c}}^2·f_x(n_{\mathrm{c}}+A)\mathrm{d}{n}_{\mathrm{c}}\hfill \\ \hfill & =2·{\int }_A^{\infty }{(x-A)}^2·f_x\left(x\right)\mathrm{d}x.\hfill \end{array}$$

(9)

Now, the covariance $\mathrm{Cov}(x_{\mathrm{c}},n_{\mathrm{c}})$ has to be calculated. Combining (2) and (3), the clipping distortion $n_{\mathrm{c}}$ results in:

$$n_{\mathrm{c}}=\left\{\begin{array}{cc}0\hfill & \mathrm{for}\left|x\right|\le A,\hfill \\ x-A\hfill & \mathrm{for}x>A,\hfill \\ x+A\hfill & \mathrm{for}x<-A.\hfill \end{array}\right.$$

(10)

Thus, for the covariance $\mathrm{Cov}(x_{\mathrm{c}},n_{\mathrm{c}})$ holds:

$$\begin{array}{cc}\hfill \mathrm{Cov}(x_{\mathrm{c}},n_{\mathrm{c}})& =\mathrm{E}\{x_{\mathrm{c}}·n_{\mathrm{c}}\}\hfill \\ \hfill & =\mathrm{E}\{x·0|\left|x\right|\le A\}+\mathrm{E}\{A·(x-A)|x>A\}+\mathrm{E}\{-A·(x+A\left)\right|x<-A\}\hfill \\ \hfill & =2·\mathrm{E}\{A·(x-A\left)\right|x>A\}\hfill \\ \hfill & =2·{\int }_A^{\infty }A·(x-A)·f_x\left(x\right)\mathrm{d}x.\hfill \end{array}$$

(11)

Inserting (9) and (11) in (8), the final result for the power difference $\Delta {\sigma }^2$ is calculated as (see Appendix A.2):

$$\begin{array}{c}\hfill \Delta {\sigma }^2={\sigma }_x^2\left[\sqrt{\frac{2}{\pi }}\frac{A}{{\sigma }_x}·\exp \left[-\left(\frac{A^2}{2{\sigma }_x^2}\right)\right]+\left(1-\frac{A^2}{{\sigma }_x^2}\right)·\mathrm{erfc}\left(\frac{A}{\sqrt{2}{\sigma }_x}\right)\right].\end{array}$$

(12)

Since the summands in (3) are uncorrelated, considering (4) as well, for the power of the clipped signal ${\sigma }_{x_{\mathrm{c}}}^2$, it holds:

$${\sigma }_{x_{\mathrm{c}}}^2={\sigma }_x^2-\Delta {\sigma }^2=K^2{\sigma }_x^2+{\sigma }_u^2$$

(13)

Thus, the uncorrelated noise variance ${\sigma }_u^2$, using the results from (7) and (12), is given by:

$$\begin{array}{cc}\hfill {\sigma }_u^2& ={\sigma }_x^2(1-K^2)-\Delta {\sigma }^2\hfill \\ \hfill {\sigma }_u^2& ={\sigma }_x^2·\left[1-{\mathrm{erf}}^2\left(\frac{A}{\sqrt{2}{\sigma }_x}\right)-\sqrt{\frac{2}{\pi }}\frac{A}{{\sigma }_x}·\exp \left[-\left(\frac{A^2}{2{\sigma }_x^2}\right)\right]-\left(1-\frac{A^2}{{\sigma }_x^2}\right)·\mathrm{erfc}\left(\frac{A}{\sqrt{2}{\sigma }_x}\right)\right]\hfill \end{array}$$

(14)

This expression matches the result in [7,8] as well.

3.2. Symbol Error Probability Based on the Bussgang Theorem

To find an analytical expression for the symbol error probability in multicarrier-transmission systems that suffer from clipping based on the Bussgang Theorem, the signal-to-noise power ratio has to be calculated first. The clipped signal $x_{\mathrm{c}}$ is transformed into frequency domain using the discrete Fourier transformation (DFT) in the receiver. Due to this process and utilizing the central limit theorem, the uncorrelated additive noise u is assumed to be Gaussian distributed in frequency domain [7]. Therefore, the received signal in frequency domain results in:

$$X_{\mathrm{c}}=K·X+U,$$

(15)

where the capital quantities are the frequency correspondences of their low case versions (compare (3)) with their variances not being affected by the DFT due to Parseval’s theorem. As stated in the system model, additional thermal noise is neglected and an ideal channel is assumed. Thus, the signal-to-noise power ratio $\gamma$ results in:

$$\gamma =\frac{K^2·{\sigma }_x^2}{{\sigma }_u^2}.$$

(16)

Note that the signal-to-noise power ratio is not depending on the subcarrier index here meaning that the distortion is assumed to be frequency-independent. This is one of the main motivations for this work, because, at least for cases of strong clipping, a certain frequency dependence is expected.

For Gaussian distributed additive noise, the symbol error probability ${\mathrm{P}}_S$ of a $2^M$-PAM can be calculated with the formula [18]:

$${\mathrm{P}}_{\mathrm{S},2^M-\mathrm{PAM},1/2}=\frac{\sqrt{2^M}-1}{\sqrt{2^M}}·\mathrm{erfc}\left(\sqrt{\frac{3}{2^M-1}·\frac{\gamma }{2}}\right).$$

(17)

Note that the useful power has been divided by two since the QAM is a two-dimensional modulation technique. Thus for the symbol error probability of a $2^M$-QAM, it follows:

$${\mathrm{P}}_{\mathrm{S},2^M-\mathrm{QAM}}=1-{(1-{\mathrm{P}}_{\mathrm{S},2^M-\mathrm{PAM},1/2})}^2.$$

(18)

To verify this result, Monte Carlo simulations based on the system model in Section 2 are carried out. The most important simulation and evaluation parameters are shown in

Table 1. Parameters used in this work for the evaluation of the analytical and theoretical expressions, as well as for the Monte Carlo simulations.

Parameter	Shortcut	Value
Subcarriers	N	8192
Bandwidth	B	$200\mathrm{MHz}$
Oversampling factor	–	50
Modulation order	M	2:2:10
Signal power	${\sigma }_x^2$	1
Clipping level	A	0.1:0.1:4

.

The convergence of OFDM towards a Gaussian distribution due to the central limit theorem is becoming closer with an increasing number of subcarriers. Since all calculations are based on a Gaussian distributed transmit signal x, it is important to meet this assumption as good as possible. Thus, a high number of $N=8192\mathrm{subcarriers}$ is used in this work. The double-sided system bandwidth B is chosen to be $200\mathrm{MHz}$ resulting in the corner frequency $f_{\mathrm{c}}$ of the information signal being $100\mathrm{MHz}$. This value is chosen since it provides a fairly high transmission rate and is still in range of the modulation bandwidth of modern optical communication devices. To correctly model the clipping of analog signals, the transmit signal x is oversampled by a factor of 50. The modulation order M is varied from two to ten in steps of two. While the transmit signal variance ${\sigma }_x^2$ is constantly set to one, the clipping level A is varied to investigate differently strong clipping scenarios. If not stated otherwise, this parameters hold for the evaluations and simulations of the entire work.

First, the low-pass filter after the clipping process is not used meaning that the out-of-band power of the clipping distortion is disturbing the demodulation due to aliasing. The simulation results for this case are compared to the theoretical results based on (18) and shown in Figure 3.

It can be seen that the analytical results based on the Bussgang theorem match the simulated data very well. The small deviation that occurs for high clipping levels A is caused by the fact that the signal is still not exactly Gaussian distributed even though a very high number of subcarriers N is used [8]. Thus, it is shown that the Bussgang theorem holds very well for the case that the out-of-band clipping distortion power still disturbs the demodulation.

Next, the clipped signal $x_{\mathrm{c}}$ is low-pass filtered before analog-to-digital conversion which means that all spectral components outside of the transmission bandwidth B are filtered out. The resulting symbol error probabilities for this case are shown in Figure 4.

The performance of the simulated system has increased, proving that a part of the distortion power is located outside of the transmission bandwidth B. This investigation and the assumption of a certain frequency selectivity raise the motivation to find an alternative way to describe the non-linear distortion of hard-limited Gaussian distributed signals that solves the problems stated above. A well-fitting solution for this is presented in the upcoming Section 4.

4. Power Spectral Density of the Clipping Distortion

In this section, an analytical expression for the power spectral density of clipping noise is found. Monte Carlo simulations show that this result fits for high clipping levels A but perform poorly for strong clipping. Based on the simulated and analytical results, an approximation for the power spectral density of the uncorrelated part of the clipping distortion inside the transmission bandwidth B is made. Together with the damping factor K, representing the correlated part of the clipping distortion, this expression allows to calculate the exact signal-to-noise power ratio on every single subcarrier separately. Additionally, the power spectral density is used to investigate the spectral distribution of the clipping distortion.

4.1. Analytical Calculation of the Power Spectral Density of Clipping Noise

At first, the approximations that are assumed to calculate a closed-form expression for the power spectral density are explained.

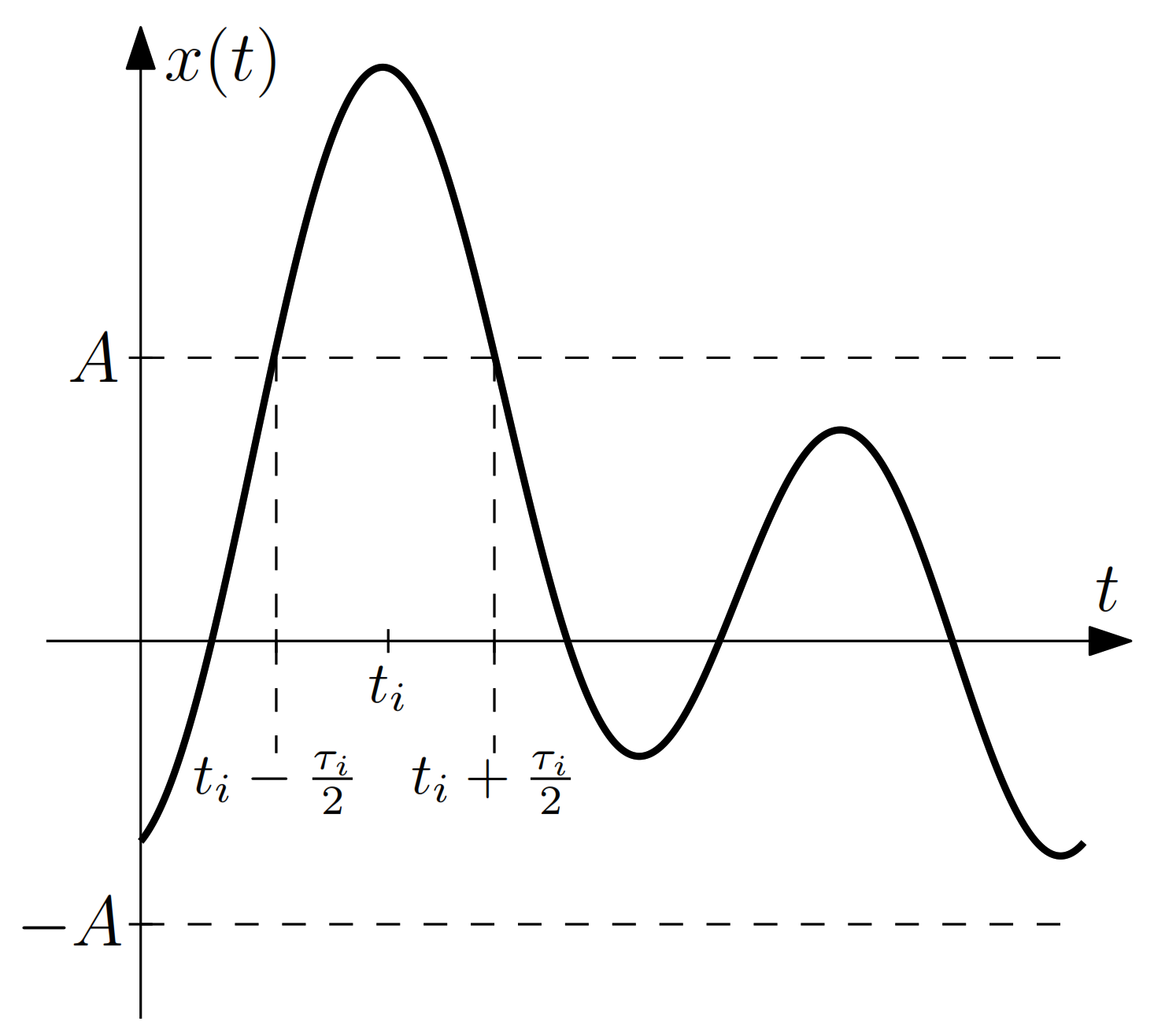
4.1.1. Clipping Level Crossing

An exemplary realization of the Gaussian distributed signal x is shown in Figure 5, crossing the positive clipping level A at the time $t_i-\frac{{\tau }_i}{2}$ where $t_i$ is the center time and ${\tau }_i$ is the duration of this i-th overshooting.

The occurrence of these overshootings of a Gaussian distributed signal x with the standard deviation ${\sigma }_x$ on a high level A is random and can be described by a Poisson process [14]. The probability that k overshootings occur in a time period T is equal to [19]:

$$\mathrm{P}\left(k\right)={\mathrm{e}}^{-\lambda ·T}·\frac{{(\lambda ·T)}^k}{k!}$$

(19)

with $\lambda$ being the intensity of the Poisson process for which, in case of one-sided clipping, holds [15]:

$${\lambda }_{\mathrm{asym}}=\frac{1}{2\pi }\frac{{\stackrel{·}{\sigma }}_x}{{\sigma }_x}\exp \left(-\frac{A^2}{2{\sigma }_x^2}\right)$$

(20)

with ${\stackrel{·}{\sigma }}_x$ being the standard deviation of the time derivative of x. Two adjustments are now made to this assumption.

First, since the case of symmetrical clipping is investigated, the intensity is doubled. This is a sufficient approximation since (20) only holds for high clipping levels. Hence, for the intensity of a symmetrical clipping process, it holds:

$${\lambda }_{\mathrm{sym}}=\frac{1}{\pi }\frac{{\stackrel{·}{\sigma }}_x}{{\sigma }_x}\exp \left(-\frac{A^2}{2{\sigma }_x^2}\right).$$

(21)

Secondly, the ratio of the standard deviations $\stackrel{·}{{\sigma }_x}/{\sigma }_x$ is calculated for the case of equally distributed power on all subcarriers in the signal bandwidth B. Furthermore, the information signal is expected to be in the baseband. Thus, the power spectral density of the signal has the constant value $S_0$ for $-B/2$ to $B/2$.

For ${\sigma }_x^2$ it holds:

$${\sigma }_x^2=\frac{1}{2\pi }{\int }_{-\pi B}^{\pi B}{S}_0\mathrm{d}\omega =S_{0}B$$

(22)

and for ${\stackrel{·}{\sigma }}_x^2$:

$${\stackrel{·}{{\sigma }_x}}^2=\frac{1}{2\pi }{\int }_{-\pi B}^{\pi B}{S}_0{\left|\mathrm{j}\omega \right|}^2\mathrm{d}\omega =\frac{S_0{B}^3{\pi }^2}{3}.$$

(23)

Hence, the ratio of the variances is given by:

$${\left[\frac{{\stackrel{·}{\sigma }}_x}{{\sigma }_x}\right]}^2=\frac{B^2{\pi }^2}{3}.$$

(24)

Finally, inserting (24) in (21), the intensity for the Poisson process results in:

$${\lambda }_{\mathrm{sym}}=\frac{B}{\sqrt{3}}\exp \left(-\frac{A^2}{2{\sigma }_x^2}\right).$$

(25)

4.1.2. Duration of an Overshooting

The duration $\tau$ of an overshooting, describing the time that the signal x is above or below the clipping level $\pm A$, is approximately Rayleigh-distributed [14]:

$$f_{\tau }\left(\tau \right)=\frac{\pi }{2}\frac{\tau }{{\overline{\tau }}^2}\exp \left(-\frac{\pi }{4}{\left(\frac{\tau }{\overline{\tau }}\right)}^2\right),\tau \ge 0$$

(26)

with $\overline{\tau }$ being the expectation of $\tau$ that can be calculated as the ratio of the intensity of the Poisson process ${\lambda }_{\mathrm{sym}}$ to the clipping probability $P_{\mathrm{clip}}$:

$${\lambda }_{\mathrm{sym}}\overline{\tau }=P_{\mathrm{clip}}\iff \overline{\tau }=\frac{P_{\mathrm{clip}}}{{\lambda }_{\mathrm{sym}}}.$$

(27)

The double-sided clipping probability can be calculated as:

$$\begin{array}{cc}\hfill P_{\mathrm{clip}}& =\mathrm{P}(x>A)+\mathrm{P}(x<-A)\hfill \\ \hfill & =2·\mathrm{P}(x>A)\hfill \\ \hfill & =2·{\int }_A^{\infty }\frac{1}{\sqrt{2\pi {\sigma }_x^2}}\exp \left(-\frac{x^2}{2{\sigma }_x^2}\right)\mathrm{d}x=\mathrm{erfc}\left(\frac{A}{\sqrt{2}{\sigma }_x}\right).\hfill \end{array}$$

(28)

Figure 6 shows the evaluation of (28) and corresponding simulation results for different clipping levels A.

Inserting (28) in (27), the expectation of $\tau$ results in:

$$\overline{\tau }=\frac{1}{{\lambda }_{\mathrm{sym}}}\mathrm{erfc}\left(\frac{A}{\sqrt{2}{\sigma }_x}\right).$$

(29)

4.1.3. Mathematical Description of an Overshooting

Note that, in this subsection, different from the rest of this work, the time dependency of the signals is noted to distinguish between time and frequency domain. The shape of one single overshooting of the signal $x\left(t\right)$ above the clipping level A at $t=0$ can be approximated as a parabolic arc $n(t,\tau )$ with the random variable $\tau$ being the width [14]:

$$n(t,\tau )=\frac{A}{2}{\left[\frac{{\stackrel{·}{\sigma }}_x}{{\sigma }_x}\right]}^2·\left[t^2-\frac{1}{4}{\tau }^2\right]$$

(30)

and the corresponding Fourier transform:

$$N(\omega ,\tau )=A{\left[\frac{{\stackrel{·}{\sigma }}_x}{{\sigma }_x}\right]}^2·\frac{\tau }{{\omega }^2}\left[\sin \mathrm{c}\left(\frac{\omega \tau }{2}\right)-\cos \left(\frac{\omega \tau }{2}\right)\right].$$

(31)

4.1.4. Closed-Form Analytical Expression of the Power Spectral Density

To calculate the power spectral density of the clipping distortion, a sample function in the time interval T is shown in Figure 7.

The clipped signal $x_{\mathrm{c}}\left(t\right)$ is equal to the input signal $x\left(t\right)$ minus the distortion $n_{\mathrm{c}}\left(t\right)$.

$$x_{\mathrm{c}}\left(t\right)=x\left(t\right)-n_{\mathrm{c}}\left(t\right).$$

(32)

The distortion can be represented by the superposition of all occurring over- and undershootings in this time interval:

$$n_{\mathrm{c}}(t,t_i,{\tau }_i)=\sum _{i=1}^{\overline{N}}{n}_i·n(t-t_i,{\tau }_i)$$

(33)

with $\overline{N}$ being the expected number of over- and undershootings in the time interval T, $t_i$ being the center and ${\tau }_i$ the duration of the i-th over- or undershooting. The random sign factors $n_i$ take the values $+1$ and $-1$ equally distributed.

Transforming this expression into frequency domain results in:

$$N_{\mathrm{c}}(\omega ,t_i,{\tau }_i)=\sum _{i=1}^{\overline{N}}{n}_i·N(\omega ,{\tau }_i)·\exp (-\mathrm{j}\omega t_i)$$

(34)

To calculate the power spectral density of the distortion induced by the symmetrical clipping of the signal $x\left(t\right)$, the Wiener–Khinchin theorem is used:

$$S_{n_{\mathrm{c}}{n}_{\mathrm{c}}}\left(\omega \right)=\underset{T\to \infty }{\lim }\frac{\mathrm{E}\left\{\right|N_{\mathrm{c}}(\omega ,t_i,{\tau }_i){|}^2\}}{T}.$$

(35)

The expectation $\mathrm{E}\{·\}$ of the squared magnitude of the spectrum of all overshootings in T is equal to $\overline{N}$ times the squared magnitude of one single overshooting [14]:

$$\mathrm{E}\left\{\right|N_{\mathrm{c}}(\omega ,t_i,{\tau }_i){|}^2\}=\overline{N}\mathrm{E}\left\{\right|N(\omega ,\tau ){|}^2\}.$$

(36)

Note that the DC-term that is neglected in [14] completely vanishes here since symmetrical clipping is investigated.

Using this and the relation $\overline{N}={\lambda }_{\mathrm{sym}}·T$, the power spectral density can be calculated as:

$$S_{n_{\mathrm{c}}{n}_{\mathrm{c}}}\left(\omega \right)={\lambda }_{\mathrm{sym}}·{\mathrm{E}\left\{\right|N(\omega ,\tau )|}^2\}.$$

(37)

In the next step, the expectation with respect to $\tau$ has to be calculated. Using (31) and substituting the term ${\left[\frac{{\stackrel{·}{\sigma }}_x}{{\sigma }_x}\right]}^{2}A=a$, the following result can be obtained:

$$\begin{array}{cc}\hfill \mathrm{E}\left\{\right|N(\omega ,& {\tau \left)\right|}^2\}=\mathrm{E}\left\{|a·\frac{\tau }{{\omega }^2}\left[\mathrm{sinc}\left(\frac{\omega \tau }{2}\right)-\cos \left(\frac{\omega \tau }{2}\right)\right]{|}^2\right\}\hfill \\ \hfill & =a^2·\mathrm{E}\left\{\frac{{\tau }^2}{{\omega }^4}{\left[\mathrm{sinc}\left(\frac{\omega \tau }{2}\right)-\cos \left(\frac{\omega \tau }{2}\right)\right]}^2\right\}\hfill \end{array}$$

(38)

The challenge is to calculate the expectation value with $\tau$ being Rayleigh distributed according to (26). In [14], a solution for this problem is given as:

$${\mathrm{E}\left\{\right|N(\omega ,\tau )|}^2\}=a^2\underset{E(\omega ,\overline{\tau })}{\underbrace{\frac{2{\overline{\tau }}^3}{{\pi }^2{\omega }^3}\left[\left(\sqrt{\pi }+\frac{2{\overline{\tau }}^2{\omega }^2}{\sqrt{\pi }}\right)\mathrm{D}\left(\frac{\overline{\tau }\omega }{\sqrt{\pi }}\right)-\overline{\tau }\omega \right]}}.$$

(39)

with $\mathrm{D}\left(x\right)$ being the Dawson integral which is defined as:

$$\mathrm{D}\left(x\right)=\exp (-x^2){\int }_0^x\exp \left(t^2\right)\mathrm{d}t.$$

(40)

Inserting (39) in (37), replacing a again and utilizing (24), the final expression for the power spectral density results in:

$$S_{n_{\mathrm{c}}{n}_{\mathrm{c}}}\left(\omega \right)={\lambda }_{\mathrm{sym}}\frac{{\pi }^4{B}^4}{9}{A}^{2}E(\omega ,\overline{\tau }),$$

(41)

where ${\lambda }_{\mathrm{sym}}$ and $\overline{\tau }$ can be calculated using (21) and (29).

This analytical closed-form solution is now evaluated for different clipping levels A and compared to simulated results in Figure 8. Note that the simulated power spectral density only represents the uncorrelated part of the clipping distortion. Although the analytical expression based on (41) match the simulated curves very well for higher clipping levels A, the deviation increases for decreasing clipping levels. To evaluate this deviation, the signal-to-noise power ratio and the resulting symbol error probability are calculated and compared to simulated data in the following subsection.

To attain an idea of how much power of the uncorrelated clipping noise actually falls into the transmission bandwidth B, the integral over the simulated power spectral density is calculated and set in relation to the total power of the uncorrelated clipping noise. The result is shown in Figure 9. Even at the highest point, around $A=1.5$, only 64% of the uncorrelated clipping noise power is located inside the transmission bandwidth. Increasing the clipping level A from this point, the relative in-band power decreases continuously. This meets the expectation that the power spectral becomes constant for infinitely high clipping levels A, because in this case, the relative in-band power approaches zero. Thus, the clipping noise power is overestimated by at least $1.9\mathrm{dB}$, if the clipped signal is low-pass filtered, but the spectral distribution is not correctly considered. Hence, the importance of this work, where such a solution is provided, is underlined.

4.2. Symbol Error Probability Based on the Analytical Power Spectral Density of Clipping Noise

Since the variance ${\sigma }_x^2$ of the information signal x is set to one and the power is distributed equally on all subcarriers, its power spectral density $S_{xx}\left(f\right)$ is given as follows:

$$S_{xx}\left(f\right)=\left\{\begin{array}{cc}\frac{1}{B},\hfill & \mathrm{for}\left|f\right|\le B/2\hfill \\ 0,\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(42)

Thus, for the signal-to-noise power ratio ${\gamma }_n$ on the n-th subcarrier holds:

$${\gamma }_n=\frac{1/B}{S_{n_{\mathrm{c}}{n}_{\mathrm{c}}}(n\Delta f)},$$

(43)

with $\Delta f=B/N$ being the subcarrier spacing. The formulas from (17) and (18) are again used to calculate the symbol error probability. Since the signal-to-noise power ratio depends on the subcarrier index n, the error probability is firstly calculated for each subcarrier separately and averaged afterwards. The result is compared with the simulated data and shown in Figure 10.

Although the curves match quite well for high clipping levels A, the analytical results deviate significantly for strong clipping. Thus, the analytical calculated power spectral density can be used to correctly describe the non-linear distortion due to clipping for high clipping levels, but for strong clipping, this is not a sufficient solution. Nevertheless, this result is already closer to the simulated curves than the one provided by the Bussgang theorem (see Figure 4).

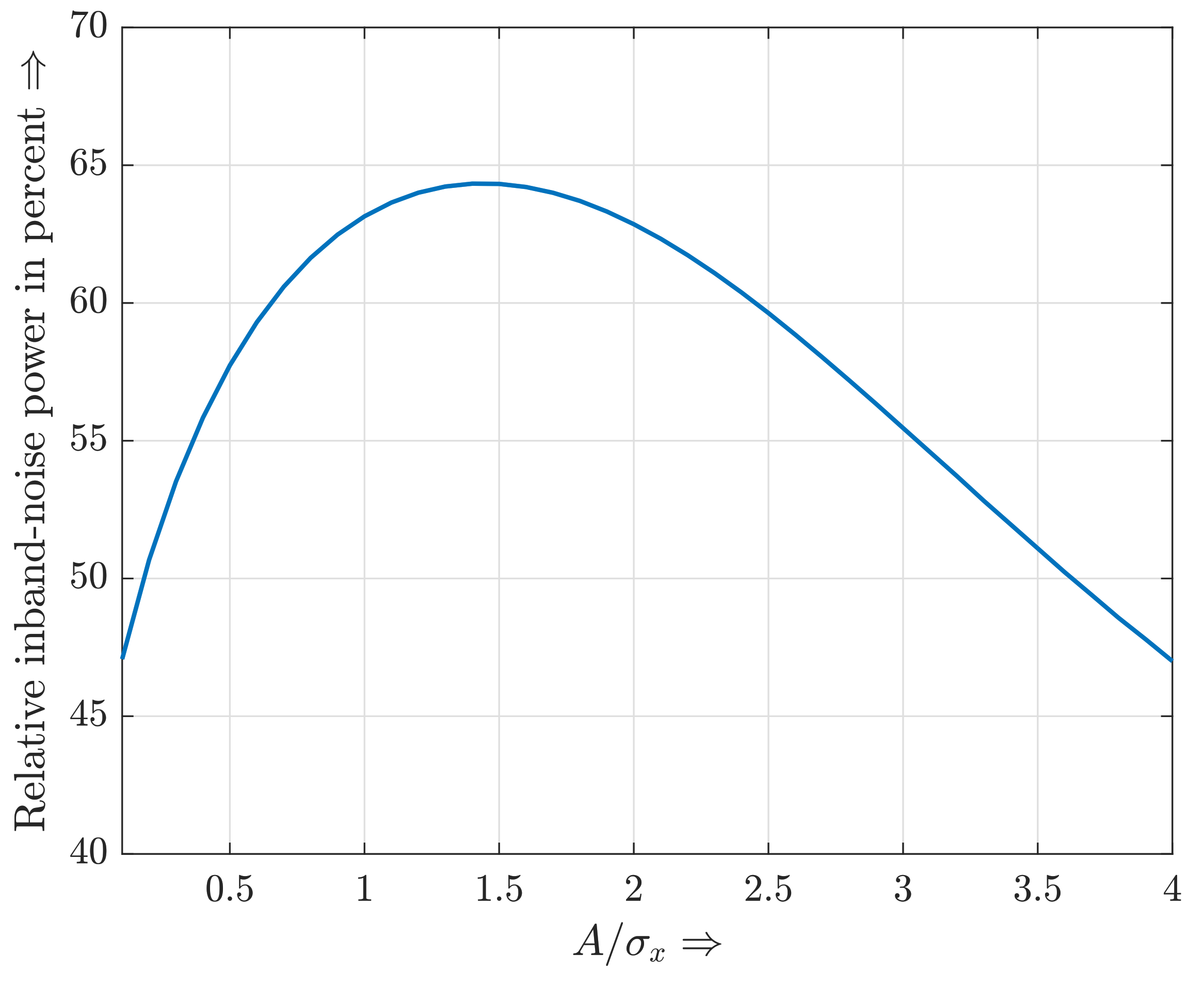
4.3. Approximated Power Spectral Density of Clipping Noise

To find an analytical expression for the power spectral density of clipping noise that provides a precise solution for strong clipping scenarios as well, an approximation based on the analytical and simulated results is made. From Figure 8, three observations are concluded:

• The simulated and analytical curves intersect at the corner frequency $f_{\mathrm{c}}=B/2$;
• The gain from $S_{n_{\mathrm{c}}{n}_{\mathrm{c}},\mathrm{dB}}(B/2)$ to $S_{n_{\mathrm{c}}{n}_{\mathrm{c}},\mathrm{dB}}\left(0\right)$ in dB appears to similar for all A; and
• The shape of the analytical curves in dB inside the transmission bandwidth can be approximated by a quadratic function and does not depend on A as well.

To verify the first point, the analytical and simulated power spectral densities are evaluated at $f=B/2$ and plotted in Figure 11. Note that only the uncorrelated part of the distortion is simulated. For $A=0$, the entire distortion is correlated and thus the power spectral density of the uncorrelated clipping noise is zero. As soon as only parts of the information signal are clipped, the correlated clipping noise decreases and additional uncorrelated clipping noise is generated, which explains the increasing trend for small values of A. As the clipping probability decreases with increasing A, a monotonically decreasing trend begins to dominate for higher clipping levels. Nevertheless, it is shown that the coincidence of the simulated and analytical power spectral density at $f=B/2$ holds for all values of A, even the very small ones.

Regarding the second point, the gain G that the simulated power spectral density in dB experiences rising from $f=B/2$ to $f=0$ is calculated from the simulated results and averaged over the clipping levels from $A=0.1$ to $A=4$. The mean ${\mu }_G$ and the standard deviation ${\sigma }_G$ are given as:

$${\mu }_G\approx 1.42\mathrm{dB};{\sigma }_G\approx 0.24\mathrm{dB}.$$

(44)

Even though the gain is slightly differing with respect to A, the standard deviation of ≈$0.24\mathrm{dB}$ is considered small enough to assume the gain to be constantly equal to the mean ${\mu }_G$. Note that an increase in the noise power of ≈$1.42\mathrm{dB}$ from the least to the most disturbed subcarrier is relatively small. In terms of practical applications, a bit-loading algorithm needs at least $3\mathrm{dB}$ to change the modulation order [20].

Based on the third observation, the slight frequency dependence of clipping noise can be described quite precisely: The shape of the power spectral density of the uncorrelated part of the clipping distortion in dB $S_{\mathrm{approx},\mathrm{dB}}\left(f\right)$ can be described by a negative quadratic function inside of the transmission band:

$$S_{\mathrm{approx},\mathrm{dB}}\left(f\right)=-{\left(\frac{f}{f_0}\right)}^2+S_0,$$

(45)

where $f_0$ represents the slope and $S_0$ is the power spectral density at $f=0$. It holds:

$$S_0=S_{n_{\mathrm{c}}{n}_{\mathrm{c}},\mathrm{dB}}(B/2)+{\mu }_G$$

(46)

and

$$f_0=\frac{B/2}{\sqrt{{\mu }_G}}.$$

(47)

The expression only depends on the analytically calculated power spectral density, evaluated at $B/2$, the empirically determined expectation of the gain ${\mu }_G$, according to (44), and the system bandwidth B. Note that ${\mu }_G$ does not depend on B itself. The result is evaluated and compared to the simulated power spectral density in Figure 12. It is shown that the approximation fits the simulated power spectral density of the uncorrelated clipping noise inside the system bandwidth B very well.

4.4. Symbol Error Probability Based on the Approximated Power Spectral Density of Uncorrelated Clipping Noise

Based on the approximated power spectral density, the signal-to-noise power ratio and symbol error probability are calculated. Since the approximated power spectral density only represents the uncorrelated part of the clipping noise, the damping factor K has to be considered as well. Thus, for the signal-to-noise power ratio ${\gamma }_{n,\mathrm{approx}}$ on the n-th subcarrier follows:

$${\gamma }_{n,\mathrm{approx}}=\frac{K^2/B}{{10}^{\frac{S_{\mathrm{approx},\mathrm{dB}}(n\Delta f)}{10}}}$$

(48)

with $\Delta f=B/N$ being the subcarrier spacing. The overall symbol error probability is calculated, such as in Section 4.2, inserting the new expression for the signal-to-noise power ratio. The result is shown in Figure 13.

The curves match the simulated data very well. The deviation for high clipping levels resulting in very rare clipping is again caused by the OFDM-signal not being perfectly Gaussian distributed even though a very high number of subcarriers $N=8192$ was used in the simulations. Overall, a very well-fitting solution to analytically describe the signal-to-noise power ratio on every single subcarrier for an OFDM-transmission system that suffers from clipping is presented and verified.

5. Conclusions

In this work, the Bussgang theorem, which is commonly used to analytically describe the non-linear distortion of Gaussian distributed signals that suffer from clipping, is reviewed. First, the mathematical calculations are carried out and explained step by step in a comprehensive way. To the best of the author’s knowledge, such a detailed derivation is not available in the literature yet. Afterwards, the Bussgang theorem is used to theoretically calculate the signal-to-noise power ratio of an OFDM transmission system that suffers from clipping. Based on the signal-to-noise power ratio, the symbol error probability is determined and verified by Monte Carlo simulations. It is shown that the Bussgang theorem provides a sufficient solution, as long as the clipped signal is not low-pass filtered before being further processed at the receiver. However, in order to minimize the error probability, the received signal needs to be low-pass filtered. For this case, the resulting symbol error probability decreases significantly and the result provided by the Bussgang theorem does not match any more. This proves that a part of the clipping distortion is located outside of the transmission bandwidth. Furthermore, the Bussgang theorem does not take into account the frequency-dependent power spectral density of the clipping noise.

To solve both of these problems, an analytical expression for the power spectral density of the clipping noise is derived, which can be used to calculate the signal-to-noise power ratio on each subcarrier separately. To find a closed-form solution, approximations are made. It was verified by simulations that the result is only valid for rare clipping scenarios, leading to the conclusion that the approximations are invalid for strong clipping. By investigating the simulated result for the power spectral density and comparing it with the analytical solution, an approximation for the power spectral density of the uncorrelated part of the clipping noise inside of the transmission bandwidth is made. This approximation only depends on the analytically calculated power spectral density, evaluated at the corner frequency, the bandwidth of the transmitted signal and an empirically determined gain value. A verification by the simulated symbol error probabilities results in a very good match. Thus, a very easy-to-apply solution has been found to correctly describe the non-linear distortion of hard limited Gaussian distributed signals.

Furthermore, it is shown that at least 36% of the power of the uncorrelated clipping noise, depending on the clipping level, is not located inside the transmission bandwidth. Additionally, the clipping distortion is showing a slight frequency dependence.

This work points out the relevance of correctly considering the spectral distribution of clipping noise in multicarrier transmission systems. In the future, the exact knowledge of the power spectral density of the clipping noise can be utilized to calculate important quantities such as the channel capacity or optimal bit allocation tables for bit-loading algorithms. Additionally, the analytical calculation of the bit error probability in an optical wireless communication system can be calculated more precisely than in the literature, since the Bussgang theorem overestimates the clipping noise.