A Study of Seven Asymmetric Kernels for the Estimation of Cumulative Distribution Functions
Abstract
:- Gamma, inverse Gamma, LogNormal, inverse Gaussian, reciprocal inverse Gaussian, Birnbaum–Saunders and Weibull kernels, when the target density is supported on , see, e.g., Chen [3], Jin and Kawczak [21], Scaillet [22], Bouezmarni and Scaillet [23], Fernandes and Monteiro [14], Bouezmarni and Rombouts [16], fBouezmarni and Rombouts [24], Bouezmarni and Rombouts [25], Igarashi and Kakizawa [26,27], Charpentier and Flachaire [28], Igarashi [29], Zougab and Adjabi [30], Kakizawa and Igarashi [31], Kakizawa [32], Zougab et al. [33], Zhang [34], Kakizawa [35];
1. The Models
- distribution (with the shape/scale parametrization);
- distribution (with the shape/scale parametrization);
- distribution;
- distribution;
- distribution;
- distribution;
- distribution.
- The mode of the kernel function in (1) is x;
2. Outline, Assumptions and Notation
2.1. Outline
2.2. Assumptions
- The target c.d.f. F has two continuous and bounded derivatives;
- The smoothing (or bandwidth) parameter satisfies as .
2.3. Notation
3. Asymptotic Properties of the c.d.f. Estimator with Gam Kernel
4. Asymptotic Properties of the c.d.f. Estimator with IGam Kernel
5. Asymptotic Properties of the c.d.f. Estimator with LN Kernel
6. Asymptotic Properties of the c.d.f. Estimator with IGau Kernel
7. Asymptotic Properties of the c.d.f. Estimator with RIG Kernel
8. Numerical Study
- Burr , with the following parametrization for the density function:
- Gamma , with the following parametrization for the density function:
- Gamma , with the following parametrization for the density function:
- GeneralizedPareto , with the following parametrization for the density function:
- HalfNormal , with the following parametrization for the density function:
- LogNormal , with the following parametrization for the density function:
- Weibull , with the following parametrization for the density function:
- Weibull , with the following parametrization for the density function:
- denotes the estimator from (1) applied to the k-th sample;
- denotes the estimator from (2) applied to the k-th sample;
- denotes the estimator from (3) applied to the k-th sample;
- denotes the estimator from (4) applied to the k-th sample;
- denotes the estimator from (5) applied to the k-th sample;
- denotes the estimator from (6) applied to the k-th sample;
- denotes the estimator from (7) applied to the k-th sample;
- , where
- denotes the c.d.f. of the Epanechnikov kernel;
- is selected by minimizing the Leave-None-Out criterion from page 197 in [61];
- is the boundary modified kernel estimator from Example 2.3 in [57], where
- denotes the c.d.f. of the Epanechnikov kernel;
- is selected by minimizing the Cross-Validation criterion from page 180 in [57];
- is the empirical c.d.f. applied to the k-th sample.

| i | Gam () | IGam () | LN () | IGau () | RIG () | B-S () | W () | OK () | BK () | EDF () | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | ||
| 256 | 1 | 1.39 | 1.27 | 1.37 | 1.34 | 1.31 | 1.26 | 1.37 | 1.32 | 1.37 | 1.32 | 1.31 | 1.26 | 1.37 | 1.32 | 1.54 | 1.43 | 1.47 | 1.34 | 1.54 | 1.44 |
| 2 | 2.59 | 2.36 | 2.50 | 2.53 | 2.36 | 2.42 | 2.49 | 2.46 | 2.49 | 2.47 | 2.36 | 2.42 | 2.50 | 2.51 | 2.76 | 2.44 | 2.67 | 2.57 | 2.76 | 2.45 | |
| 3 | 6.70 | 6.28 | 6.77 | 6.58 | 6.62 | 6.28 | 6.69 | 6.45 | 6.69 | 6.45 | 6.62 | 6.28 | 6.74 | 6.54 | 7.44 | 7.01 | 6.70 | 6.39 | 7.44 | 7.00 | |
| 4 | 3.74 | 3.14 | 3.60 | 3.27 | 3.36 | 3.15 | 3.61 | 3.20 | 3.61 | 3.21 | 3.36 | 3.14 | 3.60 | 3.26 | 3.96 | 3.24 | 3.80 | 3.27 | 3.97 | 3.24 | |
| 5 | 1.14 | 1.10 | 1.18 | 1.13 | 1.18 | 1.07 | 1.17 | 1.13 | 1.17 | 1.13 | 1.18 | 1.07 | 1.17 | 1.12 | 1.26 | 1.19 | 1.10 | 1.14 | 1.26 | 1.19 | |
| 6 | 1.93 | 1.83 | 1.91 | 1.89 | 1.81 | 1.80 | 1.91 | 1.87 | 1.91 | 1.87 | 1.81 | 1.80 | 1.91 | 1.88 | 2.13 | 1.94 | 2.05 | 1.93 | 2.13 | 1.95 | |
| 7 | 1.75 | 1.82 | 1.77 | 1.99 | 1.68 | 1.83 | 1.76 | 1.96 | 1.76 | 1.96 | 1.68 | 1.83 | 1.76 | 1.95 | 1.95 | 1.93 | 1.73 | 2.04 | 1.95 | 1.92 | |
| 8 | 2.69 | 2.71 | 2.75 | 2.78 | 2.81 | 2.66 | 2.67 | 2.71 | 2.67 | 2.71 | 2.81 | 2.66 | 2.75 | 2.75 | 3.02 | 2.88 | 2.56 | 2.59 | 3.03 | 2.88 | |
| 1000 | 1 | 0.40 | 0.36 | 0.39 | 0.36 | 0.38 | 0.35 | 0.39 | 0.36 | 0.39 | 0.36 | 0.38 | 0.35 | 0.39 | 0.36 | 0.43 | 0.39 | 0.41 | 0.36 | 0.43 | 0.39 |
| 2 | 0.72 | 0.70 | 0.70 | 0.69 | 0.67 | 0.67 | 0.70 | 0.69 | 0.70 | 0.69 | 0.67 | 0.67 | 0.70 | 0.69 | 0.75 | 0.71 | 0.73 | 0.72 | 0.75 | 0.71 | |
| 3 | 2.01 | 2.09 | 2.05 | 2.22 | 2.02 | 2.16 | 2.04 | 2.15 | 2.04 | 2.15 | 2.02 | 2.16 | 2.05 | 2.20 | 2.23 | 2.29 | 1.99 | 2.09 | 2.23 | 2.30 | |
| 4 | 0.99 | 0.79 | 0.97 | 0.82 | 0.93 | 0.80 | 0.97 | 0.81 | 0.97 | 0.81 | 0.93 | 0.80 | 0.97 | 0.82 | 1.03 | 0.82 | 1.00 | 0.82 | 1.03 | 0.83 | |
| 5 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.30 | 0.31 | 0.31 | 0.31 | 0.31 | 0.31 | 0.30 | 0.31 | 0.31 | 0.33 | 0.32 | 0.30 | 0.32 | 0.33 | 0.32 | |
| 6 | 0.47 | 0.43 | 0.47 | 0.43 | 0.46 | 0.42 | 0.47 | 0.43 | 0.47 | 0.43 | 0.46 | 0.42 | 0.47 | 0.43 | 0.50 | 0.45 | 0.49 | 0.43 | 0.50 | 0.45 | |
| 7 | 0.46 | 0.46 | 0.46 | 0.48 | 0.44 | 0.45 | 0.46 | 0.48 | 0.46 | 0.48 | 0.44 | 0.45 | 0.46 | 0.48 | 0.49 | 0.50 | 0.46 | 0.48 | 0.49 | 0.50 | |
| 8 | 0.72 | 0.74 | 0.74 | 0.75 | 0.75 | 0.74 | 0.73 | 0.75 | 0.73 | 0.75 | 0.75 | 0.74 | 0.74 | 0.75 | 0.78 | 0.80 | 0.70 | 0.72 | 0.78 | 0.81 | |
| i | Gam () | IGam () | LN () | IGau () | RIG () | B-S () | W () | OK () | BK () | EDF () | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Diff. with | Diff. with | Diff. with | Diff. with | Diff. with | Diff. with | Diff. with | Diff. with | Diff. with | Diff. with | ||
| Lowest | Lowest | Lowest | Lowest | Lowest | Lowest | Lowest | Lowest | Lowest | Lowest | ||
| Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | ||
| 256 | 1 | 0.08 | 0.06 | 0.00 | 0.06 | 0.06 | 0.00 | 0.06 | 0.23 | 0.16 | 0.23 |
| 2 | 0.23 | 0.14 | 0.00 | 0.14 | 0.13 | 0.00 | 0.14 | 0.40 | 0.32 | 0.40 | |
| 3 | 0.08 | 0.15 | 0.01 | 0.08 | 0.07 | 0.00 | 0.12 | 0.82 | 0.09 | 0.82 | |
| 4 | 0.38 | 0.24 | 0.00 | 0.25 | 0.24 | 0.00 | 0.23 | 0.60 | 0.43 | 0.60 | |
| 5 | 0.05 | 0.08 | 0.09 | 0.07 | 0.07 | 0.08 | 0.08 | 0.16 | 0.00 | 0.17 | |
| 6 | 0.12 | 0.10 | 0.00 | 0.10 | 0.10 | 0.00 | 0.10 | 0.32 | 0.24 | 0.32 | |
| 7 | 0.07 | 0.10 | 0.00 | 0.09 | 0.09 | 0.00 | 0.08 | 0.27 | 0.05 | 0.27 | |
| 8 | 0.13 | 0.19 | 0.25 | 0.11 | 0.11 | 0.25 | 0.19 | 0.46 | 0.00 | 0.46 | |
| total | 1.14 | 1.07 | 0.35 | 0.89 | 0.88 | 0.34 | 0.99 | 3.26 | 1.29 | 3.28 | |
| 1000 | 1 | 0.02 | 0.01 | 0.00 | 0.01 | 0.01 | 0.00 | 0.01 | 0.05 | 0.03 | 0.05 |
| 2 | 0.04 | 0.02 | 0.00 | 0.02 | 0.02 | 0.00 | 0.02 | 0.07 | 0.06 | 0.08 | |
| 3 | 0.02 | 0.06 | 0.03 | 0.05 | 0.05 | 0.03 | 0.06 | 0.24 | 0.00 | 0.24 | |
| 4 | 0.06 | 0.04 | 0.00 | 0.04 | 0.04 | 0.00 | 0.04 | 0.10 | 0.07 | 0.10 | |
| 5 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 | 0.03 | 0.00 | 0.03 | |
| 6 | 0.02 | 0.02 | 0.00 | 0.02 | 0.02 | 0.00 | 0.02 | 0.04 | 0.04 | 0.04 | |
| 7 | 0.01 | 0.02 | 0.00 | 0.02 | 0.02 | 0.00 | 0.02 | 0.05 | 0.02 | 0.05 | |
| 8 | 0.02 | 0.04 | 0.05 | 0.03 | 0.03 | 0.05 | 0.04 | 0.08 | 0.00 | 0.08 | |
| total | 0.20 | 0.23 | 0.10 | 0.20 | 0.20 | 0.10 | 0.24 | 0.66 | 0.22 | 0.68 | |
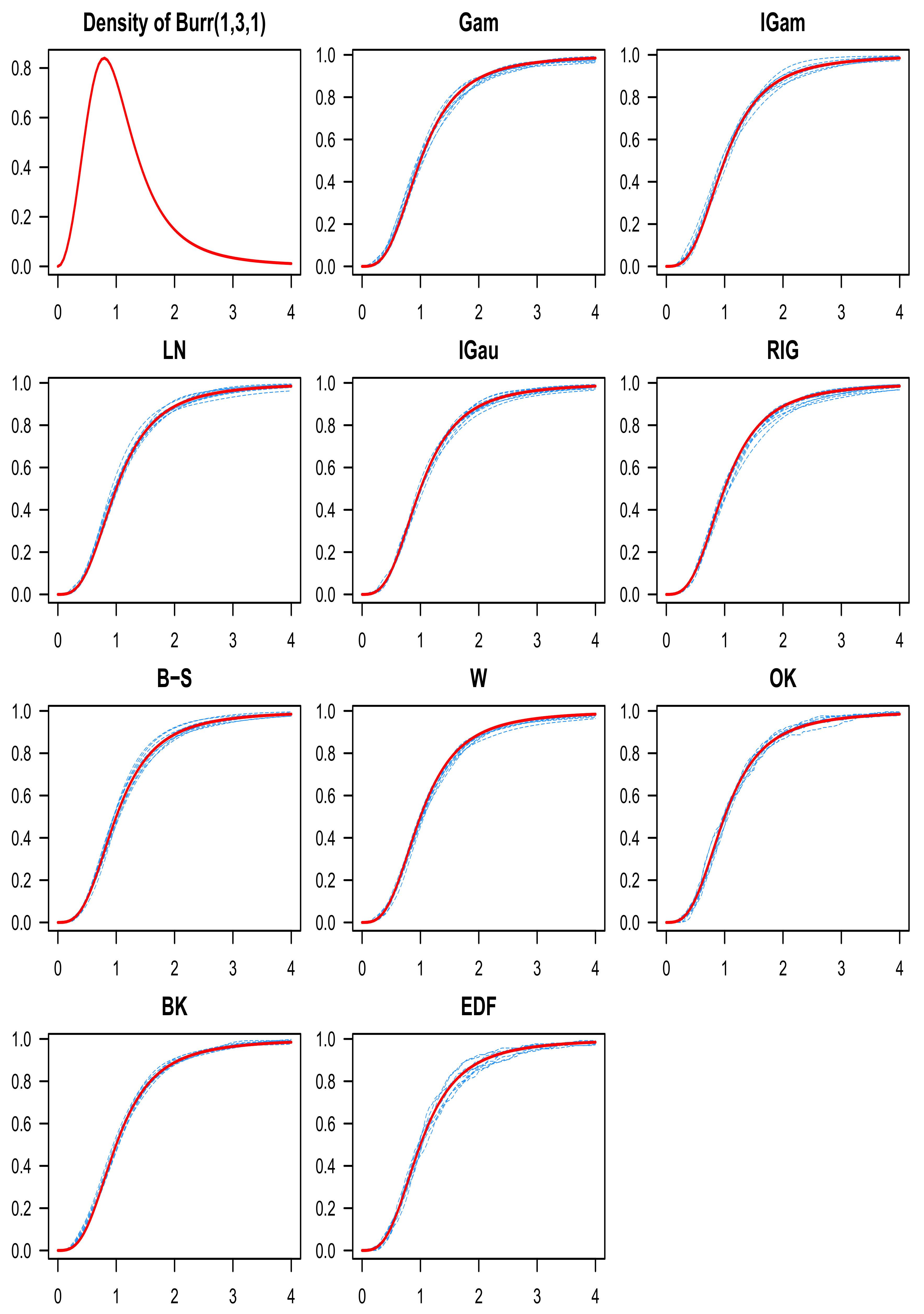
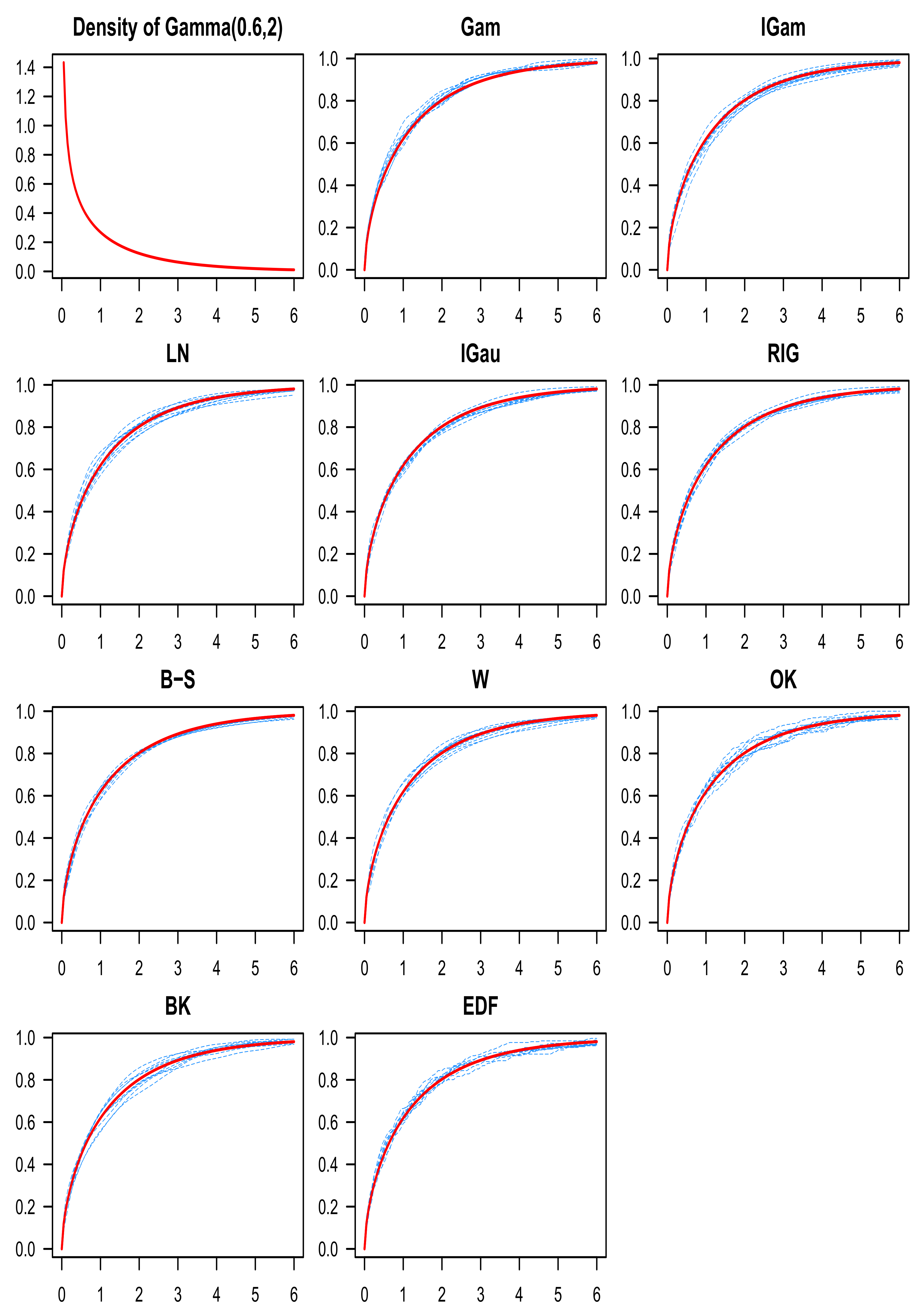
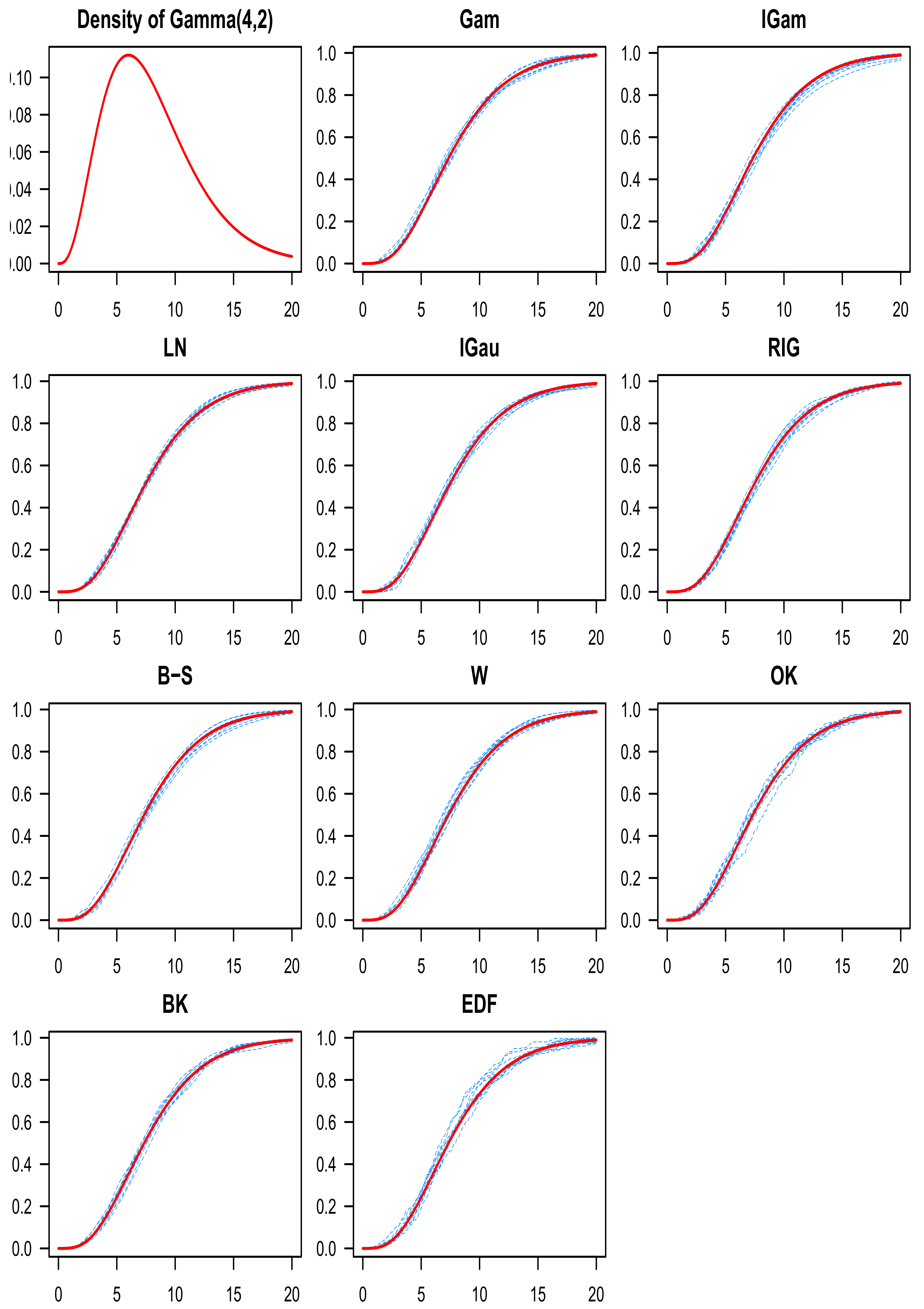

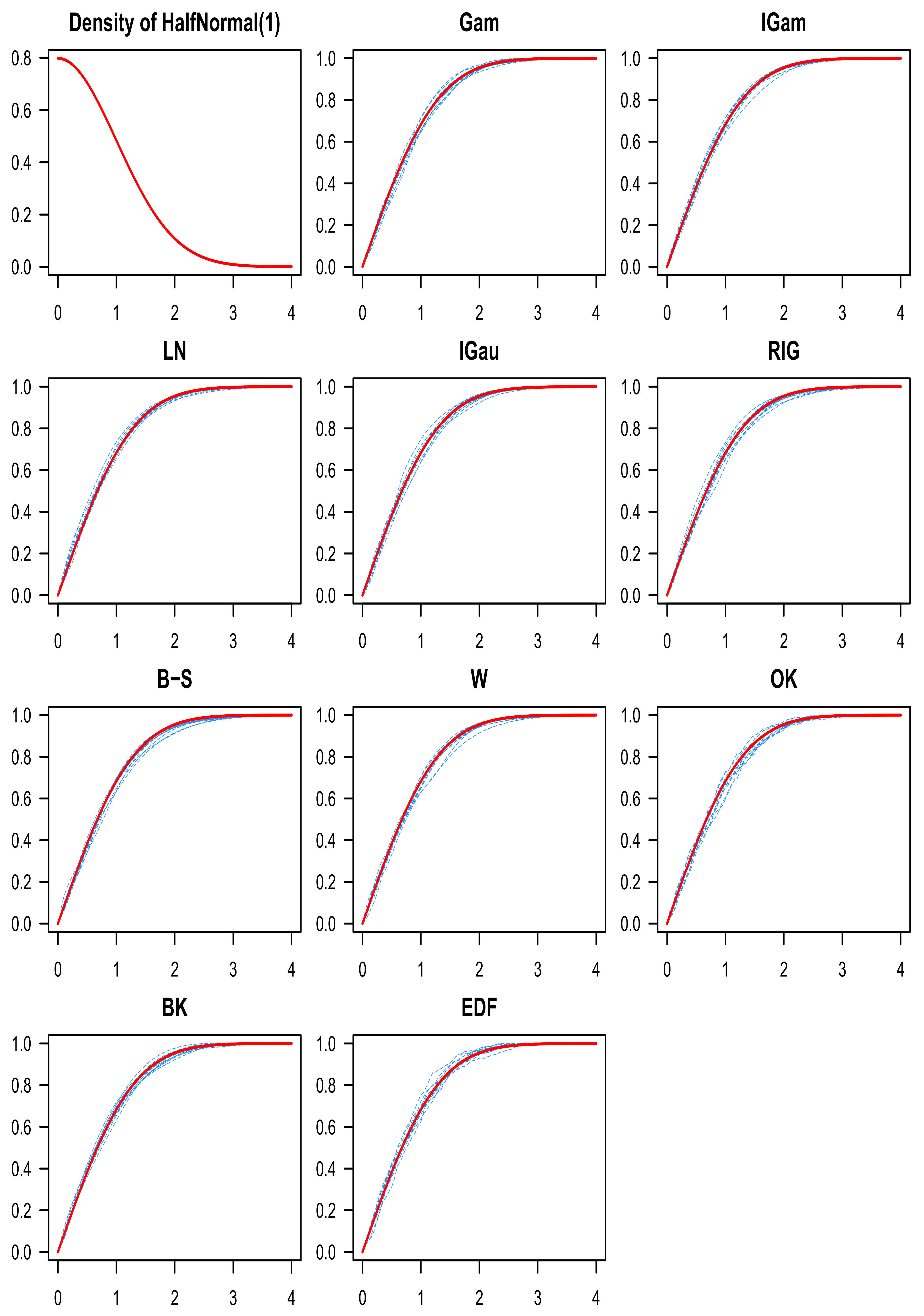

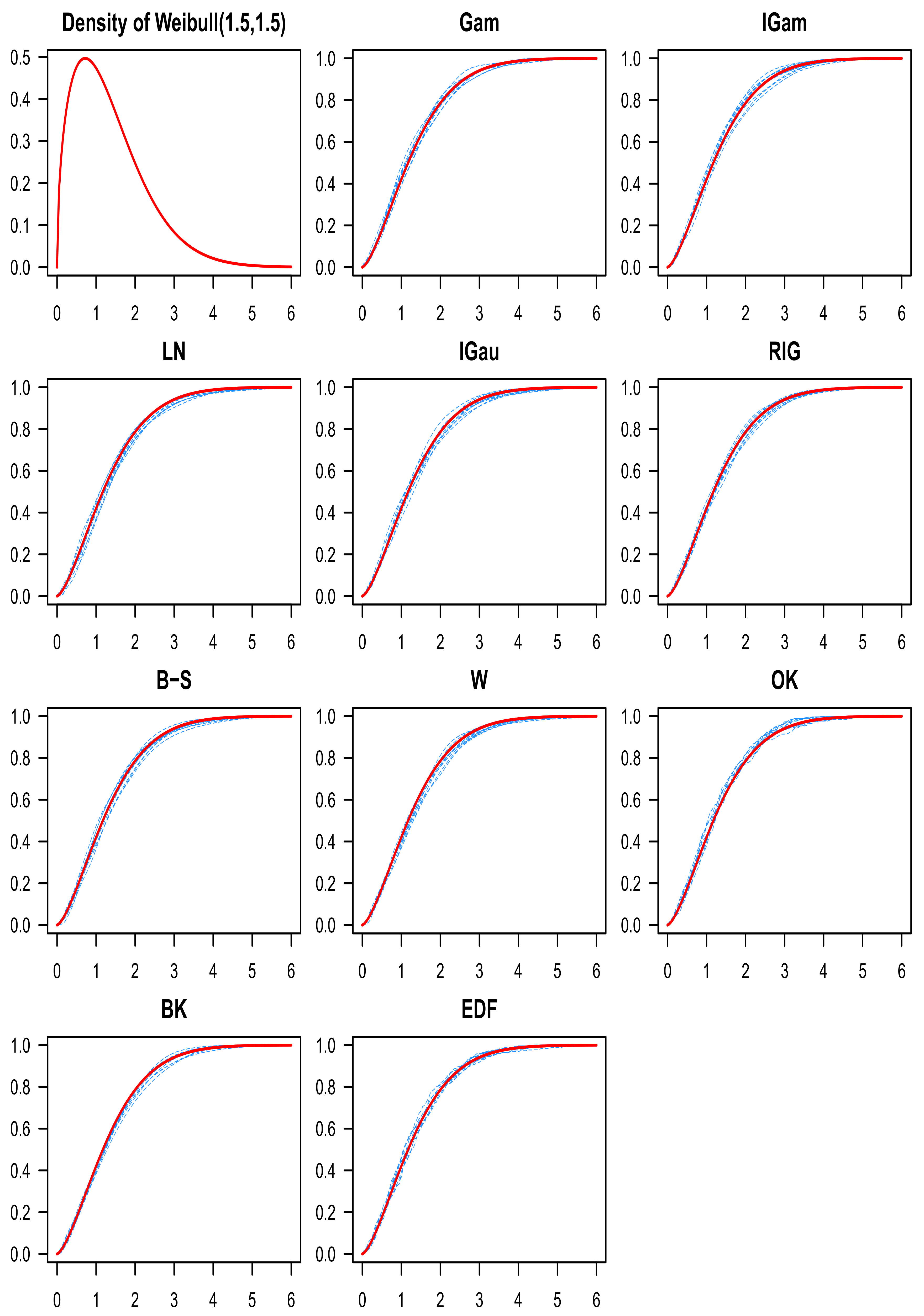

9. Discussion of the Simulation Results
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of the Results for the Gam Kernel
Appendix B. Proof of the Results for the IGam Kernel
Appendix C. Proof of the Results for the LN Kernel
Appendix D. Proof of the Results for the IGau Kernel
Appendix E. Proof of the Results for the RIG Kernel
Appendix F. Technical Lemmas
References
- Aitchison, J.; Lauder, I.J. Kernel density estimation for compositional data. J. R. Stat. Soc. Ser. C 1985, 34, 129–137. [Google Scholar] [CrossRef]
- Chen, S.X. Beta kernel estimators for density functions. Comput. Stat. Data Anal. 1999, 31, 131–145. [Google Scholar] [CrossRef]
- Chen, S.X. Probability density function estimation using gamma kernels. Ann. Inst. Stat. Math. 2000, 52, 471–480. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Gasser, T.; Müller, H.G. Kernel estimation of regression functions. In Smoothing Techniques for Curve Estimation; Springer: Berlin/Heidelberg, Germany, 1979; pp. 23–68. [Google Scholar]
- Rice, J. Boundary modification for kernel regression. Comm. Stat. A Theory Methods 1984, 13, 893–900. [Google Scholar]
- Gasser, T.; Müller, H.G.; Mammitzsch, V. Kernels for nonparametric curve estimation. J. R. Stat. Soc. Ser. B 1985, 47, 238–252. [Google Scholar] [CrossRef]
- Müller, H.G. Smooth optimum kernel estimators near endpoints. Biometrika 1991, 78, 521–530. [Google Scholar] [CrossRef]
- Zhang, S.; Karunamuni, R.J. On kernel density estimation near endpoints. J. Stat. Plann. Inference 1998, 70, 301–316. [Google Scholar] [CrossRef]
- Zhang, S.; Karunamuni, R.J. On nonparametric density estimation at the boundary. J. Nonparametr. Stat. 2000, 12, 197–221. [Google Scholar] [CrossRef]
- Bouezmarni, T.; Rolin, J.M. Consistency of the beta kernel density function estimator. Canad. J. Stat. 2003, 31, 89–98. [Google Scholar] [CrossRef]
- Renault, O.; Scaillet, O. On the way to recovery: A nonparametric bias free estimation of recovery rate densities. J. Bank. Financ. 2004, 28, 2915–2931. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, M.; Monteiro, P.K. Central limit theorem for asymmetric kernel functionals. Ann. Inst. Stat. Math. 2005, 57, 425–442. [Google Scholar] [CrossRef]
- Hirukawa, M. Nonparametric multiplicative bias correction for kernel-type density estimation on the unit interval. Comput. Stat. Data Anal. 2010, 54, 473–495. [Google Scholar] [CrossRef]
- Bouezmarni, T.; Rombouts, J.V.K. Nonparametric density estimation for multivariate bounded data. J. Stat. Plann. Inference 2010, 140, 139–152. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Karunamuni, R.J. Boundary performance of the beta kernel estimators. J. Nonparametr. Stat. 2010, 22, 81–104. [Google Scholar] [CrossRef]
- Bertin, K.; Klutchnikoff, N. Minimax properties of beta kernel estimators. J. Stat. Plann. Inference 2011, 141, 2287–2297. [Google Scholar] [CrossRef]
- Bertin, K.; Klutchnikoff, N. Adaptive estimation of a density function using beta kernels. ESAIM Probab. Stat. 2014, 18, 400–417. [Google Scholar] [CrossRef]
- Igarashi, G. Bias reductions for beta kernel estimation. J. Nonparametr. Stat. 2016, 28, 1–30. [Google Scholar] [CrossRef]
- Jin, X.; Kawczak, J. Birnbaum-Saunders and lognormal kernel estimators for modelling durations in high frequency financial data. Ann. Econ. Financ. 2003, 4, 103–124. Available online: http://aeconf.com/Articles/May2003/aef040106.pdf (accessed on 15 September 2021).
- Scaillet, O. Density estimation using inverse and reciprocal inverse Gaussian kernels. J. Nonparametr. Stat. 2004, 16, 217–226. [Google Scholar] [CrossRef] [Green Version]
- Bouezmarni, T.; Scaillet, O. Consistency of asymmetric kernel density estimators and smoothed histograms with application to income data. Econom. Theor. 2005, 21, 390–412. [Google Scholar] [CrossRef] [Green Version]
- Bouezmarni, T.; Rombouts, J.V.K. Density and hazard rate estimation for censored and α-mixing data using gamma kernels. J. Nonparametr. Stat. 2008, 20, 627–643. [Google Scholar] [CrossRef] [Green Version]
- Bouezmarni, T.; Rombouts, J.V.K. Nonparametric density estimation for positive time series. Comput. Stat. Data Anal. 2010, 54, 245–261. [Google Scholar] [CrossRef] [Green Version]
- Igarashi, G.; Kakizawa, Y. Re-formulation of inverse Gaussian, reciprocal inverse Gaussian, and Birnbaum-Saunders kernel estimators. Stat. Probab. Lett. 2014, 84, 235–246. [Google Scholar] [CrossRef]
- Igarashi, G.; Kakizawa, Y. Generalised gamma kernel density estimation for nonnegative data and its bias reduction. J. Nonparametr. Stat. 2018, 30, 598–639. [Google Scholar] [CrossRef]
- Charpentier, A.; Flachaire, E. Log-transform kernel density estimation of income distribution. L’actualité Économique Rev. D’analyse Économique 2015, 91, 141–159. [Google Scholar] [CrossRef] [Green Version]
- Igarashi, G. Weighted log-normal kernel density estimation. Comm. Stat. Theory Methods 2016, 45, 6670–6687. [Google Scholar] [CrossRef]
- Zougab, N.; Adjabi, S. Multiplicative bias correction for generalized Birnbaum-Saunders kernel density estimators and application to nonnegative heavy tailed data. J. Korean Stat. Soc. 2016, 45, 51–63. [Google Scholar] [CrossRef]
- Kakizawa, Y.; Igarashi, G. Inverse gamma kernel density estimation for nonnegative data. J. Korean Stat. Soc. 2017, 46, 194–207. [Google Scholar] [CrossRef]
- Kakizawa, Y. Nonparametric density estimation for nonnegative data, using symmetrical-based inverse and reciprocal inverse Gaussian kernels through dual transformation. J. Stat. Plann. Inference 2018, 193, 117–135. [Google Scholar] [CrossRef]
- Zougab, N.; Harfouche, L.; Ziane, Y.; Adjabi, S. Multivariate generalized Birnbaum-Saunders kernel density estimators. Comm. Stat. Theory Methods 2018, 47, 4534–4555. [Google Scholar] [CrossRef]
- Zhang, S. A note on the performance of the gamma kernel estimators at the boundary. Stat. Probab. Lett. 2010, 80, 548–557. [Google Scholar] [CrossRef]
- Kakizawa, Y. Multivariate non-central Birnbaum-Saunders kernel density estimator for nonnegative data. J. Stat. Plann. Inference 2020, 209, 187–207. [Google Scholar] [CrossRef]
- Ouimet, F.; Tolosana-Delgado, R. Asymptotic properties of Dirichlet kernel density estimators. J. Multivar. Anal. 2022, 187, 104832. [Google Scholar] [CrossRef]
- Kokonendji, C.C.; Libengué Dobélé-Kpoka, F.G.B. Asymptotic results for continuous associated kernel estimators of density functions. Afr. Diaspora J. Math. 2018, 21, 87–97. [Google Scholar]
- Kokonendji, C.C.; Somé, S.M. On multivariate associated kernels to estimate general density functions. J. Korean Stat. Soc. 2018, 47, 112–126. [Google Scholar] [CrossRef]
- Kokonendji, C.C.; Somé, S.M. Bayesian bandwidths in semiparametric modelling for nonnegative orthant data with diagnostics. Stats 2021, 4, 162–183. [Google Scholar] [CrossRef]
- Hirukawa, M. Asymmetric Kernel Smoothing; SpringerBriefs in Statistics; Springer: Singapore, 2018; p. xii+110. [Google Scholar]
- Mombeni, H.A.; Masouri, B.; Akhoond, M.R. Asymmetric Kernels for Boundary Modification in Distribution Function Estimation. Revstat 2019, 1–27. Available online: https://www.ine.pt/revstat/pdf/Asymmetrickernelsforboundarymodificationindistributionfunctionestimation.pdf (accessed on 15 September 2021).
- Babu, G.J.; Canty, A.J.; Chaubey, Y.P. Application of Bernstein polynomials for smooth estimation of a distribution and density function. J. Stat. Plann. Inference 2002, 105, 377–392. [Google Scholar] [CrossRef]
- Leblanc, A. Chung-Smirnov property for Bernstein estimators of distribution functions. J. Nonparametr. Stat. 2009, 21, 133–142. [Google Scholar] [CrossRef]
- Leblanc, A. On estimating distribution functions using Bernstein polynomials. Ann. Inst. Stat. Math. 2012, 64, 919–943. [Google Scholar] [CrossRef]
- Leblanc, A. On the boundary properties of Bernstein polynomial estimators of density and distribution functions. J. Stat. Plann. Inference 2012, 142, 2762–2778. [Google Scholar] [CrossRef]
- Dutta, S. Distribution function estimation via Bernstein polynomial of random degree. Metrika 2016, 79, 239–263. [Google Scholar] [CrossRef]
- Jmaei, A.; Slaoui, Y.; Dellagi, W. Recursive distribution estimator defined by stochastic approximation method using Bernstein polynomials. J. Nonparametr. Stat. 2017, 29, 792–805. [Google Scholar] [CrossRef]
- Erdoğan, M.S.; Dişibüyük, C.; Ege Oruç, O. An alternative distribution function estimation method using rational Bernstein polynomials. J. Comput. Appl. Math. 2019, 353, 232–242. [Google Scholar] [CrossRef]
- Wang, X.; Song, L.; Sun, L.; Gao, H. Nonparametric estimation of the ROC curve based on the Bernstein polynomial. J. Stat. Plann. Inference 2019, 203, 39–56. [Google Scholar] [CrossRef]
- Babu, G.J.; Chaubey, Y.P. Smooth estimation of a distribution and density function on a hypercube using Bernstein polynomials for dependent random vectors. Stat. Probab. Lett. 2006, 76, 959–969. [Google Scholar] [CrossRef]
- Belalia, M. On the asymptotic properties of the Bernstein estimator of the multivariate distribution function. Stat. Probab. Lett. 2016, 110, 249–256. [Google Scholar] [CrossRef]
- Dib, K.; Bouezmarni, T.; Belalia, M.; Kitouni, A. Nonparametric bivariate distribution estimation using Bernstein polynomials under right censoring. Comm. Stat. Theory Methods 2020, 1–11. [Google Scholar] [CrossRef]
- Ouimet, F. Asymptotic properties of Bernstein estimators on the simplex. J. Multivariate Anal. 2021, 185, 104784. [Google Scholar] [CrossRef]
- Ouimet, F. On the boundary properties of Bernstein estimators on the simplex. arXiv 2021, arXiv:2006.11756. [Google Scholar]
- Hanebeck, A.; Klar, B. Smooth distribution function estimation for lifetime distributions using Szasz-Mirakyan operators. Ann. Inst. Stat. Math. 2021, 1–19. [Google Scholar] [CrossRef]
- Ouimet, F. On the Le Cam distance between Poisson and Gaussian experiments and the asymptotic properties of Szasz estimators. J. Math. Anal. Appl. 2021, 499, 125033. [Google Scholar] [CrossRef]
- Tenreiro, C. Boundary kernels for distribution function estimation. REVSTAT Stat. J. 2013, 11, 169–190. [Google Scholar]
- Tiago de Oliveira, J. Estatística de densidades: Resultados assintóticos. Rev. Fac. Ciências Lisb. 1963, 9, 111–206. [Google Scholar]
- Nadaraja, E.A. Some new estimates for distribution functions. Teor. Verojatnost. i Primenen. 1964, 9, 550–554. [Google Scholar]
- Watson, G.S.; Leadbetter, M.R. Hazard analysis. II. Sankhyā Ser. A 1964, 26, 101–116. [Google Scholar]
- Altman, N.; Léger, C. Bandwidth selection for kernel distribution function estimation. J. Stat. Plann. Inference 1995, 46, 195–214. [Google Scholar] [CrossRef] [Green Version]
- Serfling, R.J. Approximation Theorems of Mathematical Statistics; Wiley Series in Probability and Mathematical Statistics; John Wiley & Sons, Inc.: New York, NY, USA, 1980; p. xvi+371. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lafaye de Micheaux, P.; Ouimet, F. A Study of Seven Asymmetric Kernels for the Estimation of Cumulative Distribution Functions. Mathematics 2021, 9, 2605. https://doi.org/10.3390/math9202605
Lafaye de Micheaux P, Ouimet F. A Study of Seven Asymmetric Kernels for the Estimation of Cumulative Distribution Functions. Mathematics. 2021; 9(20):2605. https://doi.org/10.3390/math9202605
Chicago/Turabian StyleLafaye de Micheaux, Pierre, and Frédéric Ouimet. 2021. "A Study of Seven Asymmetric Kernels for the Estimation of Cumulative Distribution Functions" Mathematics 9, no. 20: 2605. https://doi.org/10.3390/math9202605
APA StyleLafaye de Micheaux, P., & Ouimet, F. (2021). A Study of Seven Asymmetric Kernels for the Estimation of Cumulative Distribution Functions. Mathematics, 9(20), 2605. https://doi.org/10.3390/math9202605






