Preservice Teachers’ Eliciting and Responding to Student Thinking in Lesson Plays
Abstract
:1. Introduction
2. Related Literature
2.1. Teacher Questioning, Talk Moves, and Eliciting and Responding to Students’ Thinking
2.2. Studies on PSTs’ Eliciting and Responding to Student Thinking
2.3. Lesson Play as a Medium for Approximation
3. Method
3.1. Participants and Context
3.2. Task and Procedures
- These imagined assessment interviews would serve as diagnostic assessments of a randomly chosen student whose personal and academic background was unknown. Using the planned assessment, it was the goal of the PSTs to determine the level of the student’s understanding against the chosen standards by eliciting their thinking. Thus, there was no predetermined profile of the student as used in the prior study [4]. It was intentionally left open to see how the PSTs’ anticipation of the students’ confusion and their improvisation of the breadth and depth of elicitation could be tailored to various imaginary students in the lesson play scripts.
- There was no required minimum or maximum number of talk turns included in the lesson play scripts.
- The PSTs needed to include all the teacher talk and student talk from the beginning to the end, imagining they met a new student for an assessment interview.
- The PSTs could end the lesson play scripts once they determined that they fully elicited the student’s thinking.
4. Data Analysis
5. Findings
5.1. Frequency of Teacher Talks
5.2. Types of Teacher Talk
5.3. Illustrative Examples from Active Elicitation
5.4. Looking into Some Short Scripts
5.5. Looking into Some Longer Scripts
6. Discussion and Implications for Teacher Educators
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
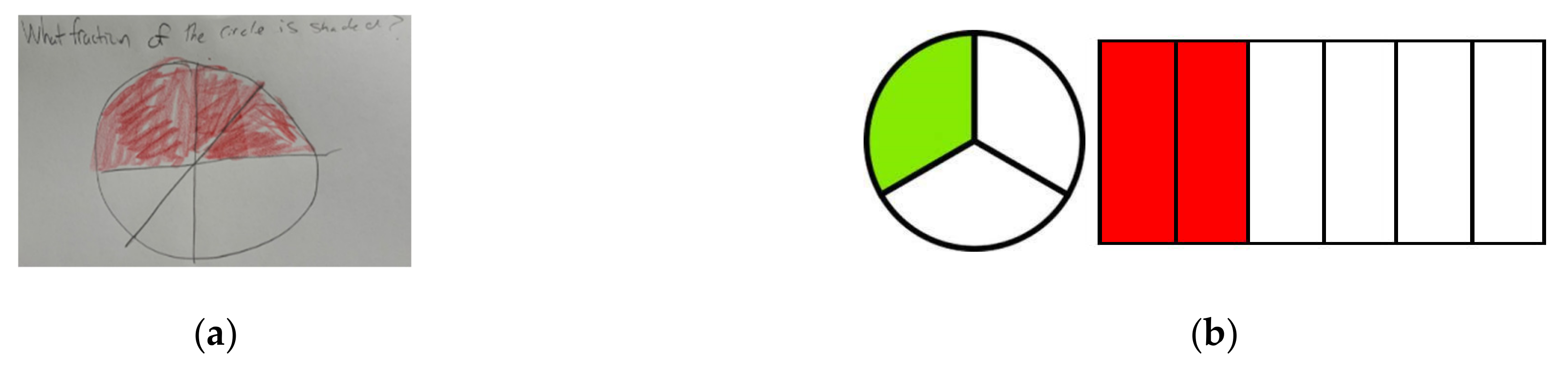
| Core Question | What fraction of the rectangle is shaded? | |
| Anticipated Confusion | The shaded squares are not all together so it may be different from how the student has seen the area model being used; students might not have a clear concept of numerators, denominators, and fractions and it may confuse them. | |
| Differentiated Tasks | Less challenging question: What fraction of the rectangle is shaded? | More challenging question: What fraction of the rectangle is shaded?  |
| Follow-up Prompts |
| |
| Anticipated Student Explanation |
| |
| Lesson Play Script |
| |
Appendix B
| Inductive Categories and Descriptions | Example of Teacher Talk | Frequency of Occurrence (n = 748) | Low Group (n = 113) | Middle Group (n = 234) | High Group (n = 401) |
|---|---|---|---|---|---|
| Eliciting methods or reasoning for actions | 224 (30%) | 47 (42%) | 76 (32%) | 101 (25%) | |
| Asking to describe the methods used (how) | “Can you tell me what you used and what you did?” “How did you get that answer?” | 123 | 28 | 44 | 58 |
| Asking to describe the reason (why) | “Why do you think that?” “Could you explain why you put the 1/2 and 4/6 where you did?” | 63 | 7 | 12 | 18 |
| Asking without specification (open) | “Can you explain your answer?” | 58 | 12 | 20 | 25 |
| Follow-up probing | 198 (26%) | 17 (15%) | 49 (21%) | 132 (33%) | |
| Gets the student to further explain their thinking | “Okay, so you counted five squares. How did you know it was 5/8 though?” | 160 | 14 | 38 | 108 |
| Ask the student to show/explain the process step-by-step | “Okay, what is your next step after that?” | 20 | 0 | 6 | 14 |
| Asks the student to explain/clarify underlying meaning | “What do you mean by ‘half way’?” “So, you got six. So, what does six mean?” | 18 | 3 | 5 | 10 |
| Teacher-led process | 102 (14%) | 9 (8%) | 30 (13%) | 63 (16%) | |
| Leads the student through a specific method or towards an answer Explicitly explains or models the concept, procedure, or strategy Gives an alternative strategy for the students to use after they give their answer | “How about we try to find the common denominator? We want to try to make it the same to see which one is bigger. Do you know how to find the common denominator?” “First, you need to find a common denominator by multiplying denominators.” “Another skill you could also try is drawing dotted lines and breaking up B into as many pieces of A as possible.” | 80 | 8 | 23 | 39 |
| Draws the student’s attention to certain details or differences | “Are all the pieces evenly divided?” | 16 | 1 | 6 | 9 |
| Shows the student how to record the answer (e.g., writing down the answer or drawing the answer for the student before the student answers) | “Yes, then you can put ¼ under here.” | 6 | 0 | 1 | 5 |
| Making connections | 100 (13%) | 19 (17%) | 37 (16%) | 44 (11%) | |
| Asks the student to use different representations | “Can you draw a picture to help me understand your thinking?” “Could you show what that would look like if you use fraction circles?” | 52 | 9 | 23 | 20 |
| Asks if the situation can be extended to other situations | “So now how would we do this with non-unit fractions?” | 48 | 10 | 14 | 24 |
| Modifying questions | 57 (8%) | 10 (9%) | 23 (10%) | 24 (6%) | |
| Gives a slightly harder or an easier prepared question | “Show 1/2 in a pie circle drawing instead of 4/6.” “Can you tell me one fraction that is larger than 6/10 and one fraction that is smaller than 6/10?” | 26 | 3 | 12 | 11 |
| Breaks down the question into parts | “Let’s look at the square for the corn only. How much of the square does the corn take up?” | 18 | 3 | 7 | 8 |
| Rephrases or represents the question in a different form for the student due to confusion | “Let me rephrase.” “Let me write it down.” | 13 | 4 | 4 | 5 |
| Revoicing | 41 (5%) | 5 (4%) | 13 (6%) | 23 (6%) | |
| Restate the student’s response to confirm | “Because you had a whole circle and you cut it in half. Is it what you are saying?” | 41 | 5 | 13 | 23 |
| Other miscellaneous | 26 (3%) | 6 (5%) | 6 (3%) | 14 (3%) | |
| Offers the student time to think or work | (When the student seems unsure, the teacher does not speak and uses wait time.) “I’ll give you a minute.” | 10 | 4 | 2 | 4 |
| Checks for the student’s confusion | “So, did the parts of the shaded circle confuse you?” | 7 | 1 | 2 | 4 |
| Teacher asks the student to recall prior problem or statement to help solve current problem | “Do you remember what we talked about a fraction being in the first question?” | 6 | 0 | 1 | 5 |
| Reminds the student of what to do | “Remember to utilize that number line.” “So, remember there are two parts to this question.” | 3 | 1 | 1 | 1 |
References
- Schack, E.O.; Fisher, M.H.; Wilhelm, J. (Eds.) Teacher Noticing—Bridging and Broadening Perspectives, Contexts, and Frameworks; Springer: New York, NY, USA, 2017. [Google Scholar]
- Sherin, M.G.; Jacobs, V.R.; Philipp, R.A. (Eds.) Mathematics Teacher Noticing: Seeing through Teachers’ Eyes; Routledge: Lodon, UK, 2011. [Google Scholar]
- Lampert, M.; Beasley, H.; Ghousseini, H.; Kazemi, K.; Franke, M.L. Instructional explanations in the disciplines. In Using Designed Instructional Activities to Enable Novices to Manage Ambitious Mathematics Teaching; Stein, M.K., Kucan, L., Eds.; Springer: New York, NY, USA, 2010; pp. 129–141. [Google Scholar]
- Shaughnessy, M.; Boerst, T.A. Uncovering the Skills That Preservice Teachers Bring to Teacher Education: The Practice of Eliciting a Student’s Thinking. J. Teach. Educ. 2017, 69, 40–55. [Google Scholar] [CrossRef] [Green Version]
- Shaughnessy, M.; Boerst, T.A.; Farmer, S.O. Complementary assessments of prospective teachers’ skill with eliciting student thinking. J. Math. Teach. Educ. 2019, 22, 607–638. [Google Scholar] [CrossRef]
- Sztajn, P.; Confrey, J.; Wilson, P.; Edgington, C. Learning trajectory based instruction: Toward a theory of teaching. Educ. Res. 2012, 41, 147–156. [Google Scholar] [CrossRef]
- Ball, D.L.; Forzani, F.M. The Work of Teaching and the Challenge for Teacher Education. J. Teach. Educ. 2009, 60, 497–511. [Google Scholar] [CrossRef]
- Grossman, P.; Compton, C.; Igra, D.; Ronfeldt, M.; Shahan, E.; Williamson, P. Teaching practice: A cross-professional per-spective. Teach. Coll. Rec. 2009, 111, 2055–2100. [Google Scholar]
- Zazkis, R.; Liljedahl, P.; Sinclair, N. Lesson plays: Planning teaching versus teaching planning. Learn. Math. 2009, 29, 40–47. [Google Scholar]
- Zazkis, R.; Sinclair, N.; Liljedahl, P. Lesson Play in Mathematics Education: A Tool for Research and Professional Development; Springer: New York, NY, USA, 2013. [Google Scholar]
- Moyer, P.S.; Milewicz, E. Learning to question: Categories of questioning used by preservice teachers during diagnostic mathematics interviews. J. Math. Teach. Educ. 2002, 5, 293–315. [Google Scholar] [CrossRef]
- Jacobs, V.R.; Lamb, L.L.C.; Philipp, R.A. Professional Noticing of Children’s Mathematical Thinking. J. Res. Math. Educ. 2010, 41, 169–202. [Google Scholar] [CrossRef]
- Grossman, P.; McDonald, M. Back to the Future: Directions for Research in Teaching and Teacher Education. Am. Educ. Res. J. 2008, 45, 184–205. [Google Scholar] [CrossRef]
- TeachingWorks. (n.d.). High-Leverage Practices. Available online: http://www.teachingworks.org/work-of-teaching/high-leverage-practices (accessed on 5 December 2019).
- Levin, T.; Long, R. Effective Instruction; Association for Supervision and Curriculum Development: Alexandria, VA, USA, 1981. [Google Scholar]
- Stevens, R. The Question as a Means of Efficiency in Instruction: A Critical Study of Classroom Practice; Teachers College, Columbia University: New York, NY, USA, 1912. [Google Scholar]
- Boaler, J.; Brodie, K. The importance, nature and impact of teacher questions. In North American Chapter of the International Group for the Psychology of Mathematics Education, Proceedings of the Twenty-Sixth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education; Toronto, ON, Canada, 21–24 October 2004; McDougall, D.E., Ross, J.A., Eds.; University of Toronto: Toronto, ON, Canada, 2004; Volume 2, pp. 774–782. [Google Scholar]
- Amy, C.; Brualdi, T. Classroom questions. Pract. Assess. Res. Eval. 1998, 6, 6. [Google Scholar] [CrossRef]
- Wood, D. Teaching talk. In Thinking Voices: The Work of the National Oracy Project; Norman, K., Ed.; Hodder & Stoughton: London, UK, 1992; pp. 203–214. [Google Scholar]
- Mercer, N.; Dawes, L. The study of talk between teachers and students, from the 1970s until the 2010s. Oxf. Rev. Educ. 2014, 40, 430–445. [Google Scholar] [CrossRef]
- Wells, G. Dialogic Inquiry: Towards a Sociocultural Practice and Theory of Education; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Chapin, S.H.; O’Connor, C.; Anderson, N.C. Classroom Discussions in Math: A teacher’s Guide for Using Talk Moves to Support the Common Core and More; Math Solutions: Sausalito, CA, USA, 2013. [Google Scholar]
- Lim, W.; Lee, J.; Tyson, K.; Kim, H.; Kim, J. An integral part of facilitating mathematical discussions: Follow-up questioning. Int. J. Sci. Math. Educ. 2020, 18, 377–398. [Google Scholar] [CrossRef]
- Lampert, M. When the problem is not the question and the solution is not the answer: Mathematical knowing and teaching. Am. Educ. Res. J. 1990, 27, 29–63. [Google Scholar] [CrossRef]
- Borko, H. Professional Development and Teacher Learning: Mapping the Terrain. Educ. Res. 2004, 33, 3–15. [Google Scholar] [CrossRef]
- Grossman, P. Teaching Core Practices in Teacher Education; Harvard Education Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Zeichner, K.M. The Turn Once Again Toward Practice-Based Teacher Education. J. Teach. Educ. 2012, 63, 376–382. [Google Scholar] [CrossRef]
- Groth, R.E.; Bergner, J.A.; Burgess, C.R. An exploration of prospective teachers’ learning of clinical interview techniques. Math. Teach. Educ. Dev. 2016, 18, 48–71. [Google Scholar]
- Weiland, I.; Hudson, R.; Amador, J. Preservice formative assessment interviews: The development of competent questioning. Int. J. Sci. Math. Educ. 2014, 12, 329–352. [Google Scholar] [CrossRef]
- Herbst, P.; Chieu, V.; Rougee, A. Approximating the practice of mathematics teaching: What learning can web-based, mul-timedia storyboarding software enable? Contemp. Issues Technol. Teach. Educ. 2014, 14, 356–383. [Google Scholar]
- Kabar, M.G.D.; Tasdan, B.T. Examining the change of pre-service middle school mathematics teachers’ questioning approaches through clinical interviews. Math. Teach. Educ. Dev. 2020, 22, 115–138. [Google Scholar]
- Zazakis, R.; Herbst, P. (Eds.) Scripting Approaches in Mathematics Education; Springer: Cham, Switzerland, 2017. [Google Scholar]
- National Governors Association Center for Best Practices & Council of Chief State School Officers. Common Core State Standards for Mathematics; NGA & CCSSO: Washington, DC, USA, 2010. [Google Scholar]
- National Council of Teachers of Mathematics. Principles to Actions: Ensuring Mathematics Success for All; NCTM: Reston, VA, USA, 2014. [Google Scholar]
- Creswell, J.W.; Creswell, J.D. Research Design: Qualitative, Quantitative, and Mixed Method Approaches, 5th ed.; Sage Publication: Thousand Oaks, CA, USA, 2017. [Google Scholar]
- Decuir-Gunby, J.T.; Marshall, P.L.; McCulloch, A.W. Developing and Using a Codebook for the Analysis of Interview Data: An Example from a Professional Development Research Project. Field Methods 2010, 23, 136–155. [Google Scholar] [CrossRef]
- Grbich, C. Qualitative Data Analysis: An Introduction, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Riffe, D.; Lacy, S.; Fico, F. Analyzing Media Messages: Using Quantitative Content Analysis in Research; Erlbaum: Mahwah, NJ, USA, 1998. [Google Scholar]
- Rourke, L.; Anderson, T.; Garrison, D.R.; Archer, W. Assessing social presence in asynchronous text-based computer con-ferencing. J. Distance Educ. 2001, 14, 50–71. [Google Scholar]
- Lamon, S. The development of unitizing: Its role in children’s partitioning strategies. J. Res. Math. Educ. 1996, 27, 170–193. [Google Scholar] [CrossRef]
- Yoshida, H.; Sawano, K. Overcoming cognitive obstacles in learning fractions: Equal-partitioning and equal-whole. Jpn. Psychol. Res. 2002, 44, 183–195. [Google Scholar] [CrossRef]
- Banner, D. Frameworks for noticing in mathematics education research. In Proceedings of the 42nd Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Mazatlán, Mexico, 14–18 October 2020; pp. 1572–1576. [Google Scholar]
- Mason, J. Learning about noticing, by, and through, noticing. ZDM 2021, 53, 231–243. [Google Scholar] [CrossRef]


| Study/Participants/Context | Categories of PST Interactions Identified and Examined |
|---|---|
| Moyer and Milewics [11] 48 elementary PSTs (the senior year before final internship placement for teacher certification) One-on-one diagnostic mathematics interviews with children ranging in age from 5 to 12 | Making a checklist (the PST proceeds from one question to the next with little regard for the child’s response):
|
| Groth, Bergner, and Burgess [28] Four PSTs (two elementary and two secondary) One-on-one pre- and post-assessment interviews with elementary students (Grades 3 and 5) |
|
| Weiland, Hudson, and Amador [29] One pair of elementary PSTs Formative assessment interview over ten weeks with two elementary students to examine changes over time | Problem-Posing Questions
|
| Shaughnessy and Boerst [4] 47 elementary PSTs in the initial stage of teacher education One-on-one interview with a hypothetical student | Moves that Require New Learning
|
| Kabar and Taşdan [31] 22 PSTs in nine working groups Three clinical interviews of middle-school students over a semester | Question Types Identified:
|
| Problem Set | Focus of the Question and Required Representations | Relevant Standards |
|---|---|---|
| 1 | Basic concepts of fractions using the area model | Understand a fraction 1/b as the quantity formed by one part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b. |
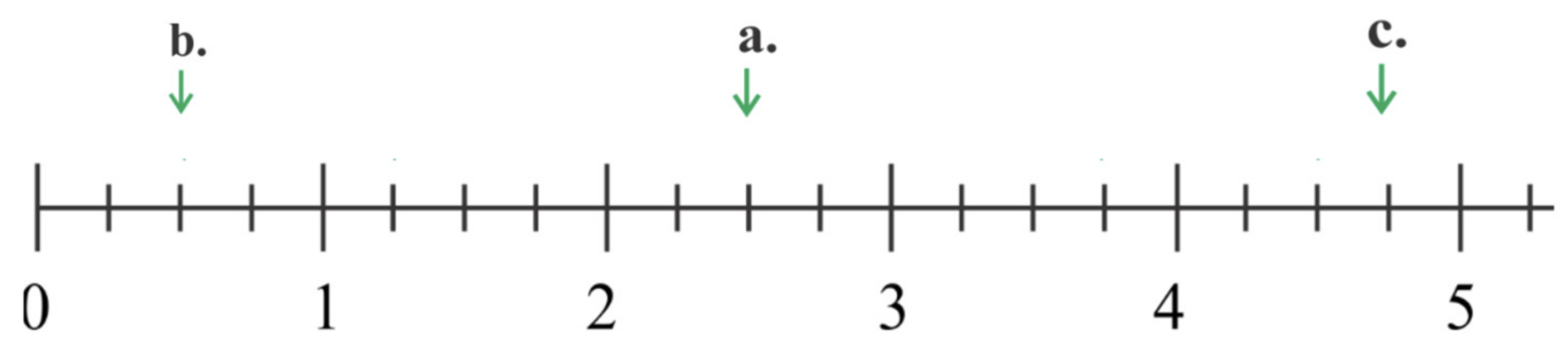
| 2 | Basic concepts of fractions using the number line representations | Understand a fraction as a number on the number line; represent fractions on a number line diagram. |
| 3 | Comparing two fractions (no required representation) | Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size. |
| Frequency Level Based on the Number of Turns of Teacher Talk | Number of Lesson Play Scripts (n = 95 Scripts) |
|---|---|
| Low (1–5 turns) | 30 scripts (Set 1: 13 scripts, Set 2: 10 scripts, Set 3: 7 scripts) |
| Middle (6–9 turns) | 33 scripts (Set 1: 11 scripts, Set 2: 11 scripts, Set 3: 11 scripts) |
| High (10+ turns) | 32 scripts (Set 1: 8 scripts, Set 2: 11 scripts, Set 3: 13 scripts) |
| Inductive Categories and Descriptions | Example | Total (n = 95 Scripts) | Low (n = 30 Scripts) | Middle (n = 33 Scripts) | High (n = 32 Scripts) |
|---|---|---|---|---|---|
| Presenting prepared written problems only | 66 (69%) | 22 (73%) | 23 (70%) | 21(66%) | |
| Reads or asks to read prepared problems as written | Teacher read: “What fraction of the square is shaded?” “Could you read the question?” | 45 (47%) | 16 (53%) | 14 (43%) | 15 (47%) |
| Slightly elaborates/rephrases problems | The problem: “What fraction is on the number line?” Teacher said: “We are going to find the number that is shown on the number line. We have four choices here. Can you find the number that’s marked here?” | 21 (22%) | 6 (20%) | 9 (27%) | 6 (19%) |
| Additional talks in addition to presenting written problems | 29 (31%) | 8 (27%) | 10 (30%) | 11 (34%) | |
| Checks on background knowledge/experience | “Have you ever used these [fraction circles] before?” “Do you ever see fractions outside of school?” | 13 (14%) | 6 (20%) | 5 (15%) | 5 (16%) |
| Describes protocol for interview | “Here are some markers and papers. Feel free to use them whenever you need.” | 9 (9%) | 2 (7%) | 4 (12%) | 4 (13%) |
| Informs math topics to be asked | “We’ll be comparing, testing for equivalency, and decomposing fractions.” | 7 (7%) | 3 (10%) | 2 (6%) | 2 (6%) |
| Checks on key terms | “Do you know what unit fractions mean?” | 7 (7%) | 2 (7%) | 2 (6%) | 5 (16%) |
| Inductive Categories and Description | Frequency of Occurrence (n = 748) | Low Group (n = 113) | Middle Group (n = 234) | High Group (n = 401) |
|---|---|---|---|---|
| Elicitation of methods or reasoning for actions * | 224 (30%) | 47 (42%) | 76 (32%) | 101 (25%) |
| Follow-up probing | 198 (26%) | 17 (15%) | 49 (21%) | 132 (33%) |
| Teacher-led process | 102 (14%) | 9 (8%) | 30 (13%) | 63 (16%) |
| Making connections | 100 (13%) | 19 (17%) | 37 (16%) | 44 (11%) |
| Modifying questions | 57 (8%) | 10 (9%) | 23 (10%) | 24 (6%) |
| Revoicing | 41 (5%) | 5 (4%) | 13 (6%) | 23 (6%) |
| Other miscellaneous | 26 (3%) | 6 (5%) | 6 (3%) | 14 (3%) |
| Inductive Categories and Descriptions | Example | Total (n = 95 Scripts) | Low (n = 30 Scripts) | Middle (n = 33 Scripts) | High (n = 32 Scripts) |
|---|---|---|---|---|---|
| Ends with student answer without teacher’s closure | Student: I don’t know (unable to tell me). | 51 (54%) | 25 (66%) | 16 (53%) | 10 (37%) |
| Wraps up with a neutral comment | “I see.” “Okay.” “I think I understand what you mean.” “Thank you.” | 19 (20%) | 9 (24%) | 7 (23%) | 3 (11%) |
| Praises the student | “That is well done. I like how you drew arrows to show the simplified area model.” “Wow, that’s fast!” “You are very good with mental math.” | 19 (20%) | 3 (8%) | 7 (23%) | 9 (33%) |
| Wraps up with an evaluative/confirmative comment on the final answer or strategies used | “So, when we’re comparing fractions it helps to look at the denominators.” “That’s correct. 2/4 or 1/2 because those are equivalent.” | 14 (14%) | 4 (11%) | 6 (15%) | 4 (14%) |
| Empathizes that the problem was difficult | “This problem was difficult because the model isn’t something we normally see.” | 2 (2%) | 0 (0%) | 0 (0%) | 2 (7%) |
| Asks if the offered tools were helpful | “Did it help using these fraction circles?” | 2 (2%) | 0 (0%) | 0 (0%) | 2 (7%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-E.; Lim, W. Preservice Teachers’ Eliciting and Responding to Student Thinking in Lesson Plays. Mathematics 2021, 9, 2842. https://doi.org/10.3390/math9222842
Lee J-E, Lim W. Preservice Teachers’ Eliciting and Responding to Student Thinking in Lesson Plays. Mathematics. 2021; 9(22):2842. https://doi.org/10.3390/math9222842
Chicago/Turabian StyleLee, Ji-Eun, and Woong Lim. 2021. "Preservice Teachers’ Eliciting and Responding to Student Thinking in Lesson Plays" Mathematics 9, no. 22: 2842. https://doi.org/10.3390/math9222842
APA StyleLee, J.-E., & Lim, W. (2021). Preservice Teachers’ Eliciting and Responding to Student Thinking in Lesson Plays. Mathematics, 9(22), 2842. https://doi.org/10.3390/math9222842






