Diffusion Model of Parallel Plate Crack Grouting Based on Foaming Expansion Characteristics of Polymer Slurry
Abstract
:1. Introduction
2. Grout Diffusion Model
2.1. Density Model
2.2. Basic Hypothesis
2.3. Diffusion Model Derived
3. Numerical Simulation of Polymer Slurry Diffusion in Parallel Plate Cracks
3.1. Governing Equations
3.2. Level Set Method
3.3. Numerical Realization (Boundary and Initial Conditions)
3.4. Numerical Verification of Diffusion Model
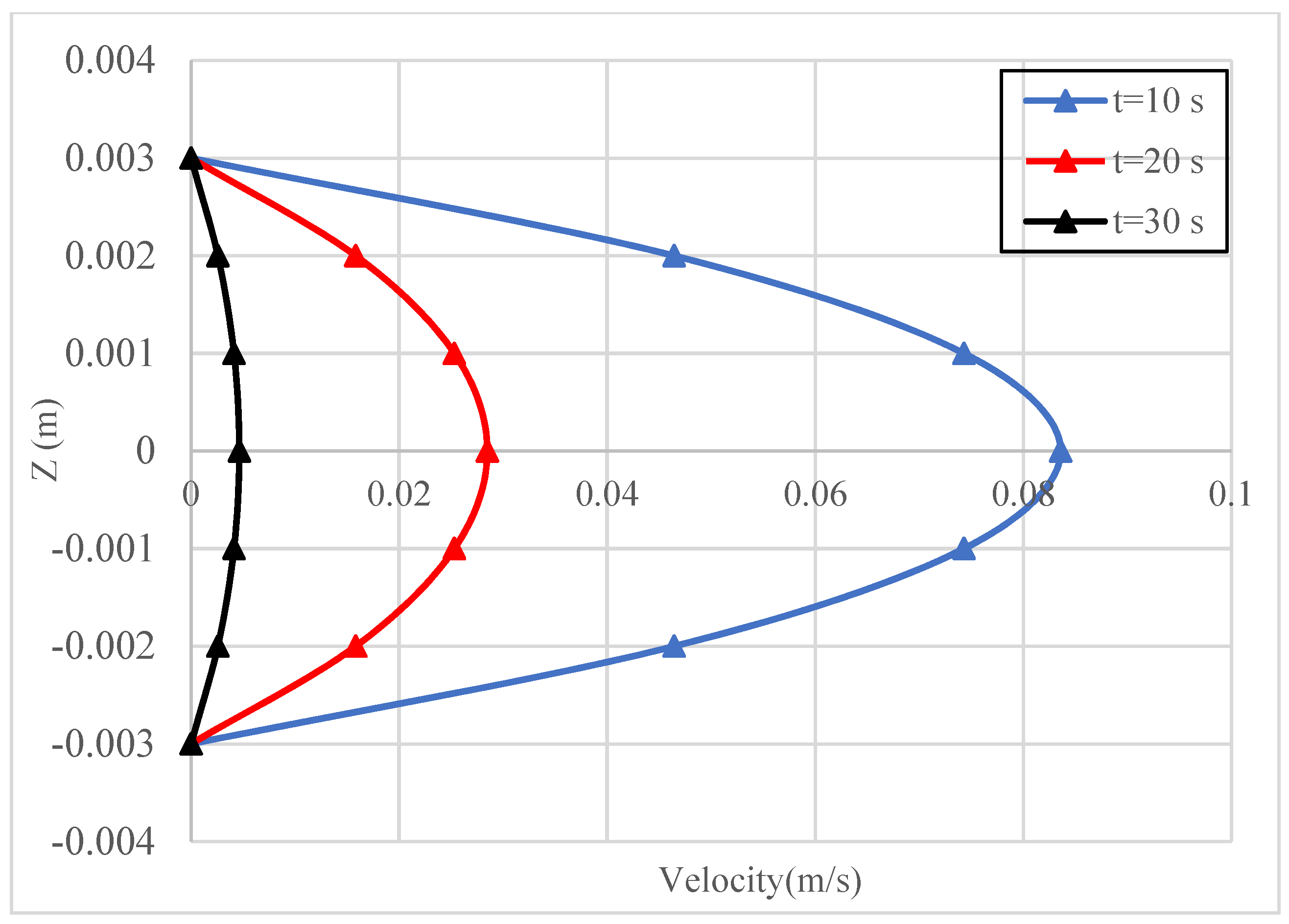
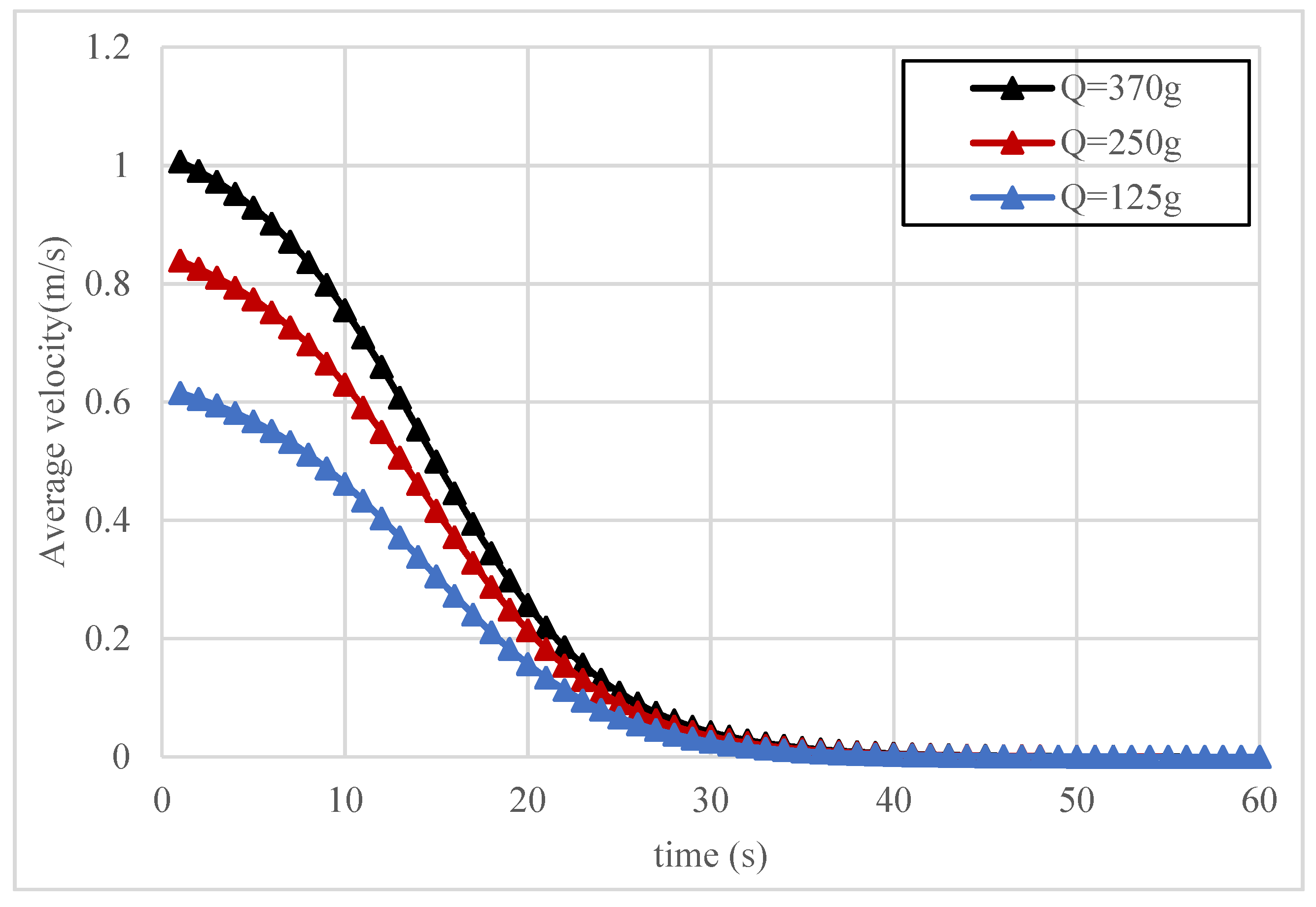
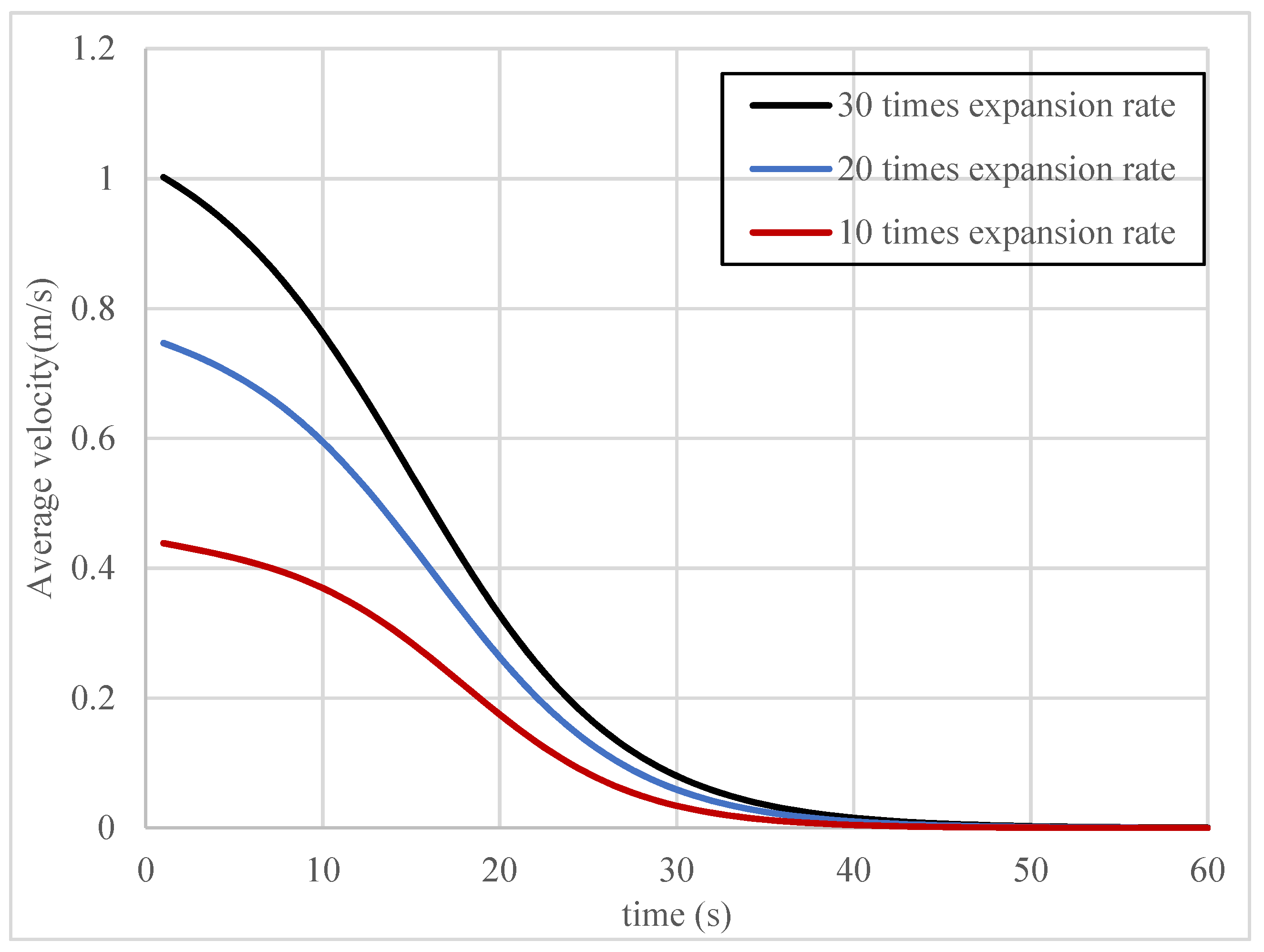
4. Analysis of Slurry Diffusion Characteristics
4.1. Analysis of Slurry Pressure Field
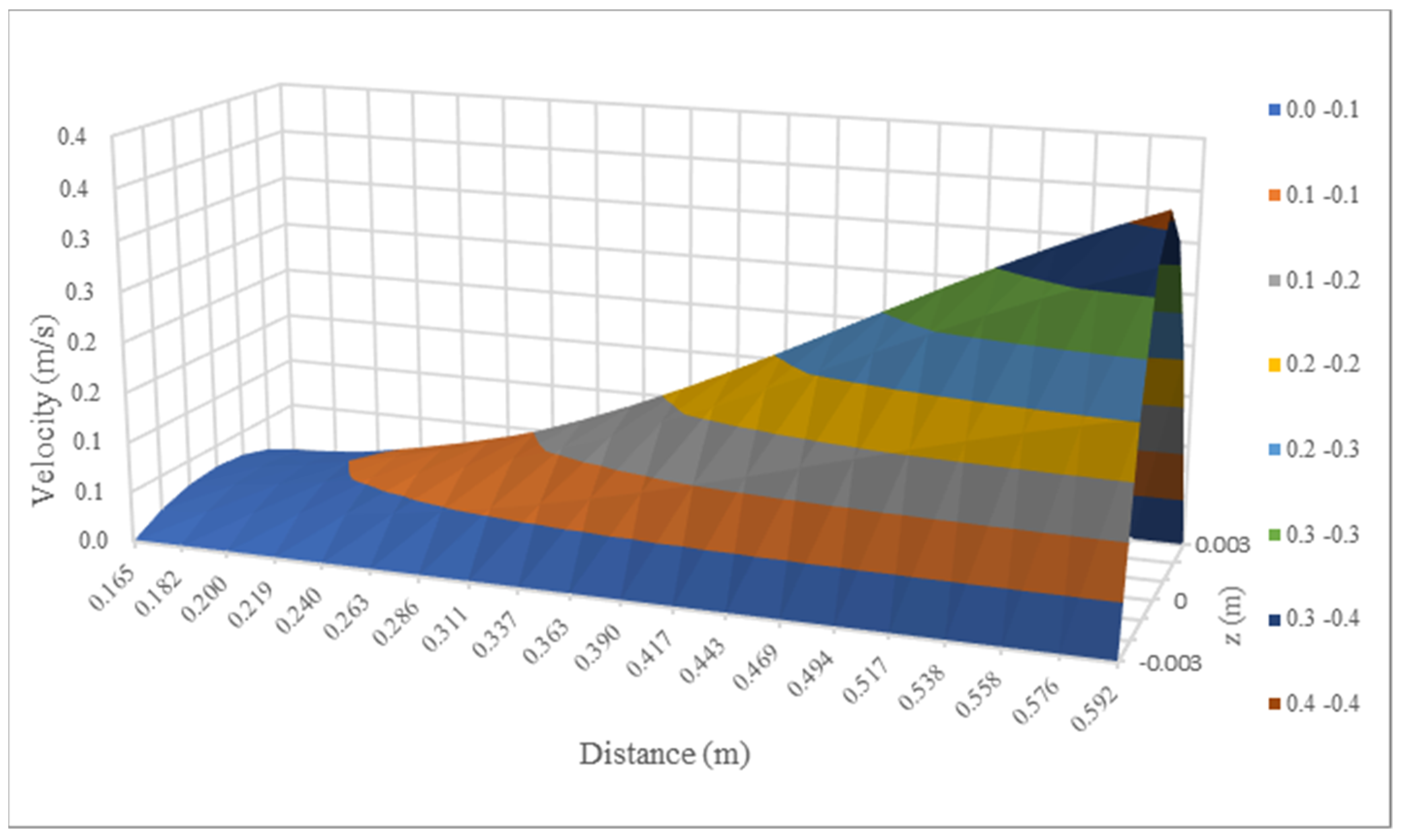
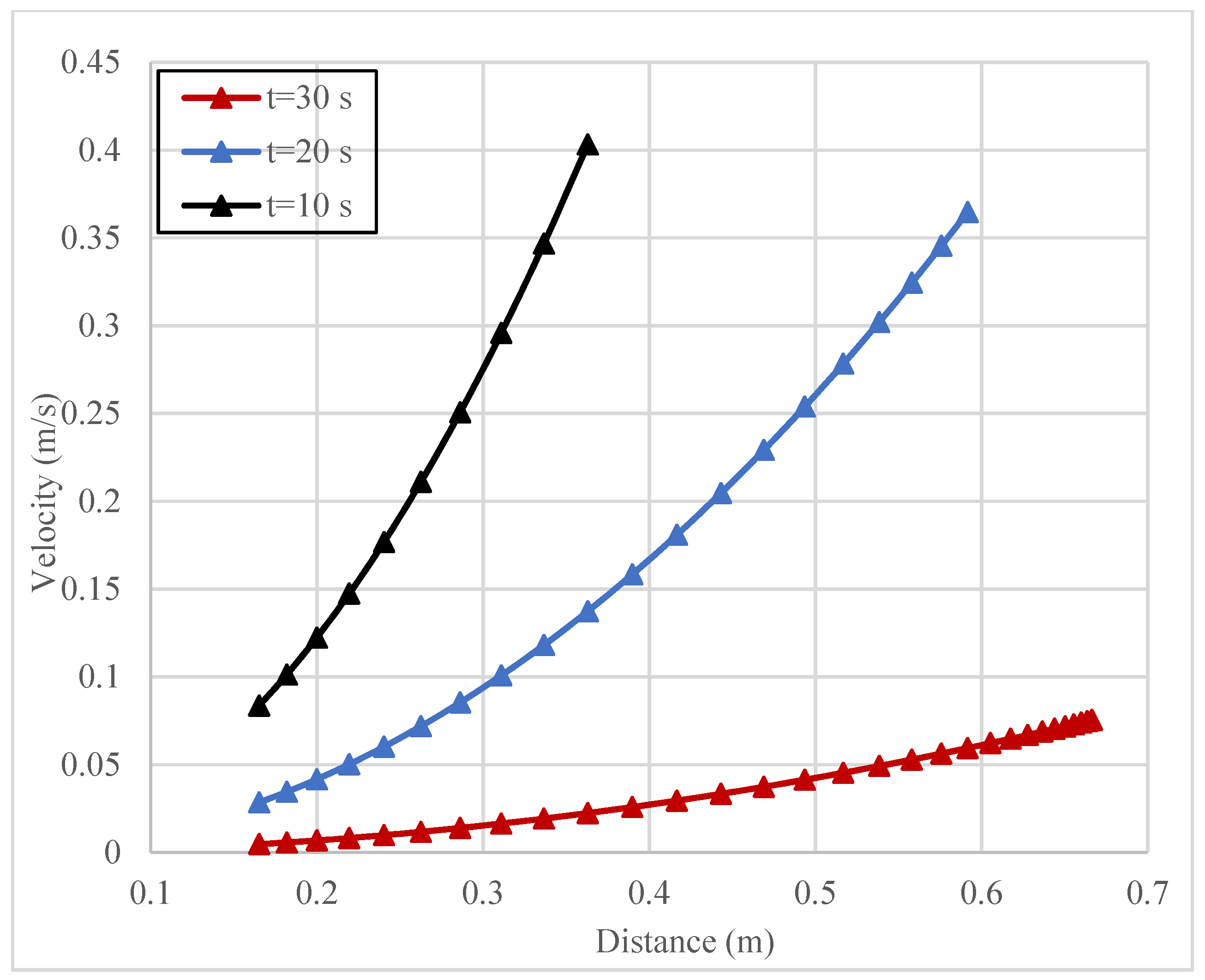
4.2. Analysis of Slurry Diffusion Flow Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, X.M.; Fang, H.Y.; Wang, S.Y.; Xue, B.H. Experimental and practical investigation of the sealing efficiency of cement grouting in tortuous fractures with flowing water. Tunn. Undergr. Space Technol. 2021, 108, 103693. [Google Scholar] [CrossRef]
- Algin, H.M. Optimised design of jet-grouted raft using response surface method. Comput. Geotech. 2016, 74, 56–73. [Google Scholar] [CrossRef]
- Maghous, S.; Saada, Z.; Dormieux, L.; Canou, J.; Dupla, J.C. A model for in situ grouting with account for particle filtration. Comput. Geotech. 2006, 34, 164–174. [Google Scholar] [CrossRef]
- Wang, Z.F.; Shen, S.L.; Modoni, G. Enhancing discharge of spoil to mitigate disturbance induced by horizontal jet grouting in clayey soil: Theoretical model and application. Comput. Geotech. 2019, 111, 222–228. [Google Scholar] [CrossRef]
- Wang, S.F.; Tang, Y.; LI, X.B.; Du, K. Analyses and predictions of rock cuttabilities under different confining stresses and rock properties based on rock indentation tests by conical pick. Trans. Nonferrous Met. Soc. China 2021, 31, 1766–1783. [Google Scholar] [CrossRef]
- Wang, S.F.; Tang, Y.; Wang, S.Y. Influence of brittleness and confining stress on rockcuttability based on rock indentation tests. J. Cent. South Univ. 2021, 28, 2786–2800. [Google Scholar] [CrossRef]
- Editorial Committee of Foundation Treatment Manual. Foundation Treatment Manual; China Construction Industry Press: Beijing, China, 1988; pp. 283–287, 331–371. [Google Scholar]
- Shi, M.S. Research on Polymer Grouting Material Properties and Directional Fracturing Grouting Mechanism for Dykes and Dams. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- El Tani, M. Grouting rock fractures with cement grout. Rock Mech. Rock Eng. 2012, 45, 547–561. [Google Scholar] [CrossRef]
- El Tani, M.; Stille, H. Grout spread and injection period of silica solution and cement mix in rock fractures. Rock Mech. Rock Eng. 2017, 50, 2365–2380. [Google Scholar] [CrossRef]
- Yang, M.J.; Yue, Z.Q.; Lee, P.K.; Su, B.; Tham, L.G. Prediction of grout penetration in fractured rocks by numerical simulation. Can. Geotech. J. 2002, 39, 1384–1394. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.S.; Zhang, L.Z.; Liu, R.T. Grouting mechanism of quick setting slurry in rock fissure with consideration of viscosity variation with space. Tunn. Undergr. Space Technol. 2017, 70, 262–273. [Google Scholar] [CrossRef]
- Zhang, L.H. Seepage Mechanism and Mechanics of Geotechnical Grouting. Ph.D. Thesis, Northern Jiaotong University, Beijing, China, 1996. [Google Scholar]
- Li, X.L.; Jin, D.; Wang, F.M.; Zhong, Y.H.; Zhang, B. Diffusion model of an ideal expansible grout in single fracture. Chin. J. Rock Mech. Eng. 2018, 37, 37–1207. [Google Scholar]
- Funehag, J.; Gustafson, G. Design of grouting with silica sol in hard rock-new methods for calculation of penetration length. part I. Tunn. Undergr. Space Technol. 2008, 23, 1–8. [Google Scholar] [CrossRef]
- Li, S.F.; Li, S.C.; Liu, R.T. Grouting reinforcement experiment for water-rich broken rock mass. Chin. J. Rock Mech. Eng. 2017, 36, 198–207. [Google Scholar]
- Ruan, W.J. Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts. Chin. J. Rock Mech. Eng. 2005, 24, 2709–2714. [Google Scholar]
- Amadei, B.; Savage, W.Z. An analytical solution for transient flow of Bingham viscoplastic materials in rock fractures. Int. J. Rock Mech. Min. Sci. 2001, 38, 285–296. [Google Scholar] [CrossRef]
- Luo, P.P.; Li, Z.P.; Fan, B. Theoretical study on flow model for tilted single fracture Binghamian grout. J. Shandong Univ. Sci. Technol. 2010, 29, 43–47. [Google Scholar]
- Zhan, K.Y.; Sui, W.H.; Gao, Y. A model for grouting into single fracture with flowing water. Rock Soil Mech. 2011, 32, 1659–1663. [Google Scholar]
- Tian, M.X. A model for grouting into fracture with flowing water based on time-dependent behavior of viscosity. J. Chongqing Jiaotong Univ. Nat. Sci. 2011, 30, 536–537. [Google Scholar]
- Zhang, Q.S.; Zhang, L.Z.; Zhang, X. Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity. Chin. J. Rock Mech. Eng. 2015, 34, 1198–1210. [Google Scholar]
- Guo, C.C.; Wang, F.M. Mechanism Study on the Construction of Ultra-Thin Antiseepage Wall by Polymer Injection. J. Mater. Civ. Eng. 2012, 24, 1183–1192. [Google Scholar]
- Zheng, C.C. Simulation study on Grouting of Fractured Rock Mass. Ph.D. Thesis, Central South University of Technology, Changsha, China, 1999. [Google Scholar]
- Ruan, W.J. Study on Basic Properties of Grout and Grouting Diffusion in Rock Cracks. Ph.D. Thesis, Jilin University, Changchun, China, 2003. [Google Scholar]
- Zheng, Y.H. Research on Grouting and Grouting Control Method for Fractured Rock Mass. Ph.D. Thesis, Jilin University, Changchun, China, 2005. [Google Scholar]

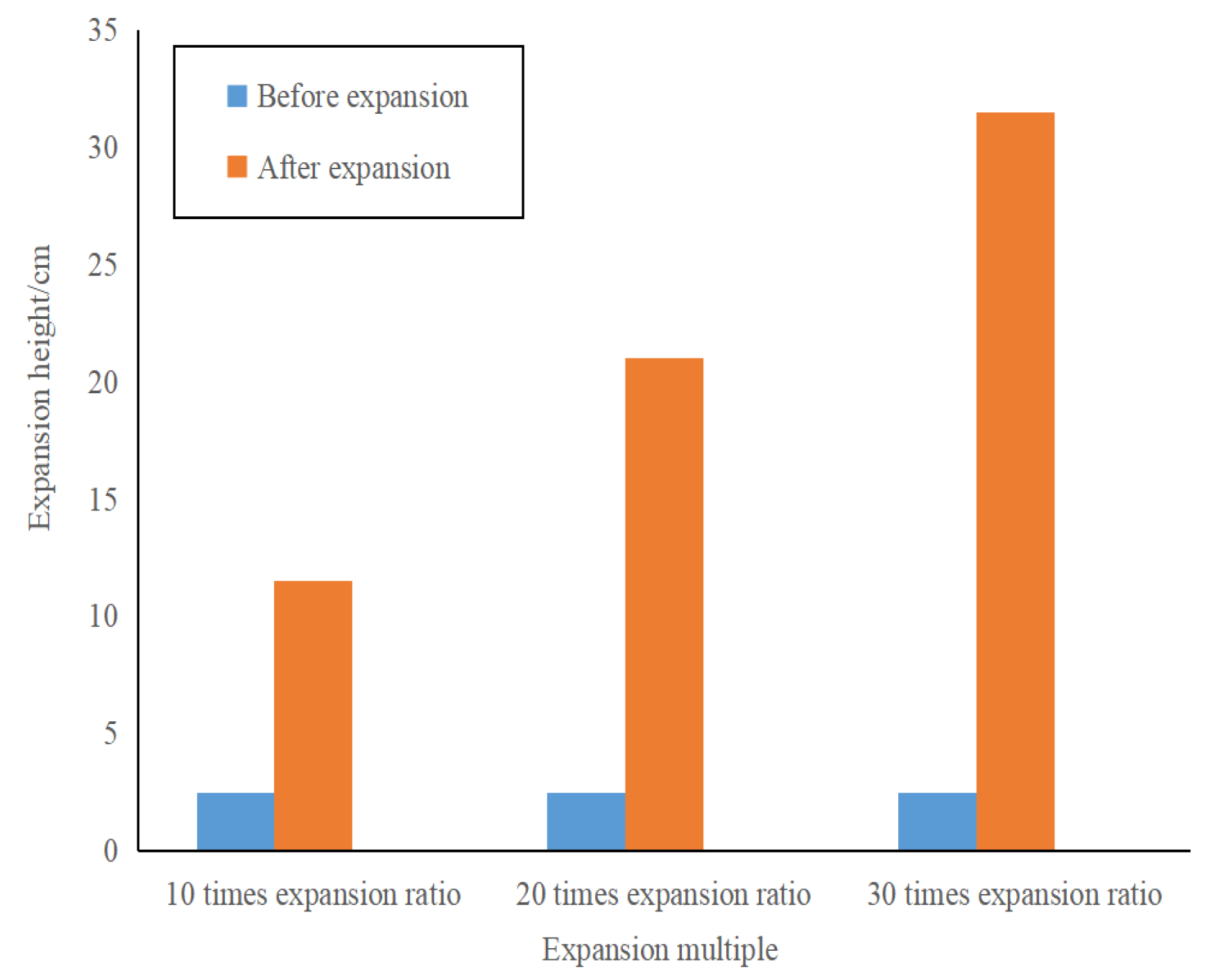
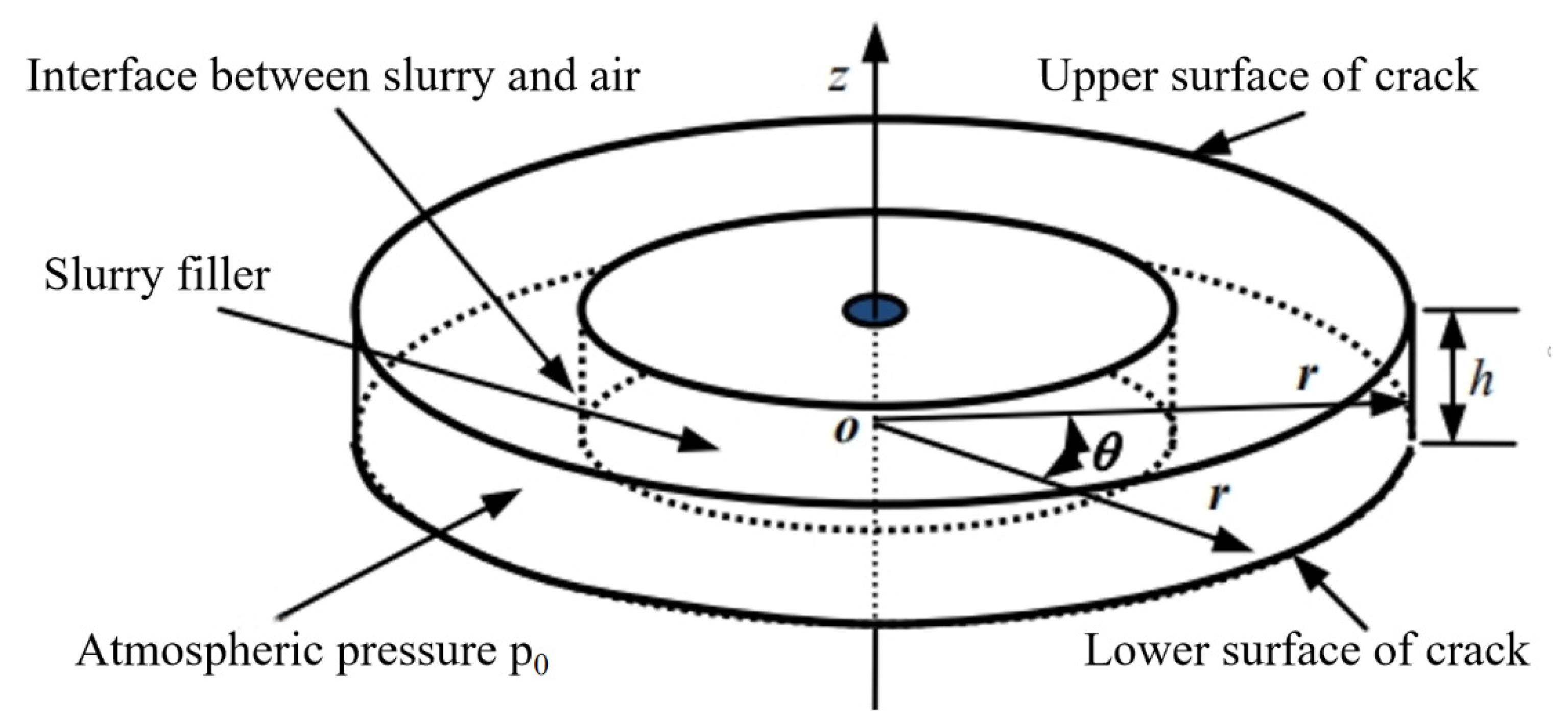
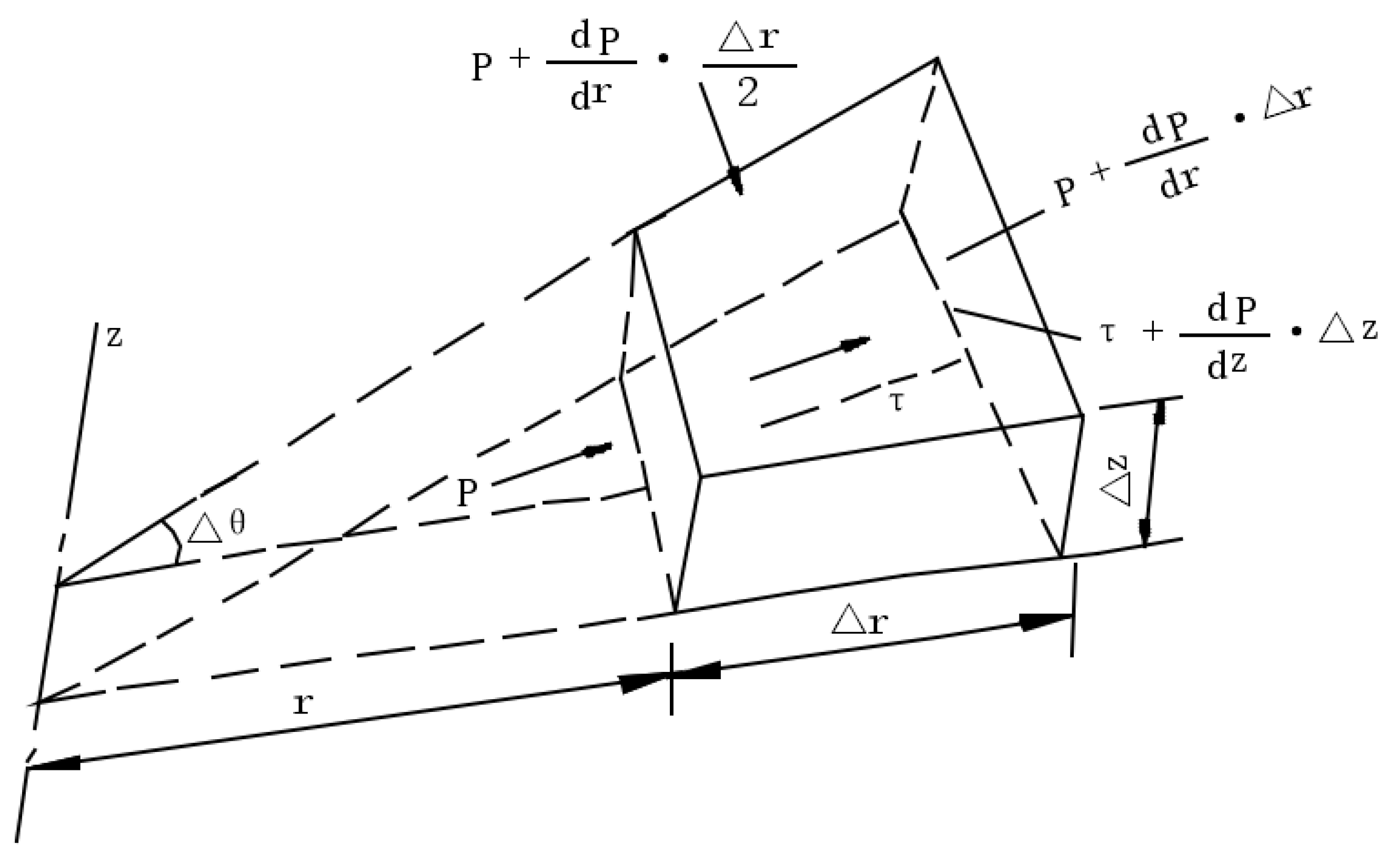
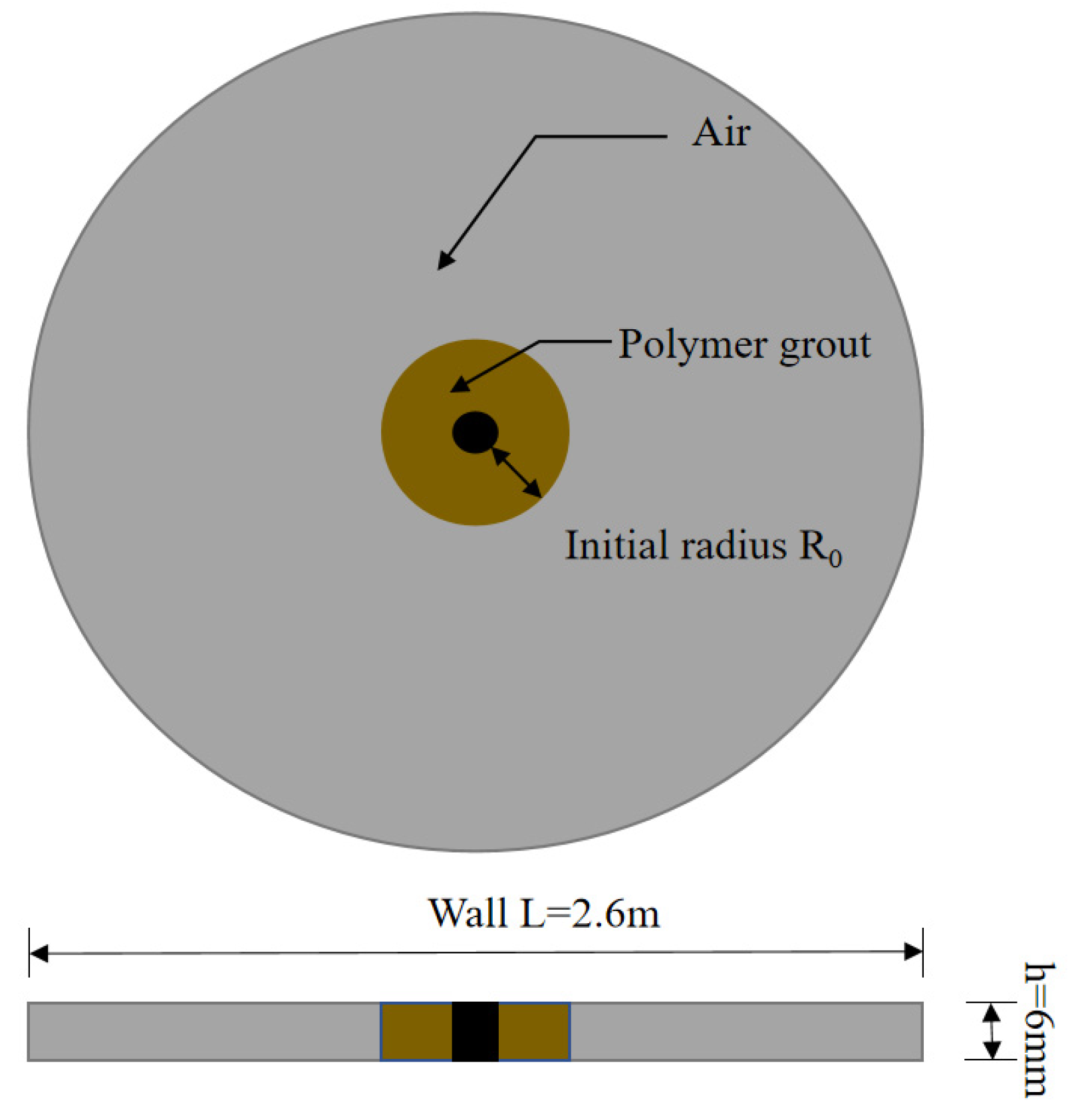


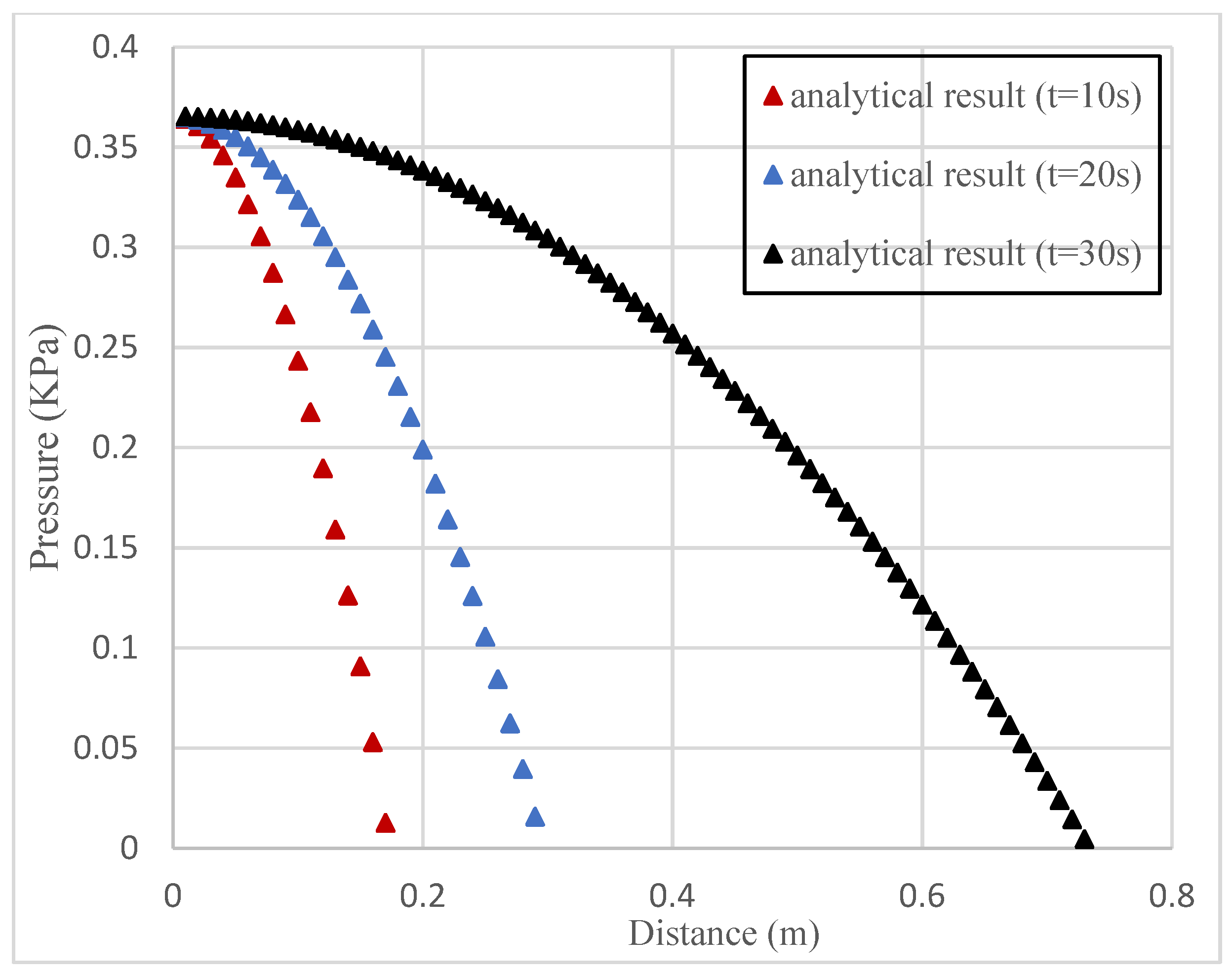

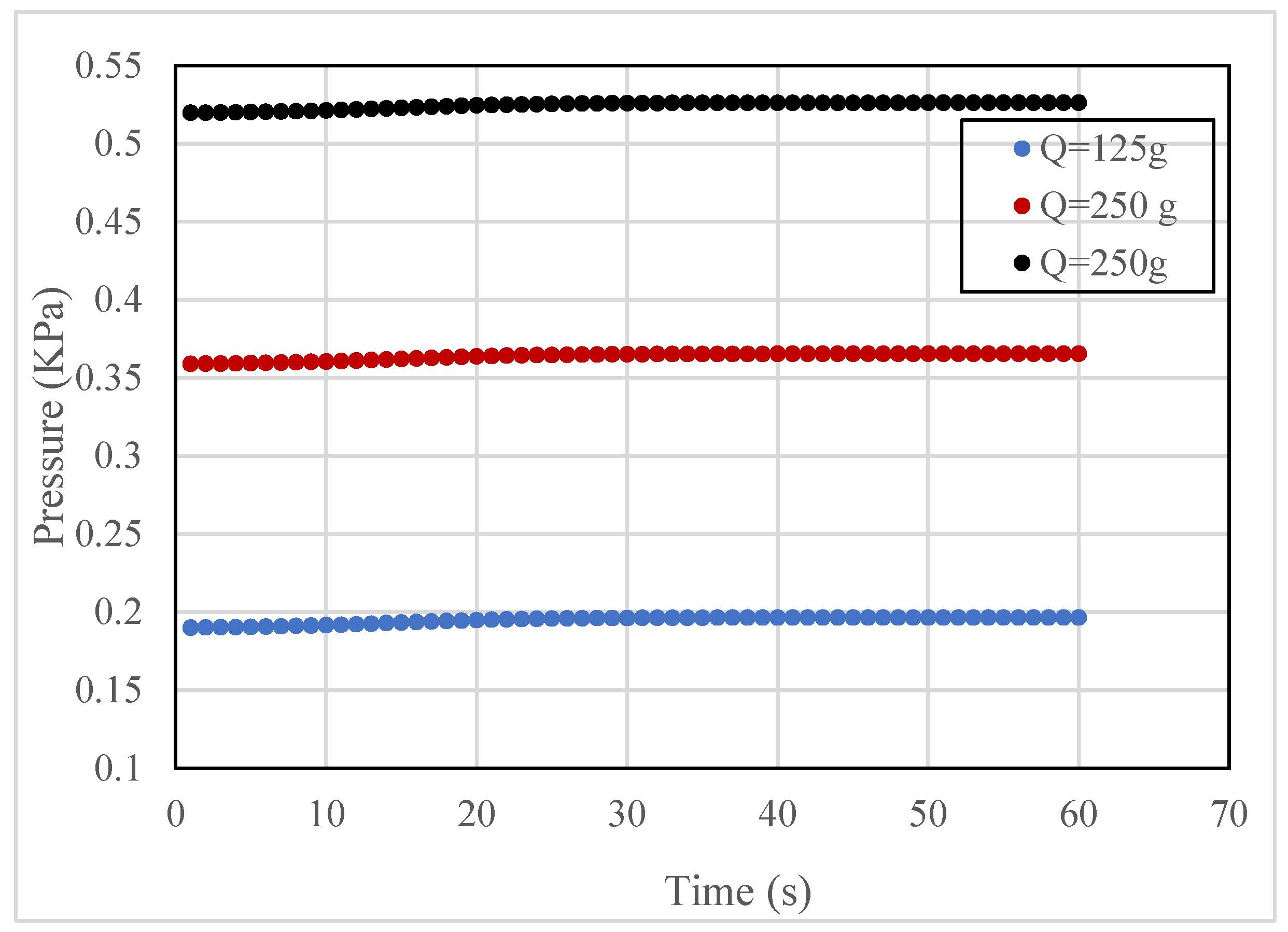
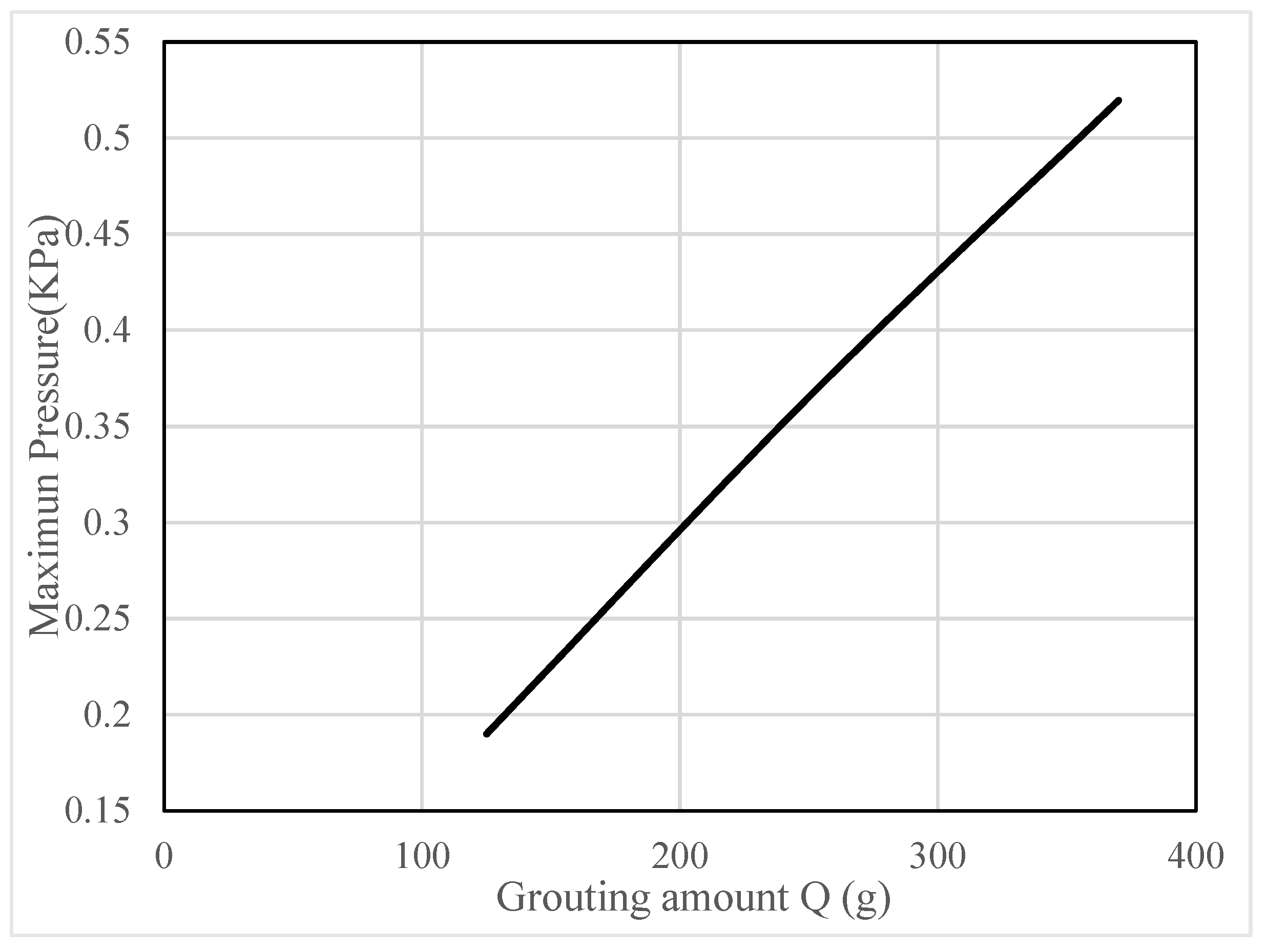

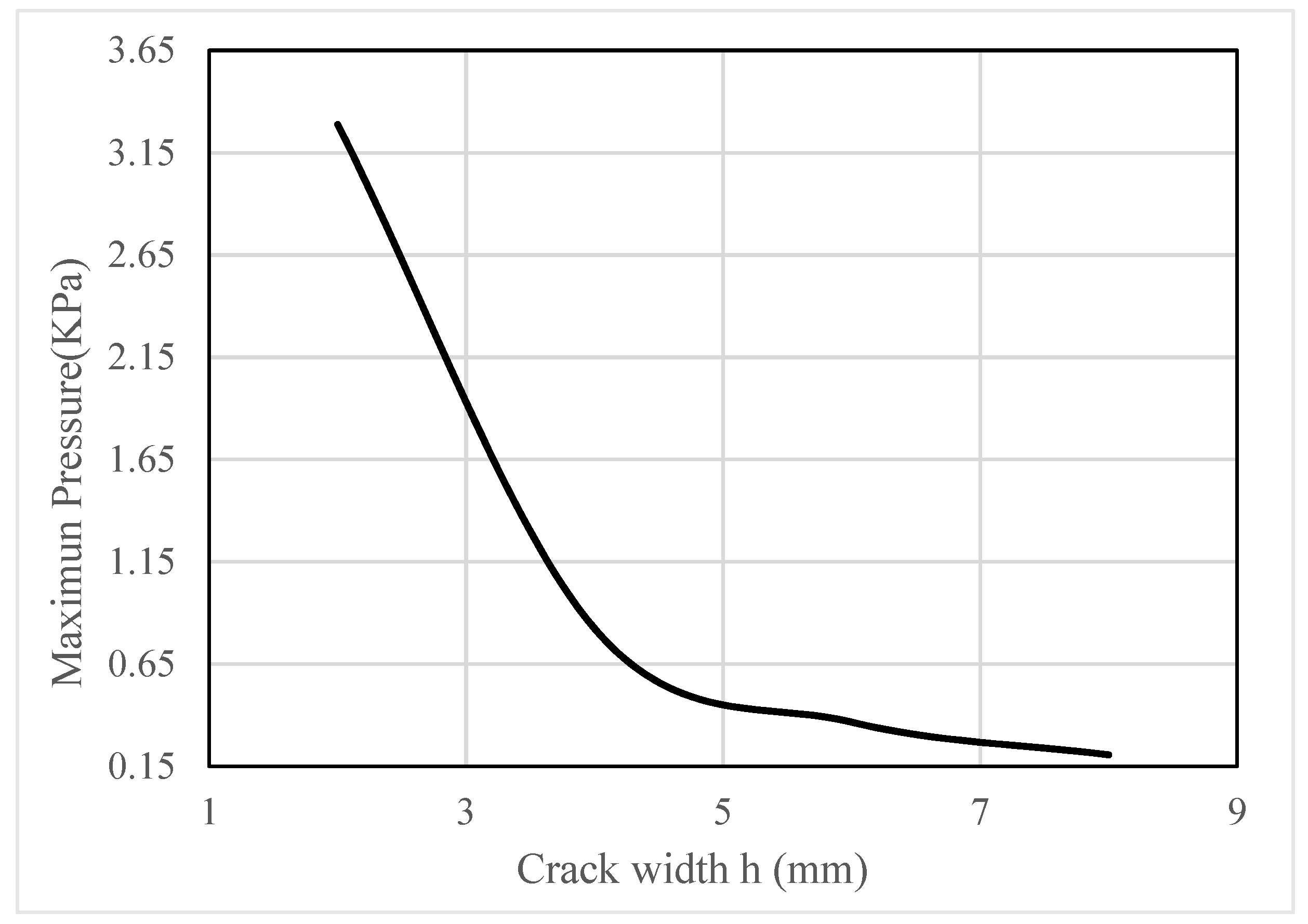
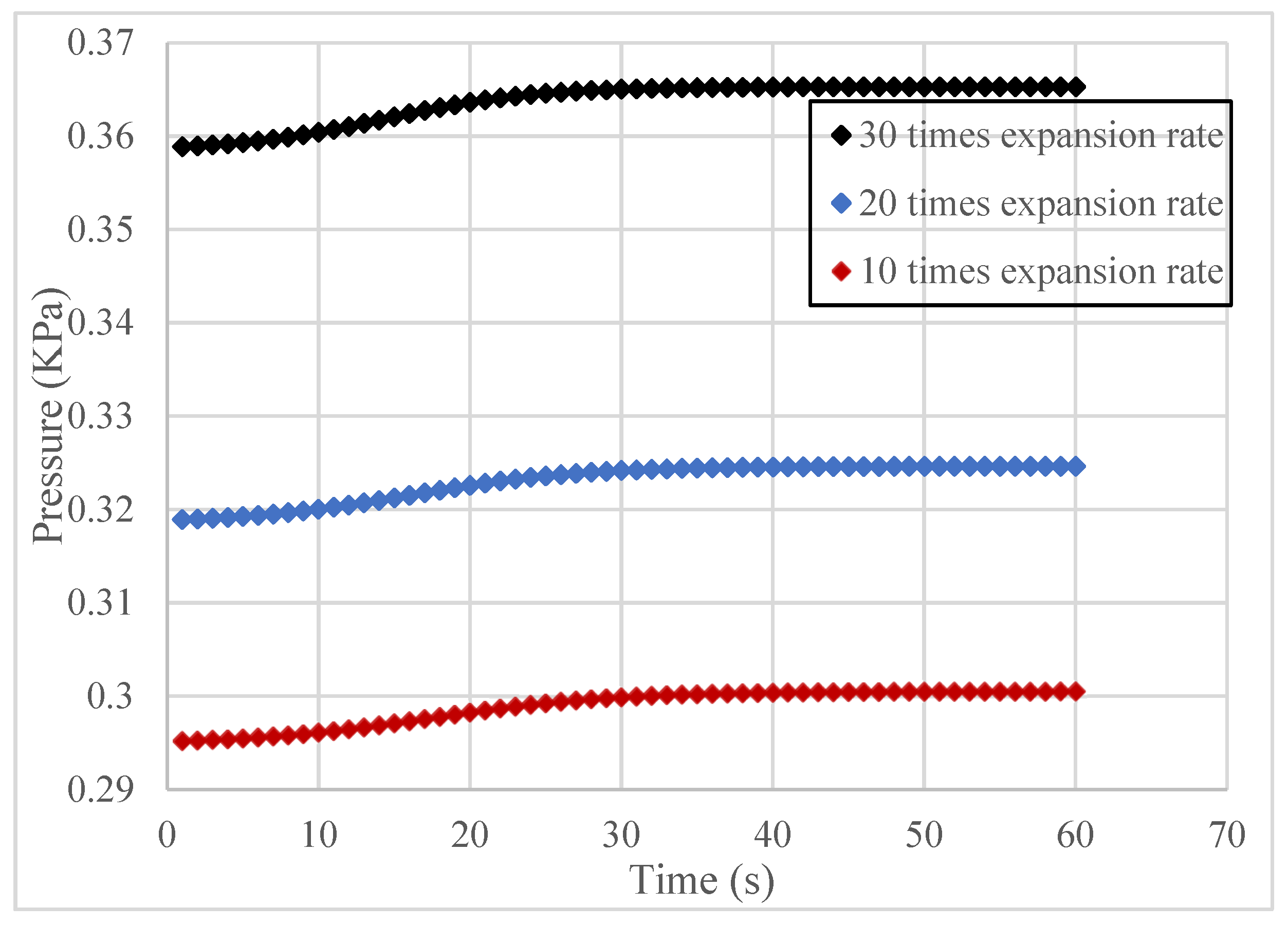
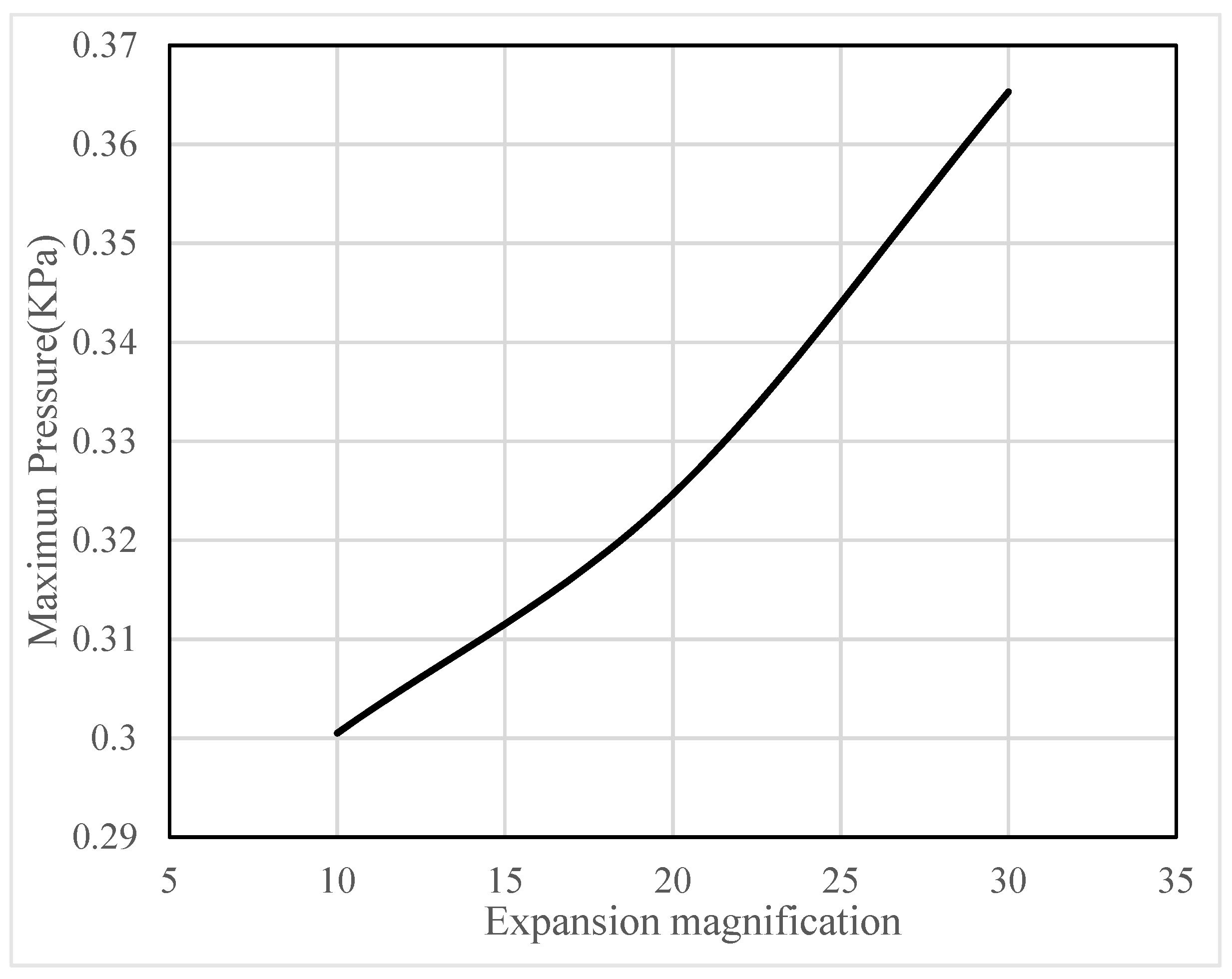
| Position r (cm) | Time t (s) | Diffusion Pressure (KPa) | Relative Error | |
|---|---|---|---|---|
| Numerical Solution | Theoretical Solution | |||
| r = 2 | 0 | 0.3554 | 0.3589 | 0.9% |
| 10 | 0.3591 | 0.3604 | 0.4% | |
| 20 | 0.3634 | 0.3636 | 0.1% | |
| 30 | 0.3652 | 0.3650 | 0.1% | |
| 40 | 0.36581 | 0.3653 | 0.1% | |
| 50 | 0.3662 | 0.3653 | 0.2% | |
| 60 | 0.3662 | 0.3653 | 0.2% | |
| Time t (s) | Position r (cm) | Diffusion Pressure (KPa) | Relative Error | |
|---|---|---|---|---|
| Numerical Solution | Theoretical Solution | |||
| t = 30 | 2 | 0.3630 | 0.3651 | 0.5% |
| 4 | 0.3592 | 0.3643 | 0.5% | |
| 6 | 0.3579 | 0.3629 | 1.3% | |
| 8 | 0.3560 | 0.3610 | 1.0% | |
| 10 | 0.3535 | 0.3585 | 1.3% | |
| 12 | 0.3506 | 0.3556 | 1.0% | |
| 14 | 0.3470 | 0.3520 | 1.4% | |
| Position(x)/m | z/m | ||||||
|---|---|---|---|---|---|---|---|
| −0.0030 | −0.0020 | −0.0010 | 0.0000 | 0.0010 | 0.0020 | 0.0030 | |
| 0.1653 | 0 | 0.0158 | 0.0253 | 0.0285 | 0.0253 | 0.0158 | 0 |
| 0.1820 | 0 | 0.0192 | 0.0307 | 0.0345 | 0.0307 | 0.0192 | 0 |
| 0.2000 | 0 | 0.0232 | 0.0370 | 0.0417 | 0.0370 | 0.0232 | 0 |
| 0.2195 | 0 | 0.0279 | 0.0446 | 0.0502 | 0.0446 | 0.0279 | 0 |
| 0.2404 | 0 | 0.0334 | 0.0535 | 0.0602 | 0.0535 | 0.0334 | 0 |
| 0.2627 | 0 | 0.0399 | 0.0639 | 0.0719 | 0.0639 | 0.0399 | 0 |
| 0.2862 | 0 | 0.0474 | 0.0759 | 0.0854 | 0.0759 | 0.0474 | 0 |
| 0.3110 | 0 | 0.0560 | 0.0896 | 0.1008 | 0.0896 | 0.0560 | 0 |
| 0.3367 | 0 | 0.0656 | 0.1050 | 0.1181 | 0.1050 | 0.0656 | 0 |
| 0.3631 | 0 | 0.0763 | 0.1221 | 0.1373 | 0.1221 | 0.0763 | 0 |
| 0.3899 | 0 | 0.0880 | 0.1408 | 0.1584 | 0.1408 | 0.0880 | 0 |
| 0.4167 | 0 | 0.1005 | 0.1608 | 0.1809 | 0.1608 | 0.1005 | 0 |
| 0.4432 | 0 | 0.1137 | 0.1819 | 0.2046 | 0.1819 | 0.1137 | 0 |
| 0.4689 | 0 | 0.1273 | 0.2037 | 0.2291 | 0.2037 | 0.1273 | 0 |
| 0.4936 | 0 | 0.1410 | 0.2256 | 0.2538 | 0.2256 | 0.1410 | 0 |
| 0.5168 | 0 | 0.1546 | 0.2474 | 0.2783 | 0.2474 | 0.1546 | 0 |
| 0.5384 | 0 | 0.1678 | 0.2684 | 0.3020 | 0.2684 | 0.1678 | 0 |
| 0.5581 | 0 | 0.1803 | 0.2884 | 0.3245 | 0.2884 | 0.1803 | 0 |
| 0.5758 | 0 | 0.1919 | 0.3071 | 0.3455 | 0.3071 | 0.1919 | 0 |
| 0.5916 | 0 | 0.2026 | 0.3241 | 0.3646 | 0.3241 | 0.2026 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Ma, S.; Du, X. Diffusion Model of Parallel Plate Crack Grouting Based on Foaming Expansion Characteristics of Polymer Slurry. Mathematics 2021, 9, 2907. https://doi.org/10.3390/math9222907
Liang J, Ma S, Du X. Diffusion Model of Parallel Plate Crack Grouting Based on Foaming Expansion Characteristics of Polymer Slurry. Mathematics. 2021; 9(22):2907. https://doi.org/10.3390/math9222907
Chicago/Turabian StyleLiang, Jiasen, Shaokun Ma, and Xueming Du. 2021. "Diffusion Model of Parallel Plate Crack Grouting Based on Foaming Expansion Characteristics of Polymer Slurry" Mathematics 9, no. 22: 2907. https://doi.org/10.3390/math9222907
APA StyleLiang, J., Ma, S., & Du, X. (2021). Diffusion Model of Parallel Plate Crack Grouting Based on Foaming Expansion Characteristics of Polymer Slurry. Mathematics, 9(22), 2907. https://doi.org/10.3390/math9222907







