Period of Arrhythmia Anchored around an Infarction Scar in an Anatomical Model of the Human Ventricles
Abstract
:1. Introduction
2. Materials and Methods
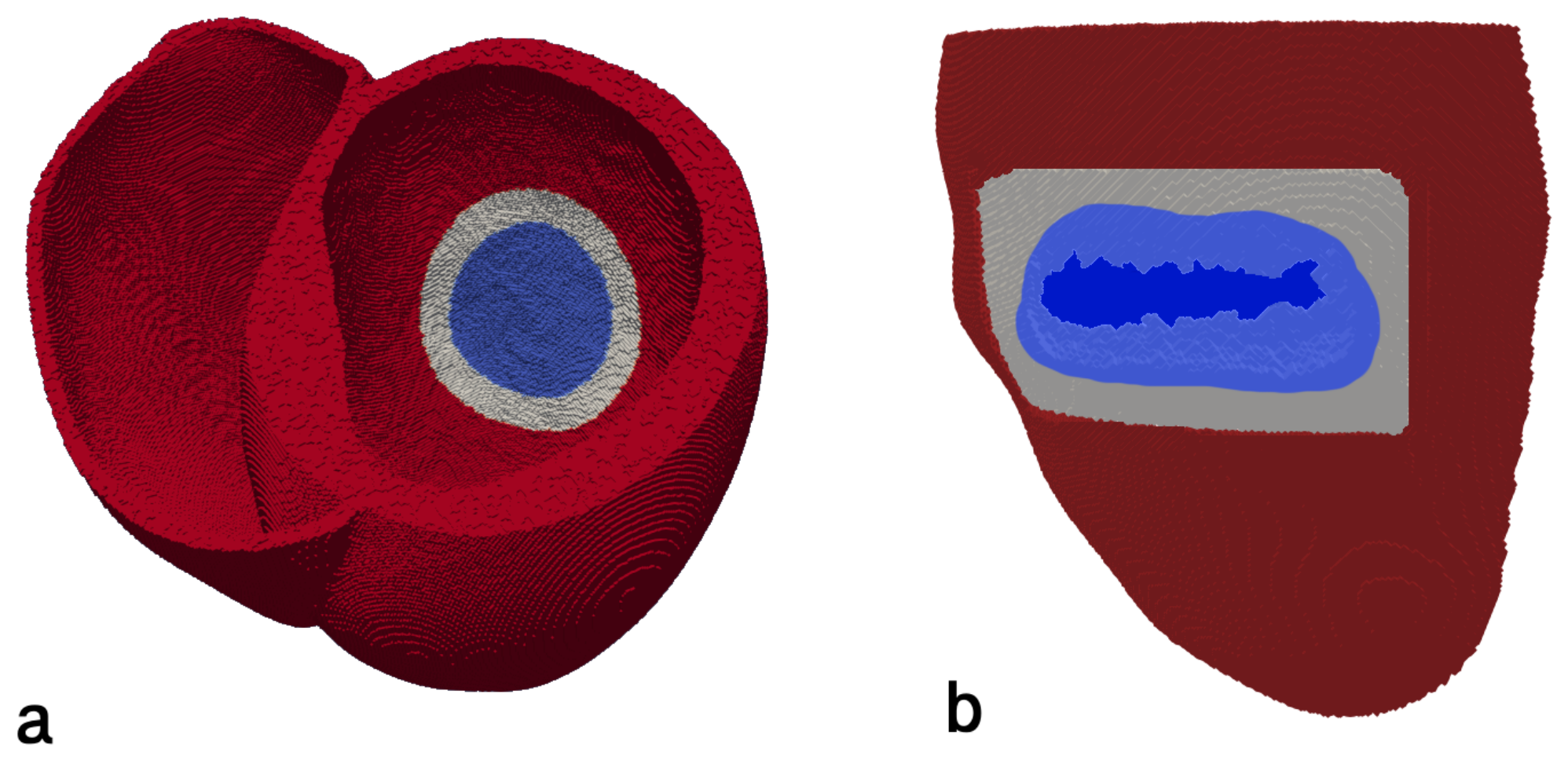
2.1. Model of the Ventricular Geometry
2.2. Infarction Scar Construction
2.3. Electrophysiological Model of Healthy Myocardium and Gray Zone
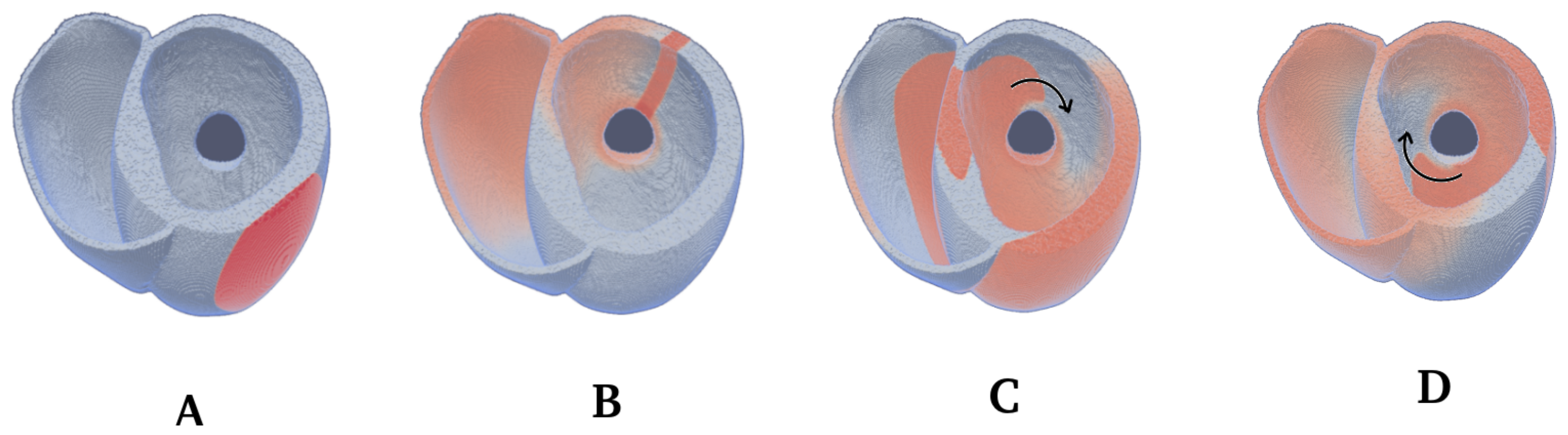
2.4. Spiral Wave Initiation
Numerical Methods
3. Results
3.1. Rotation Period
3.2. Wave Rotation Regimes
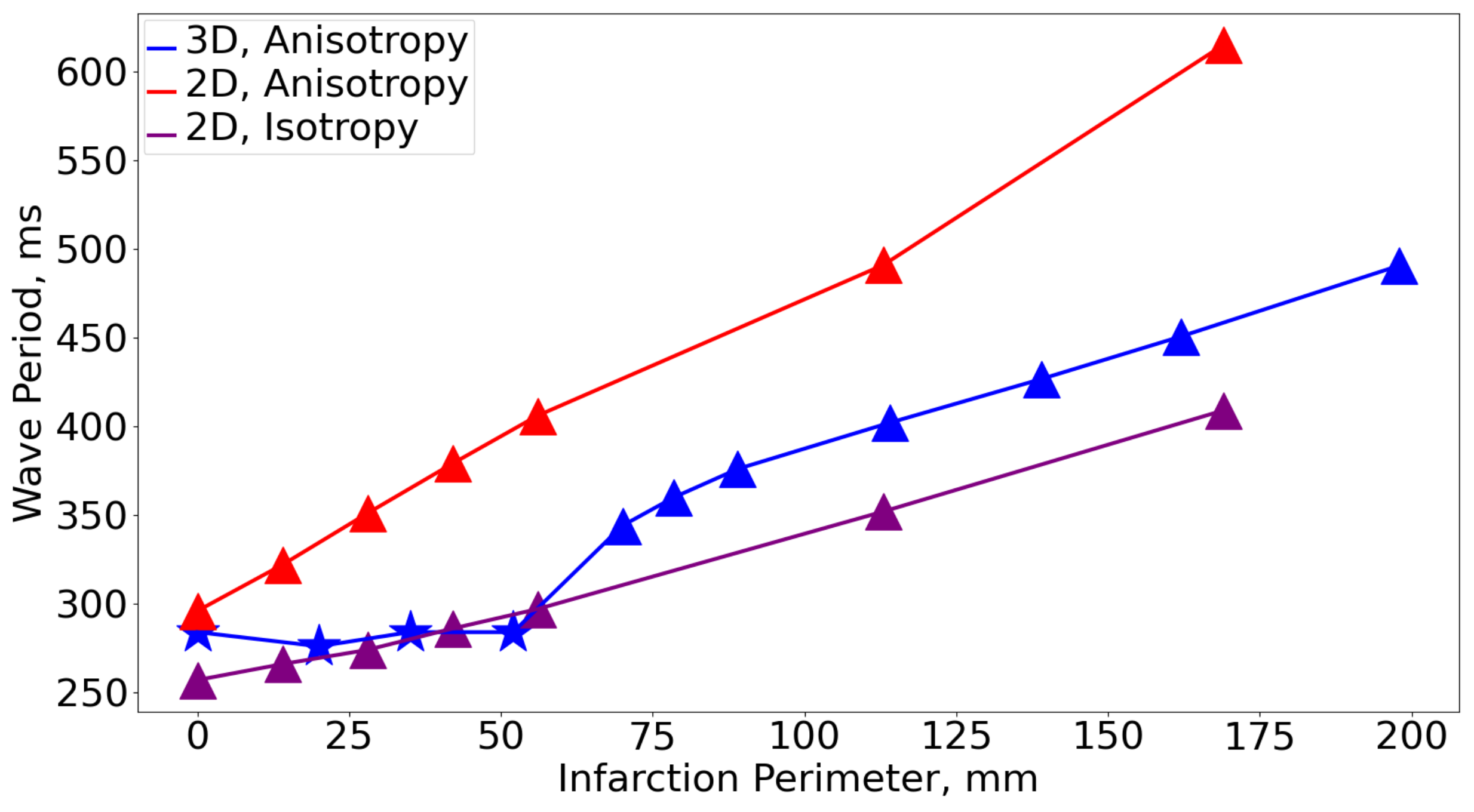
3.3. Comparison with 2D
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CV | Conduction Velocity |
| FR | Functional Rotation |
| GZ | Gray Zone |
| GZR | Gray Zone Rotation |
| IS | Post-infarction Scar |
| NT | Normal Tissue |
| SR | Scar Rotation |
| SR2 | Scar Rotation Two |
References
- Pertsov, A.M.; Ermakova, E.A.; Panfilov, A.V. Rotating spiral waves in a modified Fitz-Hugh-Nagumo model. Phys. D Nonlinear Phenom. 1984, 14, 117–124. [Google Scholar] [CrossRef]
- Davidenko, J.M.; Pertsov, A.V.; Salomonsz, R.; Baxter, W.; Jalife, J. Stationary and drifting spiral waves of excitation in isolated cardiac muscle. Nature 1992, 355, 349–351. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Feng, X.; Li, T.C.; Qu, S.; Wang, X.; Zhang, H. Dynamics of spiral waves rotating around an obstacle and the existence of a minimal obstacle. Phys. Rev. E 2017, 95, 052218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panfilov, A.V.; Holden, A.V. Computer simulation of re-entry sources in myocardium in two and three dimensions. J. Theor. Biol. 1993, 161, 271–285. [Google Scholar] [CrossRef]
- Xie, F.; Qu, Z.; Garfinkel, A. Dynamics of reentry around a circular obstacle in cardiac tissue. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1998, 58, 6355. [Google Scholar] [CrossRef]
- Courtemanche, M.; Glass, L.; Keener, J.P. Instabilities of a propagating pulse in a ring of excitable media. Phys. Rev. Lett. 1993, 70. [Google Scholar] [CrossRef] [PubMed]
- Balaban, G.; Halliday, B.P.; Bai, W.; Porter, B.; Malvuccio, C.; Lamata, P.; Rinaldi, C.A.; Plank, G.; Rueckert, D.; Prasad, S.K.; et al. Scar shape analysis and simulated electrical instabilities in a non-ischemic dilated cardiomyopathy patient cohort. PLoS Comput. Biol. 2019, 15, e1007421. [Google Scholar] [CrossRef]
- Nattel, S.; Burstein, B.; Dobrev, D. Atrial remodeling and atrial fibrillation: Mechanisms and implications. Circ. Arrhythmia Electrophysiol. 2008, 1, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, A.; Azevedo, C.F.; Cheng, A.; Gupta, S.N.; Bluemke, D.A.; Foo, T.K.; Gerstenblith, G.; Weiss, R.G.; Marbán, E.; Tomaselli, G.F. Infarct tissue heterogeneity by magnetic resonance imaging identifies enhanced cardiac arrhythmia susceptibility in patients with left ventricular dysfunction. Circulation 2007, 115, 2006–2014. [Google Scholar] [CrossRef]
- Arevalo, H.J.; Vadakkumpadan, F.; Guallar, E.; Jebb, A.; Malamas, P.; Wu, K.C.; Trayanova, N.A. Arrhythmia risk stratification of patients after myocardial infarction using personalized heart models. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef]
- Arevalo, H.; Plank, G.; Helm, P.; Halperin, H.; Trayanova, N. Tachycardia in Post-Infarction Hearts: Insights from 3D Image-Based Ventricular Models. PLoS ONE 2013, 8, e68872. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Perez, A.; Sebastian, R.; Izquierdo, M.; Ruiz, R.; Bishop, M.; Ferrero, J.M. Personalized cardiac computational models: From clinical data to simulation of infarct-related ventricular tachycardia. Front. Physiol. 2019, 10, 580. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colli-Franzone, P.; Gionti, V.; Pavarino, L.F.; Scacchi, S.; Storti, C. Role of infarct scar dimensions, border zone repolarization properties and anisotropy in the origin and maintenance of cardiac reentry. Math. Biosci. 2019, 315, 108228. [Google Scholar] [CrossRef] [PubMed]
- Bernus, O.; Zemlin, C.W.; Zaritsky, R.M.; Mironov, S.F.; Pertsov, A.M. Alternating conduction in the ischaemic border zone as precursor of reentrant arrhythmias: A simulation study. Europace 2005, 7, S93–S104. [Google Scholar] [CrossRef]
- Konovalov, P.; Mangileva, D.; Dokuchaev, A.; Solovyova, O.; Panfilov, A. Rotational Activity Around an Obstacle in 2D Cardiac Tissue in Presence of Cellular Heterogeneity. bioRxiv 2021. [Google Scholar] [CrossRef]
- Strocchi, M.; Augustin, C.M.; Gsell, M.A.F.; Karabelas, E.; Neic, A.; Gillette, K.; Razeghi, O.; Prassl, A.J.; Vigmond, E.J.; Behar, J.M.; et al. A Publicly Available Virtual Cohort of Four- chamber Heart Meshes for Cardiac Electro-mechanics Simulations. PLoS ONE 2020, 15, e0235145. [Google Scholar] [CrossRef]
- Bayer, J.; Prassl, A.J.; Pashaei, A.; Gomez, J.F.; Frontera, A.; Neic, A.; Plank, G.; Vigmond, E.J. Universal ventricular coordinates: A generic framework for describing position within the heart and transferring data. Med. Image Anal. 2018, 45, 83–93. [Google Scholar] [CrossRef]
- Mendonca Costa, C.; Neic, A.; Kerfoot, E.; Gillette, K.; Porter, B.; Sieniewicz, B.; Gould, J.; Sidhu, B.; Chen, Z.; Elliott, M.; et al. A Virtual Cohort of Twenty-four Left-Ventricular Models of Ischemic Cardiomyopathy Patients. 2020. Available online: https://www.researchgate.net/publication/343574702_A_Virtual_Cohort_of_Twenty-four_Left-ventricular_Models_of_Ischemic_Cardiomyopathy_Patients (accessed on 13 August 2021). [CrossRef]
- Tusscher, K.H.T.; Panfilov, A.V. Alternans and spiral breakup in a human ventricular tissue model. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H1088–H1100. [Google Scholar] [CrossRef]
- Taggart, P.; Sutton, P.M.; Opthof, T.; Coronel, R.; Trimlett, R.; Pugsley, W.; Kallis, P. Inhomogeneous transmural conduction during early ischaemia in patients with coronary artery disease. J. Mol. Cell. Cardiol. 2000, 32, 621–630. [Google Scholar] [CrossRef]
- Bayer, J.D.; Blake, R.C.; Plank, G.; Trayanova, N.A. A novel rule-based algorithm for assigning myocardial fiber orientation to computational heart models. Ann. Biomed. Eng. 2012, 40, 2243–2254. [Google Scholar] [CrossRef] [Green Version]
- Bayer, J.D.; Beaumont, J.; Krol, A. Laplace–Dirichlet energy field specification for deformable models. An FEM approach to active contour fitting. Ann. Biomed. Eng. 2005, 33, 1175–1186. [Google Scholar] [CrossRef] [PubMed]
- Bishop, M.J.; Boyle, P.M.; Plank, G.; Welsh, D.G.; Vigmond, E.J. Modeling the role of the coronary vasculature during external field stimulation. IEEE Trans. Biomed. Eng. 2010, 57, 2335–2345. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Streeter, D. Handbook of Physiology. Sec. 2. Vol. I. The Heart. In Gross Morphology and Fiber Geometry of the Heart; American Physiology Society: Bethesda, MD, USA, 1979; pp. 61–112. [Google Scholar]
- Decker, K.F.; Rudy, Y. Ionic mechanisms of electrophysiological heterogeneity and conduction block in the infarct border zone. Am. J. Physiol. Heart Circ. Physiol. 2010, 299. [Google Scholar] [CrossRef] [Green Version]
- Keldermann, R.H.; Tusscher, K.H.T.; Nash, M.P.; Bradley, C.P.; Hren, R.; Taggart, P.; Panfilov, A.V. A computational study of mother rotor VF in the human ventricles. Am. J. Physiol. Heart Circ. Physiol. 2009, 296. [Google Scholar] [CrossRef] [Green Version]
- De Coster, T. The Role of Adipose Tissue in Arrhythmogenesis: An In Silico Study. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2019. [Google Scholar]
- Rush, S.; Larsen, H. A Practical Algorithm for Solving Dynamic Membrane Equations. IEEE Trans. Biomed. Eng. 1978, BME-25. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.Y.; Yun, C.H.; Kuo, J.Y.; Lai, Y.H.; Sung, K.T.; Yuan, P.J.; Tsai, J.P.; Huang, W.H.; Lin, Y.H.; Hung, T.C.; et al. Aortic Root Remodeling as an Indicator for Diastolic Dysfunction and Normative Ranges in Asians: Comparison and Validation with Multidetector Computed Tomography. Diagnostics 2020, 10, 712. [Google Scholar] [CrossRef]
- Pravdin, S.; Konovalov, P.; Dierckx, H.; Solovyova, O.; Panfilov, A.V. Drift of Scroll Waves in a Mathematical Model of a Heterogeneous Human Heart Left Ventricle. Mathematics 2020, 8, 776. [Google Scholar] [CrossRef]
- Nappi, F.; Carotenuto, A.R.; Avtaar Singh, S.S.; Mihos, C.; Fraldi, M. Euler’s elastica-based biomechanics of the papillary muscle approximation in ischemic mitral valve regurgitation: A simple 2d analytical model. Materials 2019, 12, 1518. [Google Scholar] [CrossRef] [Green Version]
- Caenen, A.; Pernot, M.; Kinn Ekroll, I.; Shcherbakova, D.; Mertens, L.; Swillens, A.; Segers, P. Effect of ultrafast imaging on shear wave visualization and characterization: An experimental and computational study in a pediatric ventricular model. Appl. Sci. 2017, 7, 840. [Google Scholar] [CrossRef] [Green Version]
- Berenfeld, O.; Pertsov, A.M. Dynamics of intramural scroll waves in three-dimensional continuous myocardium with rotational anisotropy. J. Theor. Biol. 1999, 199, 383–394. [Google Scholar] [CrossRef]
- Young, R.J.; Panfilov, A.V. Anisotropy of wave propagation in the heart can be modeled by a Riemannian electrophysiological metric. Proc. Natl. Acad. Sci. USA 2010, 107, 15063–15068. [Google Scholar] [CrossRef] [Green Version]
- Bernus, O.; Wellner, M.; Pertsov, A. Intramural wave propagation in cardiac tissue: Asymptotic solutions and cusp waves. Phys. Rev. E 2004, 70, 061913. [Google Scholar] [CrossRef]
- Vandersickel, N.; Kazbanov, I.V.; Nuitermans, A.; Weise, L.D.; Pandit, R.; Panfilov, A.V. A study of early afterdepolarizations in a model for human ventricular tissue. PLoS ONE 2014, 9, e84595. [Google Scholar] [CrossRef] [Green Version]
- Stevenson, W.G.; Soejima, K. Catheter ablation for ventricular tachycardia. Circulation 2007, 115, 2750–2760. [Google Scholar] [CrossRef]
- Codreanu, A.; Odille, F.; Aliot, E.; Marie, P.Y.; Magnin-Poull, I.; Andronache, M.; Mandry, D.; Djaballah, W.; Régent, D.; Felblinger, J.; et al. Electroanatomic characterization of post-infarct scars: Comparison with 3-dimensional myocardial scar reconstruction based on magnetic resonance imaging. J. Am. Coll. Cardiol. 2008, 52, 839–842. [Google Scholar] [CrossRef] [PubMed]
- Vigmond, E.; Pashaei, A.; Amraoui, S.; Cochet, H.; Hassaguerre, M. Percolation as a mechanism to explain atrial fractionated electrograms and reentry in a fibrosis model based on imaging data. Heart Rhythm 2016, 13, 1536–1543. [Google Scholar] [CrossRef] [PubMed]

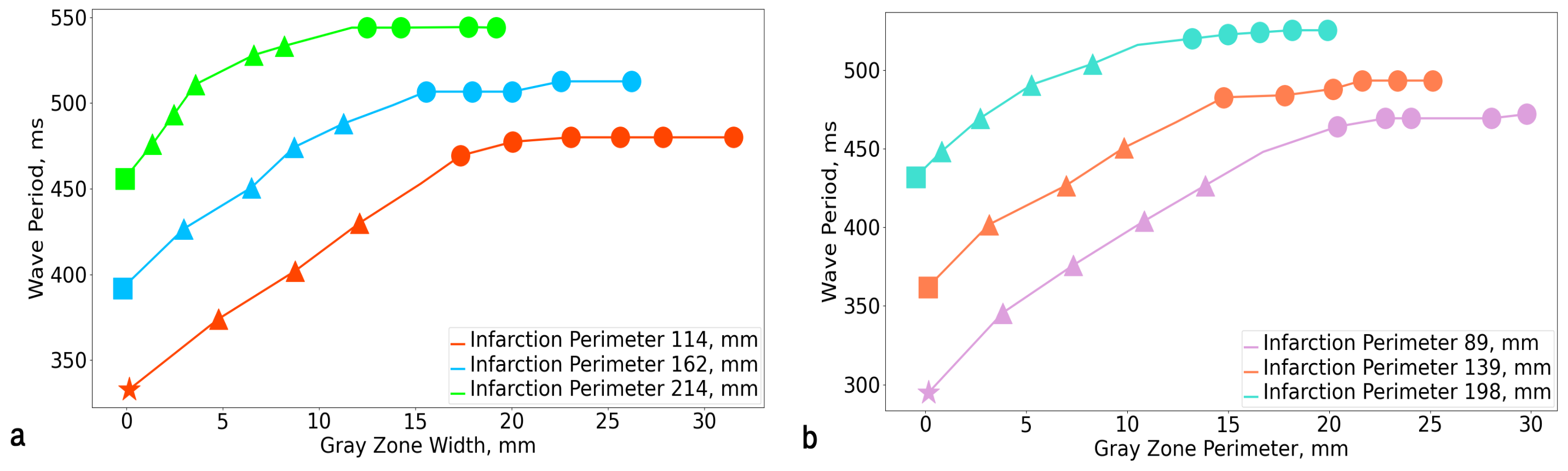
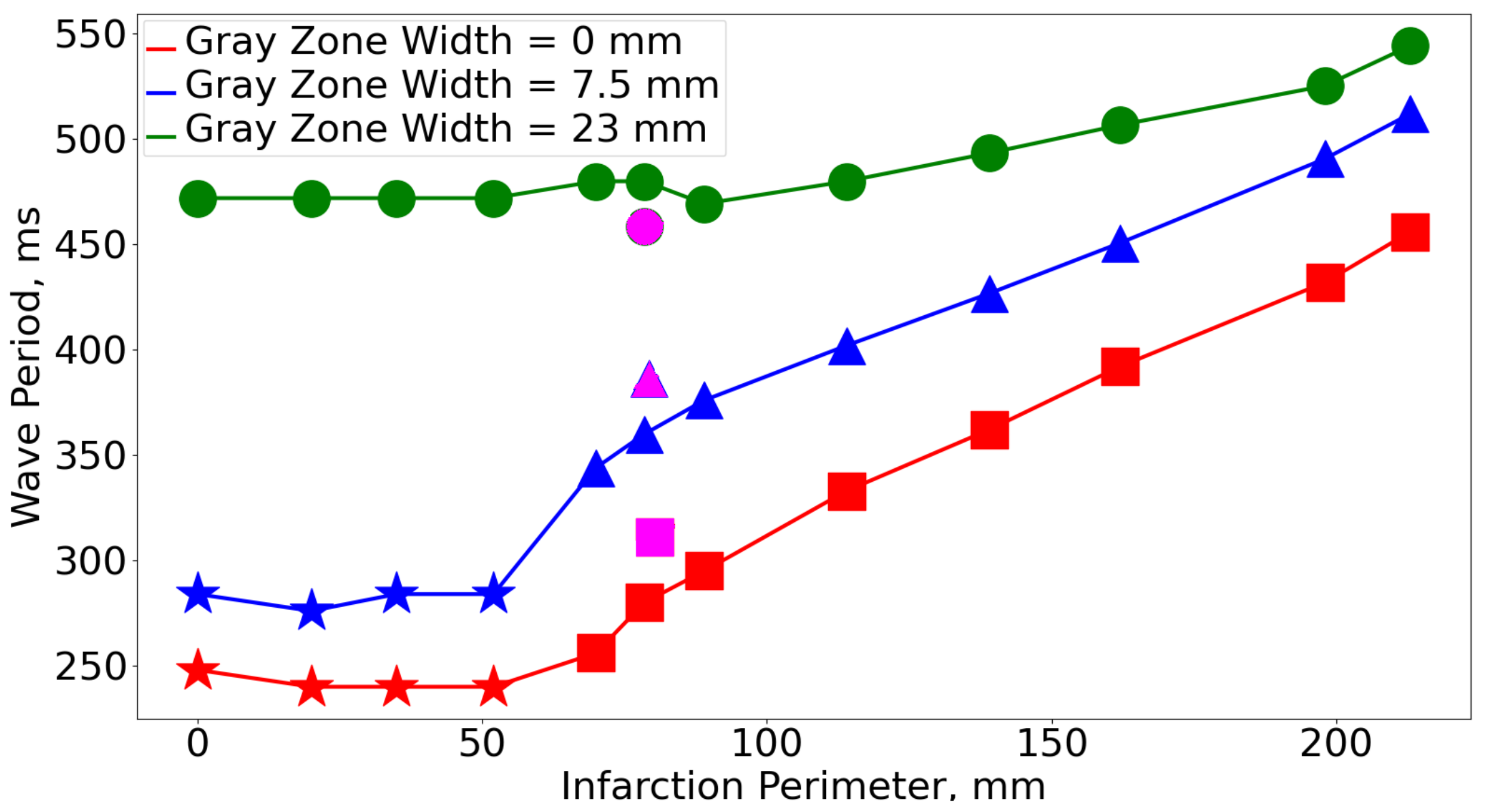
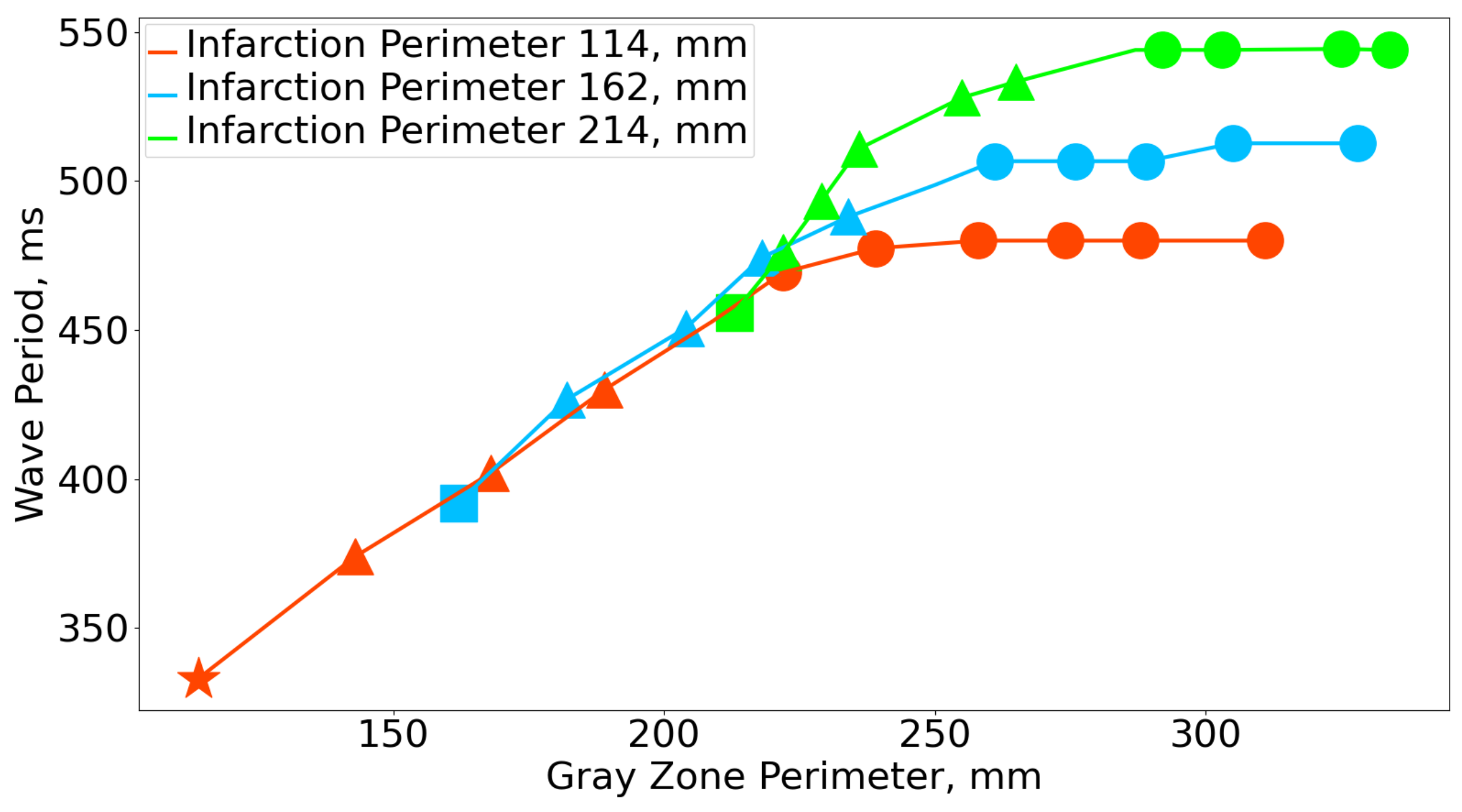

| GZ Scar | 0% | 2.5% | 5% | 7.5% | 10% | 12.5% | 15% | 17.5% | 20% | 22.5% | 25% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 295 | 346 | 376 | 404 | 427 | 448 | 464 | 469 | 469 | 469 | 472 |
| 5% | 333 | 374 | 400 | 417 | 448 | 469 | 469 | 480 | 504 | 480 | 480 |
| 7.5% | 362 | 402 | 427 | 451 | 467 | 483 | 483 | 488 | 493 | 493 | 493 |
| 10% | 392 | 427 | 451 | 474 | 488 | 499 | 499 | 507 | 513 | 513 | 513 |
| 12.5% | 432 | 442 | 469 | 491 | 504 | 516 | 516 | 523 | 525 | 525 | 524 |
| 15% | 456 | 464 | 493 | 511 | 528 | 533 | 533 | 544 | 549 | 544 | 544 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangileva, D.; Konovalov, P.; Dokuchaev, A.; Solovyova, O.; Panfilov, A.V. Period of Arrhythmia Anchored around an Infarction Scar in an Anatomical Model of the Human Ventricles. Mathematics 2021, 9, 2911. https://doi.org/10.3390/math9222911
Mangileva D, Konovalov P, Dokuchaev A, Solovyova O, Panfilov AV. Period of Arrhythmia Anchored around an Infarction Scar in an Anatomical Model of the Human Ventricles. Mathematics. 2021; 9(22):2911. https://doi.org/10.3390/math9222911
Chicago/Turabian StyleMangileva, Daria, Pavel Konovalov, Arsenii Dokuchaev, Olga Solovyova, and Alexander V. Panfilov. 2021. "Period of Arrhythmia Anchored around an Infarction Scar in an Anatomical Model of the Human Ventricles" Mathematics 9, no. 22: 2911. https://doi.org/10.3390/math9222911
APA StyleMangileva, D., Konovalov, P., Dokuchaev, A., Solovyova, O., & Panfilov, A. V. (2021). Period of Arrhythmia Anchored around an Infarction Scar in an Anatomical Model of the Human Ventricles. Mathematics, 9(22), 2911. https://doi.org/10.3390/math9222911







