Duality Solutions in Hydromagnetic Flow of SWCNT-MWCNT/Water Hybrid Nanofluid over Vertical Moving Slender Needle
Abstract
:1. Introduction
2. Problem Formation
3. Stability Flow Solution
4. Numerical Computation
5. Analysis of Result
6. Conclusions
- Duality Solution
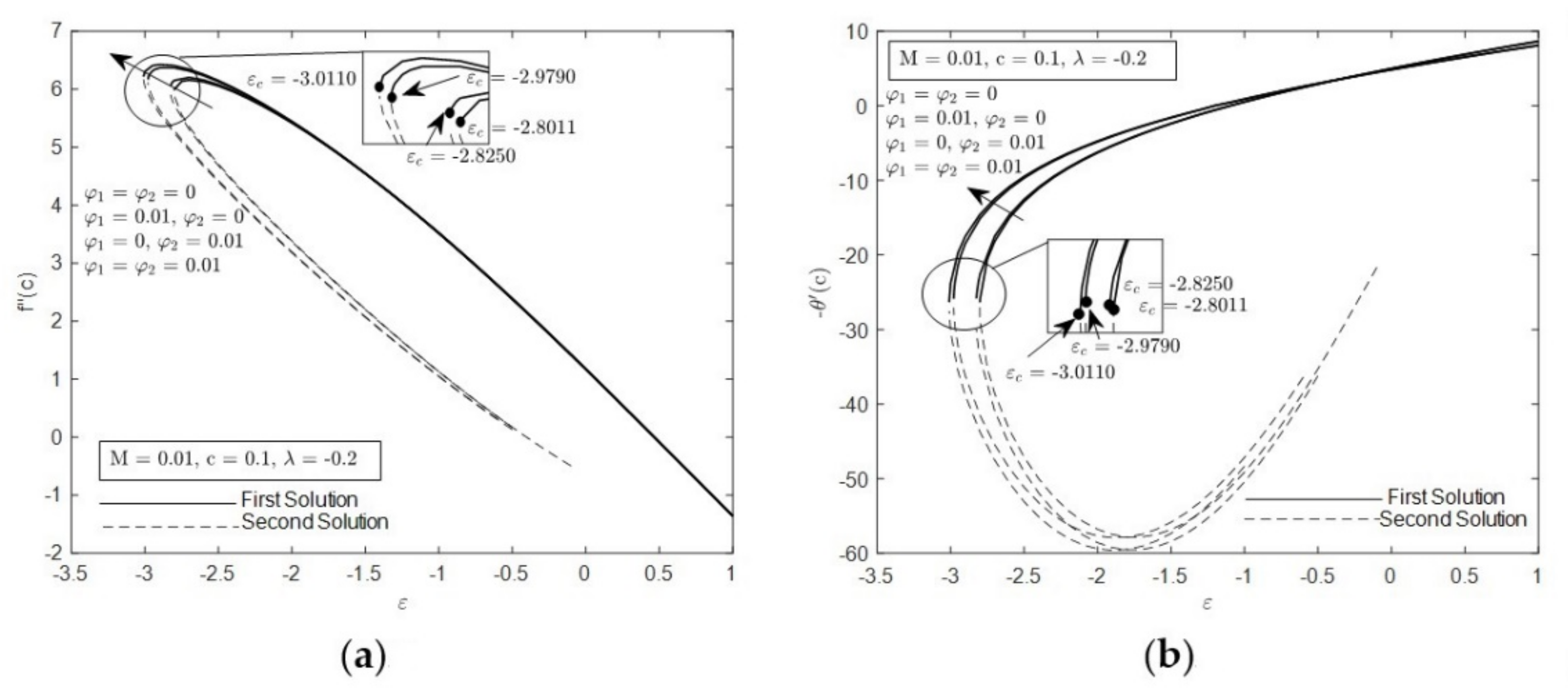
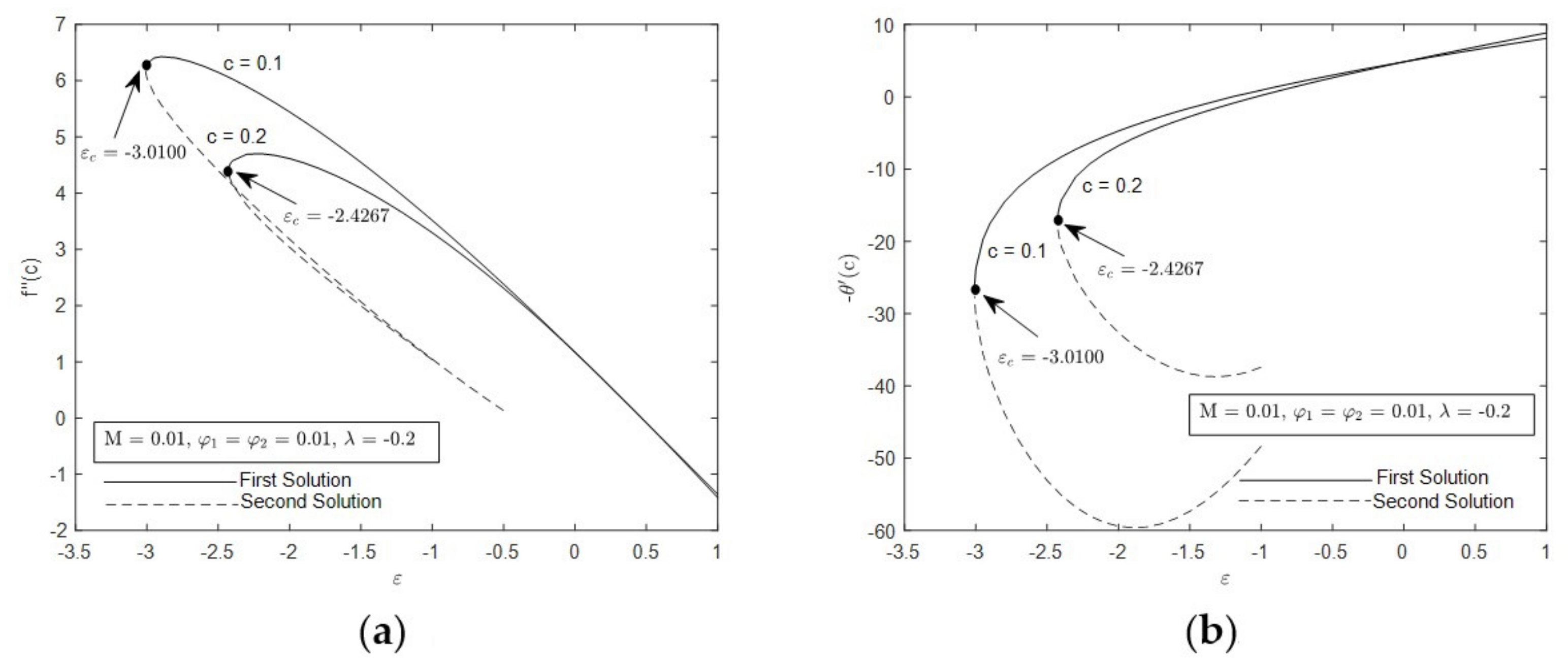
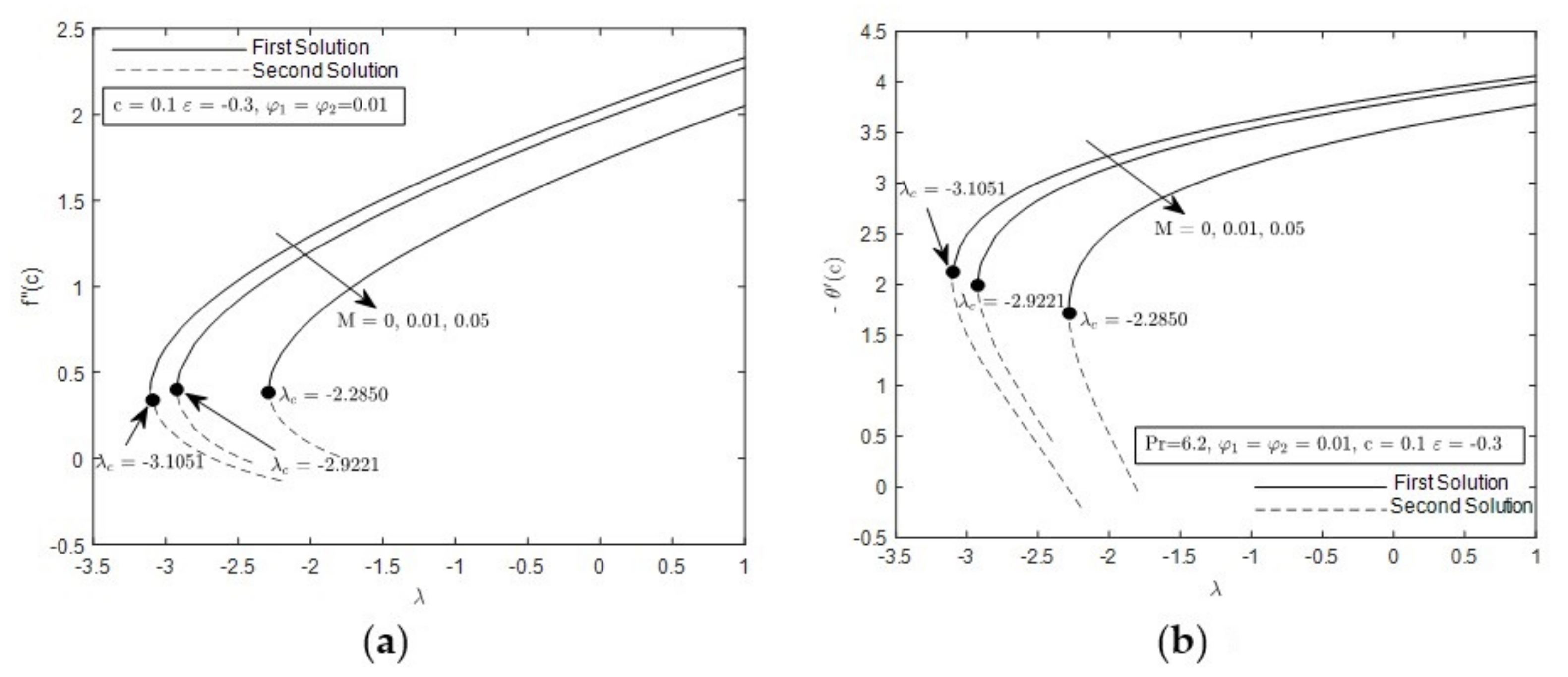
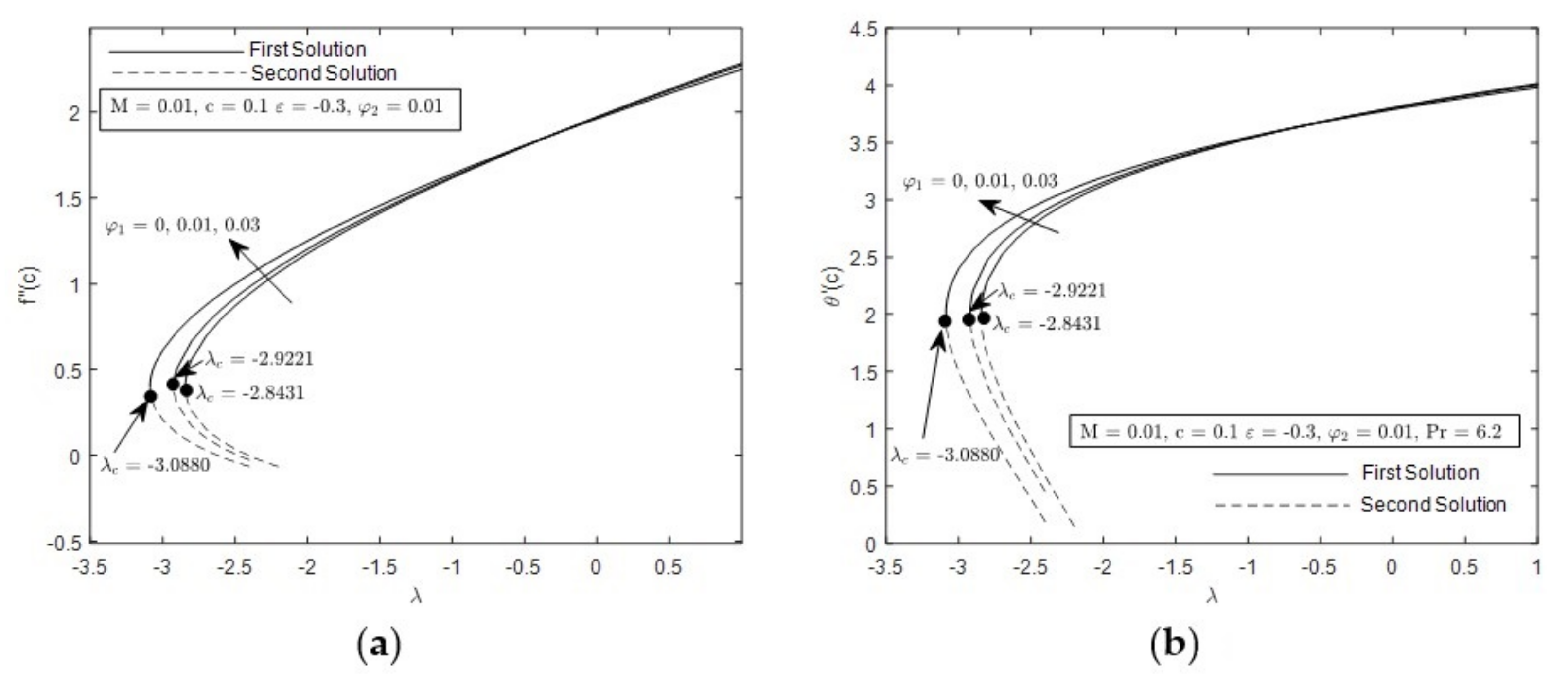
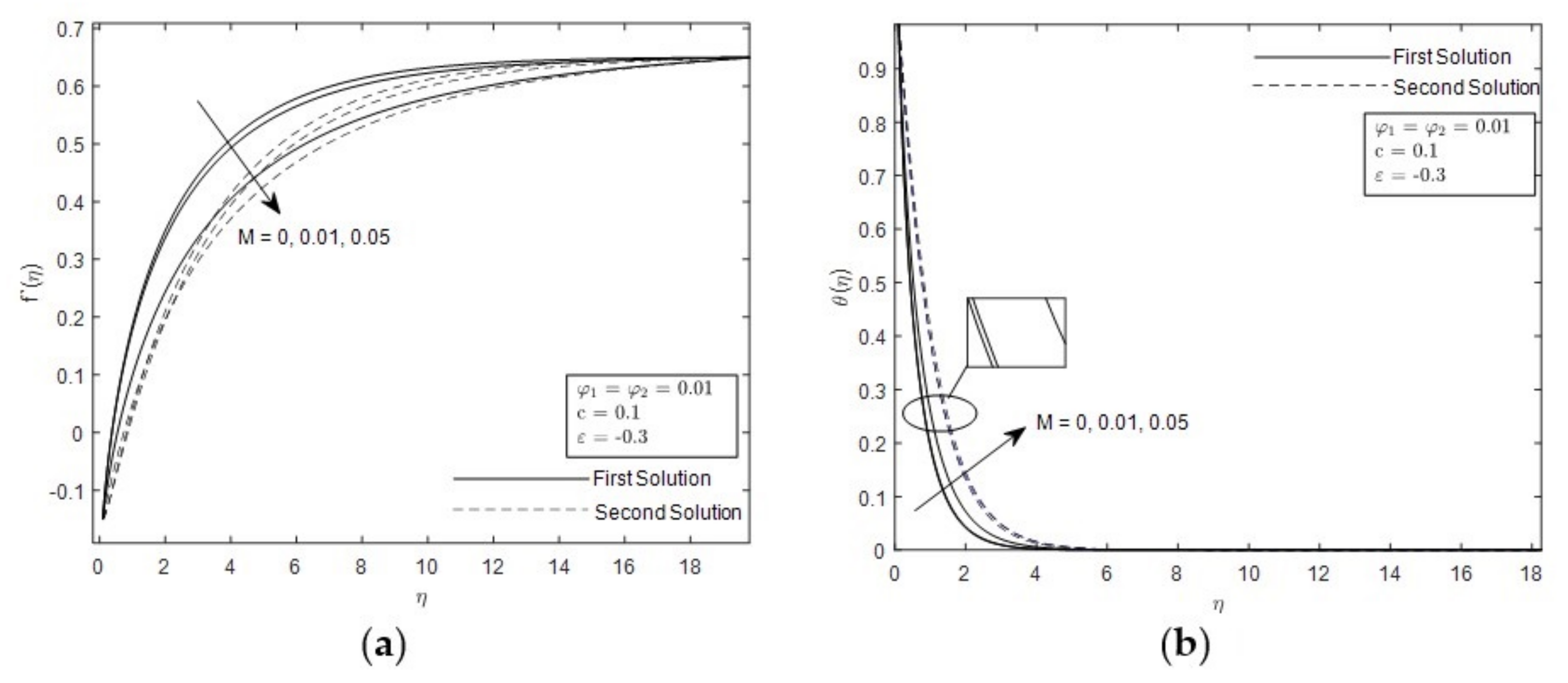
- The presence of the duality solutions is prominent when in opposing flow
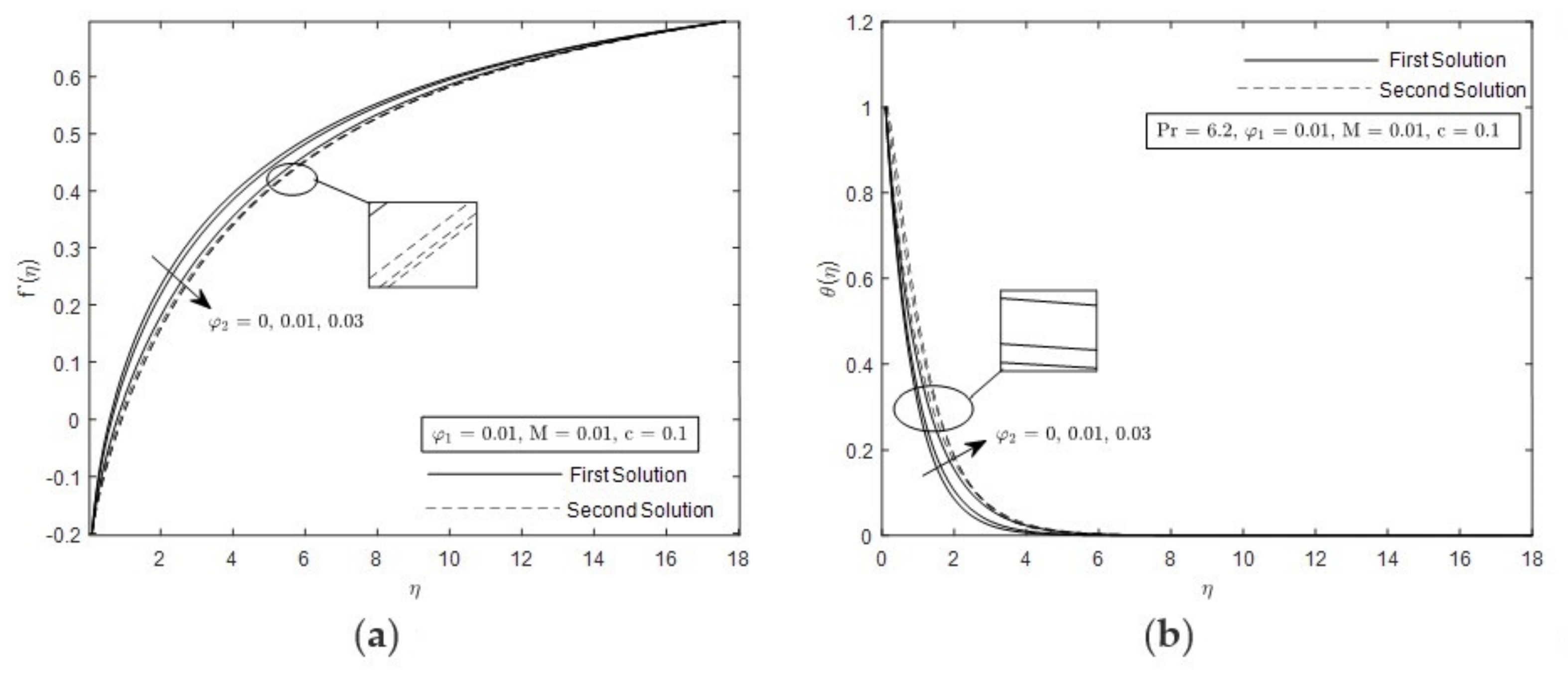
- The range of duality of solutions is widely expanded under the influence of smaller and
- Hybrid nanofluid possess faster boundary layer separation compared with viscous fluid and nanofluid.
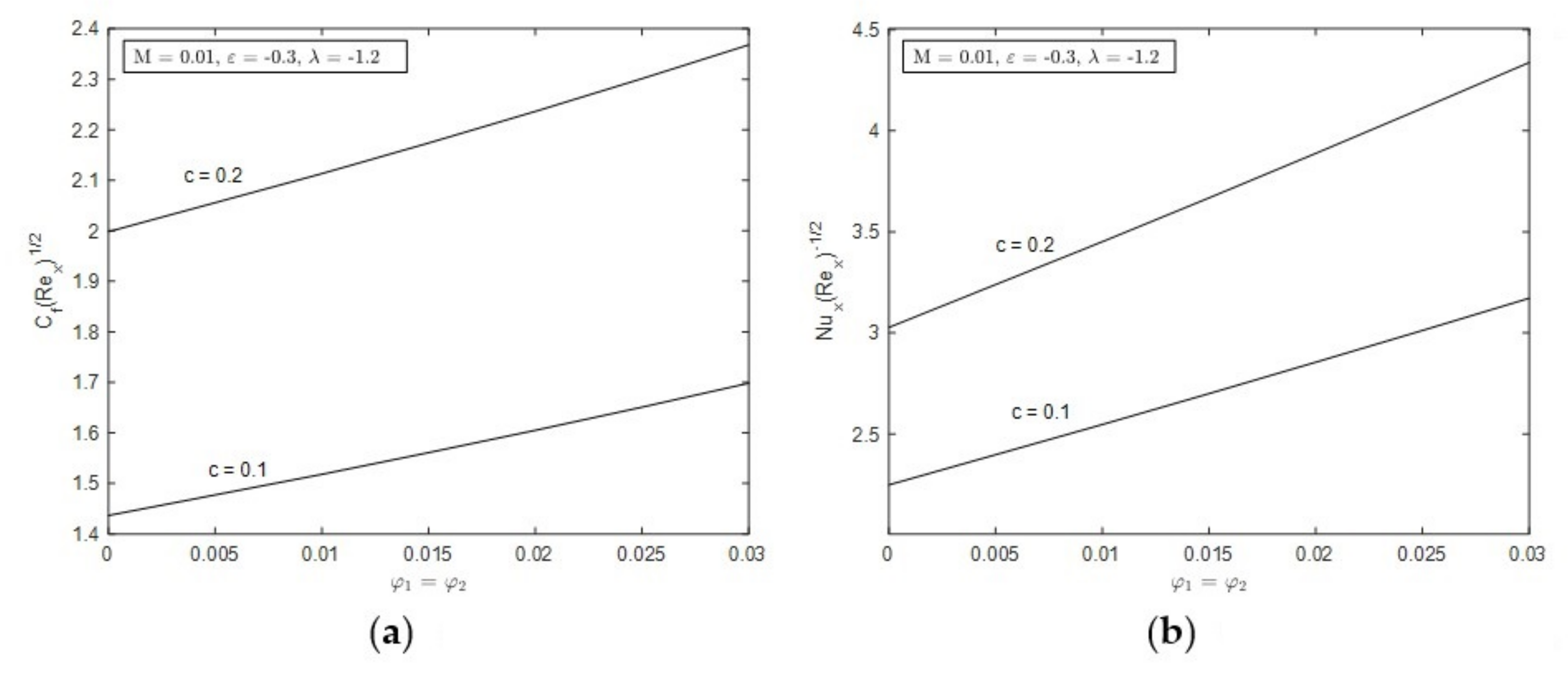
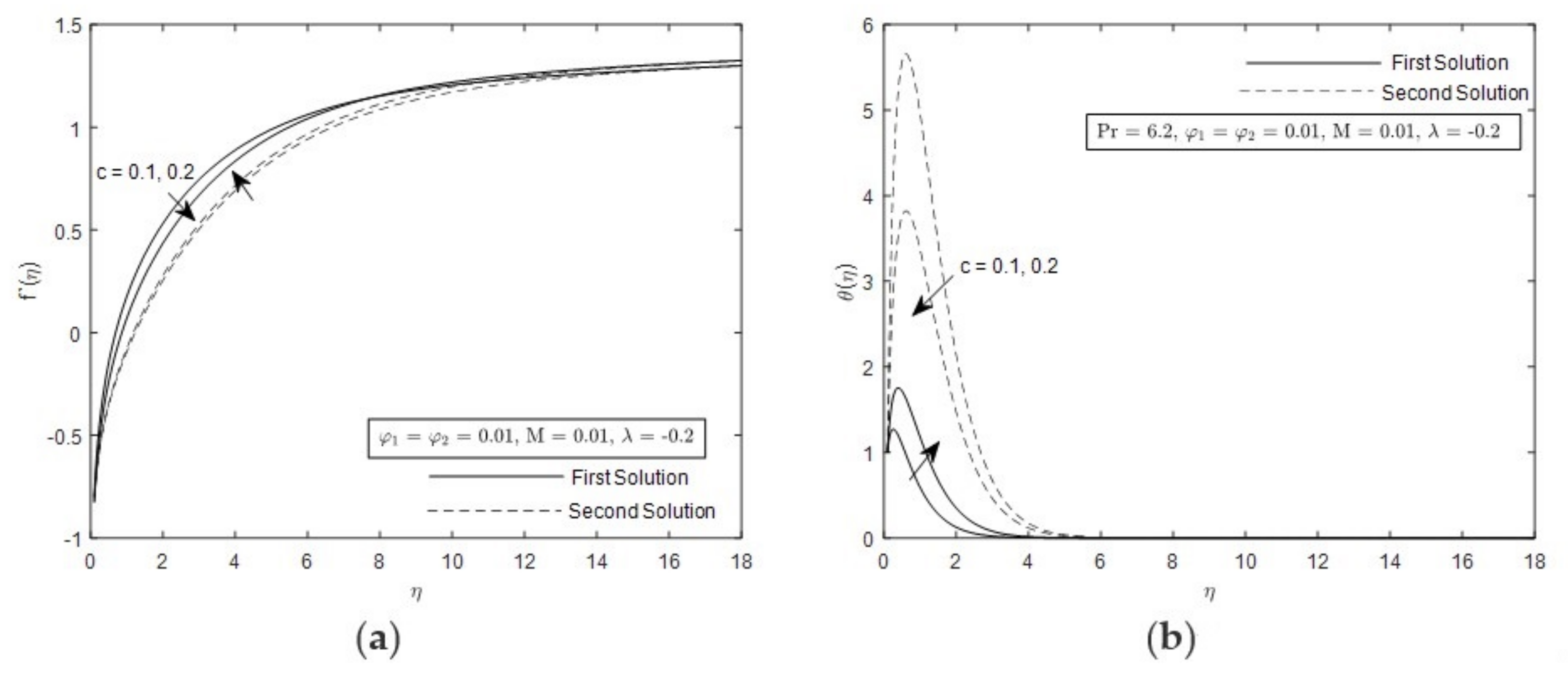
- The increment of c shortens the connection of first and second solution.
- Stability analysis shows that first solution is favorable compared with the second solution.
- Skin Friction
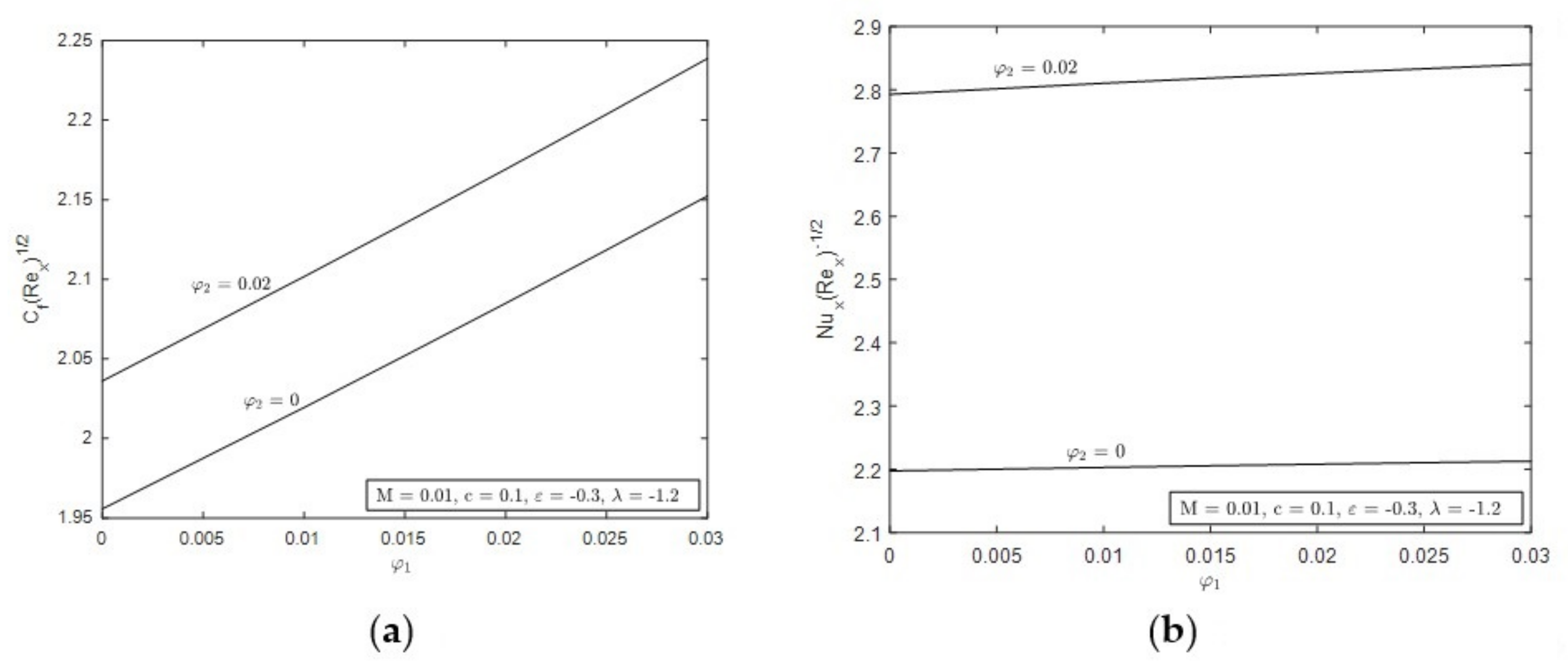
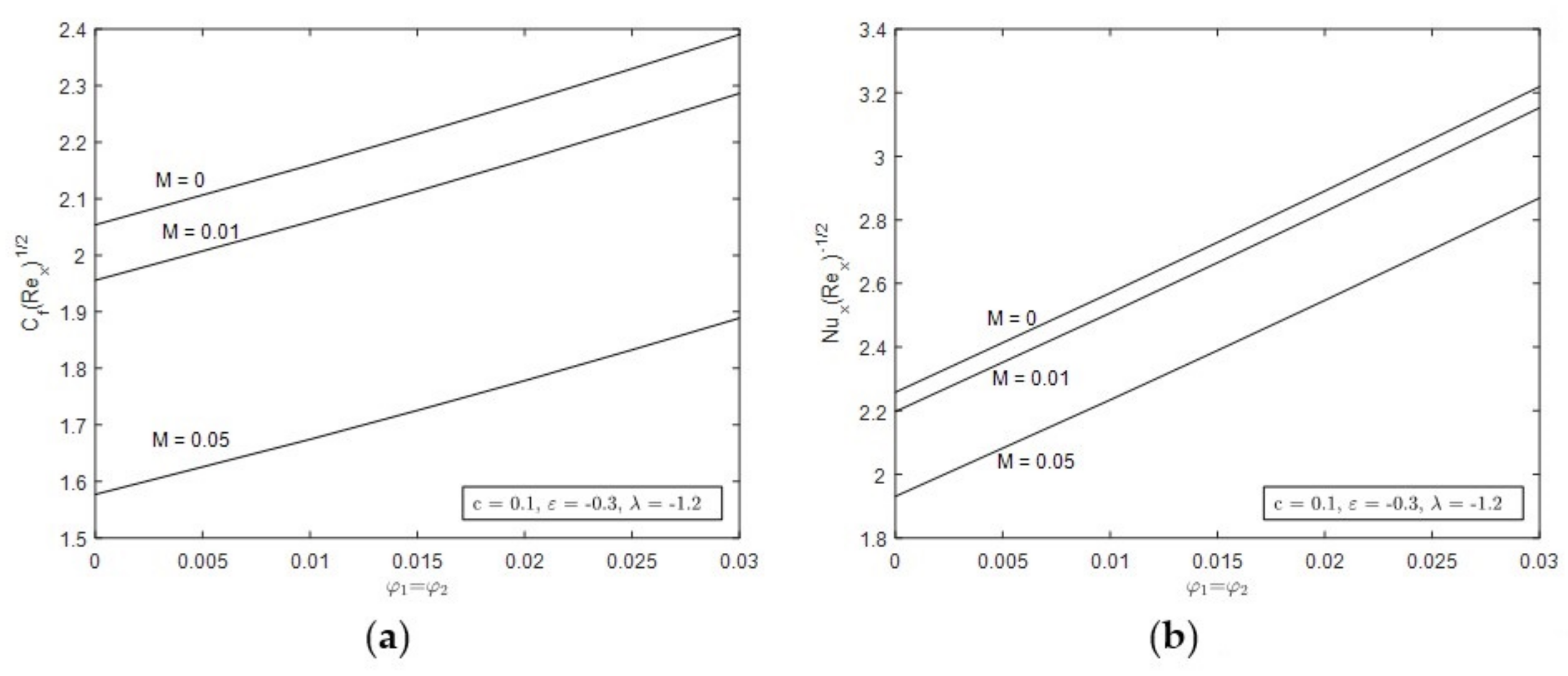
- Hybrid nanofluid reduced the value of skin friction as the value of M increased.
- Hybrid nanofluid enhanced the skin friction as the concentration of the nanoparticles and c increased.
- Heat Transfer
- Hybrid nanofluid reduced the value of heat transfer as the value of M increased.
- Hybrid nanofluid enhanced the heat transfer as the concentration of the nanoparticles and c increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ODE | Ordinary Differential Equation |
| Pr | Prandtl number |
| T | Temperature |
| U | Uniform free stream |
| qw | Plate heat flux |
| Nux | Local Nusselt number |
| Rex | Reynolds number |
| Cf | Skin friction coefficient |
| w | Condition on plate |
| ∞ | Ambient condition |
| hnf | Hybrid nanofluid |
| nf | Nanofluid |
| f | Fluid |
| α | Thermal diffusivity |
| μ | Dynamic viscosity |
| ρ | Density |
| ψ | Stream function |
| η | Similarity variables |
| θ | Dimensionless temperature |
| (ρCp)f | Specific heat for base fluid |
| Cp | Specific heat at constant pressure |
| τ | Dimensionless time |
| k | Thermal conductivity |
| Concentration of nanoparticles | |
| Eigenvalues | |
| υ | Kinematic viscosity |
| Mixed convection parameter | |
| Velocity ratio parameter |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Lemont, IL, USA, 1995.
- Rao, Y. Nanofluids: Stability, phase diagram, rheology and applications. Particuology 2010, 8, 549–555. [Google Scholar] [CrossRef]
- Lim, A.E.; Lam, Y.C. Numerical Investigation of Nanostructure Orientation on Electroosmotic Flow. Micromachines 2020, 11, 971. [Google Scholar] [CrossRef] [PubMed]
- El-Aziz, M.A.; Aly, A.M. MHD Boundary Layer Flow of a Power-Law Nanofluid Containing Gyrotactic Microorganisms Over an Exponentially Stretching Surface. CMC-Comput. Mater. Contin. 2020, 62, 525–549. [Google Scholar] [CrossRef]
- Ranga, B.J.A.; Kumar, K.K.; Rao, S.S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Haq, R.U.; Raza, A.; Algehyne, E.A.; Tlili, I. Dual nature study of convective heat transfer of nanofluid flow over a shrinking surface in a porous medium. Int. Commun. Heat Mass Transf. 2020, 114, 104583. [Google Scholar] [CrossRef]
- Xu, N.; Xu, H.A. A modified model for isothermal homogeneous and heterogeneous reactions in the boundary-layer flow of a nanofluid. Appl. Math. Mech.-Engl. Ed. 2020, 41, 479–490. [Google Scholar] [CrossRef]
- Kudenatti, R.B.; Misbah, N.E.; Bharathi, M.C. Linear Stability of Momentum Boundary Layer Flow and Heat Transfer Over a Moving Wedge. ASME J. Heat Transf. 2020, 142, 061804. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Zadeh, S.M.H.; Mehryan, S.A.M.; Pop, I.; Wen, D. Analysis of melting behavior of PCMs in a cavity subject to a non-uniform magnetic field using a moving grid technique. Appl. Math. Model. 2020, 77, 1936–1953. [Google Scholar] [CrossRef]
- Radushkevich, L.; Lukyanovich, V. O strukture ugleroda, obrazujucegosja pri termiceskom razlozenii okisi ugleroda na zeleznom kontakte. Zurn Fisic Chim 1952, 26, 88–95. [Google Scholar]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Hayat, T.; Khursheed, M.; Farooq, M.; Alsaedi, A. Melting heat transfer in stagnation point flow of carbon nanotubes towards variable thickness surface. AIP Adv. 2016, 6, 015214. [Google Scholar] [CrossRef]
- Shafiq, A.; Sindhu, T.N.; Al-Mdallal, Q.M. A sensitivity study on carbon nanotubes significance in Darcy–Forchheimer flow towards a rotating disk by response surface methodology. Sci. Rep. 2021, 11, 8812. [Google Scholar] [CrossRef] [PubMed]
- Alawi, O.A.; Mallah, A.R.; Kazi, S.N.; Sidik, N.A.C.; Najafi, G. Thermophysical properties and stability of carbon nanostructures and metallic oxides nanofluids. J. Therm. Anal. Calorim. 2019, 135, 1545–1562. [Google Scholar] [CrossRef]
- Acharya, N.; Bag, R.; Kundu, P.K. On the mixed convective carbon nanotube flow over a convectively heated curved surface. Heat Transf. 2020, 49, 1713–1735. [Google Scholar] [CrossRef]
- Kamis, N.I.; Basir, M.F.M.; Jaafar, N.A.; Shafie, S.; Khairuddin, T.K.A.; Naganthran, K. Heat Transfer and Boundary Layer Flow Through A Thin Film of Hybrid Nanoparticles Embedded in Kerosene Base Fluid Past an Unsteady Stretching Sheet. Open J. Sci. Technol. 2020, 3, 322–334. [Google Scholar]
- Olagunju, D.O. A self-similar solution forced convection boundary layer flow of a PENE-P fluid. Appl. Math. Lett. 2006, 19, 432–436. [Google Scholar] [CrossRef] [Green Version]
- Munir, A.; Shahzad, A.; Khan, M. Forced convective heat transfer in boundary layer flow of Sisko fluid over a nonlinear stretching sheet. PLoS ONE 2014, 9, e100056. [Google Scholar] [CrossRef]
- Sonawane, S.; Bhandarkar, U.; Puranik, B. Modeling Forced Convection Nanofluid Heat Transfer Using an Eulerian–Lagrangian Approach. ASME J. Therm. Sci. Eng. Appl. 2016, 8, 031001. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.M.; Yang, Z.; Fang, Y. Baffle and geometry effects on nanofluid forced convection over forward- and backward-facing steps channel by means of lattice Boltzmann method. Phys. A Stat. Mech. Its Appl. 2020, 554, 124696. [Google Scholar] [CrossRef]
- Goodrich, S.S.; Marcum, W.R. Natural convection heat transfer and boundary layer transition for vertical heated cylinders. Exp. Therm. Fluid Sci. 2019, 105, 367–380. [Google Scholar] [CrossRef]
- Saini, V.; Jauhri, S.; Gour, P.S. Study of boundary layer flow with natural convective boundary condition. Int. J. Innov. Res. Growth 2019, 8, 47–53. [Google Scholar] [CrossRef]
- Zhao, Y.; Lei, C.; Patterson, J.C. Natural transition in natural convection boundary layers. Int. Commun. Heat Mass Transf. 2016, 76, 366–375. [Google Scholar] [CrossRef]
- Fabregat, A.; Pallares, J. Heat transfer and boundary layer analyses of laminar and turbulent natural convection in a cubical cavity with differently heated opposed walls. Int. J. Heat Mass Transf. 2020, 151, 119409. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Eichhorn, R.; Gregg, J.L. Combined forced and free convection in a boundary layer flow. Phys. Fluids 1959, 2, 319–328. [Google Scholar] [CrossRef]
- Aman, F.; Ishak, A. Mixed convection boundary layer flow towards a vertical plate with a convective surface boundary condition. Math. Probl. Eng. 2012, 2012, 453457. [Google Scholar] [CrossRef]
- Galambaz, M.; Grosan, T.; Pop, I. Mixed convection boundary layer flow and heat transfer over a vertical embedded in a porous medium filled with suspension of nano-encapsulated phase change materials. J. Mol. Liq. 2019, 293, 111432. [Google Scholar] [CrossRef]
- Maleque, K.A. Similarity requirements for mixed convective boundary layer flow over a vertical curvilinear porous surface with heat generation/absorption. Int. J. Aerosp. Eng. 2020, 2020, 7486971. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.S. Natural convection from needles with variable heat flux. J. Heat Transf. 1983, 105, 403–406. [Google Scholar] [CrossRef]
- Chen, J.L.S. Mixed convection flow about slender bodies of revolution. J. Heat Transf. 1987, 109, 1033–1036. [Google Scholar] [CrossRef]
- Wang, C.Y. Free convection plume from the tip of a vertical needle. Mech. Res. Commun. 1989, 16, 95–101. [Google Scholar] [CrossRef]
- Ahmad, S.; Arifin, N.M.; Nazar, R.; Pop, I. Mixed convection boundary layer flow along vertical needles: Assisting and opposing flows. Int. Commun. Heat Mass Transf. 2008, 35, 157–162. [Google Scholar] [CrossRef]
- Trimbitas, R.; Grosan, T. Mixed convection boundary layer flow along vertical thin needles in nanofluids. Int. J. Numer. Methods Heat Fluid Flow 2012, 24, 579–594. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M.; Pop, I. Magnetohydrodynamics flow past a moving vertical thin needle in a nanofluid with stability analysis. Energies 2018, 11, 3297. [Google Scholar] [CrossRef] [Green Version]
- Suresh, S.; Venkitaraj, K.P.; Slevakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/H2O hybrid nanofluids using two steps method and its thermophysical properties. Colloid Surf. A Physichem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Salman, S.; Abu Talib, A.R.; Saadon, S.; Hameed Sultan, M.T. Hybrid nanofuid and heat transfer over backward and forward steps: A review. Powder Technol. 2020, 363, 448–472. [Google Scholar] [CrossRef]
- Khan, U.; Shafiq, A.; Zaib, A.; Baleanu, D. Hybrid nanofluid on mixed convective radiative flow from an irregular variably thick moving surface with convex and concave effects. Case Stud. Therm. Eng. 2020, 21, 100660. [Google Scholar] [CrossRef]
- Gul, T.; Khan, A.; Bilal, M.; Alreshidi, N.A.; Mukhtar, S.; Shah, Z.; Kumam, P. Magnetic Dipole Impact on the Hybrid Nanofluid Flow over an Extending Surface. Sci. Rep. 2020, 10, 8474. [Google Scholar] [CrossRef]
- Hassan, M.; Faisal, A.; Ali, I.; Bhatti, M.M.; Yousaf, M. Effects of Cu–Ag hybrid nanoparticles on the momentum and thermal boundary layer flow over the wedge. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2019, 233, 1–9. [Google Scholar] [CrossRef]
- Manjunatha, S.; Ammani Kuttan, B.; Jayanthi, S.; Chamkha, A.; Gireesha, B.J. Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon 2019, 5, e01469. [Google Scholar] [CrossRef] [Green Version]
- Tassaddiq, A.; Khan, S.; Bilal, M.; Gul, T.; Mukhtar, S.; Shah, Z.; Bonyah, E. Heat and mass transfer together with hybrid nanofluid flow over a rotating disk. AIP Adv. 2020, 10, 055317. [Google Scholar] [CrossRef]
- Sreedevi, P.; Sudarsana Reddy, P.; Chamkha, A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2020, 2, 1222. [Google Scholar] [CrossRef]
- Ebaid, A.; Aly, E.H. Exact analytical solution of the peristaltic nanofluids flow in an asymmetric channel with flexible walls and slip condition: Application to the cancer treatment. Comput. Math. Methods Med. 2013, 2013, 825376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, L.L. Boundary layer over a thin needle. Phys. Fluid 2004, 10, 820–822. [Google Scholar] [CrossRef]
- Gul, T.; Ullah, M.Z.; Ansari, K.J.; Amiri, I.S. Thin film flow of CNTs nanofluid over a thin needle surface. Surf. Rev. Lett. 2020, 27, 1950189. [Google Scholar] [CrossRef]
- Hayat, T.; Nawaz, S.; Alsaedi, A.; Rafiq, M. Impact of second-order velocity and thermal slips in the mixed convectiveperistalsis with carbon nanotubes and porous medium. J. Mol. Liq. 2016, 221, 434–442. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu Nada, E. Numerical study of natural convection in partially heated rectangular enclosure filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1985, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary layer flow near the stagnation point on a vertical surface in porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Aladdin, N.A.L.; Bachok, N.; Pop, I. Boundary layer flow and heat transfer of Cu-Al2O3/water over a moving horizontal slender needle in presence of hydromagnetic and slip effects. Int. Commun. Heat Mass Transf. 2021, 123, 105213. [Google Scholar] [CrossRef]
- Dey, D.; Borah, R.; Mahanta, B. Boundary Layer Flow and Its Dual Solutions Over a Stretching Cylinder: Stability Analysis. In Emerging Technologies in Data Mining and Information Security; Springer: Singapore, 2021; pp. 27–38. [Google Scholar]
- Shampine, L.F.; Gladwell, I.; Shampine, L.; Thompson, S. Solving ODEs with Matlab; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Ahmad, R.; Mustafa, M.; Hina, S. Buongiorno’s model for fluid flow around a moving thin needle in a flowing nanofluid: A numerical study. China J. Phys. 2017, 55, 1264–1274. [Google Scholar] [CrossRef]
- Salleh, S.N.A.; Bachok, N.; Arifin, N.M.; Ali, F.M. Numerical analysis of boundary layer flow adjacent to a thin needle in nanofluid with the presence of heat source and chemical reaction. Symmetry 2019, 11, 543. [Google Scholar] [CrossRef] [Green Version]
- Subhashini, S.V.; Samuel, N.; Pop, I. Effects of buoyancy assisting and opposing flows on mixed convection boundary layer flow over a permeable vertical surface. Int. Commun. Heat Mass Transf. 2011, 38, 499–503. [Google Scholar] [CrossRef]
- Godson, L.; Raj, V.; Raja, B.; Kancheepuram, I.; Lal, D.M. Measurement of viscosity and surface tension of silver deionized water nanofluid. In Proceedings of the 37th National & 4th International Conference on Fluid Mechanics and Fluid Power, Chennai, India, 16–18 December 2010; pp. 16–18. [Google Scholar]
- Tanvir, S.; Qiao, L. Surface tension of Nanofluid-type fuels containing suspended nanomaterials. Nanoscale Res. Lett. 2012, 7, 226. [Google Scholar] [CrossRef] [Green Version]
- Kudenatti, R.B.; Bharathi, M.C. Boundary-layer flow of the power-law fluid over a moving wedge: A linear stability analysis. Eng. Comput. 2021, 37, 1807–1820. [Google Scholar] [CrossRef]
- Ghosh, S.; Mukhopadhyay, S. Stability analysis for model-based study of nanofluid flow over an exponentially shrinking permeable sheet in presence of slip. Neural Comput. Appl. 2020, 32, 7201–7211. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Magnetohydrodynamics (MHD) boundary layer flow of hybrid nanofluid over a moving plate with Joule heating. Alex. Eng. J. 2021, in press. [Google Scholar] [CrossRef]
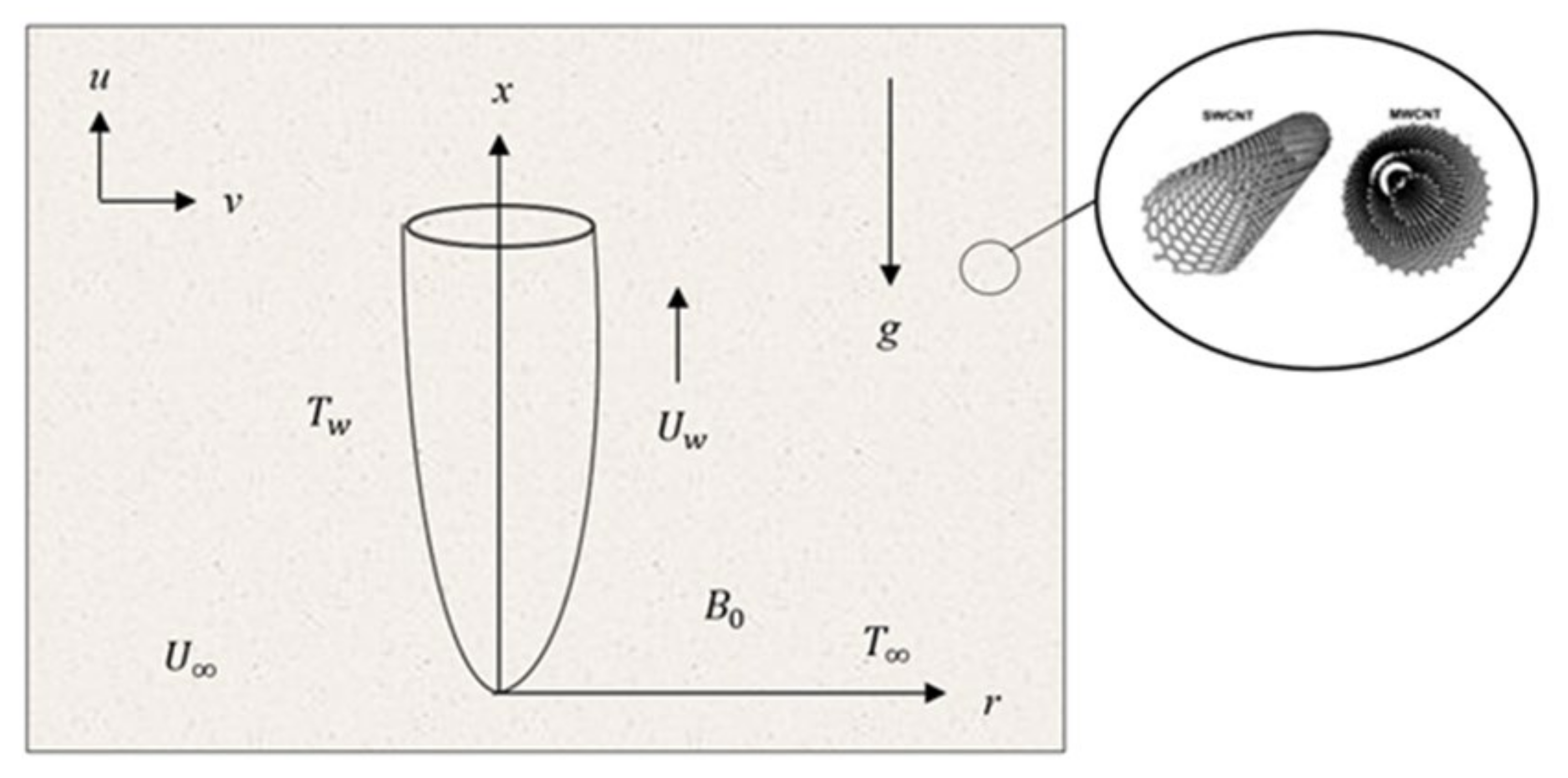

| Thermophysical Properties | k (W/mK) | Cp (J/kgK) | ρ (kg/m3) | β × 10−6 (1/K) |
|---|---|---|---|---|
| SWCNT | 6600 | 425 | 2600 | 19 |
| MWCNT | 3000 | 796 | 1600 | 21 |
| Water | 0.613 | 4179 | 997 | 210 |
| Thermophysical | Hybrid Nanofluids |
|---|---|
| Density | |
| Heat Capacity | |
| Viscosity | |
| Thermal Conductivity | |
| Thermal Expansion Coefficient |
| c | [56] | [57] | Present Study |
|---|---|---|---|
| 0.01 | 8.492436 | 8.4924453 | 8.4924451 |
| 0.1 | 1.2888171 | 1.2888300 | 1.2888300 |
| 0.15 | 0.9383388 | 0.9383388 |
| M | λ | First Solution | Second Solution | |
|---|---|---|---|---|
| 0 | −3.1048 | 0.0987 | 0.0804 | |
| −3.104 | 0.1038 | 0.0800 | ||
| −3.09 | 0.1156 | 0.0792 | ||
| 0.01 | −2.9219 | 0.0991 | 0.0908 | |
| 0.01 | −2.921 | 0.1049 | 0.0850 | |
| −2.92 | 0.1088 | 0.0811 | ||
| 0.05 | −2.2848 | 0.1037 | 0.0942 | |
| −2.284 | 0.1088 | 0.0891 | ||
| −2.28 | 0.1205 | 0.0773 | ||
| 0 | −3.2781 | 0.1004 | 0.0918 | |
| −3.278 | 0.1013 | 0.0909 | ||
| −3.27 | 0.1229 | 0.7946 | ||
| 0.01 | −3.0878 | 0.1009 | 0.0796 | |
| 0.03 | −3.087 | 0.1061 | 0.0792 | |
| −3.08 | 0.1170 | 0.0780 | ||
| 0.05 | −2.4245 | 0.1050 | 0.0971 | |
| −2.424 | 0.1088 | 0.0933 | ||
| −2.42 | 0.1213 | 0.0807 |
| c | M | ε | First Solution | Second Solution |
|---|---|---|---|---|
| 0 | −3.1121 | 0.1884 | 0.1356 | |
| −3.112 | 0.1954 | 0.1673 | ||
| −3.11 | 0.2085 | 0.1903 | ||
| 0.01 | −2.9895 | 0.2443 | 0.1311 | |
| 0.1 | −2.989 | 0.2515 | 0.1019 | |
| −2.98 | 0.2651 | 0.0871 | ||
| 0.05 | −2.5829 | 0.2011 | 0.1105 | |
| −2.582 | 0.2205 | 0.1041 | ||
| −2.58 | 0.2240 | 0.1004 | ||
| 0 | −2.5010 | 0.1720 | 0.0983 | |
| −2.495 | 0.1902 | 0.0796 | ||
| −2.49 | 0.2015 | 0.0679 | ||
| 0.01 | −2.4265 | 0.2005 | −0.2011 | |
| 0.2 | −2.426 | 0.2104 | −0.2201 | |
| −2.42 | 0.2511 | −0.2220 | ||
| 0.05 | 2.1011 | 0.1372 | 0.1013 | |
| −2.101 | 0.1518 | 0.0987 | ||
| −2.10 | 0.1729 | 0.0857 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aladdin, N.A.L.; Bachok, N. Duality Solutions in Hydromagnetic Flow of SWCNT-MWCNT/Water Hybrid Nanofluid over Vertical Moving Slender Needle. Mathematics 2021, 9, 2927. https://doi.org/10.3390/math9222927
Aladdin NAL, Bachok N. Duality Solutions in Hydromagnetic Flow of SWCNT-MWCNT/Water Hybrid Nanofluid over Vertical Moving Slender Needle. Mathematics. 2021; 9(22):2927. https://doi.org/10.3390/math9222927
Chicago/Turabian StyleAladdin, Nur Adilah Liyana, and Norfifah Bachok. 2021. "Duality Solutions in Hydromagnetic Flow of SWCNT-MWCNT/Water Hybrid Nanofluid over Vertical Moving Slender Needle" Mathematics 9, no. 22: 2927. https://doi.org/10.3390/math9222927
APA StyleAladdin, N. A. L., & Bachok, N. (2021). Duality Solutions in Hydromagnetic Flow of SWCNT-MWCNT/Water Hybrid Nanofluid over Vertical Moving Slender Needle. Mathematics, 9(22), 2927. https://doi.org/10.3390/math9222927






