Flow and Heat Transfer Past a Stretching/Shrinking Sheet Using Modified Buongiorno Nanoliquid Model

Abstract

This paper studies the boundary layer flow and heat transfer characteristics past a permeable isothermal stretching/shrinking surface using both nanofluid and hybrid nanofluid flows (called modified Buongiorno nonliquid model). Using appropriate similarity variables, the PDEs are transformed into ODEs to be solved numerically using the function bvp4c from MATLAB. It was found that the solutions of the resulting system have two branches, upper and lower branch solutions, in a certain range of the suction, stretching/shrinking and hybrid nanofluids parameters. Both the analytic and numerical results are obtained for the skin friction coefficient, local Nusselt number, and velocity and temperature distributions, for several values of the governing parameters. It results in the governing parameters considerably affecting the flow and heat transfer characteristics.

1. Introduction

Owing to the necessary improvement of the thermal conductivity of conventional fluid, the term nanofluid was introduced by Choi [1] in 1995, which aims to provide highly developed heat conductivity. Nanofluids, which are a colloidal mixture of nanoparticles (1–100 nm) and a base liquid (nanoparticle fluid suspensions), are the new class of media of nanotechnology for heat transfer (see for e.g., Buongiorno [2]). In particular, Buongiorno [2] noted that the nanoparticle absolute velocity can be viewed as the sum of the base fluid velocity and a relative velocity. He considered, in turn, seven slip mechanisms: inertia, Brownian diffusion, thermophoresis, diffusion phoresies, Magnus effect, fluid drainage, and gravity settling. He concluded that, in the absence of turbulent effects, it is the Brownian diffusion and the thermophoresis that will be important. Buongiorno proceeded to write down conservation equations based on these two effects. His model is the basis of the present study. Soon after discoveries made by Choi [1], many researchers interested in this new type of working fluid, because of its importance for the emergence and enhancement of thermal properties in practical applications, in various engineering applications such as engine cooling, diesel generator efficiency, cooling of electronics and heat exchanging devices, and solar water heating (see for e.g., Mahian et al. [3]). In a review paper, Manca et al. [4] have shown that cooling is one of the most important technical challenges facing many diverse industries, including microelectronics, transportation, solid-state lighting and manufacturing. Kamel and Lezsovits [5] found that the enrichment of thermophysical properties and heat transfer performance in nanofluid play an essential role in establishing high heat flux with small temperature differences during the boiling process in thermal engineering systems. The addition of nanometre-sized solid metal or metal oxide particles to base fluids elicits a rise in the thermal conductivity of the outgrowth fluids, see for example, Aly and Sayed [6].

To further improve nanofluids that could possess a number of favorable characteristics, researchers developed a new generation heat transfer fluid called hybrid nanofluids (HNF). They are prepared either by dispersing dissimilar nanoparticles as individual constituents or by dispersing nanocomposite particles in the base fluid. HNF may possess better thermal network and rheological properties due to synergistic effect. Researchers, to adjudge the advantages, disadvantages and their suitability for diversified applications, are extensively investigating the behavior and properties of these hybrid nanofluids. Babu et al. [7] have reviewed the contemporary investigations on synthesis, thermophysical properties, heat transfer characteristics, hydrodynamic behavior and fluid flow characteristics reported by researchers on different HNFs. This review also outlines the applications and challenges associated with hybrid nanofluid and makes some suggestions for the future scope of research in this fruitful area. On the other hand, and in an excellent review paper, Huminic and Huminic [8] discussed the HNF, which consists of two solid materials dispersed in a viscous fluid. In this work, it was shown that hybrid nanofluids lead to increased thermal conductivity and finally to a heat transfer enhancement in heat exchangers. Experimental and numerical results show that the hybrid nanofluids are working fluids, which could significantly improve the heat transfer in heat exchangers; however, research concerning to the study of different combinations of hybrid nanoparticles and their stability is still needed.

Numerous researchers have studied the flow and heat transfer of the boundary layer past a stretching/shrinking sheet with applications in manufacturing technology, for instance, glass blowing, extrusion of plastic sheets, drawing plastic films, and hot rolling (see Fisher [9]). As documented by Karwe et al. [10], the outcome quality of the required features is greatly affected by the heat transfer rate along the fluid flow and stretching/shrinking surface. Sakiadis [11] started a boundary layer flow analysis at a steady speed rate through a continuously moving flat surface by employing an integral method. Of all the fundamental fluid flow problems of a linear stretching/shrinking sheet, the current literature testifies that flow behavior due to a non-linear stretching sheet is also a crucial element in most industrial processes. Hybrid nanofluid versus the nanofluid of MHD flow and heat transfer over a stretching/shrinking sheet was introduced by Aly and Pop [12].

Unique and/or multiple (dual) solutions for a stretching/shrinking sheet have recently been presented in the works by Aly et al. [13], Waini et al. [14] and Khashi’ie et al. [15]. These papers show that unique and dual solutions exist for a stretching and shrinking sheet, respectively. In addition, Liao and Pop [16] deduced multiple solutions for both impermeable and permeable shrinking sheets. It should be noted that most of these solutions are based on the boundary layer assumptions and hence do not constitute exact solutions for Navier–Stokes equations (see for e.g., Wang [17]). It is also worth mentioning that Aly [18] has discussed the dual exact solutions of graphene–water nanofluid flow over a stretching/shrinking sheet with a suction/injection and heat source/sink, see also Roşca et al. [19], Aly [20] and Aly and Pop [21].

Finally, we mention here that Pop et al. [22], Zhu et al. [23], Uddin and Rahman [24], Rana et al. [25,26] and Pati et al. [27] have studied the boundary layer flow beneath a uniform free stream permeable continuous moving surface in a nanofluid using both Buongiorno’s [2] and Tiwari and Das’ [28] nanofluid models. However, we consider in this paper Buongiorno’s [2] nanofluid model combined with Devi and Devi’s [29] hybrid nanofluid model.

2. Mathematical Model

In this work, we consider the 2D flow and heat transfer of a hybrid nanofluid past a permeable stretching/shrinking surface, as shown in Figure 1, where $(x,y)$ are Cartesian coordinates with associated velocities $(u,v)$. The streamwise flows are directed along the $x-$ direction and y is the plate–normal coordinate. It is assumed that the surface velocity is $u_w\left(x\right)$ and the mass flux velocity is $v_0$ with $v_0<0$ for suction and $v_0>0$ for the injection or withdraw of the fluid. It is also assumed that the constant temperature and constant nanofluid volume fraction of the surface of the sheet are $T_w$ and $C_w$ while those of the ambient fluid are $T_{\infty }$ and $C_{\infty }$.

Therefore, the governing equations of the investigating physical model can be written as (Yousefi et al. [30] and Bognár et al. [31])

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2}+\delta \left[D_B\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right],$$

(3)

$$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2},$$

(4)

subject to the following boundary conditions (see for e.g., Kuznetsov and Nield [32])

$$\begin{array}{ccc}\hfill {\displaystyle }& & u=u_w\left(x\right)=U_w\left(x\right)\lambda ,v=v_0,T=T_w,D_B\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial y}=0,\mathrm{at}y=0,\hfill \end{array}$$

(5a)

$$\begin{array}{c}u=u_e\left(x\right)\to 0,T=T_{\infty },C=C_{\infty },\mathrm{as}y\to \infty .\hfill \end{array}$$

(5b)

Here, T is the temperature of the hybrid nanofluid, C is the nanoparticle concentration, $D_B$ is the Brownian diffusion coefficient, $D_T$ is the thermophoretic diffusion coefficient, $\delta ={\left(\rho C_p\right)}_s/{\left(\rho C_p\right)}_f$ is the ratio of nanoparticle heat capacity and the base fluid heat capacity. Further, ${\mu }_{hnf}$ is the dynamic viscosity of the hybrid nanofluids, ${\rho }_{hnf}$ is the density of the hybrid nanofluids, $k_{hnf}$ is the thermal conductivity of the hybrid nanofluid, ${\left(\rho C_p\right)}_{hnf}$ is the heat capacity of the hybrid nanofluid, $\lambda$ is the constant stretching/shrinking parameter with $\lambda >0$ for a stretching sheet, $\lambda <0$ for a shrinking sheet and $\lambda =0$ for a static sheet, respectively, and we assume that $U_w\left(x\right)=ax$, where a is a positive constant. Equation $D_B\partial C/\partial y+(D_T/T_{\infty })\partial T/\partial y=0$ is a statement that, with thermophoresis taken into account, the normal flux of nanoparticles is zero at the boundary. Furthermore, ${\left(\right)}_{hnf}$ denotes the hybrid nanofluid quantities, which are defined as follows (Devi and Devi [29] and Gorla et al. [33])

$$\begin{array}{ccc}\hfill \frac{{\rho }_{hnf}}{{\rho }_f}& =& \left(1-{\phi }_2\right)\left[1-{\phi }_1+{\phi }_1\frac{{\rho }_{s_1}}{{\rho }_f}\right]+{\phi }_2\frac{{\rho }_{s_2}}{{\rho }_f},\hfill \end{array}$$

(6a)

$$\begin{array}{ccc}\hfill \frac{{\mu }_{hnf}}{{\mu }_f}& =& \frac{1}{{\left(1-{\phi }_1\right)}^{2.5}{\left(1-{\phi }_2\right)}^{2.5}},\hfill \end{array}$$

(6b)

$$\begin{array}{ccc}\hfill \frac{k_{hnf}}{k_f}& =& \frac{k_{s_2}+2k_{bf}+2{\phi }_2\left(k_{s_2}-k_f\right)}{k_{s_2}+2k_{bf}-{\phi }_2\left(k_{s_2}-k_f\right)},\mathrm{where}\frac{k_{bf}}{k_f}=\frac{k_{s_1}+2k_f+2{\phi }_1\left(k_{s_1}-k_f\right)}{k_{s_1}+2k_f-{\phi }_1\left(k_{s_1}-k_f\right)},\hfill \end{array}$$

(6c)

$$\begin{array}{ccc}\hfill \frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}& =& \left(1-{\phi }_2\right)\left[1-{\phi }_1+{\phi }_1\frac{{\left(\rho C_p\right)}_{s_1}}{{\left(\rho C_p\right)}_f}\right]+{\phi }_2\frac{{\left(\rho C_p\right)}_{s_2}}{{\left(\rho C_p\right)}_f},\hfill \end{array}$$

(6d)

where ${\phi }_1$ and ${\phi }_2$ are the nanoparticle volume fraction for hybrid nanofluid (where ${\phi }_1={\phi }_2=0$ correspond to a regular fluid), ${\rho }_f$ is the density of the base fluid, ${\rho }_{s_1}$ and ${\rho }_{s_2}$ are the densities of the hybrid nanoparticles, $k_f$ is the thermal conductivity of the base fluid, $k_{s_1}$ and $k_{s_2}$ are the thermal conductivities of the hybrid nanoparticles, ${\left(\rho C_p\right)}_f$ is the heat capacity of the base fluid. ${\left(\rho C_p\right)}_{s_1}$ and ${\left(\rho C_p\right)}_{s_2}$ are the heat capacitance of the hybrid nanoparticles, and $C_p$ is the heat capacity at the constant pressure of the base fluid. Furthermore, the physical properties of the base fluid (water), alumina (Al${}_2$O${}_3$) and copper (Cu) hybrid nanofluids are given in

Table 1. Thermophysical properties of the water and nanoparticles [34].

Physical	Base Fluid	Nanoparticles
Properties	Water	${\mathrm{Al}}_2{\mathrm{O}}_3$	Cu
$\rho$ (kg/m3)	997.1	3970	8933
$C_p$ (J/kg K)	4179	765	385
k (W/m K)	0.613	40	401
$\sigma$ ($\Omega$/m)${}^{-1}$	0.05	1$\times {10}^{-10}$	5.96$\times {10}^7$

. Here, it should be noted that the hybrid nanofluid is assumed to be homogeneous, neglecting internal fluctuations of the particle density or flows.

Now, we introduce the following similarity variables

$$u=ax{f}^{\prime }\left(\eta \right),v=-\sqrt{a{\nu }_f}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_{\infty }},\eta =y\sqrt{\frac{a}{{\nu }_f}},$$

(7)

so that

$$v_0=-\sqrt{a{\nu }_f}S,$$

(8)

where S is the constant mass flux parameter with $S>0$ for suction and $S<0$ for injection or withdrawal, respectively. Invoking the similarity variables (7), Equations (2)–(4) along with the boundary conditions (5a) are transformed into the following ordinary (similarity) differential equations (see for e.g., Aly [35])

$${\alpha }_2{f}^{‴}+{\alpha }_1\left(f{f}^{″}-f^{{}^{\prime }2}\right)=0,$$

(9)

$$\frac{{\alpha }_4}{{\alpha }_{3}Pr}{\theta }^{″}+f{\theta }^{\prime }+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{\theta }^{\prime 2}=0,$$

(10)

$${\varphi }^{″}+Lef{\varphi }^{\prime }+\frac{Nt}{Nb}{\theta }^{″}=0,$$

(11)

which have to be solved subject to the following conditions:

$$\begin{array}{ccc}& & f\left(0\right)=S,f^{\prime }\left(0\right)=\lambda ,\theta \left(0\right)=1,Nb{\varphi }^{\prime }\left(0\right)+Nt{\theta }^{\prime }\left(0\right)=0,\hfill \end{array}$$

(12a)

$$\begin{array}{ccc}& & f^{″}\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0,\varphi \left(\eta \right)\to 0,\mathrm{as}\eta \to \infty ,\hfill \end{array}$$

(12b)

here, primes denote differentiation with respect to $\eta$, $Pr\left(=\frac{\nu }{\alpha }\right)$ is Prandtl number, where $\alpha \left(=\frac{k}{\rho c_p}\right)$ is the thermal diffusivity, $Le\left(=\frac{\nu }{D_B}\right)$ is Lewis number, $Nb\left(=\frac{\delta D_B({\phi }_w-{\phi }_{\infty })}{\nu }\right)$ is the Brownian motion parameter and $Nt\left(=\frac{\delta D_T(T_w-T_{\infty })}{\nu T_{\infty }}\right)$ is the thermophoresis parameter. Further, ${\alpha }_i,i=1\mathrm{to}4,$ are defined as:

$${\alpha }_1=\frac{{\rho }_{hnf}}{{\rho }_f},{\alpha }_2=\frac{{\mu }_{hnf}}{{\mu }_f},{\alpha }_3=\frac{{\left(\rho C_p\right)}_{hnf}}{{\left(\rho C_p\right)}_f}\mathrm{and}{\alpha }_4=\frac{k_{hnf}}{k_f}.$$

(13)

The physical quantities of interest are the skin friction coefficient $C_f$ and the local Nusselt number $N{u}_x$, which are defined as:

$$C_f=\frac{{\tau }_w}{{\rho }_f{U}_w^2\left(x\right)},N{u}_x=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)},$$

(14)

where ${\tau }_w$ is the skin friction or shear stress along the plate and $q_w$ is the heat flux from the plate, which are given by:

$${\tau }_w=-{\mu }_{hnf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},q_w=-k_{hnf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}.$$

(15)

On using (7) and (14), we get:

$$\mathrm{Sr}=C_f\sqrt{R{e}_x}=-{\alpha }_2{f}^{″}\left(0\right),\mathrm{Nur}=\frac{Nu}{\sqrt{R{e}_x}}=-{\alpha }_4{\theta }^{\prime }\left(0\right),$$

(16)

where ${\displaystyle {Re}_x=\frac{U_w\left(x\right)x}{{\nu }_f}}$ is the local Reynolds number.

3. Solutions of the System

On considering conditions of the dimensionless stream function in Equation (12a), $f\left(\eta \right)$ can be then deduced as:

$$f\left(\eta \right)=S+\frac{\lambda }{\beta }\left(1-e^{-\beta \eta }\right),$$

(17)

where $\beta$ is a constant to be determined and has to be positive to have a physical meaning. Therefore, by substituting the last relation in Equation (9), $\beta$ can be obtained as follows:

$$\beta =\frac{1}{2{\alpha }_2}\left[{\alpha }_{1}S\pm \sqrt{{\alpha }_1^2{S}^2+4{\alpha }_1{\alpha }_2\lambda }\right].$$

(18)

Now, when $\lambda >0$ (stretching sheet) and for any values of S, one can note that the positive sign of the second root makes $\beta$ positive. This means that there exists only a unique solution for any combination of the considered parameters (see for e.g., Aly [36]). However, for the shrinking sheet ($\lambda <0$), suppose that:

$$S_c=\left|2\sqrt{-\frac{{\alpha }_2}{{\alpha }_1}\lambda }\right|>0.$$

(19)

Then, we obtain the following three cases;

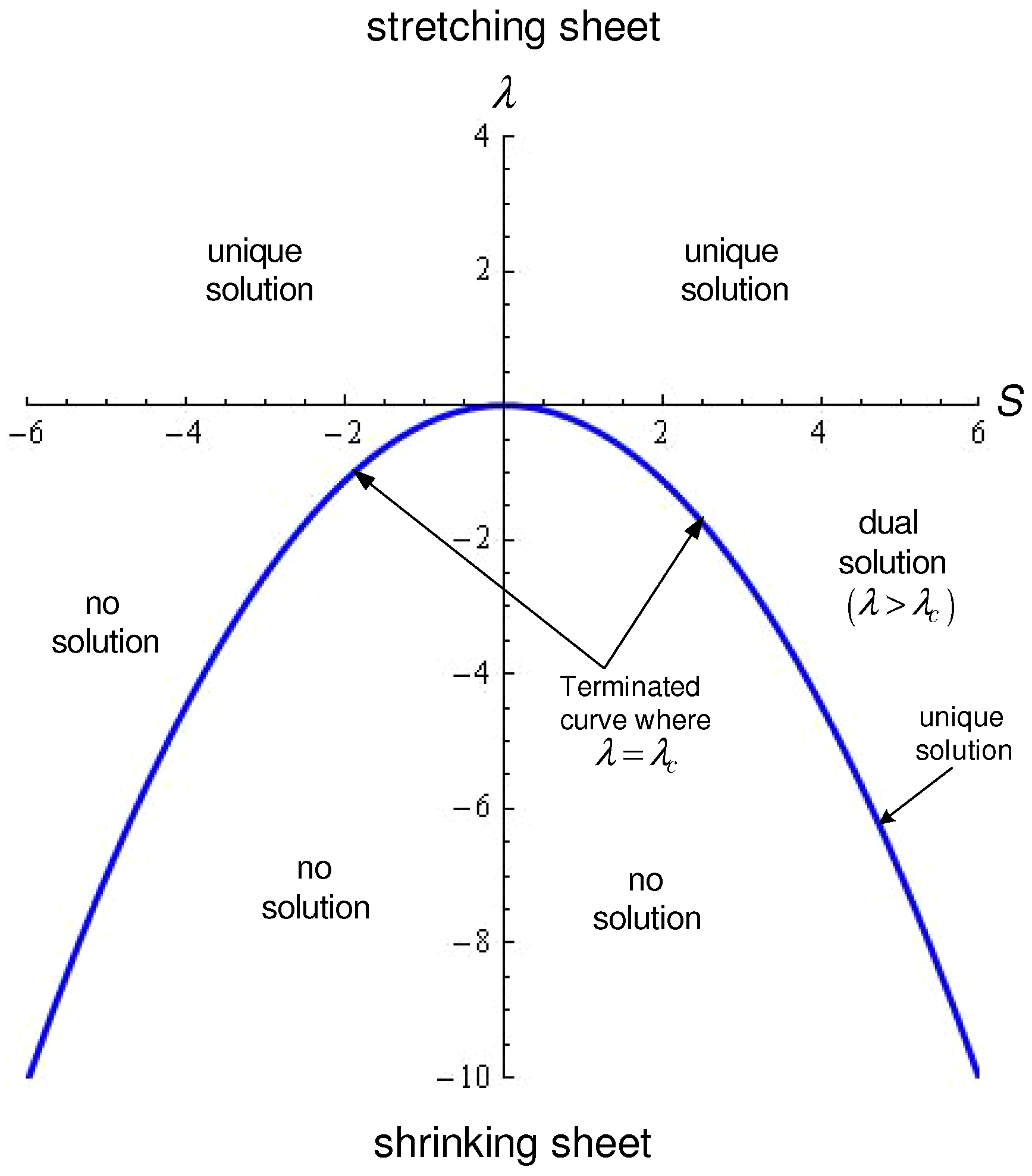
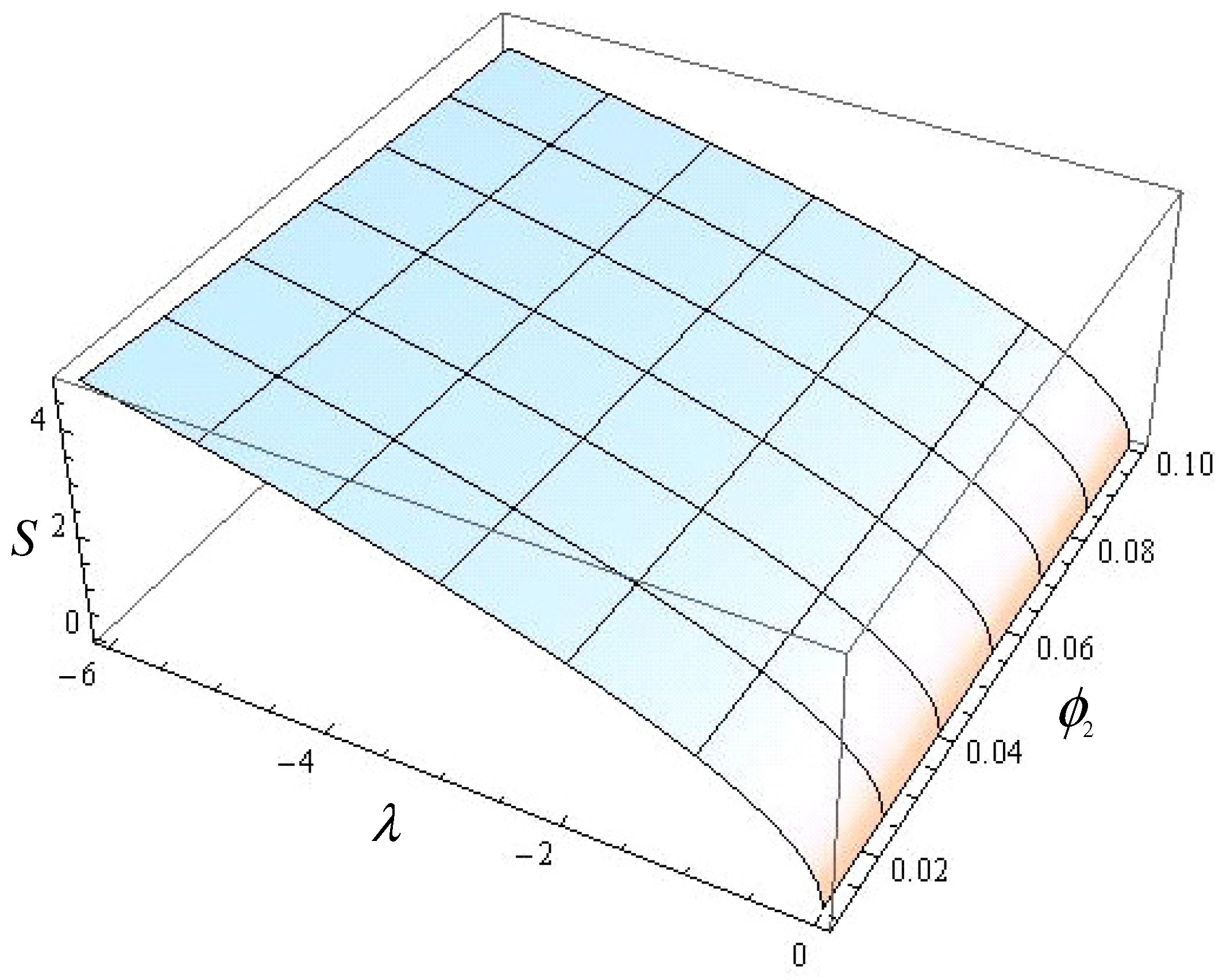
• There is no any physical solution when $S<S_c$.
• A unique solution is gotten if $S=S_c$.
• Dual solution can be only obtained for $S>S_c$.

Similarly, on supposing that

$${\lambda }_c=-\frac{S^2}{4}\frac{{\alpha }_1}{{\alpha }_2}<0,$$

(20)

there is then

• no solution when $\left[0>\lambda \ge {\lambda }_c,S<0\right]$ and $\left[\lambda <{\lambda }_c,\forall S\right]$,
• a unique solution if $\lambda ={\lambda }_c,S>0$, and
• dual solution at $\left[0>\lambda >{\lambda }_c,S>0\right]$,

where the suffix ${\left(\right)}_c$ refers the critical value of the specific parameter. Figure 2 and Figure 3 present the regions of no, unique and dual solutions of S as a function of $\lambda$ and vice versa, respectively, for a stretching/shrinking sheet. Further, 3D of the terminated curve for S as a function of $(\lambda ,{\varphi }_2)$ for a shrinking sheet is presented in Figure 4.

In addition, from Equation (16), the reduced skin friction coefficient $\left(\mathrm{Sr}\right)$ is obtained as:

$$\mathrm{Sr}=\lambda {\alpha }_2\beta .$$

(21)

With $\beta$ determined from relation (18), we obtain the analytical solution (17) for $f\left(\eta \right)$. Now, in order to calculate $\theta$ and $\varphi$, f from Equation (17) is replaced into Equations (10) and (11) to obtain the following system of differential equations:

$$\frac{{\alpha }_4}{{\alpha }_{3}Pr}{\theta }^{″}+\left[S+\frac{\lambda }{\beta }\left(1-e^{-\beta \eta }\right)\right]{\theta }^{\prime }+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{\theta }^{{}^{\prime }2}=0,$$

(22)

$${\varphi }^{″}+Le\left[S+\frac{\lambda }{\beta }\left(1-e^{-\beta \eta }\right)\right]{\varphi }^{\prime }+\frac{Nt}{Nb}{\theta }^{″}=0,$$

(23)

along with the following boundary conditions:

$$\begin{array}{ccc}& & \theta \left(0\right)=1,Nb{\varphi }^{\prime }\left(0\right)+Nt{\theta }^{\prime }\left(0\right)=0,\hfill \end{array}$$

(24a)

$$\begin{array}{ccc}& & \theta \left(\eta \right)\to 0,\varphi \left(\eta \right)\to 0,\mathrm{as}\eta \to \infty .\hfill \end{array}$$

(24b)

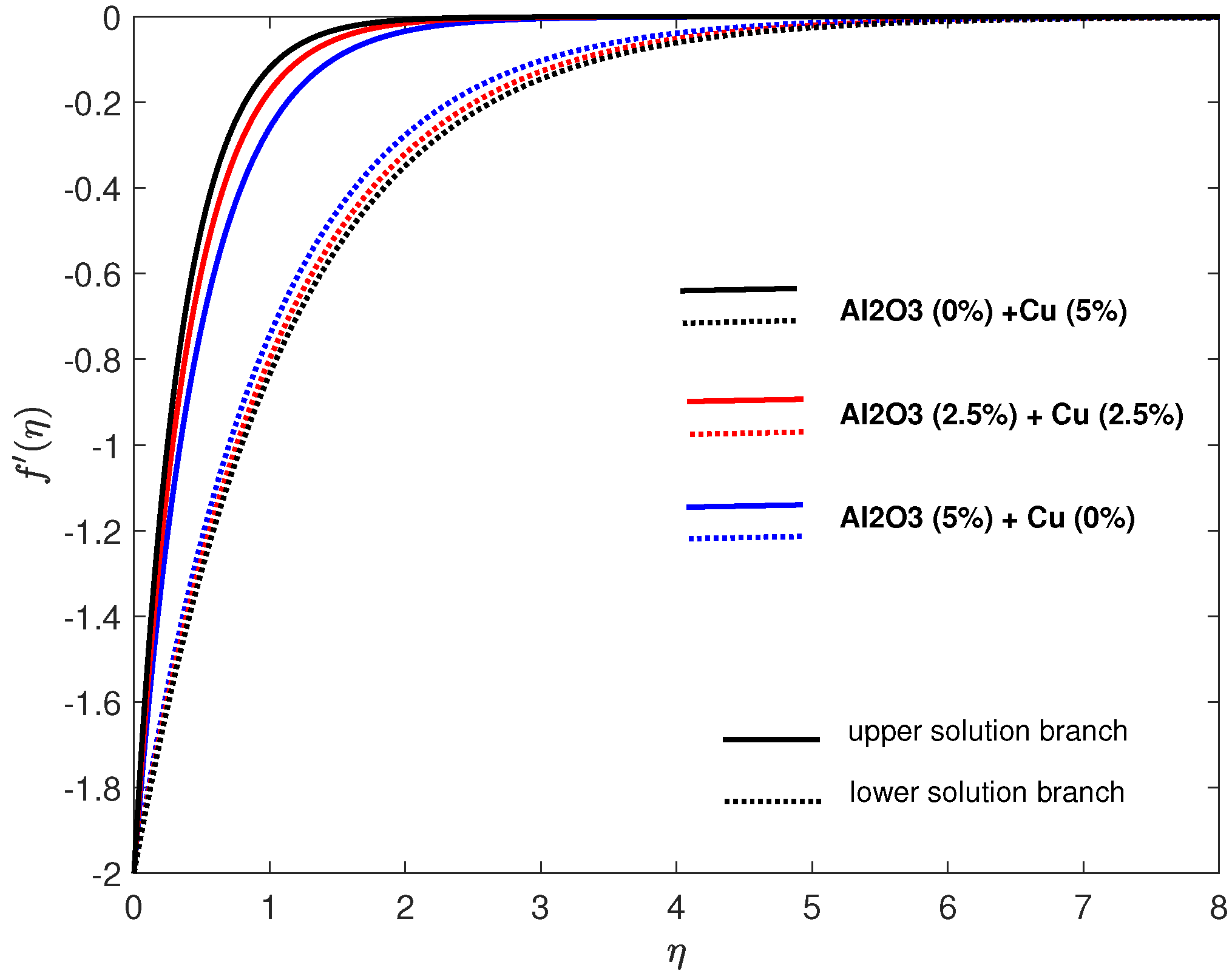
4. Results and Discussion

The boundary value problem (22)–(24) is numerically solved using the function bvp4c from MATLAB (see for e.g., Shampine et al. [37]) for different values of the included parameters $\lambda$, S, $Pr$, $Le$, $Nb$, $Nt$ with hybrid nanofluids ${\phi }_1$ and ${\phi }_2$. Brief details on the function bvp4c are introduced in the next paragraph.

The function bvp4c is a finite difference code that implements the three-stage Lobatto IIIa formula. This is a collocation formula and the collocation polynomial gives us a $C^1$–continuous solution, which is fourth-order accurate uniformly in the interval where the function is integrated. Further, in order to apply this routine, the present problem has to be rewritten as systems of first-order ODEs. In particular, we have chosen a suitable finite value of $\eta \to \infty$, namely $\eta ={\eta }_{\infty }=20$, where the relative tolerance is set at ${10}^{-7}$. Mesh selection and error control are based on the residual of the continuous solution. In addition, the starting mesh has 100 points equally distributed on the interval $[0,{\eta }_{\infty }=20]$ and then the mesh is automatically adjusted by the bvp4c routine. It is expected that the present problem may have more than one solution; therefore, a good initial guess is needed to obtain the desired solutions.

It should be noted that the results for $f\left(\eta \right)$ are to be analytically obtained from the expression (17), corresponding to the values of $\beta$. Therefore, the ODEs, (22) and (23), along with the BCs. (24) have more than one solution when $\lambda <0$ (shrinking sheet); we use the two analytical solutions described by (17) corresponding to the values of $\beta$ from (18) to numerically determine the corresponding dual (upper and lower) solutions for $\theta$ and $\varphi$.

The obtained results are displayed in terms of the skin-friction coefficient $C_f$, local Nusselt number $N{u}_x$, dimensionless velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles for different values of the parameters S, $\lambda$ and $\phi$. Both the cases of $\lambda >0$ (stretching) and $\lambda <0$ (shrinking) sheets have been studied. Because there are many cases to be considered, we limit presentation to only six figures, namely Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. This is also for sewing space.

Figure 5 and Figure 6 illustrate the variation of the reduced skin friction coefficient $f^{″}\left(0\right)$ and reduced heat transfer from the plate $-{\theta }^{\prime }\left(0\right)$ with the stretching/shrinking parameter $\lambda$ for several values of the suction parameter S. We can observe that a higher value of suction strength S is necessary to induce the dual steady similarity solutions for the shrinking case. As the shrinking parameter expands from $-1.1204$ to $-4.4817$, the required value of the suction parameter contracts from $S=4$ to $S=2$. The dual solution regions also expand with the increase of suction parameter S. Figure 7 and Figure 8 show that dual solution regions expand with the increase of the concentration of the Al${}_2$O${}_3$ particles and the decrease of the Cu nanoparticles’ concentration when the suction is present. We can see from all Figure 5, Figure 6, Figure 7 and Figure 8 that the dual solution exists only for the shrinking sheet in the case of suction $(S>0)$. All these figures show that unique solutions exist for Equations (9)–(11) with the boundary conditions (12a,b) when $\lambda >0$ (stretching sheet), dual solutions (upper and lower branch solutions) exist for ${\lambda }_c\le \lambda \le 0$ (shrinking sheet) and no solutions exist for $\lambda \le {\lambda }_c\le 0$, where ${\lambda }_c<0$ is the critical value of $\lambda <0$ for which the boundary value problems (9)–(12) have no solutions. It should be stated that, for $\lambda <{\lambda }_c<0$, the full Navier–Stokes and energy equations have to be solved.

Further, Figure 9 and Figure 10 present the velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles for shrinking case $\lambda =-2$ when the suction is presented as $S=3$. In these figures, the solid lines indicate the upper branch solution, while the dot lines refer to the lower branch solution, respectively. It is evident from these figures that the far field boundary conditions (12b) are approached asymptotically. Thus, it supports the numerical results obtained for the boundary value problems (9)–(12). Moreover, it is clearly seen from Figure 9 and Figure 10 that, for both velocity and temperature profiles, the upper branch solution displays a thinner boundary layer thickness compared to the lower branch solution. It is worth pointing out that the solution of the boundary value problem (9)–(12) exists only for large values of suction parameter $S(>0)$. This is in full agreement with the results reported by Fang et al. [38] for the problem of viscous flow over an unsteady shrinking sheet with mass transfer.

5. Conclusions

This paper considered both analytical and numerical solutions of the problem of a permeable stretching/shrinking sheet in both nanofluid and hybrid nanofluids using the mathematical models proposed by Buongiorno [2] and Devi and Devi’s [29] hybrid nanofluid model. The important conclusions of the present study are:

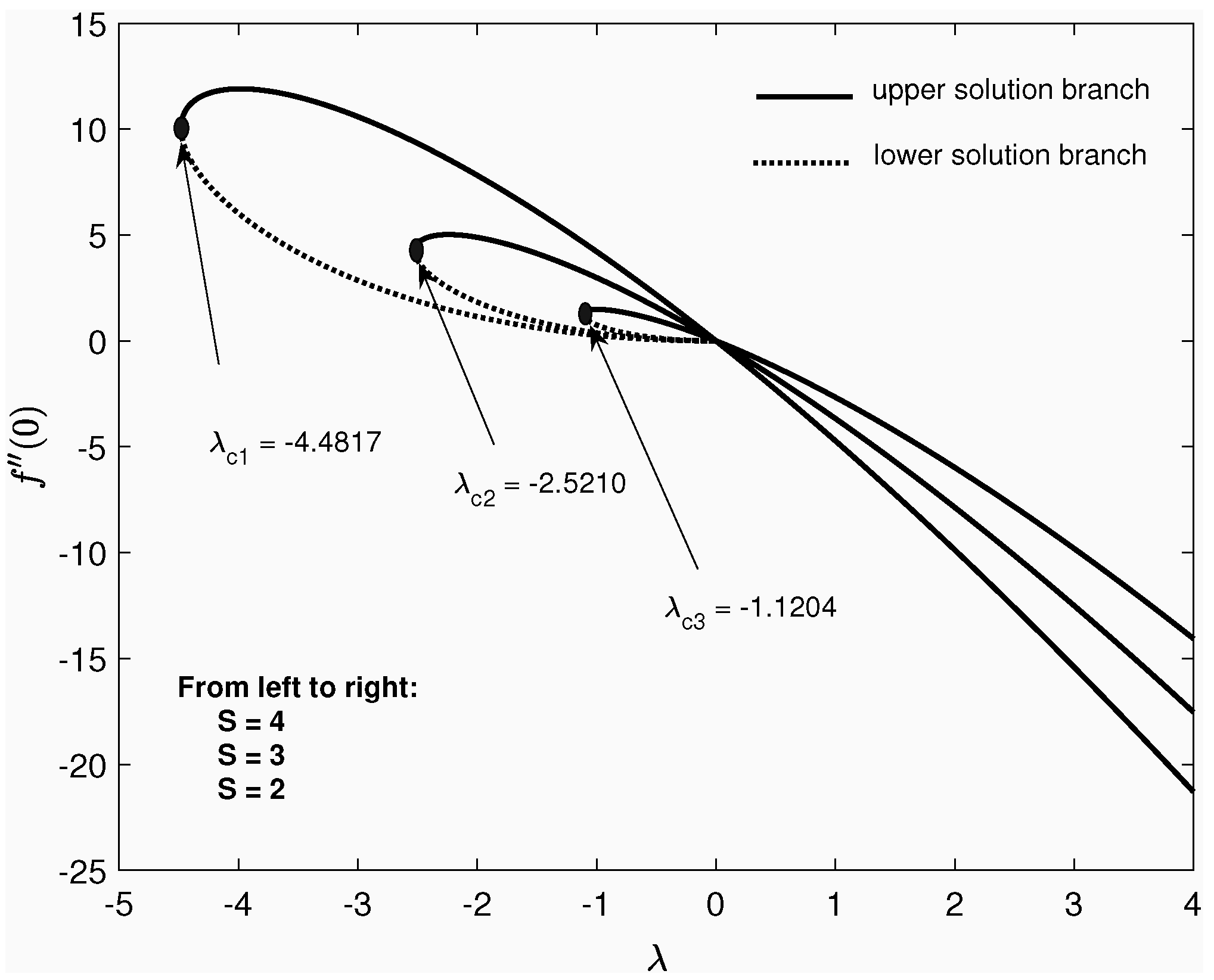
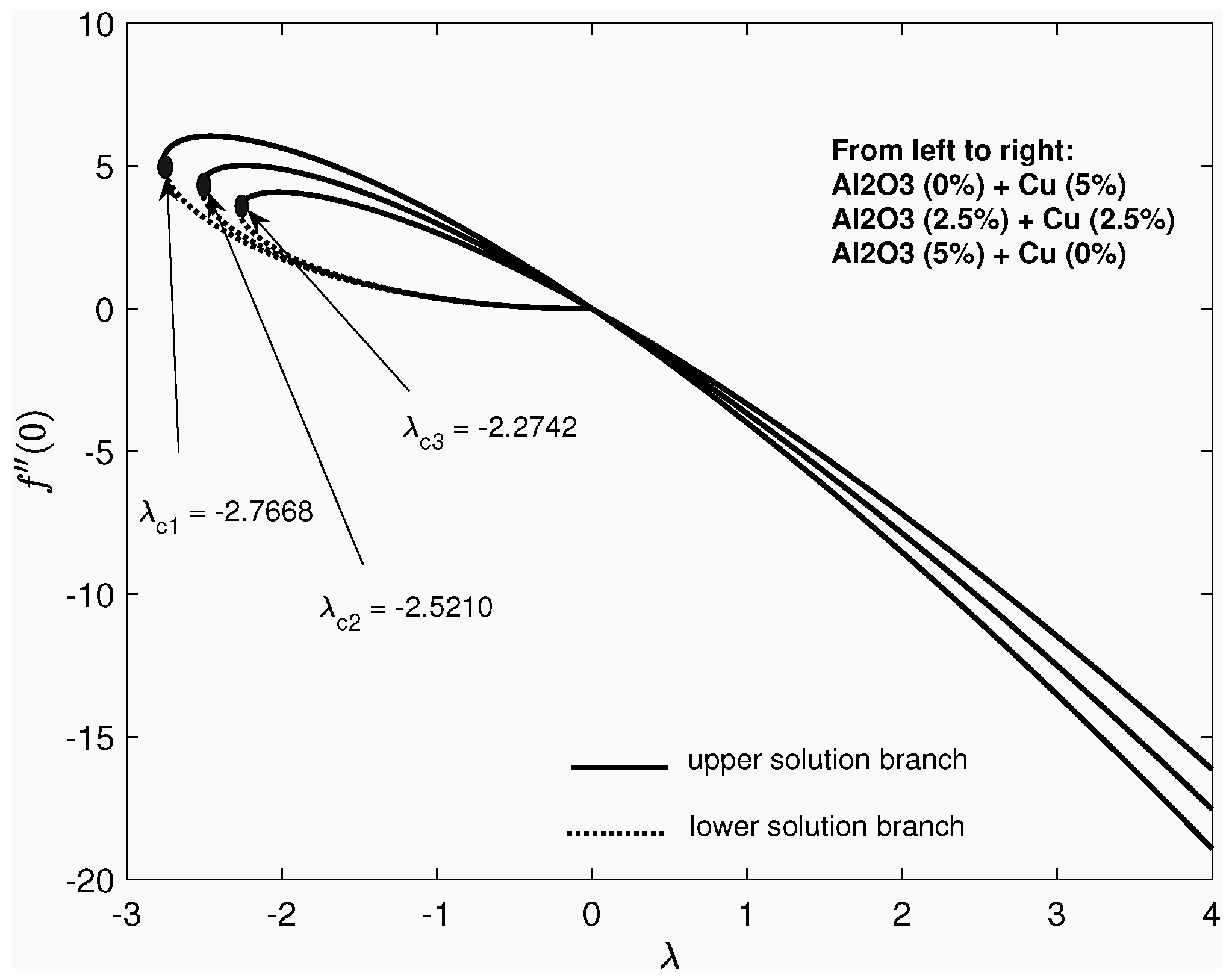
• One solution exists for stretching sheet $(\lambda >0)$.
• Dual solutions exist for shrinking case $(\lambda <0$).
• Skin friction coefficient and the local Nusselt number are increased as the rate of suction $S>0$ is increased.
• The analysis of the present investigation plays a predominant role in the applications of science and technology. Particularly, the results of the present problem are of great interest for controlled metal welding or the magnetically controlled coating of metals in fusion engineering problems, polymer engineering, metallurgy, and so forth.