Alias Structures and Sequential Experimentation for Mixed-Level Designs
Abstract
1. Introduction
2. Related Literature
3. Alias Structures for Mixed-Level Designs
3.1. Initial Design Construction Using EAs
3.2. Compute the Model Matrix
3.3. Computing the Correlation Matrix Using Pearson’s Correlation Coefficient
3.4. Creating the Alias Structure
- All main effects and interactions must belong to some chain.
- The same term cannot be included in multiple alias chains.
- Lower-order terms are considered more important than higher order terms and should appear sequentially first in the alias chain.
- Correlations take on values in the interval [−1, 1], and a value of 0 indicates no correlation (orthogonality).
4. Example
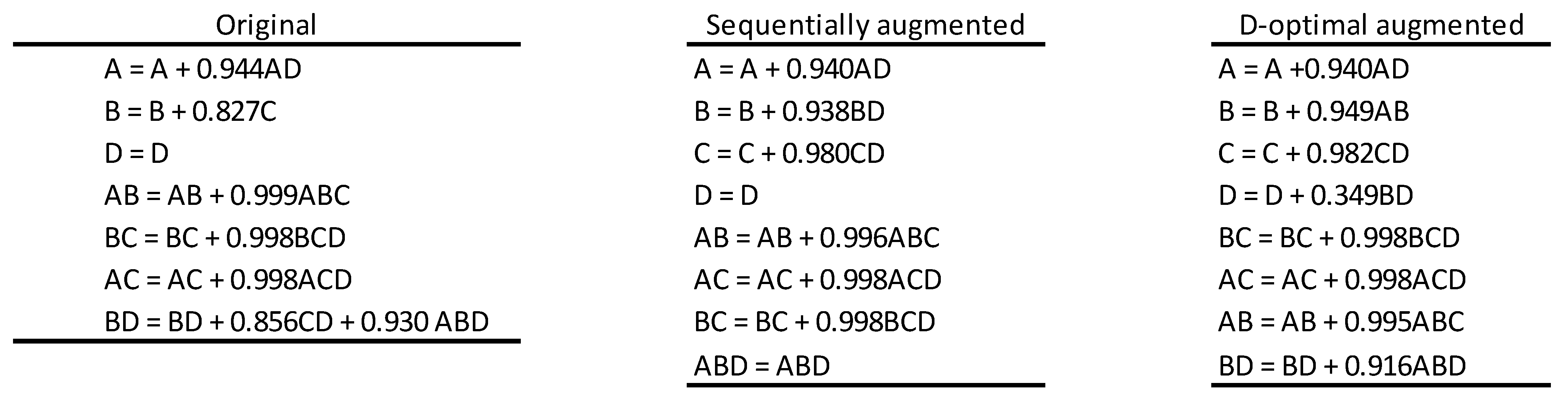
5. Sequential Experimentation Algorithm for Mixed-Level Fractions
- Use the alias structure and the correlation plot to detect the highest correlation.
- Add new runs to achieve orthogonality.
- Determine signs for remaining factors in such a way that balance is maintained.
- Compute the new alias structure and correlation plot.
- Repeat the procedure if necessary.
6. Practical Applications
7. Computer Program
| Algorithm 1. Program Alias |
|
function [ ALIASESTRUCTURE ] = GENERADORESTRUCTURAALIASITC(FRACTION) Array=FRACTION; ponderacion=0.5; [m,n]=size(Array); matrizdecorrelaciones=PASO1A3CALCULARCORRELACIONES(Array,n); PASO4; ijcontador=0; for columname=1:me-1 columname; contador=columname+1; for filame=contador:me if ijcontador==1 break end valor=W(filame,columname); if abs(valor)>=1.5 ijcontador=ijcontador+1; disp(’La fracción contiene efectos principales que estan fuertemente correlacionados (r>0.5)’ ) end contador=contador+1; end if ijcontador==1 break end end ciclo=1; while ciclo==1 if ijcontador==0 PASO5 else break end end end |
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Montgomery, D.C. Design and Analysis of Experiments, 9th ed.; Wiley and Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Guo, Y.; Simpson, J.R.; Pignatiello, J.J. Construction of Efficient Mixed-Level Fractional Factorial Designs. J. Qual. Technol. 2007, 39, 241–257. [Google Scholar] [CrossRef]
- Wang, J.C.; Wu, C.F.J. An Approach to the Construction of Asymmetrical Orthogonal Arrays. J. Am. Stat. Assoc. 1991, 86, 450. [Google Scholar] [CrossRef]
- DeCock, D.; Stufken, J. On finding mixed orthogonal arrays of strength 2 with many 2-level factors. Stat. Probab. Lett. 2000, 50, 383–388. [Google Scholar] [CrossRef]
- Xu, H. An Algorithm for Constructing Orthogonal and Nearly-Orthogonal Arrays with Mixed Levels and Small Runs. Technometrics 2002, 44, 356–368. [Google Scholar] [CrossRef]
- Koukouvinos, C.; Mantas, P. Construction of some E(fNOD) optimal mixed-level supersaturated designs. Stat. Probab. Lett. 2005, 74, 312–321. [Google Scholar] [CrossRef]
- Fang, K.-T.; Lin, D.K.J.; Liu, M.-Q. Optimal mixed-level supersaturated design. Metrika 2003, 58, 279–291. [Google Scholar] [CrossRef]
- Yan, L.; Min-Qian, L. Construction of optimal supersaturated design with large number of levels. J. Stat. Plan. Inference 2011, 141, 2035–4043. [Google Scholar]
- Sun, F.; Lin, D.K.J.; Liu, M.-Q. On construction of optimal mixed-level supersaturated designs. Ann. Stat. 2011, 39, 197–211. [Google Scholar] [CrossRef]
- Yamada, S.; Lin, D.K. Three-level supersaturated designs. Stat. Probab. Lett. 1999, 45, 31–39. [Google Scholar] [CrossRef]
- Guo, Y.; Simpson, J.R.; Pignatiello, J.J., Jr. The general balance metric for mixed-level fractional factorial designs. Qual. Reliab. Eng. Int. 2009, 25, 335–344. [Google Scholar] [CrossRef]
- Wu, C.F.; Hamada, M. Experiments: Planning, Analysis and Parameters Desing Optimization; Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mukerjee, R.; Wu, C.F. A Modern Theory of Factorial Design; Springer: New York, NY, USA, 2006. [Google Scholar]
- Pistone, G.; Rogantin, M.-P. Indicator function and complex coding for mixed fractional factorial designs. J. Stat. Plan. Inference 2008, 138, 787–802. [Google Scholar] [CrossRef]
- Grömping, U.; Xu, H. Generalized resolution for orthogonal arrays. Ann. Stat. 2014, 42, 918–939. [Google Scholar] [CrossRef]
- Guo, Y.; Simpson, J.R.; Pignatiello, J.J., Jr. Optimal foldover plans for mixed-level fractional factorial designs. Qual. Reliab. Eng. Int. 2009, 25, 449–466. [Google Scholar] [CrossRef]
- Ríos, A.J.; Simpson, J.R.; Guo, Y. Semifold plans for mixed-level designs. Qual. Reliab. Eng. Int. 2011, 27, 921–929. [Google Scholar] [CrossRef]
- Box, G.E.; Hunter, J.S. The 2k—p Fractional Factorial Designs. Technometrics 1961, 3, 311–351. [Google Scholar] [CrossRef]
- Su, H.; Wu, C.F.J. CME Analysis: A New Method for Unraveling Aliased Effects in Two-Level Fractional Factorial Experiments. J. Qual. Technol. 2017, 49, 1–10. [Google Scholar] [CrossRef]
- Xu, H. Nonregular Factorial and Supersaturated Designs. In Handbook of Design and Analysis of Experiments; Dean, A., Morris, M., Stufken, J., Bingham, D., Eds.; Taylor & Francis Group: Boca Raton, FL, USA, 2015; pp. 339–367. [Google Scholar]
- Kulahci, M.; Bisgaard, S. A generalization of the alias matrix. J. Appl. Stat. 2006, 33, 387–395. [Google Scholar] [CrossRef]
- Jones, B.; Montgomery, D.C. Alternatives to resolution IV screening designs in 16 runs. Int. J. Exp. Des. Process. Optim. 2010, 1, 285. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.A. Improving the Practice of Experimental Design in Manufacturing Engineering. Ph.D. Thesis, University of Birmingham, Birmingham, AL, USA, 2011. [Google Scholar]
- Hamada, M.; Wu, C.F.J. Analysis of Designed Experiments with Complex Aliasing. J. Qual. Technol. 1992, 24, 130–137. [Google Scholar] [CrossRef]
- Hamada, C.A.; Hamada, M.S. All-subsets regression under effect heredity restrictions for experimental designs with complex aliasing. Qual. Reliab. Eng. Int. 2010, 26, 75–81. [Google Scholar] [CrossRef]
- Wu, H.; Mee, R.; Tang, B. Fractional Factorial Designs with Admissible Sets of Clear Two-Factor Interactions. Technometrics 2012, 54, 191–197. [Google Scholar] [CrossRef]
- Tsai, P.-W.; Gilmour, S.G. A General Criterion for Factorial Designs Under Model Uncertainty. Technometrics 2010, 52, 231–242. [Google Scholar] [CrossRef]
- Cheng, C.-S.; Tsai, P.-W. Multistratum fractional factorial designs. Stat. Sin. 2011, 21, 1001–1021. [Google Scholar] [CrossRef][Green Version]
- Cheng, C.-S.; Tsai, P.-W. Templates for design key construction. Stat. Sin. 2014, 23, 1419–1436. [Google Scholar] [CrossRef]
- Zhou, Q.; Balakrishnan, N.; Zhang, R. The factor aliased effect number pattern and its application in experimental planning. Can. J. Stat. 2013, 41, 540–555. [Google Scholar] [CrossRef]
- Tyssedal, J.; Niemi, R. Graphical Aids for the Analysis of Two-Level Nonregular Designs. J. Comput. Graph. Stat. 2014, 23, 678–699. [Google Scholar] [CrossRef]
- Sartono, B.; Goos, P.; Schoen, E. Constructing General Orthogonal Fractional Factorial Split-Plot Designs. Technometrics 2015, 57, 488–502. [Google Scholar] [CrossRef]
- Jones, B.; Nachtsheim, C.J. Efficient Designs with Minimal Aliasing. Technometrics 2011, 53, 62–71. [Google Scholar] [CrossRef]
- Pantoja, Y.V.; Ríos, A.J.; Esquivias, M.T. A method for construction of mixed-level fractional designs. Qual. Reliab. Eng. Int. 2019, 35, 1646–1665. [Google Scholar] [CrossRef]
- Pantoja-Pacheco, Y.; Ríos-Lira, A.; Vázquez-López, J.; Jiménez-García, J.; Asato-España, M.; Tapia-Esquivias, M. One Note for Fractionation and Increase for Mixed-Level Designs When the Levels Are Not Multiple. Mathematics 2021, 9, 1455. [Google Scholar] [CrossRef]



















| A | B | C | BA | CA | CB | CBA |
|---|---|---|---|---|---|---|
| 1 | 1 | 7 | 1 | 7 | 7 | 7 |
| 1 | 2 | 2 | 2 | 2 | 9 | 9 |
| 1 | 3 | 5 | 3 | 5 | 19 | 19 |
| 1 | 4 | 4 | 4 | 4 | 25 | 25 |
| 1 | 5 | 3 | 5 | 3 | 31 | 31 |
| 2 | 1 | 2 | 6 | 9 | 2 | 37 |
| 2 | 2 | 5 | 7 | 12 | 12 | 47 |
| 2 | 3 | 6 | 8 | 13 | 20 | 55 |
| 2 | 4 | 7 | 9 | 14 | 28 | 63 |
| 2 | 5 | 1 | 10 | 8 | 29 | 64 |
| 3 | 1 | 4 | 11 | 18 | 4 | 74 |
| 3 | 2 | 1 | 12 | 15 | 8 | 78 |
| 3 | 3 | 2 | 13 | 16 | 16 | 86 |
| 3 | 4 | 3 | 14 | 17 | 24 | 94 |
| 3 | 5 | 6 | 15 | 20 | 34 | 104 |
| A | B | C | AB | AC | BC | |
|---|---|---|---|---|---|---|
| B | 0.000 | |||||
| C | −0.205 | 0.000 | ||||
| AB | 0.945 | 0.327 | −0.193 | |||
| AC | 0.938 | 0.000 | 0.146 | 0.887 | ||
| BC | −0.040 | 0.980 | 0.198 | 0.283 | 0.029 | |
| ABC | 0.941 | 0.331 | −0.129 | 0.998 | 0.906 | 0.299 |
| A | B | C | D | E | F | AB | AC | AD | EA | FA | BC | . | . | . | ECD | FCD | FEC | FED |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 | 3 | 1 | 1 | 3 | 2 | 3 | 1 | . | . | . | 8 | 13 | 8 | 23 |
| 1 | 2 | 1 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 1 | 2 | . | . | . | 1 | 1 | 1 | 1 |
| 1 | 1 | 2 | 2 | 3 | 1 | 1 | 3 | 3 | 3 | 1 | 3 | . | . | . | 12 | 16 | 26 | 26 |
| 1 | 2 | 1 | 1 | 3 | 2 | 3 | 1 | 1 | 3 | 2 | 2 | . | . | . | 3 | 2 | 12 | 12 |
| 1 | 1 | 2 | 1 | 2 | 2 | 1 | 3 | 1 | 2 | 2 | 3 | . | . | . | 5 | 7 | 22 | 7 |
| 1 | 2 | 2 | 2 | 1 | 5 | 3 | 3 | 3 | 1 | 5 | 4 | . | . | . | 10 | 20 | 20 | 20 |
| 1 | 1 | 1 | 2 | 3 | 4 | 1 | 1 | 3 | 3 | 4 | 1 | . | . | . | 9 | 14 | 14 | 29 |
| 1 | 2 | 2 | 2 | 2 | 4 | 3 | 3 | 3 | 2 | 4 | 4 | . | . | . | 11 | 19 | 24 | 24 |
| 1 | 1 | 2 | 1 | 1 | 3 | 1 | 3 | 1 | 1 | 3 | 3 | . | . | . | 4 | 8 | 18 | 3 |
| 1 | 2 | 1 | 1 | 2 | 5 | 3 | 1 | 1 | 2 | 5 | 2 | . | . | . | 2 | 5 | 10 | 10 |
| 2 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | 5 | 6 | 1 | . | . | . | 2 | 1 | 6 | 6 |
| 2 | 2 | 2 | 1 | 3 | 4 | 4 | 4 | 2 | 6 | 9 | 4 | . | . | . | 6 | 9 | 29 | 14 |
| 2 | 1 | 2 | 2 | 1 | 2 | 2 | 4 | 4 | 4 | 7 | 3 | . | . | . | 10 | 17 | 17 | 17 |
| 2 | 2 | 2 | 1 | 3 | 3 | 4 | 4 | 2 | 6 | 8 | 4 | . | . | . | 6 | 8 | 28 | 13 |
| 2 | 1 | 1 | 1 | 1 | 4 | 2 | 2 | 2 | 4 | 9 | 1 | . | . | . | 1 | 4 | 4 | 4 |
| 2 | 2 | 1 | 2 | 1 | 3 | 4 | 2 | 4 | 4 | 8 | 2 | . | . | . | 7 | 13 | 3 | 18 |
| 2 | 1 | 2 | 1 | 2 | 5 | 2 | 4 | 2 | 5 | 10 | 3 | . | . | . | 5 | 10 | 25 | 10 |
| 2 | 2 | 2 | 2 | 2 | 1 | 4 | 4 | 4 | 5 | 6 | 4 | . | . | . | 11 | 16 | 21 | 21 |
| 2 | 1 | 1 | 2 | 3 | 5 | 2 | 2 | 4 | 6 | 10 | 1 | . | . | . | 9 | 15 | 15 | 30 |
| 2 | 2 | 1 | 2 | 1 | 2 | 4 | 2 | 4 | 4 | 7 | 2 | . | . | . | 7 | 12 | 2 | 17 |
| A | B | C | D | E | F | AB | AC | . | . | . | EBD | FBD | FEB | ECD | FCD | FEC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0 | . | . | . | |||||||||||||
| C | 0 | 0 | . | . | . | ||||||||||||
| D | 0 | 0 | 0 | . | . | . | |||||||||||
| E | −0.06 | −0.06 | 0.062 | −0.06 | . | . | . | ||||||||||
| F | 0 | 0 | 0 | 0 | 0.088 | . | . | . | |||||||||
| AB | 0.447 | 0.894 | 0 | 0 | −0.08 | 0 | . | . | . | ||||||||
| AC | 0.447 | 0 | 0.894 | 0 | 0.028 | 0 | 0.2 | . | . | . | |||||||
| AD | 0.447 | 0 | 0 | 0.894 | −0.08 | 0 | 0.2 | 0.2 | . | . | . | ||||||
| EA | 0.875 | −0.03 | 0.03 | −0.03 | 0.429 | 0.043 | 0.364 | 0.418 | . | . | . | ||||||
| FA | 0.87 | 0 | 0 | 0 | −0.01 | 0.492 | 0.389 | 0.389 | . | . | . | ||||||
| BC | 0 | 0.447 | 0.894 | 0 | 0.028 | 0 | 0.4 | 0.8 | . | . | . | ||||||
| BD | 0 | 0.447 | 0 | 0.894 | −0.08 | 0 | 0.4 | 0 | . | . | . | ||||||
| EB | −0.03 | 0.875 | 0.03 | −0.03 | 0.429 | 0.043 | 0.769 | 0.013 | . | . | . | ||||||
| FB | 0 | 0.87 | 0 | 0 | −0.01 | 0.492 | 0.778 | 0 | . | . | . | ||||||
| CD | 0 | 0 | 0.447 | 0.894 | −0.03 | 0 | 0 | 0.4 | . | . | . | ||||||
| EC | −0.03 | −0.03 | 0.888 | −0.03 | 0.514 | 0.041 | −0.04 | 0.781 | . | . | . | ||||||
| FC | 0 | 0 | 0.87 | 0 | 0.097 | 0.492 | 0 | 0.778 | . | . | . | ||||||
| ED | −0.03 | −0.03 | 0.03 | 0.875 | 0.429 | 0.043 | −0.04 | 0.013 | . | . | . | ||||||
| FD | 0 | 0 | 0 | 0.87 | −0.01 | 0.492 | 0 | 0 | . | . | . | ||||||
| FE | −0.06 | −0.06 | 0.057 | −0.06 | 0.947 | 0.404 | −0.08 | 0.026 | . | . | . | ||||||
| ABC | 0.218 | 0.436 | 0.873 | 0 | 0.014 | 0 | 0.488 | 0.878 | . | . | . | ||||||
| ABD | 0.218 | 0.436 | 0 | 0.873 | −0.1 | 0 | 0.488 | 0.098 | . | . | . | ||||||
| EAB | 0.429 | 0.872 | 0.015 | −0.02 | 0.155 | 0.021 | 0.972 | 0.205 | . | . | . | ||||||
| FAB | 0.434 | 0.867 | 0 | 0 | −0.06 | 0.245 | 0.969 | 0.194 | . | . | . | ||||||
| ACD | 0.218 | 0 | 0.436 | 0.873 | −0.04 | 0 | 0.098 | 0.488 | . | . | . | ||||||
| EAC | 0.418 | −0.01 | 0.879 | −0.01 | 0.259 | 0.02 | 0.174 | 0.973 | . | . | . | ||||||
| FAC | 0.434 | 0 | 0.867 | 0 | 0.048 | 0.245 | 0.194 | 0.969 | . | . | . | ||||||
| EAD | 0.429 | −0.02 | 0.015 | 0.872 | 0.155 | 0.021 | 0.178 | 0.205 | . | . | . | ||||||
| FAD | 0.434 | 0 | 0 | 0.867 | −0.06 | 0.245 | 0.194 | 0.194 | . | . | . | ||||||
| FEA | 0.856 | −0.03 | 0.03 | −0.03 | 0.435 | 0.209 | 0.357 | 0.409 | . | . | . | ||||||
| BCD | 0 | 0.218 | 0.436 | 0.873 | −0.04 | 0 | 0.195 | 0.39 | . | . | . | ||||||
| EBC | −0.01 | 0.418 | 0.879 | −0.01 | 0.259 | 0.02 | 0.367 | 0.78 | . | . | . | ||||||
| FBC | 0 | 0.434 | 0.867 | 0 | 0.048 | 0.245 | 0.388 | 0.776 | . | . | . | ||||||
| EBD | −0.02 | 0.429 | 0.015 | 0.872 | 0.155 | 0.021 | 0.377 | 0.007 | . | . | . | ||||||
| FBD | 0 | 0.434 | 0 | 0.867 | −0.06 | 0.245 | 0.388 | 0 | . | . | . | 0.947 | |||||
| FEB | −0.03 | 0.856 | 0.03 | −0.03 | 0.435 | 0.209 | 0.753 | 0.013 | . | . | . | 0.457 | 0.397 | ||||
| ECD | −0.02 | −0.02 | 0.452 | 0.861 | 0.208 | 0.021 | −0.02 | 0.398 | . | . | . | 0.806 | 0.745 | 0.089 | |||
| FCD | 0 | 0 | 0.434 | 0.867 | −0.01 | 0.245 | 0 | 0.388 | . | . | . | 0.768 | 0.812 | 0.038 | 0.947 | ||
| FEC | −0.03 | −0.03 | 0.871 | −0.03 | 0.518 | 0.199 | −0.04 | 0.766 | . | . | . | 0.086 | 0.012 | 0.255 | 0.478 | 0.402 | |
| FED | −0.03 | −0.03 | 0.03 | 0.856 | 0.435 | 0.209 | −0.04 | 0.013 | . | . | . | 0.85 | 0.781 | 0.215 | 0.864 | 0.806 | 0.255 |
| True Model | A | B | C | AB |
|---|---|---|---|---|
| Original | X | X | ||
| Sequentially Augmented | X | X | X | X |
| D-optimal Augmented | X | X | X | X |
| N | A | B | C | D | Y | Desirability |
|---|---|---|---|---|---|---|
| Original | 3 | 2 | 1 * | 1 * | 4.020 | 0.987 |
| Sequentially Augmented | 3 | 2 | 5 | 1 * | 4.145 | 1 |
| D-optimal Augmented | 3 | 2 | 5 | 1 | 4.059 | 0.997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ríos-Lira, A.J.; Pantoja-Pacheco, Y.V.; Vázquez-López, J.A.; Jiménez-García, J.A.; Asato-España, M.L.; Tapia-Esquivias, M. Alias Structures and Sequential Experimentation for Mixed-Level Designs. Mathematics 2021, 9, 3053. https://doi.org/10.3390/math9233053
Ríos-Lira AJ, Pantoja-Pacheco YV, Vázquez-López JA, Jiménez-García JA, Asato-España ML, Tapia-Esquivias M. Alias Structures and Sequential Experimentation for Mixed-Level Designs. Mathematics. 2021; 9(23):3053. https://doi.org/10.3390/math9233053
Chicago/Turabian StyleRíos-Lira, Armando Javier, Yaquelin Verenice Pantoja-Pacheco, José Antonio Vázquez-López, José Alfredo Jiménez-García, Martha Laura Asato-España, and Moisés Tapia-Esquivias. 2021. "Alias Structures and Sequential Experimentation for Mixed-Level Designs" Mathematics 9, no. 23: 3053. https://doi.org/10.3390/math9233053
APA StyleRíos-Lira, A. J., Pantoja-Pacheco, Y. V., Vázquez-López, J. A., Jiménez-García, J. A., Asato-España, M. L., & Tapia-Esquivias, M. (2021). Alias Structures and Sequential Experimentation for Mixed-Level Designs. Mathematics, 9(23), 3053. https://doi.org/10.3390/math9233053








