Pre-Service Primary School Teachers’ Knowledge and Their Interpretation of Students’ Answers to a Measurement Division Problem with Fractions
Abstract
:1. Introduction
2. Theoretical Background
2.1. Measurement Division Problems
2.2. Teachers’ Knowledge of Division with Fractions
2.3. Teachers Noticing in the Specific Mathematical Domain: Division with Fractions
- How do PPTs solve measurement division problems with fractions?
- How do PPTs interpret (score and justify) the answers of primary school students in measurement division problems with fractions?
3. Materials and Methods
3.1. Participants and Context
3.2. Instruments
- ○
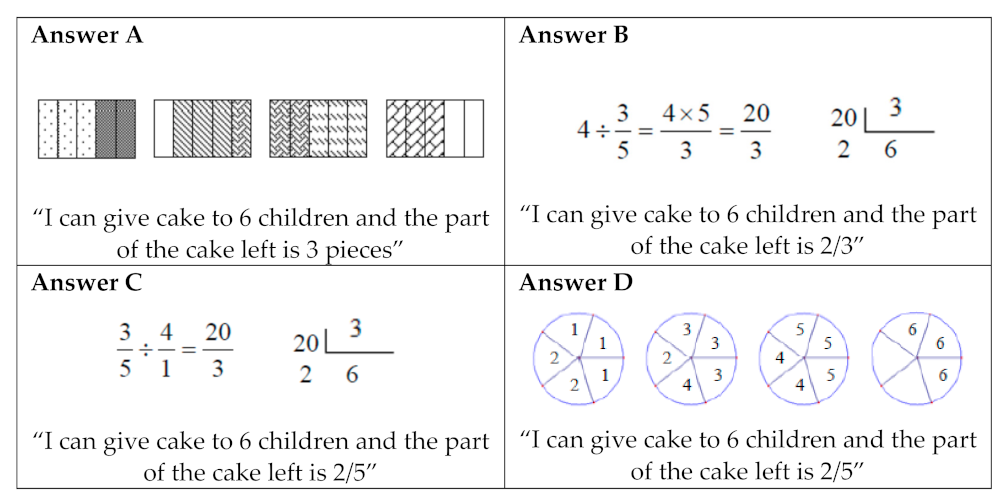
- Students’ answers were selected considering problem-solving procedures and the erroneous concepts identified in prior research on division problems with fractions [34]. The four answers chosen show procedures for measuring and the use of fractions [22,26]; in some answers, there are conceptual or procedural errors [27], and two of them made use of graphic representations.
- For Answer A, the student represents each cake by a rectangle, divides each cake into fifths, and uses a unit of measure equal to the piece of cake that must be given to each of the children (3/5). The student counts out how many times 3/5 is in the total. Because of the way the student colors the parts, he/she makes a procedural counting error, and in giving the answer regarding how much is left over, he/she answers that “three pieces” (conceptual error).
- For Answer B, the student carries out a division (4:3/5), dividing four cakes by the fraction represented by the amount of cake to be given to each child (3/5). The student uses the algorithm for division correctly, multiplying crosswise the numerator by the denominator, and obtaining 20/3. In response to the questions asked, he/she divides 20:3 and gets a quotient of 6 and a remainder of 2, giving an answer of 6 children, with 2/3 left over. The answer that says that 2/3 is left indicates that the student is using thirds as a unit of measure for the remainder rather than the entire cake, as asked. The student “read” the remainder without considering that it is the part of 3/5 (the unit) that is left (conceptual error; which is to say that 2/5 of the entire cake is left over).
- For Answer C, the student does a division but inverts the terms (dividing 3/5 by 4), as if the commutative property were true for this operation (conceptual error). The student applies the algorithm incorrectly (procedural error), but the two errors cancel each other out, leading to the right answer.
- For Answer D, the student using direct modeling draws circles to represent the 4 cakes, dividing each into five parts and enumerating each group of 1/5 that can be given to each child (3/5 cake), giving a correct answer.
- The PPTs completed Task 1, and fifteen days later, they did so with Task 2.
3.3. Analysis
- Use of natural numbers. When the PPTs considered the 4 cakes to be 20 fifths and justified the answer by using natural numbers.
- Measurement. When the PPTs created a unit of measure equal to the piece they were supposed to give to each child (3/5 of a rectangle or circle) and applied this measure to the 4 cakes.
- Use of fractions. When the PPTs used operations with fractions (such as repeated additions, or subtractions, or multiplication, or division with fractions).
- Justifications based on the validity of the method. When the PPTs deemed that the procedure used by the primary school student was or was not valid for the problem.
- Justifications based on the generalizability of the method. When the PPTs believed the procedures could or could not be applied to other problems with higher quantities.
- Justifications based on the clarity of the method. When the PPTs felt that the procedure was explained with clarity.
- Other justifications. When the PPTs considered only the correctness of the result or other aspects.
4. Results
4.1. How Do Pre-Service Teachers Solve the Measurement Division Problem?
4.2. Relationship between Problem Solving and the Scoring Assigned to the Primary Students’ Answers
- Answer A, which uses a measurement procedure with a graphic representation for support, with one procedural and one conceptual error, was given a score of 0.5 by 69.5% of the PPTs. The majority argued that the result was incorrect: “Incorrect solution, since there is 2/5 of a piece left over”. This group of teachers considered in their scoring how the primary school student expressed the amount “left over”.
- Answer B, which uses division with fractions with a conceptual error in the interpretation of the remainder, was given a score of 0.5 by 68.3% of the PPTs. These teachers maintained that the result was not correct: “The result of the operation or conclusion the student reaches is not correct”, but without indicating that the whole had been divided into five parts and therefore what was left over could not be thirds, but fifths.
- Firstly, 68.5% of the PPTs that gave answer C a score of 1 said that both the procedure used and the result were correct: “The strategy and the solution are correct, and I am giving the student the highest score since he/she understood the problem and has also carried out the right operations to solve it”. These PPTs focused their attention on the fact that the result for answer C was correct, but did not notice the two errors in the procedure (inversion of terms and algorithm).
- Secondly, 18.1% of the PPTs gave answer C a score of 0.5, arguing that the result was correct and noticing only one error, whether in the algorithm: “I gave him/her a score of 0.5 because even though the solution is correct, in the division there is a mistake since in division with fractions you can’t multiply like that”; or due to the inversion of terms of the operation: “The result is correct. The division by a fraction would be 4:3/5, but in the end the student gets the right result”.
- Finally, 13.4% of the PPTs that gave answer C a score of 0 gave at times the same reasons as those who scored it with 0.5 points: “It’s incorrect because he/she divided what has to be given to each person by the number of people there are. Later the student realized that 3:20 could not be right and corrected it; he/she gives the right answer but the approach, which is the important thing, is all wrong”. Only two of them noticed both mistakes; in these cases, the teachers based their score on the incorrect procedure and not on the answer.
4.3. How the PPTs Interpreted the Procedures and Errors of the Primary School Students
5. Discussion and Conclusions
Implications for Teacher Training
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dindyal, J.; Schack, E.O.; Choy, B.H.; Sherin, M.G. Exploring the terrains of mathematics teacher noticing. ZDM-Math. Educ. 2021, 53, 1–16. [Google Scholar] [CrossRef]
- Fernández, C.; Sánchez-Matamoros, G.; Valls, J.; Callejo, M.L. Noticing students’ mathematical thinking: Characterization, development and contexts. Av. Investig. Educ. Matemática 2018, 13, 39–61. [Google Scholar] [CrossRef] [Green Version]
- Jacobs, V.R.; Spangler, D.A. Research on core practices in K-12 mathematics teaching. In Compendium for Research in Mathematics Education; Cai, J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2017; pp. 766–792. [Google Scholar]
- Sherin, M.G. The development of teachers’ professional vision in video clubs. In Video Research in the Learning Sciences, 1st ed.; Goldman, R., Pea, R., Barron, B., Denny, S.J., Eds.; Routlege: New York, NY, USA, 2007; pp. 397–410. [Google Scholar] [CrossRef]
- Van Es, E.A.; Sherin, M.G. Learning to notice: Scaffolding new teachers’ interpretations of classroom interactions. J. Technol. Teach. Educ. 2002, 10, 571–595. [Google Scholar]
- Jacobs, V.; Lamb, L.; Philipp, R. Professional noticing of children’s mathematical thinking. J. Res. Math. Educ. 2010, 41, 169–202. [Google Scholar] [CrossRef]
- Thomas, J.; Fisher, M.H.; Jong, C.; Schack, E.O.; Krause, L.R.; Kasten, S. Professional noticing: Learning to teach responsively. Math. Teach. Middle Sch. 2015, 21, 238–243. [Google Scholar] [CrossRef]
- Brown, L.; Fernández, C.; Helliwell, T.; Llinares, S. Prospective mathematics teachers as learners in university and school contexts: From university–based activities to classroom practice. In International Handbook of Mathematics Teacher Education: Volume 3. Participants in Mathematics Teacher Education, 2nd ed.; Lloyd, G.M., Chapman, O., Eds.; Brill Academic Publishers: Leiden, The Netherlands, 2020; pp. 343–366. [Google Scholar] [CrossRef]
- Ball, D.L.; Thames, M.H.; Phelps, G. Content Knowledge for Teaching: What makes it Special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef] [Green Version]
- Thomas, J.; Jong, C.; Fisher, M.H.; Schack, E.O. Noticing and knowledge. Exploring theoretical connections between professional noticing and mathematical knowledge for teaching. Math. Educ. 2017, 26, 3–25. [Google Scholar]
- Magiera, M.; van den Kieboom, L.; Moyer, J. An exploratory study of preservice middle school teachers’ knowledge of algebraic thinking. Educ. Stud. Math. 2013, 84, 93–113. [Google Scholar] [CrossRef]
- Buforn, A.; Llinares, S.; Fernández, C.; Coles, A.; Brown, L. Pre-service teachers’ knowledge of the unitizing process in recognizing students’ reasoning to propose teaching decisions. Int. J. Math. Educ. Sci. Technol. 2020, 1–19. [Google Scholar] [CrossRef]
- Son, J. How preservice teachers interpret and respond to student errors: Ratio and proportion in similar rectangles. Educ. Stud. Math. 2013, 84, 49–70. [Google Scholar] [CrossRef]
- Ivars, P.; Fernández, C.; Llinares, S.; Choy, B.H. Enhancing noticing: Using a hypothetical learning trajectory to improve pre-service primary teachers’ professional discourse. Eurasia J. Math. Sci. Technol. Educ. 2018, 14, 3m1599. [Google Scholar] [CrossRef]
- Dick, L.K. Investigating the relationship between professional noticing and specialized content knowledge. In Teacher Noticing: Bridging and Broadening Perspectives, Contexts and Frameworks; Schack, E.O., Fisher, M.H., Wilhelm, J.A., Eds.; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 445–466. [Google Scholar]
- Schack, E.; Fisher, M.; Thomas, J.; Eisenhardt, S.; Tassell, J.; Yoder, M. Prospective elementary school teachers’ professional noticing of children’s early numeracy. J. Math. Teach. Educ. 2013, 16, 379–397. [Google Scholar] [CrossRef]
- Sánchez-Matamoros, G.; Fernández, C.; Llinares, S. Relationships among prospective secondary mathematics teachers’ skills of attending, interpreting and responding to students’ understanding. Educ. Stud. Math. 2019, 100, 83–99. [Google Scholar] [CrossRef]
- Dreher, A.; Kuntze, S. Teachers’ professional knowledge and noticing: The case of multiple representations in the mathematics classroom. Educ. Stud. Math. 2015, 88, 89–114. [Google Scholar] [CrossRef]
- Yang, X.; Kaiser, G.; König, J.; Blömeke, S. Relationship between Chinese mathematics teachers’ knowledge and their professional noticing. Int. J. Sci. Math. Educ. 2021, 19, 815–837. [Google Scholar] [CrossRef]
- Friezen, M.; Kuntze, S. How context specific is teachers’ analysis of how representations are dealt with in classroom situations? Approaching context-aware measure for teacher noticing. ZDM-Math. Educ. 2021, 53, 181–193. [Google Scholar] [CrossRef]
- Behr, M.; Harel, G.; Post, T.; Lesh, R. Rational number, ratio, and proportion. In Handbook of Research on Mathematics Teaching and Learning; Grows, D., Ed.; Macmillan: New York, NY, USA, 1992; pp. 296–333. [Google Scholar]
- Empson, S.B.; Levi, L. Extending Children’s Mathematics: Fractions and Decimals; Heinemann: Portsmouth, NH, UK, 2011. [Google Scholar]
- Lamon, S. Rational number and proportional reasoning: Towards a theoretical framework for research. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Jr., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2007; pp. 629–667. [Google Scholar]
- Greer, B. Multiplication and division as models of situation. In Handbook of Research on Mathematics Teaching and Learning; Grows, D., Ed.; McMillan: New York, NY, USA, 1992; pp. 276–295. [Google Scholar]
- Vergnaud, G. Multiplicative conceptual field: What and why? In The Development of Multiplicative Reasoning in the Learning of the Mathematics; Harel, G., Confrey, J., Eds.; State University of New York Press: New York, NY, USA, 1994; pp. 41–59. [Google Scholar]
- Bulgar, S. Children’s sense-making of division of fractions. J. Math. Behav. 2003, 22, 319–334. [Google Scholar] [CrossRef]
- Cramer, K.; Monson, D.; Whitney, S.; Leavitt, S.; Wyberg, T. Dividing fractions and problem solving. Math. Teach. Middle Sch. 2010, 15, 338–346. [Google Scholar] [CrossRef]
- Graeber, A.O.; Tirosh, D.; Glover, R. Preservice teachers’ misconceptions in solving verbal problems in multiplication and division. J. Res. Math. Educ. 1986, 20, 95–102. [Google Scholar]
- Ball, D.L. Prospective elementary and secondary teachers’ understanding division. J. Res. Math. Educ. 1990, 21, 132–144. [Google Scholar] [CrossRef]
- Nillas, L. Division of fractions: Preservice teachers’ understanding and use of problem solving strategies. Math. Educ. 2003, 7, 96–113. [Google Scholar]
- Koichu, B.; Harel, G.; Manaster, A. Ways of thinking associated with mathematics teachers’ problem posing in the context of division of fractions. Instr. Sci. 2013, 41, 681–698. [Google Scholar] [CrossRef]
- Lo, J.-J.; Lou, F. Prospective elementary teachers’ knowledge of fractions division. J. Math. Teach Educ. 2012, 15, 481–500. [Google Scholar] [CrossRef]
- Osana, H.P.; Royea, D.A. Obstacles and challenges in preservice teachers’ explorations with fractions: A view from a small-scale intervention study. J. Math. Behav. 2011, 30, 333–352. [Google Scholar] [CrossRef]
- Tirosh, D. Enhancing prospective teachers’ knowledge of children’s conceptions: The case of division of fractions. J. Res. Math. Educ. 2000, 31, 5–25. [Google Scholar] [CrossRef]
- Jakobsen, A.; Ribeiro, C.M.; Mellone, M. Norwegian prospective teachers’ MKT when interpreting pupils’ productions on a fraction task. Nord. Stud. Math. Educ. 2014, 19, 135–150. [Google Scholar]
- Montero, E.; Callejo, M.L. How prospective teachers interpret primary students’ answers to fractions division-measure problems. In Investigación en Educación Matemática XXII; Rodríguez-Muñiz, L.J., Muñiz-Rodríguez, L., Aguilar-González, A., Alonso, P., García, F.J., Bruno, A., Eds.; SEIEM: Gijón, Spain, 2018; pp. 378–386. [Google Scholar]
- Callejo, M.L.; Vila, A. Approach to mathematical problem solving and students’ belief systems: Two case studies. Educ. Stud. Math. 2009, 72, 11–126. [Google Scholar] [CrossRef]
- Fernández, C.; Callejo, M.L.; Márquez, M. Conocimiento de los estudiantes para maestro cuando interpretan respuestas de estudiantes de primaria a problemas de división-medida. Ensen. Cienc. 2014, 32, 407–424. [Google Scholar] [CrossRef] [Green Version]
- Buchbinder, O.; Kuntze, S. Mathematics Teachers Engaging with Representations of Practice; A Dynamically Evolving Field; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Downton, A. A study of comparative performance on partitive and measurement division in solving division word problems. In Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education; Tzekaki, M., Kaldrimidou, M., Sakonidis, H., Eds.; PME: Thessaloniki, Greece, 2009; Volume 2, pp. 465–472. [Google Scholar]
- Li, Y.; Silver, E.A. Can younger students succeed where older students fail? An examination of third graders’ solutions of a division-with-remainder (DWR) problem. J. Math. Behav. 2000, 19, 233–246. [Google Scholar] [CrossRef]
- Fernández, C.; Choy, B.H. Theoretical lenses to develop mathematics teacher noticing. In International Handbook of Mathematics Teacher Education: Volume 2. Tools and Processes in Mathematics Teacher Education, 2nd ed.; Llinares, S., Chapman, O., Eds.; Brill Academic Publishers: Leiden, The Netherlands, 2020; pp. 337–360. [Google Scholar]
| Answers | Examples | |
|---|---|---|
| Correct | 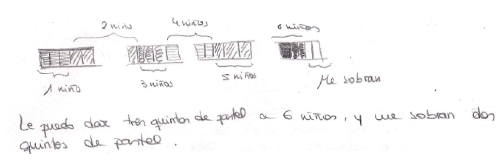 | The PPT represented graphically the cakes dividing each cake in five equal parts. He/she said that “I can give 3/5 of the cake to 6 children and the part of the cake left is 2/5” |
| Almost correct |  | The PPT made a division correctly and indicated that he/she could give 3/5 of the cake to 6 children. However, he/she indicated that the part of the cake left is 2 pieces |
| Incorrect |  | The PPT answer made no sense |
| Method | Example |
|---|---|
| “The use of natural numbers” This answer was classified as almosst correct since the PPT did not interpret the remainder | “The first cake is divided in 5 pieces. The second cake in 5 pieces. The third and fourth cake also in 5 pieces. So, we have 20 pieces (5 · 4 = 20). If we give to each child 3 pieces, we divide the number of pieces between the number of pieces that we have to give to each child”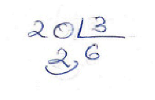 “We can give cake to 6 children and the part of the cake left is 2 pieces” |
| “Measurement” This answer was classified as correct | 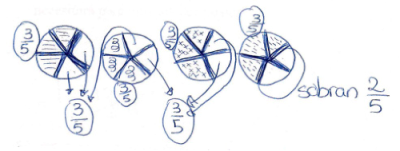 “You can give 3/5 of the cake to 6 children. The part of the cake left is 2/5” |
| “The use of fractions” This answer was classified as correct | 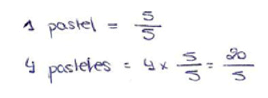 If you want to give 3/5 of the cake (pastel) to each child 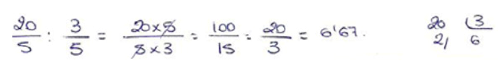 “You can give cake to 6 children and the part of the cake left is 2/5” |
| Pre-Service Teacher’s Justification | Category |
|---|---|
| “The student applies and develops an appropriate strategy to this problem, and arrives at the right answer” | Validity of the method |
| “This is a correct procedure, but it is not the best one. If the student had larger numbers the procedure would not work” | Validity-generalizability of the method |
| “The procedure used to solve the problem (a drawing) clearly shows that the student understands the problem and knows how to solve it. With this procedure we can clearly see the 2/5 of the cake” | Validity/clarity of the method |
| Procedure | Correct | Almost Correct | Incorrect | Total |
|---|---|---|---|---|
| Natural numbers | 11.9 | 8.3 | 0.0 | 20.2 |
| Measurement | 27.4 | 2.4 | 14.3 | 44.1 |
| Fractions | 15.5 | 4.8 | 7.1 | 27.4 |
| Others | 0.0 | 1.2 | 7.1 | 8.3 |
| Total | 54.8 | 16.7 | 28.5 |
| Pre-Service Teachers’ Answers Task 1 | Pre-Service Teachers’ Scores Questionnaire 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Answer A (Incorrect-Measurement) | Answer B (Incorrect-Use of Fractions without Interpretation of Remainder) | Answer C (Incorrect-Use of Fractions with Two Errors) | Answer D (Correct-Measurement) | |||||||||
| 0 | 0.5 | 1 | 0 | 0.5 | 1 | 0 | 0.5 | 1 | 0 | 0.5 | 1 | |
| Correct (45; 54.9%) * | 14.6 | 36.6 | 3.7 | 8.6 | 35.4 | 10.9 | 8.6 | 10.9 | 35.4 | 2.5 | 4.8 | 47.6 |
| Almost Correct (14; 17%) | 2.4 | 14.6 | 0 | 4.8 | 8.5 | 3.7 | 2.4 | 2.4 | 12.2 | 0 | 3.6 | 13.4 |
| Incorrect (23; 28.1%) | 9.8 | 18.3 | 0 | 0 | 24.4 | 3.7 | 2.4 | 4.8 | 20.9 | 0 | 1.2 | 26.9 |
| Total (82 **, 100%) | 26.8 | 69.5 | 3.7 | 13.4 | 68.3 | 18.3 | 13.4 | 18.1 | 68.5 | 2.5 | 9.6 | 87.9 |
| Answer A | Answer B | Answer C | Answer D | Total | |
|---|---|---|---|---|---|
| Validity | 73.8 | 79.8 | 76.2 | 55.9 | 71.4 |
| Validity/generalizability | 7.2 | 0.0 | 2.4 | 17.8 | 6.9 |
| Validity/clarity | 1.2 | 2.4 | 3.6 | 16.7 | 6.0 |
| Other | 17.8 | 17.8 | 17.8 | 9.6 | 15.7 |
| Type of Error | Answer A | Answer B | Answer C |
|---|---|---|---|
| Conceptual | 4.7 | 23.8 | 4.8 |
| Procedural | 32.5 | - | 7.2 |
| Conceptual/procedural | 0.0 | - | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Márquez, M.; Fernández, C.; Callejo, M.L. Pre-Service Primary School Teachers’ Knowledge and Their Interpretation of Students’ Answers to a Measurement Division Problem with Fractions. Mathematics 2021, 9, 3163. https://doi.org/10.3390/math9243163
Márquez M, Fernández C, Callejo ML. Pre-Service Primary School Teachers’ Knowledge and Their Interpretation of Students’ Answers to a Measurement Division Problem with Fractions. Mathematics. 2021; 9(24):3163. https://doi.org/10.3390/math9243163
Chicago/Turabian StyleMárquez, Maximina, Ceneida Fernández, and Maria Luz Callejo. 2021. "Pre-Service Primary School Teachers’ Knowledge and Their Interpretation of Students’ Answers to a Measurement Division Problem with Fractions" Mathematics 9, no. 24: 3163. https://doi.org/10.3390/math9243163
APA StyleMárquez, M., Fernández, C., & Callejo, M. L. (2021). Pre-Service Primary School Teachers’ Knowledge and Their Interpretation of Students’ Answers to a Measurement Division Problem with Fractions. Mathematics, 9(24), 3163. https://doi.org/10.3390/math9243163





