Physical and Mechanical Properties Evolution of Coal Subjected to Salty Solution and a Damage Constitutive Model under Uniaxial Compression
Abstract
:1. Introduction
2. Experimental Materials and Methods
2.1. Preparation of Coal Samples
2.2. Salt Solution
2.3. Experimental Procedure
3. Results and Discussion
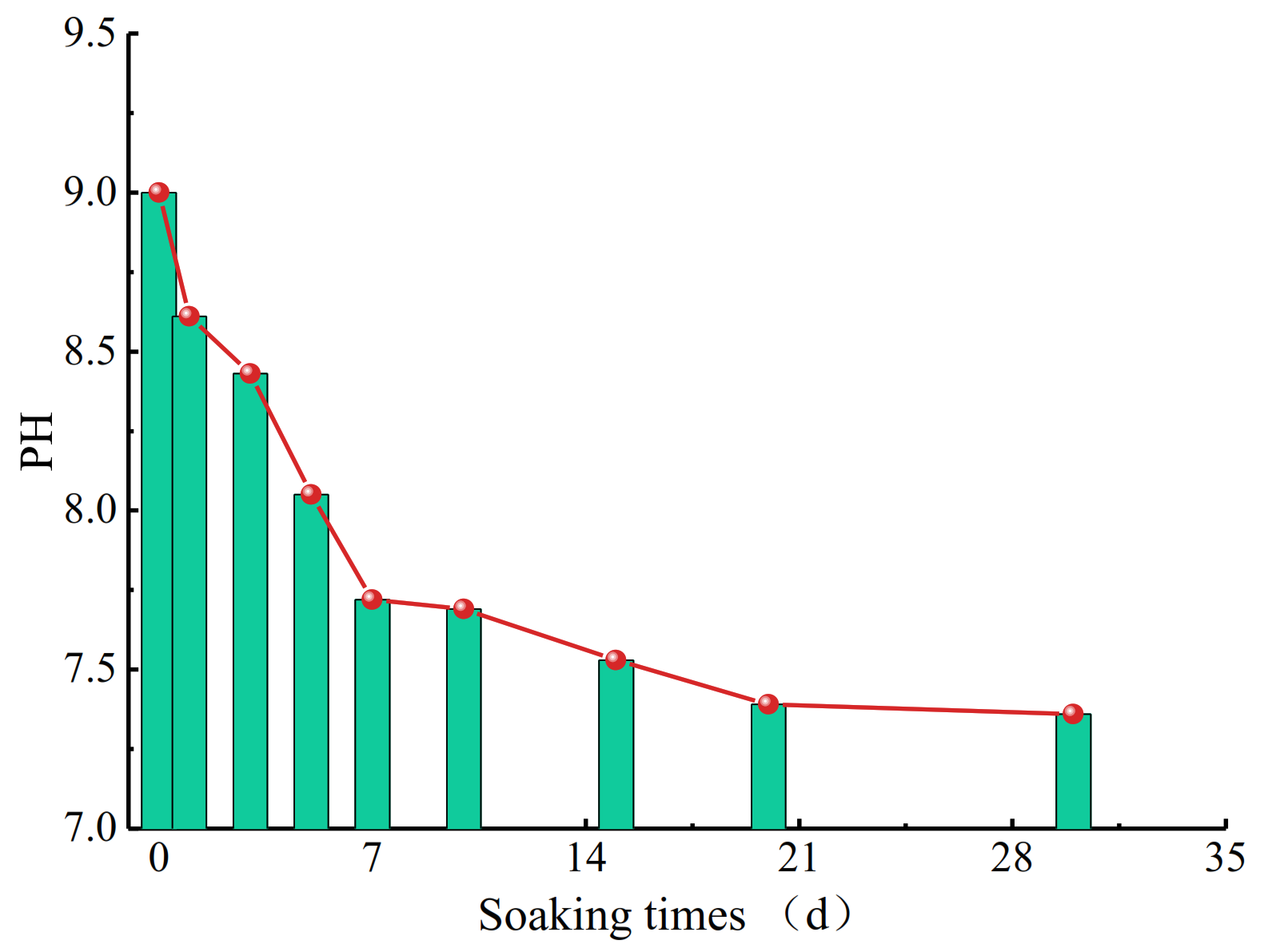
3.1. Changes in PH Values of Salt Solution
3.2. Variation Law of Longitudinal Wave Velocity of Coal Samples
3.3. Mass Changes of Coal Samples
3.4. Porosity of Coal Samples
3.5. Microscopic Morphological Characteristics of Coal Samples
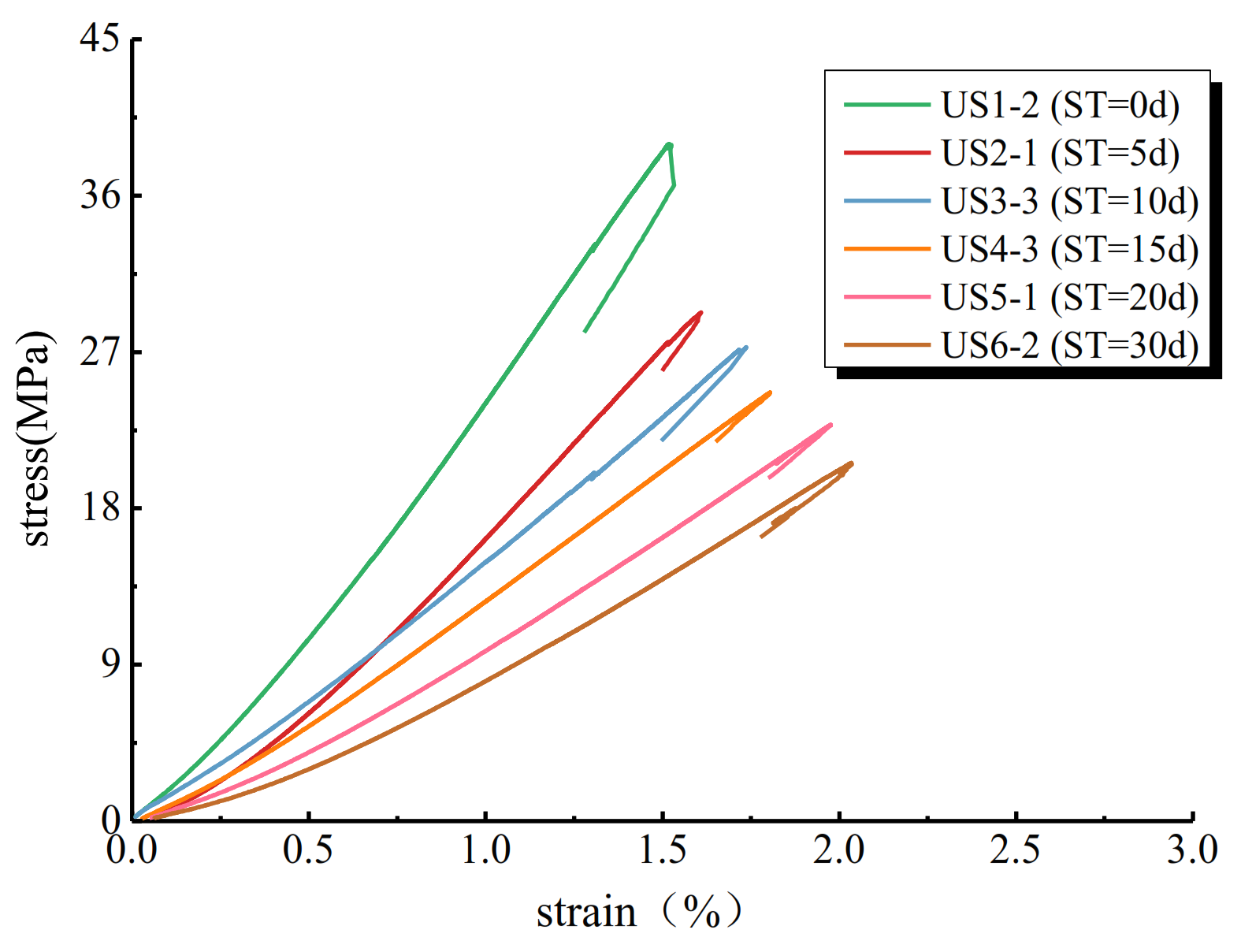
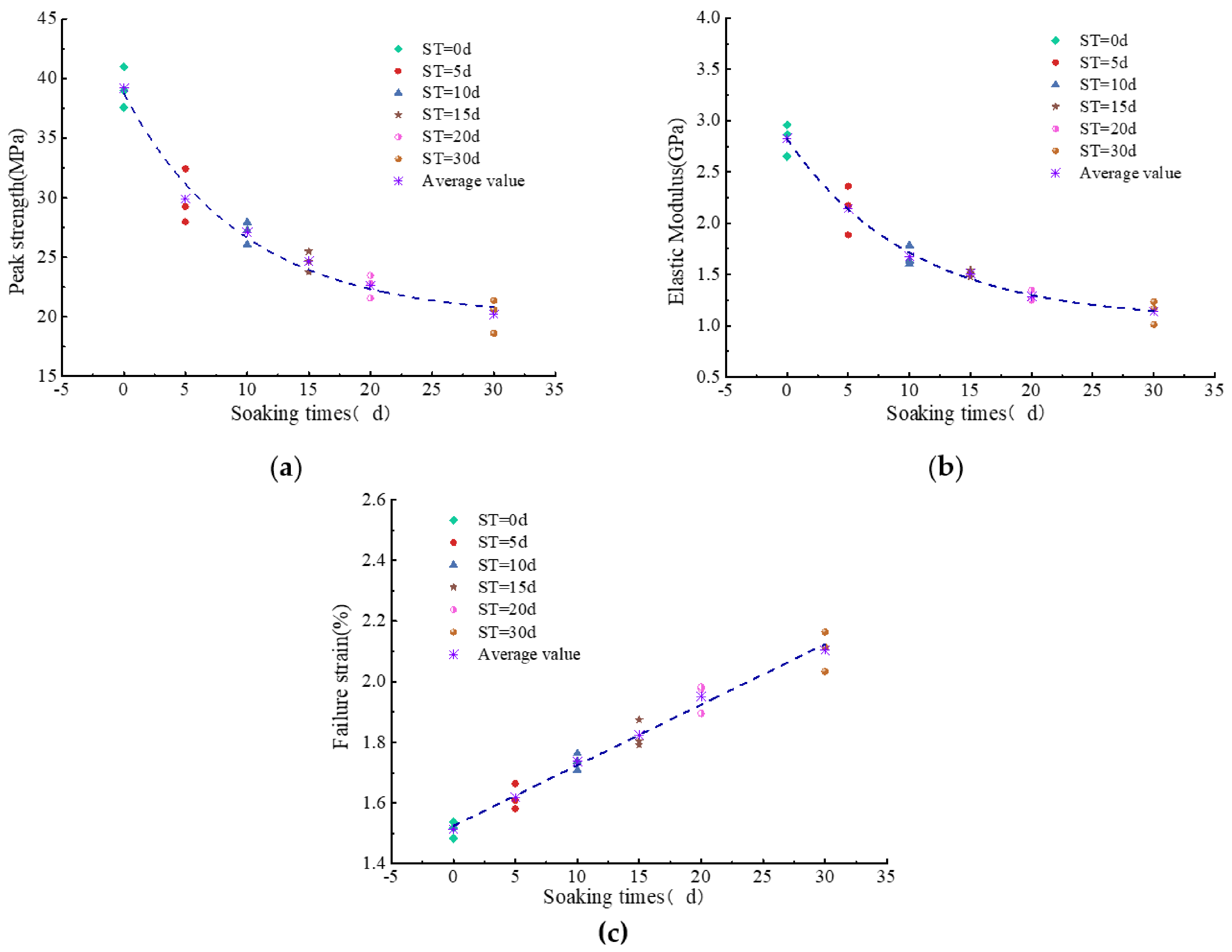
3.6. Mechanical Properties of Coal Samples
4. Statistical Damage Constitutive Relationship of Coal Samples under the Coupling Action of Salty Solution and Uniaxial Compression
4.1. Damage Constitutive Relationship and Damage Evolution Equation under Uniaxial Compression
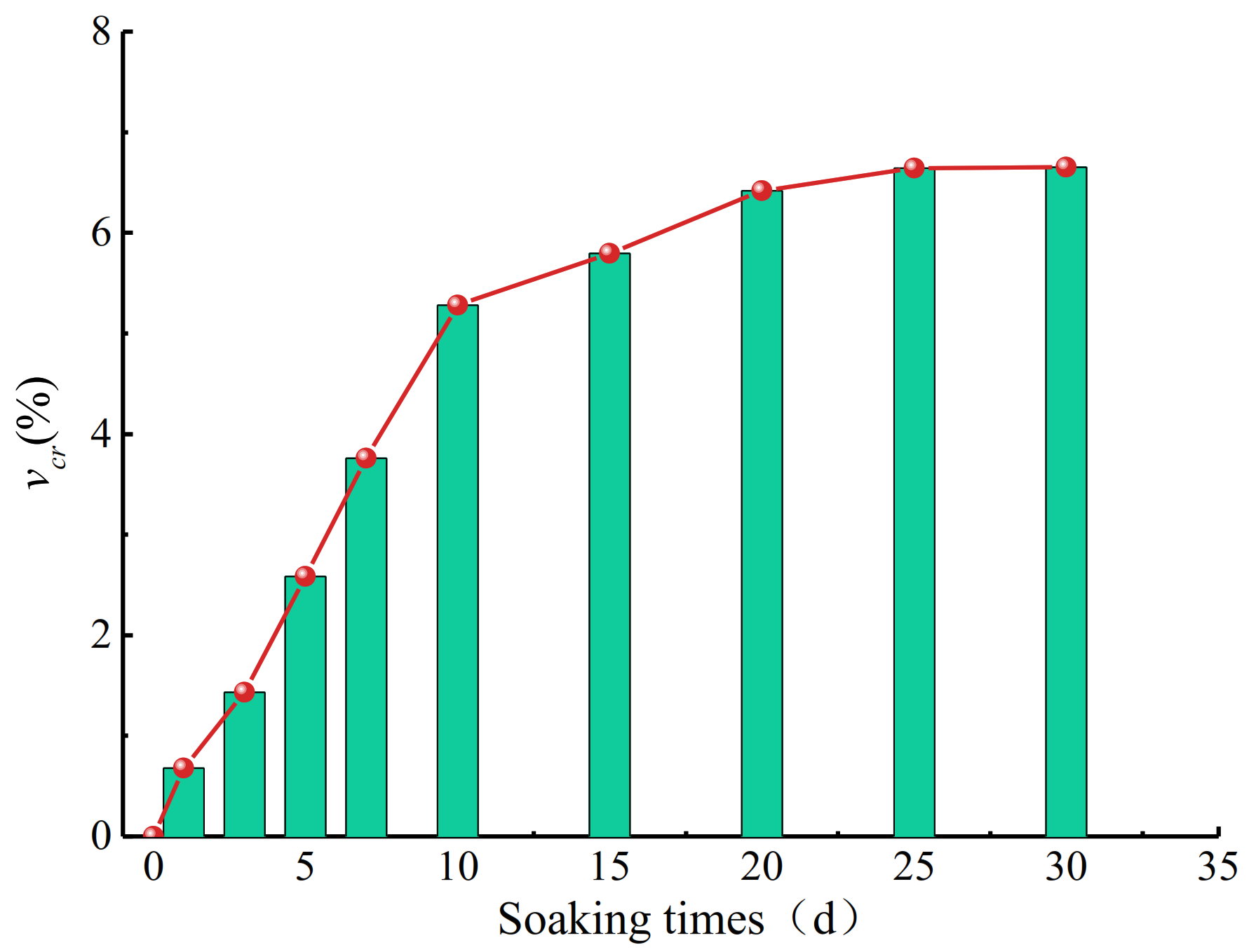
4.2. The Chemical Damage Variable under the Action of Salty Solution
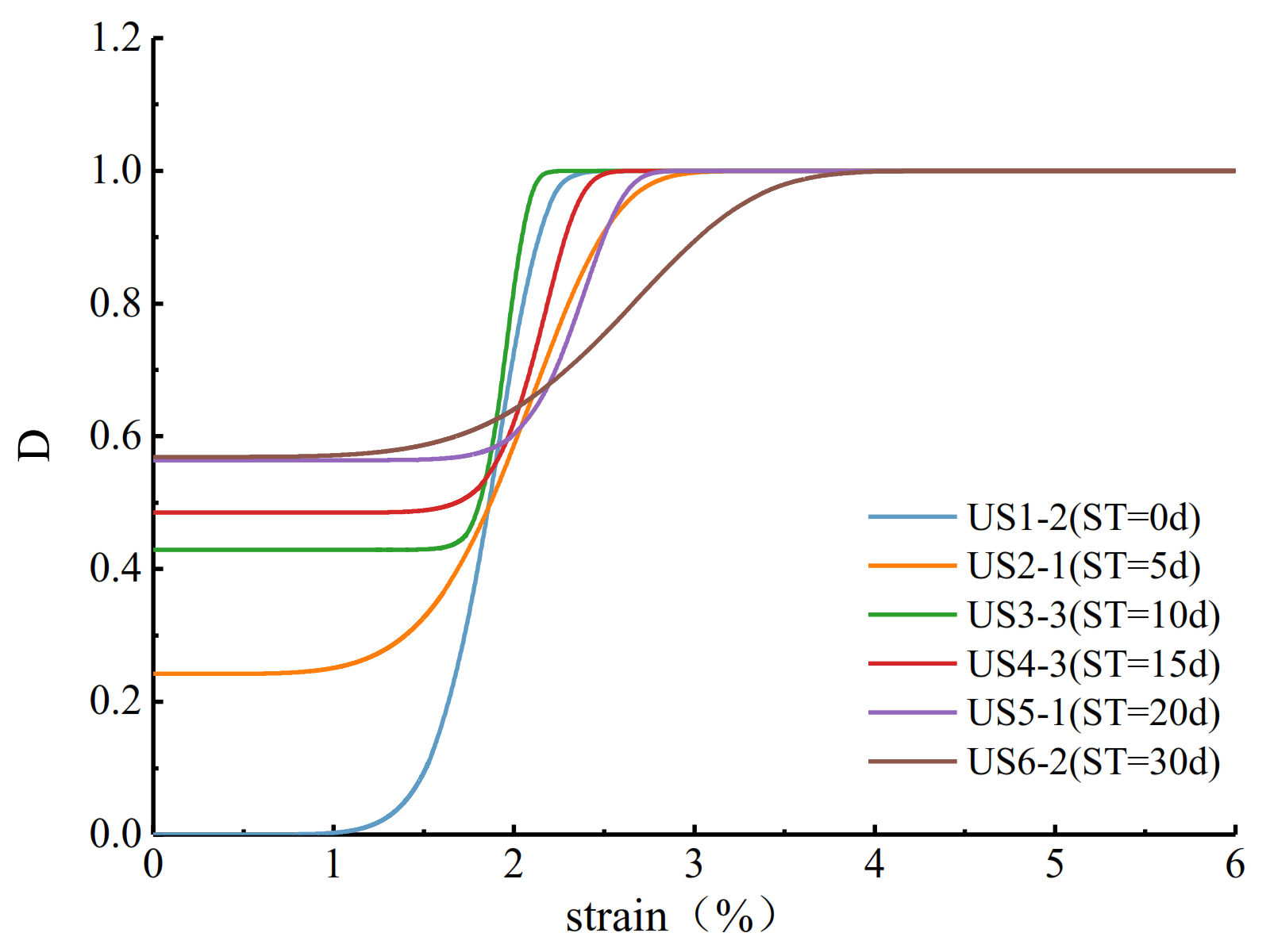
4.3. The Damage Evolution Law under the Coupling Action of Uniaxial Compression and Salty Solution Immersion
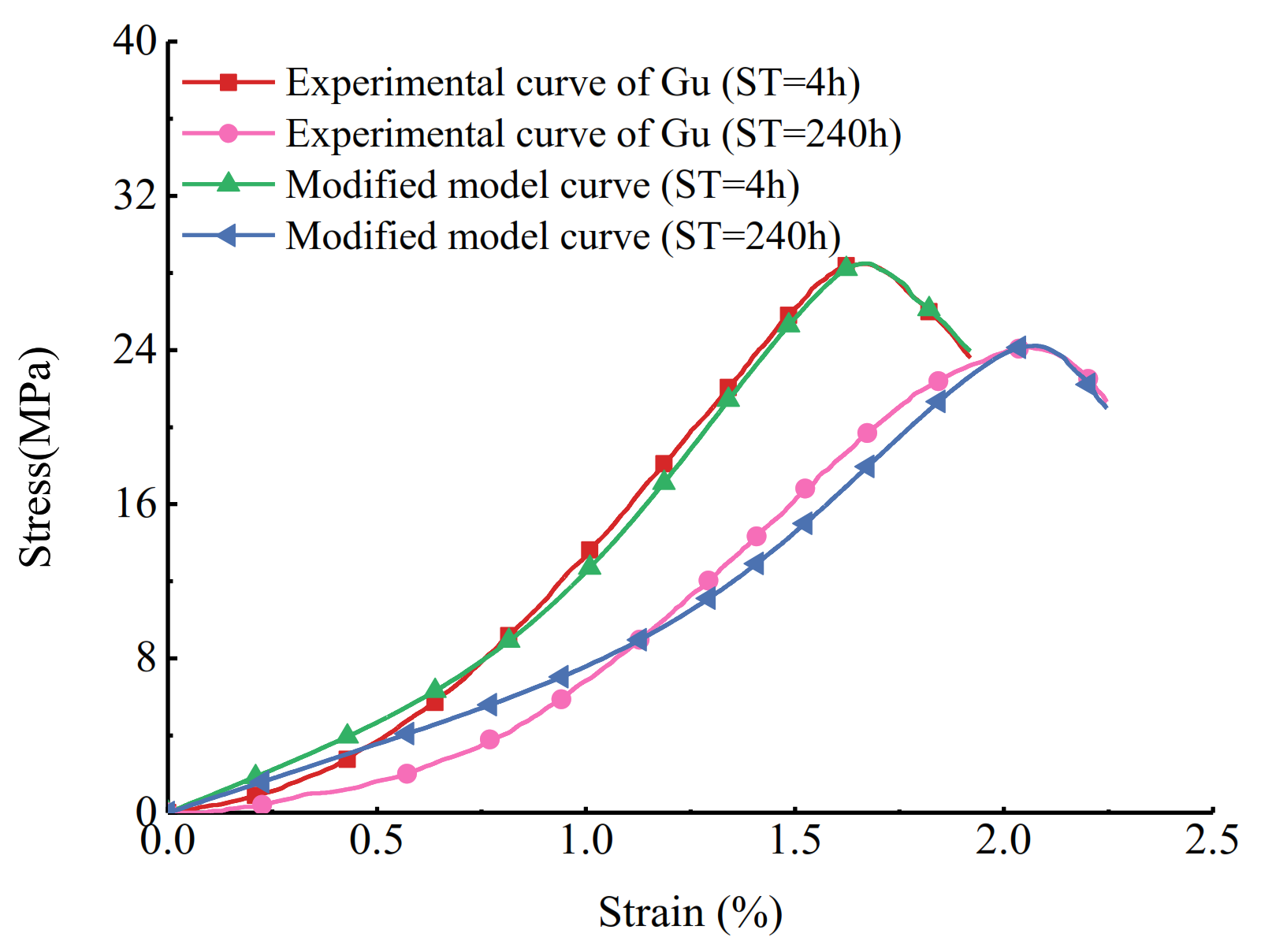
4.4. Damage Constitutive Model Considering Chemical-Stress Coupling Factor
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hamawand, I.; Yusaf, T.; Hamawand, S.G. Coal seam gas and associated water: A review paper. Renew. Sustain. Energy Rev. 2013, 22, 550–560. [Google Scholar] [CrossRef]
- Gu, D.Z.; Li, J.F.; Cao, Z.G.; Wu, B.Y.; Jiang, B.B.; Yang, Y.; Yang, J.; Chen, Y.P. Technology and engineering development strategy of water protection and utilization of coal mine in China. J. China Coal Soc. 2021, 46, 3079–3089. (In Chinese) [Google Scholar]
- Xu, H.; Lai, X.; Zhang, S.; Zhang, Y.; Shan, P.; Zhang, X.; Liu, B.; Wan, P. Multiscale Intelligent Inversion of Water-Conducting Fractured Zone in Coal Mine Based on Elastic Modulus Calibration Rate Response and Its Application: A Case Study of Ningdong Mining Area. Lithosphere 2021, 2021. [Google Scholar] [CrossRef]
- Gu, D.Z. Theory framework and technological system of coal mine underground reservoir. J. China Coal Soc. 2015, 40, 239–246. (In Chinese) [Google Scholar]
- Dyke, C.; Dobereiner, L. Evaluating the Strength and Deformability of Sandstones; Geological Society of London: London, UK, 1991. [Google Scholar]
- Hawkins, A.B.; McConnell, B.J. Sensitivity of sandstone strength and deformability to changes in moisture content. Q. J. Eng. Geol. Hydrogeol. 1992, 25, 115–130. [Google Scholar] [CrossRef]
- Vasarhelyi, B. Statistical Analysis of the Influence of Water Content on the Strength of the Miocene Limestone. Rock Mech. Rock Eng. 2004, 38, 69–76. [Google Scholar] [CrossRef]
- Erguler, Z.; Ulusay, R. Water-induced variations in mechanical properties of clay-bearing rocks. Int. J. Rock Mech. Min. Sci. 2008, 46, 355–370. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, S.; Jiang, Y.; Wang, K.; Huang, Y. Dynamic Tensile Strength of Coal under Dry and Saturated Conditions. Rock Mech. Rock Eng. 2015, 49, 1709–1720. [Google Scholar] [CrossRef]
- Gu, H.; Tao, M.; Li, X.; Li, Q.; Cao, W.; Wang, F. Dynamic response and failure mechanism of fractured coal under different soaking times. Theor. Appl. Fract. Mech. 2018, 98, 112–122. [Google Scholar] [CrossRef]
- Gu, H.; Tao, M.; Li, X.; Cao, W.; Li, Q. Dynamic tests and mechanical model for water-saturated soft coal with various particle gradations. Int. J. Rock Mech. Min. Sci. 2020, 132, 104386. [Google Scholar] [CrossRef]
- Karfakis, M.G.; Akram, M. Effects of chemical solutions on rock fracturing. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 1253–1259. [Google Scholar] [CrossRef]
- Feucht, L.; Logan, J.M. Effects of chemically active solutions on shearing behavior of a sandstone. Tectonophysics 1990, 175, 159–176. [Google Scholar] [CrossRef]
- Feng, X.; Ding, W.X. Coupled chemical stress processes in rock fracturing. Mater. Res. Innov. 2011, 15, s547–s550. [Google Scholar] [CrossRef]
- Feng, X.-T.; Chen, S.; Zhou, H. Real-time computerized tomography (CT) experiments on sandstone damage evolution during triaxial compression with chemical corrosion. Int. J. Rock Mech. Min. Sci. 2004, 41, 181–192. [Google Scholar] [CrossRef]
- Feng, X.-T.; Ding, W. Experimental study of limestone micro-fracturing under a coupled stress, fluid flow and changing chemical environment. Int. J. Rock Mech. Min. Sci. 2007, 44, 437–448. [Google Scholar] [CrossRef]
- Han, T.; Wang, X.; Li, Z.; Li, D.; Xing, F.; Han, N. Laboratory investigation of the mode-I fracture of sandstone caused by a combination of freeze-thaw cycles and chemical solutions. Bull. Int. Assoc. Eng. Geol. 2020, 79, 3689–3706. [Google Scholar] [CrossRef]
- Hutchinson, A.; Johnson, J.; Thompson, G.; Wood, G.; Sage, P.; Cooke, M. Stone degradation due to wet deposition of pollutants. Corros. Sci. 1993, 34, 1881–1898. [Google Scholar] [CrossRef]
- Qiao, L.; Wang, Z.; Huang, A. Alteration of Mesoscopic Properties and Mechanical Behavior of Sandstone Due to Hydro-Physical and Hydro-Chemical Effects. Rock Mech. Rock Eng. 2016, 50, 255–267. [Google Scholar] [CrossRef]
- Lin, Y.; Gao, F.; Zhou, K.; Gao, R.; Guo, H. Mechanical Properties and Statistical Damage Constitutive Model of Rock under a Coupled Chemical-Mechanical Condition. Geofluids 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Xie, S.; Shao, J.; Xu, W. Influences of chemical degradation on mechanical behaviour of a limestone. Int. J. Rock Mech. Min. Sci. 2011, 48, 741–747. [Google Scholar] [CrossRef]
- Li, H.; Zhong, Z.; Liu, X.; Sheng, Y.; Yang, D. Micro-damage evolution and macro-mechanical property degradation of limestone due to chemical effects. Int. J. Rock Mech. Min. Sci. 2018, 110, 257–265. [Google Scholar] [CrossRef] [Green Version]
- Ozdemir, O.; Taran, E.; Hampton, M.; Karakashev, S.; Nguyen, A. Surface chemistry aspects of coal flotation in bore water. Int. J. Miner. Process. 2009, 92, 177–183. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Zhu, J.; Yang, F.; He, H.; Qin, Z.; Shi, Q.; Pan, G. Experimental and emulational study on the role of ion in coal adsorbing kerosene: Water–kerosene interface and catenoid characteristics. Fuel 2021, 294, 120540. [Google Scholar] [CrossRef]
- Guanhua, N.; Qian, S.; Meng, X.; Hui, W.; Yuhang, X.; Weimin, C.; Gang, W. Effect of NaCl-SDS compound solution on the wettability and functional groups of coal. Fuel 2019, 257, 116077. [Google Scholar] [CrossRef]
- ISRM. SM for Determining the Uniaxial Compressive Strength and Deformability of Rock Materials; ISRM Lisbon: Lisbon, Portugal, 1979; pp. 137–140. [Google Scholar]
- Huang, Y.-H.; Yang, S.-Q.; Hall, M.R.; Zhang, Y.-C. The Effects of NaCl Concentration and Confining Pressure on Mechanical and Acoustic Behaviors of Brine-Saturated Sandstone. Energies 2018, 11, 385. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.; Frühwirt, T.; Konietzky, H. Inhomogeneous mechanical behaviour of concrete subjected to monotonic and cyclic loading. Int. J. Fatigue 2019, 132, 105383. [Google Scholar] [CrossRef]
- Zheng, H.; Feng, X.-T.; Pan, P.-Z. Experimental investigation of sandstone properties under CO2–NaCl solution-rock interactions. Int. J. Greenh. Gas Control. 2015, 37, 451–470. [Google Scholar] [CrossRef]
- Song, Z.; Wang, Y.; Konietzky, H.; Cai, X. Mechanical behavior of marble exposed to freeze-thaw-fatigue loading. Int. J. Rock Mech. Min. Sci. 2021, 138, 104648. [Google Scholar] [CrossRef]
- Wang, S.; Tang, Y.; Wang, S. Influence of brittleness and confining stress on rock cuttability based on rock indentation tests. J. Cent. South Univ. 2021, 2021. 28, 2786–2800. [Google Scholar] [CrossRef]
- Wang, S.; Sun, L.; Li, X.; Wang, S.; Du, K.; Li, X.; Feng, F. Experimental Investigation of Cuttability Improvement for Hard Rock Fragmentation Using Conical Cutter. Int. J. Geomech. 2021, 21, 06020039. [Google Scholar] [CrossRef]
- Xu, J.; Zhai, C.; Liu, S.; Qin, L.; Wu, S. Pore variation of three different metamorphic coals by multiple freezing-thawing cycles of liquid CO2 injection for coalbed methane recovery. Fuel 2017, 208, 41–51. [Google Scholar] [CrossRef]
- Zhang, Z.; Weller, A. Fractal dimension of pore-space geometry of an Eocene sandstone formation. Geophysics 2014, 79, D377–D387. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, D.; Cai, Y.; Yao, Y. Fractal characterization of pore–fracture in low-rank coals using a low-field NMR relaxation method. Fuel 2016, 181, 218–226. [Google Scholar] [CrossRef]
- Chen, S.; Tang, D.; Tao, S.; Ji, X.; Xu, H. Fractal analysis of the dynamic variation in pore-fracture systems under the action of stress using a low-field NMR relaxation method: An experimental study of coals from western Guizhou in China. J. Pet. Sci. Eng. 2018, 173, 617–629. [Google Scholar] [CrossRef]
- Hongchao, X.; Guanhua, N.; Shang, L.; Qian, S.; Kai, D.; Jingna, X.; Gang, W.; Yixin, L. The influence of surfactant on pore fractal characteristics of composite acidized coal. Fuel 2019, 253, 741–753. [Google Scholar] [CrossRef]
- Lemaître, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. Trans. ASME 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Lemaitre, J. A Course on Damage Mechanics; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar]
- Song, Z.; Konietzky, H.; Herbst, M. Bonded-particle model-based simulation of artificial rock subjected to cyclic loading. Acta Geotech. 2018, 14, 955–971. [Google Scholar] [CrossRef]
- Tang, C.A. Catastrophe in the Process of Rock Rupture.; China Coal Industry Publishing House: Beijing, China, 1993. (In Chinese) [Google Scholar]
- Zhang, Z.Z.; Gao, F.; Xu, X.L. Experimental study of temperature effect of mechanical properties of granite. Rock Soil Mech. 2011, 32, 2346–2352. (In Chinese) [Google Scholar]








| PH | TDS | K+ | Na+ | Ca2+ | Cl− | SO42− |
|---|---|---|---|---|---|---|
| mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | |
| 8.79 | 4720 | 10.7 | 1350 | 86 | 1230 | 1145 |
| Soaking Times/d | P-1 | P-2 | P-3 | |||
|---|---|---|---|---|---|---|
| Mass/g | vp/km·s−1 | Mass/g | vp/km·s−1 | Mass/g | vp/km·s−1 | |
| 0 | 257.79 | 1.83 | 255.32 | 1.76 | 253.07 | 1.80 |
| 0.25 | 261.15 | - | 258.85 | - | 256.12 | - |
| 0.5 | 265.33 | - | 263.13 | - | 261.18 | - |
| 1 | 270.91 | 1.82 | 268.24 | 1.75 | 265.86 | 1.79 |
| 3 | 269.92 | 1.80 | 267.06 | 1.73 | 264.99 | 1.77 |
| 5 | 269.54 | 1.79 | 267.30 | 1.71 | 264.44 | 1.76 |
| 7 | 269.04 | 1.76 | 266.50 | 1.69 | 264.49 | 1.73 |
| 10 | 268.40 | 1.73 | 265.71 | 1.67 | 263.32 | 1.71 |
| 15 | 268.02 | 1.73 | 265.73 | 1.66 | 262.73 | 1.70 |
| 20 | 266.85 | 1.72 | 264.47 | 1.65 | 262.04 | 1.69 |
| 25 | 266.80 | 1.71 | 264.28 | 1.64 | 262.00 | 1.68 |
| 30 | 266.77 | 1.71 | 264.26 | 1.64 | 262.02 | 1.68 |
| Soaking Times/d | Porosity/% | Adsorption Pores | Seepage Pores | Fractures |
|---|---|---|---|---|
| 0 | 21.28 | 9809 | 2570 | 213 |
| 3 | 21.91 | 9819 | 2765 | 354 |
| 5 | 22.96 | 10,041 | 2983 | 517 |
| 10 | 23.66 | 10,062 | 3172 | 688 |
| 15 | 24.88 | 10,385 | 3749 | 710 |
| 20 | 25.25 | 10,208 | 3982 | 807 |
| 30 | 25.58 | 9915 | 4210 | 1026 |
| Sample No. | Soaking Time (d) | Peak Strength (MPa) | Elastic Modulus (GPa) | Failure Strain (%) |
|---|---|---|---|---|
| US1-1 | 0 | 40.980 | 2.957 | 1.483 |
| US1-2 | 0 | 38.974 | 2.865 | 1.519 |
| US1-3 | 0 | 37.584 | 2.651 | 1.538 |
| US2-1 | 5 | 29.269 | 2.172 | 1.609 |
| US2-2 | 5 | 32.427 | 2.361 | 1.581 |
| US2-3 | 5 | 27.985 | 1.886 | 1.664 |
| US3-1 | 10 | 26.087 | 1.785 | 1.763 |
| US3-2 | 10 | 27.953 | 1.603 | 1.709 |
| US3-3 | 10 | 27.266 | 1.636 | 1.737 |
| US4-1 | 15 | 23.758 | 1.508 | 1.874 |
| US4-2 | 15 | 25.481 | 1.545 | 1.792 |
| US4-3 | 15 | 24.663 | 1.475 | 1.804 |
| US5-1 | 20 | 22.806 | 1.250 | 1.976 |
| US5-2 | 20 | 23.469 | 1.347 | 1.895 |
| US5-3 | 20 | 21.568 | 1.257 | 1.983 |
| US6-1 | 30 | 21.357 | 1.166 | 2.113 |
| US6-2 | 30 | 20.605 | 1.235 | 2.034 |
| US6-3 | 30 | 18.624 | 1.013 | 2.164 |
| Sample | εc/10−2 | A/10−2 | w/10−2 | μ0 | Correlation Coefficient |
|---|---|---|---|---|---|
| US2-1 | 1.609 | 0.28 | 0.56 | 0.60 | 0.93 |
| US2-2 | 1.581 | 0.26 | 0.46 | 0.55 | 0.95 |
| US2-3 | 1.664 | 0.28 | 0.55 | 0.59 | 0.96 |
| US3-1 | 1.763 | 0.51 | 0.81 | 0.50 | 0.94 |
| US3-2 | 1.709 | 0.42 | 0.82 | 0.60 | 0.98 |
| US3-3 | 1.737 | 0.15 | 0.80 | 0.85 | 0.98 |
| US4-1 | 1.874 | 0.32 | 0.78 | 0.68 | 0.97 |
| US4-2 | 1.792 | 0.23 | 0.80 | 0.78 | 0.98 |
| US4-3 | 1.804 | 0.25 | 0.85 | 0.76 | 0.98 |
| US5-1 | 1.976 | 0.30 | 0.85 | 0.72 | 0.96 |
| US5-2 | 1.895 | 0.35 | 0.83 | 0.68 | 0.94 |
| US5-3 | 1.983 | 0.34 | 0.81 | 0.66 | 0.95 |
| US6-1 | 2.113 | 0.41 | 0.81 | 0.60 | 0.93 |
| US6-2 | 2.034 | 0.40 | 0.80 | 0.60 | 0.95 |
| US6-3 | 2.164 | 0.21 | 0.85 | 0.82 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Guo, Q.; Tian, Y.; Dai, B. Physical and Mechanical Properties Evolution of Coal Subjected to Salty Solution and a Damage Constitutive Model under Uniaxial Compression. Mathematics 2021, 9, 3264. https://doi.org/10.3390/math9243264
Wang M, Guo Q, Tian Y, Dai B. Physical and Mechanical Properties Evolution of Coal Subjected to Salty Solution and a Damage Constitutive Model under Uniaxial Compression. Mathematics. 2021; 9(24):3264. https://doi.org/10.3390/math9243264
Chicago/Turabian StyleWang, Min, Qifeng Guo, Yakun Tian, and Bing Dai. 2021. "Physical and Mechanical Properties Evolution of Coal Subjected to Salty Solution and a Damage Constitutive Model under Uniaxial Compression" Mathematics 9, no. 24: 3264. https://doi.org/10.3390/math9243264
APA StyleWang, M., Guo, Q., Tian, Y., & Dai, B. (2021). Physical and Mechanical Properties Evolution of Coal Subjected to Salty Solution and a Damage Constitutive Model under Uniaxial Compression. Mathematics, 9(24), 3264. https://doi.org/10.3390/math9243264






