Approximating the Density of Random Differential Equations with Weak Nonlinearities via Perturbation Techniques

Abstract

We combine the stochastic perturbation method with the maximum entropy principle to construct approximations of the first probability density function of the steady-state solution of a class of nonlinear oscillators subject to small perturbations in the nonlinear term and driven by a stochastic excitation. The nonlinearity depends both upon position and velocity, and the excitation is given by a stationary Gaussian stochastic process with certain additional properties. Furthermore, we approximate higher-order moments, the variance, and the correlation functions of the solution. The theoretical findings are illustrated via some numerical experiments that confirm that our approximations are reliable.

1. Introduction and Motivation

The analysis of stochastic perturbations in nonlinear dynamical systems is a hot topic in applied mathematics [1,2] with many applications in apparently different areas such as control [3], economy [4] and especially in dealing with nonlinear vibratory systems. The study of systems subject to vibrations is encountered, for example, in Physics (in the analysis of different types of oscillators) and in Engineering (in the analysis of road vehicles, response of structures to earthquakes’ excitations or to sea waves). The nature of vibrations in this type of systems is usually random because they are spawned by complex factors that are not known in a deterministic manner but statistically characterized via measurements that often contain errors and uncertainties. Although, oscillators in Physics and Engineering systems have been extensively studied in the deterministic case [5,6], and particularly, in the nonlinear case [7,8,9], due to the above-mentioned facts the stochastic analysis is more suitable since provides better understanding of their dynamics.

Many vibratory systems are governed by differential equations with small nonlinear terms of the following form,

$$\ddot{X}(t)+\beta \dot{X}(t)+{\omega }_0^2(X(t)+ϵg(X(t)))=Y(t),t>0.$$

(1)

Here, $X(t)$ denotes the position (usually of the angle w.r.t. an origin) of the oscillatory system at the time instant t, the parameter $\beta$ is given by $\beta ≔2\xi {\omega }_0$, being $\xi$ the damping constant and ${\omega }_0>0$ the undamped angular frequency, and finally, $ϵ$ is a small perturbation ($\left|ϵ\right|\ll 1$) affecting a nonlinear function of the position, $g(X(t))$. The expression $X(t)+ϵg(X(t))$ is referred to as the nonlinear restoring term. The right-hand side term, $Y(t)$, stands for an external source/forcing term (vibration) acting upon the system. In the setting of random vibration systems, $Y(t)$ is assumed to be a stochastic process, termed stochastic excitation, having certain characteristics that in the present study will be specified later.

Notice that the nonlinear restoring term in Equation (1) involves the parameter $ϵ$, which determines the magnitude of the nonlinear perturbation, whose shape is given by $g(X(t))$. When $ϵ=0$, Equation (1) describes a random linear oscillator. In [10], authors analyze this class of oscillators considering two cases for the stochastic source term $Y(t)$, first when is Gaussian and, secondly, when it can be represented via a Karhunen–Loève expansion. In the case that $ϵ\ne 0$, the inclusion of the nonlinear term makes more difficult (even simply impossible) to exactly solve Equation (1). An effective method to construct reliable approximations of Equation (1) in the case that $ϵ$ represents a small parameter is the perturbation technique [11,12,13,14,15]. In the stochastic setting, this method has been successfully applied to study different type of oscillators subject to random vibrations. After pioneer contributions by Crandall [16,17], the analysis of random vibration systems has attracted many researchers (see, for instance, in [15,18,19] for a full overview of this topic). In [20], approximations of quadratic and cubic nonlinear oscillators subject to white noise excitations are constructed by combining the Wiener–Hermite expansion and the homotopy perturbation technique. The aforementioned approximations correspond to the first statistical moments (mean and variance) because, as authors indicate in the introduction section, the computation of the probability density function (PDF) is usually very difficult to obtain. In [21], the authors extend the previous analysis to compute higher-order statistical moments of the oscillator response in the case the nonlinearity is only quadratic. The previous methodology is extended and algorithmically automated in [22]. In [23], the author considers the interesting scenario of an harmonic oscillator with a random mass and analyses important dynamic characteristics such as the stochastic stability and the resonance phenomena. To conduct that study, a new type of Brownian motion is introduced. The perturbation technique has also been used to approximate the first moments, mainly the mean and the variance, of some oscillators subject to small nonlinearities. The computational procedures of this method often requires amendments to the existing solution codes, so it is classified as an intrusive method. A spectral technique that allows overcoming this drawback is non-intrusive polynomial chaos expansion (PCE) in which simulations are used as black boxes and the calculation of chaos expansion coefficients for response metrics of interest is based on a set of simulation response evaluations. In the recent paper [24], authors design an interesting hybrid non-intrusive procedure that combine PCE with Chebyshev Surrogate Method to analyze a number of uncertain physical parameters and the corresponding transient responses of a rotating system.

Besides computing the first statistical moments of the response or performing a stability analysis of systems under stochastic vibrations, we must emphasize that the computation of the finite distribution (usually termed “fidis”) associated to the stationary solution, and particularly of the stationary PDF, is also a major goal in the realm of vibratory systems with uncertainties. Some interesting contributions in this regard include [25,26]. In [25], the authors first present a complete overview of methods and techniques available to determine the stationary PDF of nonlinear oscillators excited by random functions. Second, nonlinear stochastic oscilators excited by a combination of Gaussian and Poisson white noises are fully analyzed. The study is based on solving the forward generalized Kolmogorov partial differential equation (PDE) using the exponential-polynomial closure method. The theoretical analysis is accompanied with several illustrative examples. In the recent contribution [26], authors propose a new method to compute a closed-form solution of stationary PDF of single-degree-of-freedom vibro-impact systems under Gaussian white noise excitation. The density is obtained by solving the Fokker–Planck–Kolmogorov PDE using the iterative method of weighted residue combined with the concepts of the circulatory and potential probability flows. Apart from obtaining the density of the solutions, it is worth to pointing out that in some recent contributions one also determines the densities of key quantities, that belong to Reliability Theory, like the first-passage time for vibro-impact systems with randomly fluctuating restoring and damping terms (see [27] and references therein).

In this paper, we address the study of random cross-nonlinear oscillators subject to small perturbations affecting the nonlinear term, g, which depend on both the position, $X(t)$, and the velocity, $\dot{X}(t)$,

$$\ddot{X}(t)+2\zeta {\omega }_0\dot{X}(t)+ϵg(X(t),\dot{X}(t))+{\omega }_0^{2}X(t)=Y(t).$$

(2)

Here, the stochastic derivatives are understood in the mean square sense [28] (Chapter 4). In our subsequent analysis, we will consider the case that $g(X(t),\dot{X}(t))=X^2(t)\dot{X}(t)$ and the excitation $Y(t)$ is a mean square differentiable and stationary zero-mean Gaussian stochastic process whose correlation function, ${\Gamma }_{YY}(\tau )$, is known. On the other hand, assuming that $Y(t)$ is a stationary and Gaussian stochastic process is a rather intuitive concept, which has been extensively used in both theoretical and practical studies [29,30]. Stationarity means that the statistical properties of the process do not vary significantly over time/space. This feature is usually met in a number of modeling problems as the surface of the sea in both spatial and time coordinates, noise in time in electric circuits under steady-state operations, homogeneous impurities in engineering materials and media, for example [28] (Chapter 3).

Now, we list the main novelties of our contribution.

• We combine mean square calculus and the stochastic perturbation method to study a class of nonlinear oscillators whose nonlinear term, g, involves both position, $X(t)$, as velocity, $\dot{X}(t)$, specifically, we consider the case $g=g(X(t),\dot{X}(t))=X^2(t)\dot{X}(t)$. This corresponds to the most complicated case, usually termed cross-nonlinearity.
• The oscillator is subject to random excitations driven by a stochastic process, $Y(t)$, having the following properties: $Y(t)$ is mean square differentiable and stationary zero-mean Gaussian.
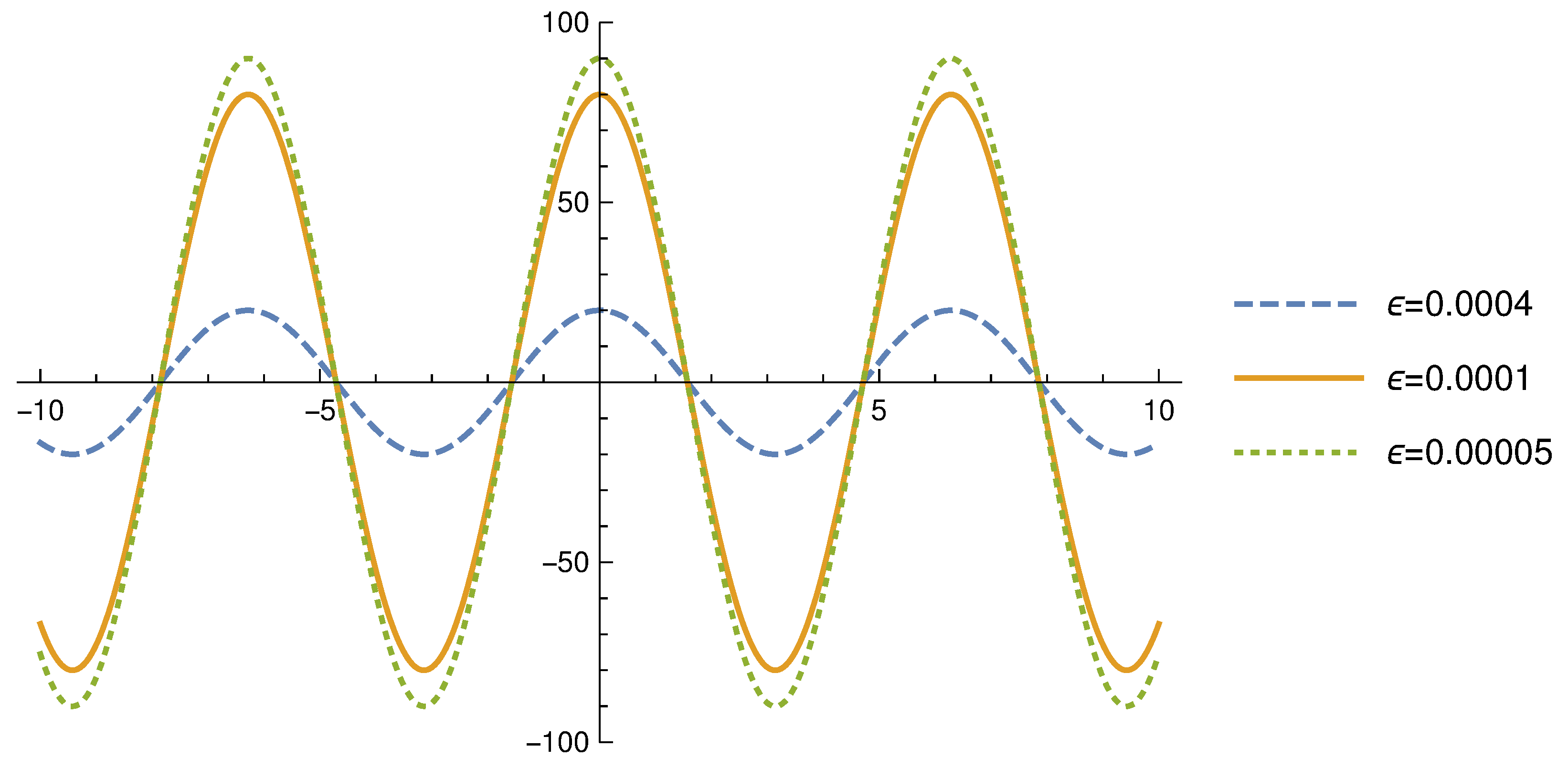
• We compute reliable approximations, not only of the mean, the variance, and the covariance (as is usually done), but also of higher moments (including the asymmetry and the kurtosis) of the steady-state of the above-described nonlinear oscillator.
• We combine the foregoing information related to higher moments and the entropy method to construct reliable approximations of the probability density function of the steady-state solution. The approximation is quite accurate as it is based on higher moments.

To the best of our knowledge, this is the first time that stochastic nonlinear oscillators with the above-described type of cross-nonlinearities is studied using our approach, i.e., combining mean square calculus and the stochastic perturbation method. In this sense, we think that our approach may be useful to extend our study to stochastic nonlinear oscillators having more general cross-nonlinearities, in particular of the form $g(X(t),\dot{X}(t))=X^n(t){\dot{X}}^m(t)$, for $n\ge 3$ and $m\ge 2$.

The paper is organized as follows. In Section 2, we introduce the auxiliary stochastic results that will be used throughout the whole paper. This section is intended to help the reader to better understand the technical aspects of the paper. Section 3 is divided into two parts. In Section 3.1, we apply the perturbation technique to construct a first-order approximation of the stationary solution stochastic process of model (2) with $g(X(t),\dot{X}(t))=X^2(t)\dot{X}(t)$. In Section 3.2, we determine expressions for the first higher-order moments, the variance, the covariance, and the correlation of the aforementioned first-order approximation. These expressions will be given in terms of certain integrals of the correlation function of the Gaussian noise, $Y(t)$, and of the classical impulse response function to the linearized oscillator associated to Equation (2). In Section 4, we take advantage of the results given in Section 3 to construct reliable approximations of the PDF of the stationary solution using the principle of maximum entropy. In Section 5, we illustrate all theoretical findings by means of several illustrative examples. Our numerical results are compared with Monte Carlo simulations and with the application of Euler–Maruyama numerical scheme, showing full agreement. Conclusions are drawn in Section 6.

2. Stochastic Preliminaries

For the sake of completeness, in this section we will introduce some technical stochastic results that will be required throughout the paper.

Hereinafter, we will work on a complete probability space $(\mathsf{\Omega },\mathcal{F},\mathbb{P})$, i.e., $\mathsf{\Omega }$ is a sample space; $\mathcal{F}$ is a $\sigma$-algebra of sets of $\mathsf{\Omega }$, usually called events; and $\mathbb{P}$ is a probability measure. To simplify, we will omit the sample notation, so the input and the solution stochastic processes involved in Equation (2) will be denoted by $Y(t)\equiv \{Y(t):t\ge 0\}$ and $X(t)\equiv \{X(t):t\ge 0\}$, respectively, rather than $\{Y(t;\omega ):t\ge 0,\omega \in \mathsf{\Omega }\}$ and $\{X(t;\omega ):t\ge 0,\omega \in \mathsf{\Omega }\}$, respectively.

The following result will be applied to calculate some higher-order moments of the solution stochastic process, $X(t)$, of the random differential Equation (2), since as it shall be seen later, $X(t)$ depends on a product of the stochastic excitation, $Y(t)$, evaluated at a finite number of instants, say $t_1,t_2,\dots ,t_n$, $Y(t_i)=Y_i$, $1\le i\le n$.

Proposition 1.

(p. 28, [28]). Let the random variables $Y_1,Y_2,\dots ,Y_n$ be jointly Gaussian with zero mean, $\mathbb{E}\left\{Y_i\right\}=0$, $1\le i\le n$. Then, all odd order moments of these random variables vanish and for n even,

$$\mathbb{E}\{Y_1{Y}_2\dots Y_n\}=\sum _{m_1,m_2,\dots ,m_n}\mathbb{E}\left\{Y_{m_1}{Y}_{m_2}\right\}\mathbb{E}\left\{Y_{m_3}{Y}_{m_4}\right\}\dots \mathbb{E}\left\{Y_{m_{n-1}}{Y}_{m_n}\right\}.$$

The sum above is taken over all possible combinations of $n/2$ pairs of n random variables. The number of terms in the summation is $1·3·5\dots (n-3)·(n-1)$.

The two following results permit interchange the expectation operator with the mean square derivative and the mean square integral. In [28] (Equation (4.130) in Section 4.4.2), the first result is established for $n=2$ and then it follows straightforwardly by induction.

Proposition 2.

Let $\{Y(t):t\ge 0\}$ be a mean square differentiable stochastic process. Then,

$$\mathbb{E}\{Y(t_1)\dots Y(t_{n-1})\dot{Y}(t_n)\}=\frac{\partial }{\partial t_n}(\mathbb{E}\{Y(t_1)\dots Y(t_n)\}),t_1,\dots ,t_n\ge 0,$$

provided the above expectations exists.

Proposition 3.

(p. 104, [28]). Let $\{Y(t):-\infty \le a\le t\le b\le +\infty \}$ be a second-order stochastic process integrable in the mean square sense and $h(t)$ a Riemann integrable deterministic function on $t\in (a,b)$. Then,

$$\mathbb{E}\left\{{\int }_a^{b}h(t)Y(t)\mathrm{d}t\right\}={\int }_a^{b}h(t)\mathbb{E}\left\{Y(t)\right\}\mathrm{d}t.$$

The following is a distinctive property of Gaussian processes since they preserve Gaussianity under mean square integration.

Proposition 4.

(p. 112, [28]). Let $\{Y(t):a\le t\le \infty \}$ be a Gaussian process and let $h(t)$ be a Riemann integrable deterministic function on $(a,t)$ such that the following mean square integral,

$$X(t)={\int }_a^{t}h(t,\tau )Y(\tau )\mathrm{d}\tau ,$$

exists, then $\{X(t):t\ge a\}$ is a Gaussian process.

3. Probabilistic Model Study

As it has been indicated in Section 1, in this paper we will study, from a probabilistic standpoint, the random cross-nonlinear oscillator

$$\ddot{X}(t)+2\zeta {\omega }_0\dot{X}(t)+ϵX^2(t)\dot{X}(t)+{\omega }_0^{2}X(t)=Y(t).$$

(3)

The analysis will be divided into two steps. First, in Section 3.1 we will apply the perturbation technique to obtain an approximation, $\widehat{X}(t)$, of the stationary solution stochastic process, $X(t)$. Then, in Section 3.2 we will take advantage of $\widehat{X}(t)$ to determine reliable approximations of the main statistical functions of $X(t)$, namely, the first higher-order moments, $\mathbb{E}\left\{X^n(t)\right\},n=1,\dots ,5$; the variance, $\mathbb{V}\left\{X(t)\right\}$; the covariance, $\mathbb{C}\mathrm{ov}\left\{X(t_1),X(t_2)\right\}$; and the correlation, ${\Gamma }_{XX}(\tau )$.

3.1. Perturbation Technique

Let us consider the Equation (3). The main idea of the stochastic perturbation technique is to consider that the solution $X(t)$ can be expanded in the powers of the small parameter $ϵ$ ($\left|ϵ\right|\ll 1$),

$$X(t)=X_0(t)+ϵX_1(t)+{ϵ}^2{X}_2(t)+\dots$$

(4)

Replacing expression (4) into Equation (3), yields the following sequence of linear differential equations, with random inputs

$$\begin{array}{c}\hfill \begin{array}{ccccc}{ϵ}^0\hfill & :& {\ddot{X}}_0(t)+2\zeta {\omega }_0{\dot{X}}_0(t)+{\omega }_0^2{X}_0(t)& =& Y(t),\\ {ϵ}^1\hfill & :& {\ddot{X}}_1(t)+2\zeta {\omega }_0{\dot{X}}_1(t)+{\omega }_0^2{X}_1(t)& =& -X_0^2(t){\dot{X}}_0(t),\\ {ϵ}^2\hfill & :& {\ddot{X}}_2(t)+2\zeta {\omega }_0{\dot{X}}_2(t)+{\omega }_0^2{X}_2(t)& =& -2X_0(t)X_1(t){\dot{X}}_0(t)-X_0^2(t){\dot{X}}_1,\\ ⋮\hfill & ⋮& ⋮& ⋮& ⋮\end{array}\end{array}$$

(5)

Notice that each equation can be solved in cascade. As usual, when applying the perturbation technique, we take the first-order approximation

$$\widehat{X}(t)=X_0(t)+ϵX_1(t).$$

(6)

This entails that in our subsequent development we will only need the two first equations listed in (5).

As indicated in Section 1, now we will focus on the analysis of the steady-state solution. Using the linear theory, the two first equations in (5) can be solved using the convolution integral [31]:

$$X_0(t)={\int }_0^{\infty }h(s)Y(t-s)\mathrm{d}s,$$

(7)

and

$$X_1(t)={\int }_0^{\infty }h(s)\left[-X_0^2(t-s){\dot{X}}_0(t-s)\right]\mathrm{d}s,$$

(8)

where

$$\begin{array}{c}\hfill h(t)=\left\{\begin{array}{cc}{\left({\omega }_0^2-{\zeta }^2{\omega }_0^2\right)}^{-\frac{1}{2}}{e}^{-\zeta {\omega }_{0}t}sin\left[{\left({\omega }_0^2-{\zeta }^2{\omega }_0^2\right)}^{\frac{1}{2}}t\right]\hfill & \mathrm{if}t>0,\hfill \\ 0\hfill & \mathrm{if}t\le 0,\hfill \end{array}\right.\end{array}$$

(9)

is the impulse response function for the underdamped case ${\zeta }^2<1$. This situation corresponds to the condition in which damping of an oscillator causes it to return to equilibrium with the amplitude gradually decreasing to zero (in our random setting it means that the expectation of the amplitude is null); system returns to equilibrium faster but overshoots and crosses the equilibrium position one or more times. Although, they are no treated hereinafter, two more situations are also possible, namely, critical damping and overdamping. The former corresponds to ${\zeta }^2=1$ and in that case the damping of an oscillator causes it to return as quickly as possible to its equilibrium position without oscillating back and forth about this position, while the latter corresponds to ${\zeta }^2>1$, and in this situation damping of an oscillator causes it to return to equilibrium without oscillating; oscillator moves more slowly toward equilibrium than in the critically damped system [32].

3.2. Approximation of the Main Statistical Moments

This subsection is devoted to calculate the main probabilistic information of the stationary solution stochastic process, $X(t)$, of model (3). As it has been previously pointed out, to this end, we assume that the input term $Y(t)$ is a stationary zero-mean ($\mathbb{E}\{Y(t)\}=0$) Gaussian stochastic process whose correlation function, ${\Gamma }_{YY}(\tau )$, is given. We will further assume that $Y(t)$ is mean square differentiable. This additional hypothesis will be apparent later. At this point, it is convenient to recall that for any stationary stochastic process its correlation function is even, so ${\Gamma }_{YY}(\tau )={\Gamma }_{YY}(-\tau )$, (p. 47, [28]). This property will be extensively applied throughout our subsequent developments.

To compute the mean of the approximation, we first take the expectation operator in (6),

$$\mathbb{E}\left\{\widehat{X}(t)\right\}=\mathbb{E}\left\{X_0(t)\right\}+ϵ\mathbb{E}\left\{X_1(t)\right\}.$$

(10)

Therefore, we now need to determine both $\mathbb{E}\left\{X_0(t)\right\}$ and $\mathbb{E}\left\{X_1(t)\right\}$. To compute the $\mathbb{E}\left\{X_0(t)\right\}$ we again use the expectation operator in (7),

$$\mathbb{E}\left\{X_0(t)\right\}=\mathbb{E}\left\{{\int }_0^{\infty }h(s)Y(t-s)\mathrm{d}s\right\}={\int }_0^{\infty }h(s)\mathbb{E}\left\{Y(t-s)\right\}\mathrm{d}s=0,$$

(11)

where we have applied Proposition 3 and that $\mathbb{E}\{Y(t)\}=0$.

Now, we deal with the computation of $\mathbb{E}\left\{X_1(t)\right\}$ in an analogous manner but using the representation of $X_1(t)$ given in (8),

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_1(t)\right\}& =\mathbb{E}\left\{{\int }_0^{\infty }h(s)\left[-X_0^2(t-s){\dot{X}}_0(t-s)\right]\mathrm{d}s\right\}={\int }_0^{\infty }h(s)\mathbb{E}\left\{\left[-X_0^2(t-s){\dot{X}}_0(t-s)\right]\right\}\mathrm{d}s\hfill \\ & =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3)\mathbb{E}\left\{Y(t-s-s_1)Y(t-s-s_2)\dot{Y}(t-s-s_3)\right\}{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s\hfill \\ & =0.\hfill \end{array}$$

(12)

Notice that the assumption of mean square differentiability of the input process $Y(t)$ appears naturally at this stage.

Let us justify the last step in expression (12). Let us denote $u_1=t-s-s_1$, $u_2=t-s-s_2$ and $u_3=t-s-s_3$, then applying Propositions 2 and 1, both with $n=3$, one gets

$$\begin{array}{cc}\hfill \mathbb{E}\left\{Y(t-s-s_1)Y(t-s-s_2)\dot{Y}(t-s-s_3)\right\}& =\mathbb{E}\left\{Y(u_1)Y(u_2)\dot{Y}(u_3)\right\}=\frac{\partial }{\partial u_3}\mathbb{E}\left\{Y(u_1)Y(u_2)Y(u_3)\right\}=0.\hfill \end{array}$$

Therefore, substituting (11) and (12) into (10), we obtain the expectation of the approximation is null,

$$\mathbb{E}\left\{\widehat{X}(t)\right\}=\mathbb{E}\left\{X_0(t)\right\}+ϵ\mathbb{E}\left\{X_1(t)\right\}=0.$$

(13)

From the approximation (6) and neglecting the term ${ϵ}^2$, the second-order moment for $\widehat{X}(t)$ is given by

$$\mathbb{E}\left\{{\widehat{X}}^2(t)\right\}=\mathbb{E}\left\{X_0^2(t)\right\}+2ϵ\mathbb{E}\left\{X_0(t)X_1(t)\right\}.$$

(14)

The first addend can be calculated using expression (7) and Fubini’s theorem,

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_0^2(t)\right\}& ={\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1)\mathbb{E}\left\{Y(t-s)Y(t-s_1)\right\}{\mathrm{d}s}_1\mathrm{d}s\hfill \\ \hfill & ={\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\Gamma }_{YY}(s-s_1){\mathrm{d}s}_1\mathrm{d}s.\hfill \end{array}$$

(15)

Notice that we have used that $Y(t)$ is a stationary process, so

$$\mathbb{E}\left\{Y(t-s)Y(t-s_1)\right\}={\Gamma }_{YY}(t-s_1-(t-s))={\Gamma }_{YY}(s-s_1).$$

Now, we calculate the second addend in (14). To this end, we substitute the expressions of $X_0(t)$ and $X_1(t)$ given in (7) and (8), respectively,

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_0(t)\right.& \left.X_1(t)\right\}={\int }_0^{\infty }h(s)\mathbb{E}\left\{X_0(t)[-X_0^2(t-s){\dot{X}}_0(t-s)]\right\}\mathrm{d}s\hfill \\ & ={\int }_0^{\infty }h(s)\mathbb{E}\left\{-{\int }_0^{\infty }h(s_1)Y(t-s_1){\mathrm{d}s}_1{\int }_0^{\infty }h(s_2)Y(t-s-s_2){\mathrm{d}s}_2{\int }_0^{\infty }h(s_3)Y(t-s-s_3){\mathrm{d}s}_3{\int }_0^{\infty }h(s_4)\dot{Y}(t-s-s_4){\mathrm{d}s}_4\right\}\mathrm{d}s\hfill \\ & =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)\mathbb{E}\left\{Y(t-s_1)Y(t-s-s_2)Y(t-s-s_3)\dot{Y}(t-s-s_4)\right\}{\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s\hfill \\ & \stackrel{(\mathrm{I})}{=}-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)({\Gamma }_{YY}(s_1-s-s_2){\Gamma }_{YY}^{\prime }(s_3-s_4)+{\Gamma }_{YY}(s_1-s-s_3){\Gamma }_{YY}^{\prime }(s_2-s_4)\hfill \\ & +{\Gamma }_{YY}^{\prime }(s_1-s-s_4){\Gamma }_{YY}(s_2-s_3)){\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s\hfill \\ & \stackrel{(\mathrm{II})}{=}-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)(2{\Gamma }_{YY}(s_1-s-s_2){\Gamma }_{YY}^{\prime }(s_3-s_4)\hfill \\ & +{\Gamma }_{YY}^{\prime }(s_1-s-s_4){\Gamma }_{YY}(s_2-s_3)){\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s.\hfill \end{array}$$

(16)

Observe that in the step (I) of the above expression, we have first applied Proposition 2 and second Proposition 1. Indeed, let us denote by $u_1=t-s_1$, $u_2=t-s-s_2$, $u_3=t-s-s_3$ and $u_4=t-s-s_4$, then by Proposition 2, with $n=4$, one gets

$$\mathbb{E}\left\{Y(t-s_1)Y(t-s-s_2)Y(t-s-s_3)\dot{Y}(t-s-s_4)\right\}=\frac{\partial }{\partial u_4}\mathbb{E}\left\{Y(u_1)Y(u_2)Y(u_3)Y(u_4)\right\},$$

and now we apply Proposition 1, with $n=4$, to the right-hand side. This yields

$$\begin{array}{cc}\hfill \mathbb{E}\{& Y(t-s_1)Y(t-s-s_2)Y(t-s-s_3)\dot{Y}(t-s-s_4)\}=\hfill \\ & =\frac{\partial }{\partial u_4}\left(\mathbb{E}\left\{Y(u_1)Y(u_2)\right\}\mathbb{E}\left\{Y(u_3)Y(u_4)\right\}+\mathbb{E}\left\{Y(u_1)Y(u_3)\right\}\mathbb{E}\left\{Y(u_2)Y(u_4)\right\}+\mathbb{E}\left\{Y(u_1)Y(u_4)\right\}\mathbb{E}\left\{Y(u_2)Y(u_3)\right\}\right)\hfill \\ & =\frac{\partial }{\partial u_4}\left({\Gamma }_{YY}(u_2-u_1){\Gamma }_{YY}(u_4-u_3)+{\Gamma }_{YY}(u_3-u_1){\Gamma }_{YY}(u_4-u_2)+{\Gamma }_{YY}(u_4-u_1){\Gamma }_{YY}(u_3-u_2)\right)\hfill \\ & ={\Gamma }_{YY}{(u)|}_{u=s_1-s-s_2}{\Gamma }_{YY}^{\prime }{(u)|}_{u=s_3-s_4}+{\Gamma }_{YY}{(u)|}_{u=s_1-s-s_3}{\Gamma }_{YY}^{\prime }{(u)|}_{u=s_2-s_4}+{\Gamma }_{YY}^{\prime }(u){{|}_{u=s_1-s-s_4}{\Gamma }_{YY}(u)|}_{u=s_2-s_3}.\hfill \end{array}$$

In step (II) of expression (16) we have taken advantage of the symmetry of the indexes.

Then, substituing (15) and (16) in (14) one gets

$$\begin{array}{cc}\hfill \mathbb{E}\left\{{\widehat{X}}^2(t)\right\}=& {\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\Gamma }_{YY}(s-s_1){\mathrm{d}s}_1\mathrm{d}s-2ϵ({\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)\hfill \\ & ·\left(2{\Gamma }_{YY}(s_1-s-s_2){\Gamma }_{YY}^{\prime }(s_3-s_4)+{\Gamma }_{YY}^{\prime }(s_1-s-s_4){\Gamma }_{YY}(s_2-s_3)\right){\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s).\hfill \end{array}$$

(17)

Notice that $\mathbb{E}\left\{{\widehat{X}}^2(t)\right\}$ does not depend on t. This is consistent with the fact that we are dealing with the stochastic analysis of the stationary solution. The same feature will hold when computing higher-order moments, $\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}$, $n>2$, later.

As $\mathbb{E}\left\{\widehat{X}(t)\right\}$ is null (see (13)), then the variance of the solution coincides with $\mathbb{E}\left\{{\widehat{X}}^2(t)\right\}$.

Now, we calculate the third-order moment of $\widehat{X}(t)$ keeping up to the first-order term of perturbation $ϵ$. Therefore,

$$\mathbb{E}\left\{{\widehat{X}}^3(t)\right\}=\mathbb{E}\left\{X_0^3(t)\right\}+3ϵ\mathbb{E}\left\{X_0^2(t)X_1(t)\right\}.$$

(18)

Reasoning analogously as we have shown before, we obtain

$$\mathbb{E}\left\{X_0^3(t)\right\}={\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2)\mathbb{E}\left\{Y(t-s)Y(t-s_1)Y(t-s_2)\right\}{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s=0,$$

(19)

where we have applied Proposition 1 in the last step.

The second addend in (18) is calculated using Propositions 1 and 2,

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_0^2(t)X_1(t)\right\}& ={\int }_0^{\infty }h(s)\mathbb{E}\left\{X_0^2(t)\left[-X_0^2(t-s){\dot{X}}_0(t-s)\right]\right\}\mathrm{d}s\hfill \\ & =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4){\int }_0^{\infty }h(s_5)\mathbb{E}\{Y(t-s)Y(t-s_1)Y(t-s-s_3)Y(t-s-s_4)\hfill \\ & ·\dot{Y}(t-s-s_5)\}{\mathrm{d}s}_5{\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s=0.\hfill \end{array}$$

(20)

From (19) and (20), we obtain

$$\mathbb{E}\left\{{\widehat{X}}^3(t)\right\}=\mathbb{E}\left\{X_0^3(t)\right\}+3ϵ\mathbb{E}\left\{X_0^2(t)X_1(t)\right\}=0.$$

Using again the first-order approximation of the perturbation $ϵ$, in general, it can be straightforwardly seen that

$$\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}=0,n=1,3,5,\dots .$$

(21)

Indeed, we know that,

$$\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}=\mathbb{E}\left\{X_0^n(t)\right\}+nϵ\mathbb{E}\left\{X_0^{n-1}(t)X_1(t)\right\}.$$

(22)

On the one hand, let us observe that applying first Fubini’s theorem and Proposition 3, and second Proposition 1 for n odd, one gets

$$\mathbb{E}\left\{X_0^n(t)\right\}=\mathbb{E}\left\{{\left({\int }_0^{\infty }h(s)Y(t-s)\mathrm{d}s\right)}^n\right\}={\int }_0^{\infty }h(s_1)\dots {\int }_0^{\infty }h(s_n)\mathbb{E}\{Y(t-s_1)\dots Y(t-s_n)\}{\mathrm{d}s}_n\dots {\mathrm{d}s}_1=0.$$

On the other hand, using the same reasoning as in (20),

$$\mathbb{E}\left\{X_0^{n-1}(t)X_1(t)\right\}={\int }_0^{\infty }h(s)\mathbb{E}\left\{X_0^{n-1}(t)\left[-X_0^2(t-s){\dot{X}}_0(t-s)\right]\right\}\mathrm{d}s=0,$$

where first we have applied Proposition 2, in order to put the first derivative out of the expectation, and second, we have utilized that $X_0^{n-1}(t)$, $X_0^2(t-s)$ and ${\dot{X}}_0(t-s)$ depend upon $n-1$, 2 and 1 terms of $Y(·)$, respectively, together with Proposition 1 (notice that $n+2$ is odd as n is odd).

To complete the information of statistical moments of the approximation, we also determine $\mathbb{E}\left\{{\widehat{X}}^4(t)\right\}$.

The fourth-order moment of $\widehat{X}(t)$, based on the first-order approximation via the perturbation method, is given by

$$\mathbb{E}\left\{{\widehat{X}}^4(t)\right\}=\mathbb{E}\left\{X_0^4(t)\right\}+4ϵ\mathbb{E}\left\{X_0^3(t)X_1(t)\right\}.$$

(23)

Reasoning analogously as we have shown in previous sections, we obtain for the first addend

$$\mathbb{E}\left\{X_0^4(t)\right\}=3{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\Gamma }_{YY}(s-s_1){\Gamma }_{YY}(s_2-s_3)\mathrm{d}s{\mathrm{d}s}_1{\mathrm{d}s}_2{\mathrm{d}s}_3,$$

(24)

and for the second addend

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_0^3(t)X_1(t)\right\}& =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4){\int }_0^{\infty }h(s_5){\int }_0^{\infty }h(s_6)\mathbb{E}\{Y(t-s_1)\hfill \\ & ·Y(t-s_2)Y(t-s_3)Y(t-s-s_4)Y(t-s-s_5)\dot{Y}(t-s-s_6)\}\mathrm{d}s{\mathrm{d}s}_1{\mathrm{d}s}_2{\mathrm{d}s}_3{\mathrm{d}s}_4{\mathrm{d}s}_5{\mathrm{d}s}_6\hfill \\ & =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4){\int }_0^{\infty }h(s_5){\int }_0^{\infty }h(s_6)(6{\Gamma }_{YY}^{\prime }(s_5-s_6)\hfill \\ & ·{\Gamma }_{YY}(s_1-s_2){\Gamma }_{YY}(s_3-s-s_4)+3{\Gamma }_{YY}^{\prime }(s_1-s-s_6)(2{\Gamma }_{YY}(s_2-s-s_4){\Gamma }_{YY}(s_3-s-s_5)\hfill \\ & +{\Gamma }_{YY}(s_2-s_3){\Gamma }_{YY}(s_4-s_5)))\mathrm{d}s{\mathrm{d}s}_1{\mathrm{d}s}_2{\mathrm{d}s}_3{\mathrm{d}s}_4{\mathrm{d}s}_5{\mathrm{d}s}_6.\hfill \end{array}$$

(25)

Observe that in the last step of the above expression, first we have used Proposition 2, and second, Proposition 1. From this last proposition, we know that exist 15 combinations, but we can reduce the expression by the symmetry of involved indexes.

Now we deal with the approximation of the correlation function of $X(t)$ via (6), i.e., taking the first-order approximation of the perturbation expansion,

$${\Gamma }_{\widehat{X}\widehat{X}}(\tau )=\mathbb{E}\left\{\widehat{X}(t)\widehat{X}(t+\tau )\right\}=\mathbb{E}\left\{X_0(t)X_0(t+\tau )\right\}+ϵ[\mathbb{E}\left\{X_0(t)X_1(t+\tau )\right\}+\mathbb{E}\left\{X_1(t)X_0(t+\tau )\right\}].$$

(26)

The first addend in (26) corresponds to the correlation function of $X_0(t)$. It can be expressed as

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_0(t)X_0(t+\tau )\right\}& ={\int }_0^{\infty }{\int }_0^{\infty }h(s)h(s_1)\mathbb{E}\left\{Y(t-s)Y(t+\tau -s_1)\right\}\mathrm{d}s{\mathrm{d}s}_1\hfill \\ & ={\int }_0^{\infty }{\int }_0^{\infty }h(s)h(s_1){\Gamma }_{YY}(\tau -s_1+s){\mathrm{d}s}_1\mathrm{d}s.\hfill \end{array}$$

The two last addends in (26) represent the cross-correlation of $X_0(t)$ and $X_1(t)$. They are given, respectively, by

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_0(t)X_1(t+\tau )\right\}& ={\int }_0^{\infty }h(s)\mathbb{E}\left\{X_0(t)[-X_0^2(t+\tau -s){\dot{X}}_0(t+\tau -s)]\right\}\mathrm{d}s\hfill \\ & =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)\{2{\Gamma }_{YY}(\tau -s-s_2+s_1){\Gamma }_{YY}^{\prime }(s_3-s_4)\hfill \\ & +{\Gamma }_{YY}^{\prime }(\tau -s-s_4+s_1){\Gamma }_{YY}(s_2-s_3)\}{\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s.\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathbb{E}\left\{X_1(t)X_0(t+\tau )\right\}& =\mathbb{E}\left\{{\int }_0^{\infty }-h(s)X_0^2(t-s){\dot{X}}_0(t-s)X_0(t+\tau )\right\}\mathrm{d}s\hfill \\ & =-{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)\{{\Gamma }_{YY}(s_1-s_2){\Gamma }_{YY}^{\prime }(\tau -s_4+s+s_3)\hfill \\ & +2{\Gamma }_{YY}^{\prime }(s_1-s_3){\Gamma }_{YY}(\tau -s_4+s+s_2)\}{\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s.\hfill \end{array}$$

Summarizing,

$$\begin{array}{cc}\hfill {\Gamma }_{\widehat{X}\widehat{X}}(\tau )& ={\int }_0^{\infty }{\int }_0^{\infty }h(s)h(s_1){\Gamma }_{YY}(\tau -s_1+s)\mathrm{d}s{\mathrm{d}s}_1\hfill \\ & -ϵ{\int }_0^{\infty }h(s){\int }_0^{\infty }h(s_1){\int }_0^{\infty }h(s_2){\int }_0^{\infty }h(s_3){\int }_0^{\infty }h(s_4)\{2{\Gamma }_{YY}(\tau -s-s_2+s_1){\Gamma }_{YY}^{\prime }(s_3-s_4)\hfill \\ & +{\Gamma }_{YY}^{\prime }(\tau -s-s_4+s_1){\Gamma }_{YY}(s_2-s_3)+{\Gamma }_{YY}(s_1-s_2){\Gamma }_{YY}^{\prime }(\tau -s_4+s+s_3)\hfill \\ & +2{\Gamma }_{YY}^{\prime }(s_1-s_3){\Gamma }_{YY}(\tau -s_4+s+s_2)\}{\mathrm{d}s}_4{\mathrm{d}s}_3{\mathrm{d}s}_2{\mathrm{d}s}_1\mathrm{d}s.\hfill \end{array}$$

(27)

As $\mathbb{E}\left\{\widehat{X}(t)\right\}=0$, we observe that the covariance and correlation functions of $\widehat{X}(t)$ coincide,

$$\mathbb{C}\mathrm{ov}\{\widehat{X}(t_1),\widehat{X}(t_2)\}={\Gamma }_{\widehat{X}\widehat{X}}(\tau ),\tau =|t_1-t_2|.$$

4. Approximating the PDF via the Maximum Entropy Principle

So far, we have calculated approximations of the moments $\mathbb{E}\left\{{\widehat{X}}^n(t)\right\},n=1,\dots ,5$ to the first-order approximation, $\widehat{X}(t)$, via the perturbation method, of the steady-state solution of the random nonlinear oscillator (3). Although this is an important information, a more ambitious goal is the approximation of the PDF, say $f_{\widehat{X}(t)}(x)$, as from it one can calculate key stochastic information as the probability that the output lies in a specific interval of interest, say $[a_1,a_2]$,

$$\mathbb{P}\left\{a_1\le \widehat{X}(t)\le a_2\right\}={\int }_{a_1}^{a_2}{f}_{\widehat{X}(t)}(x)\mathrm{d}x,$$

for any arbitrary fixed time t. Furthermore, from the knowledge of the PDF one can easily compute confidence intervals at a specific confidence level $\alpha \in (0,1)$,

$$1-\alpha =\mathbb{P}\left\{{\mu }_{\widehat{X}}(t)-k{\sigma }_{\widehat{X}}(t)\le \widehat{X}(t)\le {\mu }_{\widehat{X}}(t)+k{\sigma }_{\widehat{X}}(t)\right\}={\int }_{{\mu }_{\widehat{X}}(t)-k{\sigma }_{\widehat{X}}(t)}^{{\mu }_{\widehat{X}}(t)+k{\sigma }_{\widehat{X}}(t)}{f}_{\widehat{X}(t)}(x)\mathrm{d}x,$$

where ${\mu }_{\widehat{X}}(t)=\mathbb{E}\left\{\widehat{X}(t)\right\}=0$ (see (13)) and ${\sigma }_{\widehat{X}}(t)=\sqrt{\mathbb{V}\left\{\widehat{X}(t)\right\}}$. Usually $\alpha$ is taken as $\alpha =0.05$ so that $95\%$ confidence intervals are built, and $k>0$ must be determined numerically.

As we have calculated the approximations $\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}$, $n=1,\dots ,5,$ a suitable method to approximate the PDF, $f_{\widehat{X}(t)}(x)$, is the Principle of Maximum Entropy (PME), [33]. For t fixed, the PME seeks for a PDF, $f_{\widehat{X}(t)}(x)$, that maximizes the so-called Shannon’s Entropy, of random variable $\widehat{X}(t)$ with support $[a,b]$, defined via the following functional,

$$\mathcal{S}\left\{f_{\widehat{X}(t)}(x)\right\}=-{\int }_a^b{f}_{\widehat{X}(t)}(x)log(f_{\widehat{X}(t)}(x))\mathrm{d}x,$$

(28)

satisfying the following restrictions

$${\int }_a^b{f}_{\widehat{X}(t)}(x)\mathrm{d}x=1,$$

(29)

$$\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}={\int }_a^b{x}^n{f}_{\widehat{X}(t)}(x)\mathrm{d}x=m_n,n=1,\dots ,M.$$

(30)

Condition (29) guarantees $f_{\widehat{X}(t)}(x)$ is a PDF, and the M conditions given in (30) impose that the sampled moments, $m_n$, match the moments, $\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}$, obtained in our setting by the stochastic perturbation method. For each t fixed, the maximization of functional (28) subject to the constrains (29)–(30) can be solved via the auxiliary Lagrange function

$$\mathcal{L}\left\{f_{\widehat{X}(t)},{\lambda }_0,\dots ,{\lambda }_M\right\}=\mathcal{S}\left\{f_{\widehat{X}(t)}(x)\right\}+\sum _{i=0}^M{\lambda }_i\left[m_i-{\int }_a^b{x}^i{f}_{\widehat{X}(t)}(x)\mathrm{d}x\right],$$

where $m_0=1$. It can be seen that the form of the PDF is given by [33]

$$f_{\widehat{X}(t)}(x)={𝟙}_{[a,b]}{e}^{-{\sum }_{i=0}^M{\lambda }_i{x}^i},$$

where ${𝟙}_{[a,b]}$ denotes the characteristic function on the interval $[a,b]$.

In Section 3, we have approximated, via the stochastic perturbation technique, the moments $\mathbb{E}\left\{{\widehat{X}}^n(t)\right\}$ for $n=1,2,\dots ,5$. Therefore, to apply the PME we will take $M=5$ in (30). Notice that, in practice, to calculate the parameters ${\lambda }_i$, $i=0,1,\dots ,5$, we will need to numerically solve the system of nonlinear Equations (29) and (30).

5. Numerical Examples

This section is devoted to illustrate the theoretical findings obtained in previous sections. We take the following data for the parameters of the random nonlinear oscillator (3), $\zeta =0.05({\zeta }^2<1)$ and ${\omega }_0=1$.

Example 1.

Let us consider as input excitation the trigonometric stochastic process defined by $Y(t)={\xi }_{1}cos(t)+{\xi }_{2}sin(t)$, where ${\xi }_1,{\xi }_2\sim \mathrm{N}(0,1)$ are independent. Observe that $Y(t)$ satisfies the hypotheses, i.e., $\mathbb{E}\{Y(t)\}=0$, $Y(t)$ is Gaussian, mean square differentiable with respect to t, and stationary, with its correlation being ${\Gamma }_{YY}(t_1,t_2)=cos(t_1-t_2)$ or ${\Gamma }_{YY}(\tau )=cos(\tau )$. Substituting this data into Equation (3), we obtain

$$\ddot{X}(t)+0.1\dot{X}(t)+ϵX^2(t)\dot{X}(t)+X(t)={\xi }_{1}cos(t)+{\xi }_{2}sin(t),{\xi }_1,{\xi }_2\sim \mathrm{N}(0,1).$$

(31)

Now we shall obtain approximations to the first moments, $\mathbb{E}\left\{{\widehat{X}}^i(t)\right\},i=1,\dots ,5$, the correlation function and the variance, $\mathbb{V}\left\{\widehat{X}(t)\right\}$, of the approximate solution $\widehat{X}(t)$ of random nonlinear oscillator (31).

As we have seen in the expression (21), the moments of odd order are null, so, in this case, $\mathbb{E}\left\{\widehat{X}(t)\right\}=\mathbb{E}\left\{{\widehat{X}}^3(t)\right\}=\mathbb{E}\left\{{\widehat{X}}^5(t)\right\}=0$. Now, we sequentially derive some bounds for the perturbation parameter ϵ using the positiveness of even order moments, i.e., $\mathbb{E}\left\{{\widehat{X}}^2(t)\right\}>0$ and $\mathbb{E}\left\{{\widehat{X}}^4(t)\right\}>0$. First, it is easy to check that, using expression (17), the second-order moment is given by

$$\mathbb{E}\left\{{\widehat{X}}^2(t)\right\}=100-200000ϵ,$$

(32)

so we obtain the bound $ϵ<0.0005$. Since $E\left\{\widehat{X}(t)\right\}=0$, observe that the variance of the first-order approximation is given by (32). Second, using expressions (23)–(25),

$$\mathbb{E}\left\{{\widehat{X}}^4(t)\right\}=30,000-\frac{1,153,800,000,000}{6409}ϵ.$$

(33)

This provides a stronger bound, $ϵ<0.000166641$.

Now, applying (27), we obtain the following approximation of the correlation function,

$${\Gamma }_{\widehat{X}\widehat{X}}(\tau )=100(1-2000ϵ)cos(\tau ).$$

(34)

In Figure 1, we show the graphical representation of the correlation function, ${\Gamma }_{\widehat{X}\widehat{X}}(\tau )$, given in the expression (34) for different values of ϵ. We can see the higher the perturbation ϵ, the lower the variability. This graphical behavior is in full agreement with the physical interpretation of the oscillator dynamics. Indeed, let us rewrite Equation (31) as follows,

$$\ddot{X}(t)+(0.1+ϵX^2(t))\dot{X}(t)+X(t)={\xi }_{1}cos(t)+{\xi }_{2}sin(t).$$

As $ϵ>0$ increases, the damped coefficient $0.1+ϵX^2(t)$ does, so the mechanical system reduces its oscillations. It should be noted that $ϵ=0.0004$ only satisfies the first bound ($ϵ<0.0005$); however, we can observe that the corresponding approximation preserves symmetry of correlation function. This might be due to the sample regularity of the random excitation, $Y(t)$, which is differentiable.

For the approximation of the PDF, $f_{\widehat{X}(t)}(x)$, we apply the results exhibited in Section 4 based on PME by taking $ϵ=0.00005$, which satisfies the stronger bound previously determined ($ϵ<0.000166641$). We first compute the approximation based on the three first moments

$$f_{\widehat{X}(t)}(x)=e^{-1-2.181+1.045·{10}^{-5}x-0.005x^2-4.9217·{10}^{-8}{x}^3},$$

and, second, the approximation based on the five first moments

$$f_{\widehat{X}(t)}(x)=e^{-1-2.243+2.552·{10}^{-8}x-0.004x^2-2.177·{10}^{-9}{x}^3-3.789·{10}^{-6}{x}^4+6.754·{10}^{-13}{x}^5}.$$

In Figure 2, we compare both graphical representations. From them, we can observe that both plots are quite similar, so giving evidence that computations are consistent.

Finally, to check that our approximations are reliable, we compare the mean and standard deviation of the approximate solution obtained via the perturbation method against the ones calculated by Monte Carlo. The results are collected in

Table 1. Comparison between perturbation method and Monte Carlo simulations using $ϵ=0.00005$. Example 1.

	Perturbation Method	Monte Carlo (1000 Simulations)	Monte Carlo (10,000 Simulations)
Mean	0	0.188808	−0.114379
Standard deviation	9.48714	9.31356	9.49534

. We can observe that both approximations agree.

Example 2.

To previously perform our theoretical analysis, we have required the stationary Gaussian stochastic excitation $Y(t)$ be differentiable in the mean square sense (or equivalently, its correlation function, ${\Gamma }_Y(\tau )$, be twice differentiable in the ordinary sense at $\tau =0$ [28] (Chapter 4)), so having differentiable sample trajectories [34]. If we carefully revise our previous development, we can notice this is an hypothesis coming from the fact the nonlinearity cross-term depends upon $\dot{X}(t)$. In this second example, we shall show that using the general concept of differentiability, in the sense of distributions, we can still obtain good results via the perturbation techniques when the excitation is not differentiable. To this end, we have chosen, $Y(t)=\xi (t)$, a Gaussian white-noise process with zero-mean and correlation function ${\Gamma }_{YY}(\tau )=\frac{1}{2}W\delta (\tau )$, where $\delta (\tau )$ is the Dirac delta function and W is the noise power. This type of random noise has been extensively used in the literature since the earliest contributions [17]. Observe that $Y(t)=\xi (t)$ is a stationary zero-mean Gaussian process but is not mean square differentiable (as its correlation function, given by the Dirac delta function, is not differentiable) and, consequently, its sample trajectories are not differentiable either. In this case, Equation (3) becomes

$$\ddot{X}(t)+0.1\dot{X}(t)+ϵX^2(t)\dot{X}(t)+X(t)=\xi (t).$$

(35)

As in the previous example, we are going to obtain approximations to the five first moments, $\mathbb{E}\left\{{\widehat{X}}^i(t)\right\}$, $i=1,\dots ,5$, the correlation function and the variance, $\mathbb{V}\left\{\widehat{X}(t)\right\}$, of the approximate solution $\widehat{X}(t)$ of Equation (35). To implement the corresponding formulas derived throughout Section 3.2 saving computational time in Mathematica, we have taken into account the following properties of Dirac delta function,

$${\int }_{-\infty }^{\infty }h(t)\delta (t-s)\mathrm{d}t=h(s),{\int }_{-\infty }^{\infty }h(t){\delta }^{\prime }(t-s)\mathrm{d}t=-h^{\prime }(s).$$

As mentioned in Example 1, the moments of odd order are null and using the positiveness of even order moments we can obtain some bounds for the perturbation parameter ϵ. First, using expression (17), the second-order moment is determined by

$$\mathbb{E}\left\{{\widehat{X}}^2(t)\right\}=\frac{1}{40}-\frac{ϵ}{160},$$

(36)

so we obtain the bound $ϵ<4$. Since $\mathbb{E}\left\{\widehat{X}(t)\right\}=0$, expression (36) is also the variance of the first-order approximation. Second, using expression (23)–(25),

$$\mathbb{E}\left\{{\widehat{X}}^4(t)\right\}=\frac{3}{1600}-\frac{759}{644800}ϵ.$$

(37)

This provides a stronger bound, $ϵ<1.59289$.

Now, applying (27), we obtain the following approximation of the correlation function,

$${\Gamma }_{\widehat{X}\widehat{X}}(\tau )=\left\{\begin{array}{cc}{\displaystyle \frac{e^{-\tau /20}\left(-399\left(-399+5ϵ\tau \right)cos\left(\frac{\sqrt{399}\tau }{20}\right)+\sqrt{399}(399+100ϵ)sin\left(\frac{\sqrt{399}\tau }{20}\right)\right)}{6,368,040}}\hfill & \mathrm{if}\tau \ge 0,\hfill \\ \\ {\displaystyle \frac{e^{\tau /20}\left(-399(-399+5ϵ\tau )cos\left(\frac{\sqrt{399}\tau }{20}\right)+\sqrt{399}(-399+100ϵ)sin\left(\frac{\sqrt{399}\tau }{20}\right)\right)}{6,368,040}}\hfill & \mathrm{if}\tau <0.\hfill \end{array}\right.$$

(38)

In Figure 3, we show the plot of the correlation function, ${\Gamma }_{\widehat{X}\widehat{X}}(\tau )$, given in the expression (38) for different values of ϵ satisfying the weaker and the stronger bounds previously determined. We can observe that for smaller values of ϵ the obtained approximation of the correlation function better preserves the symmetry as expected.

Applying the results presented in Section 4, we obtain the approximation of the PDF, $f_{\widehat{X}(t)}(x)$, for $ϵ=0.5$, which satisfies the stronger bound $1.59289$. We first compute the approximation based on the three first moments

$$f_{\widehat{X}(t)}(x)=e^{-1+1.992+1.438·{10}^{-8}x-22.857x^2-2.197·{10}^{-7}{x}^3},$$

and, second, the approximation based on the five first moments

$$f_{\widehat{X}(t)}(x)=e^{-1+1.940-5.226·{10}^{-11}x-17.837x^2+1.580·{10}^{-9}{x}^3-42.679x^4-7.904·{10}^{-9}{x}^5}.$$

In Figure 4, we compare both graphical representations. We can observe, again, the similarity between them, thus showing full agreement in our numerical computations.

Finally, to check that our approximations are accurate, we compare the mean and standard deviation of $\widehat{X}(t)$ obtained via the perturbation method against the ones computed by Euler–Maruyama numerical scheme [35]. The results are shown in

Table 2. Comparison between perturbation method and Euler–Maruyama simulations using $ϵ=0.5$. Example 2.

	Perturbation Method	Euler-Maruyama (1000 Simulations)	Euler-Maruyama (10,000 Simulations)
Mean	0	0.00146868	0.00128423
Standard deviation	0.147902	0.157353	0.156475

. We can observe that both approximations are similar.

6. Conclusions

We have studied, from a probabilistic standpoint, a family of oscillators subject to small perturbations on the nonlinear term that depends both upon the position and the velocity (cross-nonlinearity) and whose forcing source is driven by a mean square differentiable stationary zero-mean Gaussian process. Despite the hypothesis of differentiability for the stochastic excitation, we have checked, via a numerical example, the method also provides good results when this hypothesis is not fulfilled, but involved computations are performed using the concept of general differentiability in the sense of distributions. We must point out that the majority of contributions dealing with this type of stochastic oscillators focus on the computation of the mean, the variance and correlation function. Our main contribution is the computation of reliable approximations of the probability density function of the stationary solution, by combining the stochastic perturbation method and the principle of maximum entropy. In this manner, we provide a fuller probabilistic description of the solution since from the density one can determine any one-dimensional moment as well as further probabilistic information of the steady-state. The proposed approach can be very useful to open new avenues in the analysis to other kind of nonlinear oscillators subject to small fluctuations and whose forcing term is a stochastic process that satisfies certain hypotheses. In our future research, we will work to continue contributing in this direction.