Dynamics of Rössler Prototype-4 System: Analytical and Numerical Investigation
Abstract
:1. Introduction
2. Analytical Investigation
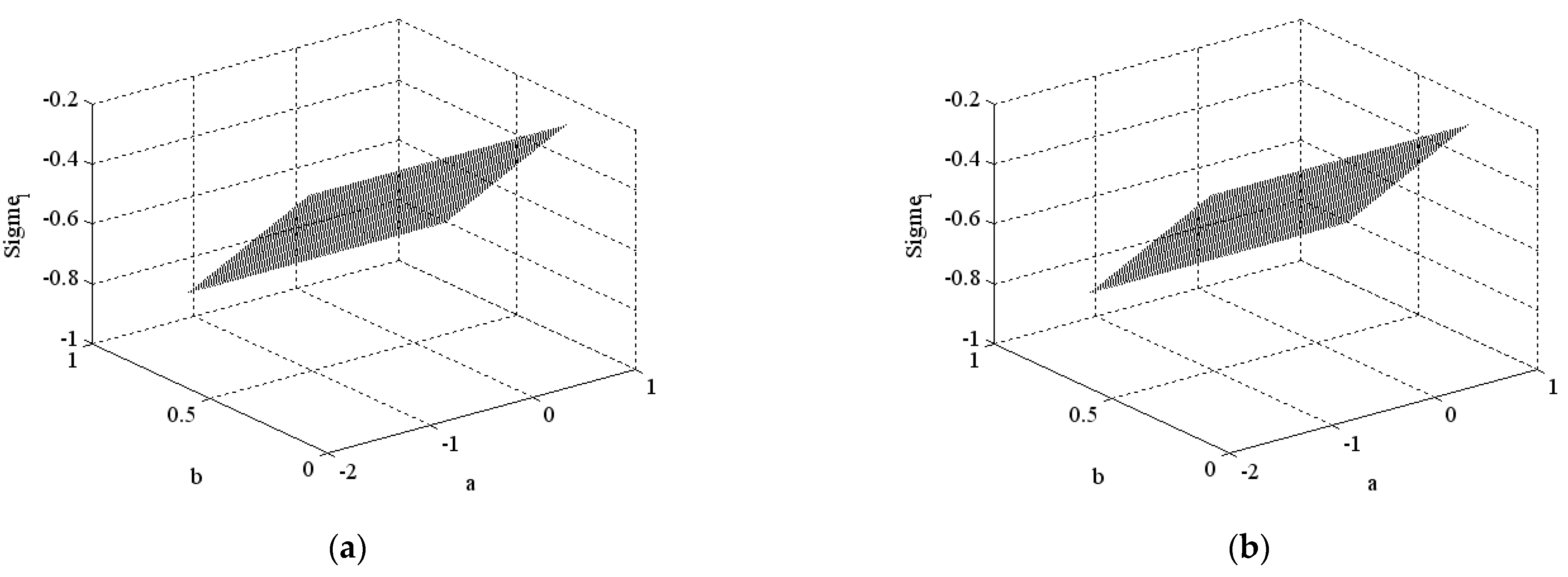
2.1. Local Analysis and First Lyapunov Value-
2.2. Special Cases
2.2.1. Conservative Case
2.2.2. Dissipative Case
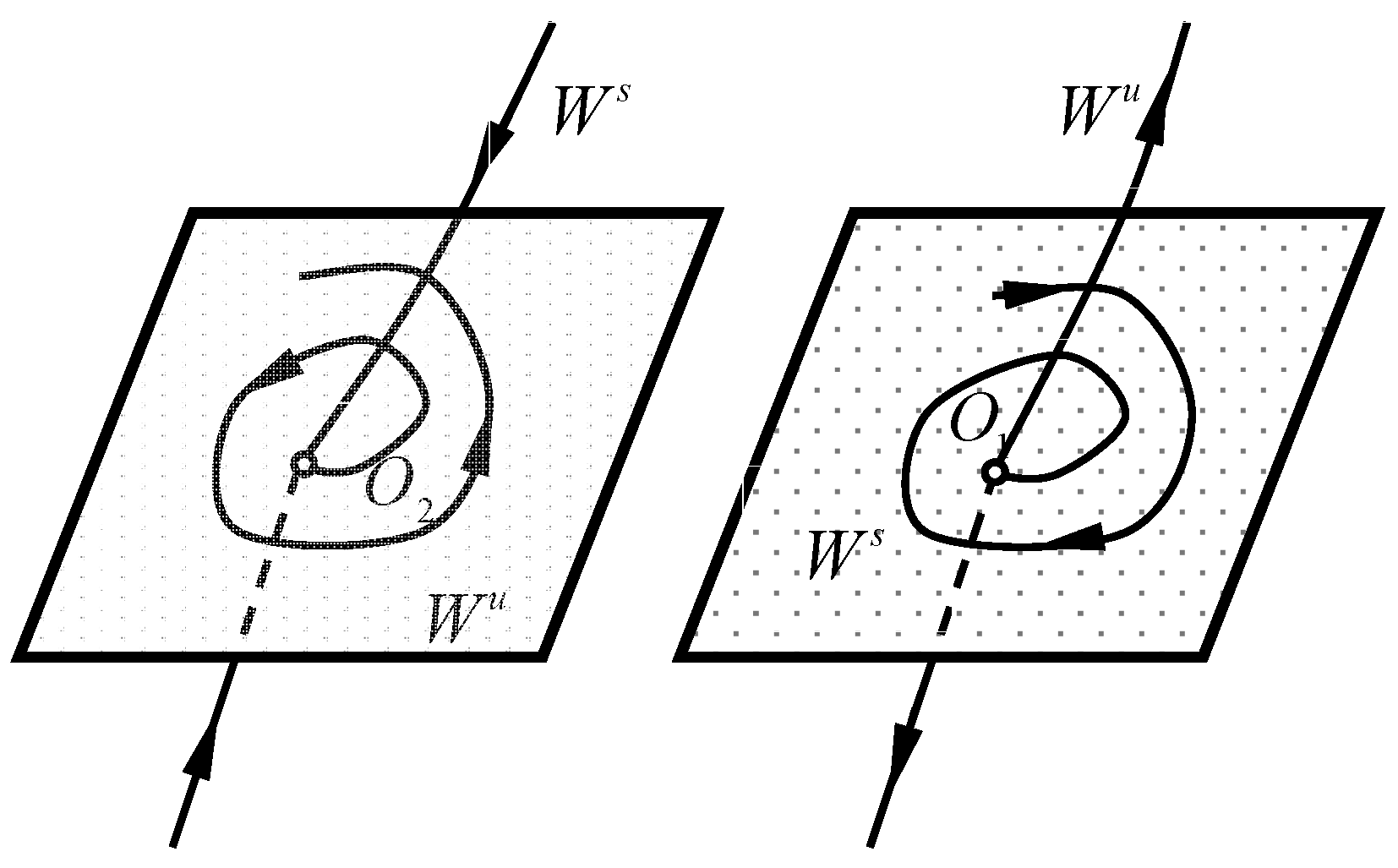
2.3. Global Analysis
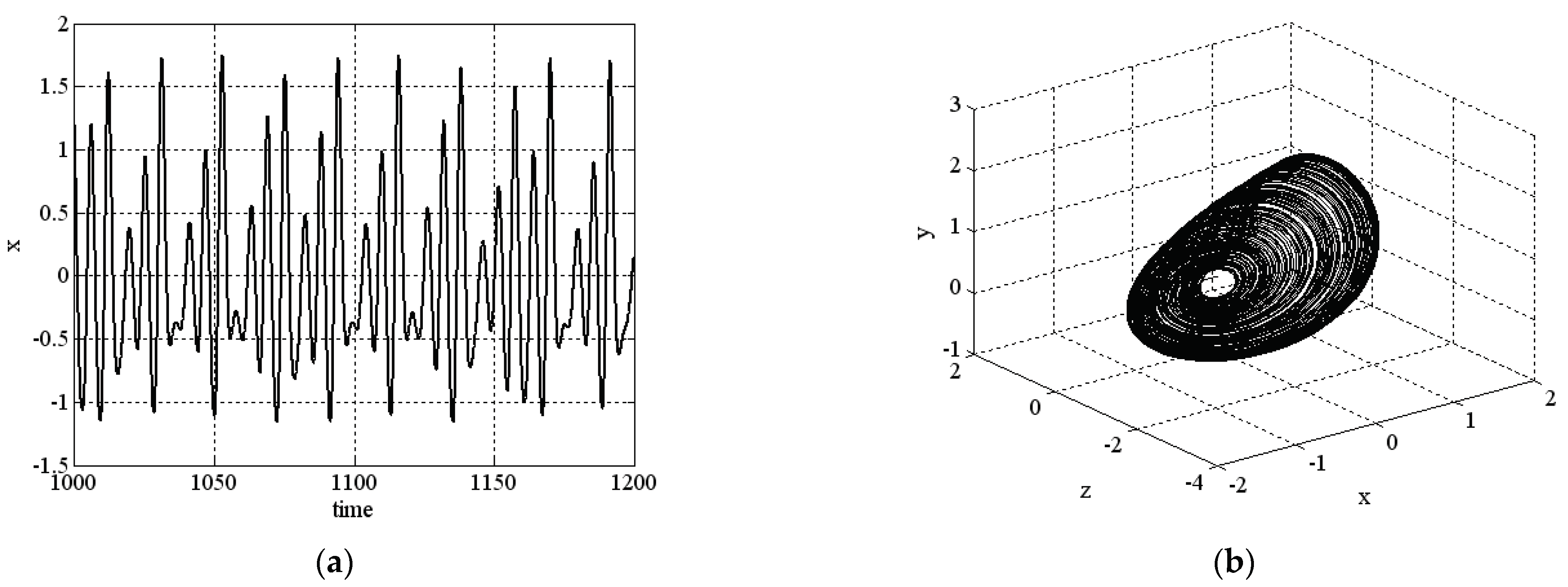
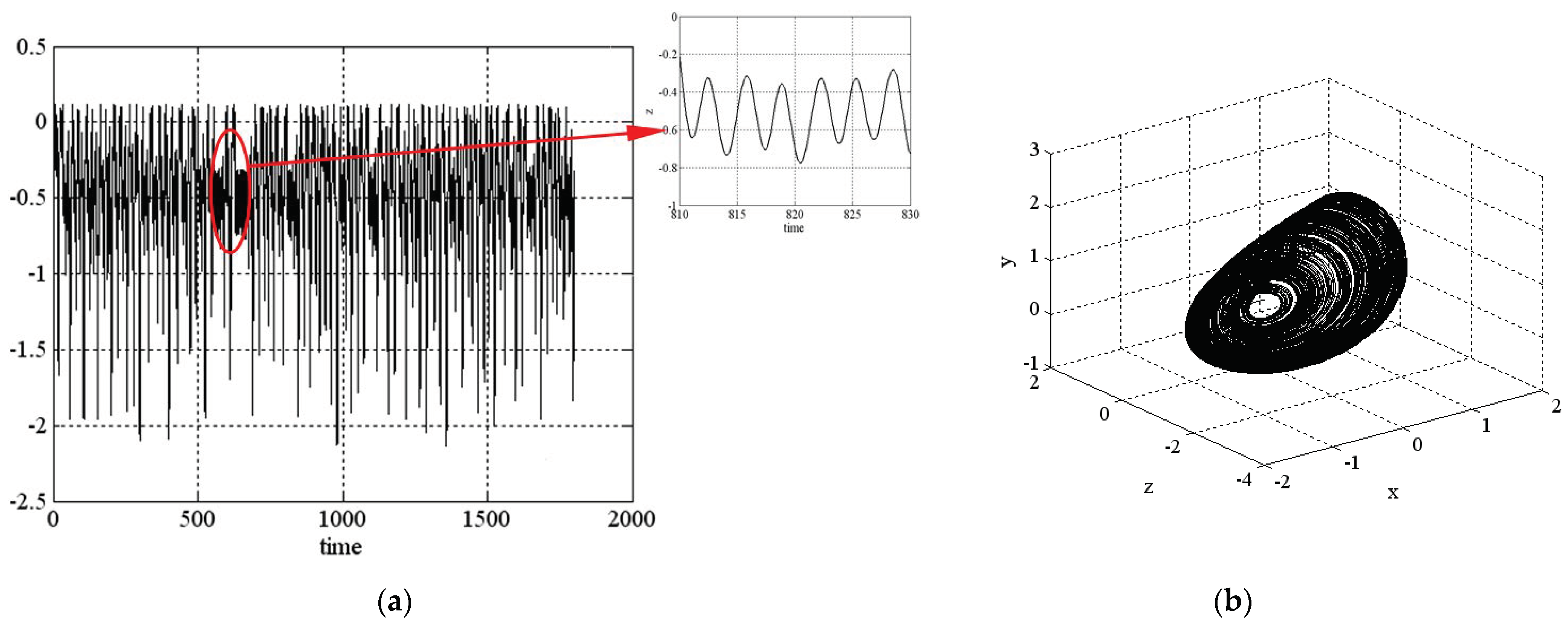
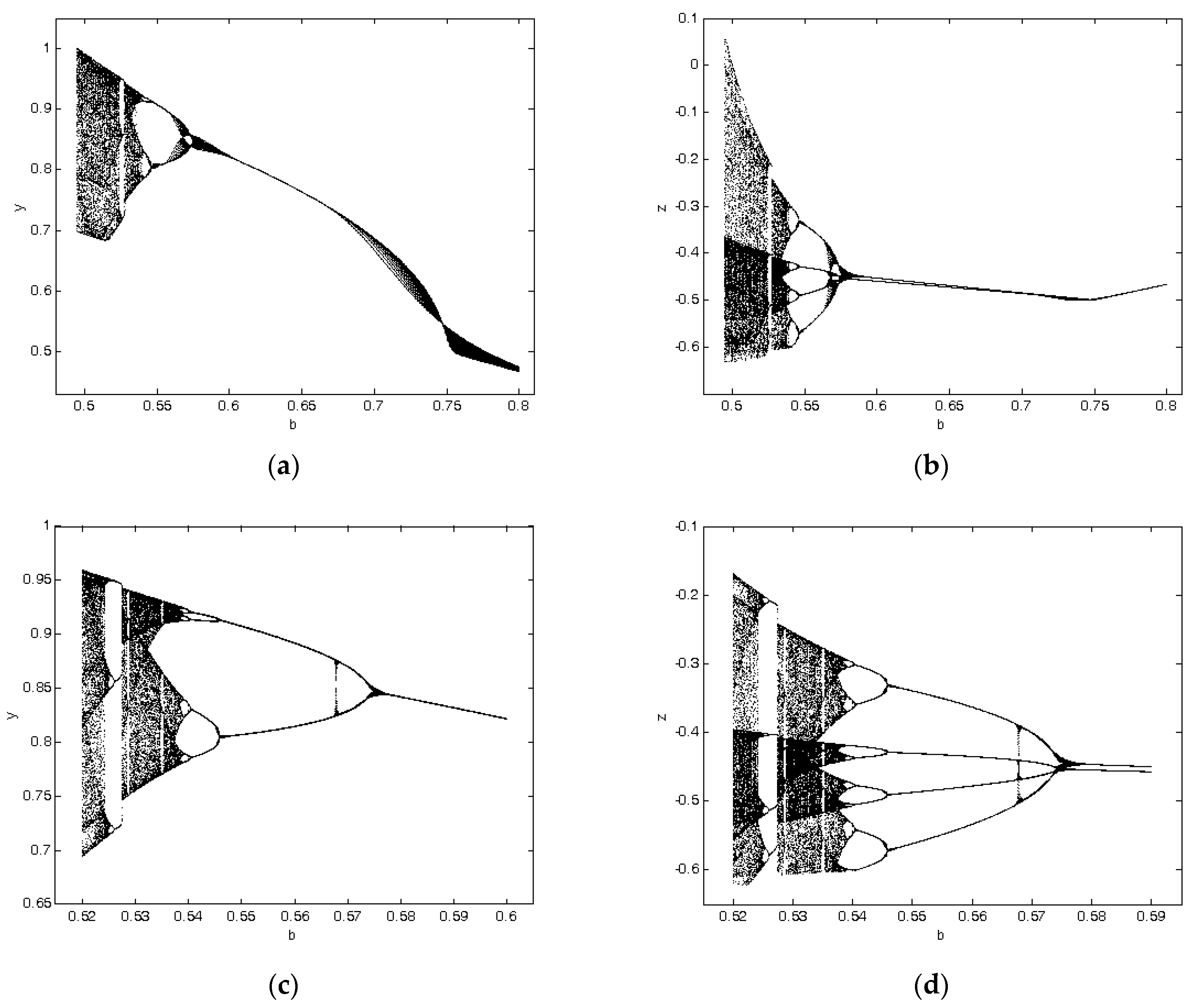
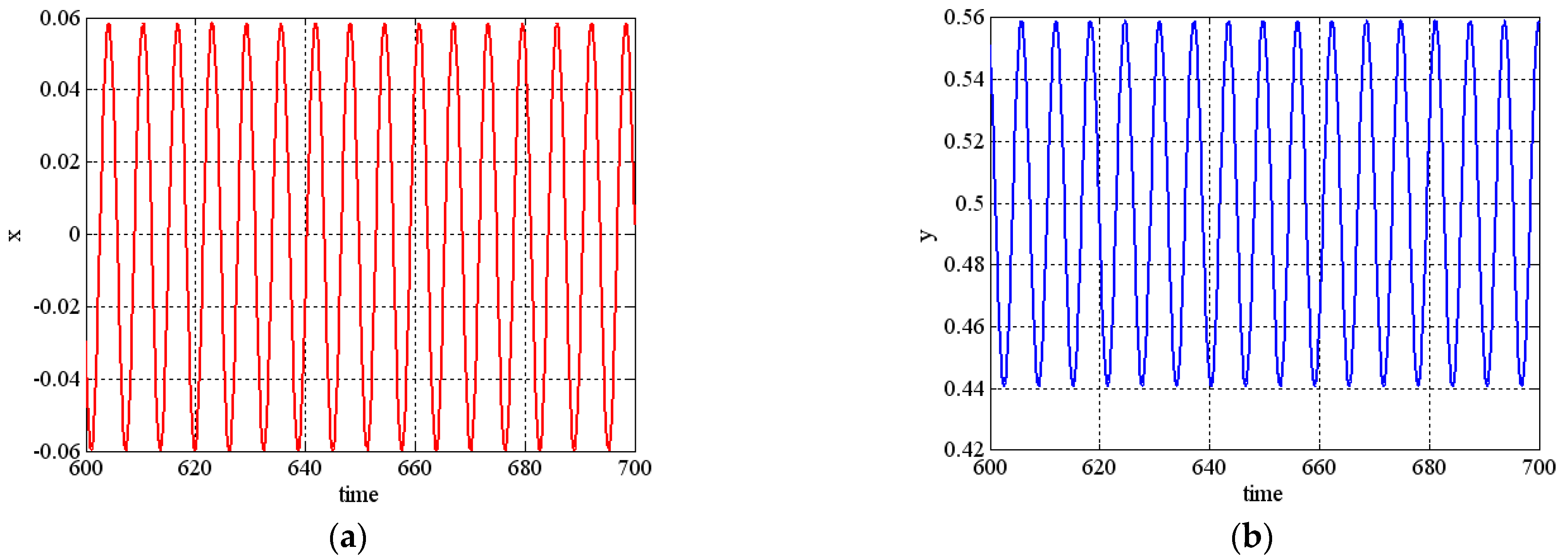
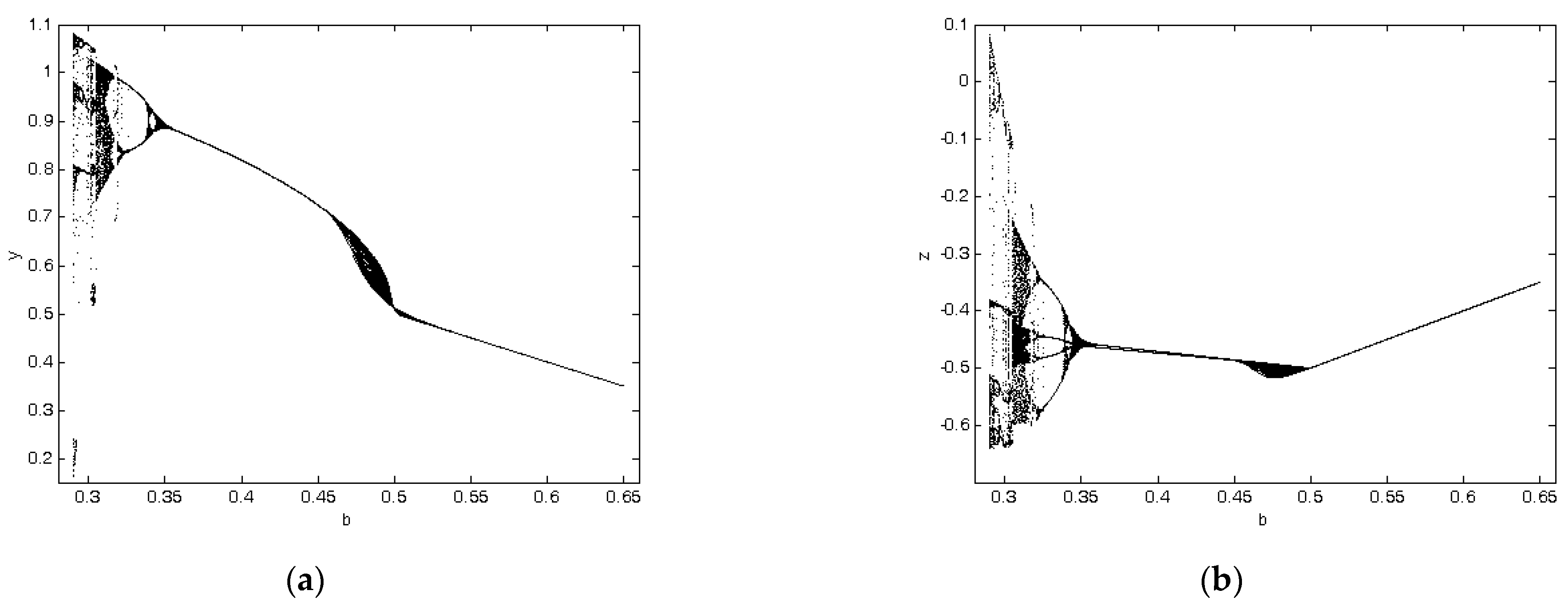
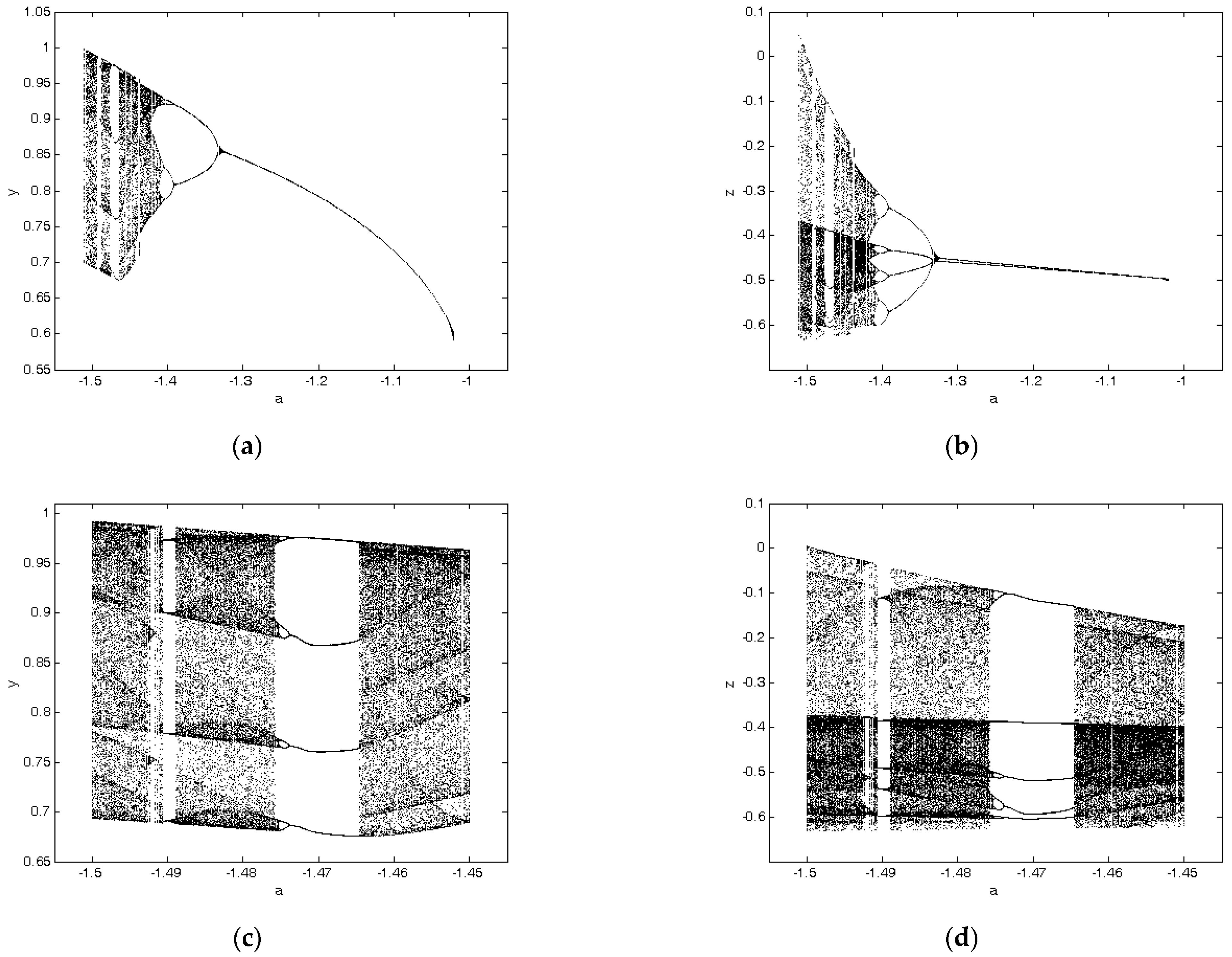
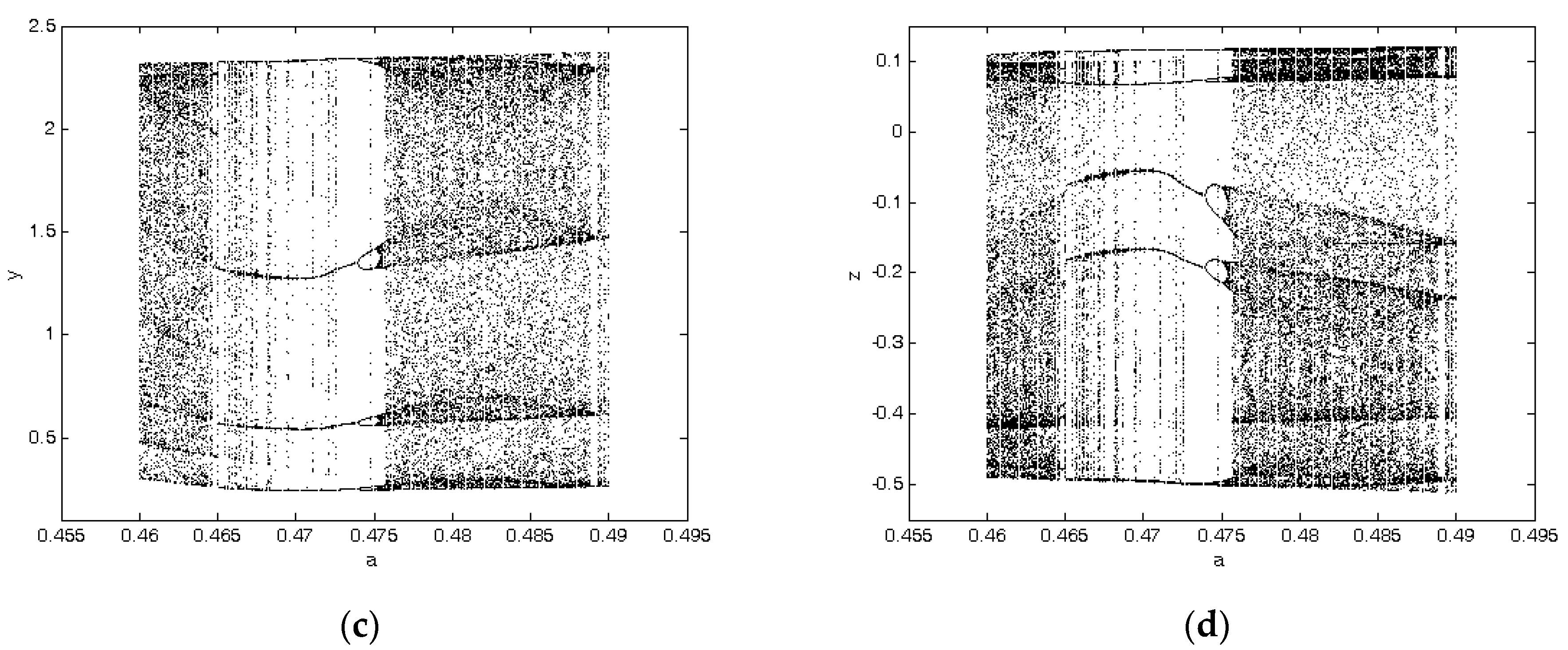
3. Numerical Investigation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C

References
- Rössler, O. Chaos and strange attractors in chemical kinetics. Springer Ser. Synerg. 1979, 3, 107–113. [Google Scholar]
- Arneodo, A.; Coullet, P.; Tresser, C. Possible new strange attractors with spiral structure. Commun. Math. Phys. 1981, 79, 573–579. [Google Scholar] [CrossRef]
- Gurel, D.; Gurel, O. Oscillations in Chemical Reactions; Springer: New York, NY, USA, 1983. [Google Scholar]
- Sprott, J. Elegant Chaos. Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Islam, M.; Islam, N.; Nikolov, S. Adaptive control and synchronization of Sprott J system with estimation of fully unknown parameters. J. Theor. Appl. Mech. 2015, 45, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Awrejcewicz, J. Bifurcation and Chaos in Simple Dynamical Systems; World Scientific: London, UK, 1989. [Google Scholar]
- Awrejcewicz, J. Bifurcation and Chaos: Theory and Applications; Springer: Berlin, Germany, 1995. [Google Scholar]
- Nikolov, S.; Nedkova, N. Gyrostat model regular and chaotic behaviour. J. Theor. Appl. Mech. 2015, 45, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Shilnikov, L.; Shilnikov, A.; Turaev, D.; Chua, L. Methods of Qualitative Theory in Nonlinear Dynamics; Part II; World Scientific: London, UK, 2001. [Google Scholar]
- Andronov, A.; Witt, A.; Chaikin, S. Theory of Oscillations; Addison-Wesley Reading: Boston, MA, USA, 1966. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1998. [Google Scholar]
- Bautin, N. Behaviour of Dynamical Systems Near the Boundary of Stability; Nauka: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Marsden, J.; Cracken, M. The Hopf Bifurcation and Its Applications; Springer: New York, NY, USA, 1976. [Google Scholar]
- Homburg, A.J.; Sandstede, B. Homoclinic and heteroclinic bifurcations in vector fields. Handb. Dyn. Syst. 2010, 3, 379–524. [Google Scholar]
- Glendinning, P.; Sparrow, C. Local and global behavior near homoclinic orbits. J. Statist. Phys. 1984, 34, 645–696. [Google Scholar] [CrossRef]
- Guckenheimer, J.; Worfolk, P. Dynamical systems: Some computational problems. In Bifurcations and Periodic Orbits of Vector Fields; Schlomiuk, D., Ed.; Kluwer Academic Publishers: Berlin/Heidelberg, Germany, 1992; pp. 241–279. [Google Scholar]
- Nikolov, S.; Nedkova, N. Dynamical behavior of a rigid body with one fixed point (gyroscope). Basic concepts and results. Open problems: A review. J. Appl. Comput. Mech. 2015, 1, 187–206. [Google Scholar]
- Peixoto, M. Structural stability on two-dimensional manifolds. Topology 1962, 1, 101–120. [Google Scholar] [CrossRef] [Green Version]
- Scott, S. Chemical Chaos; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Schuster, H.; Just, W. Deterministic Chaos: An Introduction; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Phillipson, P.; Schuster, P. Analytics of bifurcation. Int. J. Bifurc. Chaos 1998, 8, 471–482. [Google Scholar] [CrossRef]
- Nikolov, S. First Lyapunov value and bifurcation behavior of specific class of three-dimensional systems. Int. J. Bifurc. Chaos 2004, 14, 2811–2823. [Google Scholar] [CrossRef]
- Shilnikov, L. A case of the existence of a denumerable set of periodic motions. Sov. Math. Dokl. 1965, 6, 163–166. (In Russian) [Google Scholar]
- Shilnikov, L. A contribution to the problem of the structure of an extended neighborhood of a rough equilibrium of saddle-focus type. Math. USSR-Sb. 1970, 10, 91–102. (In Russian) [Google Scholar] [CrossRef]
- Tresser, C. About some theorems by Shilnikov, L.P. Ann. Inst. Henri Poincare Phys. Theor. 1984, 40, 441–461. [Google Scholar]
- Glendinning, P. Subsidiary bifurcations near bifocal homoclinic orbits. Math. Camb. Philos. Soc. 1989, 105, 597–605. [Google Scholar] [CrossRef]
- Fowler, A.; Sparrow, C. Bifocal homoclinic orbits in four dimensions. Nonlinearity 1991, 4, 1159–1182. [Google Scholar] [CrossRef] [Green Version]
- Laing, C.; Glendinning, P. Bifocal homoclinic bifurcations. Phys. D Nonlinear Phenom. 1997, 102, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Rössler, O. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Olsen, L.; Degn, H. Chaos in an enzyme reaction. Nature 1977, 267, 177–178. [Google Scholar] [CrossRef]
- Olsen, L.; Degn, H. Oscillatory kinetics of the peroxidase-oxidase reaction in an open system. Experimental and theoretical studies. Biochim. Biophys. Acta 1978, 523, 321–334. [Google Scholar] [CrossRef]
- Nikolov, S. Analysis of a Rossler type dynamical system. Mech. Transp. Commun. 2020, 18. in press. [Google Scholar]
- Garcia, I.; Llibre, J.; Maza, S. Periodic orbits and their stability in Rössler prototype-4 system. Phys. Lett. A 2012, 376, 2234–2237. [Google Scholar] [CrossRef] [Green Version]
- Sprott, J.; Linz, S. Algebraically simple chaotic flows. Int. J. Chaos Theory Appl. 2000, 5, 1–20. [Google Scholar]
- Zhang, Z.; Fu, J. Hopf bifurcation and amplitude control of a Rössler prototype-4 system. Math. Pract. Theory 2016, 2016, 225–234. [Google Scholar]
- Kuate, P.; Tchendjeu, A.; Fotsin, H. A modified Rössler prototype-4 system based on Chua’s diode nonlinearity: Dynamics, multistability, multiscroll generation and FPGA implementation. Chaos Solitons Fractals 2020, 140, 0213. [Google Scholar] [CrossRef]
- Marzec, C.; Spiegel, E. Ordinary differential equations with strange attractors. SIAM J. Appl. Math. 1980, 38, 403–421. [Google Scholar] [CrossRef]
- Nikolov, S.; Petrov, V. New results about route to chaos in Rossler system. Int. J. Bifurc. Chaos 2004, 14, 293–308. [Google Scholar] [CrossRef]
- Nikolov, S.; Nedev, V. Bifurcation analysis and dynamic behaviour of an inverted pendulum with bounded control. J. Theor. Appl. Mech. 2016, 46, 17–32. [Google Scholar] [CrossRef] [Green Version]
- Lichtenberg, A.; Lieberman, M. Regular and Chaotic Dynamics, 2nd ed.; Springer: New York, NY, USA, 1992. [Google Scholar]
- Arnold, V.; Kozlov, V.; Neishtadt, A. Mathematical Aspects of Classical and Celestial Mechanics, 3rd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Llibre, J. Centers; their integrability and relations with the divergence. Appl. Math. Nonlinear Sci. 2016, 1, 79–86. [Google Scholar] [CrossRef] [Green Version]
- Krupa, M. Robust heteroclinic cycles. J. Nonlinear Sci. 1997, 7, 129–176. [Google Scholar] [CrossRef]
- Kuznecov, A.; Afraimovich, V. Heteroclinic cycles in the repressilator model. Chaos Solitons Fractals 2012, 45, 660–665. [Google Scholar] [CrossRef]
- Shilnikov, L. The existence of a denumerable set of periodic motions in four-dimensional space in an extended neighborhood of a saddle-focus. Soviet Math. Dokl. 1967, 8, 54–58. (In Russian) [Google Scholar]
- Shilnikov, A.; Shilnikov, L.; Barrio, R. Symbolic dynamics and spiral structures due to the saddle-focus bifurcations. In Chaos, CNN, Memristors and Beyond: A Festschrift for Leon Chua with DVD-ROM; Bilotta, E., Adamatzky, A., Chen, G., Eds.; World Scientific: London, UK, 2013; pp. 428–439. [Google Scholar]
- Gonchenko, S.; Turaev, D.; Gaspard, P.; Nicolis, G. Complexity in the bifurcation structure of homoclinic loops to a saddle-focus. Nonlinearity 1997, 10, 409. [Google Scholar] [CrossRef]
- Dufraine, E.; Danckaert, J. Some topological invariants for three-dimensional flows. Chaos 2001, 11, 443–448. [Google Scholar] [CrossRef]
- Awrejcewicz, J. Numerical investigations of the constant and periodic motions of the human vocal cords including stability and bifurcation phenomena. Dyn. Stab. Syst. Int. J. 1990, 5, 11–28. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Supel, B.; Lamarque, C.H.; Kudra, G.; Wasilewski, G.; Olejnik, P. Numerical and experimental study of regular and chaotic motion of triple physical pendulum. Int. J. Bifurc. Chaos 2008, 18, 2883–2915. [Google Scholar] [CrossRef]
- Alligood, A.; Sauer, T.; Yorke, J. An Introduction to Dynamical Systems and Chaos; Springer: New York, NY, USA, 1996. [Google Scholar]
- Fan, Y.; Chay, T. Crisis and topological entropy. Phys. Rev. E 1995, 51, 1012–1019. [Google Scholar] [CrossRef]
- Sanjuan, M. Symmetry-restoring crises, period-adding and chaotic transitions in the cubic Van der Pol oscillator. J. Sound Vib. 1996, 193, 863–875. [Google Scholar] [CrossRef]
- Uzunov, I.M.; Nikolov, S.G. Influence of the higher-order effects on the solutions of complex cubic-quintic Ginzburg–Landau equation. J. Mod. Opt. 2020, 67, 606–618. [Google Scholar] [CrossRef]
- Gonchenko, S.; Ovsyannikov, I. On bifurcations of three-dimensional diffeomorphisms with a non-transversal heteroclinic cycle containing saddle-foci. Nonlinear Dyn. 2010, 6, 61–77. (In Russian) [Google Scholar]
- Afraimovich, V.; Gonchenko, S.; Lerman, L.; Shilnikov, A.; Turaev, D. Scientific heritage of L.P. Shilnikov. Regul. Chaotic Dyn. 2014, 19, 435–460. [Google Scholar] [CrossRef]
- Shilnikov, L. On a new type of bifurcation of multidimensional dynamical systems. Sov. Math. Dokl. 1969, 10, 1368–1371. (In Russian) [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolov, S.G.; Vassilev, V.M. Dynamics of Rössler Prototype-4 System: Analytical and Numerical Investigation. Mathematics 2021, 9, 352. https://doi.org/10.3390/math9040352
Nikolov SG, Vassilev VM. Dynamics of Rössler Prototype-4 System: Analytical and Numerical Investigation. Mathematics. 2021; 9(4):352. https://doi.org/10.3390/math9040352
Chicago/Turabian StyleNikolov, Svetoslav G., and Vassil M. Vassilev. 2021. "Dynamics of Rössler Prototype-4 System: Analytical and Numerical Investigation" Mathematics 9, no. 4: 352. https://doi.org/10.3390/math9040352
APA StyleNikolov, S. G., & Vassilev, V. M. (2021). Dynamics of Rössler Prototype-4 System: Analytical and Numerical Investigation. Mathematics, 9(4), 352. https://doi.org/10.3390/math9040352






