Construction of a Class of High-Dimensional Discrete Chaotic Systems
Abstract
:1. Introduction
2. Basic Concepts and Lemmas
2.1. Matrix Theoretical Analysis
- If , let ; then, ; namely,
- If , let ; then, ; namely,
2.2. Overview of Multivariate Polynomials
2.3. Marotto Theorem
- There is a real numbersuch that the moduli of all eigenvalues of the Jacobian matrixof any pointinare greater than 1.
- There is a pointinand a natural numberthat yield, and pointis nondegenerate, that is,.
3. Construction of High-Dimensional Linear Chaos Theory
3.1. is a Linear System
- (1)
- Select to satisfy , such that becomes the exclusion domain including . The Jacobian matrix at any point in is , from which is a strictly over-one diagonally dominant matrix. According to Lemma 5, it is known that the moduli of the eigenvalues of are greater than one.
- (2)
- There exists in and the natural number such that , and since , we know that is nondegenerate. In summary, we know that is a snap-back repeller. The proof is completed. □
3.2. is a Multinomial System
- (1)
- Let satisfy , and define the closed sphere. According to the above condition, the Jacobian matrix of any point in is a strictly over-one diagonally dominant matrix. Therefore, according to Lemma 5, the modulus of the eigenvalue of any point of is greater than one.
- (2)
- There exists in and a natural number that satisfy , where the components of satisfy . Becausewe know that is nondegenerate.
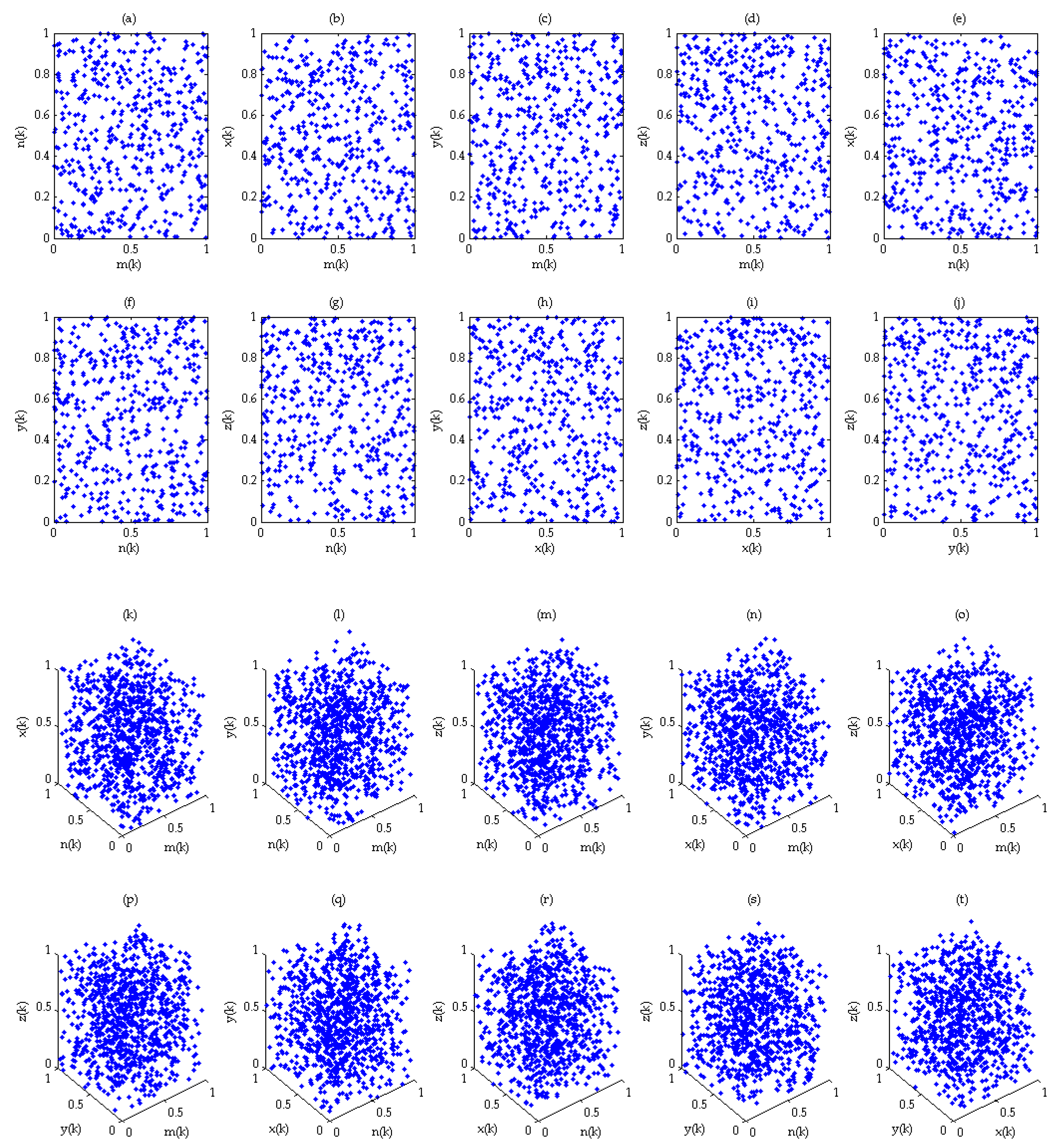
4. Numerical Simulation
4.1. Numerical Simulation of System (2)
4.2. Numerical Simulation of System (3)
5. Conclusions of this Paper
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lambić, D. A new discrete-space chaotic map based on the multiplication of integer numbers and its application in S-box design. Nonlinear Dyn. 2020, 100, 699–711. [Google Scholar] [CrossRef]
- Vaseghi, B.; Pourmina, M.A.; Mobayen, S. Secure communication in wireless sensor networks based on chaos synchronization using adaptive sliding mode control. Nonlinear Dyn. 2017, 89, 1689–1704. [Google Scholar] [CrossRef]
- Ouannas, A.; Bendoukha, S.; Volos, C.; Boumaza, N.; Karouma, A. Synchronization of Fractional Hyperchaotic Rabinovich Systems via Linear and Nonlinear Control with an Application to Secure Communications. Int. J. Control Autom. Syst. 2019, 17, 52211–52219. [Google Scholar] [CrossRef]
- Xiuping, Y.; Lequan, M.; Xue, W. A cubic map chaos criterion theorem with applications in generalized synchronization based pseudorandom number generator and image encryption. Chaos 2015, 25, 053104. [Google Scholar]
- Wang, C.; Fan, C.; Ding, Q. Constructing Discrete Chaotic Systems with Positive Lyapunov Exponents. Int. J. Bifurc. Chaos 2018, 28, 17. [Google Scholar] [CrossRef]
- Min, L.; Yang, X.; Chen, G.; Wang, D. Some Polynomial Chaotic Maps Without Equilibria an Application to Image Encryption with Avalanche Effects. Int. J. Bifurc. Chaos 2015, 25, 1550124. [Google Scholar] [CrossRef]
- Zhuosheng, L.; Simin, Y.; Jinhu, L.; Shuting, C.; Guanrong, C. Design and ARM-Embedded Implementation of a Chaotic Map-Based Real-Time Secure Video Communication System. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 1203–1216. [Google Scholar] [CrossRef]
- Lin, Z.; Yu, S.; Feng, X.; Lü, J. Cryptanalysis of a Chaotic Stream Cipher and Its Improved Scheme. Int. J. Bifurc. Chaos 2018, 28, 27. [Google Scholar] [CrossRef]
- Li, T.-Y.; Yorke, J.A. Period three implies chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Marotto, F.R. Snap-back repellers imply chaos in Rn. J. Math. Anal. Appl. 1978, 63, 199–223. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Chen, G. Discrete chaos in banach spaces. Sci. China Ser. A Math. 2005, 48, 222–238. [Google Scholar] [CrossRef]
- Lin, W.; Chen, G. Heteroclinical repellers imply chaos. Int. J. Bifurc. Chaos 2006, 16, 1471–1489. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, P. Study on chaos induced by turbulent maps in noncompact sets. Chaos Solitons Fractals 2006, 28, 1165–1180. [Google Scholar] [CrossRef]
- Da Costa, D.R.; Medrano-T, R.O.; Leonel, E.D. Route to chaos and some properties in the boundary crisis of a generalized logistic mapping. Phys. A Stat. Mech. Its Appl. 2017, 486, 674–680. [Google Scholar] [CrossRef]
- Elsadany, A.; Yousef, A.; Elsonbaty, A. Further analytical bifurcation analysis and applications of coupled logistic maps. Appl. Math. Comput. 2018, 338, 314–336. [Google Scholar] [CrossRef]
- Zang, H.; Huang, H.; Chai, H. Study on homogenization method of a class of quadratic polynomial chaotic system. J. Electron. Inf. 2019, 41, 1618–1624. [Google Scholar]
- Chen, G.; Lai, D. Feedback control of lyapunov exponents for discrete-time dynamical systems. Int. J. Bifurc. Chaos 1996, 6, 1341. [Google Scholar] [CrossRef]
- Zang, H.; Li, J.; Li, G. A one-dimensional discrete chaos determination theorem and its application in pseudorandom number generator. J. Electron. Inf. 2018, 40, 1992–1997. [Google Scholar]
- Wang, X.; Chen, G. Yet Another Algorithm for Chaotifying Control of Discrete Chaos. Control Theory Appl. 2000, 17, 336–340. [Google Scholar]
- Yu, S.; Lu, J.; Chen, G. Anti Control Method of Power System and Its Application; Science Press: Beijing, China, 2013. [Google Scholar]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, H.; Liu, J.; Li, J. Construction of a Class of High-Dimensional Discrete Chaotic Systems. Mathematics 2021, 9, 365. https://doi.org/10.3390/math9040365
Zang H, Liu J, Li J. Construction of a Class of High-Dimensional Discrete Chaotic Systems. Mathematics. 2021; 9(4):365. https://doi.org/10.3390/math9040365
Chicago/Turabian StyleZang, Hongyan, Jianying Liu, and Jiu Li. 2021. "Construction of a Class of High-Dimensional Discrete Chaotic Systems" Mathematics 9, no. 4: 365. https://doi.org/10.3390/math9040365
APA StyleZang, H., Liu, J., & Li, J. (2021). Construction of a Class of High-Dimensional Discrete Chaotic Systems. Mathematics, 9(4), 365. https://doi.org/10.3390/math9040365






