A Novel Geometric Modeling and Calculation Method for Forward Displacement Analysis of 6-3 Stewart Platforms
Abstract
:1. Introduction
2. Conformal Geometric Algebra
2.1. Foundations of CGA
2.2. Conformal Geometric Entities
3. Two Formulas under the Framework of CGA
3.1. Derivation of the First Formula
3.2. Derivation of the Second Formula
4. CGA-Based Geometric Modeling and Calculation Procedure
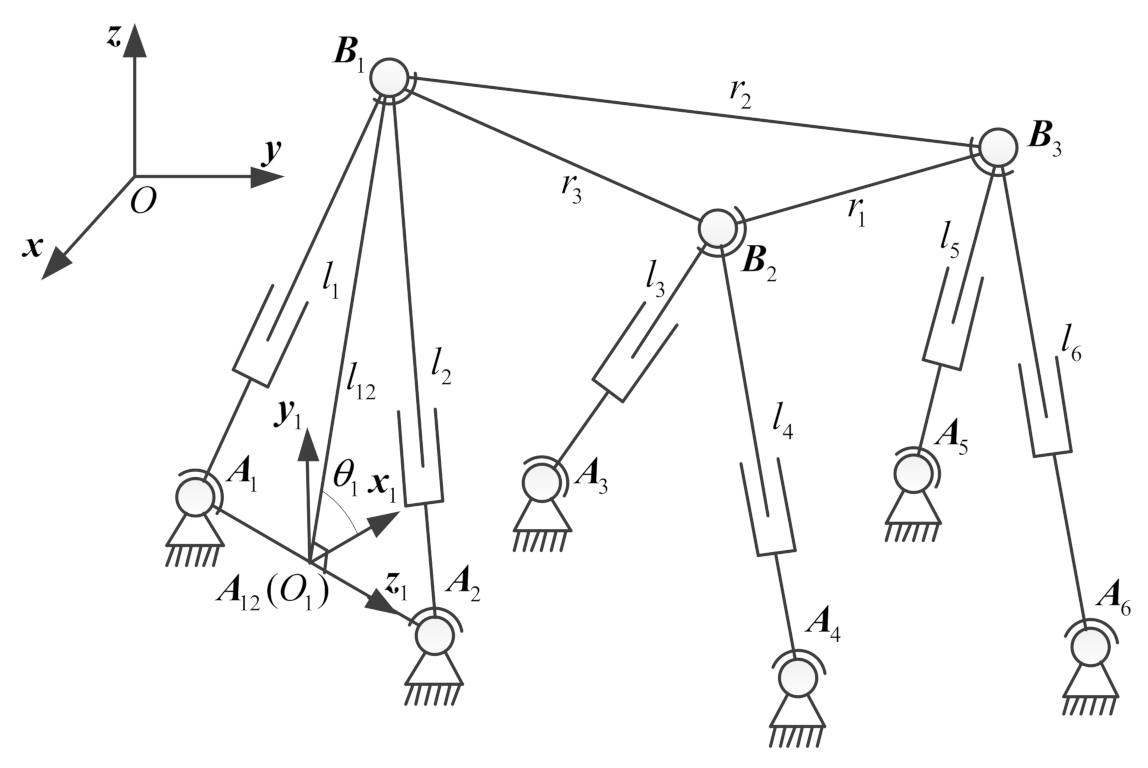
4.1. The Structure and Coordinate System of the 6-3 Stewart Platforms
4.2. The Expressions for Two Point Pairs and .
4.3. The Coordinate-Invariant Geometric Constraint Equation
4.4. The Univariate Polynomial Equation for Forward Displacement Analysis
4.5. Back Substitution
4.6. Two Comparisons
5. Numerical Example
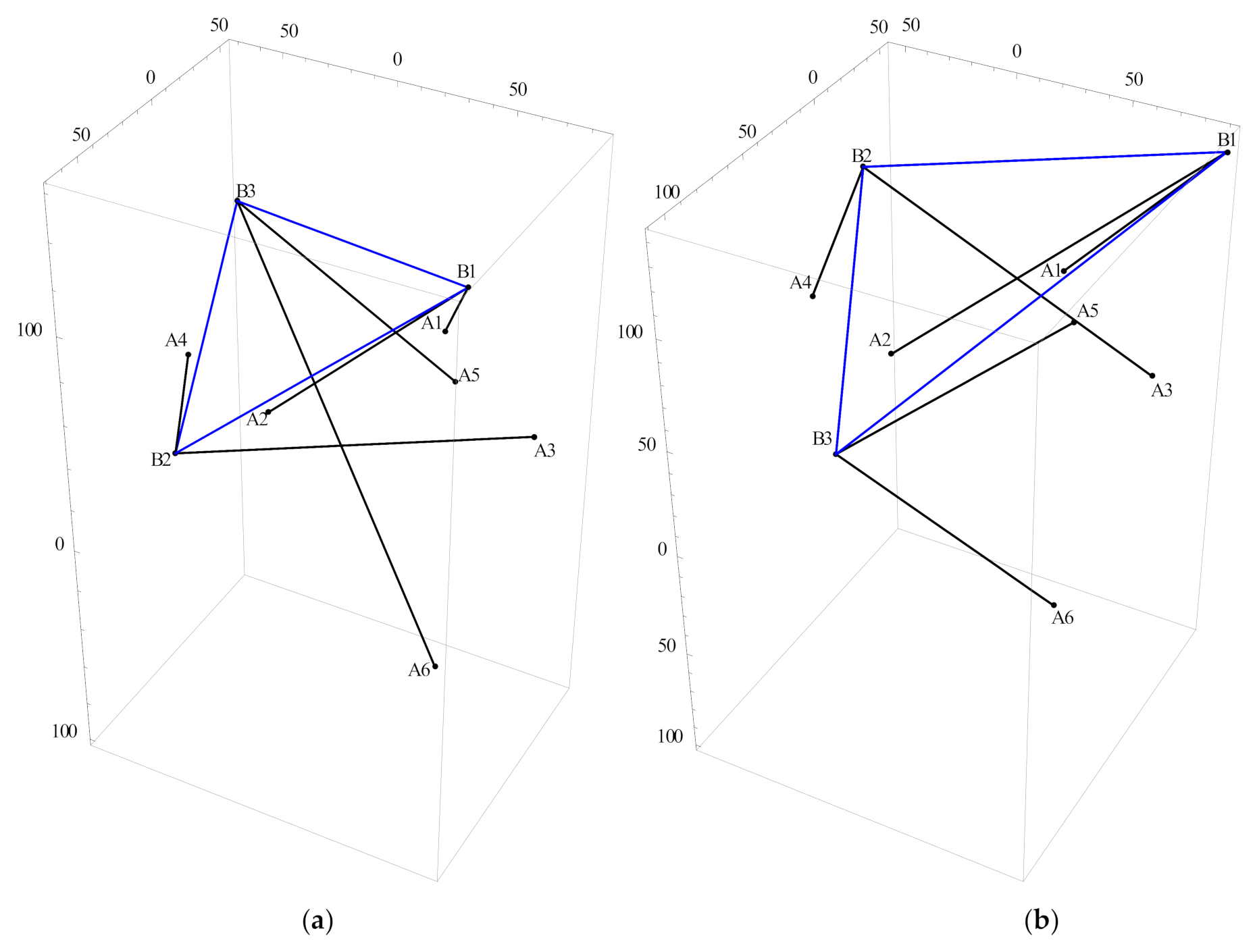
5.1. Example 1
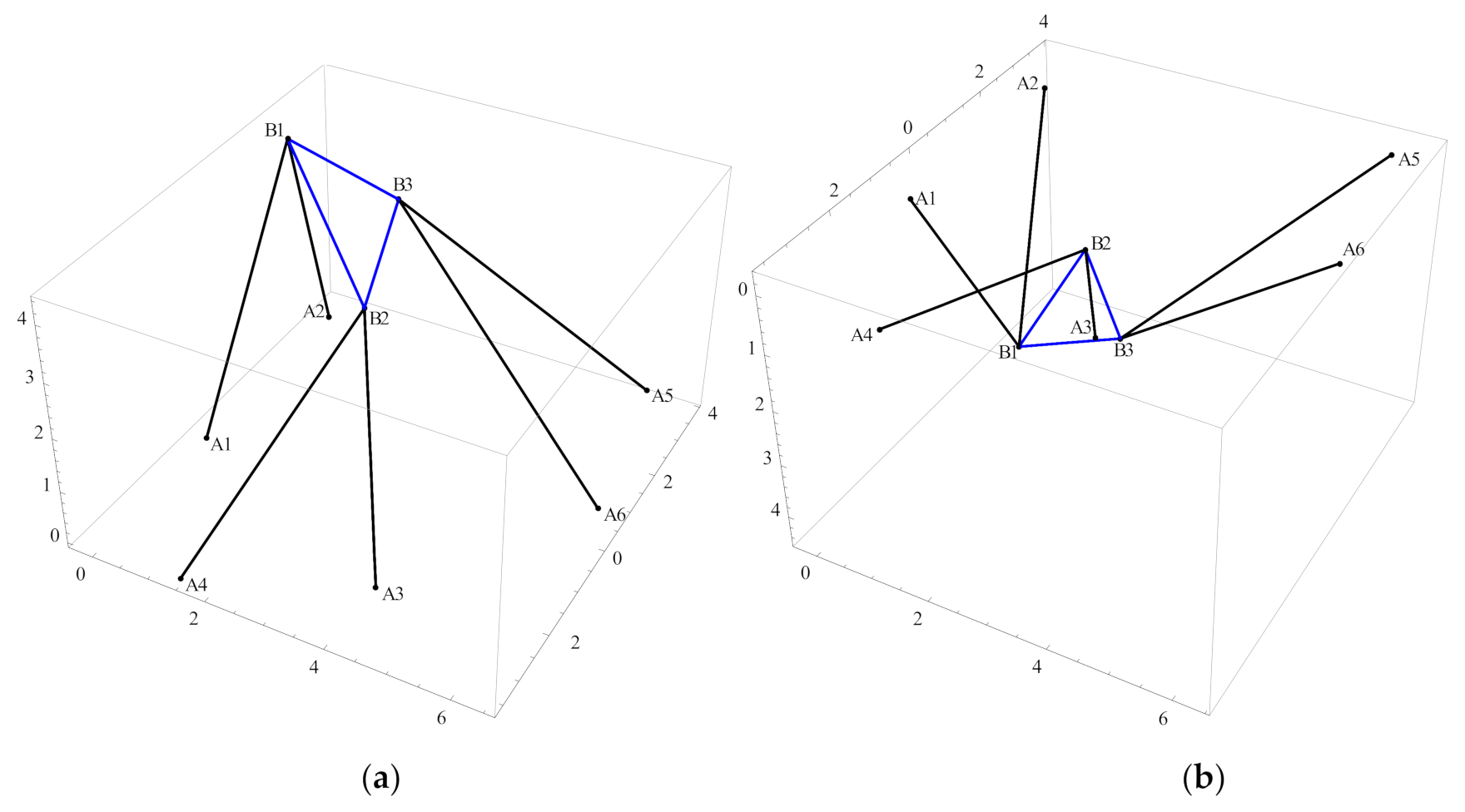
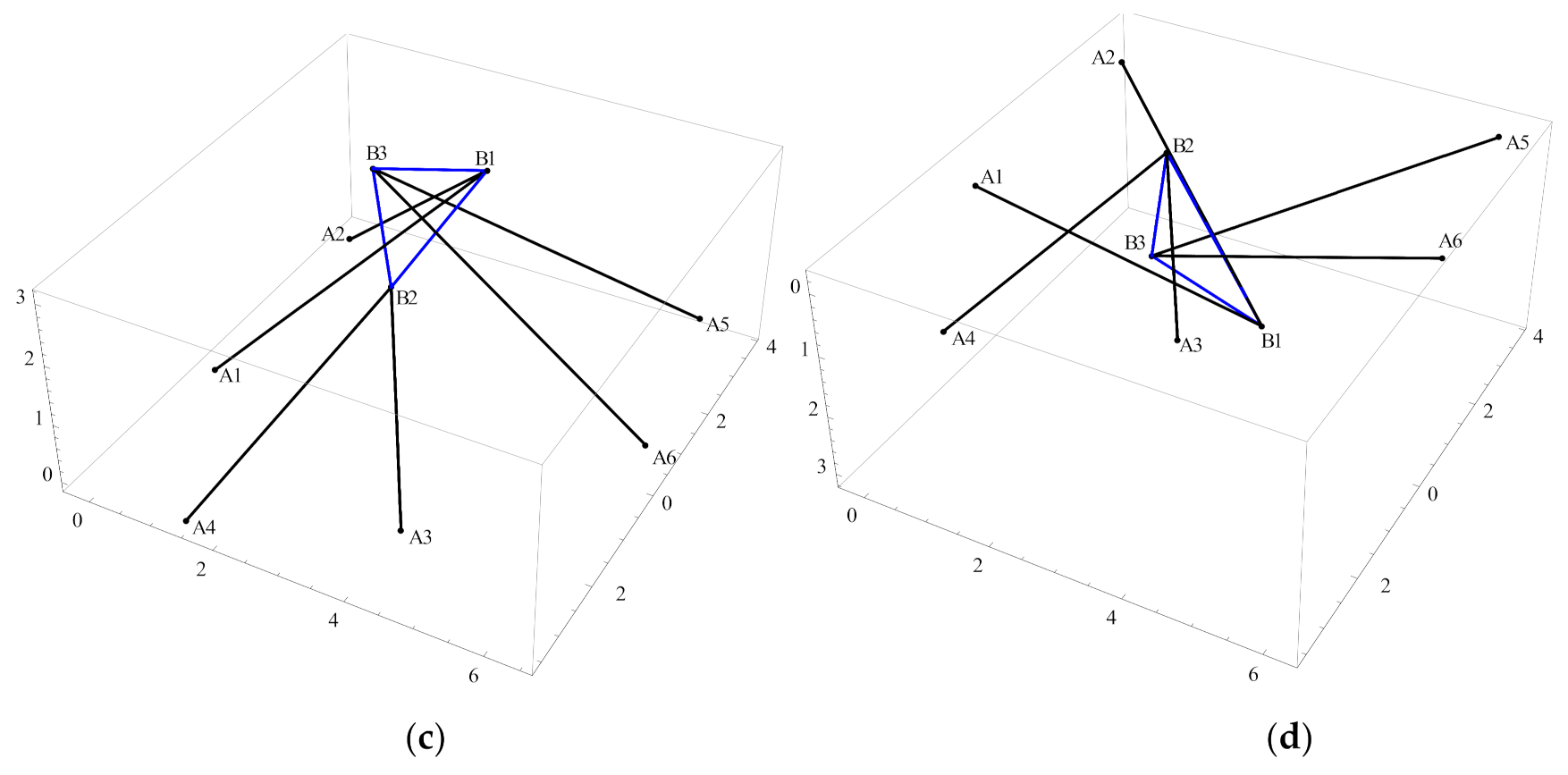
5.2. Example 2
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Equation (12)
Appendix B. Derivation of Equations (37)–(41)
References
- Gough, V.E. Contribution to discussion of papers on research in automobile stability, control and tyre performance. Proc. Automot. Div. Inst. Mech. Eng. 1956, 171, 392–394. [Google Scholar]
- Stewart, D. A platform with six degree of freedom. Proceedings of the Institution of Mechanical Engineers. Part. I: J. Syst. Control. Eng. 1965, 180, 371–386. [Google Scholar]
- Luces, M.; Mills, J.K.; Benhabib, B. A Review of Redundant Parallel Kinematic Mechanisms. J. Intell. Robot. Syst. 2016, 86, 175–198. [Google Scholar] [CrossRef]
- Karger, A.; Husty, M. Classification of all self-motions of the original Stewart-Gough platform. Comput. Des. 1998, 30, 205–215. [Google Scholar] [CrossRef]
- Study, E. Geometrie der Dynamen—Die Zusammensetzung von Kraftenund verwandte Gegenstande der Geometrie, Leipzig, Verlag und Druck von B.G. Teubner, 1903. Math. Gaz. 1904, 3, 15–16. [Google Scholar]
- Ypma, T.J. Historical Development of the Newton–Raphson Method. Siam Rev. 1995, 37, 531–551. [Google Scholar] [CrossRef] [Green Version]
- Barton, M.; Shragai, N.; Elber, G. Kinematic Simulation of Planar and Spatial Mechanisms Using a Polynomial Constraints Solver. Comput. Des. Appl. 2009, 6, 115–123. [Google Scholar] [CrossRef]
- Griffis, M.; Duffy, J. A forward displacement analysis of a class of stewart platforms. J. Robot. Syst. 1989, 6, 703–720. [Google Scholar] [CrossRef]
- Nanua, P.; Waldron, K.J.; Murthy, V. Direct kinematic solution of a Stewart platform. IEEE Trans. Robot. Autom. 1990, 6, 438–443. [Google Scholar] [CrossRef]
- Innocenti, C.; Parenti-Castelli, V. Direct position analysis of the Stewart platform mechanism. Mech. Mach. Theory 1990, 25, 611–621. [Google Scholar] [CrossRef]
- Merlet, J.-P. Direct kinematics and assembly modes of parallel manipulators. Int. J. Robot. Res. 1992, 11, 150–162. [Google Scholar] [CrossRef]
- Zhang, Y.; Liao, Q.; Wei, S.; Wei, F.; Li, D. A Novel Geometric Modeling and Solution Method for Forward Displacement Analysis of 6-3 Stewart Platforms. In Proceedings of the Lecture Notes in Electrical Engineering; Springer: Singapore, 2017; pp. 911–924. [Google Scholar]
- Wei, F.; Wei, S.; Zhang, Y.; Liao, Q. Forward Displacement Analysis of a General 6-3 Stewart Platform Using Conformal Geometric Algebra. Math. Probl. Eng. 2017, 2017 Pt 2, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, X.; Wei, S.; Li, D.; Liao, Q. CGA-Based approach to direct kinematics of parallel mechanisms with the 3-RS structure. Mech. Mach. Theory 2018, 124, 162–178. [Google Scholar] [CrossRef]
- Li, H.; Hestenes, D.; Rockwood, A. Generalized Homogeneous Coordinates for Computational Geometry. In Geometric Computing with Clifford Algebras; Springer: Berlin/Heidelberg, Germany, 2001; pp. 27–59. [Google Scholar]
- Li, H. Conformal Geometric Algebra-A new framework for computational geometry. J. Comput. Aided Des. Comput. Graph. 2005, 17, 2383–2393. [Google Scholar]
- Rosenhahn, B.; Sommer, G. Pose Estimation in Conformal Geometric Algebra Part I: The Stratification of Mathematical Spaces. J. Math. Imaging Vis. 2005, 22, 27–48. [Google Scholar] [CrossRef] [Green Version]
- Hildenbrand, D.; Fontijne, D.; Perwass, C.; Dorst, L. Geometric algebra and its application to computer graphics. In Proceedings of the Euro Graphics 2004 Tutorial, Grenoble, France, 30 August–3 September 2004; pp. 1–49. [Google Scholar]
- Kim, J.S.; Jeong, J.H.; Park, J.H. Inverse kinematics and geometric singularity analysis of a 3-SPS/S redundant motion mechanism using conformal geometric algebra. Mech. Mach. Theory 2015, 90, 23–36. [Google Scholar] [CrossRef]
- Kleppe, A.L.; Egeland, O. Inverse Kinematics for Industrial Robots using Conformal Geometric Algebra. Model. Identif. Control. A Nor. Res. Bull. 2016, 37, 63–75. [Google Scholar] [CrossRef]
- Tørdal, S.S.; Hovland, G.; Yapin, I. Efficient Implementation of Inverse Kinematics on a 6-DOF Industrial Robot using Con-formal Geometric Algebra. Adv. Appl. Clifford Algebras 2017, 27, 2067–2082. [Google Scholar] [CrossRef]
- Song, Y.; Han, P.; Wang, P. Type synthesis of 1T2R and 2R1T parallel mechanisms employing conformal geometric algebra. Mech. Mach. Theory 2018, 121, 475–486. [Google Scholar] [CrossRef]
- Hrdina, J.; Návrat, A.; Vašík, P.; Matoušek, R. CGA-based robotic snake control. Adv. Appl. Clifford Algebras 2016, 27, 621–632. [Google Scholar] [CrossRef]
- Hrdina, J.; Návrat, A.; Vašík, P.; Matoušek, R. Geometric Control of the Trident Snake Robot Based on CGA. Adv. Appl. Clifford Algebras 2016, 27, 633–645. [Google Scholar] [CrossRef]
- Hrdina, J.; Návrat, A.; Vašík, P. Control of 3-Link Robotic Snake Based on Conformal Geometric Algebra. Adv. Appl. Clifford Algebras 2015, 26, 1069–1080. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Wei, S.; Wang, Y.; Zhang, X.; Zhang, P.; Liang, C. A Geometric Modeling and Computing Method for Direct Kinematic Analysis of 6-4 Stewart Platforms. Math. Probl. Eng. 2018, 2018 Pt 2, 1–9. [Google Scholar] [CrossRef]
- Huang, X.; Ma, C.; Su, H. A geometric algebra algorithm for the closed-form forward displacement analysis of 3-PPS parallel mechanisms. Mech. Mach. Theory 2019, 137, 280–296. [Google Scholar] [CrossRef]

| Entity | IPNS | Grade | OPNS | Grade |
|---|---|---|---|---|
| Point | 1 | 4 | ||
| Sphere | 1 | 4 | ||
| Plane | 1 | 4 | ||
| Line | 2 | 3 | ||
| Circle | 2 | 3 | ||
| Point pair | 3 | 2 |
| Coordinates | B1 | B2 | B3 | ||
|---|---|---|---|---|---|
| 1 | 0.8920 + 0.4520i | 79.5345 | −26.0943 | −70.9222 | |
| −45.8809 | −68.9458 | 54.3105 | |||
| 152.9020 | 62.3955 | 94.3853 | |||
| 2 | −0.9997 + 0.0231i | 90.9017 | −40.7764 | 14.0676 | |
| 53.3945 | 6.28516 | −108.359 | |||
| 135.3850 | 117.424 | 71.8847 | |||
| 3 | −0.9597 + 0.2809i | 82.5389 | −48.8262 | −6.78228 | |
| 51.0783 | 24.7277 | −100.5170 | |||
| 145.9150 | 101.985 | 74.2181 | |||
| 4 | 0.6405 + 0.7680i | 68.8676 | −47.0212 | 21.2493 | |
| −33.0062 | 21.0887 | 137.061 | |||
| 165.8070 | 106.44 | 95.7391 |
| O-XYZ | A1 | A2 | A3 | A4 | A5 | A6 |
|---|---|---|---|---|---|---|
| aix | 0 | 0 | 4.0803 | 1.4802 | 5.7676 | 6.2278 |
| aiy | −0.6749 | 3.2366 | −2.3929 | −3.5971 | 3.8962 | 0.7516 |
| aiz | 0 | 0 | 0 | 0 | 0 | 0 |
| Coordinates | B1 | B2 | B3 | ||
|---|---|---|---|---|---|
| 1 | 0.0366 − 0.9993i | 0.1570 | 1.6474 | 2.0248 | |
| 1.8880 | 1.6311 | 2.0987 | |||
| 4.2903 | 1.6994 | 3.6070 | |||
| 2 | 0.0366 + 0.9993i | 0.1570 | 1.6474 | 2.0248 | |
| 1.8880 | 1.6311 | 2.0987 | |||
| −4.2903 | −1.6994 | −3.6070 | |||
| 3 | 0.7239 − 0.6899i | 3.1079 | 1.5287 | 1.1961 | |
| 1.8880 | 1.8873 | 1.9774 | |||
| 2.9618 | 0.4111 | 2.3812 | |||
| 4 | 0.7239 + 0.6899i | 3.1079 | 1.5287 | 1.1961 | |
| 1.8880 | 1.8873 | 1.9774 | |||
| −2.9618 | −0.4111 | −2.3812 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Wei, S.; Zhang, Y.; Liao, Q. A Novel Geometric Modeling and Calculation Method for Forward Displacement Analysis of 6-3 Stewart Platforms. Mathematics 2021, 9, 442. https://doi.org/10.3390/math9040442
Zhu G, Wei S, Zhang Y, Liao Q. A Novel Geometric Modeling and Calculation Method for Forward Displacement Analysis of 6-3 Stewart Platforms. Mathematics. 2021; 9(4):442. https://doi.org/10.3390/math9040442
Chicago/Turabian StyleZhu, Ganmin, Shimin Wei, Ying Zhang, and Qizheng Liao. 2021. "A Novel Geometric Modeling and Calculation Method for Forward Displacement Analysis of 6-3 Stewart Platforms" Mathematics 9, no. 4: 442. https://doi.org/10.3390/math9040442
APA StyleZhu, G., Wei, S., Zhang, Y., & Liao, Q. (2021). A Novel Geometric Modeling and Calculation Method for Forward Displacement Analysis of 6-3 Stewart Platforms. Mathematics, 9(4), 442. https://doi.org/10.3390/math9040442





