Flow towards a Stagnation Region of a Vertical Plate in a Hybrid Nanofluid: Assisting and Opposing Flows
Abstract
1. Introduction
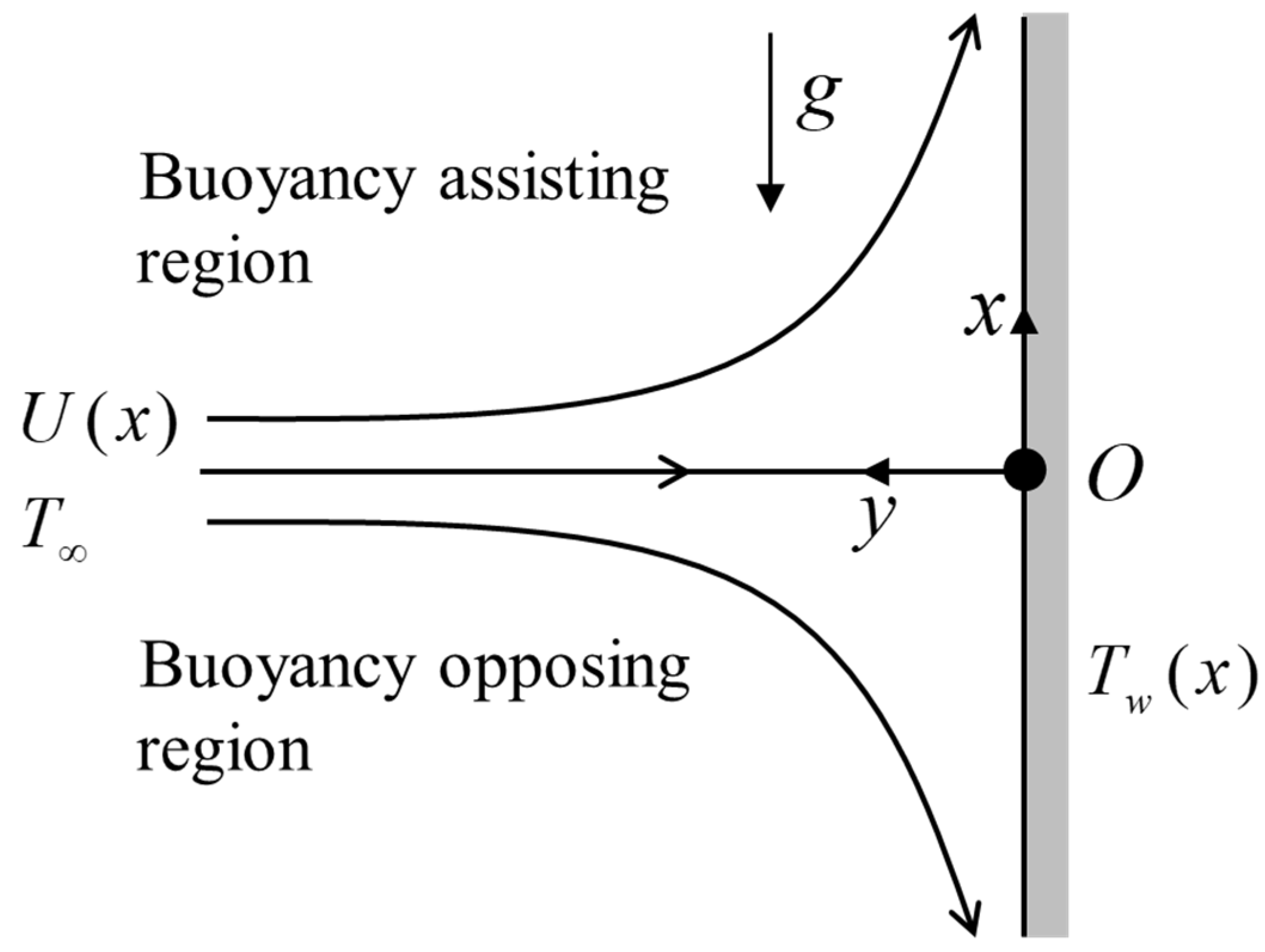
2. Mathematical Formulation
3. Stability Analysis
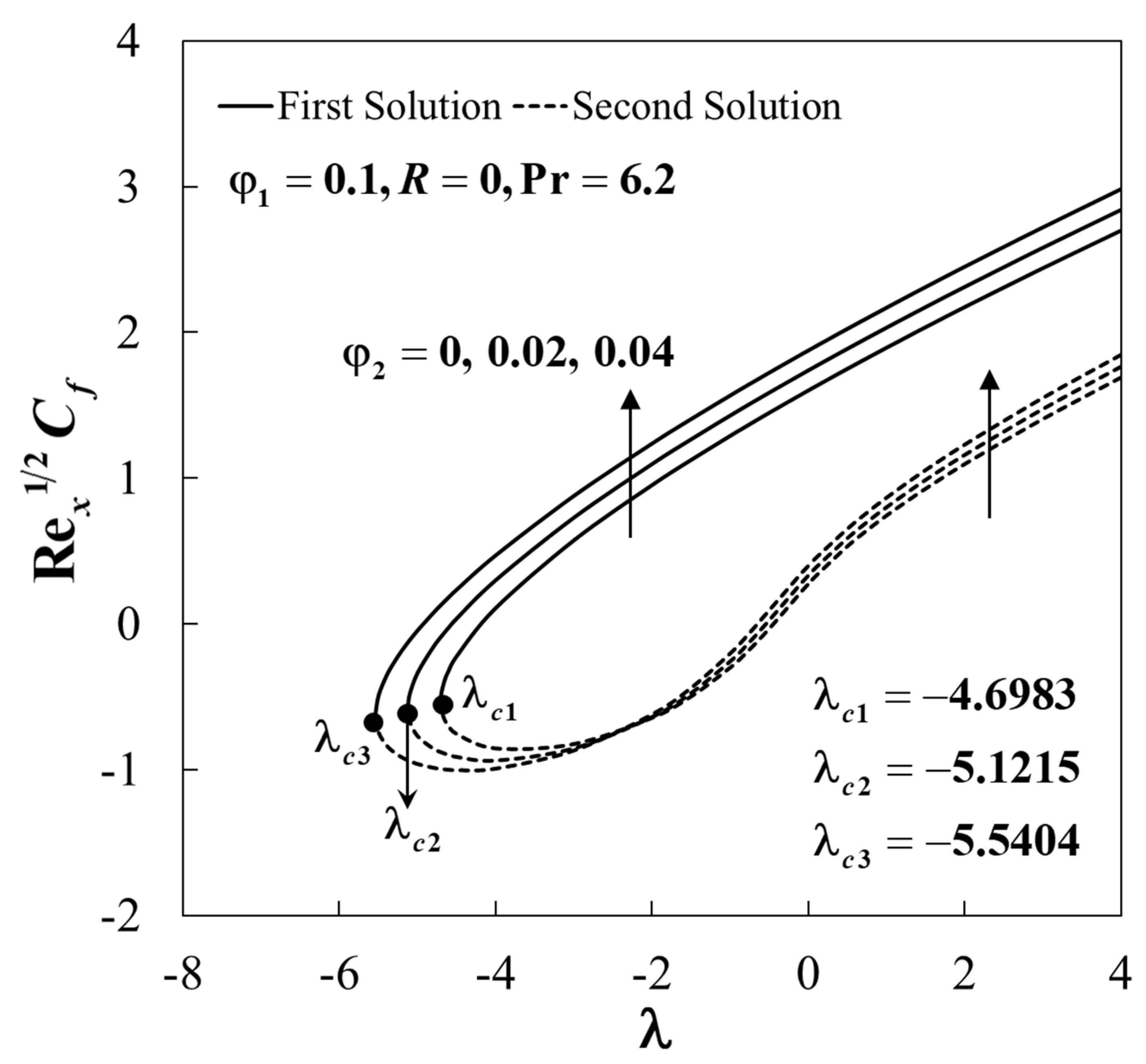
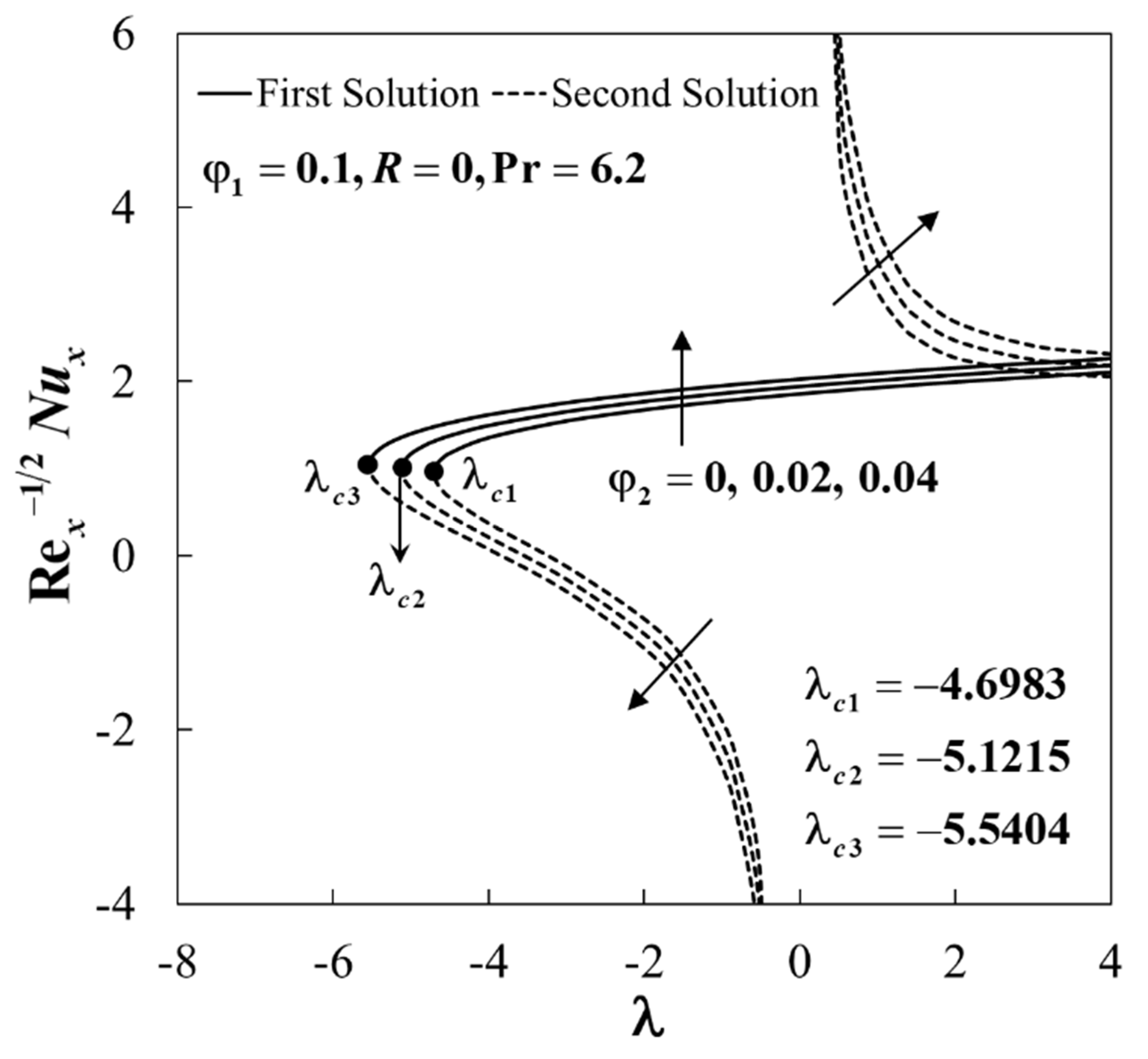
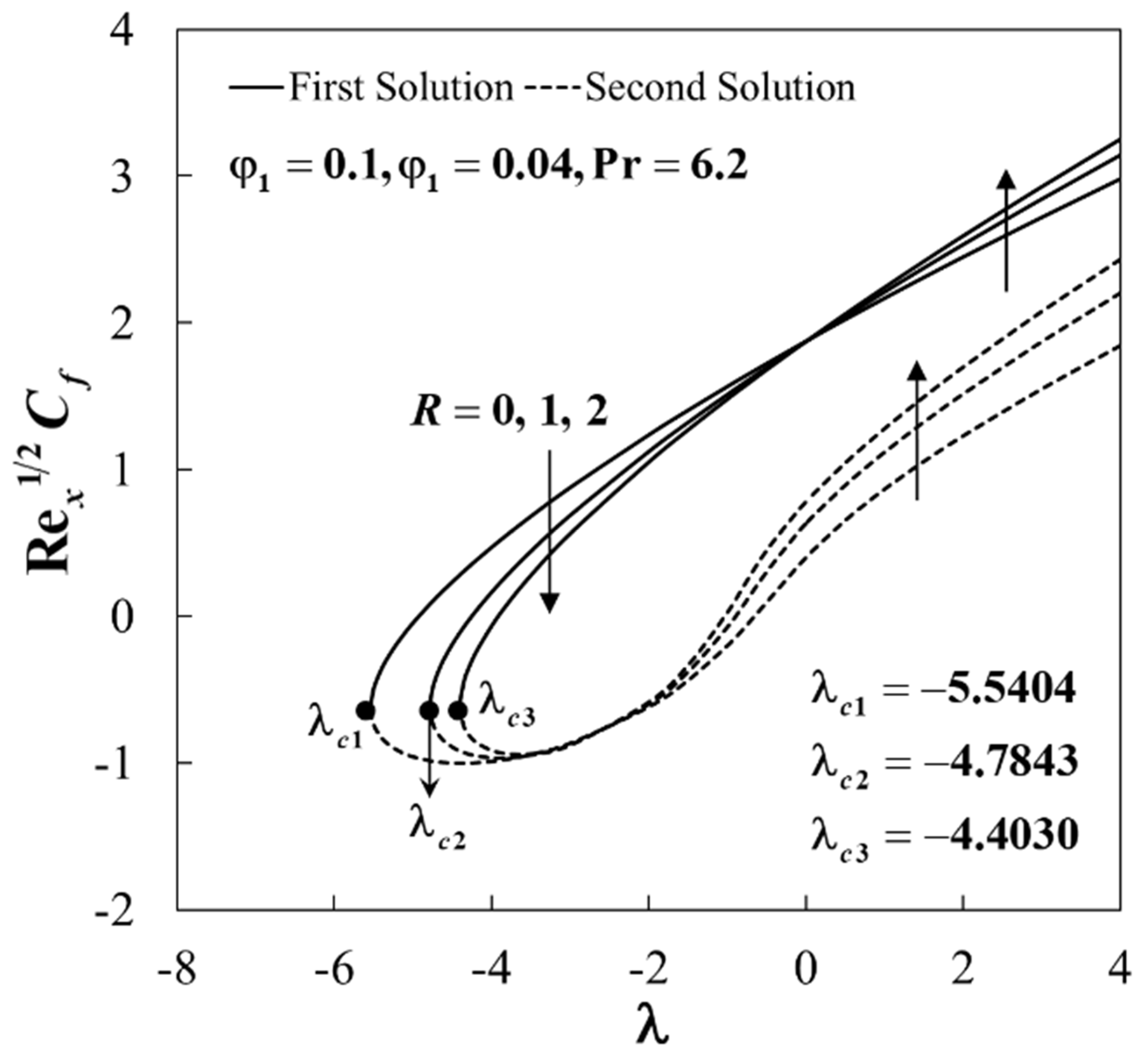
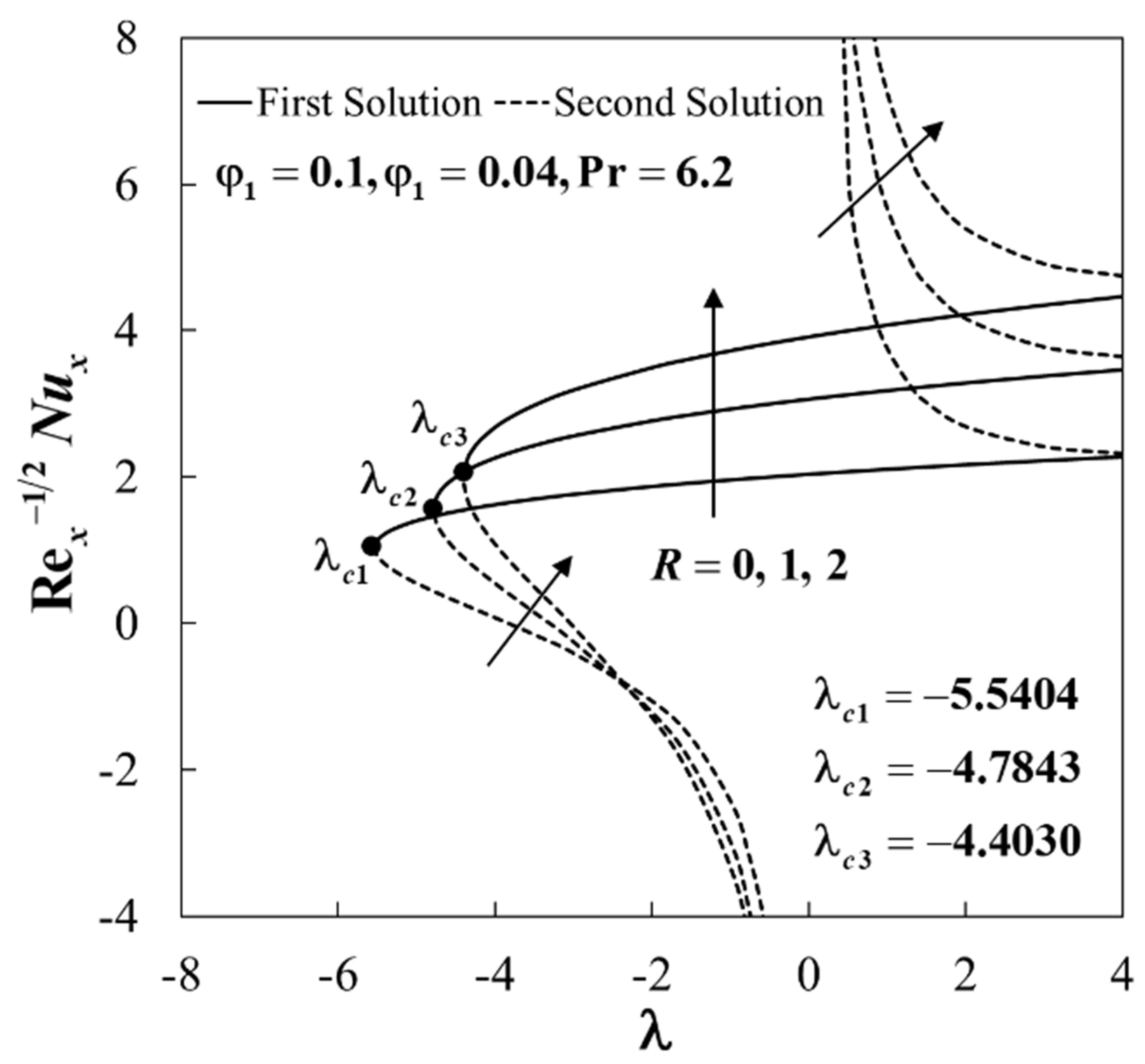
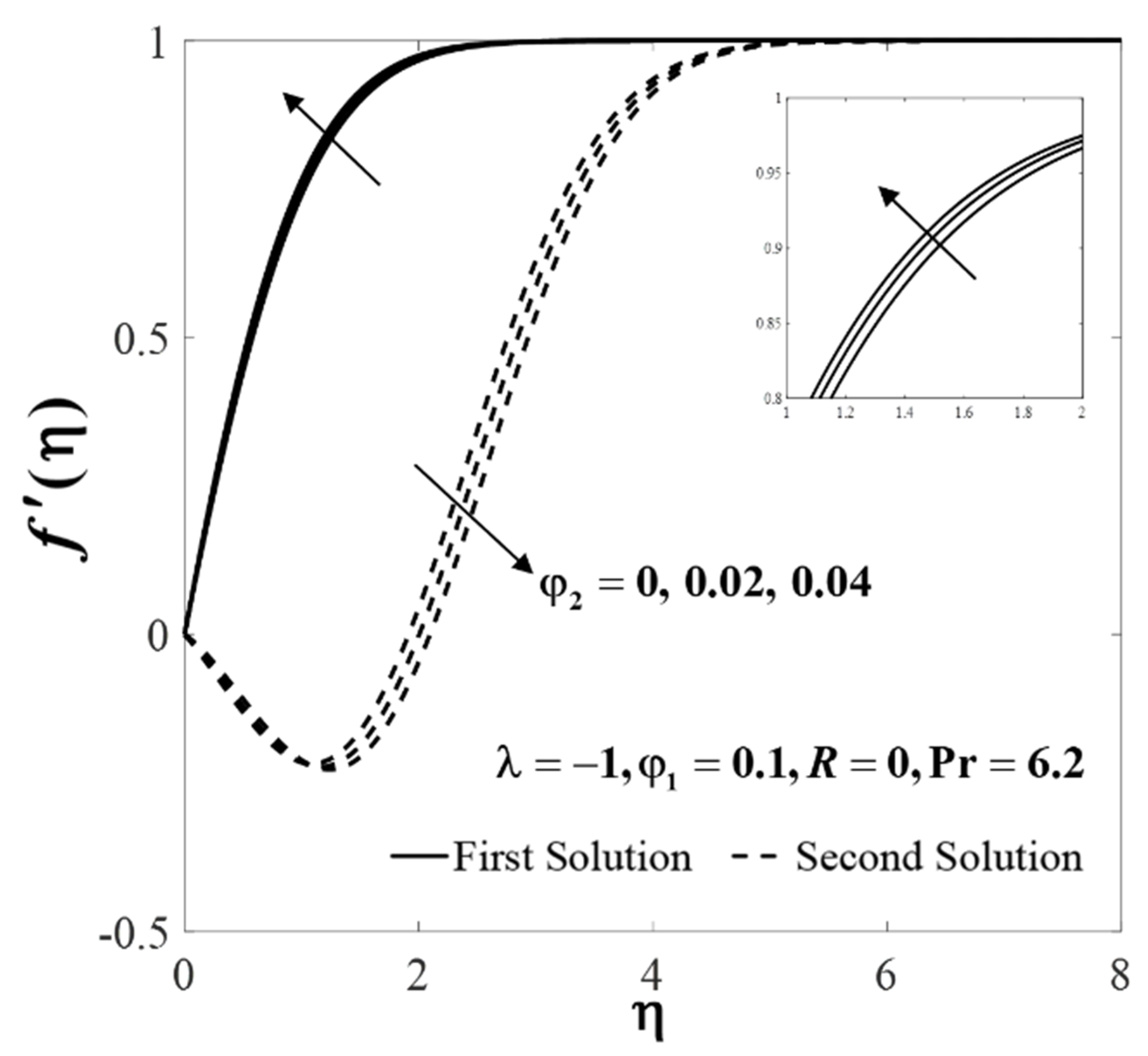
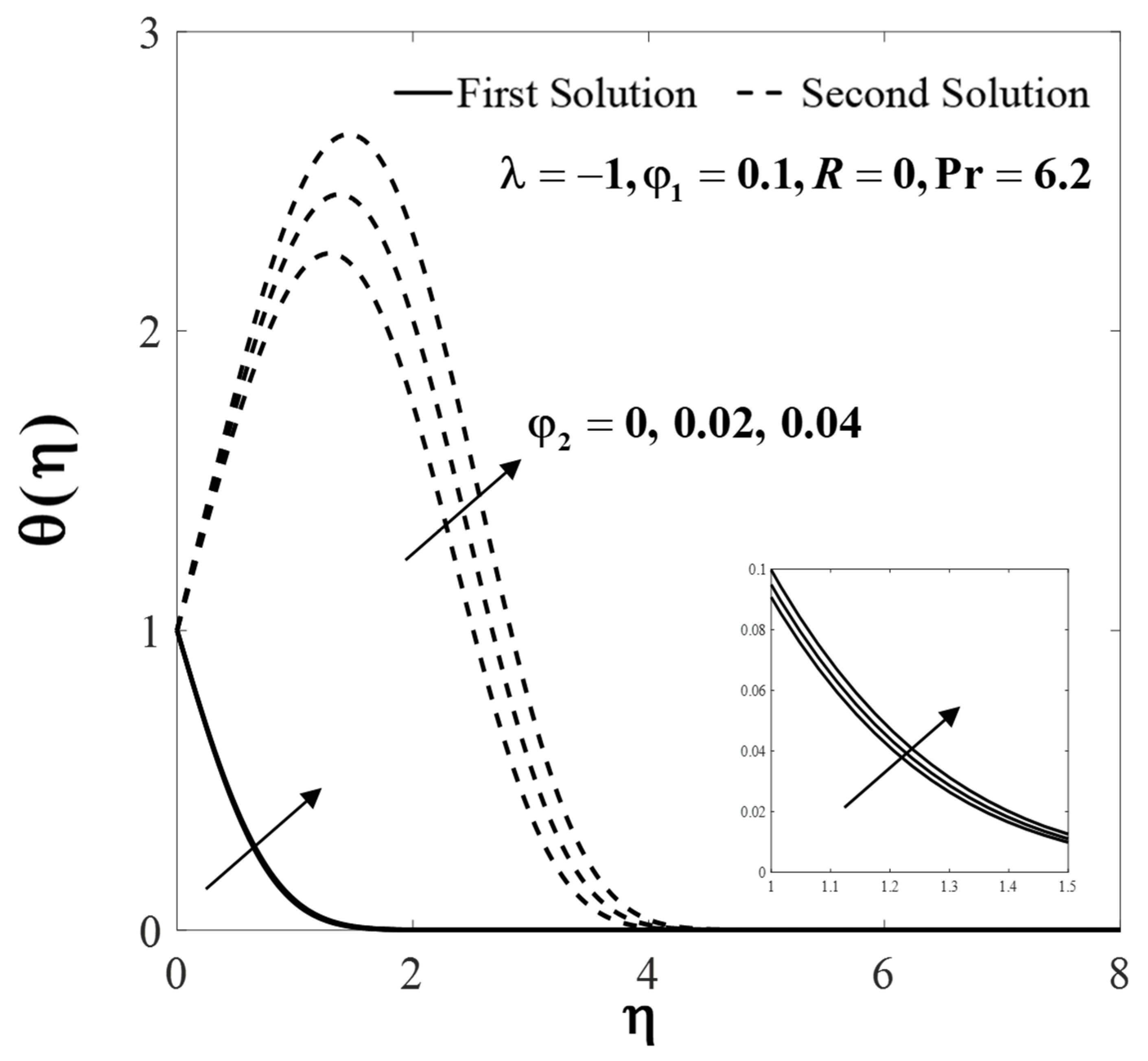
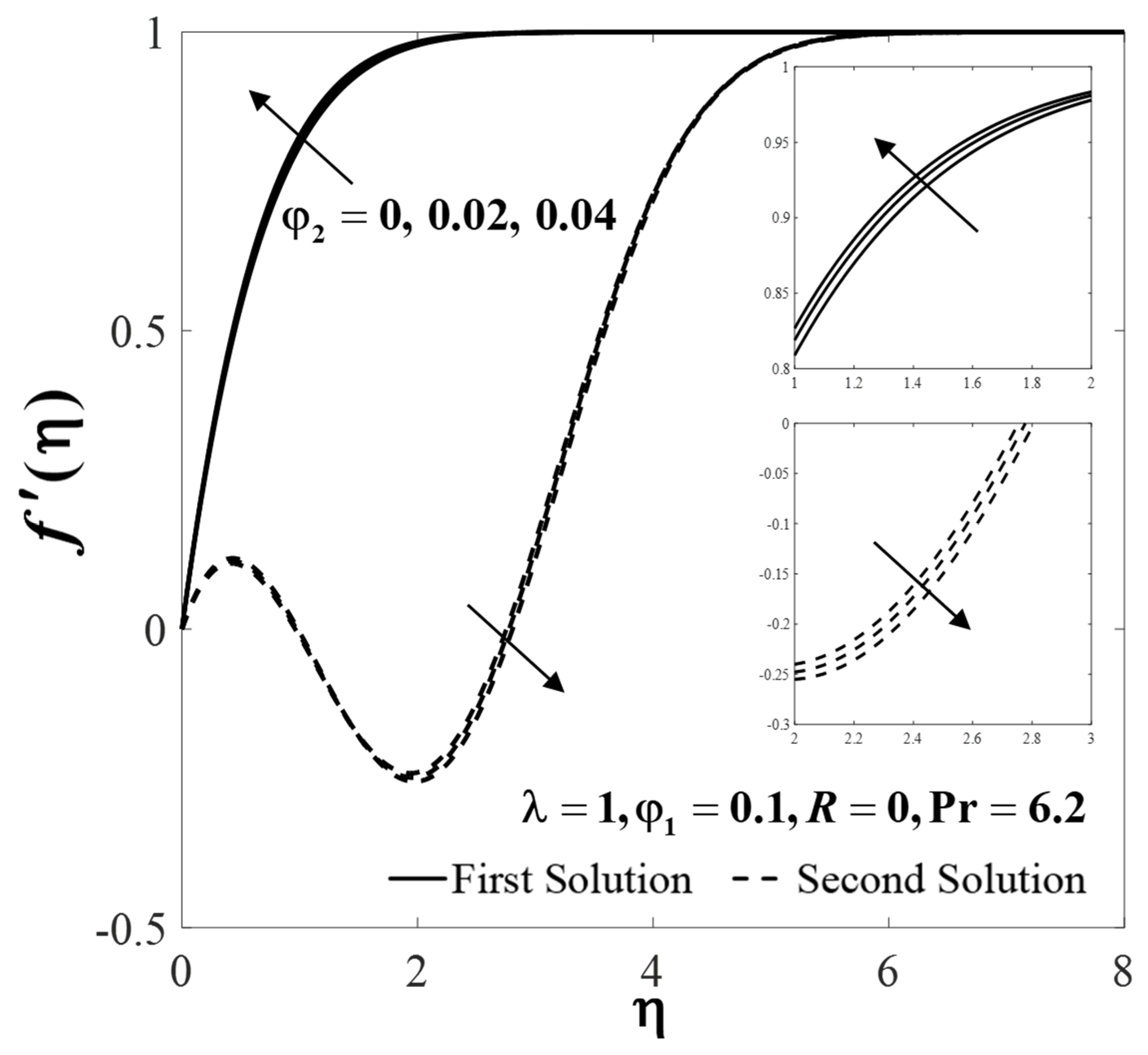
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hiemenz, K. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–410. [Google Scholar]
- Homann, F. Der Einflub grober Zähigkeit bei der Strömung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 1936, 16, 153–164. [Google Scholar] [CrossRef]
- Chiam, T.C. Stagnation-point flow towards a stretching plate. J. Phys. Soc. Jpn. 1994, 63, 2443–2444. [Google Scholar] [CrossRef]
- Merkin, J.H. Mixed convection boundary layer flow on a vertical surface in a saturated porous medium. J. Eng. Math. 1980, 14, 301–313. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Arifin, N.M.; Pop, I. Dual solutions in mixed convection flow near a stagnation point on a vertical porous plate. Int. J. Therm. Sci. 2008, 47, 417–422. [Google Scholar] [CrossRef]
- Subhashini, S.V.; Samuel, N.; Pop, I. Effects of buoyancy assisting and opposing flows on mixed convection boundary layer flow over a permeable vertical surface. Int. Commun. Heat Mass Transf. 2011, 38, 499–503. [Google Scholar] [CrossRef]
- Roşca, A.V.; Roşca, N.C.; Pop, I. Note on dual solutions for the mixed convection boundary layer flow close to the lower stagnation point of a horizontal circular cylinder: Case of constant surface heat flux. Sains Malays 2014, 43, 1239–1247. [Google Scholar]
- Khashi’ie, N.S.; Arifin, N.M.; Rashidi, M.M.; Hafidzuddin, E.H.; Wahi, N. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Anal. Calorim. 2019, 8, 1–14. [Google Scholar] [CrossRef]
- Ali, F.M.; Naganthran, K.; Nazar, R.; Pop, I. MHD mixed convection boundary layer stagnation-point flow on a vertical surface with induced magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4697–4710. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: Lemont, IL, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Stagnation-point flow over a stretching/shrinking sheet in a nanofluid. Nanoscale Res. Lett. 2011, 6, 623. [Google Scholar] [CrossRef]
- Yacob, N.A.; Ishak, A.; Pop, I.; Vajravelu, K. Boundary layer flow past a stretching/shrinking surface beneath an external uniform shear flow with a convective surface boundary condition in a nanofluid. Nanoscale Res. Lett. 2011, 6, 314. [Google Scholar] [CrossRef] [PubMed]
- Waini, I.; Ishak, A.; Pop, I. Dufour and Soret effects on Al2O3-water nanofluid flow over a moving thin needle: Tiwari and Das model. Int. J. Numer. Methods Heat Fluid Flow 2020, in press. [Google Scholar] [CrossRef]
- Turcu, R.; Darabont, A.; Nan, A.; Aldea, N.; Macovei, D.; Bica, D.; Vekas, L.; Pana, O.; Soran, M.L.; Koos, A.A.; et al. New polypyrrole-multiwall carbon nanotubes hybrid materials. J. Optoelectron. Adv. Mater. 2006, 8, 643–647. [Google Scholar]
- Jana, S.; Salehi-Khojin, A.; Zhong, W.H. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim. Acta 2007, 462, 45–55. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surfaces A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Devi, S.P.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid. Alex. Eng. J. 2020, 59, 1881–1891. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Squeezed hybrid nanofluid flow over a permeable sensor surface. Mathematics 2020, 8, 898. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hiemenz flow over a shrinking sheet in a hybrid nanofluid. Results Phys. 2020, 19, 103351. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow on a shrinking cylinder with prescribed surface heat flux. Int. J. Numer. Methods Heat Fluid Flow 2020, in press. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Melting heat transfer of a hybrid nanofluid flow towards a stagnation point region with second-order slip. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2020, in press. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady hybrid nanofluid flow on a stagnation point of a permeable rigid surface. ZAMM Z. Angew. Math. Mech. 2020, in press. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3012–3038. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Baleanu, D.; Nisar, K.S. Enhanced heat transfer in moderately ionized liquid due to hybrid MoS2/SiO2 nanofluids exposed by nonlinear radiation: Stability analysis. Crystals 2020, 10, 142. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Baleanu, D.; Sherif, E.S.M. Comparative investigation on MHD nonlinear radiative flow through a moving thin needle comprising two hybridized AA7075 and AA7072 alloys nanomaterials through binary chemical reaction with activation energy. J. Mater. Res. Technol. 2020, 9, 3817–3828. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Thermally stratified flow of Cu-Al2O3/water hybrid nanofluid past a permeable stretching/shrinking circular cylinder. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 63, 154–163. [Google Scholar]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on a stretching/shrinking cylinder. Sci. Rep. 2020, 10, 9296. [Google Scholar] [CrossRef] [PubMed]
- Khashi’ie, N.S.; Arifin, N.M.; Wahi, N.; Pop, I.; Nazar, R.; Hafidzuddin, E.H. Thermal marangoni flow past a permeable stretching/shrinking sheet in a hybrid Cu-Al2O3/water nanofluid. Sains Malays 2020, 49, 211–222. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady three-dimensional MHD nonaxisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Impact of anisotropic slip on the stagnation-point flow past a stretching/shrinking surface of the Al2O3-Cu/H2O hybrid nanofluid. Appl. Math. Mech. 2020, 41, 1401–1416. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Babu, J.A.R.; Kumar, K.K.; Rao, S.S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Yang, L.; Ji, W.; Mao, M.; Huang, J. An updated review on the properties, fabrication and application of hybrid-nanofluids along with their environmental effects. J. Clean. Prod. 2020, 257, 120408. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik und Atom-Theoretische Grundlagen; Springer: Berlin/Heidelberg, Germany, 1931. [Google Scholar]
- Cortell, R. Heat and fluid flow due to non-linearly stretching surfaces. Appl. Math. Comput. 2011, 217, 7564–7572. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
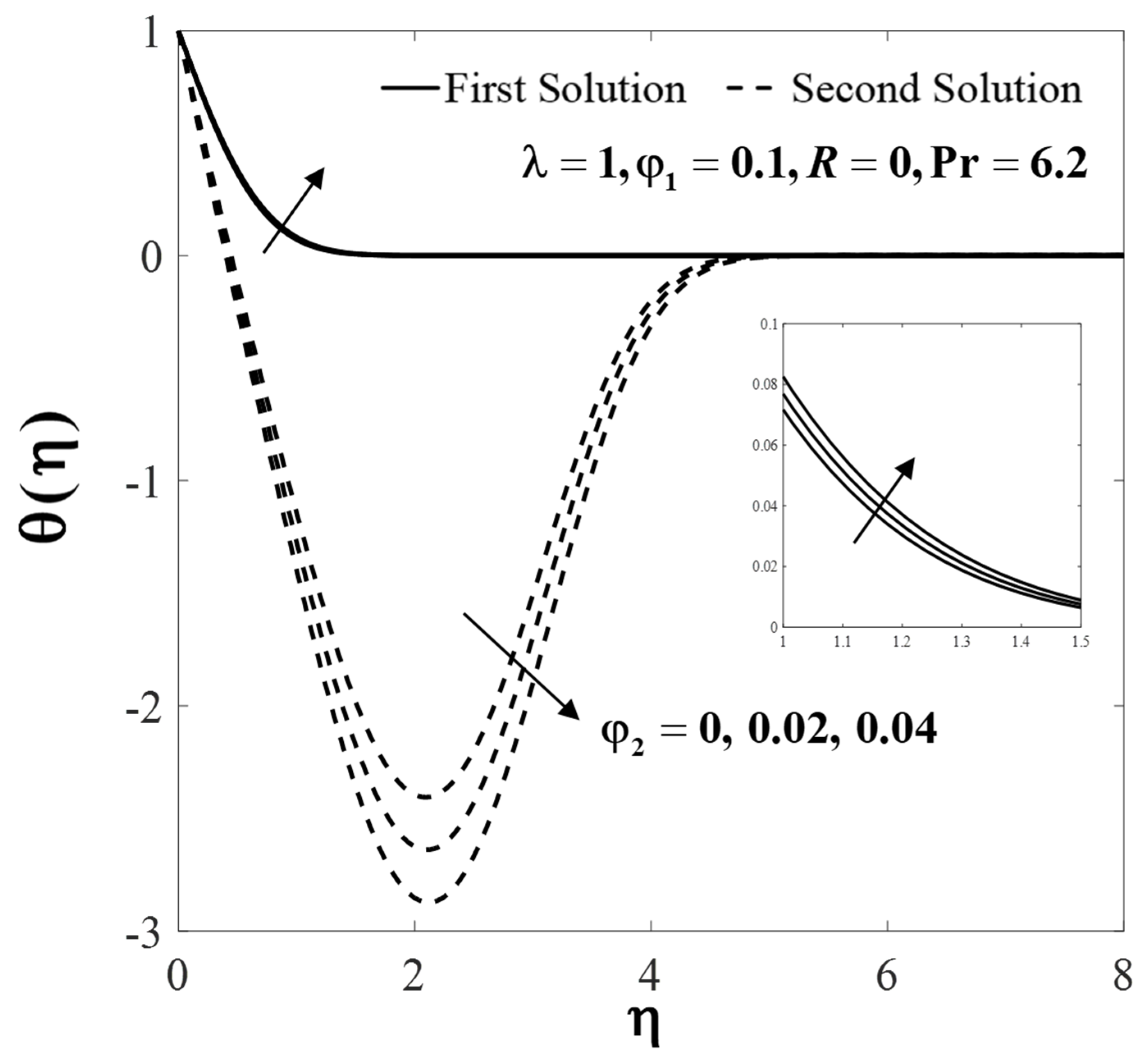
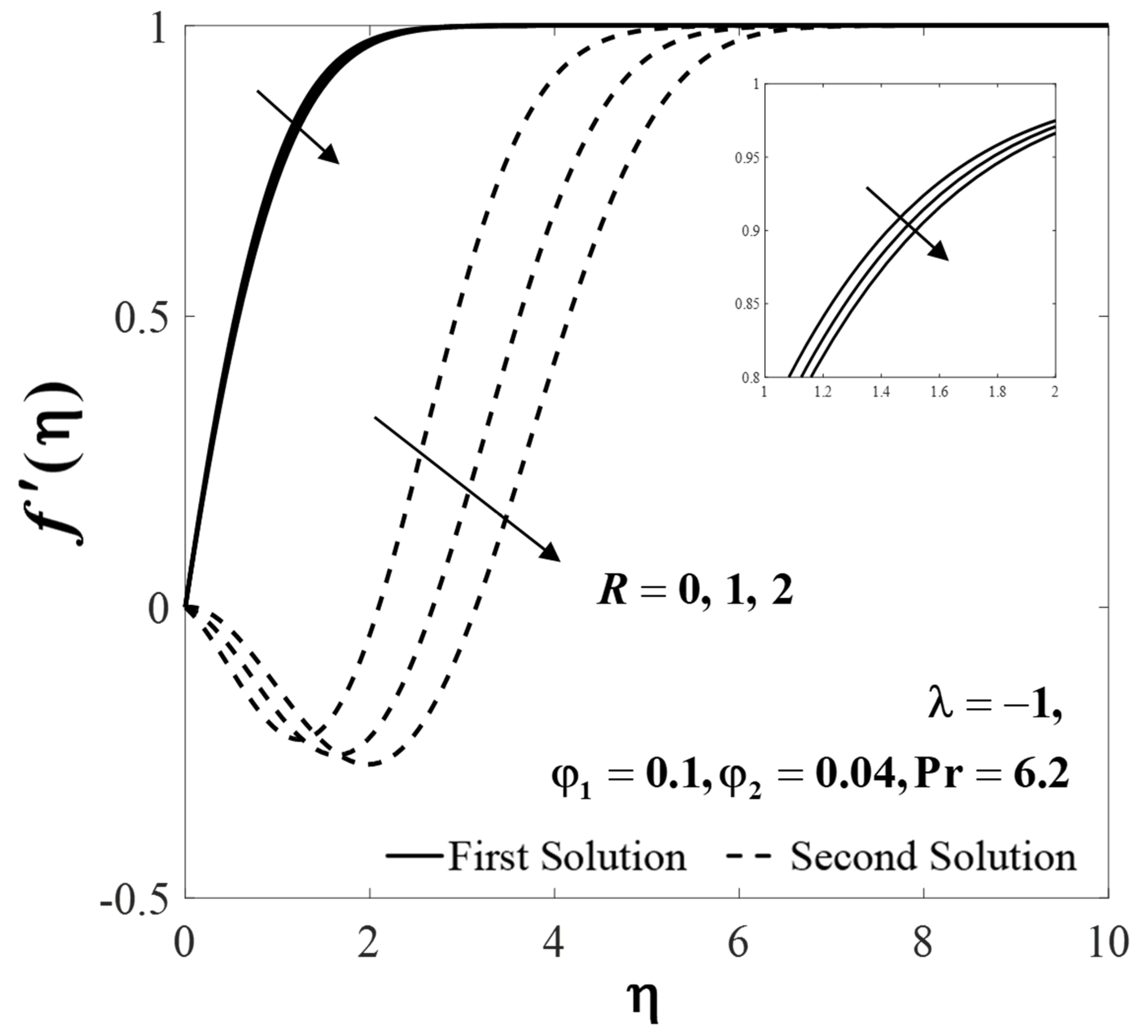
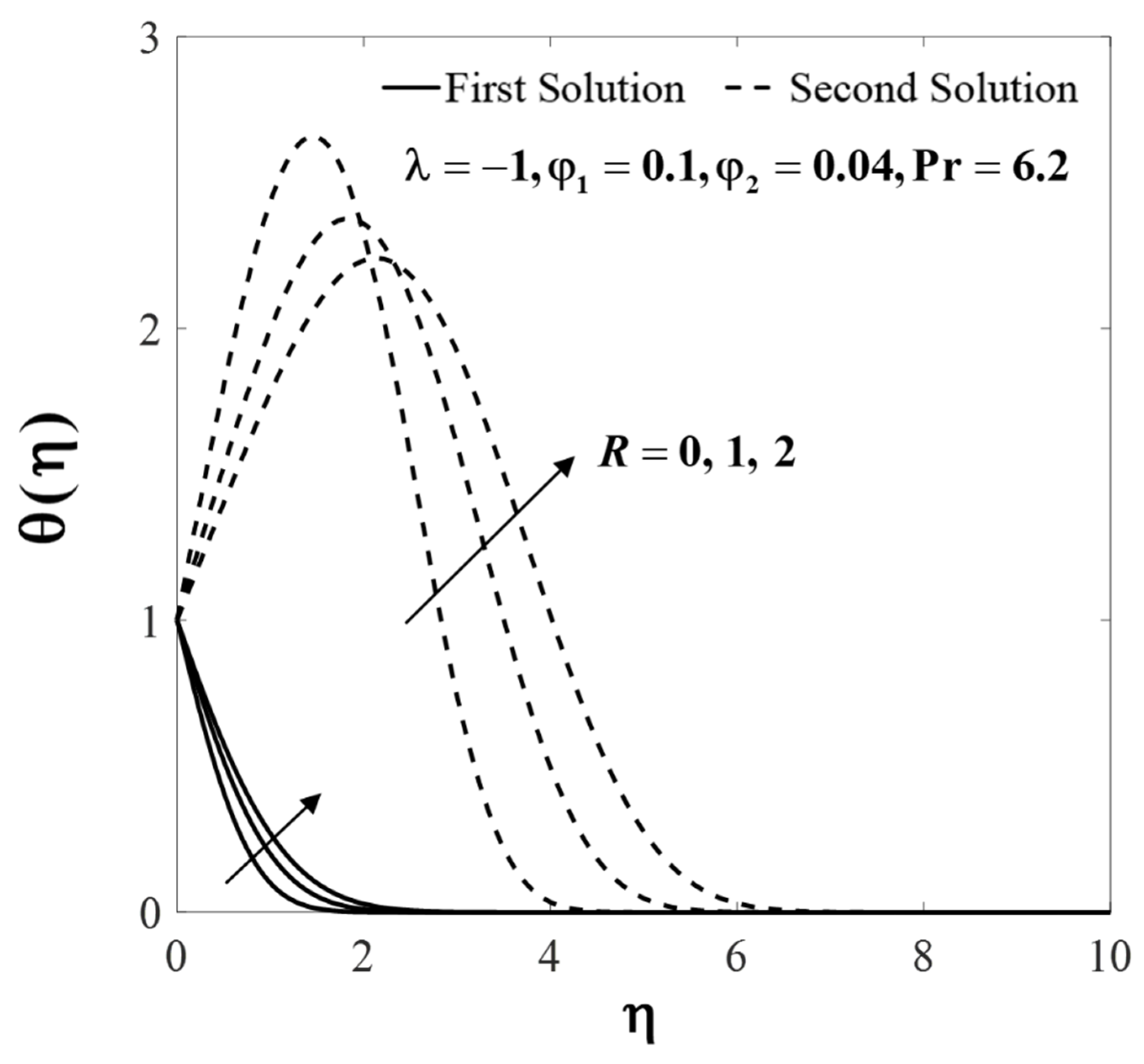


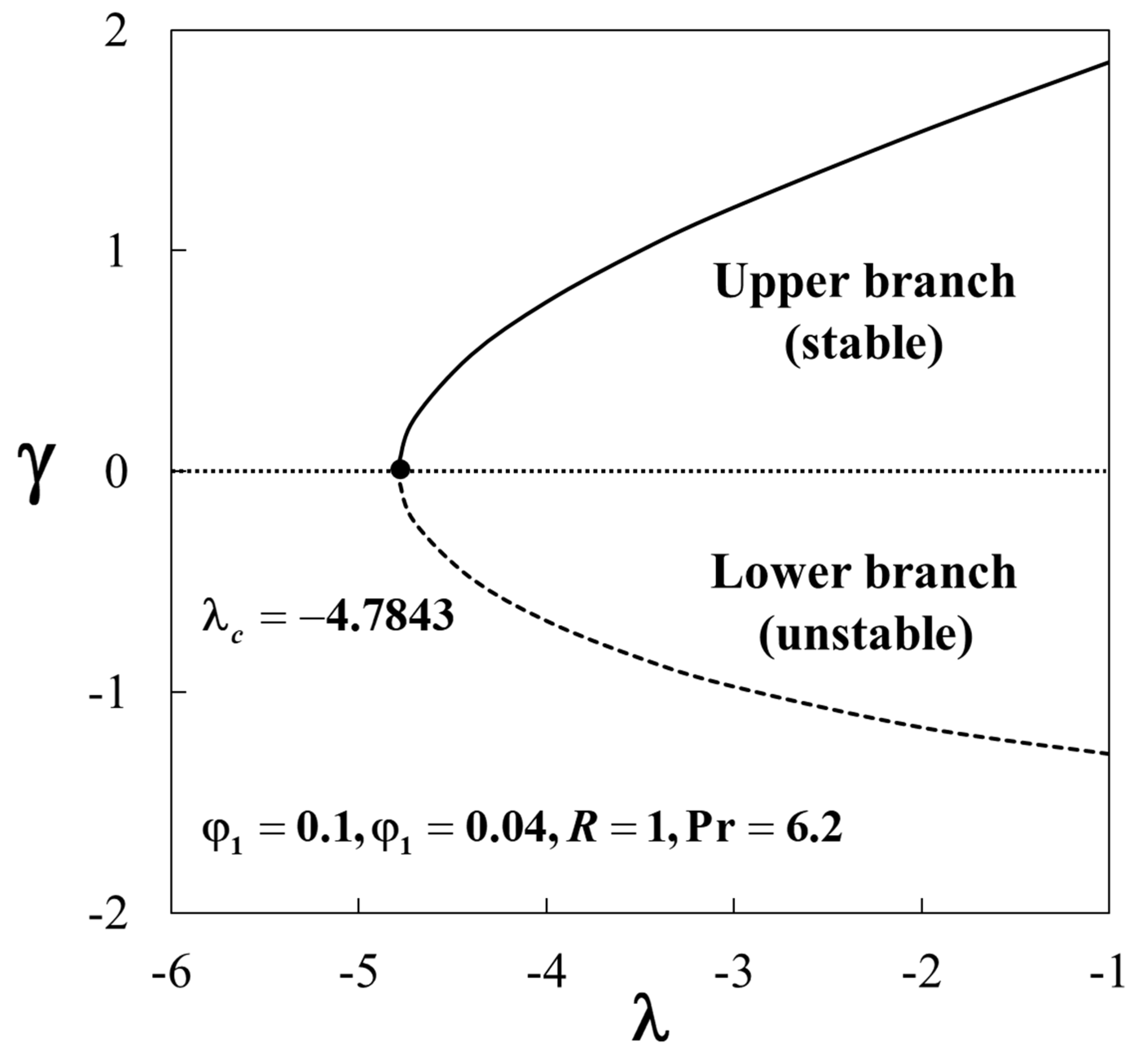
| Properties | Base Fluid | Nanoparticles | |
|---|---|---|---|
| Water | Al2O3 | Cu | |
| 997.1 | 3970 | 8933 | |
| 21 | 0.85 | 1.67 | |
| 4179 | 765 | 385 | |
| 0.613 | 40 | 400 | |
| Prandtl number, | 6.2 | ||
| Properties | Nanofluid | Hybrid Nanofluid |
|---|---|---|
| Dynamic viscosity | ||
| Density | ||
| Thermal expansion | ||
| Heat capacity | ||
| Thermal conductivity | where |
| Ishak et al. [5] | Present Results | Ishak et al. [5] | Present Results | |
|---|---|---|---|---|
| 0.7 | 1.7063 [1.2387] | 1.70632 [1.23873] | 0.7641 [1.0226] | 0.76406 [1.02263] |
| 1 | 1.6754 [1.1332] | 1.67544 [1.13319] | 0.8708 [1.1691] | 0.87078 [1.16913] |
| 6.2 | 1.52677 [0.61317] | 1.65242 [2.13399] | ||
| 7 | 1.5179 [0.5824] | 1.51791 [0.58240] | 1.7224 [2.2192] | 1.72238 [2.21919] |
| 10 | 1.4928 [0.4958] | 1.49284 [0.49578] | 1.9446 [2.4940] | 1.94462 [2.49403] |
| 20 | 1.4485 [0.3436] | 1.44848 [0.34364] | 2.4576 [3.1646] | 2.45759 [3.16461] |
| Bachok et al. [14] | Present Results | Present Results | ||
|---|---|---|---|---|
| −1 | 0.1 | 1.5811 [−0.1602] | 1.8967 [−2.3965] | |
| 0.2 | 2.3161 [0.1908] | 2.2872 [−3.8078] | ||
| 0 | 0.1 | 1.8843 | 1.8843 | 1.9692 |
| 0.2 | 2.6226 | 2.6227 | 2.3494 | |
| 1 | 0.1 | 2.1725 [0.8884] | 2.0336 [3.7324] | |
| 0.2 | 2.9183 [1.2445] | 2.4064 [5.7802] | ||
| Cu/Water | Cu-Al2O3/Water | |||||
|---|---|---|---|---|---|---|
| −1 | 0 | 0 | 0.9131 [−0.3719] | 1.4779 [−1.1835] | 1.2896 [−0.3019] | 1.7766 [−1.8984] |
| 0.02 | 1.0475 [−0.3432] | 1.5672 [−1.4219] | 1.4271 [−0.2546] | 1.8673 [−2.1625] | ||
| 0.04 | 1.1801 [−0.3071] | 1.6528 [−1.6605] | 1.5656 [−0.2008] | 1.9563 [−2.4313] | ||
| 1 | 0 | 0.8342 [−0.3440] | 2.5034 [−1.5160] | 1.2300 [−0.2235] | 2.7541 [−2.3870] | |
| 0.02 | 0.9755 [−0.2936] | 2.6044 [−1.8351] | 1.3717 [−0.1513] | 2.8430 [−2.6909] | ||
| 0.04 | 1.1136 [−0.2334] | 2.6950 [−2.1359] | 1.5137 [−0.0716] | 2.9272 [−2.9891] | ||
| 1 | 0 | 0 | 1.5268 [0.6132] | 1.6524 [2.1340] | 1.8958 [0.7439] | 1.9328 [3.0137] |
| 0.02 | 1.6524 [0.6617] | 1.7309 [2.4197] | 2.0304 [0.8031] | 2.0173 [3.3718] | ||
| 0.04 | 1.7789 [0.7136] | 1.8079 [2.7224] | 2.1675 [0.8656] | 2.1010 [3.7485] | ||
| 1 | 0 | 1.5928 [0.8445] | 2.8771 [3.7973] | 1.9481 [0.9837] | 3.0441 [4.7696] | |
| 0.02 | 1.7140 [0.9041] | 2.9422 [4.1738] | 2.0797 [1.0510] | 3.1132 [5.2068] | ||
| 0.04 | 1.8367 [0.9661] | 3.0043 [4.5633] | 2.2140 [1.1210] | 3.1807 [5.6584] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waini, I.; Ishak, A.; Pop, I. Flow towards a Stagnation Region of a Vertical Plate in a Hybrid Nanofluid: Assisting and Opposing Flows. Mathematics 2021, 9, 448. https://doi.org/10.3390/math9040448
Waini I, Ishak A, Pop I. Flow towards a Stagnation Region of a Vertical Plate in a Hybrid Nanofluid: Assisting and Opposing Flows. Mathematics. 2021; 9(4):448. https://doi.org/10.3390/math9040448
Chicago/Turabian StyleWaini, Iskandar, Anuar Ishak, and Ioan Pop. 2021. "Flow towards a Stagnation Region of a Vertical Plate in a Hybrid Nanofluid: Assisting and Opposing Flows" Mathematics 9, no. 4: 448. https://doi.org/10.3390/math9040448
APA StyleWaini, I., Ishak, A., & Pop, I. (2021). Flow towards a Stagnation Region of a Vertical Plate in a Hybrid Nanofluid: Assisting and Opposing Flows. Mathematics, 9(4), 448. https://doi.org/10.3390/math9040448








