1. Introduction
The method of event-triggered impulsive control (ETIC), which was introduced in the last decade, has been very successful. For instance, the method is based on algorithms that offer more precision to our calculations and more rapidity for the reaction to act on the system. Besides, it offers a discrete control which only allows for an intervention in critical moments when the system solution may deviate from the desired solution, in contrast with the classical method in the theory of control, which opts for a continuous control. In addition, the introduction of digital technology in recent years to control dynamic systems has given much importance to impulsive control, as this control is simpler to implement and often involves a less expensive mechanism. Furthermore, it has contributed to impressive results that have encouraged greater attention to impulsive control to control ordinary differential equations. The ETIC method transmits data packages and updates control inputs only when the predefined criterion is satisfied [
1,
2,
3]. In [
4], the stabilization of nonlinear systems was studied using the ETIC method, together with hybrid system tools.
The ETIC method was also used to stabilize networked systems (NCS) [
5,
6] and multi-agent systems (MASs) [
7,
8]. A survey of trends and techniques was given in [
9], and recently in [
10].
The success of the ETIC method in the context of controlling ordinary differential equations encouraged their generalization to be used to control partial differential equations. In [
11], the ETIC method was used to design a predictive control for spatially distributed processes with low-order dynamics and a limited number of output measurements modeled by nonlinear parabolic PDEs. In [
12], the ETIC method was used to construct a controller to achieve the exponential stabilization of a
uncertain semilinear diffusion equation under homogeneous Dirichlet or mixed boundary conditions. In [
13], the boundary controls for 1-dimensional linear hyperbolic systems of conservation laws were investigated.
More recently, based on Lyapunov analysis and the backstepping design method, an event-triggered boundary controller to stabilize a coupled linear hyperbolic system was introduced in [
14], while an observer based on boundary control for semilinear parabolic PDE with non-collocated distributed event-triggered observation was considered in [
15].
Lastly, an event-triggered boundary control to stabilize a PDE reaction-diffusion system with a Dirichlet boundary condition was proposed in [
16,
17].
Based on the main triggering events developed for input-to-state stabilization of nonlinear systems described by ODEs in [
18] and motivated by the above discussions, the main contribution of this paper is proposing a rigorous framework for the ETIC method to achieve the rapid exponential stabilization of a damped wave equation derived from brain activity.
In [
19], the equation describing the spatio-temporal behavior of brain activity, more precisely, the dynamics of excitatory synaptic activity
at instant time
t and position
x is given by the following damped wave equation:
where
denotes the neural sheet set (at the brain surface which is supposed to be continuous),
c is the excitatory propagation speed along cortico-cortical fibers, and
where
and
are real constants dependent on excitatory connection,
is a constant depending of inhibitory connection and propagation speed, and
S is a sigmoid function giving the value of the pulse from the value of the wave
u and the external input
p in the neural tissue (for more details, see [
19]).
The classical results of the stabilization of damped wave equations assert that stabilization with continuous damping is equivalent to a geometrical condition [
20]. However, for non-regular damping, the problem remains open, and no equivalent condition was found, except for a necessary condition, and a sufficient condition, which trivially come from the demonstration of the continuous case. The only known non-trivial results are a few special cases with strong stabilization without satisfying this sufficient condition. However, they still contain many important considerations towards the essence of the problem. Recently, a stabilization result of the wave equations on some spherical collectors, with approximate damping terms that do not satisfy the geometrical control condition set in [
20], was elaborated ([
21]). In this context, the event-triggered stabilization mechanism has allowed for many stabilization problems to be solved without the need for such regular damping conditions. This highlights the considerable added value of this method.
Inspired by an event-triggered impulsive control method developed for finite-dimensional systems [
18], an extension to the damped wave equation (which is of infinite dimensions) is introduced in this paper. We designed an event-triggered impulsive control that rapidly exponentially stabilizes the system under consideration. The main contribution of our work is three-fold: (i) The generalization of an ETIC method initially adopted for finite dimension systems to stabilize systems of infinite dimensions, (ii) the rapid nature of exponential stabilization, and (iii) the removal of the non-verifiable convergence condition given by [
18] (Equation (
6) p.118583).
This paper is organized as follows. In
Section 2, we formulate our problem and define the control task to be solved.
Section 3 contains the main results that are the strategy for event-triggered control. The existence and uniqueness of the solution, and the rapid exponential stability of the controlled system are discussed.
Section 4 provides a numerical example to illustrate the main result. Lastly, conclusions and perspectives are given in
Section 5.
2. Problem Statement
In this paper, we solve the stabilization problem by the event-triggered control of the brain activity which was modeled by the following damped wave equation [
19],
with initial condition
, where
is an open-bounded domain in
with a sufficiently smooth boundary
. Assume that, for some
, respectively,
a is uniformly bounded,
p is a smooth given function modeling the external input, and
is a Lipschitz function with respect to its first component with a Lipschitz constant
Notation (respectively, ) stands for the first (respectively, second) partial derivative of u with respect to time variable t, and is the classic Laplace operator. Lastly, we denote as the classical -norm, and as the -norm.
We propose to construct a control
, such that the solution of the impulsive damped system
is rapidly exponentially stable. Our method is a generalization of the ideas proposed in [
18] for input-to-state stabilization for finite-dimensional systems to an infinite-dimensional setting. We now introduce a precise definition of the rapid exponential stabilization.
Definition 1. The solution of System (7)–(9) is rapidly exponentially stable if, for all prescribed decay rates , there exists a sequence of functions (representing impulse controls), such that, under an event-triggered method, and for all initial conditions , the solution of System (7)–(9) exists, defined on , and satisfieswhere c is a positive constant. Let
be the state for System (
7)–(9). The following remark is about the existence of solutions for the impulsive System (
7)–(9).
Remark 1. To guarantee that System (7)–(9) is well-posed, it is sufficient that Equations (4) and (5) is well-posed for all initial conditions and the process continues as long as the solution exists and as long as an infinite number of discrete transitions does not occur in a finite time interval known as "Zeno behavior". System (4) and (5) can be written as a semi-linear evolution equation This equation admits a unique solution for all (see Theorem 1.5 page 187 in [22]). Remark 2. Using the Duhamel formula, we obtain for all and for all : where . It follows that Using the Gronwall inequality, we obtain 3. Main Result
In this section, we introduce the event-triggered control for our system, and we prove the rapid exponential stability of the closed-loop system.
3.1. Event-Triggered Control Design
We aim to construct an impulsive control such that the sequence of occurrences of the time and the values of the solution v at the right of each would be selected in the following way.
- :
The sequence of control time is such that:
where
q is a positive integer, and
are positive real numbers.
- :
There exists a positive real number
such that
The construction of sequence is performed in a recursive way. Let be a positive real number that is fixed later; starting from , we put and . Let us suppose that we have and , and we choose among q values , and among m values according to the occurrence of the following events:
- E1:
If , we put
where ,
.
- E2:
If we put,
where such that ,
where
3.2. Main Result
At this stage, we are able to establish our main result concerning the rapidly exponential stabilization for System (
4) and (5) according to the above definition.
Theorem 1. Assume that and are satisfied, and consider the designed events defined above. Then, System (7)–(9) is rapidly exponentially stable. Proof. First, Zeno’s behavior for System (
4) and (5) is avoided, thanks to the construction of the impulse time sequences, since we have for all
.
Let
be any positive constant, and
denotes the number of occurrences of the event
during interval
, which satisfies
. We can select parameters
and
, such that the solutions of System (
4) and (5) with designed events described above are exponentially stable with decay rate
as (
10). Let
be the solution of System (
7)–(9) with the designed events defined above and the initial conditions
. Let
; two cases arise:
First case: If
results from the occurrence of the event
, then from the definition of
, we have
Second case: If
results from the occurrence of event
, then from the definition of
, we have
It results from Inequality (
11) that
From Equations (
14) and (15), we obtain
Choosing
, and
It is clear that
and
are strictly positive reals and strictly smaller than 1; in addition, we have
from which we obtain
Now, using the fact that
, we have
, we obtain
where
. It follows that
for all
and
Hence, System (
7)–(9) is exponentially stable with decay rate
. Thus, the proof of the theorem is finished. □
Remark 3. The main issue to investigate is how to generalize the event-triggered impulsive control method for the more general class of the semi-linear evolution equation with initial condition , where A is a generator of a -semigroup, and f satisfies the hypothesis of Theorem 1.5 in [22]. Remark 4. In the original method of ETIC introduced by [18], the condition imposed to the system that guaranteed the input-to-state stabilization could not be applied to obtain rapid exponential stabilization. Indeed, the condition is expressed according to the number of occurrences of events and , which are future incidents and are, therefore, not yet produced at the beginning of the process. This makes the validation of the convergence condition impossible. Furthermore, the convergence rate in the cited paper was chosen under condition given in Theorem 1 (see [18]). However, in our work, the convergence was not formulated as a function of the numbers of these incidents. In addition, our decay rate was arbitrarily chosen. Remark 5. The above result was obtained in the absence of any kind of perturbation at the time of the impulse times; either these perturbations were due to the existence of data dropouts in the ETIC, and the state jump caused by the impulse thereby did not occur, or they were due to a delay in the ETIC, leading to a delay in triggering the impulse control. In the control of a system of time-triggered impulsive ordinary differential equations (TTC), where activities are initiated periodically at predetermined points in real-time, robustness measures of the stability property of the impulsive stabilization system relative to the perturbations of the jump moments were studied. In [23], the robustness of the global asymptotic stability (GAS) of a system of ordinary impulsive differential equations with fixed moments with respect to the jump moments was discussed, while in [24], an impulsive control based on time sequences with a finally uniformly bounded impulse frequency was discussed. This class of time sequences provides the least conservative sufficient conditions for time-triggered impulsive stabilization. It will then be very interesting to study the question of stabilization robustness by this ETIC method with respect to these types of perturbations based on the results developed in ([23,24]). 4. Numerical Application
In this section, we consider Equation (
1) modeling brain activity. In the case where the dimension is equal to
, it is obvious to suppose that all connections between the neuron sheets are made by a segment
. To simplify, we also suppose that external input
and constant
. The dynamics of the neural field then satisfy the following equation:
The value of nerve flow
S and its derivatives depends on parameter
, which represents a neuron-dependent coefficient. Here, we adopted the same expression for
S as that in [
19]:
, and we took as initial conditions
and
.
System (
19) and (20) is written as damped wave Equations (
4) and (5) with
and
. It is obvious that
a and
b are continuously differentiable;
a is uniformly bounded and
b is the Lipschitz function.
By applying our strategy for event-triggered impulsive control, we obtain the following system:
where
were chosen according to the designed events described above, and
were some constants to be designed. According to Equation (23), functions
. To compute the numerical solution, the state of the system was discretized by divided differences on a uniform grid with step
for the space variable. Discretization with respect to time was performed using the implicit Euler scheme with step size
, and numerical values
and
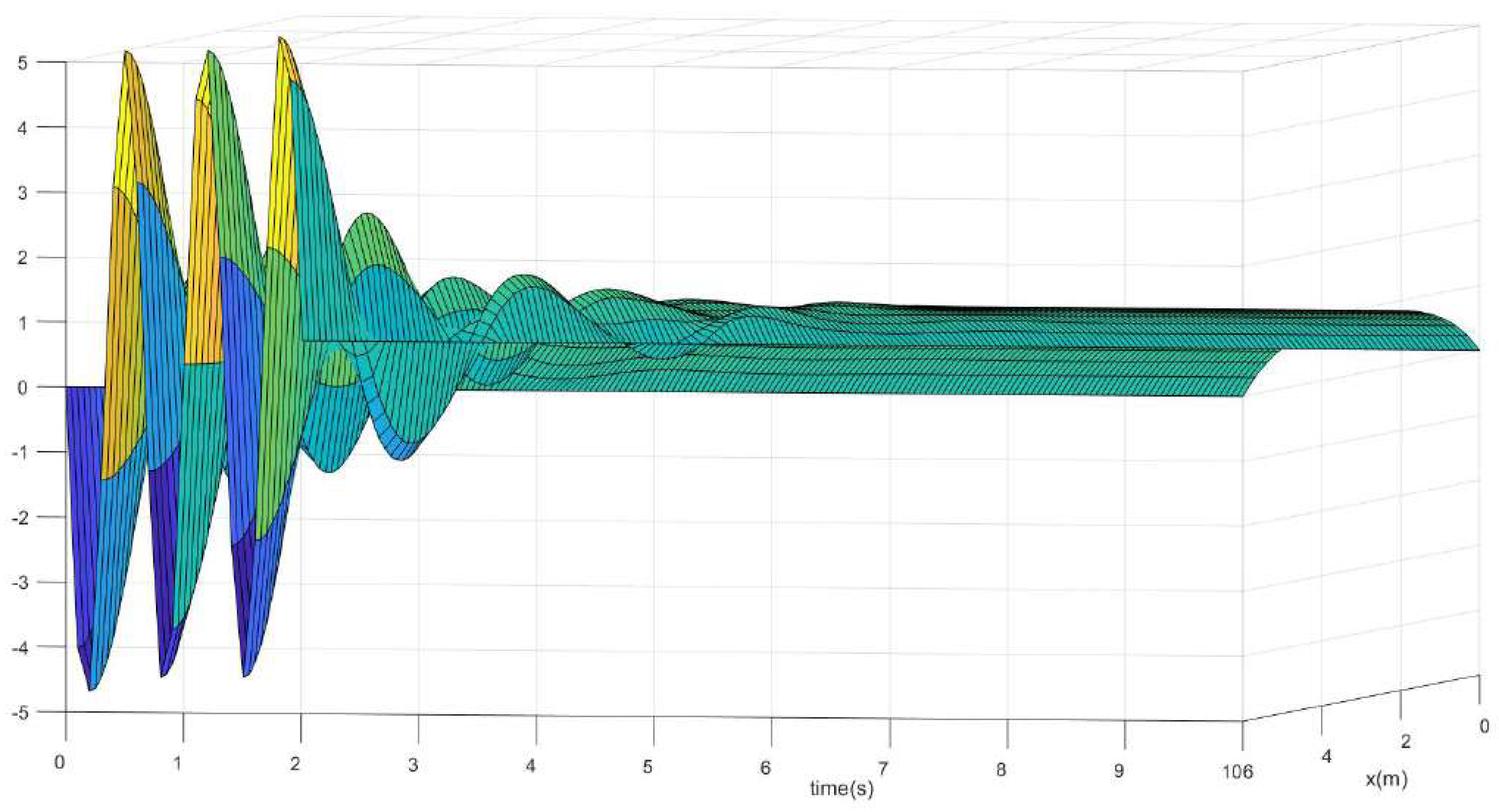
The state trajectories of System (21)–(23) without control are depicted in
Figure 1. The convergence of trajectories of control Equations (21)–(23) is depicted in
Figure 2 in 3D and in
Figure 3 in 2D, which shows that the dynamics were exponentially stable under the designed ETIC.
Figure 4 shows the exponential convergence of the norm of the solution zero, while
Figure 5 illustrates the convergence of the solution to zero under the impulsive control through successive iterations.
Finally, to compare the (ETIC) method with that of (TTC), where the jump times are predefined, we took the same numerical example, with a periodic time-jump. The results are shown in
Figure 5 and
Figure 6.
Figure 5 and
Figure 6 illustrate the behaviour of the system solution norms
under impulsive control where the time sequences are simply periodic impulsive jumps (TTC)
In
Figure 5, we have taken the minimum values taken from ETIC control
, where we notice that we do not have an exponential stability, and we arrived at the same result by taking even smaller values for
and
(
Figure 6).