Modeling and Semi-Analytic Stability Analysis for Dynamics of AC Machines
Abstract
:1. Introduction
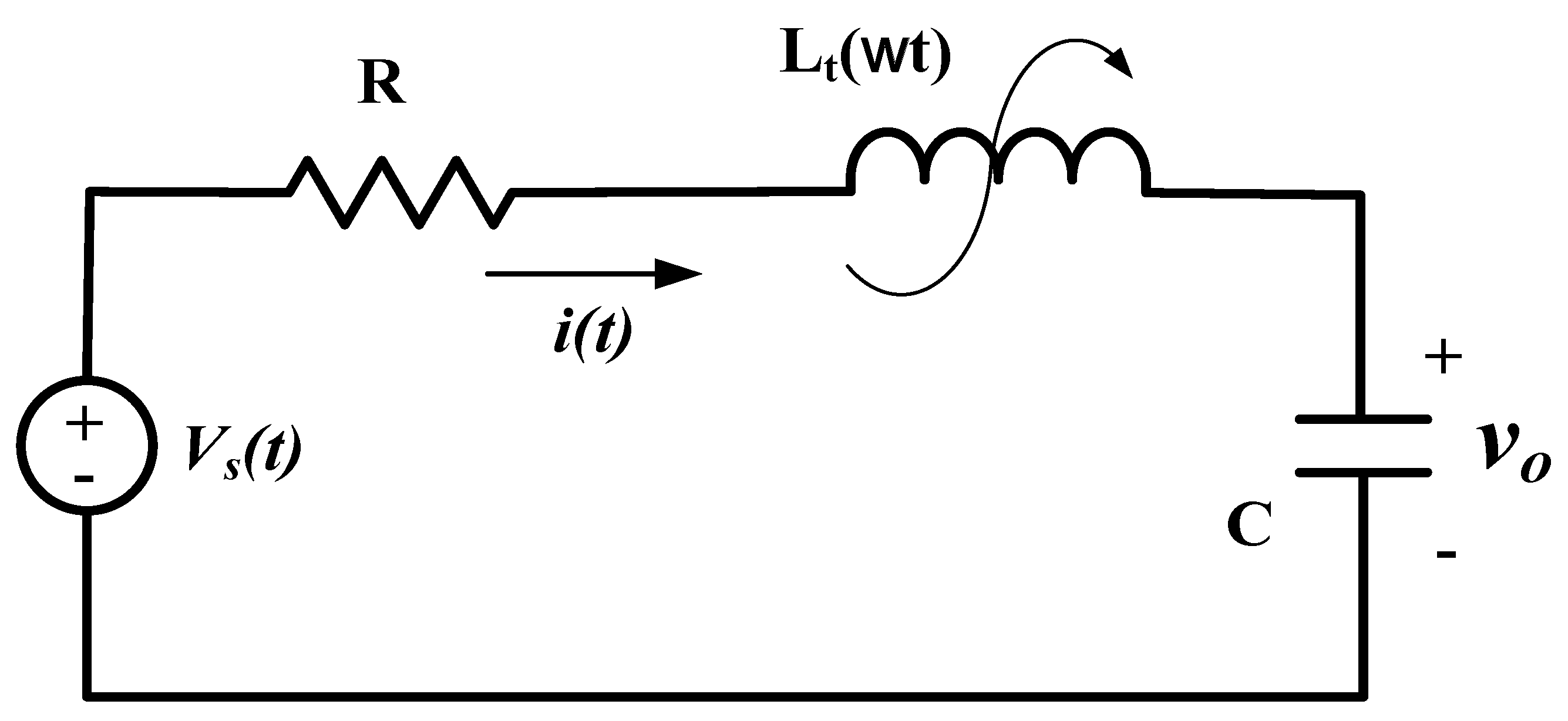
2. The Governing Dynamic Model
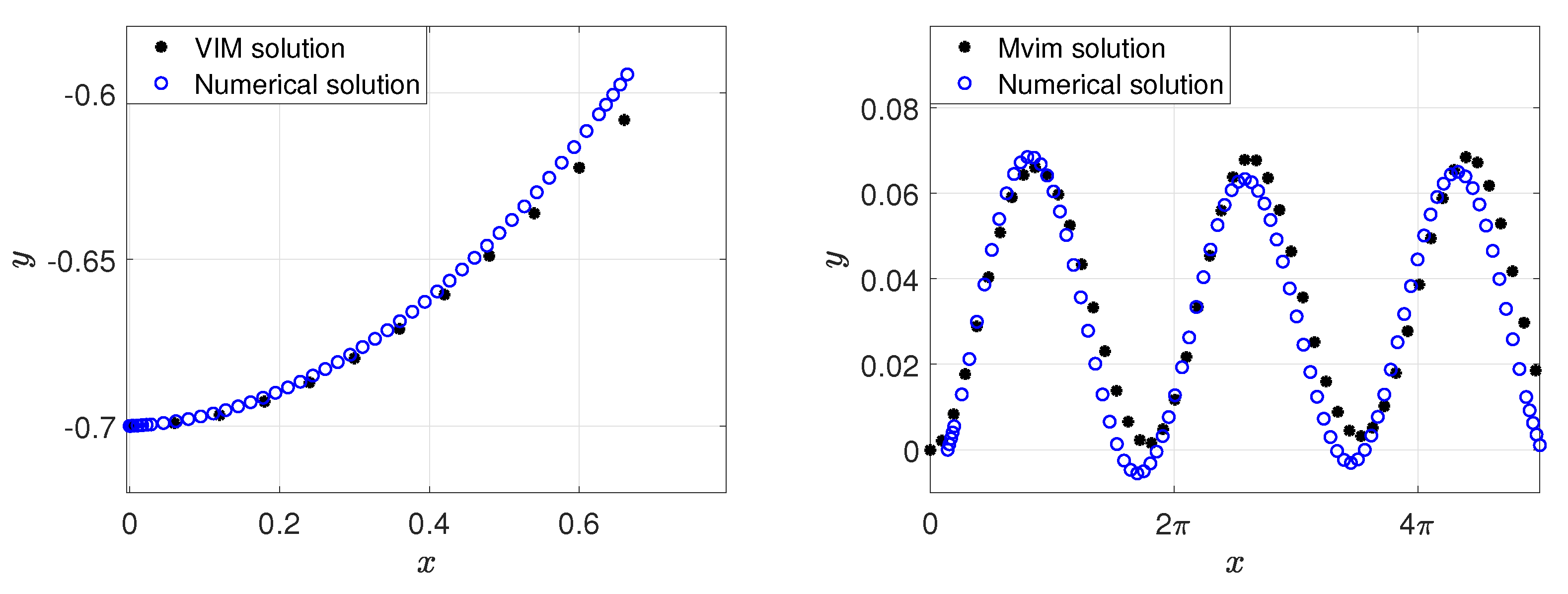
3. Construction of Semi-Analytical Solutions via VIM
4. Construction of Stability Domains
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Lacalle, L.N.L.; Lamikiz, A.; Sanchez, J.A.; de Bustos, I.F. Simultaneous measurement of forces and machine tool position for diagnostic of machining tests. IEEE Trans. Instrum. Meas. 2005, 54, 2329–2335. [Google Scholar]
- Hehenberger, P.; Poltschak, F.; Zeman, K.; Amrhein, W. Hierarchical design models in the mechatronic product development process of synchronous machines. Mechatronics 2010, 20, 864–875. [Google Scholar] [CrossRef]
- Riel, T.; Saathof, R.; Katalenic, A.; Ito, S.; Schitter, G. Noise analysis and efficiency improvement of a pulse-width modulated permanent magnet synchronous motor by dynamic error budgeting. Mechatronics 2018, 50, 225–233. [Google Scholar] [CrossRef]
- Abdel-Halim, I.A.M.; Ahmar, M.; El-Sherif, M.Z. A novel approach for the analysis of self-excited induction generators. Electr. Mach. Power Syst. 1999, 27, 879–888. [Google Scholar] [CrossRef]
- El-Borhamy, M.; Rashad, E.M.; Sobhy, I. Floquet analysis of linear dynamic RLC circuits. Open Phys. 2020, 18, 264–277. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V.; Madescu, G.; Dragan, F. Dynamic response of a permanent magnet synchronous generator to a wind gust. Energies 2019, 12, 915. [Google Scholar] [CrossRef] [Green Version]
- Matusita, K.; Omatu, S. Use of the homotopy method for excitation control of generators for multimachine power system. Electr. Eng. Jpn. 1996, 117, 96–111. [Google Scholar] [CrossRef]
- Longuski, J.M.; Tsiotras, P. Analytical solutions for a spinning rigid body subject to time-varying body-fixed torques, part 1: Constant axial torque. J. Appl. Mech. 1993, 60, 970–975. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wilkinson, S.A.; Vogt, N.; Golubev, D.S.; Cole, J.H. Approximate solutions to Mathieu’s equation. Physica E 2018, 100, 24–30. [Google Scholar] [CrossRef] [Green Version]
- Abbasbandy, S.; Jalili, M. Determination of optimal convergence-control parameter value in homotopy analysis method. Numer. Algorithms 2013, 64, 593–605. [Google Scholar] [CrossRef]
- Aksoy, Y.; Pakdemirli, M.; Abbasbandy, S.; Boyaci, H. New perturbation-iteration solutions for nonlinear heat transfer equations. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 814–828. [Google Scholar] [CrossRef]
- Gupta, A.K.; Ray, S.S. Comparison between homotopy perturbation method and optimal homotopy asymptotic method for the soliton solutions of Boussinesq-Burger equations. Comput. Fluids 2014, 103, 34–41. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method for analytic treatment for linear and nonlinear ODEs. Appl. Math. Comp. 2009, 212, 120–134. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Cent. Europ. J. Eng. 2014, 4, 64–71. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Optimal homotopy perturbation method for a non-conservative dynamical system of a rotating electrical machine. Z. Nat. A 2012, 67, 509–516. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. On the flow of a Walters-type B viscoelastic fluid in a vertical channel with porous wall. Int. J. Heat Mass Transf. 2014, 79, 146–165. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. The Optimal Homotopy Asymptotic Method; Engineering Applications; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Rashidi, M.M.; Efrani, E. The modified differential transform method for investigating nano boundary-layers over stretching surfaces. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 864–883. [Google Scholar] [CrossRef]
- Ding, H.; Gong, X.; Gong, Y. Estimation of rotor temperature of permanent magnet synchronous motor based on model reference fuzzy adaptive control. Math. Probl. Eng. 2020, 2020, 4183706. [Google Scholar] [CrossRef]
- Hou, K.; Li, Z.; Chen, L.; Xia, D.; Li, Q.; Xiao, Y. Steady-state stability of sending-end system with mixed synchronous generator and power-electronic-interfaced renewable energy. Math. Probl. Eng. 2020, 2020, 8693245. [Google Scholar] [CrossRef] [Green Version]
- Jose, J.T.; Chattopadhyay, A.B. Mathematical formulation of feedback linearizing control of doubly fed induction generator including magnetic saturation effects. Math. Probl. Eng. 2020, 2020, 3012406. [Google Scholar] [CrossRef]
- Zhang, M.; Xiao, F.; Shao, R.; Deng, Z. Robust fault detection for permanent-magnet synchronous motor via adaptive sliding-mode observer. Math. Probl. Eng. 2020, 2020, 9360939. [Google Scholar] [CrossRef]
- Dehghanzadeh, A.R.; Behjat, V.; Banaei, M.R. Dynamic modeling of wind turbine based axial flux permanent magnetic synchronous generator connected to the grid with switch reduced converter. Ain Shams Eng. J. (ASEJ) 2018, 9, 125–135. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Zhang, L.; Wang, X. AC Machine Systems: Mathematical Model and Parameters, Analysis and System Performance; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mostafa, A.S.; Mohamadein, A.L.; Rashad, E.M. Application of Floquet’s theory to the analysis of series-connected wound-rotor self-excited synchronous generator. IEEE Trans. Energy Convers. 1993, 8, 369–376. [Google Scholar] [CrossRef]
- Nabil, M.; Allam, S.M.; Rashad, E.M. Modeling and design considerations of a photovoltaic energy source feeding a synchronous reluctance motor suitable for pumping systems. Ain Shams Eng. J. (ASEJ) 2012, 3, 375–382. [Google Scholar] [CrossRef] [Green Version]
- Rashad, E.M. Theory and steady-state analysis of series-connected wound-rotor induction motor in sub-synchronous mode. In Proceedings of the 2016 IEEE International Conference on Power and Energy (PECon), Melaka City, Malaysia, 28–30 November 2016. [Google Scholar]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comp. 2000, 114, 115–123. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method: Some recent results and new interpretations. J. Comp. Appl. Math. 2007, 207, 3–17. [Google Scholar] [CrossRef] [Green Version]
- He, J.H.; Wu, X.W. Variational iteration method: New development and applications. Comput. Math. Appl. 2007, 54, 881–894. [Google Scholar] [CrossRef] [Green Version]
- Chicone, C. Ordinary Differential Equations with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hale, J.K. Ordinary Differential Equations; Dover Publications: Garden City, NY, USA, 2009. [Google Scholar]
- Nayfeh, A. H Introduction to Perturbation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Shivamoggi, B. Perturbation Methods for Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Grantham, C.; Sutanto, D.; Mismail, B. Steady-state and transient analysis of self-excited induction generators. In IEE Proceedings B (Electric Power Applications); IET Digital Library, 1989; Volume 136, pp. 61–68. Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-b.1989.0008 (accessed on 16 March 2021).
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D. Analysis of Electrical Machinery; IEEE Press: New York, NY, USA, 1995. [Google Scholar]
- Rashad, E.M. Application of Floquet Theory to the Analysis of Parametric Generator. Ph.D. Thesis, Alexandria University, Alexandria, Egypt, 1992. [Google Scholar]
- He, J.-H. Nonlinear Mathieu equation and its approximation without a small parameter. Engng. Trans. 2002, 50, 43–54. [Google Scholar]
- Jafari, H.; Alipoor, A. A new method for calculating general Lagrange multiplier in the variational iteration method. Numer. Meth. Partial. Differ. Equ. 2011, 27, 996–1001. [Google Scholar] [CrossRef]
- Jafari, H.; Saeidy, M.; Baleanu, D. The variational iteration method for solving nth order fuzzy differential equations. Open Phys. 2012, 10, 76–85. [Google Scholar] [CrossRef] [Green Version]
- El-Borhamy, M. On the existence of new integrable cases for Euler-Poisson equations in Newtonian fields. Alex. Eng. J. (AEJ) 2019, 58, 733–744. [Google Scholar] [CrossRef]
- El-Borhamy, M. Chaos transition of the generalized fractional duffing oscillator with a generalized time delayed position feedback. Nonlinear Dyn. 2020, 111, 2471–2487. [Google Scholar] [CrossRef]
- El-Borhamy, M.; Ahmed, A. Stability analysis of delayed fractional integro-differential equations with applications of RLC circuits. J. Indon. Math. Soc. 2020, 26, 74–100. [Google Scholar]
- El-Borhamy, M.; Mosalam, N. On the existence of periodic solution and the transition to chaos of Rayleigh-Duffing equation with application of gyro dynamic. Appl. Math. Nonl. Sci. 2020, 5, 43–58. [Google Scholar] [CrossRef]
- El-Borhamy, M.; Medhat, T.; Ali, M.E. Chaos prediction in fractional delayed energy-based models of capital accumulation. Complexity 2021, 2021, 8751963. [Google Scholar] [CrossRef]
- Merkin, D.R. Introduction to the Theory of Stability; Springer: Berlin/Heidelberg, Germany, 1997; ISBN-13 978-1-4612-8477-2. [Google Scholar]
- Hubinger, S.; Gattringer, H.; Bremer, H.; Mayrhofer, K. Instability maps of a system of Mathieu-Equations using different perturbation methods. PAMM Proc. Appl. Math. Mech. 2011, 11, 319–320. [Google Scholar] [CrossRef]
- Jazar, R.N.; Mahinfalah, M.; Mahmoudian, N.; Rastgaar, M.A. Energy-rate method and stability chart of parametric vibrating systems. J. Braz. Soc. Mech. Sci. Eng. 2008, 30, 182–188. [Google Scholar] [CrossRef] [Green Version]
- Kovacic, I.; Rand, R.; Sah, S.M. Mathieu’s equation and its generalizations: Overview of stability charts and their features. Appl. Mech. Rev. 2018, 70, 020802. [Google Scholar] [CrossRef] [Green Version]
- Mostafa, A.S.; Mohamadein, A.L.; Rashad, E.M. Analysis of series-connected wound-rotor self-excited induction generator. In IEE Proceedings B (Electric Power Applications); IET Digital Library, 1993; Volume 140, pp. 329–336. Available online: https://digital-library.theiet.org/content/journals/10.1049/ip-b.1993.0041 (accessed on 16 March 2021).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Borhamy, M.; Rashad, E.E.M.; Sobhy, I.; El-Sayed, M.K. Modeling and Semi-Analytic Stability Analysis for Dynamics of AC Machines. Mathematics 2021, 9, 644. https://doi.org/10.3390/math9060644
El-Borhamy M, Rashad EEM, Sobhy I, El-Sayed MK. Modeling and Semi-Analytic Stability Analysis for Dynamics of AC Machines. Mathematics. 2021; 9(6):644. https://doi.org/10.3390/math9060644
Chicago/Turabian StyleEl-Borhamy, Mohamed, Essam Eddin M. Rashad, Ismail Sobhy, and M. Kamel El-Sayed. 2021. "Modeling and Semi-Analytic Stability Analysis for Dynamics of AC Machines" Mathematics 9, no. 6: 644. https://doi.org/10.3390/math9060644






