N-Fold Darboux Transformation for the Classical Three-Component Nonlinear Schrödinger Equations and Its Exact Solutions
Abstract
:1. Introduction
2. Darboux Transformation and Exact Solutions for the NLS Equations
2.1. Darboux Transformation
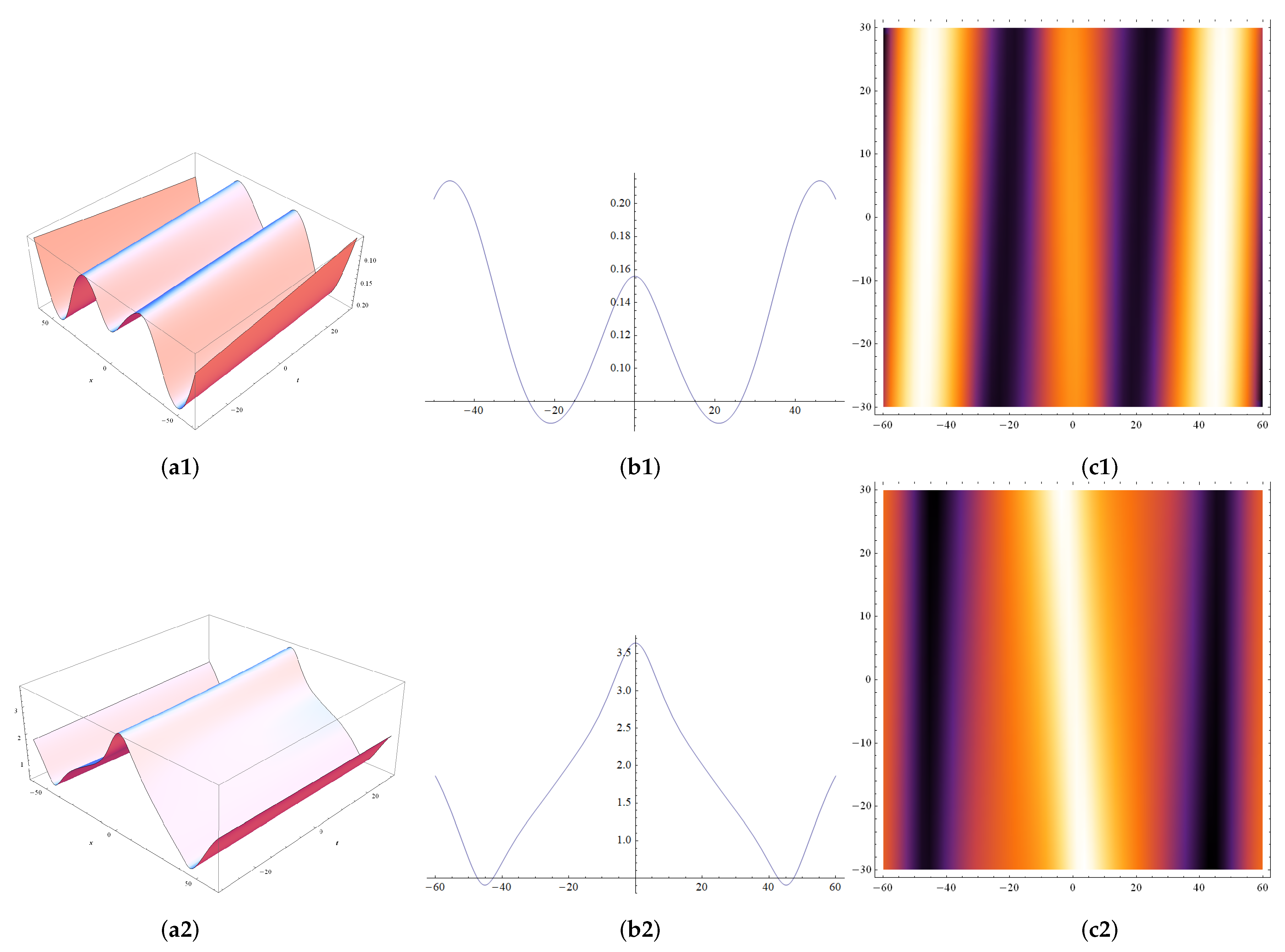
2.2. Exact Solutions for the NLS Equations
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Gu, C.-H.; Hu, H.-S.; Zhou, Z.-X. Darboux Transformation of Soliton Theory and Its Geometric Application; Shanghai Science and Technology Press: Shanghai, China, 1999. [Google Scholar]
- Ablowitz, M.J.; Ablowitz, M.A.; Clarkson, P.A. Solitons Nonlinear Evolution Equations and In-Verse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Ma, W.-X. Darboux transformations for a Lax integrable system in 2n-dimensions. Lett. Math. Phys. 1997, 39, 33–49. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.-X.; Zhang, J.Y. Darboux transformatins of integrable couplings and applications. Rev. Math. Phys. 2018, 30, 1850003. [Google Scholar] [CrossRef]
- Geng, X.-G. Darboux transformation of the discrete Ablowitz–Ladik eigenvalue problem. Acta Math. Sci. 1989, 9, 21–26. [Google Scholar] [CrossRef]
- Bagrov, V.G.; Samsonov, B.F. Darboux transformation of the Schrödinger equation. Phys. Part. Nuclei 1997, 28, 374–397. [Google Scholar] [CrossRef]
- Xin, X.-P.; Xia, Y.-R.; Liu, H.-Z.; Zhang, L.L. Darboux transformation of the variable coefficient nonlocal equation. J. Math. Anal. Appl. 2020, 490, 124–227. [Google Scholar] [CrossRef]
- Gürsesl, M.; Pekcan, A. Nonlocal nonlinear Schrödinger equations and their soliton solutions. J. Math. Phys. 2018, 59, 051501. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Chen, Y. Several reverse-time integrable nonlocal nonlinear equations: Rogue-wave solutions. Chaos 2018, 28, 053104. [Google Scholar] [CrossRef] [PubMed]
- Meng, D.-X.; Li, K.-Z. Darboux transformation of the second-type nonlocal derivative nonlinear Schrödinger equation. Mod. Phys. Lett. B 2019, 33, 1950123. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Prinari, B.; Trubatch, A.D. Discrete and Continuous Nonlinear Schrödinger Systems; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Duval, C.; Horvthy, P.A. On Schrödinger superalgebras. J. Math. Phys. 1994, 35, 2516. [Google Scholar] [CrossRef] [Green Version]
- Leblanc, M.; Lozano, G.; Min, H. Extended superconformal Galilean symmetry in Chern–Simons matter systems. Ann. Phys. 1992, 219, 328–348. [Google Scholar] [CrossRef] [Green Version]
- Nakayama, Y.; Sakaguchi, M.; Yoshida, K. Non-relativistic M2-brane gauge theory and new superconformal algebra. J. High. Energy Phys. 2009, 941–944. [Google Scholar] [CrossRef] [Green Version]
- Galajinsky, A.; Masterov, I. Remark on quantum mechanics with N = 2 Schrödinger supersymmetry. Phys. Lett. B. 2009, 675, 116. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quantum Semiclass. Opt. 2005, 7, R53–R72. [Google Scholar] [CrossRef]
- Carretero-Gonzalez, R.; Frantzeskakis, D.J.; Kevrekidis, P.G. Nonlinear waves in Bose–Einstein condensates. Nonlinearity 2008, 21, R139–R202. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.-Y. Nonlocal general vector nonlinear Schrödinger equations: Integrability, PT symmetribility, and solutions. Appl. Math. Lett. 2016, 62, 101–109. [Google Scholar] [CrossRef]
- Yan, Z.Y.; Konotop, V.V. Exact solutions to threedimensional generalized nonlinear Schrödinger equa-tions with varying potential and nonlinearities. Phys. Rev. E 2009, 80, 036607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, F.J. Nonautonomous rogue waves and ‘catch’ dynamics for the combined Hirota-LPD equation with variable coefficients. Commun. Nonlinear. Sci. Numer. Simul. 2016, 34, 142–153. [Google Scholar] [CrossRef]
- Malomed, B.; Torner, L.; Wise, F.; Mihalache, D. On multidimensional solitons and their legacy in contem-poraryatomic, molecular and optical physics. J. Phys. B Mol. Opt. Phys. 2016, 49, 170502. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Feng, L.; Li, L. Darboux transformations for super-Schrödinger equation, super-Dirac equation and their exact solutions. Nonlinear Dyn. 2017, 88, 1257–1271. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear Schrödinger equation. Phys. Rev. Lett. 2013, 110, 064105. [Google Scholar] [CrossRef] [Green Version]
- Ablowitz, M.J.; Musslimani, Z.H. Integrable nonlocal nonlinear equations. Stud. Appl. Math. 2017, 139, 7–59. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.Y.; Hang, C. Analytical three-dimensional bright solitons and soliton-pairs in Bose–Einstein conden-sates with time-space modulation. Phys. Rev. A 2009, 80, 063626. [Google Scholar] [CrossRef] [Green Version]
- Hovhannisyan, G.; Ruff, O. Darboux transformations on a space scale. J. Math. Anal. Appl. 2016, 434, 1690–1718. [Google Scholar] [CrossRef]
- Duan, C.; Yu, F. N-Fold Darboux Transformation for the Nonlocal Nonlinear Schrödinger (NNLS) Equation with the Self-Induced PT-Symmetric Potential. J. Appl. Math. Phys. 2018, 6, 888–900. [Google Scholar] [CrossRef] [Green Version]
- Hobby, D.; Shemyakova, E. Classification of Multidimensional Darboux Transformations: First Order and Continued Type. Symmetry Integr. Geom. Methods Appl. 2017, 13, 010. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.X.; Batwa, S. A binary Darboux transformation for multicomponent NLS equations and their reduc-tions. Anal. Math. Phys. 2021, 11, 44. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The inverse scattering transform-Fourier analysis for nonlinear problems. Stud. Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Ma, W.X. Integrable couplings of vector AKNS soliton equations. J. Math. Phys. 2005, 46, 033507. [Google Scholar] [CrossRef]
- Ma, W.X.; Wu, H. Time–space integrable decompositions of nonlinear evolution equations. J. Math. Anal. Appl. 2006, 324, 134–149. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.X. Multi-component bi-Hamiltonian Dirac integrable equations. Chaos Solitons Fractals 2009, 39, 282–287. [Google Scholar] [CrossRef]
- Ma, W.X. Long-time asymptotics of a three-component coupled nonlinear Schrödinger system. J. Geom. Phys. 2020, 153, 103669. [Google Scholar] [CrossRef]
- Yu, J.; Chen, S.-T.; Ma, W.X. N-fold Darboux Transformation for Integrable Couplings of AKNS Equations. Commun. Theor. Phys. 2018, 69, 367. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.-S.; Su, P.-X.; Ma, W.-X. N-Fold Darboux Transformation for the Classical Three-Component Nonlinear Schrödinger Equations and Its Exact Solutions. Mathematics 2021, 9, 733. https://doi.org/10.3390/math9070733
Bai Y-S, Su P-X, Ma W-X. N-Fold Darboux Transformation for the Classical Three-Component Nonlinear Schrödinger Equations and Its Exact Solutions. Mathematics. 2021; 9(7):733. https://doi.org/10.3390/math9070733
Chicago/Turabian StyleBai, Yu-Shan, Peng-Xiang Su, and Wen-Xiu Ma. 2021. "N-Fold Darboux Transformation for the Classical Three-Component Nonlinear Schrödinger Equations and Its Exact Solutions" Mathematics 9, no. 7: 733. https://doi.org/10.3390/math9070733
APA StyleBai, Y.-S., Su, P.-X., & Ma, W.-X. (2021). N-Fold Darboux Transformation for the Classical Three-Component Nonlinear Schrödinger Equations and Its Exact Solutions. Mathematics, 9(7), 733. https://doi.org/10.3390/math9070733