Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition
Abstract
:1. Introduction
2. Materials and Methods
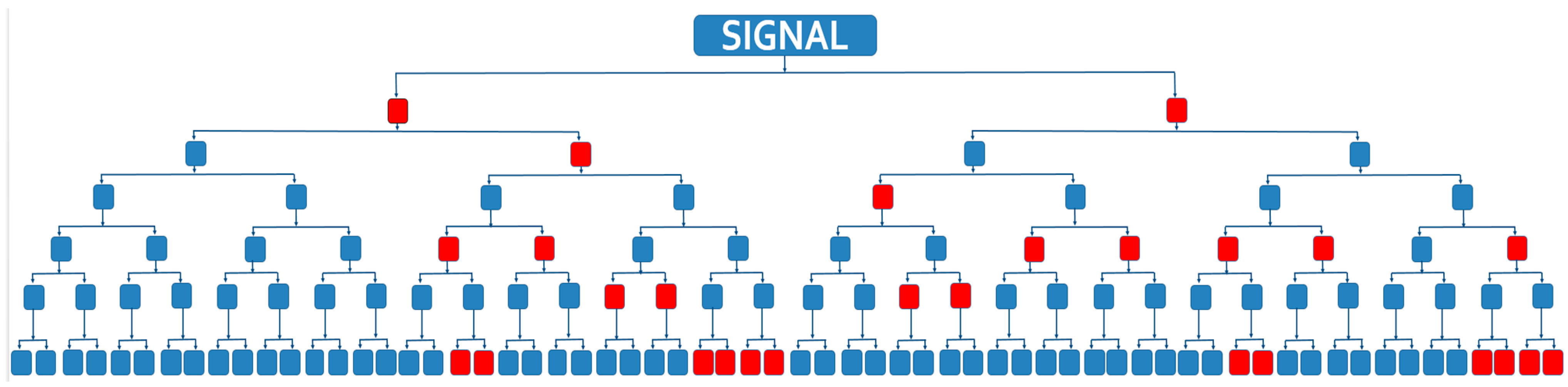
2.1. Nonlinear Signal Approximation Based on Its Expansion in Basis
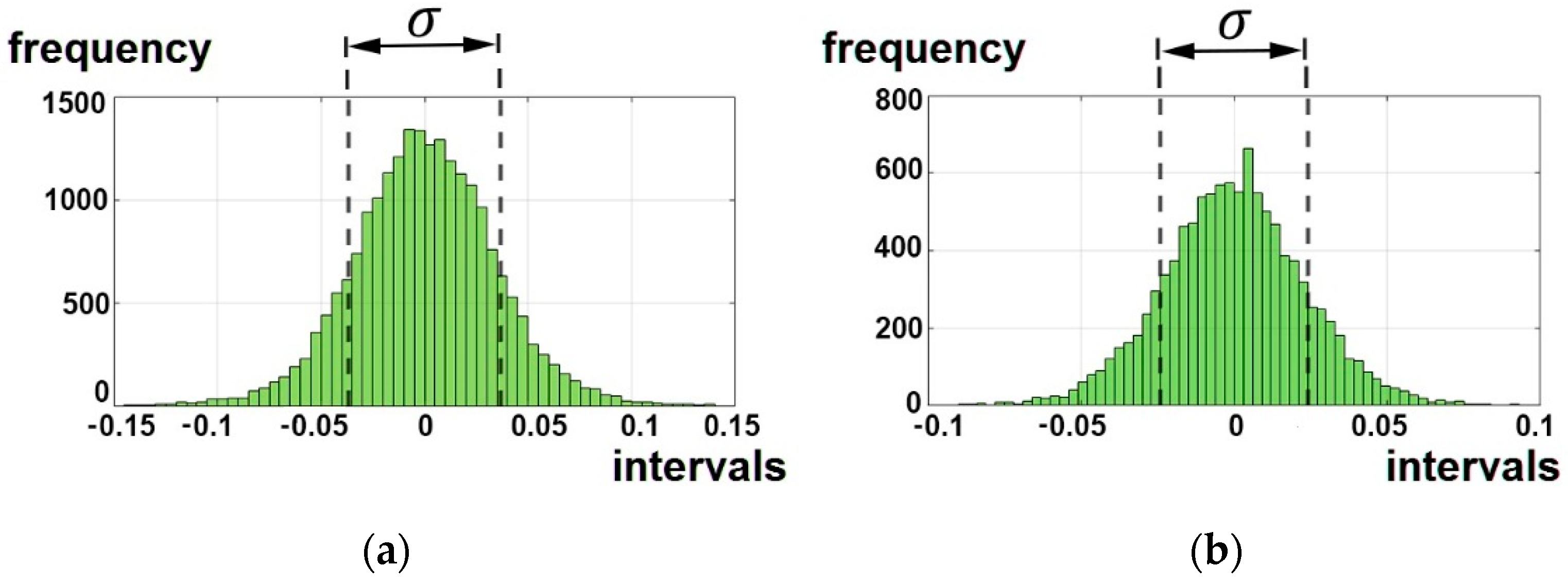
2.2. Nonlinear Approximation of a Noisy Signal
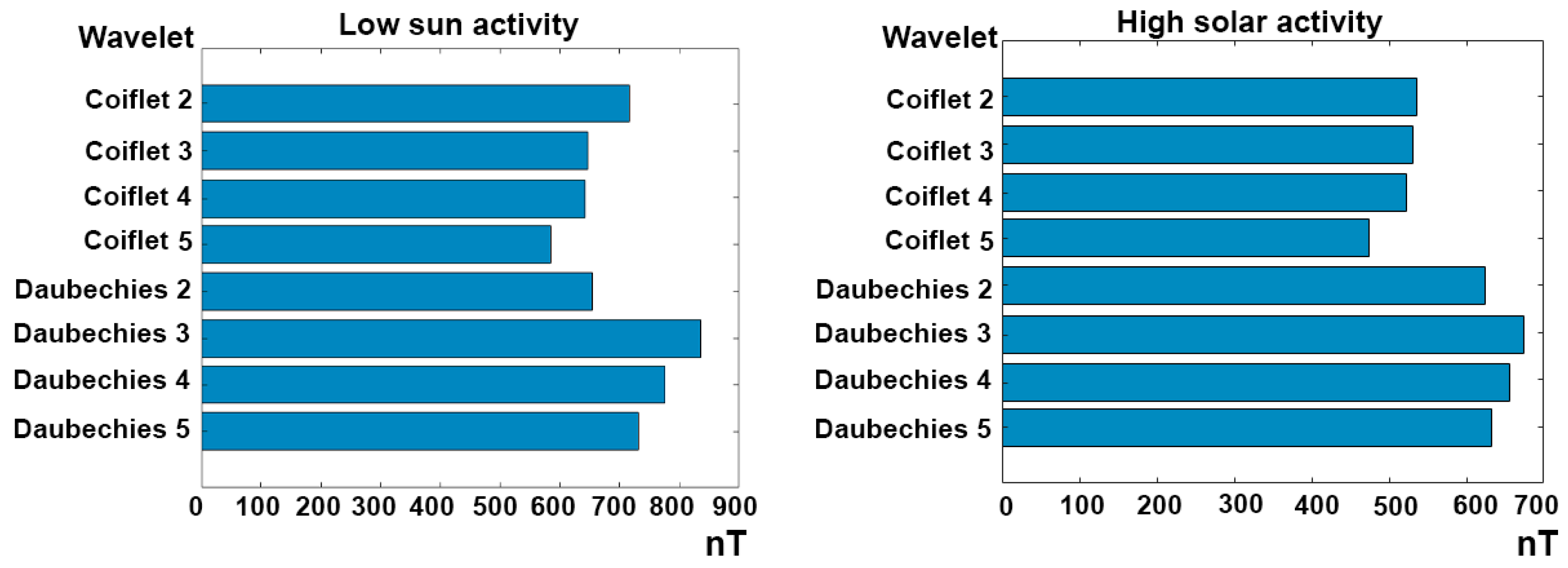
3. Results
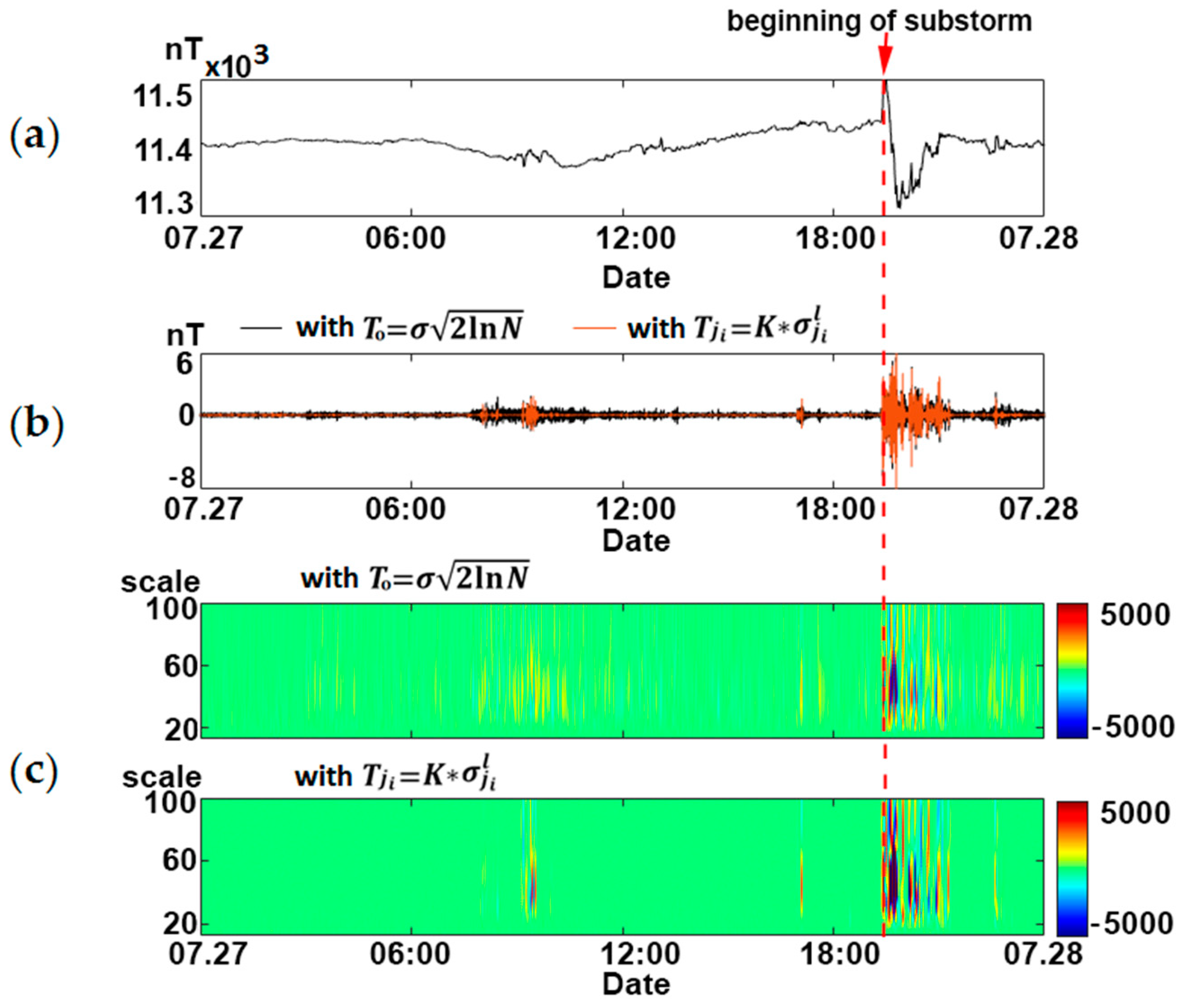
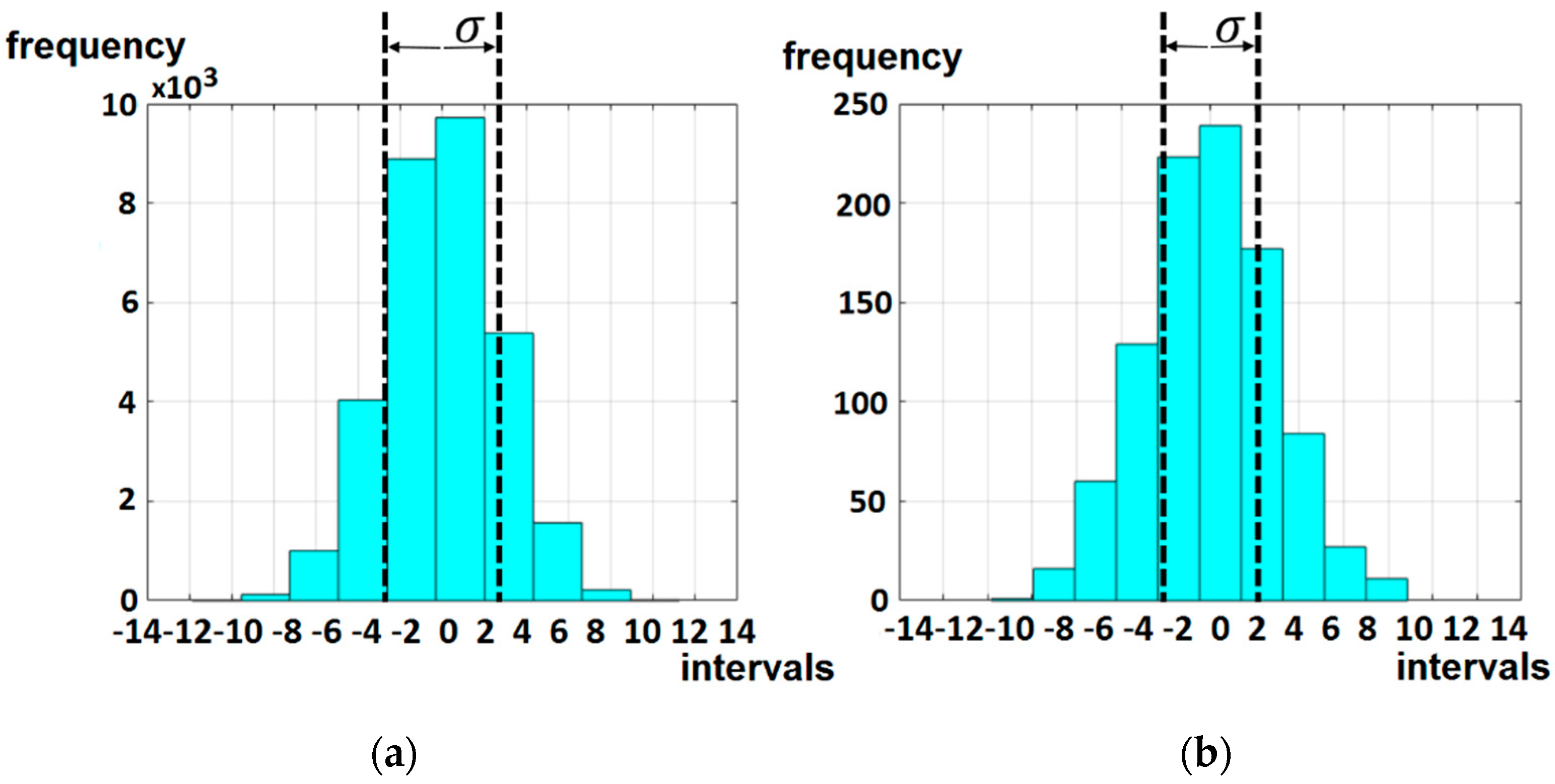
3.1. Detection of Geomagnetic Pulsations in Geomagnetic Data
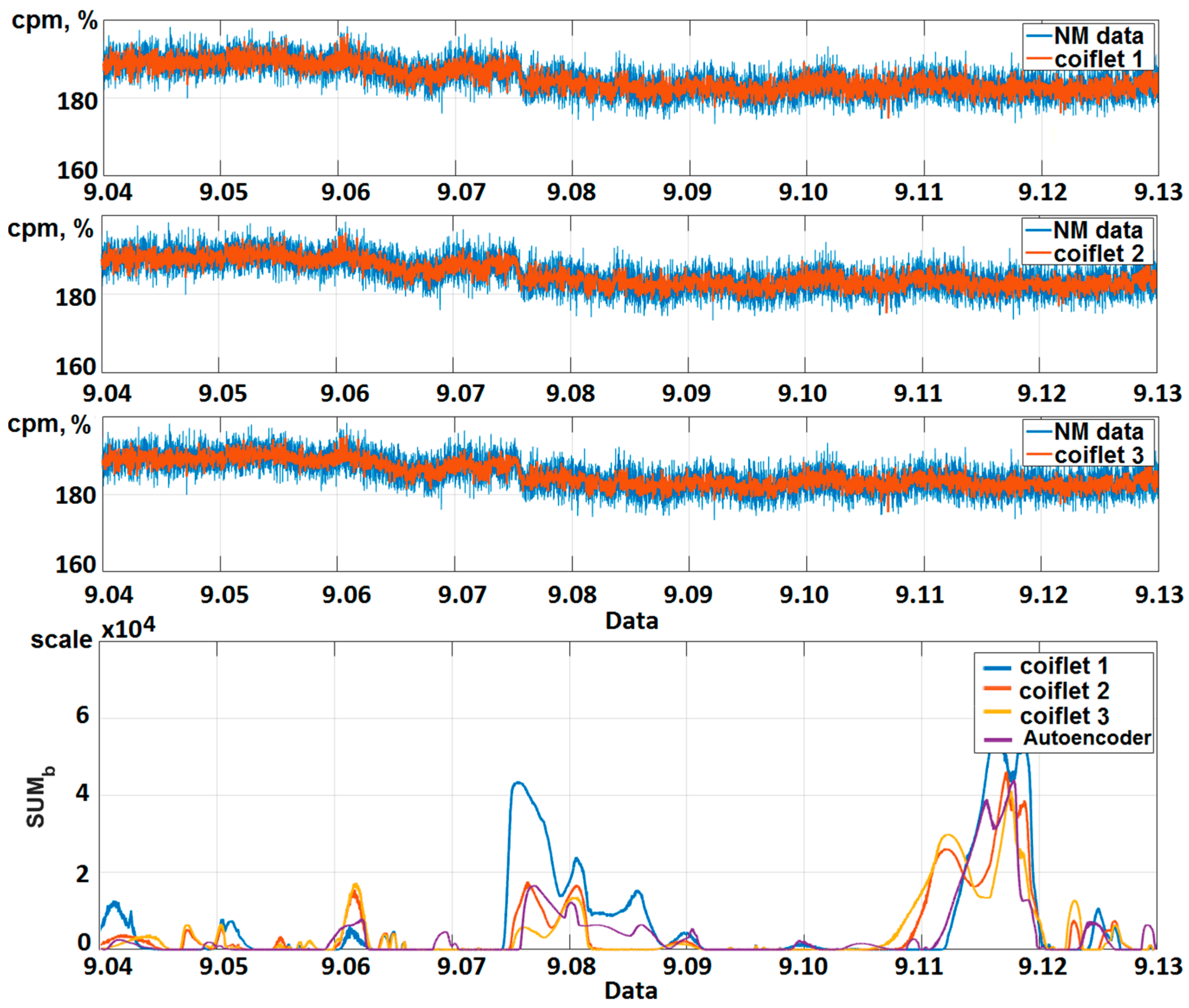
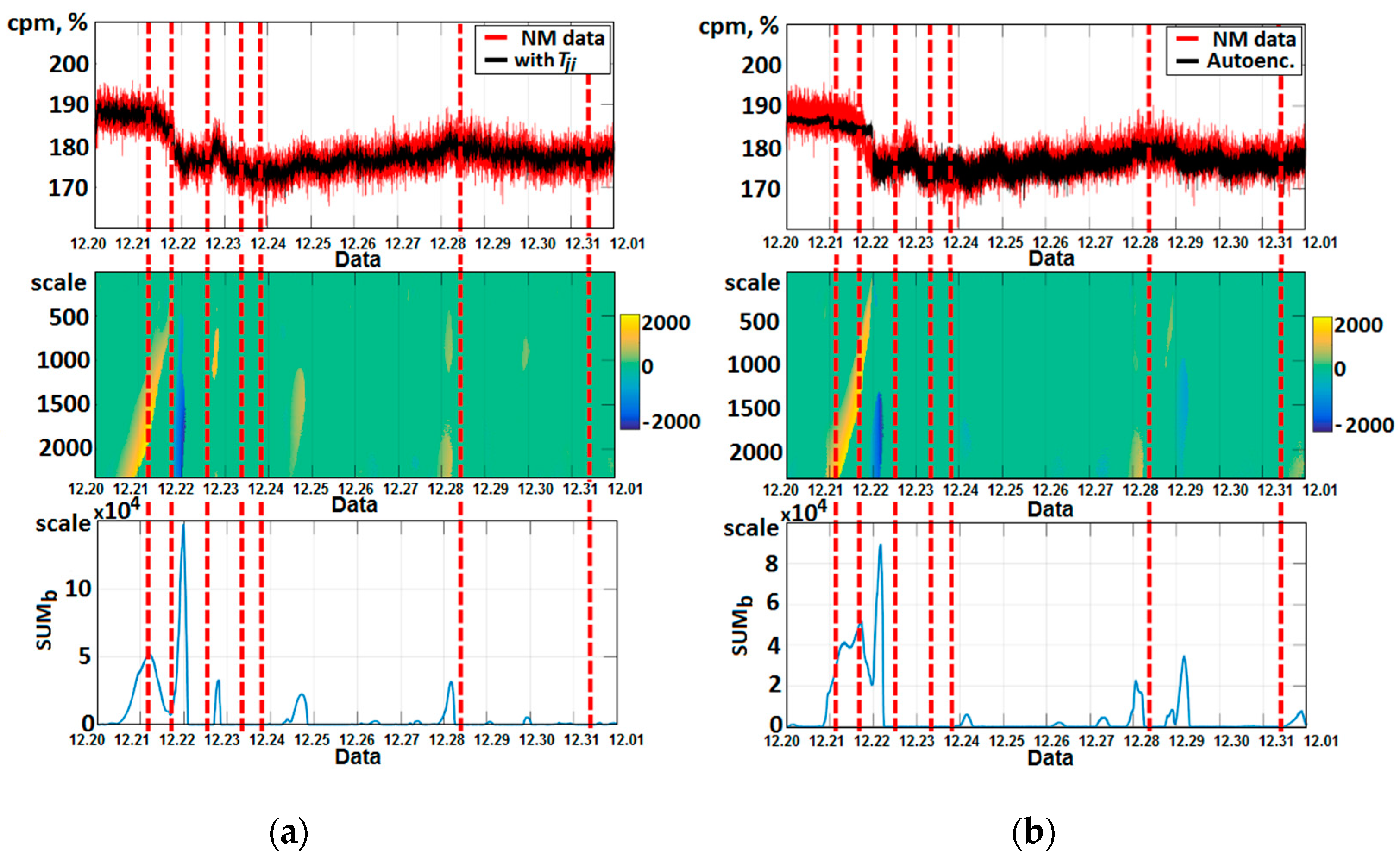
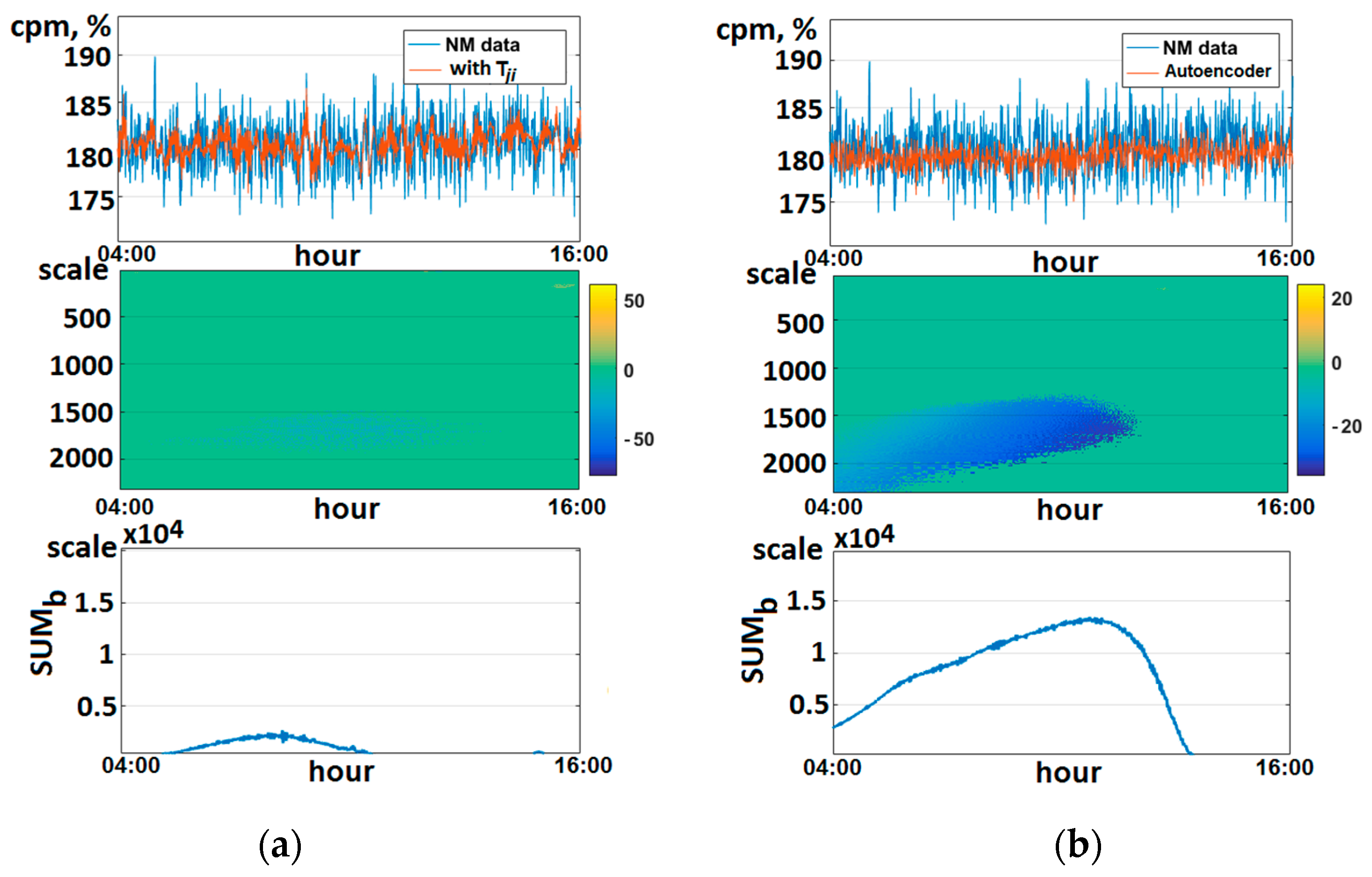
3.2. Detection of Sporadic Features in Neutron Monitor Data
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Perez-Sanchez, A.V.; Perez-Ramirez, C.A.; Valtierra-Rodriguez, M.; Dominguez-Gonzalez, A.; Amezquita-Sanchez, J.P. Wavelet Transform-Statistical Time Features-Based Methodology for Epileptic Seizure Prediction Using Electrocardiogram Signals. Mathematics 2020, 8, 2125. [Google Scholar] [CrossRef]
- Shestakov, O. Wavelet Thresholding Risk Estimate for the Model with Random Samples and Correlated Noise. Mathematics 2020, 8, 377. [Google Scholar] [CrossRef] [Green Version]
- Alperovich, L.; Eppelbaum, L.; Zheludev, V.; Dumoulin, J.; Soldovieri, F.; Proto, M.; Bavusi, M.; Loperte, A. A new combined wavelet methodology: Implementation to GPR and ERT data obtained in the Montagnole experiment. J. Geophys. Eng. 2013, 10, 025017. [Google Scholar] [CrossRef]
- Abunina, M.A.; Belov, A.V.; Eroshenko, E.A.; Abunin, A.A.; Yanke, V.G. Ring of Stations Method in Cosmic Rays Variations Research. Sol. Phys. 2020, 295, 1–20. [Google Scholar] [CrossRef]
- Zaitsev, A.N.; Dalin, P.A.; Zastenker, G.N. Sharp variations in the flux of solar wind ions and their response to disturbances of the earth’s magnetic field. Geomagn. Aeron. 2002, 6, 752–759. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: London, UK, 1999; p. 620. [Google Scholar]
- Singh, J.; Barabanov, N. Stability of discrete time recurrent neural networks and nonlinear optimization problems. Neural Netw. 2016, 74, 58–72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chui, C.K. An Introduction in Wavelets; Academic Press: New York, NY, USA, 1992; p. 264. [Google Scholar]
- Mandrikova, O.V.; Solovev, I.S.; Zalyaev, T.L. Methods of analysis of geomagnetic field variations and cosmic ray data. Earth Planet Space 2014, 66, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Alperovich, L.; Zheludev, V.; Hayakawa, M. Application of a wavelet technique for the detection of earthquake signatures in the geomagnetic field. Nat. Hazards Earth Syst. Sci. 2001, 1, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Alperovich, L.; Zheludev, V.; Hayakawa, M. Use of wavelet analysis for detection of seismogenic ULF emissions. Radio Sci. 2003, 38, 1093. [Google Scholar] [CrossRef]
- Cao, K.; Zeng, X. Adaptive Wavelet Estimations in the Convolution Structure Density Model. Mathematics 2020, 8, 1391. [Google Scholar] [CrossRef]
- Herley, C.; Kovacevic, J.; Ramchandran, K.; Vetterli, M. Tilings of the time-frequency plane: Construction of arbitrary orthogonal bases and feist tiling algorithms. IEEE Trans. Signal Proc. 1993, 41, 3341–3359. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Donoho, D. Atomic Decomposition by Basis Pursuit; Technical Report; Stanford University: Stanford, CA, USA, 1995. [Google Scholar]
- Mallat, S.G.; Zhang, Z.F. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Ten Lectures on Wavelets; CBMS-NSF Lecture Notes; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Wald, A. Statistical Decision Functions; John Wiley & Sons: New York, NY, USA; Chapman & Hall: London, UK, 1950. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation via wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Jaffard, S. Pointwise smoothness, two-microlocalization and wavelet coefficients. Publ. Mat. 1991, 35, 155–168. [Google Scholar] [CrossRef] [Green Version]
- Bansal, A.K. Bayesian Parametric Inference; Narosa Publishing House Pvt. Ltd.: New Delhi, India, 2007. [Google Scholar]
- Kuznetsov, V.D. Space weather and risks of space activities. Space Technol. Technol. 2014, 3, 3–13. [Google Scholar]
- Despirac, I.V.; Kleimenova, N.G.; Gromova, L.I.; Gromov, S.V.; Malysheva, L.M. Supersubstorms during storms on 7–8 September 2017. Geomagn. Aeron. 2020, 60, 308–317. [Google Scholar] [CrossRef]
- Real Time Data Base for the Measurements of High-Resolution Neutron Monitor. Available online: www.nmdb.eu (accessed on 1 November 2020).
- Ian, G.; Yoshua, B.; Aaron, C. Deep Learning; Random House: New York, NY, USA; p. 808.
- Mandrikova, O.; Polozov, Y.; Fetisova, N.; Zalyaev, T. Analysis of the dynamics of ionospheric parameters during periods of increased solar activity and magnetic storms. J. Atmos. Sol. Terr. Phys. 2018, 181, 116–126. [Google Scholar] [CrossRef]
- IZMIRAN Space Weather Forecast Center. Catalog of Forbush Effects and Interplanetary Disturbances. Available online: http://spaceweather.izmiran.ru/rus/fds2019.html (accessed on 11 November 2020).



| Wavelet, Ψ | Number of Tree Nodes | Approximation Error, ϵ[M] |
|---|---|---|
| Daubechies 2 | 44 | 57.95443552 |
| Daubechies 2 | 44 | 57.95443552 |
| Daubechies 3 | 44 | 95.03347346 |
| Daubechies 4 | 37 | 73.25697093 |
| Daubechies 5 | 61 | 63.16288707 |
| Coiflet 2 | 42 | 77.63664436 |
| Coiflet 3 | 40 | 70.45379894 |
| Coiflet 4 | 44 | 61.81353236 |
| Coiflet 5 | 48 | 56.32646977 |
| Signal/Noise | Threshold Coefficient K = 2.5 | Threshold Coefficient K = 1.5 | ||
|---|---|---|---|---|
| Part of Detected (%) | Part of False (%) | Part of Detected (%) | Part of False (%) | |
| 1 | 89 | 4 | 87 | 13 |
| 0.8 | 81 | 7 | 49 | 15 |
| 0.7 | 72 | 10 | 66 | 17 |
| Method | Approximation Error, ϵ[M] |
|---|---|
| Autoencoder, training | 310.2346 |
| Autoencoder testing | 4.2870 × 105 |
| Threshold , Coiflet 1 | 7.2196 × 10−10 |
| Threshold , Coiflet 1 | 176.0616 |
| Threshold , Coiflet 1 | 273.2969 |
| Threshold , Coiflet 1 | 376.4855 |
| Threshold , Coiflet 2 | 177.1038 |
| Threshold , Coiflet 2 | 273.45 |
| Threshold , , Coiflet 2 | 375.741 |
| Threshold , , Coiflet 3 | 176.9381 |
| Threshold , , Coiflet 3 | 274.2327 |
| Threshold , Coiflet 3 | 376.1264 |
| Year | The Number of Forbush Effects in the Signal | Proposed Method | Autoencoder |
|---|---|---|---|
| 2013 | 98 | Detected: 86% | Detected: 79% |
| Not detected: 14% | Not detected: 21% | ||
| False alarm: 16 events | False alarm: 11 events | ||
| 2014 | 96 | Detected: 89% | Detected: 84% |
| Not detected: 11% | Not detected: 16% | ||
| False alarm: 12 events | False alarm: 9 events | ||
| 2015 | 91 | Detected: 84% | Detected: 76% |
| Not detected: 16% | Not detected: 24% | ||
| False alarm: 10 events | False alarm: 8 events |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandrikova, O.; Mandrikova, B.; Rodomanskay, A. Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition. Mathematics 2021, 9, 737. https://doi.org/10.3390/math9070737
Mandrikova O, Mandrikova B, Rodomanskay A. Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition. Mathematics. 2021; 9(7):737. https://doi.org/10.3390/math9070737
Chicago/Turabian StyleMandrikova, Oksana, Bogdana Mandrikova, and Anastasia Rodomanskay. 2021. "Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition" Mathematics 9, no. 7: 737. https://doi.org/10.3390/math9070737
APA StyleMandrikova, O., Mandrikova, B., & Rodomanskay, A. (2021). Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition. Mathematics, 9(7), 737. https://doi.org/10.3390/math9070737





