Abstract
The reasonable distribution of supply chain profits among supply chain members is the core of the stability of a supply chain. Manufacturer rebates are a normal method to improve the performance of a supply chain and balance profit distribution. Based on consideration of the behavior preferences of supply chain members, in this paper, we study the influence of rebate distribution on supply chain utility. We establish a supply chain utility model, including the proportion of distribution, fairness concern coefficient and effort level, and discuss three different situations of supply chain members. The results show that (i) a manufacturer’s rebate can more effectively improve the utility in a supply chain with fairness perception; (ii) with other conditions unchanged, the fairness perception of supply chain members will have a positive impact on their own utility; and (iii) at the same time, when the party who has more discourse power in the supply chain has a sense of fairness, this is conducive to realizing the stable development of the supply chain through changes in the proportion of rebate distribution.
1. Introduction
Economic globalization accelerates the development of the supply chain, which makes the traditional competition mode between enterprises gradually change into competition between supply chains. Therefore, maintaining efficient and stable operation of the supply chain is key to the success of enterprises in the future. Therefore, ensuring the reasonable distribution of supply chain profits among supply chain members is the core of the stability of the supply chain. Only in this way can supply chain members obtain a sense of belonging and the supply chain achieve its goal.
Wal-Mart, the world famous retail giant, achieved great success worldwide by virtue of its strategy of “Every day low price” and also consolidated its core position in the supply chain. As its core position in the supply chain, Wal-Mart continues lowering the wholesale price of suppliers and prolonging the payment cycle, which leads to complaints from suppliers. In China, suppliers have protested against this, saying that if Wal-Mart does not respect the interests of suppliers, it will stop supplying products and terminate cooperation.
From the perspective of the “rational man” hypothesis, although Wal-Mart’s behavior has seriously squeezed the interests of suppliers, suppliers can make profits in cooperation. There may be much unfairness in the process of cooperation, but at least it is profitable. In this case, why would the suppliers protest or even terminate the cooperation? Once the cooperation is terminated, it means that the original meager profits will all return to zero, which is not in line with the “rational man” hypothesis in economics. The research of behavioral economics provides a way to explain this phenomenon. Through experiments, scholars found that people not only pay attention to their own income but also pay attention to whether they are treated fairly [1].
Guth was the first to design the ultimatum game experiment, and he proposed that a proportion of people would not only pay attention to material gains [2]. In addition to the ultimatum game, there are gift exchange games, trust games, dictator games, and public product games, which can prove that people have fairness preferences. Supply chain members should focus on sustainable development to pursue supply chain long-term interest and should pay attention to the interest of both the internal and external participants [3,4].
In the actual operation process, the enterprises downstream of the supply chain will compare their own income with that of other members in the supply chain. When they find that their income is quite different from those of other members, they may think that they have been treated unfairly. In this case, they may take measures to change this situation in order to seek a fair result.
The consequence may be the emergence of double marginalization due to the lack of effective coordination among supply chain members [5]. To pursue the absolute fairness of income, they will take extreme actions, which may harm the interests of all members of the supply chain and eventually lead to the rupture of the supply chain [6].
At present, the manufacturer’s rebate is widely used in the supply chain. This method has a wide application scope and is applicable in practice. In this case, distributors and retailers can not only obtain their own operating profits, but also obtain the performance rebate given by upstream manufacturers. Different from the existing and popular method of using contracts to coordinate the supply chain, there is no contractual constraint between distributors and retailers but simply negotiation of the rebate distribution ratio to obtain a satisfactory result for both parties.
This makes the operation of the supply chain simpler and more efficient. In this process, different bodies have a different degrees of fairness, and different distribution ratios will directly affect the supply chain utility. Our research is to clarify the impact of different rebate distribution ratios on the utility of supply chain members and provides a theoretical basis for a more efficient distribution strategy in practice.
2. Literature Review
In general, our paper is related to two streams of literature: fairness concerns in the supply chain and supply chain coordination contracts as well as the role of sales effort in supply chain coordination.
The first stream of the research mainly focuses on the fairness concern in supply chain and supply chain coordination contracts. Since Rabin first defined the concept of fairness concern through behavioral experiments, research on introducing the concept of fairness concern into supply chain operation and management has been emerging [7]. Camerer and Thaler studied the ultimatum game to make it clear that when people think they are being treated unfairly, they will take measures to punish those who are unfair to them [8].
Cui et al. further introduced fairness concerns into the determined supply chain model and analyzed the impact of fairness concerns on supply chain coordination in a manufacturer-led supply chain. They pointed out that, under certain conditions, wholesale price contracts can coordinate the supply chain when retailers have fairness concerns [9]. Caliskan Demirag et al. extended Cui’s study with Cui’s model studied under the condition of linear demand. They found that, under the condition of nonlinear demand, manufacturers could achieve supply chain coordination only through wholesale price contracts in many situations [10].
Gerchak and Wang studied the supply chain performance of assembly systems under uncertain demands. They compared the revenue-sharing contract and wholesale-price contract and found that a wholesale-price-only scheme degraded with the number of suppliers, while the situation with only a revenue-sharing contract was the opposite [11]. Ullah et al. studied a joint inventory and dynamic pricing policy for stochastic price-dependent demand, and they developed a multi-period newsvendor model to help retailers increase profit and market share [12].
Cachon and Lariviere studied the strengths and limitations of a revenue-sharing contract under the newsvendor model. They demonstrated that revenue-sharing can coordinate a supply chain, including multiple competing retailers and can explain why revenue-sharing contracts are not prevalent in all industries [13]. Jian et al. studied the competing supply chain with revenue-sharing contract and fairness concern. They established two game models to explore the Pareto improvements in supply chains, and they found that manufacture’s fairness concern could achieve the increase in supply chain profits [14].
Jin found that there was a partial substitution relationship between the online recommendations of e-commerce enterprises and the experienced service of offline stores, which may lead to an imbalance of the incentive contract and eventually aggravate an imbalance in the supply chain [15]. Katok, Olsen, and Pavlov studied the information regarding fairness concern behavior from supply chain members with wholesale price contracts, and found that when the fairness concern information of supply chain members is private, the strength of fairness concern behavior will have different effects on the operation decision, and the asymmetry of fairness preference information may make the supply chain unable to achieve coordination [16].
Wei and Li’s pricing strategy for dual channel supply chains takes into account the fairness concern behavior and risk aversion behavior of decision-makers in the supply chain [17]. Sarkar et al. studied a single-period newsvendor problem with a consignment policy and introduced a new policy that both consignors and consignees shared the fixed fee under the Stackelberg approach, which can reduce the cost of the retailers [18].
The fairness perception of supply chain participants will have an impact on the supply chain utility, the degree of sales effort of participants will also have a direct impact on supply chain utility. The sales efforts of supply chain participants include hiring more sales personnel, increasing product publicity, and improving product quality. Mela concluded that from 1990 to 1995, nearly 70% of enterprises significantly increased their investment in commodity promotion, which can be interpreted as efforts toward sales [19].
Lin B also pointed out that, in 2010, the total turnover of advertising and promotion activities in the United States exceeded 300 billion dollars, and the total amount of advertising and promotion activities in the world exceeded 500 billion dollars [20]. Previous studies demonstrated that sales efforts have a positive impact on supply chain utility.
Most studies on effort level are related to supply chain coordination, market demand, and supply chain decision-making. Taylor’s research shows that under a linear rebate, the supplier can improve the retail profit margin by combining the buyback contract with the sales rebate contract, prompting the retailer to make more efforts and increase the order quantity [21]. Manikas and Godfrey established a new coordinating mechanism for a two-echelon service chain with a single service retailer and multiple suppliers, and the mechanism could coordinate the supply chain while simplifying the calculation as well [22].
Krishnan et al. introduced the quick response mechanism into the supply chain, and found that the quick response mechanism would reduce the retailer’s effort level [23]. Therefore, to avoid the decline of the retailer’s enthusiasm, the cooperation of a minimum order contract and discount contract is needed. Under the assumption that the supplier and retailer are risk neutral, Krishnan et al. pointed out that the buyback strategy will reduce the retailer’s sales effort level and indirectly reduce the utility of the whole supply chain through the research on the inventory and effort level of both parties [24].
Yue et al. studied the pricing and promotion efforts of the supply chain when both manufacturers and retailers offer price discounts—that is, advertising investment decision-making. They found that, in the supply chain, the situation dominated by the manufacturer has a greater advantage over the situation with equal rights [25]. Song et al. first considered that when product quality and sales efforts affect demand at the same time, the power structure of different channels will have different effects on the production decisions of manufacturers and retailers [26]. Ma studied the supply chain decision-making model under the conditions of information symmetry and asymmetry, considering that marketing efforts can improve corporate social responsibility [27].
In this paper, we studied the literature on the aspects of supply chain coordination contracts, the fairness concern and effort level. From the perspective of supply chain utility, we established a game model consisting of the rebate distribution proportion, fairness concern coefficient, and effort level and analyzed the impact of rebate distribution proportion on supply chain utility. We discuss the utility of supply chains under three different scenarios, which provides theoretical support for solving common problems in reality. The results of this study can not only improve the utility of supply chain but also balance the profit distribution among members in a supply chain and finally achieve stable development of a supply chain.
3. Model Description
3.1. Prior Assumptions
In this paper, we studied a two-level supply chain model composed of one distributor and one retailer. In this model, a distributor buys products from upstream manufacturers at price c, which is defined as the cost of the distributors. After that, the distributor sells the products to the retailer at the wholesale price w, and finally the retailer sells the products to the consumers at the retail price p. We assumed that the effort behavior of distributors and retailers for product sales will have an impact on the market demand of products and will be directly reflected in the sales volume of products.
In the business process, distributors and retailers can obtain the sales rebate given by the manufacturer at the end of each sales cycle. There is a positive correlation between the amount of sales rebate and the amounts of products sold—that is, the more products sold, the more rebate the manufacturer will give. After the manufacturer returns the rebate to the downstream distributors and retailers, the distributors will discuss with the retailers to determine the distribution proportion of the rebate. Due to the profit seeking nature of merchants, there are three kinds of distribution situations in the actual distribution process.
- (1)
- Distributor obtains a higher proportion of the distribution.
- (2)
- Distributor and retailer obtain the same distribution ratio.
- (3)
- Retailer obtains a higher proportion of the distribution.
In the supply chain model without considering fairness concerns, distributors and retailers guard their own interests according to the proportion of negotiation, and the proportion of distribution will not affect the effort level of the distributors and retailers, that is, both sides will maintain the original level of effort. However, in the model considering fairness concerns, if only the distributors have a sense of fairness and the retailers remain in a fairness neutral (i.e., rational) state, when the distributors know that their income is lower than that of the retailers, the distributors who have adverse unfair aversion will feel that they have been treated unfairly.
To seek a fair result, the distributors will lower their effort level. For example, they may reduce the amount of advertising, cut down product publicity activities, and a series of other measures. These practices will eventually be reflected in the market demand for products. The decrease in distributor effort level will lead to the decrease in market demand, which will also lead to a decrease in product sales.
As the manufacturer’s rebate is directly related to the amounts of products sold, the actions of distributors will lead to a reduction in their own and the retailer’s revenue, and the utility of the whole supply chain will also be harmed. Similarly, when the retailer has a sense of fairness and the distributor remains fairness neutral, a similar situation will occur. Therefore, a reasonable proportion of rebate distribution can lead to both distributors and retailers obtaining better profits and can improve the utility of the supply chain.
3.2. Model Development
3.2.1. Symbol Description
c: distributor’s cost;
w: wholesale price;
p: retail price;
Q: demand of the product;
a: market size, ;
b: Price sensitivity coefficient, ;
: distributor’s effort level, ;
: retailer’s effort level, ;
: distributor’s effort efficiency, ;
: retailer’s effort efficiency, ;
: Effort cost coefficient of distributors, ;
: Effort cost coefficient of retailers, ;
: sales rebate, ;
: rebate ratio;
: distribution proportion of distributors in rebate,;
distribution proportion of retailers in rebate;
: distributor’s effort cost;
: retailer’s effort cost;
: unfair aversion coefficient of distributors, ; and
: unfair aversion coefficient of retailer, .
3.2.2. Model Development
In a supply chain composed of a retailer and a distributor, the market demand is linearly related to the retailer’s retail price, the effort level of the retailer, and the distributor. All the information in the market is shared by the retailer and the distributor, and the information of the two parties are completely symmetric. The effort level of distributors and retailers is decided by themselves independently, and the effort level of the other side will not affect their own effort level.
- Situation I: both distributor and retailer are fairness neutral
When both distributor and retailer are fairness neutral, the profit functions of distributor and retailer are as follows:
In situation I, we find the partial derivative of Equation (2) with respect to . Equation (4) is obtained.
Let (4) be equal to zero. We obtain the following:
We find the partial derivative of Equation (3) with respect to and let the partial derivative equal 0. Equations (6) and (7) are obtained.
Remark 1:
and are, respectively, the best effort level of distributors and retailers under situation I. By observing Equations (5) and (7), we find that the effort level of distributors increases with the increase in , while the effort level of retailers decreases with the increase in . In reality, there is a positive correlation between the amount of reward and the sales volume of products, that is, the more the sales volume of products, the greater the amount of reward.
When distributors have a higher proportion of the rebate distribution, the total amount of bonus will be more, which will have an incentive effect on the distributors, and distributors will further improve their efforts to obtain higher profits. In the same way, if the distributors obtain a higher proportion of bonus distribution, then the retailer can only obtain less bonus, which will undoubtedly have a negative impact on the retailer’s sales enthusiasm, and eventually lead to a reduction in the retailer’s effort level.
Remark 2:
By observing Equations (5) and (7), we suppose that distributors and retailers decide to distribute the rebate equally, that is, λ = 0.5. In addition, the effort efficiency and effort cost of distributors and retailers are the same, that is, . In this case, the only factors that affect the effort level of distributors and retailers are the distributor’s cost c, wholesale price w, and retail price p. The distributor can decide (w − c) and the retailer can decide (p − w). It is not difficult to find that both sides can maximize the profit of a single commodity by increasing the selling price.
However, because the market demand has a direct relationship with the retail price of the product, when the retail price of the product increases, the market demand of the product will decrease. In this case, the total profit of retailers and distributors is difficult to maintain, which means that if distributors do not leave reasonable profit space for retailers, the retailer’s effort level is difficult to guarantee.
Substituting Equations (5) and (7) into Equation (2), we obtain the following:
Equation (8) shows the maximum profit function under the level of effort maintained by the distributors to maximize their own interests without considering fairness concerns. Substituting Equations (5) and (7) into Equation (3), we obtain the following:
Equation (9) shows the maximum profit function of retailers in order to maximize their own interests without considering fairness concerns.
- Situation II: only retailers have fairness concerns
In situation I, we consider a two-echelon supply chain composed of one retailer and one distributor. However, in this supply chain, retailers have adverse unfair aversion (which means that when their profits are less than those of distributors, they will be jealous), while distributors maintain a fairness neutral.
In this paper, we analyzed the change of effort level of distributors and retailers with different distribution proportions of rebate, and then studied the influence of the distribution proportion of rebate on the utility of both sides. We used the F-S model proposed by Fehr and Schmidt to characterize the fair utility function of distributors and retailers [28]. In the FS model, any difference in income between individuals will lead to unfair aversion, which reflects the negative effect of unfair aversion in the model.
In this case, the utility function of the retailer is as follows:
and the utility function of the distributor is as follows:
We find the partial derivative of Equation (10) with respect to , and Equation (12) is obtained.
Let ; we can then obtain the following:
As the effort levels of distributors and retailers involve their own decisions and are not affected by each other’s decisions, when retailers have adverse unfair aversion, the effort level of distributors follows.
Substituting Equations (13) and (14) into Equations (10) and (11), we obtain
Equation (15) shows the utility function of the retailer when the retailer has adverse unfair aversion, and Equation (16) shows the utility function of the retailer when the retailer has adverse unfair aversion.
- Situation III: only distributors have fairness concerns
Situation III considered is the opposite to situation II, in which the distributor has adverse unfairness aversion while the retailer remains fairness neutral. In this case, the utility function of the distributors is as follows:
The utility function of the retailer is as follows:
We find the partial derivative of Equation (17) with respect to , and Equation (19) is obtained.
We let , and we can obtain the following:
The same is true.
Substituting Equations (20) and (21) into Equations (17) and (18), and the utility function of the distributor is:
The utility function of the retailer is:
Equation (22) shows the utility function of the retailer when the distributor has adverse unfair aversion, and Equation (23) shows the utility function of the retailer when the distributor has adverse unfair aversion.
4. Numerical Simulation
To explain the meaning of the equation more intuitively, we calculated the function equation through numerical calculation.
4.1. Both Distributor and Retailer Are Fairness Neutral
In situation I, both the retailer and the distributor are fairness neutral. Suppose that the retailer and the distributor discuss the average distribution of the rebate, namely .
The utility function of the distributor is followed. , By simplifying the function, we can obtain the following results. .
Remark 3:
The result shows that there is a negative correlation between the profit of the distributor and the retail price of products. The higher the retail price of products is, the less the profit of distributors will be. From the actual situation, because retailers want to ensure their own interests, the minimum retail price should be greater than 1.3 to ensure no loss. When , the utility of the distributor is . Under the same conditions, the retailer’s utility function is . By simplifying the function, we can obtain the following results..
Remark 4:
The retailer’s profit is a quadratic function of the retail price . After calculation, we found that when the retail price , the retailer’s profit reaches the highest, , then the profit of the distributor is . When the retail price , the retailer is on the edge of loss. It can be seen that retail price has a great impact on the profit of distributors and retailers.
The profit of the supply chain is . At this time, . After calculation, when , the total profit of the supply chain reaches the highest, , the profit of distributors is , and the retailer’s profit is as shown in Figure 1.
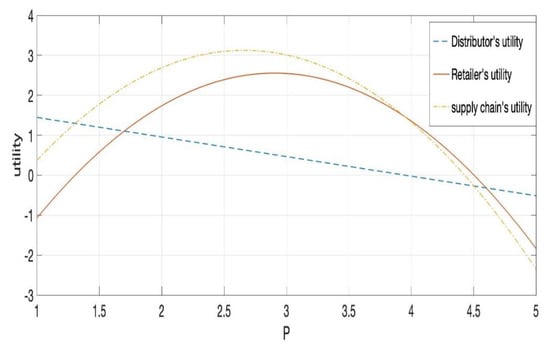
Figure 1.
The relationship between the retail price and supply chain profit.
Remark 5:
It can be seen from Figure 1 that the overall profit of the supply chain and the profit of the retailer are affected by the retail price to a similar extent, and both increase and then decrease with the increase in retail price. In the market, keeping a certain level of gross profit rate and setting an appropriate price can effectively improve profits; however, if the product price deviates too much from the product value, this will lead to a reduction in market demand, making the products unsalable and supply chain loss. It can also be seen from the figure that the influence of the retail price on distributors is obvious.
When the retail price increases, the profit of distributors decreases rapidly. This is because the distributors cannot control the retail price in the market. They can only suppose that the retailers can set a reasonable retail price to achieve the goal of small profit and quick turnover. Once the retailers cannot reach an agreement with the distributors to increase the retail price for personal profit, the distributors cannot intervene. At this time, the distributor’s approach is often to increase the wholesale price, and increase their gross profit margin to resist the impact of reduced sales on their own profits.
Under the above conditions, the calculation shows that the profit of the supply chain reaches the maximum value when the wholesale price . To study the influence of both sides’ effort level on the profit of the supply chain, we set Under these conditions, the profit of the distributor is , and the retailer’s profit is . When and vary from 0 and 1, the changes of the distributor and retail profits are shown in Figure 2.
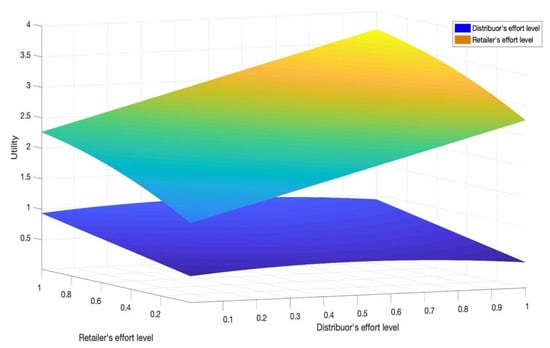
Figure 2.
The effects of the effort level of distributors and retailers on supply chain profit.
Remark 6:
According to the results of the above analysis, combined with Figure 2, we found that, because the retail price makes the retailer obtain a higher marginal profit, when the retailer improves their own effort level, their own profit increases faster, which can also be understood as the incentive effect of high marginal profit for the retailer to improve their own effort level being more obvious. For distributors, the incentive level of relatively low and fixed marginal profit is significantly lower than that of retailers. Therefore, in the process of operation, it is more conducive to the healthy and sustainable development of the whole supply chain to appropriately increase the wholesale price and ensure their own reasonable interests.
When , we consider the impact of the retail price and rebate distribution ratio on the profit of distributors and retailers. At this time, the profit of distributors is , and the retailer’s profit is . The results are shown in Figure 3 and Figure 4.
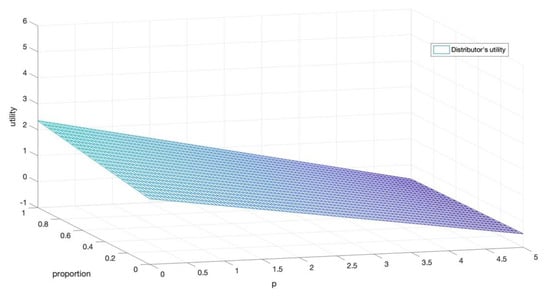
Figure 3.
The impact of changes in the retail price and distribution ratio on distributor profits.
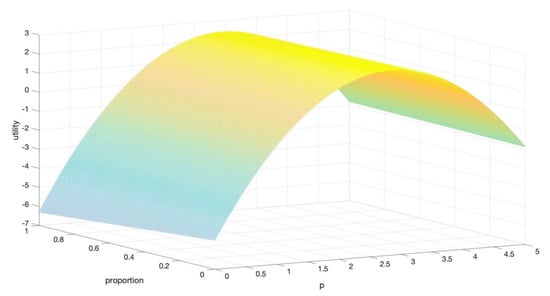
Figure 4.
The impact of the retail price and distribution ratio on retailer profits.
4.2. Simulation Calculation and Data Analysis of Retailer Fairness Concern
In situation II, the retailer in the two-echelon supply chain remains fairness neutral, and the retailer has the fairness concern behavior of adverse unfairness aversion.
Suppose .
The utility function of the retailer is
The utility function of the distributor is .
The best effort level of the distributor is . The retailer’s optimal effort level is . Substituting the parameter into the equation, we can obtain the following.
To study the impact of rebate distribution on the utility of distributors, retailers, and the whole supply chain, we considered the situation under different distribution ratios. We selected ten distribution ratios with λ = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1 and considered the adverse unfair aversion coefficient under each distribution ratio = 0.2, 0.5, and 0.8. The utility of the distributors and retailers and the total utility of the supply chain were calculated in each case as shown in Table 1.

Table 1.
The utility values of retailers, distributors, and supply chains under different distribution ratios.
Remark 7:
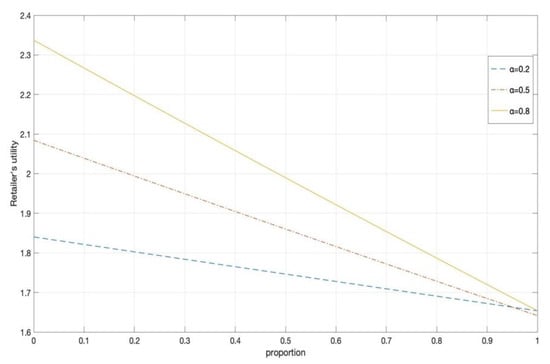
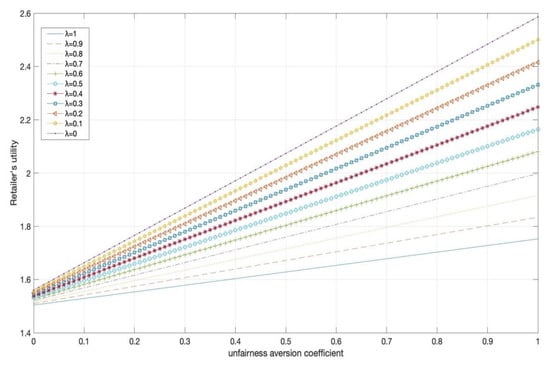
By analyzing each group of data, we can see that under the same distribution ratio, with the increase in the retailer’s adverse unfair aversion coefficient, the retailer’s utility value increases. The distributor’s utility decreases with the increase in the retailer’s aversion coefficient. Combined with Figure 5 and Figure 6, this fully shows that fairness concern behavior does play a role in daily operation, and people are not completely rational people. While pursuing interests, people are also pursuing fairness, and sometimes they can give up their interests for the sake of fairness.

Figure 5.
The effects of different adverse unfair aversion coefficients on the retailer utility.

Figure 6.
The effect of different distribution proportion on the retailer utility.
Remark 8:
According to Table 1, when , the retailer’s utility reaches the maximum value , and the utility of the distributor reaches the minimum value . This means that retailers can obtain 90% of the rebate, and distributors can only obtain 10%. Retailers have a high degree of aversion to adverse unfairness, and even if the utility of distributors is a little higher than themselves, this will also cause jealousy.
Therefore, under this condition, there will be an extreme situation, that is, the retailer’s utility reaches the highest and the distributor’s utility reaches the lowest. At the same time, we find that the supply chain’s utility reaches the highest. By analyzing the reasons, we can infer that the supply chain may be dominated by retailers, because in the process of operation, retailers obtain very high marginal profit, and can also obtain 90% of the rebate, which indicates that retailers control the sales channel. At this time, the rich rebate can effectively stimulate the sales enthusiasm of retailers, so that the supply chain utility can reach the maximum.
Remark 9:
When , the utility of the distributor reaches the maximum value and the retailer’s utility is . In this case, the retailer will obtain all the rebate, while the retailer has a low degree of adverse unfair aversion. When , the utility of the distributor is 0.853, and the utility of retailer is . It is also the distributors who obtain all the rebate.
However, due to the different degrees of aversion of retailers to the adverse unfairness, the perceived intensity of unfairness will be different. Higher perceived intensity of unfairness will lead to a negative service attitude of retailers, a reduction in the number of employees, and a lack of promotions, which will eventually affect the individual utility and the overall utility of the supply chain.
Remark 10:
Through comparative analysis, we found that when the retailer’s adverse unfair aversion coefficient and , the total utility of the supply chain increased with the increase in the rebate distribution proportion. The main reason is that the retailer’s profit is higher than that of the distributor in the fixed price, and the rebate distribution can make up the profit gap between the retailer and the distributor.
This can effectively motivate the distributor to improve their effort level and strive for more outstanding performance. The distributors obtain more rebate just to make up for the profit difference, and this will not trigger the unfair aversion of retailers, and, thus, this will not produce negative effects on profits. When , the total utility of the supply chain decreases with the increase in the rebate distribution proportion.
At this time, the retailer’s aversion to adverse unfairness is very high, which will eventually affect their effort level, and then affect the utility of the whole supply chain. Especially in the supply chain dominated by retailers, the reduction in the retailers’ effort level has a great impact on the operation and stability of the supply chain. Both sides in the supply chain should maintain a moderate fairness concern behavior and pay high effort to obtain higher supply chain utility.
4.3. Simulation Calculation and Data Analysis of Distributor Fairness Concerns
In situation III, the situation considered is opposite to situation II, in which the distributor has adverse unfairness aversion while the retailer remains fairness neutral. All the parameter settings are consistent with situation II, assuming . The utility function of the distributor and retailer are as follows.
The best effort level of the distributor is: . The best effort level of the retailer is: . Substituting the parameter into the equation, we can obtain the following.
In this paper, we selected ten distribution ratios of λ = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1 and considered the adverse unfair aversion coefficient α under each distribution ratio, S = 0.2, 0.5, and 0.8. The utility of the distributors and retailers and the total utility of the supply chain were calculated in each case as shown in Table 2.

Table 2.
The utility values of the retailers, distributors, and supply chains under different distribution ratios.
We found that the value of distributor utility in Table 1 was lower than that in Table 2 under the conditions that the retailers and distributors both had the fairness concern behavior and the fairness coefficient α = 0.2. As the marginal profit of the distributor is always less than that of the retailer in situation III, the distributor is always in the aversion state of adverse unfairness, and thus it can be inferred that appropriate fairness concern behavior can improve its own utility. Similarly, when the party with higher marginal profit has fairness concern behavior, this will produce higher overall utility in the supply chain as shown in Table 3.

Table 3.
Comparison of the utility of the supply chain under adverse unfair aversion of distributors and retailers.
5. Conclusions
In this paper, fairness concerns were introduced into the study of the utility of a two-echelon supply chain. On this basis, the influence of different rebate distribution ratios on the utility of the supply chain in different situations was studied. By establishing a mathematical model, we calculated the changes in distributor utility, retailer utility, and the total supply chain utility under three scenarios of fairness concern. We analyzed the influence of the change of distribution proportion and the change of fairness concern on the utility of supply chain in different situations, and made a comparative analysis of the results.
Finally, we obtained the following conclusions.
First, we studied the role of fairness concern behavior in the supply chain. In the supply chain, members will also pursue fairness in the process of pursuing profits. In practice, ignoring the sense of fairness of partners and focusing only on their own profit maximization may lead to rupture of the supply chain. Therefore, a reasonable profit distribution mechanism is very important for the stable development of supply chains, and supply chain members should consider various factors to distribute profits, such as price and the marginal profit of both sides. We also found that fairness perception helped supply chain members to achieve better utility.
Second, we analyzed the effect of the manufacturer rebate, a traditional supply chain incentive strategy. We found that a manufacturer rebate played the role of balancing profit distribution in a supply chain, particularly in supply chains with a sense of fairness. Our model provides theoretical support for manufacturers to seek the most efficient rebate ratio, and can also provide support for the optimal rebate distribution ratio between distributors and retailers and ultimately, help to improve the performance of a supply chain.
Third, in the process of supply chain operation, if the member with more discourse power in the supply chain has a sense of fairness, this is more conducive to realize stable development of the supply chain through the change of rebate distribution proportion as they tend to focus on the long-term benefits, and are willing to transfer part of the rebate in exchange for better supply chain utility.
Finally, our model reduces the difficulty of application in practice, enriches the theory of supply chain coordination, and simplifies the calculations.
Based on the above conclusions, the paper has the following insights for supply chain management. First, manufacturers should formulate reasonable incentive policies, strengthen communication and coordination with downstream distributors and retailers, and moderately intervene in the distribution of rebate among downstream participants. Secondly, as the upstream and downstream enterprises of the supply chain, distributors and retailers are interdependent. Setting reasonable marginal profit and protecting the income of partners are the basis for stable development of the supply chain. Retailers need to build a long-term cooperative relationship with distributors to achieve a win-win situation in the supply chain. Thirdly, it is an effective way to improve the quality and efficiency of the supply chain for distributors and for retailers to improve their operation efficiency and reduce their effort cost.
This paper only studied the benefit comparison between distributors and retailers in the supply chain vertically, without considering the benefit comparison when the manufacturer corresponds to multiple distributors and the distributors correspond to multiple retailers. In future research, we can investigate horizontal research between multiple distributors and retailers in a supply chain, which is more complex.
Author Contributions
Conceptualization, X.J.; Writing—original draft, X.J.; Writing review and editing, X.J. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ho, T.H.; Su, X.; Wu, Y. Distributional and Peer-Induced Fairness in Supply Chain Contract Design. Prod. Oper. Manag. 2014, 23, 161–175. [Google Scholar] [CrossRef]
- Güth, W.; Schmittberger, R.; Schwarze, B. An experimental analysis of ultimatum bargaining. J. Econ. Behav. Organ. 1982, 3, 367–388. [Google Scholar] [CrossRef]
- Pucci, T.; Casprini, E.; Galati, A.; Zanni, L. The virtuous cycle of stakeholder engagement in developing a sustainability culture: Salcheto winery. J. Bus. Res. 2020, 119, 364–376. [Google Scholar] [CrossRef]
- Giacomarra, M.; Crescimanno, M.; Sakka, G.; Galati, A. Stakeholder engagement toward value co-creation in the F&B packaging industry. EuroMed J. Bus. 2019, 15, 315–331. [Google Scholar] [CrossRef]
- Spengler, J.J. Vertical Integration and Antitrust Policy. J. Political Econ. 1950, 58, 347–352. [Google Scholar] [CrossRef]
- Nie, T.F.; He, B.Y.; Du, S.F. Supply chain operations considering fairness concerns with bargaining disagreement point. J. Manag. Sci. China 2017, 20, 92–102. [Google Scholar]
- Rabin, M. Incorporating Fairness into Game Theory and Economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Thaler, C.R.H. Anomalies: Ultimatums, Dictators and Manners. J. Econ. Perspect. 1995, 9, 209–219. [Google Scholar]
- Cui, T.H.; Raju, J.S.; Zhang, Z.J. Fairness and Channel Coordination. Manag. Sci. 2007, 53, 1303–1314. [Google Scholar] [CrossRef]
- Caliskan-Demirag, O.; Chen, Y.; Li, J. Channel coordination under fairness concerns and nonlinear demand. Eur. J. Oper. Res. 2010, 207, 1321–1326. [Google Scholar] [CrossRef]
- Gerchak, Y.; Wang, Y. Revenue-Sharing vs. Wholesale-Price Contracts in Assembly Systems with Random Demand. Prod. Oper. Manag. 2009, 13, 23–33. [Google Scholar] [CrossRef]
- Ullah, M.; Khan, I.; Sarkar, B. Dynamic Pricing in a Multi-Period Newsvendor Under Stochastic Price-Dependent Demand. Mathematics 2019, 7, 520. [Google Scholar] [CrossRef]
- Cachon, G.P.; Lariviere, M.A. Supply Chain Coordination with Revenue-Sharing Contracts: Strengths and Limitations. Manag. Sci. 2005, 51, 30–44. [Google Scholar] [CrossRef]
- Jian, J.; Zhang, Y.; Jiang, L.; Su, J. Coordination of Supply Chains with Competing Manufacturers considering Fairness Concerns. Complex 2020, 2020, 4372603. [Google Scholar] [CrossRef]
- Liang, J. Optimal Online Referral Strategy and Incentive Mechanism in Offline to Online (O2O)Supply Chain. Manag. Rev. 2019, 31, 242–253. [Google Scholar]
- Katok, E.; Olsen, T.; Pavlov, V. Wholesale Pricing under Mild and Privately Known Concerns for Fairness. Prod. Oper. Manag. 2014, 23, 285–302. [Google Scholar] [CrossRef]
- Wei, G.; Li, K. A Review of Economic Theoretical Model on Fairness Preference. Lect. Notes Manag. Sci. 2013, 19, 38–43. [Google Scholar]
- Sarkar, B.; Zhang, C.; Majumder, A.; Sarkar, M.; Seo, Y.W. A distribution free newsvendor model with consignment policy and retailer’s royalty reduction. Int. J. Prod. Res. 2018, 56, 5025–5044. [Google Scholar] [CrossRef]
- Mela, C.F.; Gupta, S.; Lehmann, D.R. The long-term impact of promotion and advertising on consumer brand choice. J. Mark. Res. 1997, 34, 248–261. [Google Scholar] [CrossRef]
- Liu, B.; Cai, G.; Tsay, A.A. Advertising in Asymmetric Competing Supply Chains. Prod. Oper. Manag. 2014, 23, 1845–1858. [Google Scholar] [CrossRef]
- Taylor, T.A. Supply Chain Coordination Under Channel Rebates with Sales Effort Effects. Manag. Sci. 2002, 48, 992–1007. [Google Scholar] [CrossRef]
- Manikas, A.; Godfrey, M. Service Chain Coordination Using Salvage Manipulation. Int. J. Manag. Mark. Res. 2016, 7, 15–27. [Google Scholar]
- Krishnan, H.; Kapuscinski, R.; Butz, D.A. Quick Response and Retailer Effort. Manag. Sci. 2010, 56, 962–977. [Google Scholar] [CrossRef]
- Krishnan, H.; Kapuscinski, R.; Butz, D.A. Coordinating Contracts for Decentralized Supply Chains with Retailer Promotional Effort. Manag. Sci. 2004, 50, 48–63. [Google Scholar] [CrossRef]
- Yue, J.; Austin, J.; Huang, Z.; Chen, B. Pricing and advertisement in a manufacturer–retailer supply chain. Eur. J. Oper. Res. 2013, 231, 492–502. [Google Scholar] [CrossRef]
- Song, J.; Li, F.; Wu, D.D.; Liang, L.; Dolgui, A. Supply chain coordination through integration of innovation effort and advertising support. Appl. Math. Model. 2017, 49, 108–123. [Google Scholar] [CrossRef]
- Ma, P.; Shang, J.; Wang, H. Enhancing corporate social responsibility: Contract design under information asymmetry. Omega 2017, 67, 19–30. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A Thoery of fairness, competition and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).