Networked Analysis of a Teaching Unit for Primary School Symmetries in the Form of an E-Book
Abstract
1. Introduction
2. Review of Literature
3. Theoretical Framework
3.1. The Van Hiele Levels of Mathematical Reasoning
- Level 1 (visual recognition): geometric objects are recognized globally by their shape and appearance, and classified or differentiated on a visual basis. Students can name geometric objects, but they do not recognize their mathematical components or attributes. Students can identify a symmetrical figure or a pair of symmetrical figures by sight, folding a sheet of paper or using a mirror. They can use paper folding to draw symmetries and to get axes of symmetry. They can also discover visual properties of symmetrical figures, like equidistance to the axis or position at both sides of the axis, and learn some mathematical terms, like axis, symmetry, or image.
- Level 2 (analysis): mathematical components and properties of geometric objects are identified and used to describe and classify the objects. Students can discover experimentally the main properties of symmetrical figures and axes (equidistance and perpendicularity respect to the axis) and prove them empirically. They describe informally transformations observed after dragging GeoGebra figures and mathematical properties identified, and can verbalize a definition of symmetry as a list of known properties. They can draw the image of a figure and the axis of a symmetrical figure or a pair of symmetrical figures by using properties of the perpendicular bisector. They can also obtain the image of a shape after a product of two symmetries. Students learn to use geometric symbols when writing their solution or talking about them, like P, P’, Se, and others, but cannot understand complex symbolic expressions.
- Level 3 (informal deduction): mathematical definitions of geometric objects (as minimum sets of properties) are meaningful for students, and they are able to use different definitions for the same concept; in particular, they can obtain and use the mathematical definition of symmetry. Students can discover properties of symmetry or symmetrical figures and prove them by assembling informal deductive arguments by means of known definitions and properties. They can also discover and understand the relationships between products of two symmetries and translations or rotations, in particular that there are infinitely many decompositions of translations and rotations into pairs of symmetries.
- Level 4 (formal deduction): the algebraic structure of the group of the plane isometries can be understood and properties of the group can be discovered, and students can prove them by means of formal proofs.
3.2. The Levels of Cognitive Demand
- Memorization: Activities only requiring the reproduction of previously memorized definitions, properties, formulas, etc., which are explicitly and clearly mentioned in the statement. There is no connection to the concepts or relationships to be learned. The solution of these activities requires a minimum cognitive effort.
- Procedures without connections: Activities requiring algorithmic solutions, consisting of following a previously mastered simple procedure that is explicitly called for or is evident from the statement of the activity. There is no connection to the concepts or relationships to be learned. The solution of these activities requires a limited cognitive effort.
- Procedures with connections: Activities requiring algorithmic solutions, consisting of following a previously mastered procedure which, unlike the previous level, is complex and requires students to be mindful and take some decisions. The way to follow the procedure is not evident and, to succeed, students have to understand and use consciously the mathematical contents or relationships to be learned which are implicit in the activity. The solution of these activities requires a moderately high cognitive effort.
- Doing mathematics: Activities requiring non-algorithmic thinking, since they do not explicitly suggest a way of solution. Students have to use the mathematical contents or relationships to be learned implicit in the activity in innovative and original ways. The solution of these activities requires a high cognitive effort.
3.3. Networking Theories in Mathematics Education
4. Methodology
4.1. Selection of the Mathematical Contents
- Visual approach to symmetries: visual identification of symmetrical shapes, pairs of symmetrical shapes, and axes of symmetry.
- Manipulative approach to symmetries: folding and cutting out to produce symmetrical shapes and axes of symmetrical shapes (the electronic environment of the e-book does not favor the use of a mirror).
- Discovery of the equidistance of any two symmetrical points from the axis of symmetry.
- Discovery of the perpendicularity to the axis of any segment ending in two symmetrical points.
- Equidistance and perpendicularity as the main characteristics of symmetries. Mathematical definition of axial symmetry.
- Accurate constructions with the DGS of the images of given shapes and the axis of given (pairs of) symmetrical shapes.
- Relationship between the axis of symmetry and the perpendicular bisector of any pair of symmetrical points.
- Symmetries of triangles, quadrilaterals, and regular polygons. Generalization of the relationship between the number of sides of a regular polygon, its number of symmetries, and the position of their axes.
- Products of two symmetries with parallel axes.
- Products of two symmetries with secant axes.
- Creation of frieze patterns and rosette (dihedral) patterns.
- Decomposition of translations and rotations into products of two symmetries. Infiniteness of solutions.
4.2. Didactical Criteria for Designing the Teaching Unit
4.3. Structure and Components of the Electronic Book
5. The Contents of the E-Book for the Learning of Plane Symmetries
6. Discussion: Analysis of the Mathematical Content of the E-Book
7. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sinclair, N.; Cirillo, M.; de Villiers, M. The Learning and Teaching of Geometry. In Compendium for Research in Mathematics Education; Cai, J., Ed.; NCTM: Reston, VA, USA, 2017; pp. 457–489. [Google Scholar]
- Swoboda, E.; Vighi, P. Early Geometrical Thinking in the Environment of Patterns, Mosaics and Isometries; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Sinclair, N.; Bussi, M.G.B.; De Villiers, M.; Jones, K.; Kortenkamp, U.; Leung, A.; Owens, K. Recent Research on Geometry Education: An ICME-13 Survey Team Report. ZDM 2016, 48, 691–719. [Google Scholar] [CrossRef]
- Roschelle, J.; Noss, R.; Blikstein, P.; Jackiw, N. Technology for Learning Mathematics. In Compendium for Research in Mathematics Education; Cai, J., Ed.; NCTM: Reston, VA, USA, 2017; pp. 853–876. [Google Scholar]
- Wu, H. Key Mathematical Ideas in Grades 5–8. In Proceedings of the National Council of Teachers of Mathematics Annual Meeting, Anaheim, CA, USA, 4–6 April 2005. [Google Scholar]
- Thaqi, X.; Gimenez, J. Geometrical Transformations in the Mathematics Textbooks in Kosovo and Catalonia. Univ. J. Educ. Res. 2016, 4, 1944–1949. [Google Scholar] [CrossRef]
- Faggiano, E.; Montone, A.; Mariotti, M.A. Synergy between Manipulative and Digital Artefacts: A Teaching Experiment on Axial Symmetry at Primary School. Int. J. Math. Educ. Sci. Technol. 2018, 49, 1165–1180. [Google Scholar] [CrossRef]
- Seago, N.; Jacobs, J.; Driscoll, M.; Matassa, M.; Callahan, M. Developing Teachers’ Knowledge of a Transformations-Based Approach to Geometric Similarity. Math. Teach. Educ. 2013, 2, 74–85. [Google Scholar] [CrossRef]
- Knuchel, C. Teaching Symmetry in the Elementary Curriculum. Math. Enthus. 2004, 1, 3–8. [Google Scholar]
- NCTM. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Clements, D.H.; Battista, M.T. Geometry and Spatial Reasoning. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; MacMillan: New York, NY, USA, 1992; pp. 420–464. [Google Scholar]
- Sinclair, N.; Bruce, C.D. New Opportunities in Geometry Education at the Primary School. ZDM 2015, 47, 319–329. [Google Scholar] [CrossRef]
- Küchemann, D. Children’s Difficulties with Single Reflections and Rotations. Math. Sch. 1980, 9, 12–13. [Google Scholar]
- Hart, K. Children’s Understanding of Mathematics: 11–16; John Murray: London, UK, 1981. [Google Scholar]
- Herscovics, N. Cognitive Obstacles Encountered in the Learning of Algebra. In Research Issues in the Learning and Teaching of Algebra; Wagner, S., Kieran, C., Eds.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1989; Volume 4, pp. 60–86. [Google Scholar]
- Yılmaz, G.K. The Effect of Dynamic Geometry Software and Physical Manipulatives on Candidate Teachers’ Transformational Geometry Success. Educ. Sci. Theory Pract. 2015, 16, 1417–1435. [Google Scholar] [CrossRef]
- Gutiérrez, P. Teaching Symmetries in Primary Education; Apple Books Store: Cupertino, CA, USA, 2021; Available online: https://books.apple.com/us/book/teaching-symmetries-in-primary-education/id1553392856?ls=1 (in English) (accessed on 10 April 2021). Available online: https://books.apple.com/us/book/enseñanza-de-las-simetrías-en-educación-primaria/id1553394353?ls=1 (in Spanish) (accessed on 10 April 2021).
- Diezmann, C.M.; Watters, J.J. Summing up the Education of Mathematically Gifted Students. In Proceedings of the 25th Annual Conference of the MERGA, Sidney, Australia, 7–10 July 2002; pp. 219–226. [Google Scholar]
- Karatas, F.I.; Bostan, M.I. Mathematically Gifted Students’ Reflections on using History of Mathematics in Mathematics Classrooms. In Proceedings of the 11th International Conference on Mathematical Creativity and Giftedness (MCG 11), Hamburg, Germany, 22–24 August 2019; pp. 191–196. [Google Scholar]
- Sriraman, B.; Haavold, P. Creativity and Giftedness in Mathematics Education: A Pragmatic View. In Compendium for Research in Mathematics Education; Cai, J., Ed.; NCTM: Reston, VA, USA, 2017; pp. 908–916. [Google Scholar]
- Cyr, S.S. Can Distance Learning Meet the Needs of Gifted Gifted Elementary Math Students? Gift. Child Today 2004, 27, 42–51. [Google Scholar] [CrossRef]
- Bikner-Ahsbahs, A.; Prediger, S. Networking of Theories as a Research Practice in Mathematics Education; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Greenes, C. Identifying the Gifted Student in Mathematics. Arith. Teach. 1981, 28, 14–17. [Google Scholar] [CrossRef]
- Jaime, A.; Gutiérrez, A. La Resolución de Problemas Para la Enseñanza a Alumnos de Educación Primaria Con Altas Capacidades Matemáticas. In Resolver Problemas. Estudios en Memoria de Fernando Cerdán; Gómez, B., Puig, L., Eds.; PUV: Valencia, Spain, 2014; pp. 147–190. [Google Scholar]
- Moya, J.A.; Gutiérrez, A.; Jaime, A. Discriminating Proof Abilities of Secondary School Students with Different Mathematical Talent. In Proceedings of the 9th Conference of the European Society for Research in Mathematics Education (CERME9), Prague, Czech Republic, 4–8 February 2015; pp. 171–177. [Google Scholar]
- Benedicto, C.; Jaime, A.; Gutiérrez, A. Análisis de la Demanda Cognitiva de Problemas de Patrones Geométricos. In Investigación en Educación Matemática XIX; Fernández, C., Molina, M., Planas, N., Eds.; SEIEM: Alicante, Spain, 2015; pp. 153–162. [Google Scholar]
- Benedicto, C.; Gutiérrez, A.; Jaime, A. When the Theoretical Model Does not fit our Data: A Process of Adaptation of the Cognitive Demand Model. In Proceedings of the 10th Congress of the European Society for Research in Mathematics Education (CERME10), Dublin, Ireland, 2 January–2 May 2017; pp. 2791–2798. [Google Scholar]
- Smith, M.S.; Stein, M.K. Reflections on Practice: Selecting and Creating Mathematical Tasks: From Research to Practice. Math. Teach. Middle Sch. 1998, 3, 344–350. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Gutiérrez, Á.; Boero, P. Handbook of Research on the Psychology of Mathematics Education; Sense Publishers: Rotterdam, The Netherlands, 2006. [Google Scholar]
- Clements, M.A.; Bishop, A.J.; Keitel, C.; Kilpatrick, J.; Leung, F.K.S. Third International Handbook of Mathematics Education; Springer: New York, NY, USA, 2013. [Google Scholar]
- Gutiérrez, A.; Leder, G.C.; Boero, P. The Second Handbook of Research on the Psychology of Mathematics Education; Sense Publishers: Rotterdam, The Netherlands, 2016. [Google Scholar]
- Cai, J. Compendium for Research in Mathematics Education; NCTM: Reston, VA, USA, 2017. [Google Scholar]
- Baya’a, N.; Daher, W.; Mahagna, S. The Effect of Collaborative Computarized Learning using GeoGebra on the Development of Concept Images of the Angle among Seventh Graders. In Proceedings of the 13th International Conference on Technology in Mathematics Teaching, Lyon, France, 3–6 July 2017; pp. 208–215. [Google Scholar]
- Ferrarello, D.; Mammana, M.F.; Pennisi, M.; Taranto, E. Teaching Intriguing Geometric Loci with DGS. In Mathematics and Technology. Advances in Mathematics Education; Aldon, G., Hitt, F., Bazzini, L., Gellert, U., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Liljedahl, P.; Santos-Trigo, M.; Malaspina, U.; Bruder, R. Problem Solving in Mathematics Education; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Battista, M.T. The Development of Geometrical and Spatial Thinking. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Ed.; NCTM: Reston, VA, USA, 2007; pp. 843–908. [Google Scholar]
- Schultz, K.A.; Austin, J.D. Directional Effects in Transformation Tasks. J. Res. Math. Educ. 1983, 14, 95. [Google Scholar] [CrossRef]
- Grenier, D. Quelques Aspects de la Symétrie Orthogonale Pour des Élèves de Classes de 4ème et 3ème. Petit x 1985, 7, 57–69. [Google Scholar]
- Jaime, A. Aportaciones a la Interpretación y Aplicación del Modelo de Van Hiele: La Enseñanza de las Isometrías del Plano. Ph.D. Thesis, Universidad de Valencia, Valencia, Spain, 1993. Available online: https://www.uv.es/angel.gutierrez/archivos1/textospdf/Jai93.pdf (accessed on 16 December 2020).
- Jaime, A.; Gutiérrez, A. Connecting Research to Teaching: Guidelines for Teaching Plane Isometries in Secondary School. Math. Teach. 1995, 88, 591–597. [Google Scholar] [CrossRef]
- Pepin, B.; Gueudet, G.; Trouche, L. Investigating Textbooks as Crucial Interfaces between Culture, Policy and Teacher Curricular Practice: Two Contrasted Case Studies in France and Norway. ZDM 2013, 45, 685–698. [Google Scholar] [CrossRef]
- Son, J.-W. Investigating Preservice Teachers Understanding and Strategies on a Student’s Errors of Reflective Symmetry. In Proceedings of the 30th Conference of the International Group for the Psychology of Mathematics Education; Novotná, J., Moraová, H., Krátká, M., Stehlíková, N., Eds.; PME: Prague, Czech Republic, 2006; Volume 5, pp. 145–152. [Google Scholar]
- Thangamani, U.; Eu, L.K. Students’ Achievement in Symmetry of Two Dimensional Shapes using Geometer’s Sketchpad. Malays. Online J. Educ. Sci. 2019, 7, 14–22. [Google Scholar]
- Healy, L. Using the Transformation Tools of Cabri-Géomètre as a Resource in the Proving Process. In Actes du Colloque Européen: Intégration des Technologies dans l’Enseignement des Mathématiques; Lagrange, J.-B., Artigue, M., Guin, D., Laborde, C., Lenne, D., Trouche, L., Eds.; IUFM Champagne-Ardenne: Reims, France, 2003; pp. 1–10. Available online: https://edutice.archives-ouvertes.fr/edutice-00001334 (accessed on 14 December 2020).
- Dello Iacono, U.; Dentice, E.F. Mathematical Walks in Search of Symmetries: From Visualization to Conceptualization. Int. J. Math. Educ. Sci. Technol. 2020, 10, 1–19. [Google Scholar] [CrossRef]
- Ng, O.-L.; Sinclair, N. Young Children Reasoning About Symmetry in a Dynamic Geometry Environment. ZDM 2015, 47, 421–434. [Google Scholar] [CrossRef]
- Pepin, B.; Gueudet, G.; Trouche, L. Refining Teacher Design Capacity: Mathematics Teachers’ Interactions with Digital Curriculum Resources. ZDM 2017, 49, 799–812. [Google Scholar] [CrossRef]
- Pepin, B.; Gueudet, G.; Yerushalmy, M.; Trouche, L.; Chazan, D. E-Textbooks in/for Teaching and Learning Mathematics: A Disruptive and Potentially Transformative Educational Technology. In Handbook of International Research in Mathematics Education; English, L., Kirshner, D., Eds.; Taylor & Francis: New York, NY, USA, 2016; pp. 636–661. [Google Scholar]
- Fahlgren, M.; Brunström, M. A Model for Task Design with Focus on Exploration, Explanation, and Generalization in a Dynamic Geometry Environment. Technol. Knowl. Learn. 2014, 19, 287–315. [Google Scholar] [CrossRef]
- Pehkonen, E. An Alternative Method to Promote Pupils’ Mathematical Understanding via Problem Solving. In Problem Solving in Mathematics Instruction and Teacher Professional Development; Felmer, P., Liljedahl, P., Koichu, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 111–122. [Google Scholar]
- Santos-Trigo, M.; Camacho Machín, M. La Resolución de Problemas Matemáticos y el Uso de Tecnología Digital en el Diseño de Libros Interactivos. Educ. Siglo XXI 2018, 36, 21–40. [Google Scholar] [CrossRef]
- Piggott, J. The Nature of Mathematical Enrichment: A Case Study of Implementation. Educate 2007, 7, 30–45. [Google Scholar]
- Piggott, J. Rich Tasks and Contexts; NRICH, University of Cambridge: Cambridge, UK, 2011; Available online: https://nrich.maths.org/5662 (accessed on 7 May 2018).
- Jaime, A.; Gutiérrez, A.; Benedicto, C. Problemas Con Extensiones: Propuesta Para Estudiantes Con Alta Capacidad Matemática. UNO 2018, 79, 7–14. [Google Scholar]
- Benedicto, C.; Gutiérrez, A.; Jaime, A. Analysis of Mathematically Gifted Students’ Answers to Cognitively Demanding School Tasks. In Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education, Umeå, Sweden, 3–8 July 2018; Volume 5, p. 18. [Google Scholar]
- Leikin, R. Stepped tasks: Top-down structure of varying mathematical challenge. In Problem Solving in Mathematics Instruction and Teacher Professional Development; Felmer, P., Liljedahl, P., Koichu, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 167–184. [Google Scholar]
- Jones, K.; Tzekaki, M. Research on the Teaching and Learning of Geometry. In The Second Handbook of Research on the Psychology of Mathematics Education, the Journey Continues; Gutiérrez, A., Leder, G.C., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2016; pp. 109–149. [Google Scholar]
- Otten, S.; Webel, C.; De Araujo, Z. Inspecting the Foundations of Claims about Cognitive Demand and Student Learning: A Citation Analysis of Stein and Lane (1996). J. Math. Behav. 2017, 45, 111–120. [Google Scholar] [CrossRef]
- Gutierrez, A.; Benedicto, C.; Jaime, A.; Arbona, E. The Cognitive Demand of a Gifted Student’s Answers to Geometric Pattern Problems. In Challenges and Strategies in Teaching Linear Algebra; J.B. Metzler: Stuttgart, Germany, 2018; pp. 169–198. [Google Scholar]
- Gutiérrez, A.; Ramírez, R.; Benedicto, C.; Beltrán-Meneu, M.J.; Jaime, A. Visualization Abilities and Complexity of Reasoning in Mathematically Gifted Students’ Collaborative Solutions to a Visualization Task: A Networked Analysis. In Broadening the Scope of Research on Mathematical Problem Solving; J.B. Metzler: Stuttgart, Germany, 2018; pp. 309–337. [Google Scholar]
- Gutiérrez, A.; Jaime, A.; Fortuny, J.M. An Alternative Paradigm to Evaluate the Acquisition of the Van Hiele Levels. J. Res. Math. Educ. 1991, 22, 237–251. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. The Teaching for Robust Understanding (TRU) Observation Guide for Mathematics: A Tool for Teachers, Coaches, Administrators, and Professional Learning Communities; TRU Project: Berkeley, CA, USA, 2016; Available online: http://map.mathshell.org/trumath/tru_observation_guide_math_v5_20161125.pdf (accessed on 7 October 2020).
- Lloyd, G.M.; Cai, J.; Tarr, J.E. Issues in Curriculum Studies: Evidence-Based Insights and Future Directions. In Compendium for Research in Mathematics Education; Cai, J., Ed.; NCTM: Reston, VA, USA, 2017; pp. 824–852. [Google Scholar]
- Chamberlin, M.T.; Chamberlin, S.A. Enhancing Preservice Teacher Development: Field Experiences with Gifted Students. J. Educ. Gift. 2010, 33, 381–416. [Google Scholar] [CrossRef]
- Resnick, L.B.; Zurawsky, C. Do the Math: Cognitive Demand Makes a Difference. Res. Points 2006, 4, 1–4. [Google Scholar]
- Malaspina, U.; Torres, C. Teaching of Discontinuous Functions of One or Two Variables: A Didactic Experience Using Problem Posing and Levels of Cognitive Demand. In Proceedings of the 11th Congress of the European Society for Research in Mathematics Education (CERME11); Jankvist, U.T., Van den Heuvel-Panhuizen, M., Veldhuis, M., Eds.; ERME: Utrecht, The Netherlands, 2019; pp. 2578–2585. [Google Scholar]
- Stein, M.K.; Smith, M.S.; Henningsen, M.A.; Silver, E.A. Implementing Standards-Based Mathematics Instruction: A Casebook for Professional Development; Teachers College Press: New York, NY, USA, 2009. [Google Scholar]
- Benedicto, C. Diseño y Aplicación de un Instrumento Para Valorar la Demanda Cognitiva de Problemas de Matemáticas Resueltos Por Estudiantes de Enseñanza Obligatoria. El Caso de Las Altas Capacidades Matemáticas; Universidad de Valencia: Valencia, Spain, 2018; Available online: http://roderic.uv.es/handle/10550/66468 (accessed on 5 November 2020).
- Bikner-Ahsbahs, A.; Prediger, S. Networking of Theories-An Approach for Exploiting the Diversity of Theoretical Approaches. In Theories of Mathematics Education; Sriraman, B., English, L., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 483–506. [Google Scholar]
- Ministerio de Educación, C.y.D. Real Decreto 126/2014, de 28 de Febrero, Por el Que se Establece el Currículo Básico de la Educación Primaria. Bol. Of. Del Estado 2014, 52, 19349–19420. [Google Scholar]
- Fujita, T. Learners’ Level of Understanding of the Inclusion Relations of Quadrilaterals and Prototype Phenomenon. J. Math. Behav. 2012, 31, 60–72. [Google Scholar] [CrossRef]
- Gutiérrez, Á.; Jaime, A. Preservice Primary Teachers’ Understanding of the Concept of Altitude of a Triangle. J. Math. Teach. Educ. 1999, 2, 253–275. [Google Scholar] [CrossRef]
- Krajcevski, M.; Sears, R. Common Visual Representations as a Source for Misconceptions of Preservice Teachers in a Geometry Connection Course. Inter. J. Math. Teach. Learn. 2019, 20, 85–105. [Google Scholar]
- Vinner, S. The Role of Definitions in the Teaching and Learning of Mathematics. In Advanced Mathematical Thinking; Tall, D., Ed.; Kluwer: Dordrecht, The Netherlands, 1991; pp. 65–81. [Google Scholar]
- Laborde, C.; Capponi, B. Cabri-Géomètre Constituant d’un Milieu Pour L’apprentissage de la Notion de Figure Géométrique. Rech. En Didact. Des Math. 1994, 14, 165–209. [Google Scholar]
- Forsythe, S.K. Dragging Maintaining Symmetry: Can it generate the Concept of Inclusivity as Well as a Family of Shapes? Res. Math. Educ. 2015, 17, 1–22. [Google Scholar] [CrossRef][Green Version]
- Battista, M.T. Development of the Shape Makers Geometry Microworld: Design Principles and Research. In Research on Technology and the Teaching and Learning of Mathematics: Cases and Perspectives; Blume, G.W., Heid, M.K., Eds.; NCTM & Information Age Publishing: Charlotte, NC, USA, 2008; Volume 2, pp. 131–156. [Google Scholar]
- Lord, E. Going Deeper: Exploring Ways to Achieve ‘Mastery at Greater Depth’ in the Primary Mathematics Classroom. BSRLM Proc. 2020, 40, 1–6. [Google Scholar]
- Fritzlar, T.; Nolte, M. Research on Mathematical Giftedness in Germany-Looking Back and Ahead. In Proceedings of the 11th International Conference on Mathematical Creativity and Giftedness, Hamburg, Germany, 22–24 August 2019; pp. 8–20. [Google Scholar]
- Gerver, R.K.; Sgroi, R.J. Creating and Using Guided-Discovery Lessons. Math. Teach. 2003, 96, 6–13. [Google Scholar]
- Teppo, A. Van Hiele Levels of Geometric Thought Revisited. Math. Teach. 1991, 84, 210–221. [Google Scholar] [CrossRef]


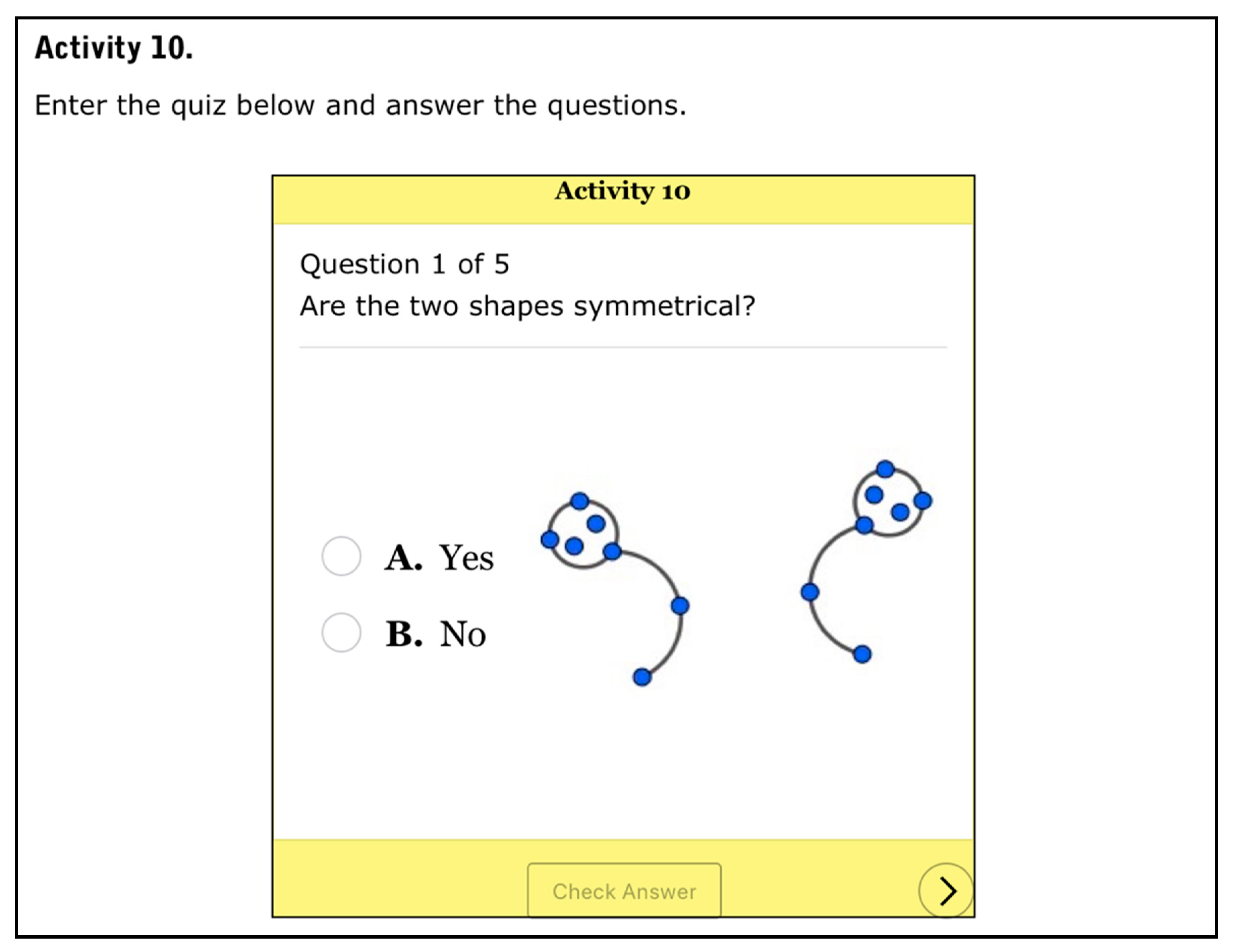


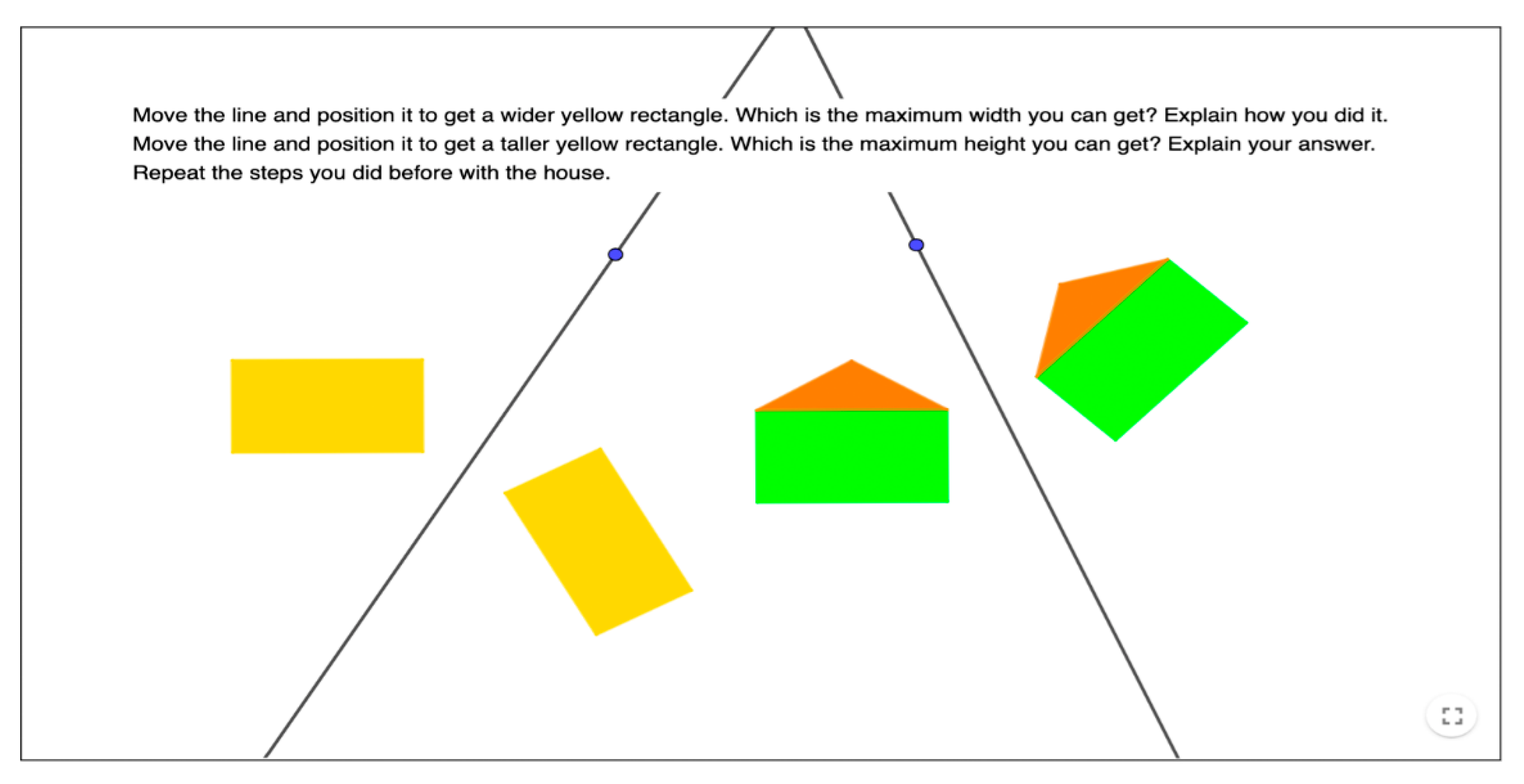

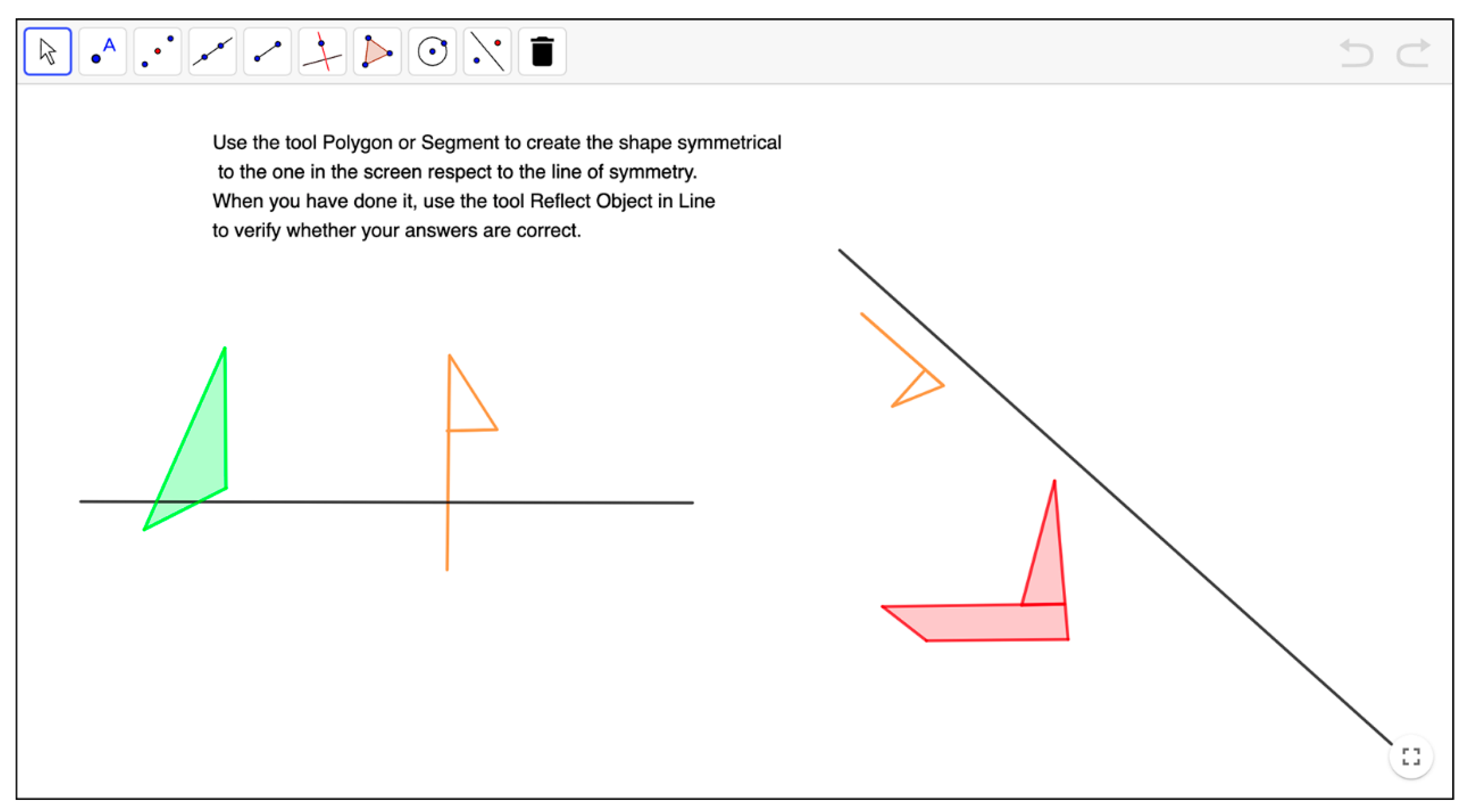
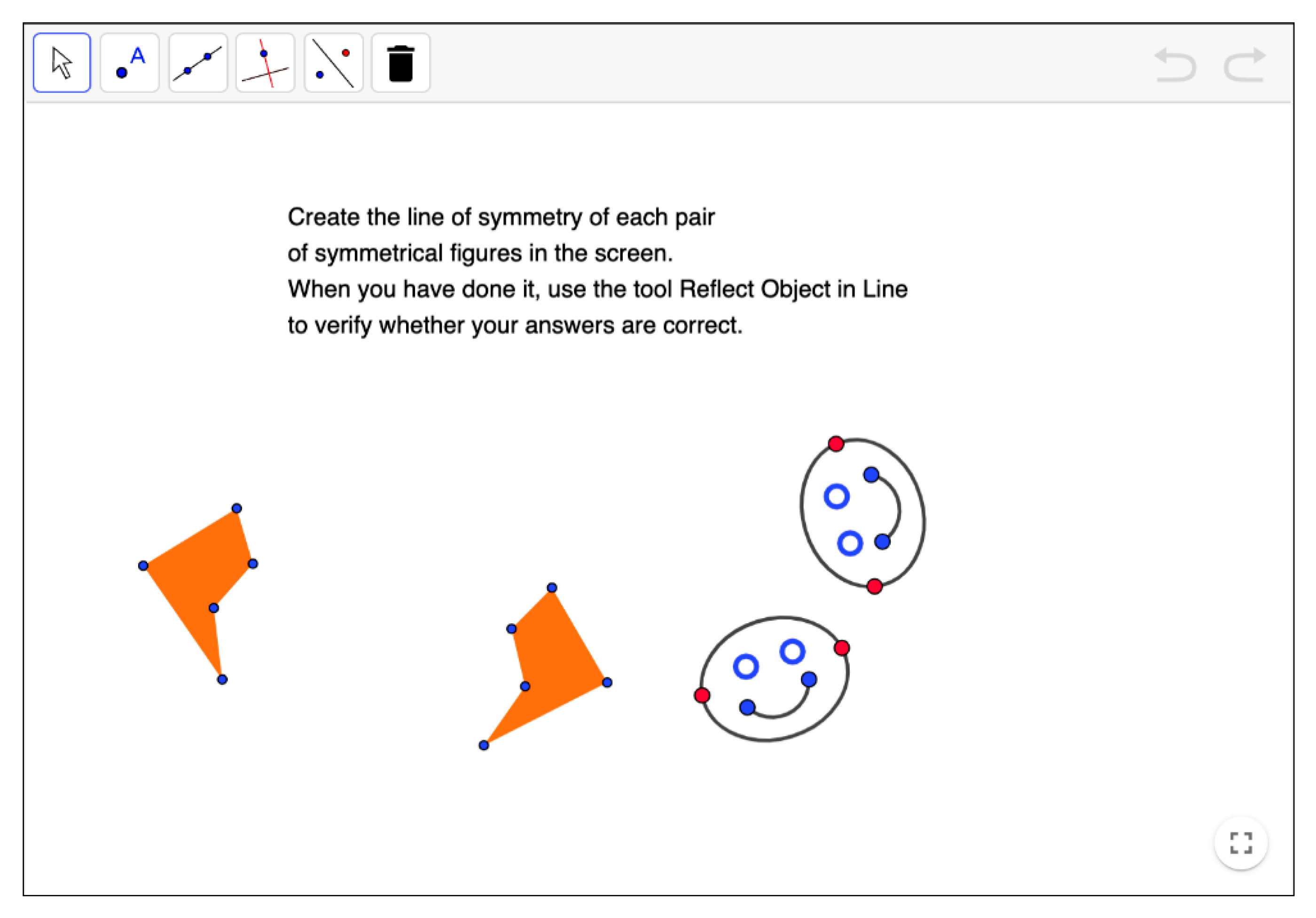

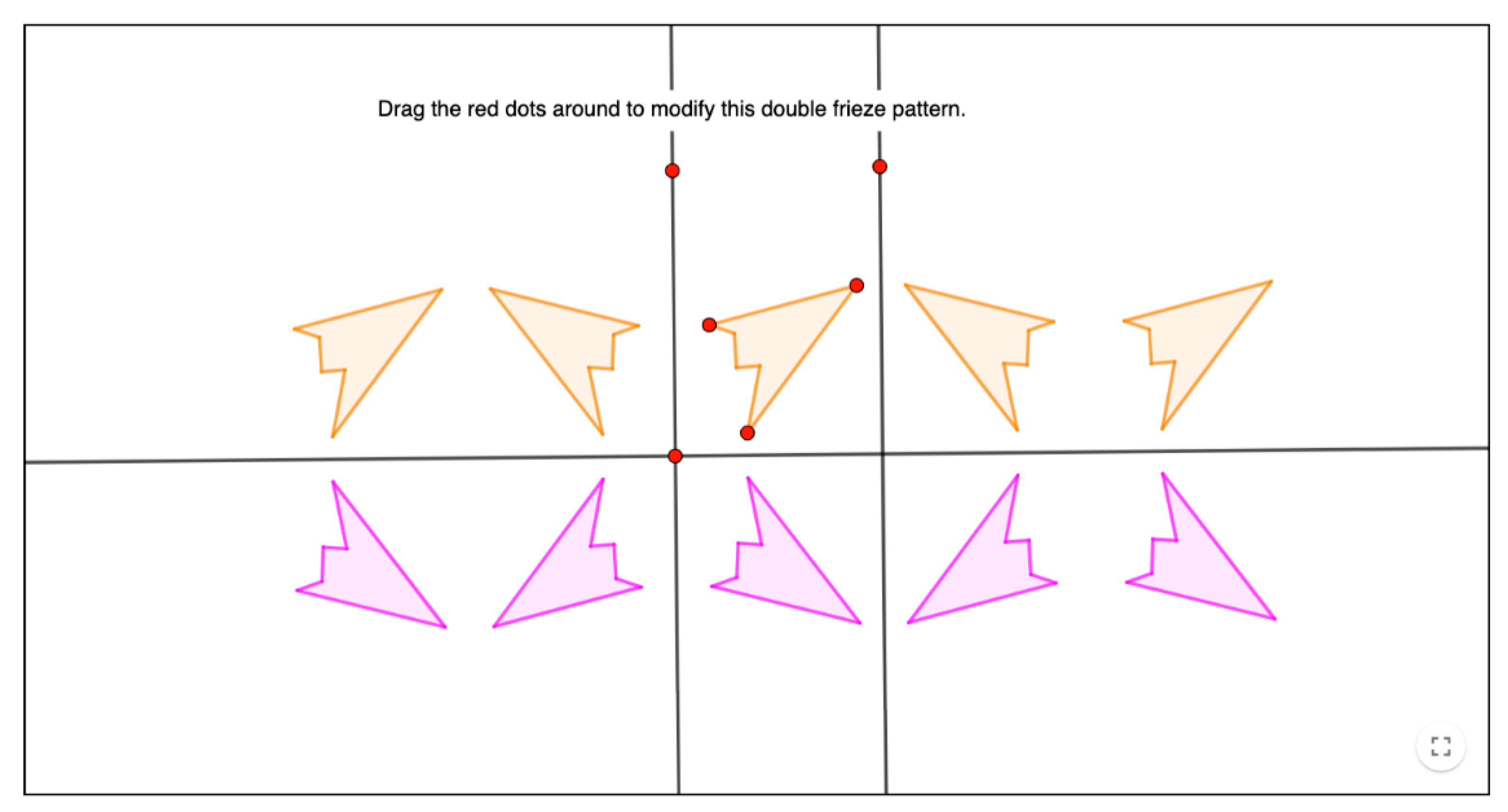
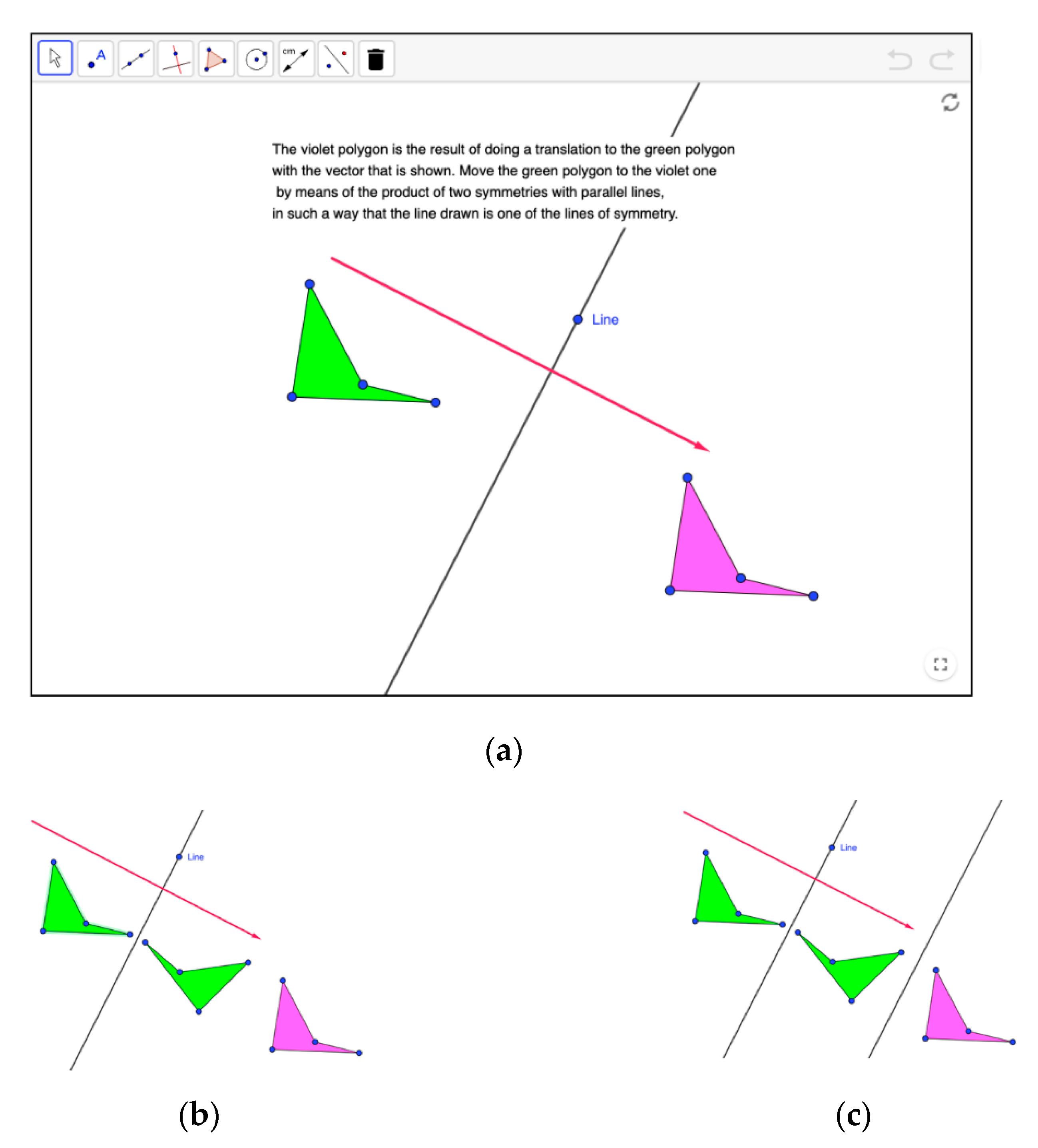
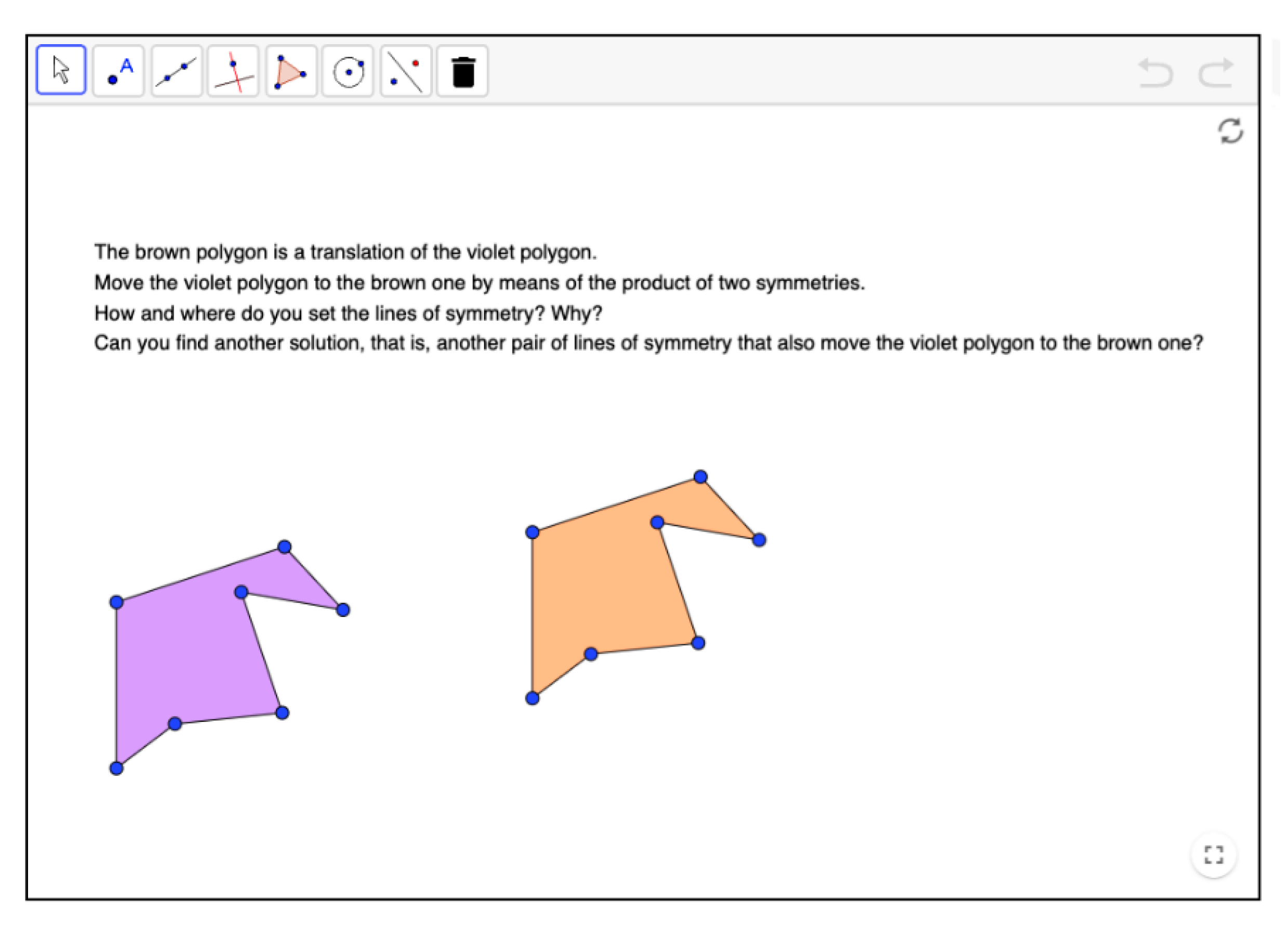
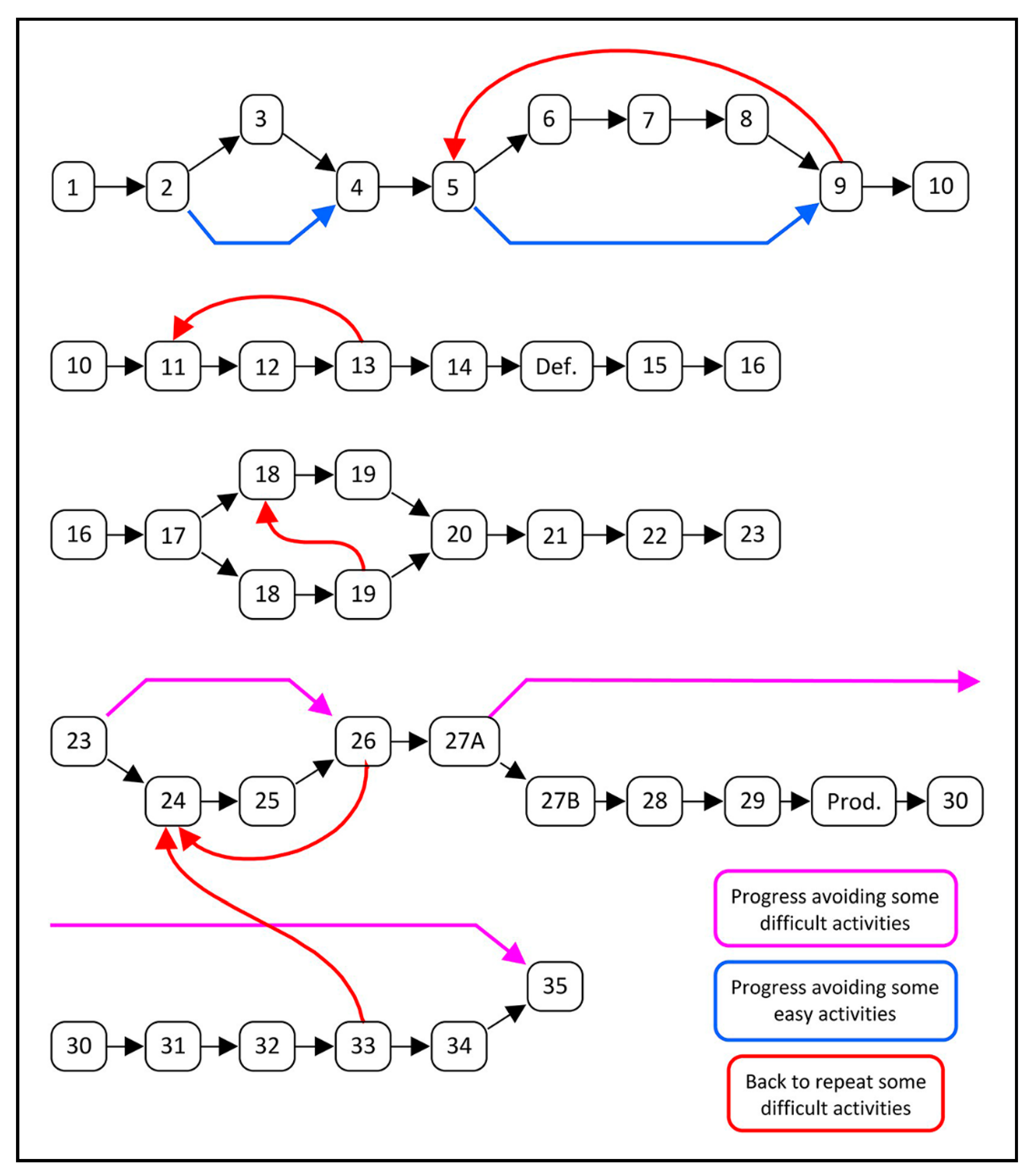
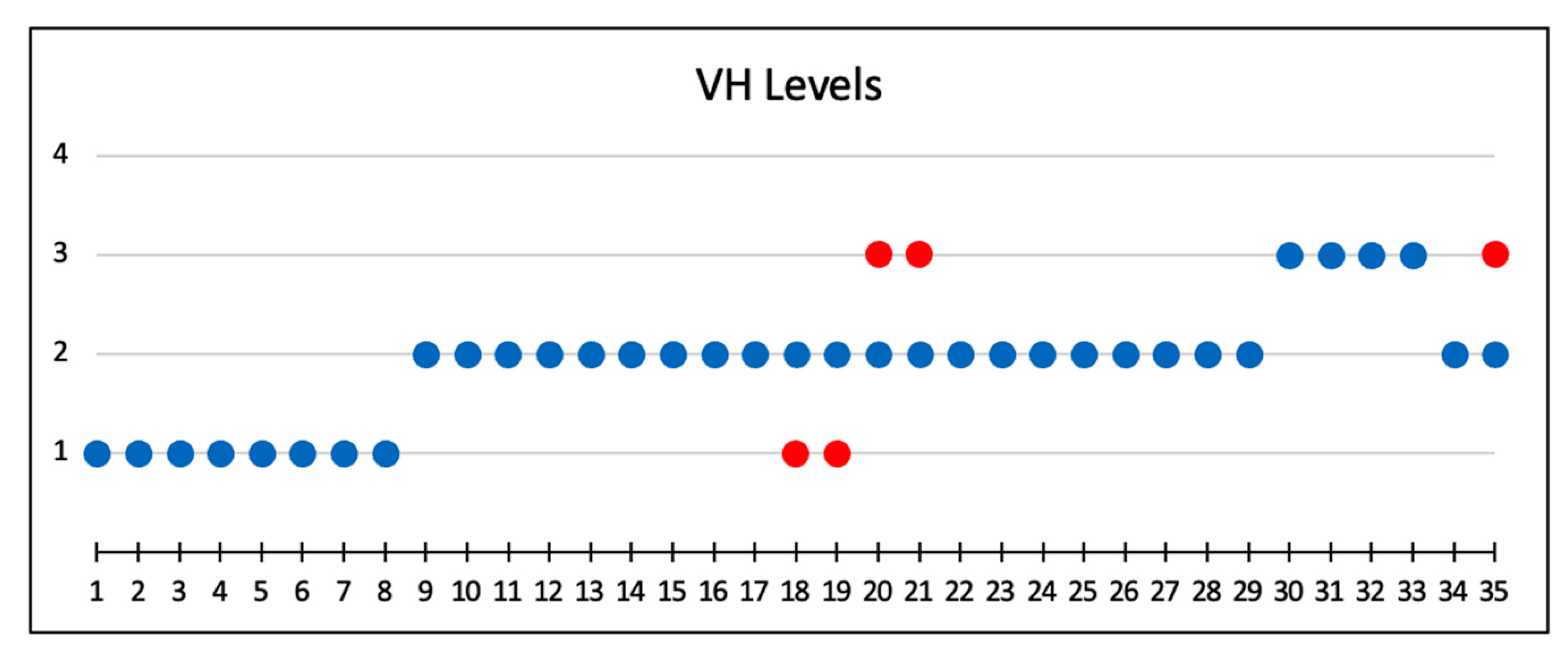

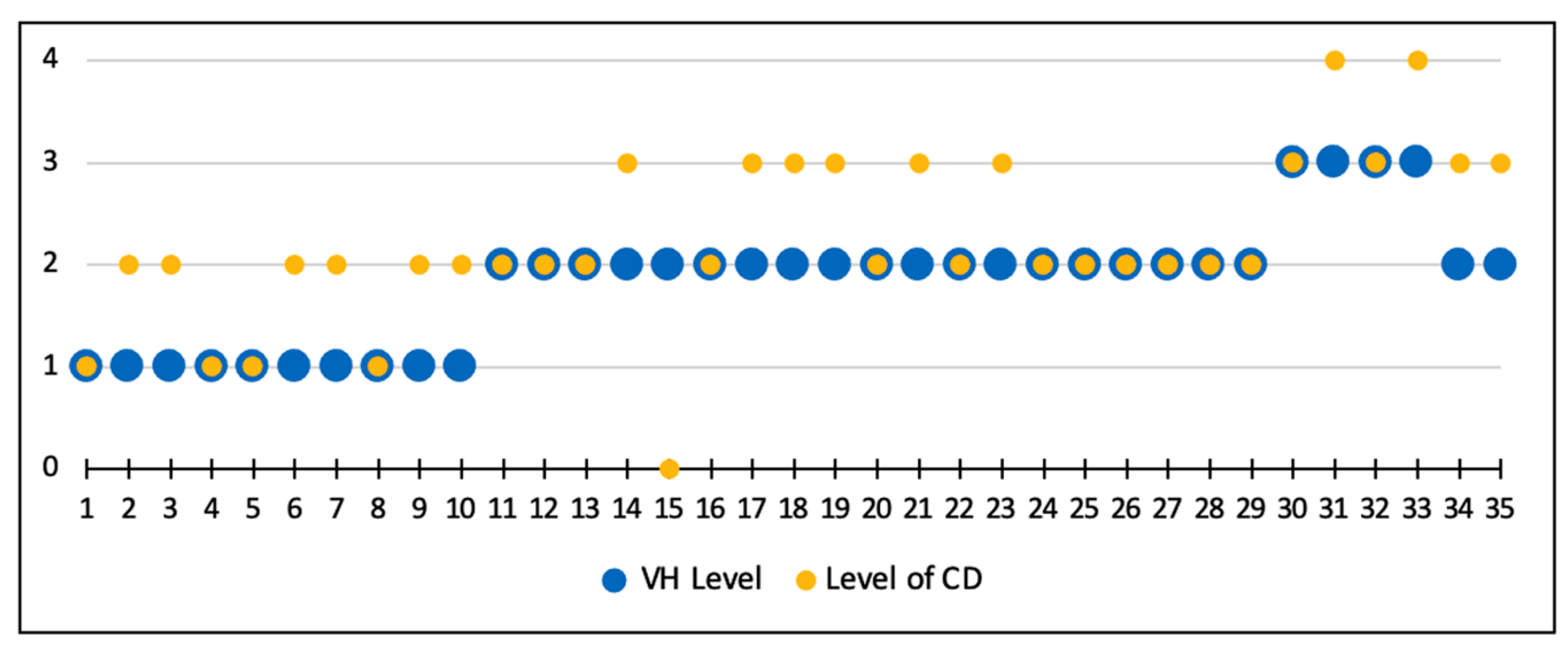
| Levels of Cognitive Demand | Categories | Characteristics of the Activity |
|---|---|---|
| Memorization | Process of solution | It is solved by observing shapes presented in the activity, making actions that automatically produce the answer or resorting to mental images or data recalled. |
| Objective | Identify visually regularities of symmetrical (pairs of) shapes or reproduce elements (visual properties, etc.) previously learned or recalled. | |
| Cognitive effort | A successful solution requires a minimum cognitive effort. The statement is not ambiguous and it only requires observing the shapes to perceive their visual characteristics of symmetry or following the given directions about what to do. | |
| Implicit content | It has no connection to the mathematical definition, properties, etc. of symmetries to be learned. Students do not need to use such knowledge to get correct answers. | |
| Explanations | It does not require explanations. | |
| Representation of the solution | The representation used may be graphical or visual, but the virtual environment may also induce verbal representations. | |
| Procedures without connections | Process of solution | Depending on the activity, the procedure may consist of observing the shapes showed in the activity to visually identify (pairs of) symmetrical shapes, axes or properties, or dragging or using DGS tools to obtain images or axes. |
| Objective | Produce a correct answer (visually complete symmetrical shapes, or identify the axes of symmetry of the given shapes, or construct images or axes with the DGS). Students do not need to apply the underlying mathematical properties of symmetry to be learned. | |
| Cognitive effort | Solving it correctly requires a limited cognitive effort. Little ambiguity exists about what to do and how to do it, because the statement clearly states it and the environment offers the adequate resources (DGS files, Internet links, etc.). | |
| Implicit content | There are implicit connections between the underlying properties of symmetries and the expected solution procedures, but students do not need to be aware of such connections since they may find the answer by using their visual conception of symmetry or the data presented by the activities. | |
| Explanations | It requires explanations that focus only on describing the procedure used. It is not necessary to explicitly connect the answer to mathematical definition or properties. | |
| Representation of the solution | Students use visual or geometrical representations, depending on whether the activities ask to observe or draw symmetry images or axes. Sometimes, they may prefer transmitting the information verbally. | |
| Procedures with connections | Process of solution | The procedure consists of, depending on the activity, considering the relative positions of the axis of symmetry and the vertices and sides of the shapes showed in the activity, to determine the position of the symmetric vertices or the axis, or decomposing a translation or rotation into a product of two symmetries. |
| Objective | Depending on the activity, guide students to note that the metric properties of symmetries (equidistance of symmetrical points from the axis and perpendicularity of the segment joining the symmetrical points respect to the axis) are characteristic of symmetry and it is necessary to use them as tools to solve graphical activities, or note that the relationship between translation/rotation and product of symmetries can be reversed. | |
| Cognitive effort | Solving it correctly requires a moderately high cognitive effort. Students may use general procedures to draw images or axes of symmetry, but they need to have some understanding of the geometric characteristics of, depending on the activities, symmetry or products of symmetries, and use them. | |
| Implicit content | To solve the activity, students need to explicitly use the properties of symmetries underlying the correct procedures of solution. | |
| Explanations | It requires explanations to justify the procedures applied in the solutions. Such explanations may be abstract or based on the specific shapes of the activity, depending on the activity. | |
| Representation of the solution | Students may use visual representations to create an approach to polygon images or axes asked and graphical representations to improve the positions of image points or axes. | |
| Doing mathematics | Process of solution | It requires complex and non-algorithmic thinking. The statement does not suggest any way to get the solution. Students have to understand, analyze, and put to work the properties of symmetry and products of symmetries they have learned to produce a correct solution. |
| Objective | Analyze the solutions to previous tasks and possible limitations to get conclusions and establish new links that allow them to find multiple decompositions of a translation or rotation into products of symmetries. | |
| Cognitive effort | Requires a high cognitive effort, since students need to use abstract reasoning to establish explicit links between adequate parts of the underlying properties of symmetries to determine an innovative way to proceed to solve correctly the activity. | |
| Implicit content | Students have to access relevant knowledge and previous experiences to make appropriate use of the underlying properties of symmetries in working through the task to get a correct solution. | |
| Explanations | Explanations consist of proving the correctness of the steps done in the DGS to get the construction asked by the activity. | |
| Representation of the solution | The solution is based on geometrical representations of figures, axis, etc. necessary to solve the activity. |
| Learning Objectives | Activities |
|---|---|
| Visual approach to symmetries | 1–10 |
| Manipulative approach to symmetries | 4 |
| Discovery of the property of equidistance | 6–15 |
| Discovery of the property of perpendicularity | 11–15 |
| Mathematical definition of axial symmetry | 14–19 |
| Accurate constructions with the DGS | 17–21 |
| Relationship between axis of symmetry and perpendicular bisector | 20–23 |
| Symmetries of polygons | 22–23 |
| Products of two symmetries with parallel axes | 24–27 |
| Products of two symmetries with secant axes | 28–29 |
| Creation of frieze and rosette patterns | 26, 27, 29 |
| Decomposition of translations into products of symmetries | 30, 31, 34 |
| Decomposition of rotations into products of symmetries | 32, 33, 34 |
| Final synthesis of the contents learned | 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez, A.; Jaime, A.; Gutiérrez, P. Networked Analysis of a Teaching Unit for Primary School Symmetries in the Form of an E-Book. Mathematics 2021, 9, 832. https://doi.org/10.3390/math9080832
Gutiérrez A, Jaime A, Gutiérrez P. Networked Analysis of a Teaching Unit for Primary School Symmetries in the Form of an E-Book. Mathematics. 2021; 9(8):832. https://doi.org/10.3390/math9080832
Chicago/Turabian StyleGutiérrez, Angel, Adela Jaime, and Pablo Gutiérrez. 2021. "Networked Analysis of a Teaching Unit for Primary School Symmetries in the Form of an E-Book" Mathematics 9, no. 8: 832. https://doi.org/10.3390/math9080832
APA StyleGutiérrez, A., Jaime, A., & Gutiérrez, P. (2021). Networked Analysis of a Teaching Unit for Primary School Symmetries in the Form of an E-Book. Mathematics, 9(8), 832. https://doi.org/10.3390/math9080832






