Networked Analysis of a Teaching Unit for Primary School Symmetries in the Form of an E-Book

Abstract

In mathematics education, technology offers many opportunities to enrich curricular contents. Plane symmetries is a topic often skipped by primary teachers. However, it is important and may be worked in attractive ways in dynamic geometry software environments. In any regular classroom there are students with different levels of mathematical attainment, some needing easy tasks while others, particularly mathematically-gifted students, need challenging problems. We present a teaching unit for plane symmetries, adequate for upper primary school grades, implemented in a fully interactive electronic book, with most activities solved in GeoGebra apps. The book allows student to choose which itinerary to follow and attention is paid to different levels of students’ mathematical attainment. The research objective of the paper is to make a networked analysis of the structure and contents of the teaching unit based on the Van Hiele levels of mathematical reasoning and the levels of cognitive demand in mathematical problem solving. The analysis shows the interest of networking both theories, the suitability of the teaching unit, as the Van Hiele levels and the cognitive demand of the activities increases, and its usefulness to fit the needs of each student, from low attainers to mathematically-gifted students.

1. Introduction

Along the last three decades, there is being a slow but constant change in the methods of teaching mathematics at primary and secondary school levels, partly induced by the appearance of new affordable technological tools that can be used in schools, like computers, tablets, electronic boards, augmented reality, smartphones, etc. There are also new kinds of software that take advantage of the possibilities of interaction offered by the modern hardware to present mathematical contents in new ways, like dynamic geometry software (DGS), computer algebra systems (CAS), podcasts, electronic books (e-books), web pages, and so on. The fusion of hardware and software allows teachers and researchers create new technological learning environments aimed to help students understand mathematics more easily and intended to be more interesting and attractive than the traditional textbooks.

Although research published in the 1990s showed benefits of students programming Logo in their learning of transformations, in particular symmetries [1] and, more recently, it has been showed that students learning in dynamic manipulative environments (either real or electronic) are more successful than those learning in static environments [2], there is a lack of research on the application of the newly available technologies in the teaching and learning of geometry [3], either as purely technological classes or blended learning [4]. Furthermore, the educational constraints to in person classes imposed by the pandemic of covid-19 give an added value to technological teaching and learning environments that can be used in virtual classrooms, so research on new electronic learning environments and blended environments is still necessary. In this paper, we present a learning environment based on the abilities of an interactive Apple iBook to present Internet links, GeoGebra files, and videos and self-evaluation questionnaires embedded in it.

Primary and secondary school mathematics curricula have a common core of content around the world, mainly arithmetic with whole numbers, decimal numbers, and fractions, polygons and circle geometry, measurement, equations, some types of functions, basic trigonometry, and others [5]. However, in some countries, other mathematics topics are only sometimes included in the curricula or are considered as “dispensable” by many teachers, who feel free to skip over those topics when, allegedly, they are short of time, one such topic being plane isometries [6,7]. Nevertheless, isometries are a very useful tool for ordinary life and many areas of elementary, middle, and higher mathematics [8], with symmetries being the most relevant one [9], since they have to do with regularities, which are easily perceived by students. Thus, it is worth to start studying symmetries in primary and secondary school [10,11,12].

The learning of symmetries has some obstacles and difficulties that should be taken into consideration by teachers when preparing the classes, to try help students bypass or overcome them. After the seminal research by Küchemann [13,14] on students’ difficulties with plane symmetries, there is a knowledge of some typical errors that should be prevented by designing specific activities, like the cognitive obstacle [15] induced by the prototypical image of the axis of symmetry drawn vertically. Technological environments, like those based on DGS, have proved to be helpful to prevent or remove this kind of students’ prototypical images when they are allowed to manipulate the axes of symmetry and get used to see them with any slope [16]. Then, although teaching and learning of isometries have not been frequently explored by mathematics education research [7], an interesting research direction is the design of technological environments where students can manipulate geometrical objects (in our case those related to symmetries) to gain experience and build on it a deep understanding of the related concepts and properties [2]. In this paper we present a teaching unit for symmetries implemented as an interactive e-book [17] that takes advantage of the possibilities of DGS played in computers and tablets.

Mathematically gifted students (m-gifted students hereafter) too often suffer a lack of adequate attention by their teachers when these devote their efforts to prepare the classes with only the slow learners and average students in mind. M-gifted students should be provided by their mathematics teachers with special curriculum adaptations to let them learn mathematics at their own pace, i.e., faster and deeper than their classmates [18]. Technological environments that can be designed to allow a diversity of learning objectives and learning speeds are adequate for primary and secondary school mathematics teachers to attend the diversity of pupils they usually have in their regular class groups [10,19]. Mathematical giftedness has not been a main focus of attention for researchers in mathematics education [20], although there is an increasing number of publications reporting research experiments with secondary school m-gifted students based on technological environments, but there is a need of such kind of research with primary school m-gifted students [21], since these students are ready to move from empirical tasks to abstract problems, and such transition poses troubles to them to gain deeper levels of understanding [2]. Most activities in the teaching unit we present are adequate for average students, but it also includes activities that are aimed to provide a deeper knowledge of symmetries to m-gifted students.

Mathematics education researchers have at their reach different theories that can be used as theoretical ground for their research. When several theories can be selected, usually none of them is “the best choice”, since each one has some strengths and weaknesses. Then, a procedure that has proved to produce good results is the networking of different theories to analyze a set of research results [22]. There is a broad consensus that the Van Hiele levels of mathematical thinking are an excellent theoretical framework to organize the teaching of geometry and scrutinize students’ ways of reasoning when performing geometric activities [1]. Therefore, we have used the Van Hiele levels to ground the design of the teaching unit on symmetries. On the other hand, when teaching m-gifted students, it is important to analyze their ways of solving problems and their learning trajectories, which tend to be different from those of average students of their age or grade. Differential characteristics of m-gifted students are that they tend to engage more, use higher-order thinking more frequently, and be more successful than average students when solving problems, which results in a faster attainment of the learning objectives [23,24,25]. It is quite frequent that, as a consequence of their harder cognitive activity, m-gifted students discover and learn concepts, properties, etc., before the moment planned by their teachers for the average students [26]. We have used the levels of cognitive demand [27,28] as the framework to analyze the potential of the activities in our teaching unit to induce higher cognitive activity in m-gifted students. Consequently, we have networked in an original way both theories to analyze the activities and the expected students’ behavior when solving them.

We denote as tasks the diversity of assignments to students like exercises, problems, evaluation questions, investigations, etc. Activities are tasks focused on a direct use, explicitly or implicitly, of a mathematical content or procedure, and problems are activities where students, after reading the statement, have difficulties to solve them, because either they do not have the necessary previous knowledge or they do not know a way to link the knowledge with the statement to find a solution, the difficulties being intellectual rather than computational or procedural [29]. A teaching unit is an organized set of activities, not necessarily sequentially ordered, having a global learning objective and several local learning objectives.

In this paper we present the results of a mathematics education research aimed to design a teaching unit for plane symmetries, based on a DGS environment, which pays attention to the diversity of students’ teaching needs, in particular of m-gifted students. The teaching unit is adequate for upper primary or lower secondary school grades, depending on the grade where symmetries are studied for the first time. The learning objectives of the teaching unit include (1) the basic properties of plane symmetry, (2) procedures to draw the symmetric of a point or shape respect to a given axis of symmetry and draw the axis of two given symmetrical points or shapes, (3) the definition of plane symmetry, and (4) products of two symmetries and decompositions of translations and rotations into products of two symmetries. We present the teaching unit in the form of an Apple’s iBook which takes advantage of the interactivity of e-books and some specific features of iBooks, like the possibilities of modifying the sequence of activities to be solved by a student and the availability of evaluation questionnaires.

The research objective of the paper is to make a networked analysis of the structure and contents of the e-book based on the theoretical models of the Van Hiele levels of mathematical reasoning and the levels of cognitive demand in mathematics problem solving, to verify the adequacy of the teaching unit for the mentioned grades and average and m-gifted students. The analysis is theoretical in the sense that it is based on the aims of the activities and the expected students’ answers.

We present the analysis of selected examples of the different types of activities and other elements of the teaching unit and a global analysis of the whole e-book from the points of view of the two networked theories. We conclude that the set of activities designed and their organization in the e-book is coherent with the mentioned theoretical models and is adequate for the teaching to different kinds of students, from slow learners to m-gifted students. The results of this research add information to current knowledge by mathematics education researchers on a successful networked use of the Van Hiele levels and the levels of cognitive demand, and also provide information to mathematics teachers on the teaching to and learning by m-gifted students of plane symmetries in the technological environment of an e-book with DGS, as an example of a teaching methodology good for virtual learning.

2. Review of Literature

The main components of the teaching unit we analyze in this paper are: use of DGS in the teaching of geometry, teaching and learning of symmetries, use of e-books to teach mathematics, and attention to m-gifted students. Each of these topics could be the focus of a wide review, but we have limited this review to mention relevant literature related to the objective of our research and the teaching unit in the e-book. The last part of the review also includes literature about the Van Hiele levels, and levels of cognitive demand, since these theoretical models are the core of our theoretical framework.

The use of information and communication technologies (ICT) in teaching mathematics has proved to be fruitful in many teaching contexts in the different educational levels. Tools like calculators, computers, tablets, videos, and other technologies offer teachers possibilities to organize different ways of teaching mathematical contents adequate to the characteristics of their pupils. The mathematics education research handbooks (e.g., the more recent ones [30,31,32,33]) show that the literature is plenty of publications, both by researchers and practitioners, showing examples of mathematical classes including ICTs for every curricular topic. These texts also make evident the evolution, from the 1980s until nowadays, of the ways technologies have been used in the classrooms. According to Sinclair et al. [3], there are several areas related to ICTs where research is necessary, the first one being “the introduction and design of new technology, both hardware and software” (p. 701). The research reported in this paper fits in this area, since we present the design of an e-book as an example of an under-used but promising technology.

Research literature has demonstrated that, in the context of regular classrooms with heterogeneous groups of students, DGS has proved to be useful to create teaching units based on the methodology of guided discovery [34,35] allowing the coexistence of different students’ learning styles and needs, from slow learners or those not interested in mathematics to m-gifted students willing to learn more [36]. The diverse ways of doing and understanding dragging, all of them implicitly based on the transformational-saliency hypothesis proposed by Battista [37], allow different students’ learning processes, from the empirical discovery of mathematical facts to the generalization and abstraction of general properties. These ideas grounded the teaching unit we have designed, since the activities based on GeoGebra applets offer students different possibilities of learning, from visual perception of regularities to identification of abstract geometrical relationships and properties. We have also designed the sequence of activities to improve students’ conceptions as they advance in the solution of the activities and to allow m-gifted or interested students go farther in the learning of properties of symmetries.

The teaching of symmetries has been an objective of mathematics education researchers for decades. They have paid attention both to students’ difficulties and to teaching strategies to prevent or overcome them. Early studies focusing on primary and secondary school students’ behavior [13,38,39,40,41] identified some typical sources of students’ misunderstandings and errors, like the direction of movement (vertical, horizontal, slanting), the distance between objects and axis, and the position of the axis (vertical, horizontal, oblique), the last one being the most frequent and persistent error. More recent studies have focused on the teaching and learning of symmetries from kindergarten to high school, like those reported in [1,12,42], and pre-service teachers [43]. Some authors have explored software environments for symmetry [1,12,42,44,45] and described primary school students’ improvements in their conceptions of symmetry from perceptual (Van Hiele level 1) to geometrical (Van Hiele level 2) conceptions and from static to dynamic embodied ways of reasoning [46,47].

There are scarce publications showing teaching experiments based on e-books, which is an evidence of the need of new research on this issue and specific proposals of mathematics e-books. A remarkable study in this direction was made by Pepin et al. [48,49], who tackled the question of defining an e-textbook and analyzing different related aspects. They identified three types of e-textbooks (integrative, evolving, and interactive, our e-book matching the last type) and analyzed several e-textbook from the points of view of their contents, structure, and changes observed in teachers and students’ interactions with e-textbooks and standard textbooks. Pepin and colleagues also presented a conceptual framework to analyze teachers’ processes of designing electronic materials, in particular e-textbooks.

A different focus was adopted by Fahlgren and Brunström [50], who presented some principles for the design of problems to be solved with DGS or CAS, which are valid for the design of e-book based teaching units. Their main principle is that there should be open problems [51], i.e., problems allowing students to explore in the screen graphical representations of the problems, generate conjectures, and prove them in different ways (empirical or deductive) depending on students’ mathematical knowledge and abilities to produce proofs. Another principle is that students should have a good knowledge of the software, to let them develop different modalities of interaction depending on the requirements of the problems. Related in some way to the previous research, Santos-Trigo and Camacho-Machín [52] presented a conceptualization of mathematical e-books, reflecting on the necessary coordination between the affordances and limitations of the technological environment and the design of the tasks posed, including suggestions of ways to transform routine textbook exercises into dynamic problems, with multiple ways of solution whenever possible and able to induce students’ reflexive thinking.

Adequate attention to m-gifted students in their regular classes is an open mathematics education question for both teachers and researchers. There have been different approaches, all of them agreeing in that problem solving should be the core content of the classes. Several researchers have identified as a desirable practice that all students in the classroom work on the same tasks or sets of problems. To put this into practice, tasks or problems have to be diverse enough to be adequate for the different students’ mathematical abilities or interests. Piggott [53,54] proposed mathematics teachers to create rich tasks; these are tasks made of several related questions or problems, starting with basic questions within all students’ reach, which focus on the key contents to be learned, and continuing with increasingly complex and challenging questions. The last kind of questions should be more adequate for the m-gifted students in the classroom, who may deepen their mathematical knowledge and improve their problem solving abilities. Rich tasks may be seen as bottom-up tasks, since they start with a simple question and each new question is a bit more complex or challenging than the previous ones. We have used this construct in previous research [55,56] and, when designing the activities for the e-book, we also adopted the spirit of rich tasks to design sequences of activities with a same teaching objective and increasing challenge.

Leikin [57] applied a similar idea when she defined a stepped task as “a mathematical activity that includes a complex mathematical problem, called the ‘target problem,’ which is accompanied by scaffolding paths that include steps of different levels of mathematical challenge. Each step includes a number of problems with a reduced level of complexity with respect to the problems at the previous step.” (p. 173). Thus, stepped tasks are top-down tasks, since they start stating a difficult question, which only a few students in a classroom can answer, and continue offering students clues to be used if they cannot solve the tasks with the available information or if they do not want to engage in solving them.

There are many publications showing applications of the Van Hiele levels of reasoning to design and implement teaching units, and to evaluate students’ outcomes [1,37,58]. In particular, [43,46] used the Van Hiele levels to investigate preservice teachers’ and grade 6 students’, respectively, understanding of plane symmetries. A difference between both authors is that Son [43] used the generic characterizations of the levels while Della Iacono and Ferrara [46] used a specific adaptation of the Van Hiele levels to the context of their experiment. In Section 3.1 we present a particularization of the Van Hiele levels to the specific context of the activities included in our e-book, to guarantee an accurate and reliable evaluation of the activities and the hypothesized students’ behavior when solving them.

Since the emergence of the levels of cognitive demand in the mid-1990s [28], they have been used many times to evaluate mathematics teachers’ design and implementation of activities or teaching units in their classes, paying attention to teachers’ intended levels of cognitive demand and the ways teachers acted during the classes to keep them or not. Otten et al. [59] offer an analytic compilation of research publications about the levels of cognitive demand. In previous research, we have used the levels of cognitive demand as theoretical framework to make theoretical analysis of problems and analysis of students’ solutions in specific contexts of pre-algebra, geometry, and visualization [26,27,60,61]. In this paper, we add a new approach by characterizing the levels of cognitive demand in the context of plane symmetries, which is an innovative contribution to mathematics education research.

3. Theoretical Framework

We present the two components of our theoretical framework, the Van Hiele levels of mathematical reasoning and the levels of cognitive demand. The general characterizations of both models are broad and generic, which makes difficult their use in a specific context like the teaching and learning of symmetries. To avoid this obstacle, we have particularized each model to this context. Then, we analyze the teaching unit from each model and network both analyses to provide a final analysis of the electronic teaching unit of symmetries we have designed.

3.1. The Van Hiele Levels of Mathematical Reasoning

The Van Hiele levels characterize the different types of mathematical reasoning used by students of different ages and mathematical abilities when they solve mathematical activities. The model includes five levels, although usually only the levels 1 to 4 are considered when dealing with primary or secondary school students. In particular, in this paper we only use levels 1 to 3, since we are focused to primary school average and m-gifted students. The main characteristics of levels 1 to 4, particularized to the study of symmetries, are [37,40,62]:

• Level 1 (visual recognition): geometric objects are recognized globally by their shape and appearance, and classified or differentiated on a visual basis. Students can name geometric objects, but they do not recognize their mathematical components or attributes. Students can identify a symmetrical figure or a pair of symmetrical figures by sight, folding a sheet of paper or using a mirror. They can use paper folding to draw symmetries and to get axes of symmetry. They can also discover visual properties of symmetrical figures, like equidistance to the axis or position at both sides of the axis, and learn some mathematical terms, like axis, symmetry, or image.
• Level 2 (analysis): mathematical components and properties of geometric objects are identified and used to describe and classify the objects. Students can discover experimentally the main properties of symmetrical figures and axes (equidistance and perpendicularity respect to the axis) and prove them empirically. They describe informally transformations observed after dragging GeoGebra figures and mathematical properties identified, and can verbalize a definition of symmetry as a list of known properties. They can draw the image of a figure and the axis of a symmetrical figure or a pair of symmetrical figures by using properties of the perpendicular bisector. They can also obtain the image of a shape after a product of two symmetries. Students learn to use geometric symbols when writing their solution or talking about them, like P, P’, S_e, and others, but cannot understand complex symbolic expressions.
• Level 3 (informal deduction): mathematical definitions of geometric objects (as minimum sets of properties) are meaningful for students, and they are able to use different definitions for the same concept; in particular, they can obtain and use the mathematical definition of symmetry. Students can discover properties of symmetry or symmetrical figures and prove them by assembling informal deductive arguments by means of known definitions and properties. They can also discover and understand the relationships between products of two symmetries and translations or rotations, in particular that there are infinitely many decompositions of translations and rotations into pairs of symmetries.
• Level 4 (formal deduction): the algebraic structure of the group of the plane isometries can be understood and properties of the group can be discovered, and students can prove them by means of formal proofs.

3.2. The Levels of Cognitive Demand

Our starting point is the conclusion that a successful way for teachers to get the highest meaningful learning from their pupils is to pose them activities that make students engage in productive struggling (intellectual challenge) and high level of reasoning to solve them [28,63]. This statement is valid for every student [64], but specially for m-gifted students [20,65]. The cognitive demand of a mathematics problem is defined as the amount of mathematical thinking called for by students when solving it [66,67] or, equivalently in other words, the kind and level of thinking used by students to engage with the problem and successfully solving it [68].

To operatize the construct of students’ cognitive demand, Smith and Stein [28] presented a graduation of levels of cognitive demand to characterize different complexities of activities on the basis of both their relationship to the mathematical contents to be learned and the expected or real students’ cognitive efforts when solving them. Smith and Stein defined four levels of cognitive demand:

• Memorization: Activities only requiring the reproduction of previously memorized definitions, properties, formulas, etc., which are explicitly and clearly mentioned in the statement. There is no connection to the concepts or relationships to be learned. The solution of these activities requires a minimum cognitive effort.
• Procedures without connections: Activities requiring algorithmic solutions, consisting of following a previously mastered simple procedure that is explicitly called for or is evident from the statement of the activity. There is no connection to the concepts or relationships to be learned. The solution of these activities requires a limited cognitive effort.
• Procedures with connections: Activities requiring algorithmic solutions, consisting of following a previously mastered procedure which, unlike the previous level, is complex and requires students to be mindful and take some decisions. The way to follow the procedure is not evident and, to succeed, students have to understand and use consciously the mathematical contents or relationships to be learned which are implicit in the activity. The solution of these activities requires a moderately high cognitive effort.
• Doing mathematics: Activities requiring non-algorithmic thinking, since they do not explicitly suggest a way of solution. Students have to use the mathematical contents or relationships to be learned implicit in the activity in innovative and original ways. The solution of these activities requires a high cognitive effort.

Based on their experience on applying the levels of cognitive demand, Benedicto et al. [27,69] modified the characterizations of the levels stated by Smith and Stein [28], summarized above, to systematize, complete, and refine them. The characteristics of each level of cognitive demand refer to the process of solution of an activity, its learning objective, the cognitive effort required from students to solve correctly the activity, the implicit (mathematical) content students have to put to work to solve correctly it, the explanations required from students, and the ways of representation of the solution (systems of signs) used in students’ answers. The representations used in the expected solutions to the activities in our teaching unit are: graphical (use of external visual elements like manipulations, dragging, drawings, etc.), geometrical (use of letters and geometrical symbols, to refer to polygons, axes, movements, etc., or measure distances or angles), visual (use of mental images) or verbal (verbal explanations with limited use of mathematical, graphical or visual elements).

In other previous research, we have successfully applied that new characterization of the levels by particularizing them to different mathematical contexts, aiming to analyze mathematics problems and students’ solutions [26,60,61]. Based on Benedicto [69], we present in this paper an innovative and original characterization of the levels of cognitive demand for the context of initial learning of symmetries by primary or secondary school students.

Table 1. Characteristics of the levels of cognitive demand for the activities on plane symmetries.

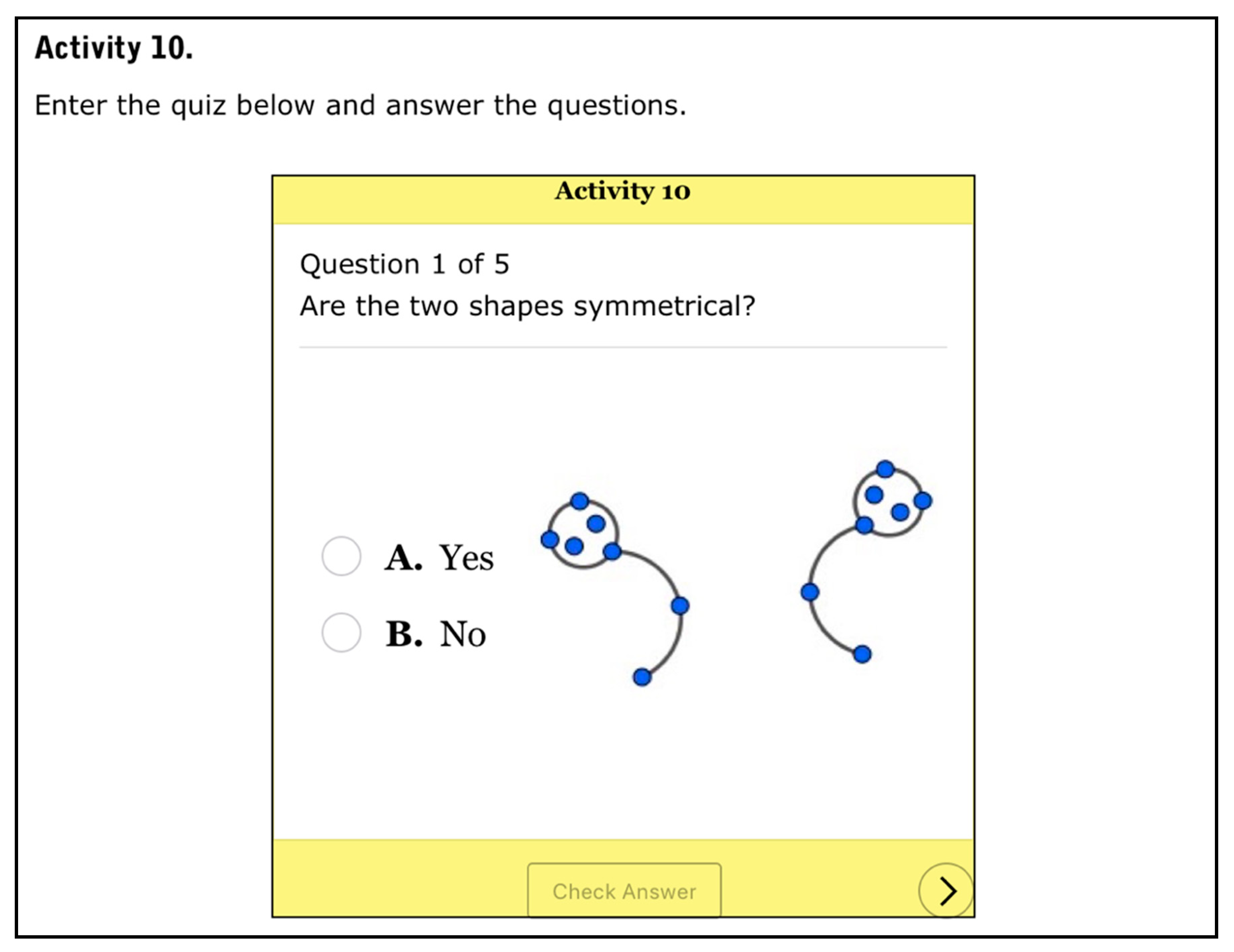
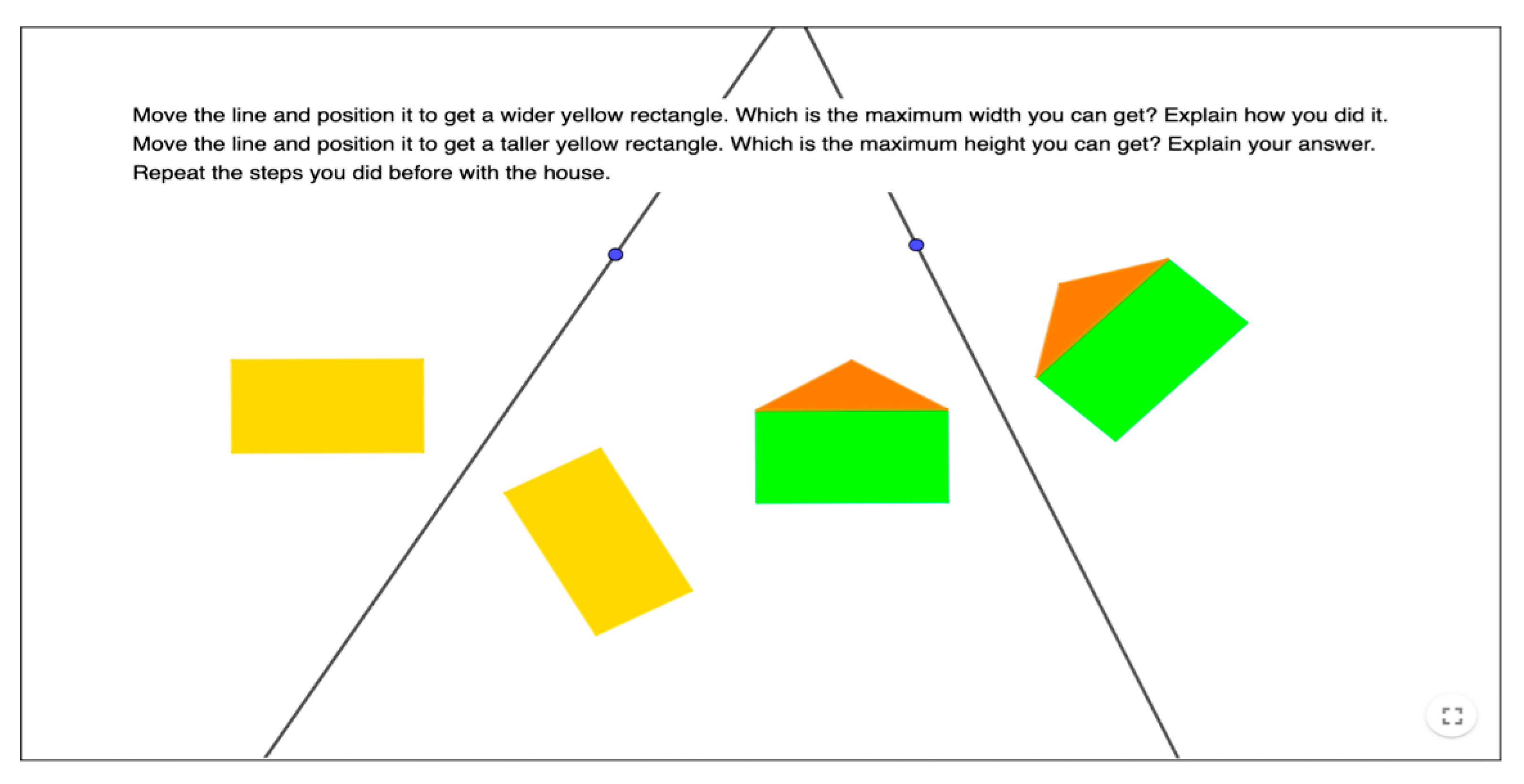
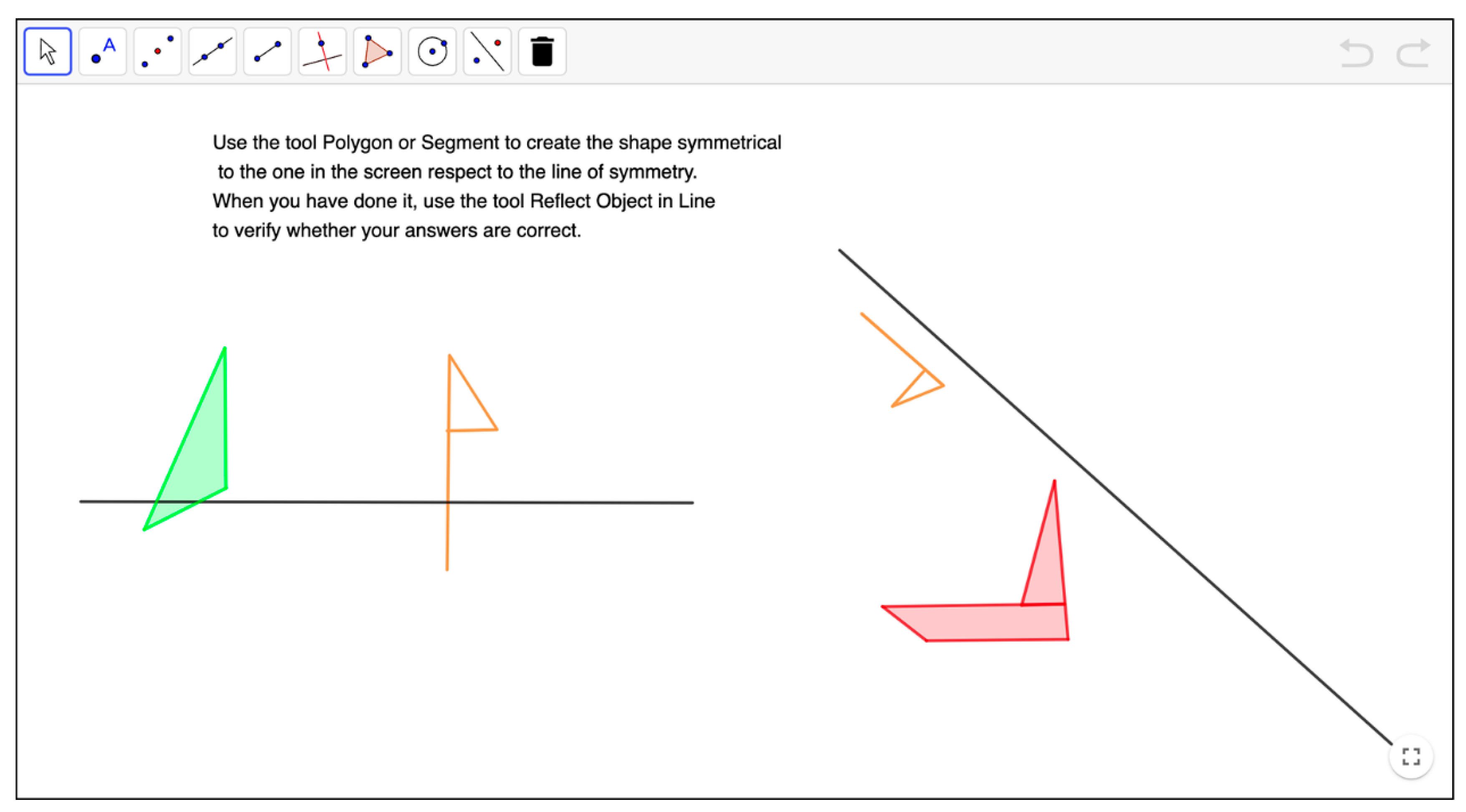
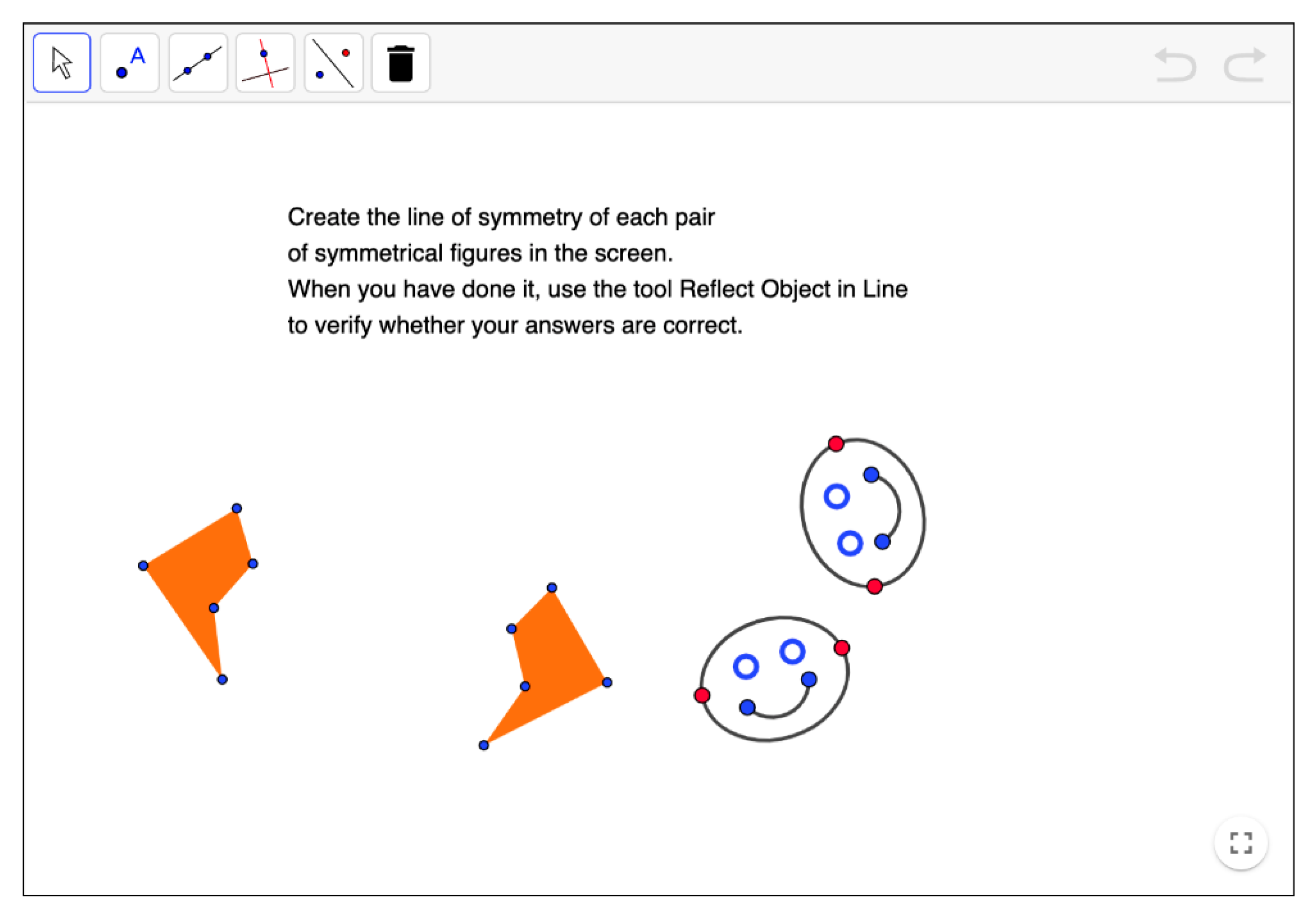
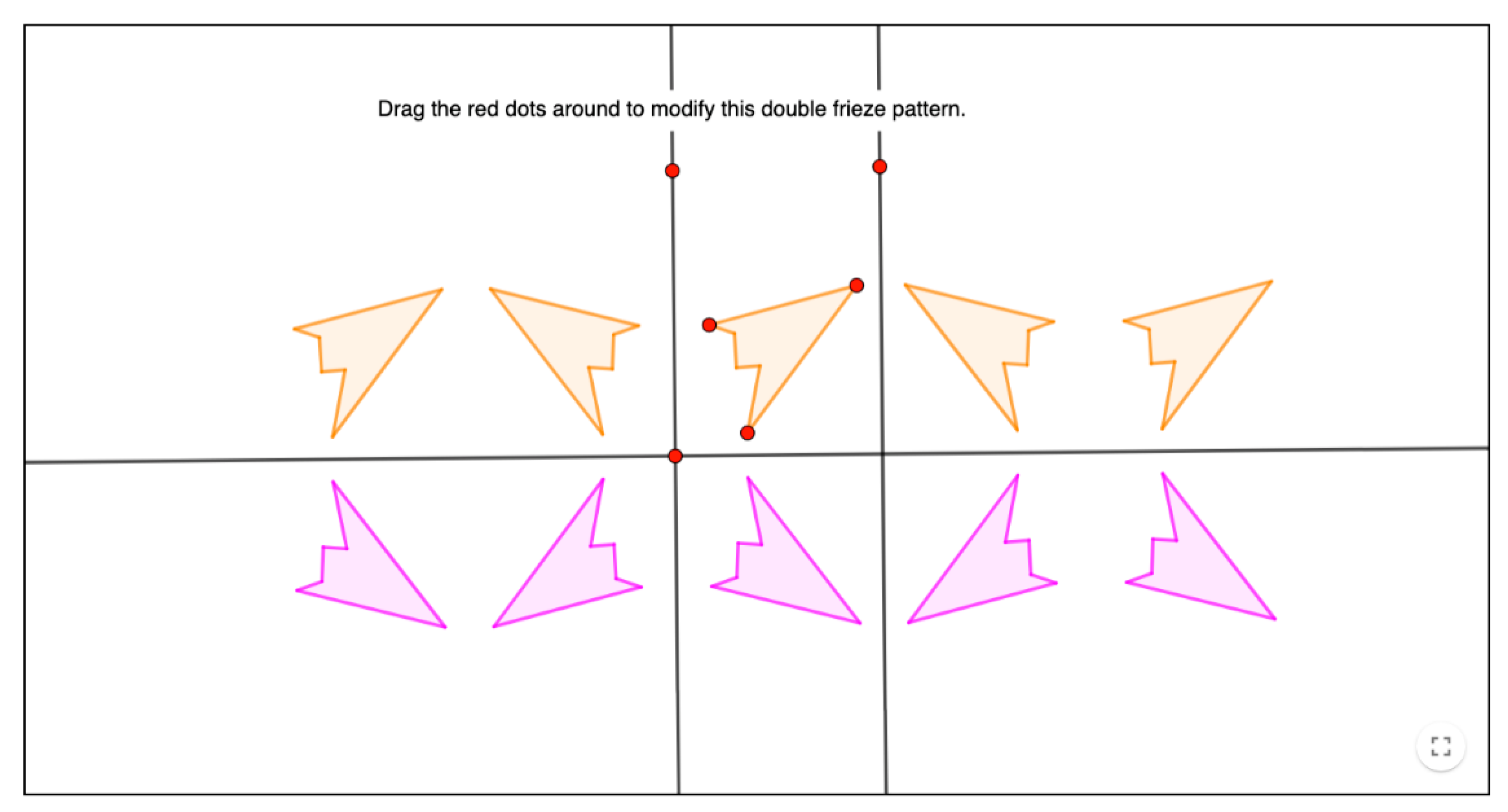
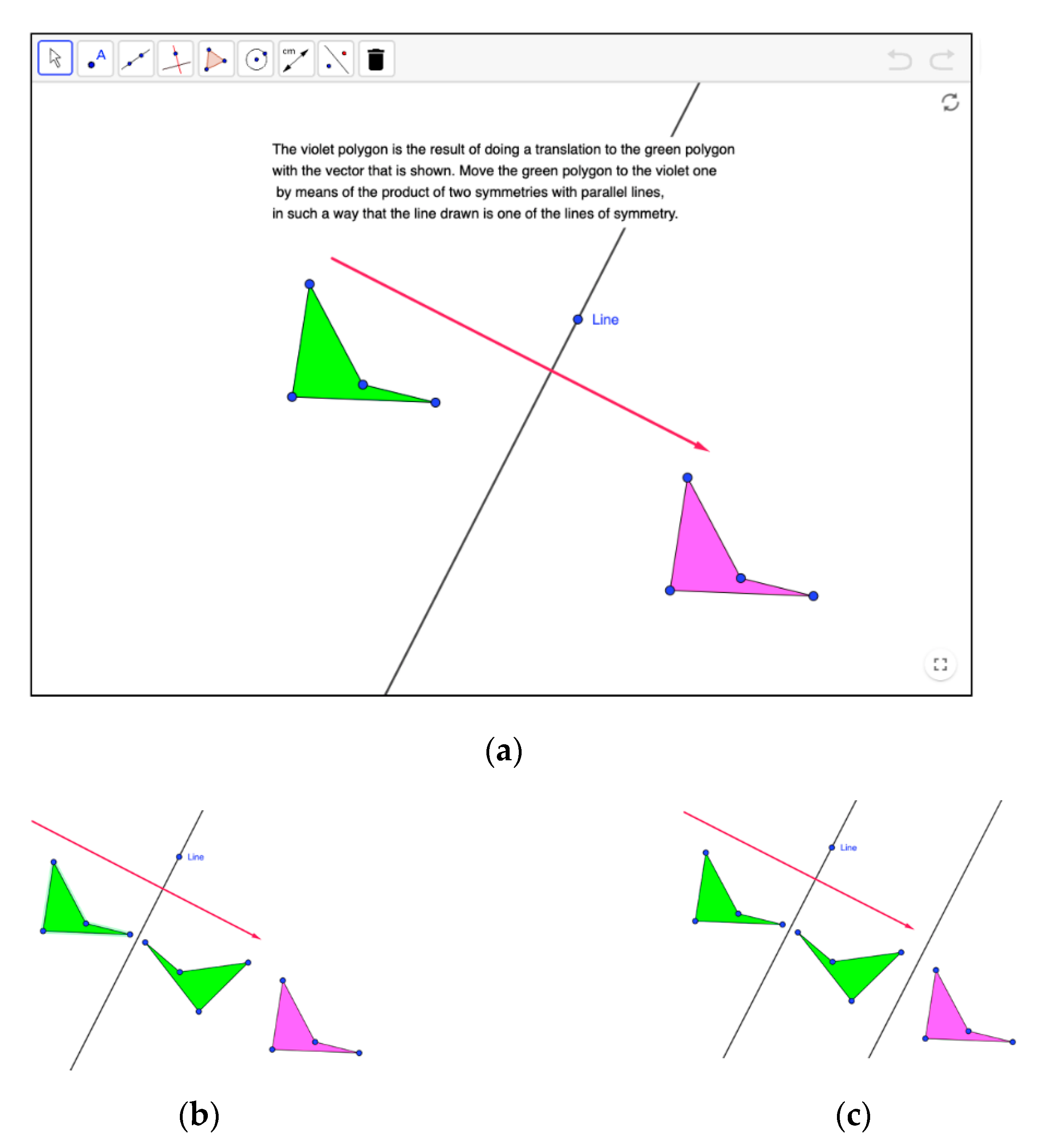
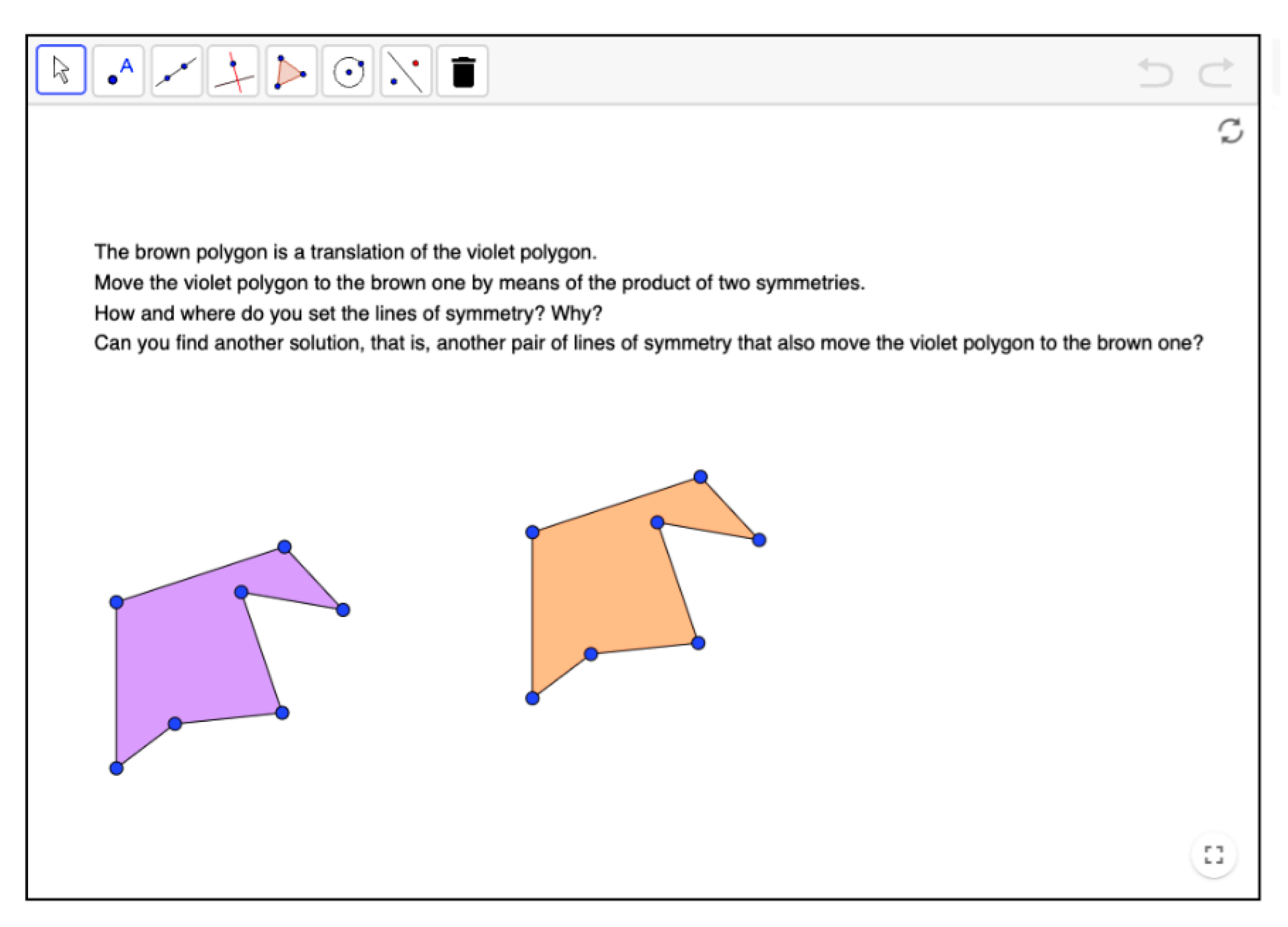
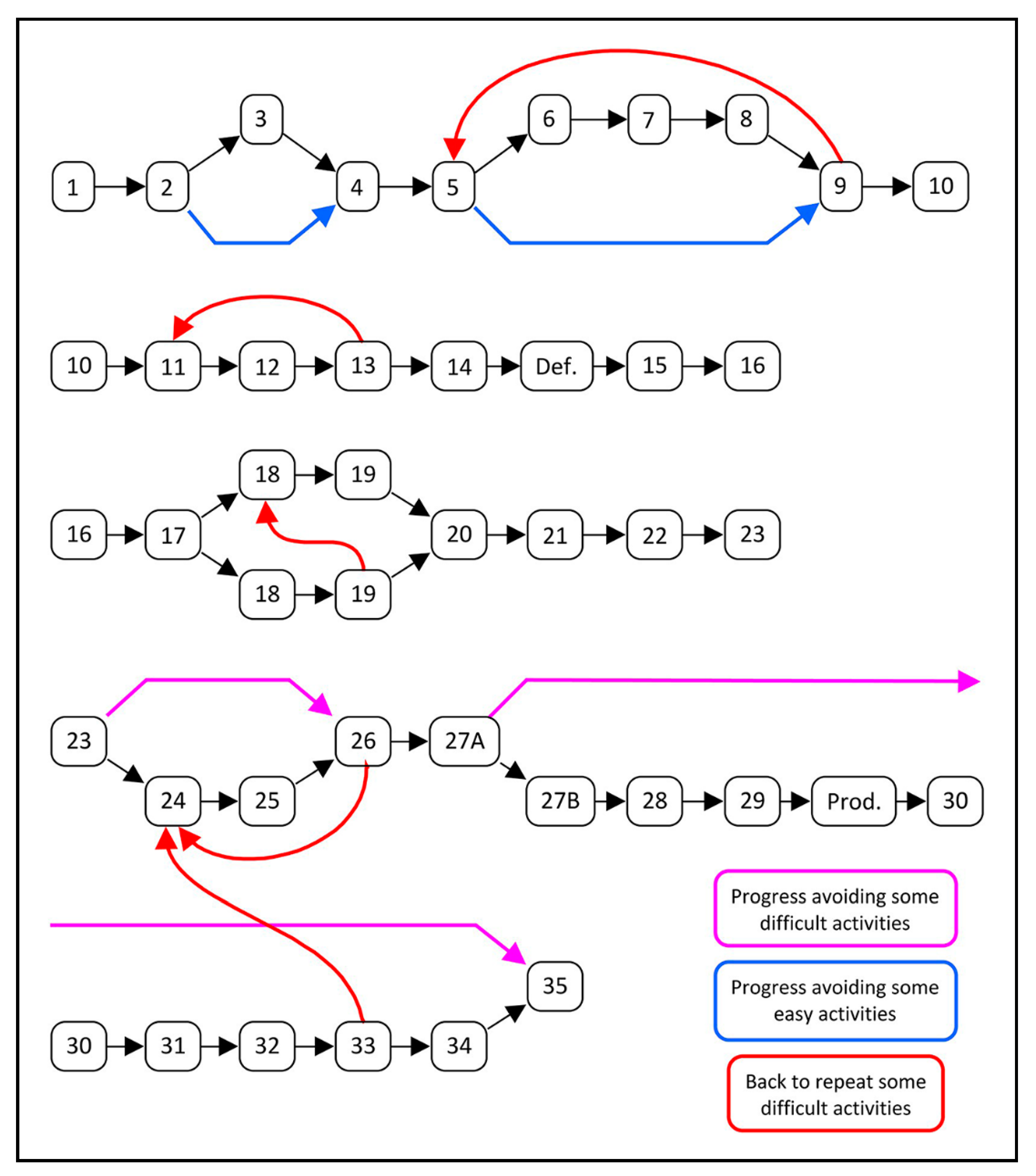
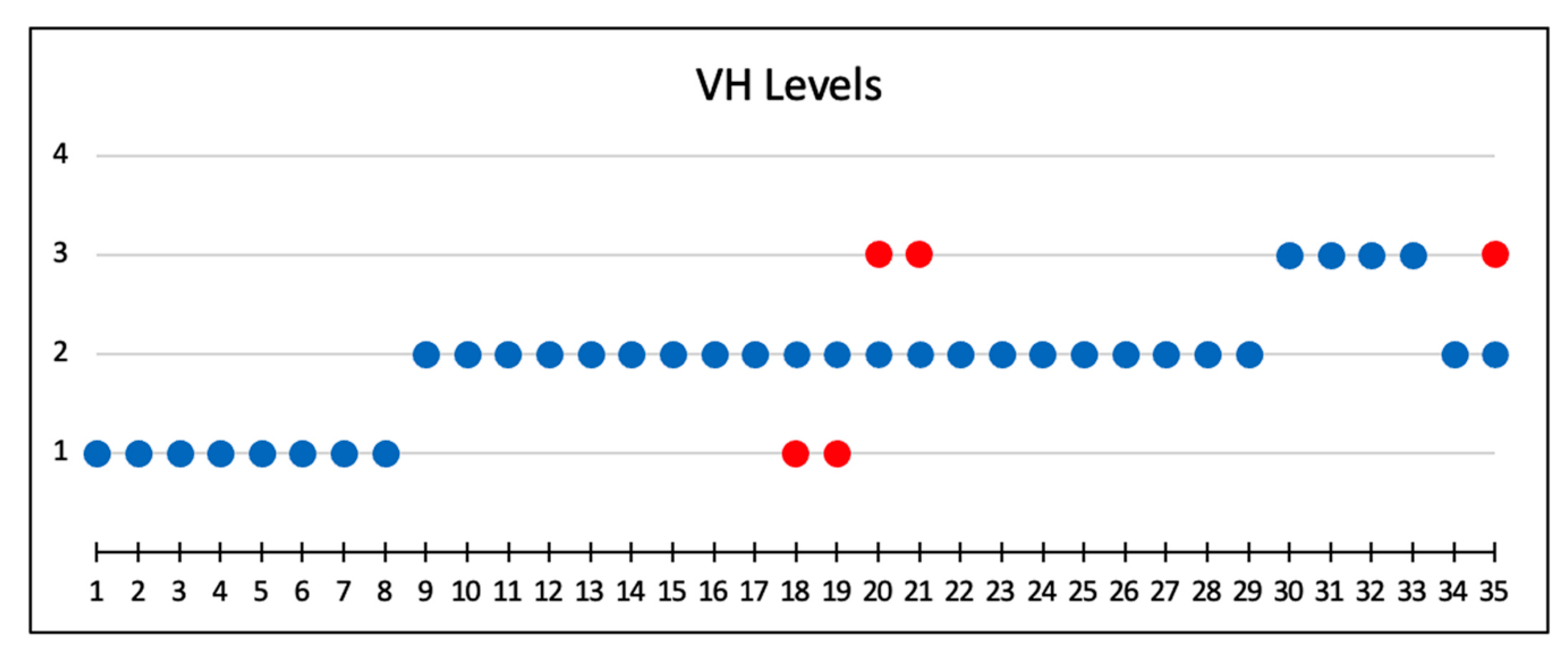
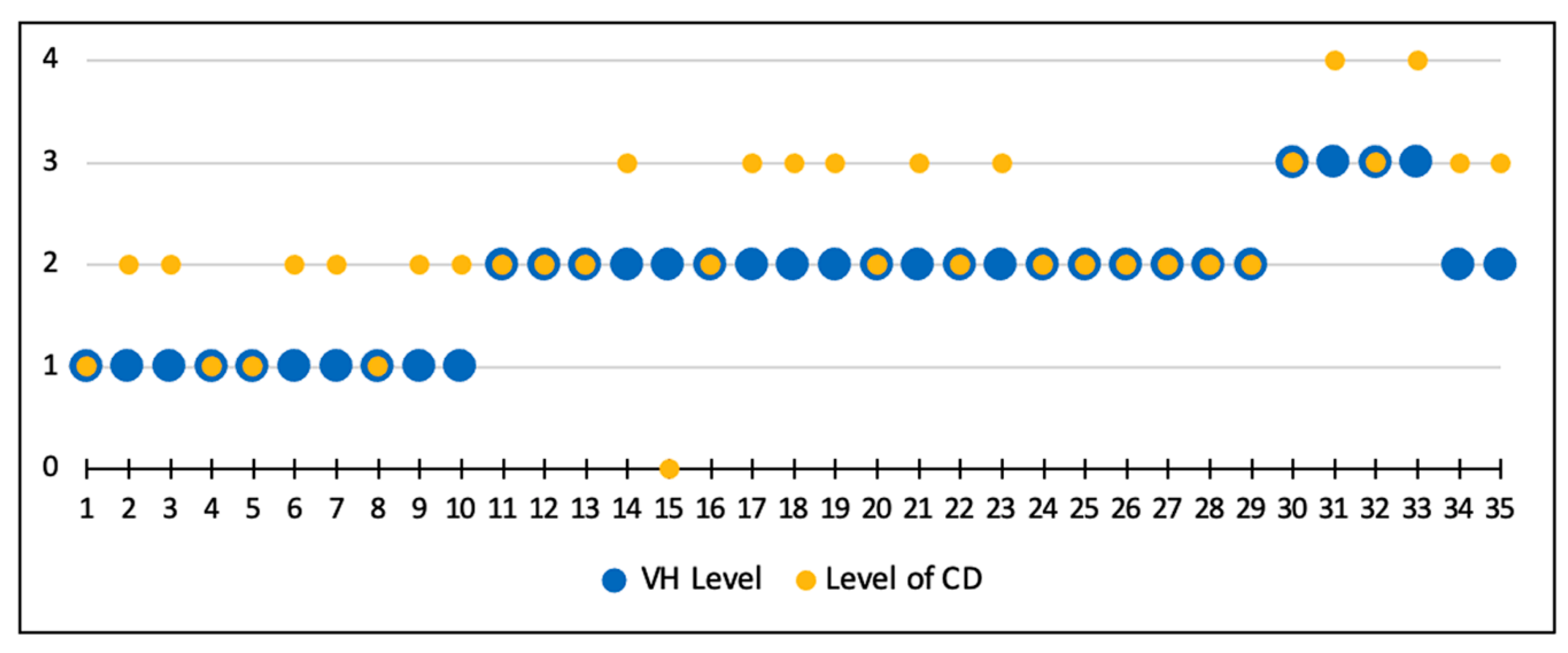
Levels of Cognitive Demand	Categories	Characteristics of the Activity
Memorization	Process of solution	It is solved by observing shapes presented in the activity, making actions that automatically produce the answer or resorting to mental images or data recalled.
	Objective	Identify visually regularities of symmetrical (pairs of) shapes or reproduce elements (visual properties, etc.) previously learned or recalled.
	Cognitive effort	A successful solution requires a minimum cognitive effort. The statement is not ambiguous and it only requires observing the shapes to perceive their visual characteristics of symmetry or following the given directions about what to do.
	Implicit content	It has no connection to the mathematical definition, properties, etc. of symmetries to be learned. Students do not need to use such knowledge to get correct answers.
	Explanations	It does not require explanations.
	Representation of the solution	The representation used may be graphical or visual, but the virtual environment may also induce verbal representations.
Procedures without connections	Process of solution	Depending on the activity, the procedure may consist of observing the shapes showed in the activity to visually identify (pairs of) symmetrical shapes, axes or properties, or dragging or using DGS tools to obtain images or axes.
	Objective	Produce a correct answer (visually complete symmetrical shapes, or identify the axes of symmetry of the given shapes, or construct images or axes with the DGS). Students do not need to apply the underlying mathematical properties of symmetry to be learned.
	Cognitive effort	Solving it correctly requires a limited cognitive effort. Little ambiguity exists about what to do and how to do it, because the statement clearly states it and the environment offers the adequate resources (DGS files, Internet links, etc.).
	Implicit content	There are implicit connections between the underlying properties of symmetries and the expected solution procedures, but students do not need to be aware of such connections since they may find the answer by using their visual conception of symmetry or the data presented by the activities.
	Explanations	It requires explanations that focus only on describing the procedure used. It is not necessary to explicitly connect the answer to mathematical definition or properties.
	Representation of the solution	Students use visual or geometrical representations, depending on whether the activities ask to observe or draw symmetry images or axes. Sometimes, they may prefer transmitting the information verbally.
Procedures with connections	Process of solution	The procedure consists of, depending on the activity, considering the relative positions of the axis of symmetry and the vertices and sides of the shapes showed in the activity, to determine the position of the symmetric vertices or the axis, or decomposing a translation or rotation into a product of two symmetries.
	Objective	Depending on the activity, guide students to note that the metric properties of symmetries (equidistance of symmetrical points from the axis and perpendicularity of the segment joining the symmetrical points respect to the axis) are characteristic of symmetry and it is necessary to use them as tools to solve graphical activities, or note that the relationship between translation/rotation and product of symmetries can be reversed.
	Cognitive effort	Solving it correctly requires a moderately high cognitive effort. Students may use general procedures to draw images or axes of symmetry, but they need to have some understanding of the geometric characteristics of, depending on the activities, symmetry or products of symmetries, and use them.
	Implicit content	To solve the activity, students need to explicitly use the properties of symmetries underlying the correct procedures of solution.
	Explanations	It requires explanations to justify the procedures applied in the solutions. Such explanations may be abstract or based on the specific shapes of the activity, depending on the activity.
	Representation of the solution	Students may use visual representations to create an approach to polygon images or axes asked and graphical representations to improve the positions of image points or axes.
Doing mathematics	Process of solution	It requires complex and non-algorithmic thinking. The statement does not suggest any way to get the solution. Students have to understand, analyze, and put to work the properties of symmetry and products of symmetries they have learned to produce a correct solution.
	Objective	Analyze the solutions to previous tasks and possible limitations to get conclusions and establish new links that allow them to find multiple decompositions of a translation or rotation into products of symmetries.
	Cognitive effort	Requires a high cognitive effort, since students need to use abstract reasoning to establish explicit links between adequate parts of the underlying properties of symmetries to determine an innovative way to proceed to solve correctly the activity.
	Implicit content	Students have to access relevant knowledge and previous experiences to make appropriate use of the underlying properties of symmetries in working through the task to get a correct solution.
	Explanations	Explanations consist of proving the correctness of the steps done in the DGS to get the construction asked by the activity.
	Representation of the solution	The solution is based on geometrical representations of figures, axis, etc. necessary to solve the activity.

proposes the characteristics of each level of cognitive demand aligned to the activities in our teaching unit.

3.3. Networking Theories in Mathematics Education

When several theories are adequate to approach a given issue but provide different solutions or focus on the issue from different points of view, researchers do not need to restrict themselves to select one theory, but they can use two theories to get richer analyses or conclusions than by using only one of those theories. According to [22,70], networking theories is a research methodology aimed to establish relationships between parts of different theories, maintaining the identity of each theory, that is, not trying to modify or merge them.

There are different ways of networking theories, depending on the objectives aimed and the strategies used for finding connections between them [22]: understanding, making understandable, comparing, contrasting, combining, coordinating, integrating, and synthesizing. The kind of networking we have used in our research to analyze the e-book is combining theories, that “means looking at the same phenomenon from different theoretical perspectives as a method for deepening insights into the phenomenon. … Combining theoretical approaches does not necessitate the complete compatibility of the theoretical approaches under consideration” ([22], pp. 119–120; italics in the source) and is adequate for networking theoretical frameworks which aim “at the use of different analytical tools for the sake of a practical problem or the analysis of a concrete empirical phenomenon” ([70], p. 495). We have identified the Van Hiele levels of reasoning and the levels of cognitive demand of the hypothesized students’ answers to each activity in the teaching sequence, and have combined both classifications to get extra information about the cognitive characteristics of the activities.

4. Methodology

In this section we describe and justify the process of designing the teaching unit and implementing it in the resulting e-book [17]. We present and discuss the mathematical contents aimed to be learned by students, the didactical criteria guiding the selection and organization of the activities, and the types of activities included in the e-book. We will denote hereafter the Van Hiele levels as VH (e.g., VH 2 for the second level) and the levels of cognitive demand as CD (e.g., CD 3 for the level of procedures with connections).

4.1. Selection of the Mathematical Contents

Some mathematics curricula for primary school introduce students to isometries by means of manipulation and drawing of simple cases, situated in the VH 2 of reasoning. Two examples of this approach are the NCTM Principles and Standards [10] and the Spanish mathematics curriculum [71]. In the upper primary grades and lower secondary grades of different countries, the study of isometries may include the use of measurements of distances and angles, the Cartesian plane, and products of isometries of the same type, presented just manipulatively and stating the formal results of the products without any justification other than a drawing, keeping the learning in the VH 2. For instance, the most used Spanish textbooks teach in primary grades 4–6 (students aged 9–12) translations, symmetries, and (sometimes) rotations informally, as movements and based on manipulations and drawings, including the basic vocabulary of each movement. Secondary school textbooks teach in grade 1 (students aged 12–13) the symmetries of polygons and they make in grade 3 (students aged 14–15) a detailed teaching of translations, rotations, and symmetries, including the mathematical definition and main properties of each isometry. In this context, clearly there is room to pose m-gifted students activities like the ones in our teaching unit, which help them gain a deeper knowledge of isometries.

Prototypical cases are frequent in textbooks, mainly horizontal vectors for translations and vertical axis for symmetries. In this context, most m-gifted students in the upper primary or lower secondary grades lose an opportunity to learn and understand isometries according to their potential to reason in the VH 3 and to solve problems requiring from them high levels of cognitive demand. The aim of our teaching unit was to help all students understand and learn the basic properties of symmetries, those included in curricula and textbooks, and provide m-gifted students with an opportunity to go farther in deepening their knowledge of symmetries, by learning some properties that are not usually included in the textbooks. The mathematical contents of the teaching unit of symmetries are:

• Visual approach to symmetries: visual identification of symmetrical shapes, pairs of symmetrical shapes, and axes of symmetry.
• Manipulative approach to symmetries: folding and cutting out to produce symmetrical shapes and axes of symmetrical shapes (the electronic environment of the e-book does not favor the use of a mirror).
• Discovery of the equidistance of any two symmetrical points from the axis of symmetry.
• Discovery of the perpendicularity to the axis of any segment ending in two symmetrical points.
• Equidistance and perpendicularity as the main characteristics of symmetries. Mathematical definition of axial symmetry.
• Accurate constructions with the DGS of the images of given shapes and the axis of given (pairs of) symmetrical shapes.
• Relationship between the axis of symmetry and the perpendicular bisector of any pair of symmetrical points.
• Symmetries of triangles, quadrilaterals, and regular polygons. Generalization of the relationship between the number of sides of a regular polygon, its number of symmetries, and the position of their axes.
• Products of two symmetries with parallel axes.
• Products of two symmetries with secant axes.
• Creation of frieze patterns and rosette (dihedral) patterns.
• Decomposition of translations and rotations into products of two symmetries. Infiniteness of solutions.

We consider that the basic contents to be learned by all students are those guiding to the discovery of the two properties which constitute the definition of axial symmetry, i.e., those contents described in 1–6 above. The expression of the definition of axial symmetry may be more or less formal depending on the Van Hiele level of reasoning of students. Most students in the upper primary school grades reason in VH 1 or 2 [3], so they are expected to understand, read and write mathematical sentences with a small quantity of mathematical symbols, but they would be unable to understand complex symbolic expressions. Then, in the e-book, we present the standard mathematical definition of symmetry expressed in an informal language which limits the use of mathematical symbols to the minimum necessary and helps students understand the definition as a synthesis of the properties they have discovered. The activities of products of symmetries and decompositions of translations and rotations, described in 7–12 of the list above, require a higher and more demanding level of reasoning, most of them in the VH 3 and CD 3 or 4, so they are more adequate for m-gifted students willing to engage in solving more complex problems.

4.2. Didactical Criteria for Designing the Teaching Unit

Didactical criteria to organize teaching of mathematics may be very different, depending on the case. To design the teaching unit and the e-book, we have mainly considered as didactical criteria: the frequent obstacles for learning symmetries, the advantages of using a DGS environment, the complexity and cognitive requirements of the activities, the possibility to offer several paths to advance in the e-book, and students’ metacognition. In the following paragraphs we unfold each criterion.

Mathematics education research has showed that there are some prototypical figures that hinder the learning of mathematical concepts, more frequently geometrical concepts like some types of polygons and polyhedra [72], altitude of triangles [73,74], or isometries [13], among others, making students create poor concept images [3,75]. For our purposes, the most relevant are the prototypes related to the symmetry. Grenier [39] analyzed the influence of different variables that may hinder or facilitate the drawing of images or axes: drawing on squared or white paper, calculating the images of points, segments or more complex figures, the orientation of the axis of symmetry respect to student’s horizontal (horizontal, vertical, slanting at different angles), the distance of the object from the axis (far, near, touching it, cutting it). A main result reported by several researchers [13,39] is that the most prototypical position for the axes of symmetry are vertical axes, inducing in students the concept image of reflection as a horizontal movement, even when the axis is not vertical. Horizontal axes also induce a similar prototypical concept image, although it is less frequent. Prototypical images make students base their solutions to the activities on basic visual reasoning where shapes, positions, sizes, etc., are unduly relevant and, therefore, students’ reasoning remain in VH 1 and CD 2. Taking into consideration the obstacles students may suffer and adopting actions when designing the activities to prevent or correct them is a way to make easier the transition of students from VH 1 to VH 2 and CD 2 to CD 3.

Research in mathematics education has repeatedly showed the positive influence of students’ use of DGS in promoting their observation of many different drawings of a same figure [76] to isolate characteristic properties and construct good conceptions of mathematical objects, dragging actions being the main element [3,37,77]. In line with such results, we have been careful in including in the statements of the activities suggestions asking students to drag points, figures, and axes whenever possible and as much as possible. The easiness to change the orientation of axes in DGS helps prevent the mentioned students’ prototypical conceptions of symmetry, by helping students detach from a physical static conception of symmetry, typical of levels VH 1 and CD 2, and start identifying its invariant geometric properties [78], so moving to the levels VH 2 and CD 3. Anyway, we have taken into consideration the didactical information about possible sources of students’ errors and misunderstanding and we have been careful when designing the activities to present the axes of symmetry in several positions. This is particularly important for activities where the axes are fixed or students who do not feel necessary dragging them. The use of GeoGebra should also help m-gifted students to solve the activities focused on learning the characteristics of products of symmetries and decompositions of translations and rotations, therefore promoting their progress from levels VH 2 and CD 3 to VH 3 and CD 4.

As the e-book is intended to be used by all students in regular classrooms, a criteria for designing and organizing the teaching unit was that the learning of new mathematical contents should start with basic introductory activities accessible by all students, requiring low demanding reasoning in levels CD 1 and CD 2, and should advance up to complex activities more adequate for m-gifted students, requiring high demanding reasoning in levels CD 3 and CD 4 (low threshold and high ceiling [79]). The teaching unit pays attention to several mathematical properties of symmetries, as described in Section 4.1. For each concept or property, there is a set of activities of increasing complexity presenting it, first isolated from other contents to be learned, as required by levels VH 1 and VH 2, which is done by means of simple manipulative activities. Next, several geometric contents are integrated to present new properties, to promote a higher abstraction of the more able students’ learning of definitions and properties of symmetries [80], adequate to introduce students in informal deductive reasoning proper of VH 3. The teaching unit also includes some reinforcement activities aimed to help average students understand the basic mathematical contents.

In general, the activities try to induce students to use their high level thinking and help them getting their higher expectations of sense making and understanding [66], but some activities may be unnecessary for the m-gifted students and other activities may be inadequate for average or slow students. To manage this diversity of interests, the e-book includes some moments for metacognition, with comments suggesting students to think on their progress and decide which activities solve next, i.e., although the e-book presents a lineal sequence of activities, it suggests possibilities of going back to reinforce understanding of difficult parts, jump over activities that may be very easy for m-gifted students, and skip over activities that may be too difficult for some students (this issue will be discussed at the beginning of Section 6).

Our interpretation of the teaching methodology of guided discovery [81] by problem solving includes teachers asking their pupils for explanations and justifications of their processes of solution and answers, and giving them, when necessary, some clue or other kind of help. This is difficult, or even impossible, to do really when students use the teaching documents on their own, but it is possible in those on-line courses that include interaction between teachers and students. Anyway, the spirit of the e-book is that students should think on their solutions and should try to check their correctness. To induce the former, the statements of some activities ask students to explain their solutions (not all activities ask it, to avoid being repetitive). To induce the latter, whenever possible, the activities offer students an alternative automatic way of getting the solution; for instance (Initial window for activity 14), if an activity asks students to draw the symmetric of a shape by hand with the GeoGebra tool Polygon, it also includes the tool Reflect Object in Line, so students, after having drawn their shape, can use this tool to construct the correct symmetric shape and compare it to their own one.

We have made some pilot experiments of the e-book with m-gifted primary school students, but the iPads used did not allow screen capture, so we could not collect detailed information of students’ interactions with the e-book, apart from the observations by the researchers and their field notes. Thus, in this paper we focus on describing the e-book, analyzing the organization of the mathematical contents, and presenting the didactical structure of the e-book relative to the Van Hiele levels and the cognitive demand.

4.3. Structure and Components of the Electronic Book

iBooks are a specific kind of e-books designed to be played in the app Books. Like most e-books, iBooks can play audio and video files, include links to web pages, and take the reader to other place in the book with a click. A distinctive characteristic of iBooks is the possibility of merging in the body of the book interactive documents (widgets) able to do things like showing sets of pictures, playing keynote presentations, creating interactive images or posing self-correcting multichoice or drag questionnaires. In our e-book [17], available as Data Availability Statement, we have merged videos, links to web pages, multichoice questionnaires, and links to other activities in the e-book. The solution of most problems integrating our teaching unit is based on offering students the opportunity of interaction with GeoGebra applets, so the e-book has many links to GeoGebra files, created by its author, housed in the GeoGebra resources web page. Figure 1 shows the statement of an activity based on GeoGebra. Students click on the figure to open the GeoGebra file, which has the menu modified to show only the tools needed to solve the activity (Figure 2).

Even for teaching methodologies based on students’ problem solving, there are some moments where a presentation by the teacher is most adequate. We have included in the e-book two short video clips to explain students how to get symmetrical shapes by folding and cutting out and to summarize the basic properties of symmetry. On the other hand, some types of activities are not adequate for solving them with GeoGebra; in these cases, the e-book offers students several links to web pages presenting interesting activities for the learning of symmetry.

To let students have some control on their self-learning progress, the teaching unit includes several activities consisting of sets of multi-choice questions (Figure 3), to evaluate students’ knowledge of the main results to be learned. The questionnaires let students verify their answer to each question before going to the next one or have a summary of correct and wrong answers after having answered all the questions. It is also possible to erase the answers and start responding the questionnaire again.

To manage the issue of the different complexity of the activities in the teaching unit and letting students self-control their progress, the e-book includes several points where students are asked to reflect on their progress and success in a given set of activities, and decide which is the best way for them to advance in the learning of the mathematical contents. The e-book may suggest students having difficulties to go back to work again on some activities or go ahead skipping over some difficult activities, while it suggests m-gifted students to go ahead skipping over some easy activities. By clicking on the adequate box, the e-book points at the next activity to be solved (Figure 4).

5. The Contents of the E-Book for the Learning of Plane Symmetries

Table 2. Learning objectives of the teaching unit and the corresponding activities.

Learning Objectives	Activities
Visual approach to symmetries	1–10
Manipulative approach to symmetries	4
Discovery of the property of equidistance	6–15
Discovery of the property of perpendicularity	11–15
Mathematical definition of axial symmetry	14–19
Accurate constructions with the DGS	17–21
Relationship between axis of symmetry and perpendicular bisector	20–23
Symmetries of polygons	22–23
Products of two symmetries with parallel axes	24–27
Products of two symmetries with secant axes	28–29
Creation of frieze and rosette patterns	26, 27, 29
Decomposition of translations into products of symmetries	30, 31, 34
Decomposition of rotations into products of symmetries	32, 33, 34
Final synthesis of the contents learned	35

presents a summary of the mathematical contents aimed to be learned and the corresponding activities in the teaching sequence. Some activities may have several related objectives. As mentioned in Section 4.1, the geometrical contents can be divided into two parts: the first one is aimed to teach all students the definition and basic properties of plane axial symmetry (activities 1–23), and the second part is aimed to teach, mainly to the m-gifted students, the concept of product of symmetries and the main properties of the products of two symmetries (activities 24–34). Finally, activity 35 asks students to write a summary of the geometrical contents they have learned. In this section, we present a sample of the different types of activities and analyze them from the networked points of view of the Van Hiele levels and the levels of cognitive demand.

Activity 1 connects to a web page showing a sequence of photographs showing symmetrical figures with one, two or more axes in vertical, horizontal and slanted positions. The aim of this activity is to have a first contact with symmetry. It is purely visual (VH 1) and it only requires from students a minimum cognitive effort to look at the figures and identify their visual symmetry (CD 1).

Activity 3 connects to another web page which presents several patterns (Figure 5) where students have to complete the blank side to make a pattern with vertical symmetry. When a tile is connected to a wrong position, the app does not register the result and the square remains blank. To solve this activity, students only need to use their concept image of a figure with vertical symmetry to visualize the colors of the blank tiles (VH 1). To solve the activity, students do not need to use equidistance or perpendicularity with respect to the axis, since there is not explicit connection to the geometrical properties of symmetries, so the cognitive effort necessary to solve it is limited (CD 2).

Activities 1–5 are based on rigid shapes, since their focus are the visual characteristics of symmetrical shapes or pairs of shapes, so students do not need to move or transform the shapes, but next activities are based on dynamic DGS shapes. Activities 6 and 7 ask students to move the axes of symmetry to position the rectangles (or the houses) in some specific positions (Figure 6 presents the activity 7). To do it, axes have to be translated and rotated. The objective of these of activities is to visually introduce students to the geometrical characteristic of symmetry of equidistance from a figure and its image to the axis. To solve activities 6 and 7, students only need to use the visual aspect of symmetry, without the explicit use of mathematical properties (VH 1) but they have to make some cognitive effort to find the correct positions of the objects, although such effort is limited, since students do not need to use geometrical properties to solve the activities (CD 2).

Activity 10 (Figure 3), like other activities along the e-book, poses students a set of multichoice questions to assess the knowledge they have acquired in the previous questions. This activity shows some pairs of congruent or similar figures and asks students to decide if they are symmetrical or not. This activity checks the visual understanding of symmetry gained in the previous nine activities, so answering it requires only visual reasoning (VH 1), without the need of using geometrical properties and having to make a limited cognitive effort (CD 2) to solve it.

Activities 11–13 add to the visualization of pairs of symmetrical shapes and points the measurement of distances to the axis. For instance, activity 13 (Figure 2) shows several pairs of symmetrical points with their distances to the axis of symmetry measured. Students are asked to transform the construction by translating and rotating the axis and to pay attention to the equidistance of symmetrical points from the axis of symmetry. They are also asked about the angles between the axis and segments joining points and their symmetric ones. We have included the tool Angle in the menu to allow students measure angles if they want. These activities intend to move students from the purely visual context of previous activities to a combined visual and geometrical context (VH 2) while maintaining a limited cognitive effort, since students still cannot apply geometrical properties of symmetries, as these are the targets to be discovered (CD 2).

To induce students to apply the properties they should have discovered and learned in the previous activities, activity 14 (Figure 7) asks them to draw by hand (by using only the tool Segment or Polygon) the symmetric to the given polygon. Slow learners may solve the activity by placing the vertices of the symmetric polygon just by sight, putting to work their concept images (VH 1), but we expect that average and m-gifted students will solve it by using their intuitive geometrical knowledge about perpendicularity and equidistance to decide the position of the vertices (basic VH 2). To solve the activity correctly, students have to pay explicit and simultaneous attention to the two required properties (perpendicularity and equidistance), which requires from them a moderately high cognitive effort (CD 3) to be successful.

After activity 14, the mathematical definition of axial symmetry is presented in a verbal style, with the minimum indispensable of geometric symbols, adequate for students reasoning in VH 2. To reinforce the learning and understanding of the definition, the teaching unit includes activities 15 (a video demonstrating properties of symmetries), 16 (a quiz to identify pairs of symmetric shapes or points), and 17–19 asking students to construct symmetric figures or axes of symmetry by using the adequate tools, like Midpoint, Perpendicular Line, or Perpendicular Bisector. The statement of activity 18 (Figure 8) is similar to that of activity 14 (Figure 7), but now students have more elaborated geometrical knowledge, so we expect them to construct the symmetric images by using the properties in the definition of symmetry (advanced VH 2), i.e., by measuring distances and constructing perpendicular lines. The expected correct solutions of activities 14 and 18 require VH 2 reasoning, although the reasoning necessary to solve activity 18 is more sophisticated than the one for activity 14 because students are expected to use consciously and explicitly the characteristic properties of symmetry to choose the tools and construct the symmetric polygon. Furthermore, both activities demand from students level 3 of cognitive demand since students have to use the same geometrical properties and relationships in similar ways.

Activity 20 asks students to compare the graphical representations of two symmetrical points with their axis and a segment with its perpendicular bisector. This activity is aimed to complete the basic knowledge we consider can be acquired by most students in any average classroom. Activity 21 (Figure 9) asks students to draw the axes of symmetry of several pairs of symmetrical shapes. The statement of this activity is similar to that of activity 17, except that the expected solutions are different: In activity 17, students are expected to construct the axis based on the definition of axial symmetry, but in activity 21 they are expected to construct it by using the tool Perpendicular Bisector. Both activities require the sequential use of the adequate geometrical properties, without the need of logical connection between them (VH 2), but students have to understand the meaning of the properties to select the adequate ones and connect the abstract formulation of the properties with the specific application, which requires from them a moderate effort (CD 3).

After activities 22 and 23, focused on learning the relationships between axes of symmetry and perpendicular bisector of regular polygons, activity 24 opens the second part of the teaching unit, devoted to products of and decompositions in pairs of symmetries. The activities are organized into two similar sets, one for parallel axes and the other for intersecting axes. Here we analyze the activities for parallel axes. Before trying to solve these activities, students should be able to visually recognize translations and rotations, and should have learned their definitions, at least operatively, i.e., to know how to apply the characteristic properties of translations and rotations to make those movements with points and polygons; otherwise, a complementary teaching unit about translations and rotations should be necessary before continuing with the e-books. On the other hand, we assume that students have never made a product of movements, so activity 24 has the double aim of introducing students to the concept of product of symmetries and presenting them, as a practical case, the product of parallel axes.

Activity 24 (Figure 10) introduces the concept of product of symmetries. Firstly, it shows the two axes of symmetry, leaf A, and the little square “Image in Line 1”. When the square is clicked, the leaf A’ and the square “Image in Line 1” appear. Students have to click successively on this square and the one appearing next, to finally obtain the construction shown in Figure 10. Then, students are asked to move the axes and analyze the changes in the construction. To solve this activity, students have to follow the steps and finally observe the relationships between the leaves (VH 2). To do it, students are only required to do a limited amount of cognitive effort, since they do not need to be aware of the geometrical properties underlying the graphical manipulations; even they are not asked to abstract such relationships from the dragging of the construction (CD 2), but only to note that leaves A and A’’ are related by a translation. Activities 25 and 26 reinforce the concept of product of symmetries by asking to calculate images of shapes by products of symmetries with parallel axes.

To conclude the set of activities devoted to the product of parallel symmetries, activity 27 first presents a frieze pattern (Figure 11) where students can drag the vertices of the base polygon and rotate and translate the axes of symmetry. The second part of the activity presents a white screen with the same set of axes, and students have to create a base polygon and the other polygons to create their own frieze pattern. To solve this activity, students have to differentiate the role of each axis in creating new copies of the base polygon, but they do not need to make any logical or deductive relationship (VH 2). The solution is quite algorithmic, and requires a limited cognitive effort, since students only need to select adequate shape and axis to create a new copy, they do not need to explicitly use the concept of product of symmetries nor its properties (CD 2).

Activities 28 and 29 are devoted to the product of intersecting axes and have the same organization as activities 24–27, ending with an activity where students are asked to construct some rosette patterns. The introduction of products of two symmetries (activities 24–29) ends with a summary of the discoveries made by presenting to students the mathematical characteristics of the products of two parallel and intersecting symmetries. As for the definition of axial symmetry, we have used a VH 2 language, by presenting a verbal description of the results of the products with two figures representing each product and avoiding the use of geometric symbols in the text. We have not tackled the case of the product of a symmetry with itself (S∘S = I) because we consider that it is too abstract for the target students of the e-book and fully understanding it requires VH 3.

Activities 30 and 31 (32 and 33) focus on the decomposition of a translation (rotation) into a product of two parallel (intersecting) symmetries. Activity 30 (and similarly activity 32) presents a pair of translated polygons, the vector of the translation and a straight line (Figure 12a). The green polygon can be modified and the line can be translated. Students have to use the give straight line to construct a pair of parallel symmetries whose product is equivalent to the given translation. The app offers students a bunch of tools to choose their way to solve the activity, since it can be solved in several ways, with different GeoGebra tools and grades of complexity. We expect that m-gifted students will solve this activity by calculating the symmetric of the green shape with the given axis (Figure 12b) and then constructing the second axis with the tool Perpendicular Bisector (Figure 12c).

Activity 30 requires the use of logical relationships to reverse the steps of calculating the result of a product of two symmetries and also to make some deductions to combine adequately the given axis and the axis to be found (VH 3). This activity demands of students a moderately high cognitive effort, since the activity is new for them and requires the explicit use of properties of symmetries and their product learned in the e-book. However, the axis of symmetry given in the statement connects this activity with activities 24–27, giving students a clue on how to solve the problem (CD 3).

Activity 31 (Figure 13) first states the same question as activity 30, but the data do not include any axis of symmetry nor the vector of translation. Then, when students have found a solution, the activity asks them to think on the possibility of finding another solution. The answer to this question should activate on some m-gifted students the idea that the pair of parallel axes can be placed anywhere in the GeoGebra window, eventually leading them to discover that there are infinite solutions. From the point of view of the Van Hiele levels, this activity requires the same level of reasoning as the previous activity (VH 3). However, the cognitive effort necessary to solve this activity is significantly higher than that of activity 30, since primary and lower secondary students are not used to deal with the infinite. Solving this activity requires from students to produce new ideas that have not been presented, nor even suggested, in previous activities. Furthermore, the statement does not suggest how to solve the problem. Students have to understand, analyze, and use the properties of symmetry and products of symmetries in an original way, by using abstract reasoning to make explicit connections between adequate properties of symmetries (in particular the solution of activity 30) to imagine an innovative way to solve the activity (CD 4).

The teaching unit ends with a quiz about products and decompositions (activity 34) and the final activity 35 asking students to write a summary of the concepts and properties they have learned.

6. Discussion: Analysis of the Mathematical Content of the E-Book

After having analyzed a representative sample of specific activities of the e-book (the whole e-book is available as supplememntary material), in this section we offer a global view of the characteristics of the whole teaching unit from the mathematical and cognitive points of view. We have presented in Section 4.1 the teaching objectives of the e-book, by stating the mathematical contents to be learned. We have also presented in Section 5 (Table 2) the distribution of activities between the objectives.

One of the methodological characteristics of the e-book is that it offers students the possibility of self-regulating their progress by deciding, in some moments, which way continue solving the activities. Figure 14 shows a flow diagram of the whole sequence of activities and the positions and different types of bifurcations.

Some activities may be easy and repetitive for students having a previous knowledge of symmetries or m-gifted students learning fast. This is the case of activity 3 and activities 6–8, making a visual approach to symmetry, so we offer students the possibility to skip those activities if they think that they already recognize symmetries visually. On the contrary, some mathematical contents and the related activities may be difficult for slow learners and even average students. We believe that, in this case, it is convenient that these students do not try solving by themselves the activities that they cannot understand or do not know how to solve, and ask their teachers for help, so the teachers can give them some advice, extra teaching, or decide that it is not necessary that the students try that part of the teaching unit. This is the case of two sets of activities in the second part of the e-book, devoted to learn the product of symmetries (activities 24, 25, and 27B–29) and the decomposition of translations and rotations into products of symmetries (activities 30–34); as we commented in Section 4.1, we designed activities 24–35 as extensions for m-gifted students, but the adequacy of these activities is something to be decided according to the characteristics (mathematical ability, interest, etc.) of each student.

The theoretical framework of this research design is integrated by the Van Hiele levels of reasoning and the levels of cognitive demand. Figure 15 shows (blue dots) the classification of the activities according to the Van Hiele levels of the expected solutions and answers. The table shows an increasing progression in the level of reasoning, from VH 1 for the introductory activities focusing on the visual approach to the symmetry to VH 3 for the activities devoted to the decomposition of translations and rotations. The teaching unit is mainly designed for students in upper primary or lower secondary school, so it is adequate that most activities require from students reasoning in the VH 2, which is the level of reasoning of most students in the mentioned grades.

There are a few exceptions to the increasing progression in the levels of reasoning required by the activities. Activity 34 is a multichoice questionnaire that assess the knowledge students have gained after solving the previous activities. The questions only require identifying the conclusions taken from the activities, without the need of any deductive activity, so VH 2 is sufficient to answer the questionnaire. Similarly, activity 35 asks students to summarize the concepts, properties, and procedures they have learned, so the summaries we expect from most students should be based on level 2 reasoning.

Other kinds of exception are the activities marked in Figure 15 with a red dot. We have analyzed the activities based on the expected solutions, but a few activities may be answered in a different level. As seen in Figure 14, after activity 19, the e-book suggests students to decide how they want to continue: “If activities 18 and 19 have been difficult, please try to solve them again, but using the tool Reflect Object in Line instead of the tools Polygon or Segment. Click here to go to activity 18.” Solving activities 18 (Figure 8) and 19 drawing the symmetric shapes by hand, as asked by their statements, requires VH 2, but solving them with the tool Reflect Object in Line only requires VH 1, since students do not need to use mathematical properties, but only click on the appropriate objects.

The typical answers we expect to activity 20 (described in Section 5) are based on the visual similarity of the figures showed in the e-book representing two symmetrical points with their axis and a segment with its perpendicular bisector, to conclude that the axis of symmetry and the perpendicular bisector are the same line because they are drawn in the same place (VH 2). However, some m-gifted students may pay attention to the mathematical properties characterizing symmetry and perpendicular bisector, to conclude that both lines are the same because they have the same relationship with a pair of points (VH 3). Similarly, the expected solution to activity 21 (Figure 9) is to use the tool Perpendicular Bisector (VH 2), but students having answered in VH 3 the activity 20 could use an ordered sequence of tools (e.g., Segment, Midpoint, and Perpendicular Line) corresponding to the geometrical properties considered in activity 20 (VH 3). These students could also answer activity 35 according to VH 3.

Figure 16 shows the classification of the activities according to their levels of cognitive demand. Activity 15 is not assigned to any level of cognitive demand because it shows a video where the properties of symmetries are summarized, but students do not have any question or problem to solve. Like for the Van Hiele levels, some activities might be solved by m-gifted students with a higher level of cognitive demand. Activity 16 presents a questionnaire showing pairs of points or shapes and asking students to decide if they are symmetric respect to the showed line. We expect that students will base their answers on visual analysis of the figures (CD 2), but some m-gifted students might answer by referring to the properties of equidistance or perpendicularity (CD 3). With respect to activity 20, the same arguments we explained in the previous paragraph are valid to justify that we expect answers with CD 2, but some students could work with CD 3.

The diagram in Figure 16 shows a global progressive increment in the level of cognitive demand required to solve the activities, but, locally, an oscillation back and forth along the teaching unit. This is typical of teaching units where new mathematical contents are introduced since each new content requires opening activities in the lower levels of cognitive demand. In our case, also the activities consisting of watching videos (4 and 15) or answering questionnaires (10, 16, and 34) require lower levels of cognitive demand than the activities before or after these ones. The case is different from activity 24, because this activity is the beginning of a set of activities with new learning objectives (product of symmetries and decomposition of translations and rotations). We observe that activities 14–23 have the learning objective of introducing and reinforcing the definition of axial symmetry and, as analyzed in Section 5, most of these activities require from students’ cognitive effort in CD 3. However, activities 24–29 introduce from scratch the product of two symmetries, by means of quite automatic and simple manipulations in GeoGebra apps only requiring CD 2. Next, activities 30 and 31 (Figure 12 and Figure 13) introduce the decomposition of translations in symmetries with increasing levels of cognitive demand, as analyzed in Section 5 (and similarly activities 32 and 33 for rotations).

Figure 17 shows the graphs in Figure 15 and Figure 16 superimposed. By doing it we do not pretend to identify Van Hiele level n and the level n of cognitive demand, but to show at the same time the information transmitted by each analysis of the teaching unit and to make a networked analysis of the activities according to both the Van Hiele levels of reasoning and the levels of cognitive demand.

Some results can be derived from the analysis of this graph. The most important and interesting one is that the graph shows that style of mathematical reasoning and cognitive demand are independent components of students’ cognitive activity when solving mathematical problems. The Van Hiele levels of mathematical reasoning refer to the “distance” between the mathematical reasoning used by a student to solve a problem and mathematicians’ way of reasoning. The cognitive demand refers to the intensity and complexity, of a student’s mathematical reasoning while solving a problem. A student’s level of reasoning is independent on that student’s characteristics like age, school grade, contents learned, etc., but the cognitive demand is relative to those student’s characteristics: young primary school students may make highly cognitive demanding reasoning although they are just reasoning in the visual VH 1 or solving elementary arithmetic problems, but undergraduate students or mathematicians may make formal reasoning in VH 4 to solve a problem while needing low cognitive demand because the problem is quite rutinary for them.

Related to the previous result is that, in the context of a teaching unit or a sequence of problems, the required level of cognitive demand may be quite variable, while the Van Hiele level of reasoning to be used in the solution may be constant. In our case, the requirement of students’ cognitive demand of the activities varied quite often, depending on their learning objective, but the level of reasoning needed to solve the activities was usually constant in each set of activities.

Then, we argue that analyzing geometrical problems or teaching units and the corresponding students’ outcomes will be much richer if we take simultaneously into consideration the different perspectives offered by the levels of cognitive demand and the Van Hiele levels of reasoning.

7. Final Remarks

In this paper we have presented a teaching unit for plane symmetries, implemented in an interactive e-book and adequate for students without previous school experience with symmetries. The teaching unit is based on the guided discovery by problem solving teaching methodology and the sequence of activities leads students to progress in the learning of visual and mathematical characteristics of symmetries. The first part of the teaching unit is aimed to be adequate for all students in regular classrooms and the second part is more adequate for more capable students, especially mathematically-gifted students, who can handle more complex properties.

The research objective is to analyze the structure and contents of the teaching unit to assess its adequacy for the mentioned grades and the m-gifted students. The analysis we have made is based on a particularization to the plane symmetries of the models of the Van Hiele levels [40,62,82] and the levels of cognitive demand [28,69]. We have used the methodology of networking theories [22], making a simultaneous analysis with both theories and integrating the results and conclusions derived from each theory.

The analysis made suggests that the design of this e-book is coherent with the intention of producing a sequence of increasingly complex problems that helps all students progress to learn the basic mathematical and practical properties of plane symmetries and allows m-gifted students to gain a deeper and more complete knowledge of the topic (low threshold and high ceiling [54]).

The analysis made also proves that the networking of the Van Hiele levels and the levels of cognitive demand is adequate and useful, since it shows that these models are different but compatible, as they provide different and complementary views of the characteristics of each activity and the whole teaching unit.

A limitation of the study is that the analysis presented is theoretical, since we made a piloting with m-gifted students, but the data obtained were not rich enough to be used as support of this analysis. Thus, future objectives are to make new experiments to obtain complete information of students’ solutions, analyze those data, and compare the theoretical analysis presented in this paper with the analysis of the real solutions.