Incremental Minimum Flow Algorithms

Abstract

There are various situations in which real-world problems can be modeled and solved as minimum flow problems. Sometimes, in these situations, minor data changes may occur, leading to corresponding changes of the networks in which the practical problems are modeled as flow problems, such as slight variations in capacity or lower bound. For instance, the capacity or the lower bound of an arc may increase or decrease in time, leaving one with no other choice than finding the new minimum network flow. Given both the various ways in which the networks can be changed and the high frequency of these changes, it is desirable to find as fast a computation method for minimum flow as possible. This paper is focused on the cases that concern increasing and decreasing the capacity or the lower bound of an arc. For these cases, both the minimum flow algorithms and the dynamic minimum flow algorithms that are already known are inefficient. Our incremental algorithms for determining minimum flow in the modified network are more efficient than both the above-mentioned types of algorithms. The proposed method starts from the initial network minimum flow and solves the minimum flow problem in a significantly faster way than recalculating the new network minimum flow starting from scratch.

1. Introduction

The complexity of the network flow field determines the occurrence of a wide range of optimization methods corresponding to specific network flow problems. Over the past 70 years researchers have delivered more and more efficient algorithms for solving several classes of problems. Starting from the 1950s, researchers designed many of the fundamental network flow algorithms, including methods for maximum flow [1,2,3,4,5,6] and minimum cost flow problems [1,2]. In the decades that followed, there were many research contributions concerning the improvement of the computational complexity of network flow algorithms by using enhanced data structures, techniques of scaling the problem data, etc.

There is, however, another kind of network flow problem, which has its own applications, often of high importance, but not dealt within such an extended manner as deserved: the minimum flow problem. Several algorithms [7,8,9,10,11,12,13,14] were developed for solving the minimum flow problem (in a static manner) and a few others for the minimum dynamic flow problem [15,16]. Nevertheless, the in between case, in which just a small change in network data occurs, has never been studied before. For instance, the capacity or the lower bound of a given arc may increase or decrease in time as a singular difference from a network in which a minimum flow was previously determined. The algorithms developed in this paper are especially designed for these cases.

Among real-life applications of the minimum flow problem, one can identify two main types: the direct applications and the indirect ones. The direct applications include various forms of flows that are demanded in a minimum amount in order to maintain certain environmental (for instance) parameters or even to preserve the integrity of the network itself. For example, methods to maintain a minimum temperature in a facility or to eliminate the risk of network freezing. An example of a minor data change that may occur is the sudden temperature drop in one of the rooms that is crossed by a technological fluid pipe, increasing the freezing risk. Modeling the HVAC (Heating Ventilation and Air Conditioning) networks, electrical networks, water supply networks, food webs and any other direct applications (for instance, transportation and communication systems described in [7]) as minimum network flow problems is very intuitive and easy to understand. On the other hand, there are the indirect applications, which at first sight have nothing to do with the minimum network flow, but can be efficiently modeled as one. In [11,15] is described the following machine setup problem. A team of workers needs to perform a number of tasks (p) in a particular day. For each task i, the starting time τ(i) and the ending time τ’(i) are known, for i = 1, 2, … , p. Additionally, a setup time τ₂(i, j) is necessary for a worker to switch from task i to task j. A particular worker must not work on more than one particular task at the same time and one particular task must be fulfilled by a single worker. The problem is to find the minimum number of workers to perform the required tasks according to the above rules. The problem can be formulated as a minimum flow problem in a network, where the value of the minimum flow is the minimum number of needed workers.

Because they arise in real life, applications of both types might be subject to data modifications. Some of these modifications will lead to small differences from the initial network through which the problem prior to the modifications was modeled and solved as a minimum flow problem. This paper presents especially designed algorithms for these cases, too.

We consider the directed network G = (N, A, l, c, s, t), where N is a set containing n nodes, A is a set with m arcs, l and c are two functions that confer to each arc (i, j) its nonnegative lower bound l(i, j) and its nonnegative capacity c(i, j), respectively. We assume that both the capacities and the lower bounds are nonnegative integers. There are two special nodes in the network G: the source node s and the sink node t.

A minimum flow is a function f:A →R+ satisfying the next conditions:

minimize v

(1)

$$\mathrm{f}\left(\mathrm{i}, \mathrm{N}\right)- \mathrm{f}\left(\mathrm{N}, \mathrm{i}\right)=\{\begin{array}{ll}\mathrm{v},& \mathrm{i} = \mathrm{s}\\ 0,& \mathrm{i} \ne \mathrm{s},\mathrm{t}\\ -\mathrm{v},& \mathrm{i} = \mathrm{t}\end{array}$$

(2)

l(i, j) ≤ f(i, j) ≤ c(i, j), (i, j)∈A

(3)

We denoted by $\mathrm{f}\left(\mathrm{i}, \mathrm{N}\right)$ the total outgoing flow from node i and by $\mathrm{f}\left(\mathrm{N}, \mathrm{i}\right)$ the total incoming flow into node i, for any node I∈N. Formally,

$$\mathrm{f}\left(\mathrm{i}, \mathrm{N}\right)={{\displaystyle \sum }}_{\mathrm{j}|\left(\mathrm{i}, \mathrm{j}\right)\in \mathrm{A}}^{}\mathrm{f}\left(\mathrm{i},\mathrm{j}\right), \mathrm{I} \in \mathrm{N} \mathrm{and} \mathrm{f}\left(\mathrm{N}, \mathrm{i}\right)={{\displaystyle \sum }}_{\mathrm{j}|\left(\mathrm{j}, \mathrm{i}\right)\in \mathrm{A}}^{}\mathrm{f}\left(\mathrm{j},\mathrm{i}\right), \mathrm{I}\in \mathrm{N}.$$

We refer to v as the value of the flow f.

Equation (2) are referred to as mass balance constraints. They state that for any node other than the source node and the sink node, the total outgoing flow equals the total incoming flow. Consequently, all the flow leaving the source node s reaches the sink node t.

Equation (3) are boundary constraints and they state that the flow on each arc is upper-bounded by the arc capacity and lower-bounded by the lower bound of the arc.

A function f:A → R+ that satisfies only conditions (2) and (3) is named a feasible flow or, shortly, a flow.

Consequently, a minimum flow is a flow f for which its value v is minimized.

A preflow is a function f:A → R+ satisfying (3) and the next conditions:

f(N, i) − f(i, N) ≥ 0, i≠ s,t

Let f be a preflow. As in [16], we define the excess of a node i∈N in the following manner:

e(i) = f(N, i) − f(i, N)

Thus, for any preflow f, we have e(i) ≥ 0, i∈N\{s, t}.

We say that a node i∈N\{s, t} is active if e(i) > 0 and balanced if e(i) = 0.

A preflow f for which

e(i) = 0, for each i∈N\{s, t}

is a flow. Consequently, a flow is a particular case of preflow.

A pseudoflow [16] is a function f: A → R+ satisfying only conditions (3)

For any pseudoflow f, we define, as in [16], the imbalance of node i as e(i) = f(N, i) − f(i, N), for all i∈N. If e(i) > 0 for some node i, we refer to e(i) as the excess of node i; if e(i) < 0, we refer to e(i) as the deficit of node i. If e(i) = 0 for some node i, we refer to node i as balanced. Consequently, a preflow is a particular case of pseudoflow.

For the minimum flow problem, the residual capacity r(i, j) of any arc (i, j)∈A, with respect to a given pseudoflow f, is given, as in [16], by

r(i, j) = f(i, j) − l(i, j) + c(j, i) − f(j, i)

By convention, if (i, j) ∈ A and (j, i) ∉ A, then we add the arc (j, i) to the set of arcs A and we set its lower bound l(j, i) = 0 and its capacity c(j, i) = 0.

The residual capacity r(i, j) of the arc (i, j) represents the maximum amount of flow from the node i to node j that can be canceled by adjusting the flow on both of the arcs(i, j) and (j, i).

The network G(f) = (N, A(f)) consisting only of those arcs with strictly positive residual capacity is named the residual network (with respect to the given pseudoflow f).

A directed path from the source node s to the sink node t in the residual network G(f) = (N, A(f)) is called a decreasing path.

The minimum flow problem in a network can be solved in two phases ([16]):

• determining a feasible flow, if there is one;
• from a given feasible flow, finding a minimum flow.

The first phase, i.e., the problem of determining a feasible flow, can be reduced to a maximum flow problem (for details see [1]).

For the second phase of the minimum flow problem there are three approaches:

• using decreasing path algorithms [11,12];
• using preflow algorithms [7,8,11,12,13,14,17,18];
• using minimax algorithms which consists of finding a maximum flow from the sink node to the source node in the residual network [10].

There are several types of problems that can be modeled and solved as minimum flow problems in networks. Sometimes the network in which we need to determine a minimum flow differs from a network in which a minimum flow is already known only by an arc capacity or a lower bound (which is reduced or augmented by a units). For instance, in the machine setup problem described above, the value of τ(i), τ′(i) or τ ₂(i, j) for some i (and j) might be modified. In this case and in other cases like this one, neither the minimum flow algorithms [7,8,9,10,11,12,13,14], nor the minimum dynamic flow algorithms [15,19] are efficient. The algorithms that we develop are especially designed for these cases.

The rest of the paper is dedicated to the study of the following four problems: minimum flow problem in a network with an underestimated lower bound (Section 2), minimum flow problem in a network with an overestimated lower bound (Section 3), minimum flow problem in a network with an overestimated capacity (Section 4) and minimum flow problem in a network with an underestimated capacity (Section 5), and it ends with some conclusions.

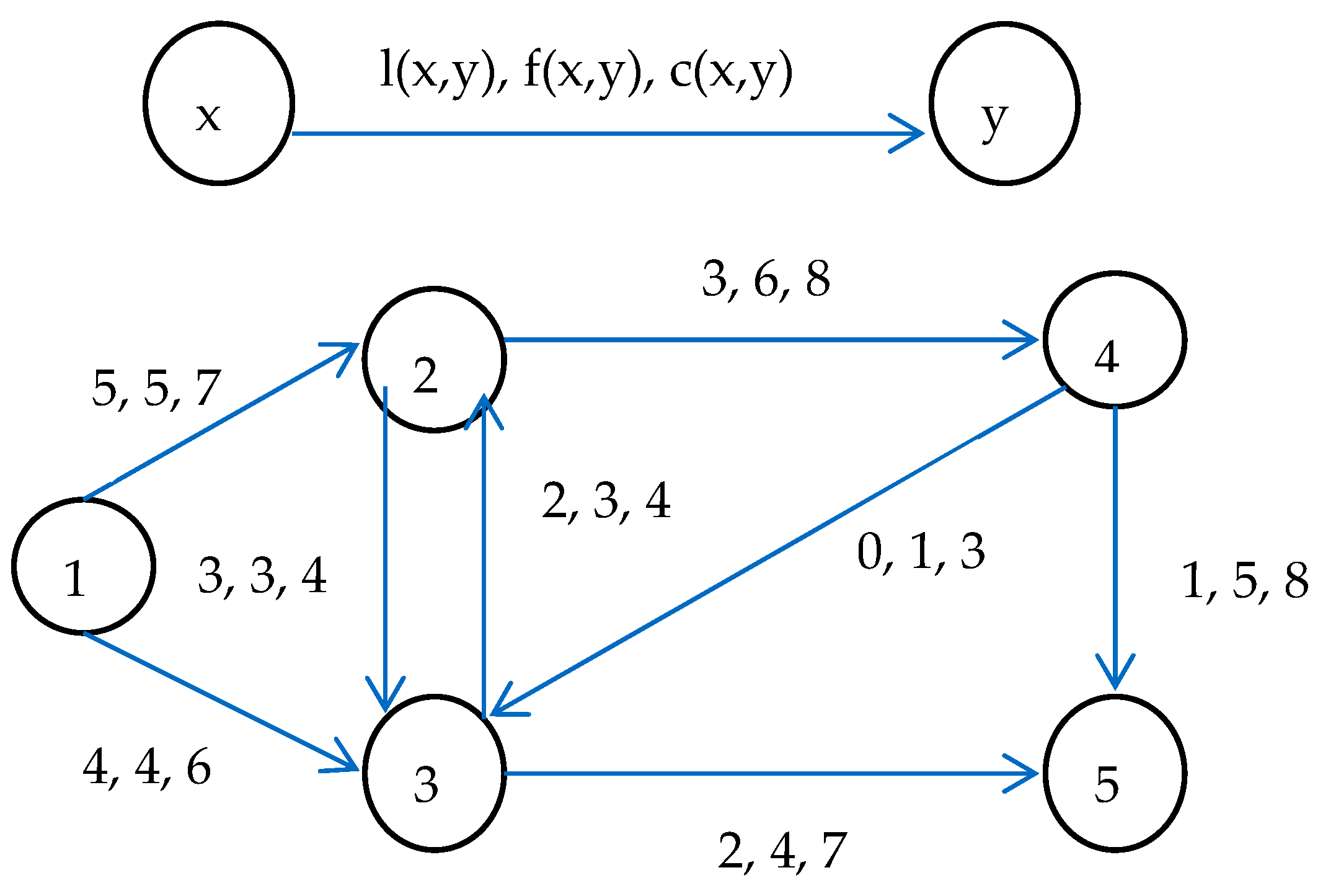
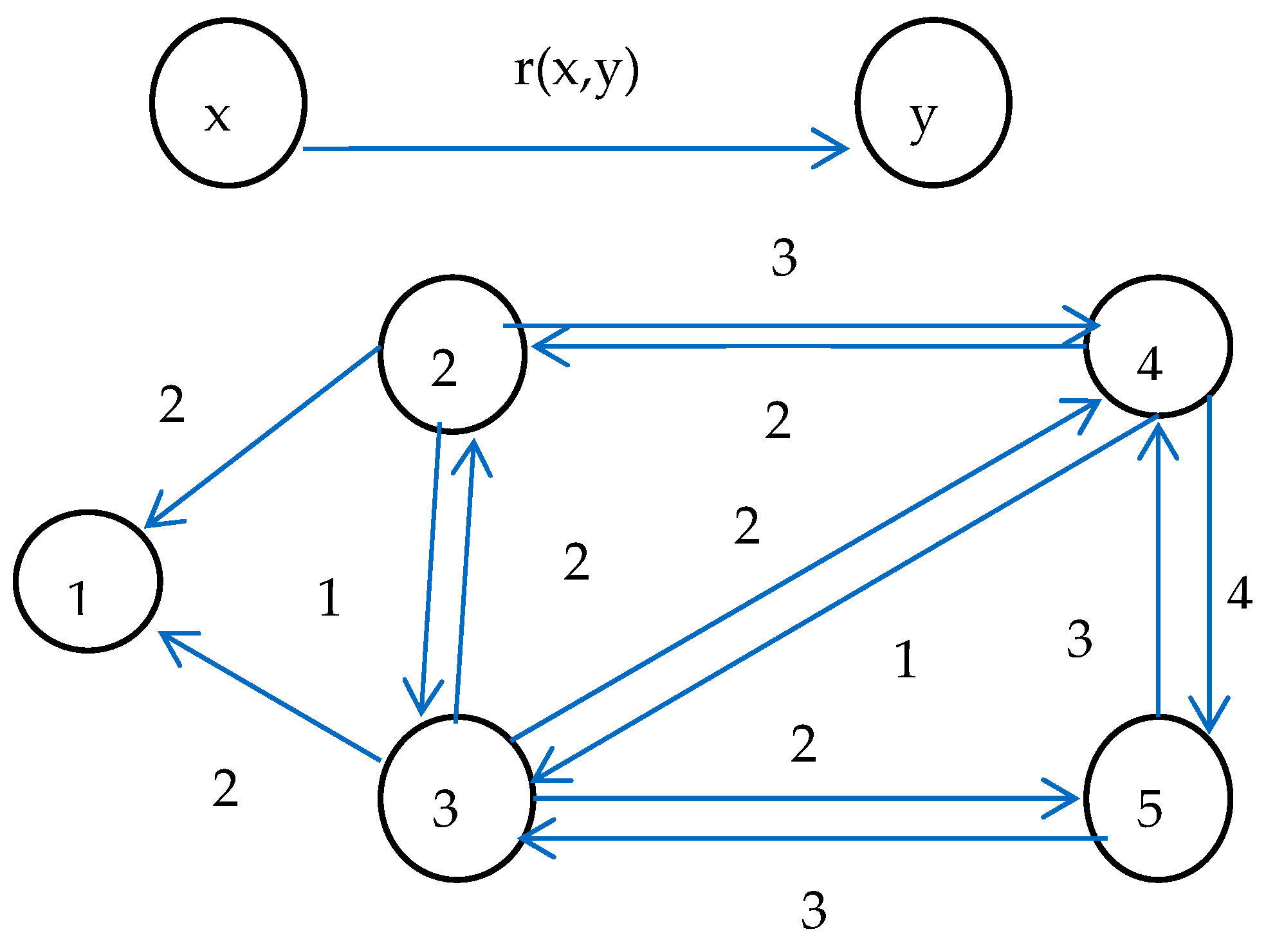
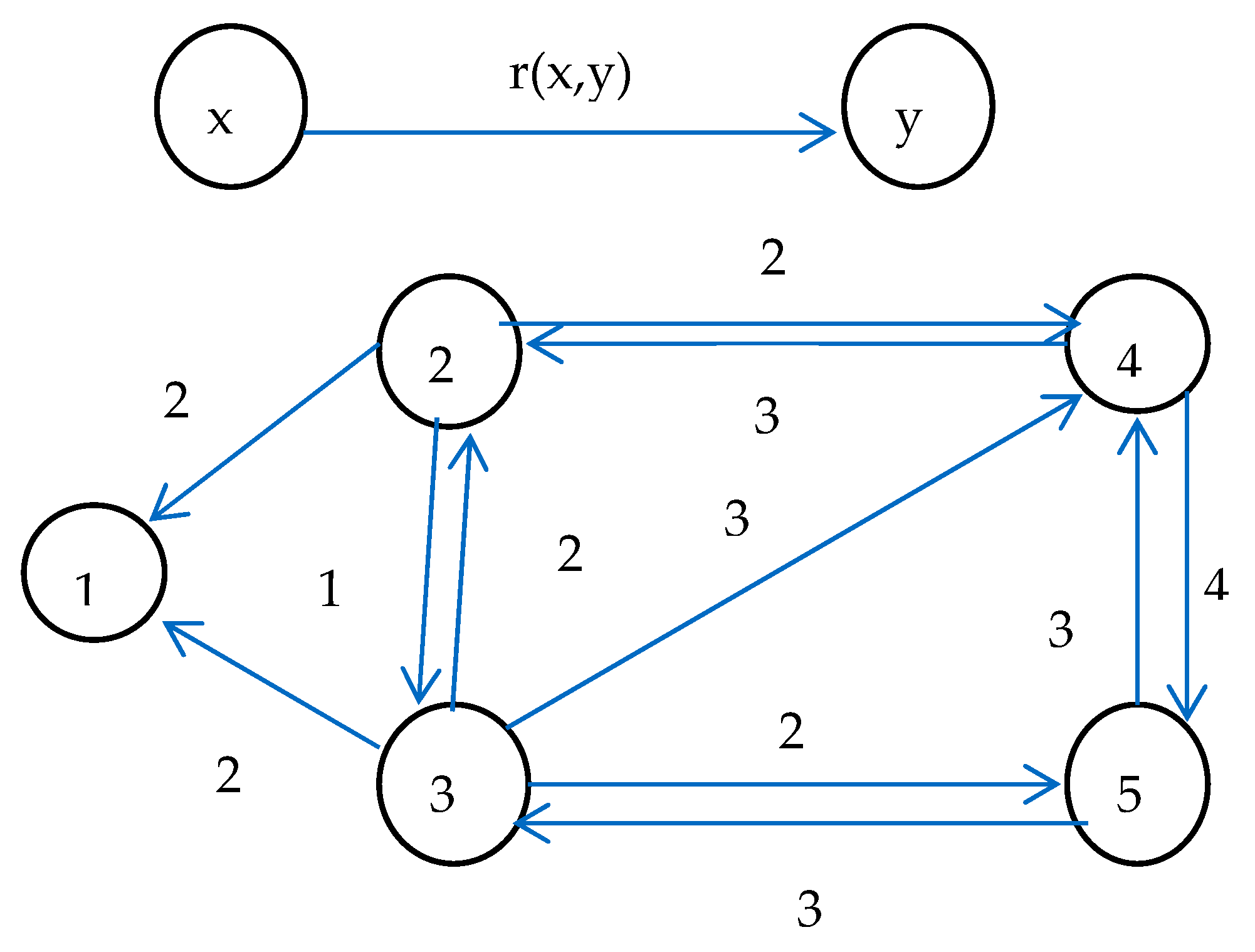
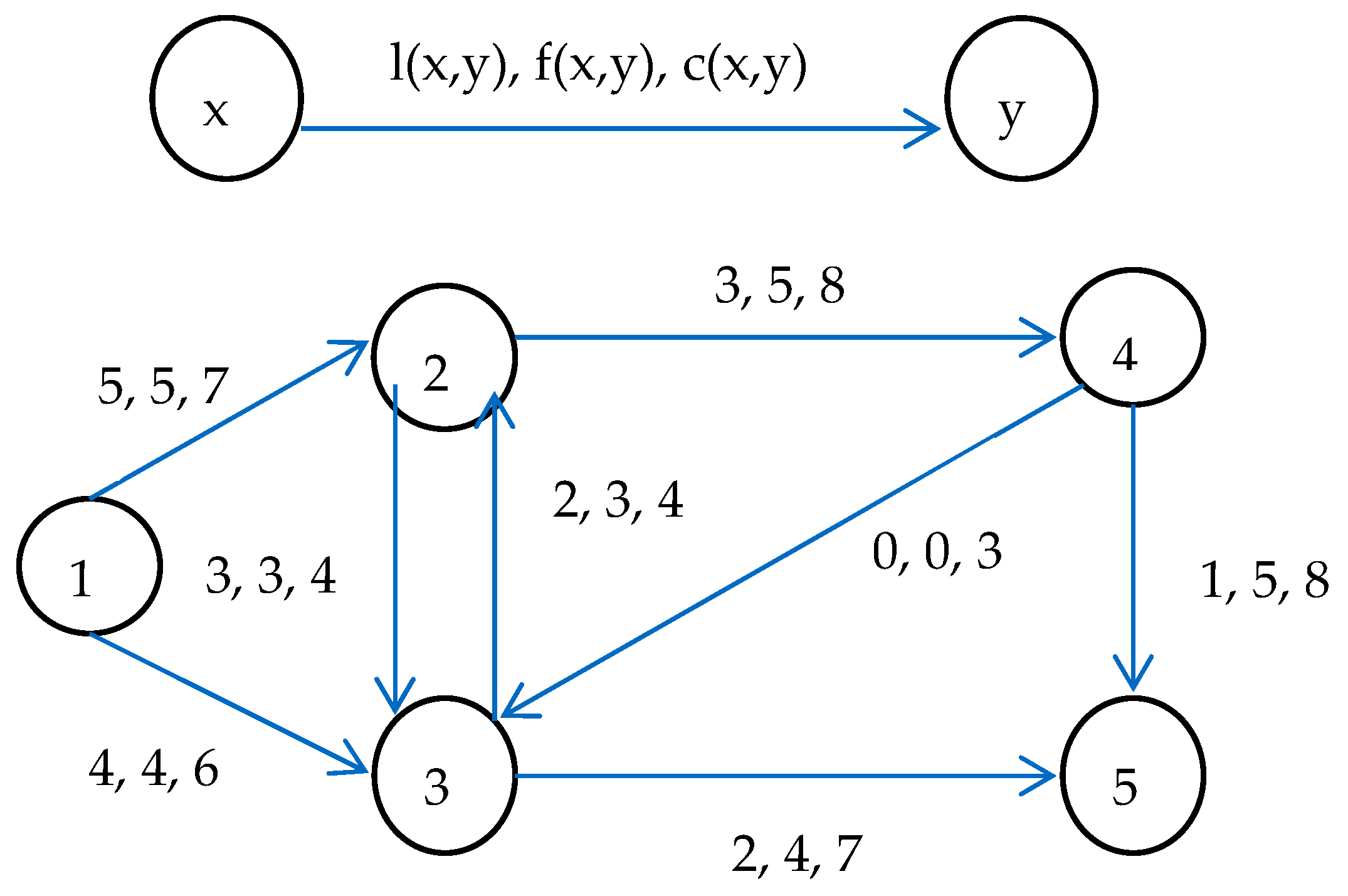
2. Determining a Minimum Flow in a Network with an Underestimated Lower Bound

In the following we will study the problem of determining a minimum flow in a network when increasing the lower bound of the arc (x, y) by a units (a > 0).

Let G = (N, A, l, c, s, t) be a network in which a minimum flow f is already determined. Let (x, y) be an arbitrary arc of G, whose endpoints are intermediate nodes and whose lower bound has been increased by a units. In this way we obtain the network G’ = (N, A, l’, c, s, t), where:

l’(i, j) = l(i, j), ∀(i,j)∈A\{(x, y)}

l’(x, y) = l(x, y) + a

There are two cases that might occur:

• f(x, y) ≥ l’(x, y). In this case fis, obviously, also a minimum flow in the network G’;
• f(x, y) < l’(x, y). In this case, b denotes the difference l’(x, y) − f(x, y) and we set f(x, y) = l’(x, y), creating in this way a deficit equal to -b in node x and an excess equal to b in node y. Hence, now f is a pseudoflow. Firstly, the algorithm will try to decrease the flow along directed paths from node x to node t and along directed paths from node s to node y in the residual network, decreasing in this way the absolute value of the deficit of node x, the excess of node t, the absolute value of the deficit of node s and the excess of node y by the same amount. If both nodes x and y become inactive, then the pseudoflow becomes a flow, which, moreover, is a minimum flow, whose value is by b units smaller than the value of the flow f; otherwise the algorithm will try to decrease the flow along directed paths from node x to node y in the residual network, decreasing the absolute value of the deficit of node x and the excess of node y by the same amount. If both of them become 0, then the pseudoflow becomes a flow, which is a minimum flow, whose value is by b units smaller than the value of the initial flow f. If the deficit of node x still remains nonzero, its absolute value can be further reduced by decreasing theflow along directed paths from x to s (if there are any), which also increases the absolute value of the deficit of node s. It is possible that the deficit of node x remains strictly negative after all these decreases. This occurs when the network G’ contains no feasible flow. If the deficit of node x becomes 0, then, to suppress the remaining excess of node y, the algorithm will decrease the flow along directed paths from t to y (if there are any), which also increases the excess of node t. Again, after all these flow decreases, the node y could still be active. This happens when the network G’ contains no feasible flow. Consequently, if there is a feasible flow in the modified network, G’, then the value of the minimum flow in G’ might be smaller than, larger than or the same as the value of the minimum flow in G.

The algorithm takes as inputs a network G and a minimum flow f in G. The algorithm output is either a minimum flow in the network G’, which differs from G only by the lower bound of a given arc (x, y), if there is a feasible one, or the message “There is no feasible flow in G’.”, if there is not.

• Underestimated Lower Bound Algorithm;
• Begin
• let f be a minimum flow in the network G;
• determine the network G’;
• if f(x, y) < l’(x, y) then
• begin
•  f(x, y) = l’(x, y);
•  determine the residual network G’(f);
•  while e(x) < 0 and there is a directed path from x to t in G’(f) and e(y) > 0 and there is a directed path from s to y in G’(f) do begin
•   determine a directed path D from x to t in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   determine a directed path D’ from s to y in G’(f);
•   r(D’) = min{r(i, j) | (i, j) ∈D’};
•   u = min{-e(x), r(D), e(y), r(D’)};
•   pull u units of flow from x to t along the path D;
•   pull u units of flow from s to y along the path D’;
•  end;
•  while e(x) < 0 and e(y) > 0 and there is a directed path from x to y in G’(f) do begin
•   determine a directed path D from x to y in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   pull min{−e(x), e(y), r(D)} units of flow from x to y along the path D;
•  end;
•  while e(x) < 0 and there is a directed path from x to s in G’(f) do begin
•   determine a directed path D from x to s in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   pull min{−e(x), r(D)} units of flow from x to s along the path D;
•  end;
•  if e(x) < 0 then write “There is no feasible flow in G’.”
•  else begin
•   while e(y) >0 and there is a directed path from t to y in G’(f) do begin
•   determine a directed path D from t to y in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   pull min{e(y), r(D)} units of flow from t to y along the path D;
•   end;
•   if e(y) > 0 then write “There is no feasible flow in G’.”
•  end;
• end;
• else write “The minimum flow f in G is also a minimum flow in G’.”
• end.

Theorem 1. (Correctness Theorem)

If there is a feasible flow in the network G’, then the Underestimated Lower Bound Algorithm correctly determines a minimum flow.

Proof. 

The algorithm starts with a pseudoflow obtained from the minimum flow f in the network G by setting the flow on the arc (x, y) equal to l’(x, y), creating, in this way, a deficit of –b units in the node x and an excess of b units in the node y. First, by decreasing the flow along directed paths from x to t and along directed paths from s to y, the algorithm simultaneously decreases the absolute value of the deficit of nodes s and x and the excess of nodes y and t. If, at this point, both nodes x and y become inactive, it means that the pseudoflow becomes a flow, which is a minimum flow in G’, whose value is by b units smaller than the value of the minimum flow in G. If the nodes x and y are still active, the algorithm will decrease the flow along directed paths from x to y, which leads to decreasing both the absolute value of the deficit of node x and the excess of the node y, while leaving the deficit of s and the excess of t unchanged. This implies that, if at this point both nodes x and y become inactive, a minimum flow in G’ is obtained and, moreover, its value is by b units smaller than the value of the minimum flow in G.If node x is still active and if there are directed paths from x to s, the algorithm identifies them and pulls flow along them, decreasing the absolute value of the deficit of x and increasing the absolute value of the deficit of the source node s. If the node x still remains active, but the residual networks contain no such paths, it means that the modified network does not contain a feasible flow. If the node x becomes balanced, but the node y is still active, then the algorithm will pull flow along directed paths from t to y until either y becomes also balanced, which means that a minimum flow is established, orthere are no more such paths, which happens when there is no feasible flow in the modified network.□

Remark. 

In order to transform the pseudoflow into a flow, the algorithm decreases the flow along five types of directed paths: from x to t, from s to y, from x to y, from x to s and from t to y. Decreasing the flow along all these directed paths reduces the absolute value of the deficit of node x and/or the excess of node y. Decreasing the flow along four out of these five types of paths also affects the flow outgoing from the source node and the flow incoming into the sink node, i.e., the value of the flow, which is decreased by using the first two types of paths and which is increased by using the last two types of paths. Consequently, decreasing the flow along these types of paths in this particular order guarantees a minimum flow, if there is one.

Theorem 2. (Complexity Theorem)

If there is a feasible flow in the network G’, then the Underestimated Lower Bound Algorithm determines a minimum flow in O(am).

Proof. 

Each flow decrease along a directed path in the residual network means that the absolute value of the deficit of node x and/or the excess of node y decrease/s by at least 1 unit, because both the capacities and the lower bounds are assumed to be nonnegative integers. At the beginning of the algorithm they are both equal to b, which is at most a. It follows that, after at most 2a flow decreases along directed paths in G’(f), the algorithm ends with a minimum flow in G’, if there is a feasible flow in the network G’. Since identifying a decreasing path means performing a graph search in the residual network, it follows that our algorithm runs in O(am) time. □

In the following, we will illustrate how the algorithm works using the network represented in Figure 1, where a minimum flow of value 9 is already determined.

The modified network G’ is derived from G by increasing the lower bound of the arc (x, y) = (2, 3) by one unit. In order to meet the boundary constraints (3) for the arc (2, 3), in the first step, the algorithm sets the flow on this arc equal to its new lower bound and obtains a pseudoflow in the modified network G’, which is depicted in Figure 2. In this network the node 2 has a deficit of one unit and the node 3 has an excess of one unit.

In the residual network corresponding to the initial pseudoflow presented in Figure 3, there are directed paths from x = 2 to t = 5, but there are not directed paths from s = 1 to y = 3. Consequently, the algorithm starts looking for paths from x = 2 to y = 3. There are several such paths. Assuming that it finds the directed path D = (2, 4, 3), it then determines its residual capacity, r(D) = 1, and it pulls one unit of flow along D, obtaining the residual network depicted in Figure 4, where both of the nodes 2 and 3 are balanced. This means that the pseudoflow is now a flow, which, moreover, is a minimum flow in G’, having the same value as the minimum flow in the initial network G.

The minimum flow of value 9 in the modified network is represented in Figure 5.

Remark 1.

If we search for the types of the paths in a different order than the one specified by the algorithm, we will obtain a flow which is not a minimum flow. For example, if we look for the paths from x to y after pulling flow along all the other available types of paths, we could pull one unit of flow along the path D = (2, 1) from x = 2 to s = 1, then one unit of flow along the path D = (5, 3) from t = 5 to y = 3, balancing both the nodes 2 and 3 and obtaining the residual network depicted in Figure 6. This residual network corresponds to the flow of value 10 (represented in Figure 7), which, obviously, is not a minimum flow.

3. Determining a Minimum Flow in a Network with an Overestimated Lower Bound

Next, we will study the minimum flow problem in a network, after decreasing the lower bound of the arc (x, y) by a units (a > 0).

Let G = (N, A, l, c, s, t) be a network in which a minimum flow f is already determined. Let (x, y) be an arbitrary arc of G, whose endpoints are intermediate nodes and whose lower bound will be decreased by a units. In this way we obtain the network G’ = (N, A, l’, c, s, t), where:

l’(i, j) = l(i, j), ∀(i,j)∈A\{(x, y)}

l’(x, y) = l(x, y) − a

There are two cases that might appear:

• f (x, y)> l(x, y). In this case fis also a minimum flow in the network G’;
• f (x, y) = l(x, y). In this case, there are two sub-cases:

  ○

  The residual network G(f) contains the arc (x, y).Then, reducing the lower bound of the arc (x, y) does not create a new arc in the residual network G’(f), nor a new decreasing path. Consequently, in this sub-case, f is also a minimum flow in the network G’;

  ○

  The residual network G(f) does not contain the arc (x, y). This implies that by reducing its lower bound by a, the residual network G’(f) will contain an additional arc (x, y), whose residual capacity is equal to a. In this case, the residual network G’(f) is obtained from G(f) by simply adding the arc (x, y), whose residual capacity is equal to a. The addition of the arc (x, y) to the residual network means that it is possible, but not mandatory, that the residual network G’(f) contains decreasing paths along which flow can be pulled. If there are such paths, they will all contain the arc (x, y). If we apply the generic decreasing path algorithm (see [11]) in G’(f), it will perform at most a flow decrease. Since the time complexity of a flow decrease is O(m), it follows that a minimum flow in G’ can be obtained in O(am) time starting with a minimum flow in G. Obviously, in this case, the minimum flow value in G’ might be smaller than the minimum flow value in G.

4. Determining a Minimum Flow in a Network with an Underestimated Arc Capacity

Now we will study the problem of determining a minimum flow in a network when increasing the capacity of the arc (x, y) by a units (a > 0).

Let G = (N, A, l, c, s, t) be a network in which a minimum flow f is already determined. Let (x, y) be an arbitrary arc of G, whose endpoints are intermediate nodes and whose capacity will be increased by a units. In this way we obtain the network G’ = (N, A, l, c’, s, t), where:

c’(i, j) = c(i, j), ∀(i,j)∈A\{(x, y)}

c’(x, y) = c(x, y) + a

There are two cases that might appear:

• f(x, y) < c(x, y). In this case f is also a minimum flow in the network G’;
• f(x, y) = c(x, y). Increasing the capacity of the arc (x, y) will imply increasing the residual capacity of the arc (y, x). Here, there are two sub-cases:

  ○

  The residual network G(f) contains the arc (y, x), which means that increasing the capacity of the arc (x, y) does not create a new arc in the residual network G’(f), nor a new decreasing path. Consequently, in this sub-case, f is also a minimum flow in the network G’;

  ○

  The residual network G(f) does not contain the arc (y, x). This implies that by increasing the capacity of the arc (x, y) by a units, the residual network G’(f) will contain an additional arc, (y, x), whose residual capacity is equal to a. Thus, in this case, the residual network G’(f) is obtained from G(f) by simply adding the arc(y, x), whose residual capacity is equal to a. The addition of the arc (y, x) to the residual network means that it is possible, yet not mandatory, that the residual network G’(f) contains decreasing paths along which flow can be pulled. If there are such paths, they will all contain the arc (y, x). If we apply the generic decreasing path algorithm (see [11]) in G’(f), it will perform at most a flow decrement. Since the time complexity of a flow decrement is O(m), it implies that a minimum flow in G’ can be obtained in O(am) time starting with a minimum flow in G. Obviously, in this case, the minimum flow value in the modified network G’ might be smaller than the minimum flow value in G.

5. Determining a Minimum Flow in a Network with an Overestimated Capacity

Now we will study the problem of determining a minimum flow in a network after decreasing the capacity of the arc (x, y) by a units (a > 0).

Let G = (N, A, l, c, s, t) be a network in which a minimum flow f is already determined. Let (x, y) be an arbitrary arc of G, whose endpoints are intermediate nodes and whose capacity will be decreased by a units. In this way we obtain the network G’ = (N, A, l, c’, s, t), where:

c’(i, j) = c(i, j), ∀(i,j)∈A\{(x, y)}

c’(x, y) = c(x, y) − a

The two cases that might appear are:

• f(x, y) ≤ c’(x, y). In this case fis also a minimum flow in the network G’;
• f(x, y) > c’(x, y). In this case, b denotes the difference f(x, y) − c’(x, y) and we set f(x, y) = c’(x, y), creating in this way an excess equal to b in the node x and a deficit in node y equal to -b. Hence, now f is a pseudoflow. Firstly, the algorithm will try to decrease the flow along directed paths from node s to node x and along directed paths from node y to node t in the residual network, decreasing in this way the absolute value of the deficit of node s, the excess of node x, the absolute value of the deficit of node y and the excess of node t by the same amount. If both nodes x and y become inactive, then the pseudoflow becomes a flow, which, moreover, is a minimum flow, whose value is by b units smaller than the value of the flow f; otherwise the algorithm will try to decrease the flow along directed paths from node y to node x in the residual network, decreasing the excess of node x and the absolute value of the deficit of node y by the same amount. If both of them become 0, then the pseudoflow becomes a flow, which is a minimum flow, whose value is by b units smaller than the value of the initial flow f. If the excess of node x still remains strictly positive, it can be further reduced by decreasing theflow along directed paths from t to x (if there are any), which increases the excess of node t. It is possible that the excess of node x remains strictly positive after all these decreases. This occurs when in the network G’ there is no feasible flow. If the excess of node x became 0, then, to suppress the remaining deficit of node y, the algorithm will decrease the flow along directed paths from y to s (if there any), which increases the absolute value of the deficit of node s. Again, after all these flow decreases, the node y could still be active. This happens when the network G’ contains no feasible flow. Consequently, if there is a feasible flow in the modified network, G’, then the value of the minimum flow in G’ might be smaller than, larger than or the same as the value of the minimum flow in G.

• Overestimated Capacity Algorithm;
• Begin
• let f be a minimum flow in the network G;
• determine the network G’;
• if f(x, y) > c’(x, y) then
• begin
•  f(x, y) = c’(x, y);
•  determine the residual network G’(f);
•  while e(x) > 0 and there is a directed path from s to x in G’(f) and e(y) <0 and there is a directed path from y to t in G’(f) do begin
•   determine a directed path D from s to x in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   determine a directed path D’ from y to t in G’(f);
•   r(D’) = min{r(i, j) | (i, j) ∈D’};
•   u = min{e(x), r(D), −e(y), r(D’)};
•   pull u units of flow from s to x along the path D;
•   pull u units of flow from y to t along the path D’;
•  end;
•   while e(x) > 0 and e(y) < 0 and there is a directed path from y to x in G’(f) do begin
•   determine a directed path D from y to x in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   pull min{e(x), -e(y), r(D)} units of flow from y to x along the path D;
•  end;
•  while e(x) > 0 and there is a directed path from t to x in G’(f) do begin
•   determine a directed path D from t to x in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   pull min{e(x), r(D)} units of flow from t to x along the path D;
•  end;
•  if e(x) > 0 then write “There is no feasible flow in G’.”
•  else begin
•  while e(y) < 0 and there is a directed path from y to s in G’(f) do begin
•   determine a directed path D from y to s in G’(f);
•   r(D) = min{r(i, j) | (i, j) ∈D};
•   pull min{−e(y), r(D)} units of flow from y to s along the path D;
•  end;
•  if e(y) < 0 then write “There is no feasible flow in G’.”
•  end;
• end;
• else write “The minimum flow f in G is also a minimum flow in G’.”
• end.

Theorem 3. (Correctness Theorem)

If there is a feasible flow in the network G’, then the Overestimated Capacity Algorithm correctly determines a minimum flow.

Proof. 

The algorithm starts with a pseudoflow obtained from the minimum flow f in the network G’ by setting the flow on the arc (x, y) equal to c’(x, y), creating in this way an excess of b units in the node x and a deficit of -b units in the node y. First, by decreasing the flow along directed paths from s to x and along directed paths from y to t, the algorithm simultaneously decreases the absolute value of the deficit of nodes s and y and the excess of nodes x and t.If, at this point, both nodes x and y become inactive, it means that the pseudoflow becomes a flow, which is a minimum flow in G’, whose value is by b units smaller than the value of the minimum flow in G. If the nodes x and y are still active, the algorithm will decrease the flow along directed paths from y to x, which leads to decreasing both the excess of node x and the absolute value of the deficit of the node y, while leaving the deficit of s and the excess of t unchanged. This implies that, if at this point both nodes x and y become inactive, a minimum flow in G’ is obtained and, moreover, its value is by b units smaller than the value of the minimum flow in G. If node x is still active and if there are directed paths from t to x, the algorithm identifies them and pulls flow along them, decreasing the excess of x and increasing the excess of the sink node t. If the node x still remains active, but the residual networks contain no such paths, it means that the modified network does not contain a feasible flow. If the node x becomes balanced, but the node y is still active, then the algorithm will pull flow along directed paths from y to s until either y becomes also balanced, which means that a minimum flow is established, or there are no more such paths, which happens when there is no feasible flow in the modified network. □

In order to transform the pseudoflow into a flow, the algorithm decreases the flow along five types of directed paths: from s to x, from y to t, from y to x, from t to x and from y to s. Decreasing the flow along all these directed paths reduces the excess of node x and/or the absolute value of the deficit of node y. Decreasing the flow along four out of these five types of paths also affects the flow outgoing from the source node and the flow incoming into the sink node, i.e., the value of the flow, which is decreased by using the first two types of paths and which is increased by using the last two types of paths. Consequently, decreasing the flow along these types of paths in this particular order guarantees a minimum flow, if there is one.

Theorem 4. (Complexity Theorem)

If there is a feasible flow in the network G’, then the Overestimated Capacity Algorithm determines a minimum flow in O(am).

Proof. 

Each flow decrease along a directed path in the residual network means that the excess of node x and/or the absolute value of the deficit of node y decreases by at least 1 unit because both the capacities and the lower bounds are assumed to be nonnegative integers. At the beginning of the algorithm they are both equal to b, which is at most a. It follows that after at most 2a flow decreases along directed paths in G’(f), the algorithm ends with a minimum flow in G’. Consequently, our algorithm, which is a decreasing path algorithm, runs in O(am) time. □

6. Conclusions

In a time of continuously increasing complexity of computer controlled processes, in which the hardware almost reaches its upper limit level, it is of great importance to find the most efficient computational methods. Among the things that can effectively improve the solution of the minimum flow problem in terms of time, finding and choosing the methods that wisely use resources is of the highest importance.

Real-life situations in which minor changes might occur imply increasing or decreasing a lower bound or a capacity of an arc in the network in which the problem is modeled and solved. In this paper, we studied all four cases (increasing and decreasing the lower bound or the capacity of a given arc) and we developed efficient algorithms that refined the solution of the minimum flow problem starting from the minimum flow in the initial network, in a faster way than any other known method.

Further research might be the study of the following problems: (1) the case in which the lower bound and the capacity of a given arc are simultaneously modified and (2) the case in which not one, but several arcs suffer minor changes, few enough not to justify the use of a dynamic minimum flow algorithm.