Developing a Fuzzy TOPSIS Model Combining MACBETH and Fuzzy Shannon Entropy to Select a Gamification App

Abstract

Due to the important advantages it offers, gamification is one of the fastest-growing industries in the world, and interest from the market and from users continues to grow. This has led to the development of more and more applications aimed at different fields, and in particular the education sector. Choosing the most suitable application is increasingly difficult, and so to solve this problem, our study designed a model which is an innovative combination of fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) with the Measuring Attractiveness by a Categorical Based Evaluation Technique (MACBETH) and Shannon entropy theory, to choose the most suitable gamification application for the Industrial Manufacturing and Organisation Systems course in the degree programmes for Electrical Engineering and Industrial and Automatic Electronics at the Higher Technical School of Industrial Engineering of Ciudad Real, part of the University of Castilla-La Mancha. There is no precedent in the literature that combines MACBETH and fuzzy Shannon entropy to simultaneously consider the subjective and objective weights of criteria to achieve a more accurate model. The objective weights computed from fuzzy Shannon entropy were compared with those calculated from De Luca and Termini entropy and exponential entropy. The validity of the proposed method is tested through the Preference Ranking Organisation METHod for Enrichment of Evaluations (PROMETHEE) II, ELimination and Choice Expressing REality (ELECTRE) III, and fuzzy VIKOR method (VIsekriterijumska optimizacija i KOmpromisno Resenje). The results show that Quizizz is the best option for this course, and it was used in two academic years. There are no precedents in the literature using fuzzy multicriteria decision analysis techniques to select the most suitable gamification application for a degree-level university course.

1. Introduction

Gamification is defined as a process that applies gaming elements to non-game contexts [1,2]. Among the most commonly included game elements are levels, points, memes, quests, leader boards, combat, badges, gifting, boss fights, avatars, social graphs, certificates, and content unlocking [3,4].

Many benefits of the application of gamification to teaching have been described, including by Torres-Toukoumidis et al. [5] and Carnero [6]: it encourages autonomous, rigorous, and methodical working; leads to healthy competition; increases the intrinsic involvement and motivation of the participants, and motivates trying again, as feedback is immediate; improves group dynamics; maintains continuous intellectual activity by interacting constantly with the computer; incorporates fun into learning; uses a high level of interdisciplinarity; combines theory and practice, facilitating knowledge acquisition; increases the use of creativity; promotes interaction with other students; develops search and information selection skills; helps in problem solving, visualising simulations; increases interest in class participation and the number of communication channels between teacher and students; drives connectivity and interoperability in mixed distance-classroom learning; combines the application with other teaching methods; improves academic performance; and modernises the educational landscape in the new digital era [7], given the great importance of digital literacy in the modern world [8]. It also allows students to be surveyed on any aspect related to teaching, or to determine their previous level of knowledge of a subject easily. It facilitates analysis of the results obtained during an academic year and comparison of the results with those of previous years, as well as with other subjects. It facilitates the teachers’ self-assessment of their own teaching and control of attendance of the students [9]. Furthermore, some applications include social media, which allows students to create, share, and exchange content with classmates, and thereby create a sense of community [10]; this goes with the fact that student assessment is undertaken in an innovative way, since the level of knowledge acquisition is measured during the learning process, and not simply given as a final mark. Moreover, gamification provides a source of data on student learning, guaranteeing more effective, accurate, and useful information for teachers, parents, administrators, and public education policy managers [11].

In the literature review carried out on the databases Emerald, MDPI, Hindawi, Proquest, Science Direct, and Scopus using the terms “select app multicriteria”, “education game multicriteria”, and “gamification multicriteria”, the only precedents found were those of Kim [12] and Rajak and Shaw [13]. Kim [12] sets out a model built via AHP to assess three gamification platforms applied to a project in a company located in South Korea using the criteria typical in the selection of business software, such as credibility of supplier, competitiveness of product, continuity of service, etc. in a model designed for business managers. Rajak and Shaw [13] assesses 10 mHealth applications on the market via AHP and fuzzy-TOPSIS, recognising that a suitable framework for assessing the efficacy of mobile applications is not to be found in the literature. Therefore, there is no study in the literature analysing the choice of gamification apps for degree-level university courses with fuzzy multicriteria techniques. However, as recognised in Boneu [14], the selection of the e-learning platform is very important, as it identifies and defines the pedagogical methodologies that can be designed based on the tools and services they offer.

This study describes a method that combines fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) with the Measuring Attractiveness by a Categorical Based Evaluation Technique (MACBETH) approach and fuzzy Shannon entropy for the choice of the most suitable gamification app for the Manufacturing Systems and Industrial Organisation course, taught in the second-year degree programmes of Electrical Engineering and Industrial and Automatic Electronic Engineering at the Higher Technical School of Industrial Engineering at the Ciudad Real campus of the University of Castilla-La Mancha. The objective weights calculated with fuzzy Shannon entropy are compared with those calculated from fuzzy De Luca and Termini entropy and exponential entropy. The feasibility and validity of the proposed method is tested through the Preference Ranking Organisation METHod for Enrichment of Evaluations (PROMETHEE) II, ELimination and Choice Expressing REality (ELECTRE) III and fuzzy VIKOR method (VIsekriterijumska optimizacija i KOmpromisno Resenje)) (some of the methods proposed by the application that recommend the most suitable Multi-Criteria Decision Analysis (MCDA) methods carried out by Wątróbski et al. [15]).

The inclusion of fuzzy logic allows the uncertainties, ambiguities, or indecisions typical of real decision-making processes to be taken into account. The choice of fuzzy TOPSIS rather than other fuzzy multicriteria decision analysis techniques is because it has been shown to be a robust technique for handling complex real-life problems [16] and is widely used in many areas [17]. This is the first study in the literature to integrate the subjective weights from the judgements given by the lecturer who teaches the course, processed using the MACBETH approach, with objective weights based on objective information (fuzzy decision matrix), calculated using fuzzy Shannon entropy. In this way, the deficiencies that occur both in a subjective and an objective approach are overcome. The subjective weighted methods are indeed highly subjective and it is difficult to fully express the effectiveness of the weights in evaluating the criteria. The objective weighted methods can easily lose key information due to the limited sample of measurement data [18]. Subsequently, fuzzy TOPSIS is used to obtain the classification of alternatives. The MACBETH approach was chosen because it provides additional tools for handling ambiguous, imprecise, or inadequate information, or the impossibility of giving precise values. In the literature, fuzzy TOPSIS is usually combined only with the subjective weighting methods AHP or fuzzy AHP to calculate the relative weights of the criteria [19], while fuzzy TOPSIS is used to rank the alternatives; examples of these combinations can be seen in Torfi et al. [20], Amiri [21], Sun [22], Kutlu and Ekmekçioğlu [23], Senthil et al. [24], Beikkhakhian et al. [25], Shaverdi et al. [26], Samanlioglu et al. [27], and Nojavan et al. [28]. This is because the strengths of the two methods are complementary, since while TOPSIS uses two for comparison and better visualisation, AHP gives the weightings of the criteria based on consistency ratio analysis [29]. However, this study chose MACBETH instead of AHP because, although both methods use pairwise comparisons, the scales used by the decision maker to give judgements are different; AHP uses a 9-point ratio scale whereas MACBETH uses an ordinal scale with six semantic values. AHP uses an eigenvalue method for determining the weights, while MACBETH uses linear programming. AHP allows up to 10% inconsistency in the judgements given in each matrix, while MACBETH does not allow any inconsistency [30]. The main advantage of MACBETH is that it provides a complete methodology for ensuring accuracy in the weightings of the criteria, such as the reference levels and the definition of a descriptor associated with each criterion; it also gives the aforementioned tools for including doubts or incomplete knowledge of the decision maker. Furthermore, MACBETH has the advantage of creating quantitative measurement scales based on qualitative judgements by linear programming.

It is difficult, but essential, to determine the most suitable MCDA method for any given problem [31], as none of the methods are perfect, nor can any one method be used for all decision problems [32]. This is an important question that is still being widely discussed in the literature, but to which no answer has yet been found. The reasons may be related to the high level of MCDA methods available, both those specific to certain areas and general-purpose methods [33]. Furthermore, different methods can give different results for the same problem [34], even when the same weights are applied to the criteria. One reason for this is that, at times, the alternatives are very similar and are close to each other. However, it may also come about because each MCDA technique can use weights in the calculations in a different way, because the algorithms are different, the algorithms try to scales the objectives, affecting the already-chosen weights, or because the algorithms introduce extra parameters which affect the classification [15]. Each method may, therefore, assign a different rating, depending on its exact working, and thus the final ranking can vary from one method to another [35]. Since the correct ranking is not known, and so cannot be compared to the results obtained, it is not possible to determine which method to choose [36]. The decision maker thus faces a paradox by which the choice of an MCDA method becomes a decision problem in itself [37,38]. It should also not be forgotten that MCDA methods include subjective information provided by the decision maker, such that a change of decision maker can lead to a change in the solution [32]. The literature agrees that a number of methods should be applied to the same problem, as in the literature review undertaken by Zavadskas et al. [39], which states that there is a significant number of publications that apply comparative analysis of separate MCDA methods (see for example [40,41,42]). If all or most of the methods agree on the first-placed alternative, it may be concluded that this alternative is the most suitable; this, however, does not lead to conclusions about how the behaviour of the methods might be generalised. As a result of this, the choice of methodology, and the framework for assessment of decisions, is a current and future line of research [15,38]. Initially, Guitouni and Martel [43] produced guidelines for the selection of the most suitable MCDA, and Zanakis et al. [34] used 12 measures of similarity of performance to compare the performance of eight MCDA methods. Subsequently, Ishizaka and Nemery [32] show how analysing the required input information (data and parameters), the outcomes (choice, sorting, or partial or complete ranking), and their granularity can be an approach making a choice of the appropriate MCDA method. Saaty and Ergu [38] proposed 16 criteria for evaluating a number of MCDA methods. More recently, Wątróbski et al. [15], set out a guideline for MCDA method selection, independently of the problem domain, taking into account the lack of knowledge about the description of the situation; an online application is also proposed to assist in making this choice at http://www.mcda.it/, accessed on 4 April 2021 [44]. Including a set of properties of the case study described in this paper, this application proposes, from a total of 56 MCDA methods, a group of suitable methods: fuzzy TOPSIS, fuzzy VIKOR, fuzzy AHP, fuzzy Analytic Network Process (ANP), fuzzy AHP + fuzzy TOPSIS, fuzzy ANP + fuzzy TOPSIS, PROMETHEE I, PROMETHEE II, ELECTRE III, ELECTRE TRI, ELECTRE IS, Organization, Rangement Et Synthese De Donnes Relationnelles (ORESTE), etc. The proposed model, combining MACBETH with fuzzy TOPSIS, will be compared with the ranking obtained from applying PROMETHEE II, ELECTRE III, and fuzzy VIKOR.

Shannon entropy was chosen as an objective weighting method because it is a method applied widely and with success in the literature and is a data-based weight-determination technique that computes optimal criteria weights based on the initial decision matrix. Therefore, its use is recognised as enhancing the reliability of results [45]. A comparison was made of the results obtained with objective fuzzy Shannon weights with those computed from fuzzy De Luca and Termini entropy and exponential Pal and Pal entropy.

TurningPoint, Socrative, Quizziz, Mentimeter, and Kahoot! are the apps assessed in this study because they are the ones most commonly used in teaching, they have a free version for the number of students signed up to the course analysed, and they do not place constraints on the number of questions that can be included in questionnaires [46].

The article is laid out as follows. Section 2 contains a review of the literature. Next, the fuzzy TOPSIS methodology is introduced. The model built is then described, with the structuring results, the subjective weighs obtained via the MACBETH approach, and the objective weights computed by fuzzy Shannon entropy, fuzzy De Luca and Termini entropy, and exponential Pal and Pal entropy, with a prior introduction to all methods. The intermediate decision matrices resulting from applying fuzzy TOPSIS are shown below. Finally, the results, the validity of the proposed method, the sensitivity analysis, the conclusions, and future lines of work are set out.

2. Literature Review

There is increasingly powerful evidence of the favourable acceptance of gamification and its effectiveness in promoting highly engaging learning experiences [7,47,48]. For example, Hamari et al. [49], in their literature review, analysed 24 empirical studies in which gamification of education or learning was the most common field of application, and all the studies considered the learning results to be mostly positive, in terms of increased motivation and participation in learning activities and enjoyment. However, some studies bring out the negative effects of greater competition, difficulties in assessing tasks, and the importance of the design characteristics of the application on the results. In their literature review of 93 studies using Kahoot!, Wang and Tahir [50], show that gamification can have a beneficial effect on learning at K-12 and higher education, reducing student anxiety and giving favourable results for attention, confidence, concentration, engagement, enjoyment, motivation, perceived learning, and satisfaction. It also has positive effects from the point of view of teachers, such as increasing their own motivation, ease of use, support for training, assessment of the knowledge of students in real time, stimulating students to express their opinions in class, increasing class participation, or reducing the teacher’s workload. Nevertheless, it also states that there are studies that show little or no effect, and that things such as unreliable internet connections, questions and answers that are difficult to read on projector screens, the impossibility of changing the answers once they have been given, the time pressure to respond, or not having enough time or fear of losing are some of the problems mentioned by students. Licorish et al. [10] note as results of the experiment with Kahoot! that the use of educational games probably minimises distractions and therefore improves the quality of teaching and learning beyond that which comes from the traditional teaching methods. Zainuddin et al. [48], in their experiment with 94 students using Socrative, Quizizz, and iSpring Learn LMS, showed that its application was effective in assessing students’ learning performance, especially with the formative assessments after finishing each unit. Dell et al. [51] describe how the performance of students during the game shows a significant correlation with the marks for the course, and also sees games as fun tools to review course content which, can serve as an effective method of determining students’ understanding, progress, and knowledge. Other authors, such as Knutas et al. [52], Iosup and Epema [53], Laskowski [54], and Dicheva et al. [55] also found improvements in the marks of the participants at all levels of the education system, especially university education [5]. Huang and Hew [56] suggest that university students in Hong Kong were more motivated to do activities using gamification outside class, while Huang et al. [57] worked with pre-degree students and concluded that the group with gamification-enhanced flipped learning was more likely to do pre-class and post-class activities on time, and achieved significantly better marks on the post-course test than those who did not use gamification.

Since the publication of the Gartner [58] and IEEE [59] reports predicting that most companies and organisations would be using gamification in the near future [60], gamification is one of the fastest-growing industries worldwide, with multi-billion-dollar profits, and interest in gamification from the market and from users is still growing [61]. This increasing interest in gamification has led to the production of evermore applications aimed at different fields, such as advertising, commerce, education, environmental behaviour, enterprise resource planning, exercise, intra-organisational communication and activity, government services and public engagement, science, health, marketing, etc. [60]. Gamification applications for the education sector include: Padlet, Blinkist, BookWidgets, Brainscape, Breakout EDU, Cerebriti, Classcraft, Mentimeter, ClassDojo, Arcademics, Coursera, Minecraft: Education Edition, Duolingo, Toovari, Edmodo Gamification, Maven, Quizlet, Goose Chase, Knowre, Tinycards, Kahoot!, keySkillset, Khan Academy, Gimkit, Memrise, Pear Deck, Google Forms and Flubaroo, Play Brighter, Udemy, Quizizz, TEDEd, CodeCombat, The World Peace Game, Trivinet, SoloLearn, Class Realm, Yousician, Edpuzzle, Virtonomics, etc. [62,63,64,65,66]; additionally, a number of applications produced for a less commercial environment or more related to research include StudyAid [67], GamiCAD [68], WeBWorK [69], the online quiz system designed by Snyder and Hartig [70] aimed at medical residents, or the gamification plugin of Domínguez et al. [1] designed as an e-learning platform, and the number of teaching apps is expected to rise considerably in the future [71].

However, the many apps available on the market make it difficult to choose the most suitable one for a particular degree or course, and although there are some studies, like that of Zainuddin et al. [7], that provide a literature review about gamification in the educational domain, and states that the platforms and apps most commonly used in research are: ClassDojo and ClassBadges, Ribbonhero of Microsoft, Rain classroom, Quizbot, Duolingo, Kahoot! and Quizizz, Math Widgets, Google + Communities, and iSpring Learn LMS. Acuña [72] says that FlipQuiz, Quizizz, Socrative, Kahoot, and uLearn Play are the five best applications for university students. Roger et al. [73] state that Kahoot! and Socrative are the two applications most commonly used in teaching, while Plump and LaRosa [74] say that Kahoot! is the most used gamification app, with more than 70 million users [50]. In the statistical study carried out by Göksün and Gürsoy [65], the activities gamified with Kahoot! had a more positive impact on academic performance and student engagement when compared with a control group and another group that did activities with Quizizz. It was seen that the impact of the activities carried out with Quizizz was lower than that of the instruction method used with the control group based both on academic performance and student engagement. [9] points out that the use of TurningPoint in the university subject pharmacology improves the performance of students by increasing their participation in class and fixing the knowledge provided by the teacher, as well as allowing the teacher to know what aspects of the class should be better explained, before taking the concepts as known. TurningPoint has also been used in the Faculty of Economics of the University of Valencia in different subjects and teaching sessions, with the result that 82.8% of students consider that its use in class is useful for the development and understanding of the subject; in addition, the participation of the attendees increased, since more than 90% of them participated in using the tool, and the interaction between the audience and the speakers increased notably [75]. Gokbulut [76] appreciates that Mentimeter actively engage students in classroom activities and enjoy learning as in Kahoot!. However, in Mentimeter, the personal information of the student is not collected or displayed on the teacher’s screen, so participation in class increases and students feel more comfortable, especially those who are less likely to participate due to the influence of cultural factors, gender, shyness, anxiety, or other factors such as speech impediments [77]. In the study carried out in [77], 68% of the students who answered indicated that Mentimeter did not increase learning, but other students, across disciplinary areas, stated that Mentimeter improved content retention and that most of the students increased their learning. A model is thus required that uses multiple criteria, objective and based on the perceptions of teachers and students, to facilitate decision-making in this field.

Contributions in the literature related to the selection of apps in different fields are very few; for example, Basilico et al. [78] analyse mobile apps for diabetes self-care, because the large number makes it difficult for patients who have no tools for judgement to assess them properly. A pictorial identification scheme was developed for diabetes self-care tools, which identifies the strengths and weaknesses of a diabetes self-care app. Similarly in the area of diabetes treatment, Krishnan and Selvam [79] use multiple regression analysis to identify success factors in diabetes smartphone apps. Mao et al. [80] propose a behavioural change technique based on an mHealth App recommendation method to choose the most suitable mHealth apps for users. They do this by codifying information on behavioural change techniques included in each mHealth app and in a similar way for each user. They next developed a prediction model which, together with the AdaBoost algorithm, related behavioural change techniques with a possible user; this then recommends the app with the highest behavioural change technique, matching levels to a possible user. Păsărelu et al. [81] identify 109 apps that analyse assessment, treatment, or both in attention-deficit/hyperactivity disorder. The following information was collected for each app: target population, confidentiality, available language besides English, cost, number of downloads, category, ratings, main purpose, and empirical support and type of developer. Descriptive statistics were produced for each of these categories. Robillard et al. [82] assess mental health apps in terms of availability, readability, and privacy-related content of the privacy policies and terms of agreement. In a field other than medicine, Beck et al. [83] identify 57 apps out of a total 2400 that target direct energy use and include an element of gamification; the apps are then assessed statistically in the categories: gamification components, game elements, and behavioural constructs.

3. Fuzzy TOPSIS

TOPSIS was developed by Hwang and Yoon [84] as a method of choosing the alternatives with the shortest distance to a positive ideal solution (PIS) and the longest distance to a negative ideal solution (NIS). While PIS is the solution preferred by the decision maker, maximises the criteria of the benefit type, and minimises the criteria of cost type, NIS acts in the opposite way. TOPSIS provides a cardinal raking of the alternatives according to the best distance to PIS and the greatest distance to NIS. It also does not matter whether the attributes are independent [85,86]. A broad literature review including 266 studies up to the year 2012 can be seen in Behzadian et al. [87].

Subsequently, Chen [88] adapted TOPSIS to the fuzzy environment. Fuzzy TOPSIS has been widely and successfully used in real-world decision problems [19]. Some examples of these applications can be seen in the literature reviews carried out by Salih et al. [89] and Palczewski and Sałabun [19].

Bottani and Rizzi [90] and Asuquo [17] explain the advantages of choosing fuzzy TOPSIS as a multicriteria technique:

• It is easy to understand;
• It is a realistic compensatory method that can include or exclude alternatives based on hard cut-offs;
• It is easy to add more criteria without the need to start again;
• The mathematical notions behind fuzzy TOPSIS are simple.

However, TOPSIS and fuzzy TOPSIS have some disadvantages, such as rank reversal [91]. That is, ranking changes in the alternatives when an alternative is added to or removed from the hierarchy, and so the validity of the method could be in question. Furthermore, in fuzzy TOPSIS, the problems are related to the fact that there are no consistency and reliability checks, and these aspects are more relevant in decision-making and may lead to misleading results [92]. The assessment of alternatives is also carried out through linguistic expressions, in which the linguistic terms must be quantified within a previously established value scale. The quantifying of qualitative values generally involves translating the standard linguistic terms into values on a previously agreed scale. Therefore, to address problems defined in this way, the uncertain information given by the linguistic terms must be taken into account [93].

Zadeh [94] proposed fuzzy set theory to formulate real decision problems in which alternative ratings and criteria weights cannot be precisely defined, due to the existence of: unquantifiable information, incomplete information, unobtainable information, and partial ignorance [95].

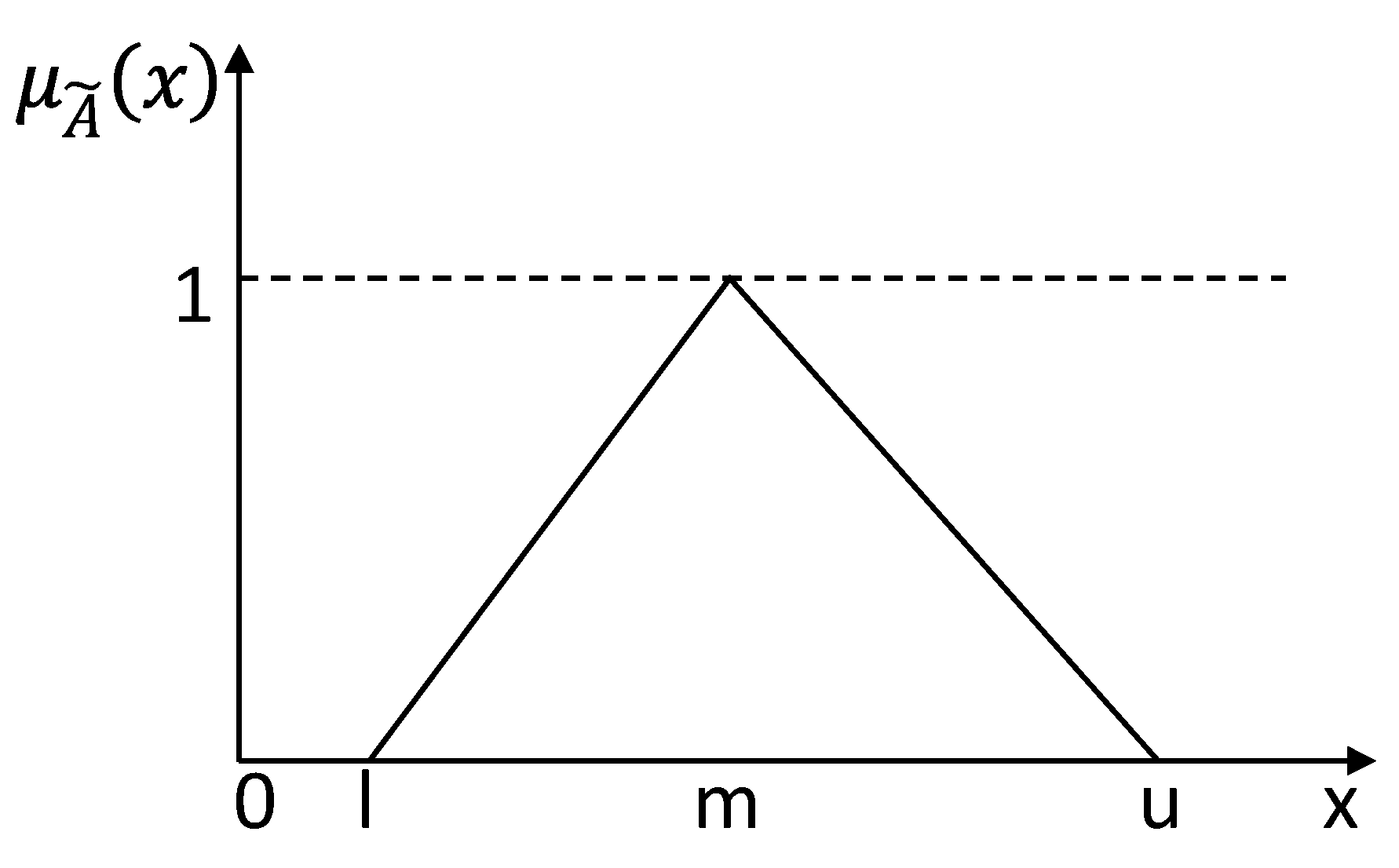
A Triangular Fuzzy Number (TFN) $\tilde{A}$ can be defined as a triplet $\left(l, m, u\right)$ with a membership function ${\mu }_{\tilde{A}}\left(x\right):\Re \stackrel{}{\to }\left[0, 1\right]$, as shown in Equation (1) [88]:

$${\mu }_{\tilde{A}}\left(x\right)=\{\begin{array}{c}0,\\ \left(x-l\right)/\left(m-l\right),\\ \left(x-u\right)/\left(m-u\right),\\ 0,\end{array}\begin{array}{c} \\ \\ \\ \begin{array}{c} \\ \\ \end{array}\end{array}\begin{array}{c}x<l\\ l\le x\le m\\ m\le x\le u\\ x>u\end{array}$$

(1)

where $l\le m\le u$, l, and u are the lower and upper value of fuzzy number $\tilde{A}$ and m the modal value (see Figure 1).

Let $\tilde{A}=\left(l_1, m_1,u_1\right)$ and $\tilde{B}=\left(l_2, m_2,u_2\right)$ be two TFNs, then the operational laws of these triangular fuzzy numbers are as follows [96]:

$$\tilde{A}\oplus \tilde{B}=\left(l_1+l_2,m_1+m_2,u_1+u_2\right)$$

(2)

$$\tilde{A}\ominus \tilde{B}=\left(l_1-u_2,m_1-m_2,u_1-l_2\right)$$

(3)

$$\tilde{A}\otimes \tilde{B}\approx \left(l_1{l}_2,m_1{m}_2,u_1{u}_2\right)$$

(4)

$$\tilde{A}\oslash \tilde{B}\approx \left(l_1/u_2,m_1/m_2,u_1/l_2\right)$$

(5)

$${\tilde{A}}^{-1}\approx \left(1/u_1,1/m_1,1/l_1\right)forl,m,u>0$$

(6)

$$k\otimes \tilde{A}\approx \left(k{l}_1,k{m}_1,k{u}_1\right),k>0,k\in R$$

(7)

and the distance between the two TFN’s $\tilde{A}$ and $\tilde{B}$ $d \left(\tilde{A}, \tilde{B}\right)$, according to the vertex method established in Chen [88] is calculated by Equation (8).

$$d (\tilde{A}, \tilde{B})={\left(\frac{1}{3}\left[{(l_1-l_2)}^2+{(m_1-m_2)}^2+{(u_1-u_2)}^2\right]\right)}^{1/2}$$

(8)

In a decision problem with criteria $\left(C_1, C_2, \mathrm{\dots }, C_n\right)$ and alternatives $\left(A_1, A_2, \mathrm{\dots }, A_m\right)$, the best alternative in fuzzy TOPSIS should have the shortest distance to a fuzzy positive ideal solution (FPIS) and the farthest distance from a fuzzy negative ideal solution (FNIS). The FPIS is computed using the best performance values for each criterion and the FNIS is generated from the worst performance values.

In fuzzy TOPSIS, the criteria should satisfy one of the following conditions to ensure that they are monotonic [17]:

• As the value of the variable increases, the other variables will also increase;
• As the value of the variable increases, the other variables decrease.

Monotonic criteria can be classified into benefit or cost type. A criterion can be classified as of benefit type if, the more desirable the alternative, the higher the score of the criterion. On the other hand, cost type criteria will classify the alternative as less desirable the higher its value in that criterion.

In fuzzy TOPSIS, the decision makers use linguistic variables to obtain the weightings of the criteria and the ratings of the alternatives. If there is a decision group made up of k individuals, the fuzzy weight and rating of the kth decision maker with respect to the ith alternative in the jth criterion are respectively:

$${\tilde{w}}_j^k=\left(w_{j1}^k, w_{j2}^k,w_{j3}^k\right)$$

(9)

$${\tilde{x}}_{ij}^k=\left(a_{ij}^k, b_{ij}^k,c_{ij}^k\right)$$

(10)

where $i=1,2, \dots , m$ and $j=1, 2, \dots , n$.

The aggregate fuzzy weights ${\tilde{w}}_{ij}^{}$ of each criterion given by k decision makers are calculated using Equation (11).

$${\tilde{w}}_j^{}=\frac{1}{K}\otimes \left({\tilde{w}}_j^1\oplus {\tilde{w}}_j^2\oplus \dots \oplus {\tilde{w}}_j^k\right)$$

(11)

Equation (12) is used to calculate the aggregate ratings of the alternatives [97].

$${\tilde{x}}_{ij}^{}=\frac{1}{K}\otimes \left({\tilde{x}}_{ij}^1\oplus {\tilde{x}}_{ij}^2\oplus \dots \oplus {\tilde{x}}_{ij}^k\right)$$

(12)

A fuzzy multicriteria decision-making problem can be expressed in matrix form as is shown in Equation (13) [88]:

$$D=\left[\begin{array}{cccc}{\tilde{x}}_{11}& {\tilde{x}}_{12}& \dots & {\tilde{x}}_{1n}\\ {\tilde{x}}_{21}& {\tilde{x}}_{22}& \dots & {\tilde{x}}_{21}\\ .& .& .& .\\ .& .& .& .\\ .& .& .& .\\ {\tilde{x}}_{m1}& {\tilde{x}}_{m2}& \dots & {\tilde{x}}_{mn}\end{array}\right]$$

$$\tilde{W}=\left({\tilde{w}}_1^{}, {\tilde{w}}_2^{},\dots , {\tilde{w}}_n^{}\right)$$

(13)

with ${\tilde{w}}_j$ and ${\tilde{x}}_{ij}$ linguistic variables be described by triangular fuzzy numbers.

The weightings of the criteria can be calculated by assigning directly the following linguistic variables:

$$\mathrm{Very}\mathrm{low}=\left(0, 0, 0.1\right)$$

$$\mathrm{Low}=\left(0, 0.1, 0.3\right)$$

$$\mathrm{Medium}\mathrm{low}=\left(0.1, 0.3, 0.5\right)$$

$$\mathrm{Medium}=\left(0.3, 0.5, 0.7\right)$$

$$\mathrm{Medium}\mathrm{high}=\left(0.5, 0.7, 0.9\right)$$

$$\mathrm{High}=\left(0.7, 0.9, 1.0\right)$$

$$\mathrm{Very}\mathrm{high}=\left(0.9, 1.0, 1.0\right)$$

The ratings of the alternatives are found using the linguistic variables of

Table 1. Linguistic variables for the ratings.

Linguistic Terms for the Ratings	Fuzzy Number	Inverse Fuzzy Number
	$\left(\mathit{l}, \mathit{m}, \mathit{u}\right)$	$\left(1/\mathit{u},1/\mathit{m}, 1/\mathit{l}\right)$
Very Poor	(0, 0, 1)	(1, 0, 0)
Poor	(0, 1, 3)	(1/3, 1, 0)
Medium Poor	(1, 3, 5)	(1/5, 1/3, 1)
Fair	(3, 5, 7)	(1/7, 1/5, 1/3)
Medium Good	(5, 7, 9)	(1/9, 1/7, 1/5)
Good	(7, 9, 10)	(1/10, 1/9, 1/7)
Very Good	(9, 10, 10)	(1/10, 1/10, 1/9)

[88].

The linear scale transformation is used to transform the various criteria scales into a comparable scale. Thus, we obtain the normalised fuzzy decision matrix $R$. The normalisation method should be used to transform the various criteria scales into a comparable scale, which ensures compatibility between the assessments of the criteria and the linguistic ratings of the subjective criteria [98].

$$\tilde{R}=\left[{\tilde{r}}_{ij}\right]{ }_{mxn} i=1,2, \dots , m;j=1, 2, \dots , n.$$

(14)

where ${\tilde{r}}_{ij}=\left(\frac{l_{ij}}{u_j^{+}},\frac{m_{ij}}{u_j^{+}},\frac{u_{ij}}{u_j^{+}}\right)and u_j^{+}=ma{x}_i{u}_{ij}$ in the case of benefit type criteria, ${\tilde{r}}_{ij}=\left(\frac{l_j^{-}}{u_{ij}},\frac{l_j^{-}}{m_{ij}},\frac{l_j^{-}}{l_{ij}}\right)and l_j^{-}=ma{x}_i{l}_{ij}$ in the case of cost type criteria

Next, the weighted normalised decision matrix $\tilde{V}$ is calculated by multiplying the weightings of the criteria ${\tilde{w}}_j$, by the elements ${\tilde{r}}_{ij}$ of the normalised fuzzy decision matrix.

$$\tilde{V}=\left[{\tilde{v}}_{ij}\right]{ }_{mxn} \mathrm{where} {\tilde{v}}_{ij}={\tilde{x}}_{ij}\otimes {\tilde{w}}_j$$

(15)

A positive ideal point $A^{+}$ and a negative ideal point $A^{-}$ should be defined using the following equations [99]:

$$A^{+}=\left\{{\tilde{v}}_1^{+},\dots ,{\tilde{v}}_n^{+} \right\}\mathrm{where}{\tilde{v}}_j^{+}=\left\{\max \left({\tilde{v}}_{ij}\right)if j\in J;\min \left({\tilde{v}}_{ij}\right)if j\in J\prime \right\} j=1, 2, \dots , n$$

(16)

$$A^{-}=\left\{{\tilde{v}}_1^{-},\dots ,{\tilde{v}}_n^{-} \right\}\mathrm{where}{\tilde{v}}_j^{-}=\left\{\min \left({\tilde{v}}_{ij}\right)if j\in J;\max \left({\tilde{v}}_{ij}\right)if j\in J\prime \right\} j=1, 2, \dots , n$$

(17)

The calculation of Euclidean distances $d_i^{+}$ and $d_i^{-}$ of each weighted alternative from the FPIS ($A^{+})$ and FNIS ($A^{-})$ are computed using Equations (18) and (19) [100].

$$d_i^{+}={\left\{{\displaystyle \sum }_{j=1}^n{\left({\tilde{\nu }}_{ij}-{\nu }_{ij}^{+} \right)}^2\right\}}^{1/2}\mathrm{i}=1,2,\dots ,\mathrm{m}$$

(18)

$$d_i^{-}={\left\{{\displaystyle \sum }_{j=1}^n{\left({\tilde{\nu }}_{ij}-{\nu }_{ij}^{-} \right)}^2\right\}}^{1/2}\mathrm{i}=1,2,\dots ,\mathrm{m}$$

(19)

Finally, the closeness coefficient, $C{C}_i$, of each alternative i is calculated using Equation (20) [88].

$$C{C}_i=\frac{d_i^{-}}{d_i^{-}+d_i^{+}}$$

(20)

The ranking of alternatives is calculated considering that an alternative is closer to the FPIS and further from the FNIS as $C{C}_i$ approaches 1.$C{C}_i$ is the fuzzy satisfaction degree in the ith alternative. $\frac{d_i^{+}}{d_i^{-}+d_i^{+}}$ is considered to be the fuzzy gap degree in the ith alternative.

4. Fuzzy TOPSIS Model Combining MACBETH and Fuzzy Shannon Entropy to Select a Gamification App

Figure 2 shows the flow diagram for this research.

This section firstly describes the structuring process, which allows the problem hierarchy to be built, then the subjective and objective weighting.

4.1. Structuring

The criteria used in this study are original and specific to the Manufacturing Systems and Industrial Organisation course, taught in the second-year degree programmes of Electrical Engineering and Industrial and Automatic Electronic Engineering (jointly) at the Higher Technical School of Industrial Engineering at the Ciudad Real campus of the University of Castilla-La Mancha (Spain).

The Manufacturing Systems and Industrial Organisation course has a large number of students registered, typically between 60 and 80 each year. For the purposes of the gamification experiment, the class was divided into two practical groups, so the number of students was half that in each experiment. Since only free versions of the gamification apps could be used, neither cost nor criteria related to the sales conditions, such as Price or Market program or Contract terms or Warranty—typical in other software selection models such as Kim [12], based on criteria used in the selection of Business Information Systems [101] and Information Security Management Systems [12]—have been considered, and therefore they are not applied to the specific field of gamification in university teaching under the conditions previously laid out. Rajak and Shaw [13] use the following criteria to choose an mHealth application: user satisfaction, compatibility, functionality, security, accessibility, ease of learning and use, empathy, information quality, and responsiveness. Thus, it is also not used in this study because issues of security of health data are not as important as the information contained in gamification apps for teaching, for example.

Therefore, after analysing the literature on gamification—as well as the international standard ISO/IEC 9126 [102] on evaluation of software quality, which takes the following factors into account: functionality, reliability, usability, efficiency, maintainability, and portability, as well as results of direct experiments on the use of gamification in the classroom with the alternatives assessed—the following decision criteria were established:

• Capacity to combine with other methodologies or novel teaching tools (C1). The possibility of using weak Just In Time Teaching (JITT) was considered, with the consequent need for a prior study (open questions about this prior study, questions about what is understood and what is not, and about material to be revised or supporting activities to be provided), and a strong JITT (closed, direct questions to check knowledge of contents). Peer Instruction where, after the teacher has explained the concept, students must answer a series of multiple-choice or yes/no questions, with the aim of examining the understanding of the fundamental concepts of the subject. In Flipped Classroom, certain learning processes are moved out of the classroom, using class time to facilitate participation of students in active learning through questions, discussions, and applied activities to encourage exploration, articulation, and application of these ideas. The possibility of connecting the questionnaires with other tools—for example, Google Classroom—was also looked at;
• Academic performance (C2). The capacity of the app to improve academic performance is also assessed. The following studies were considered in assessing the alternatives: Göksün and Gürsoy [65] about the academic results of applying Kahoot! and Quizizz, the literature review of Wang and Tahir [50] on the effects of Kahoot!, and Zainuddin et al. [48], who compare Quizizz, Socrative, and iSpring Learn LMS. The results obtained in [75] are used for TurningPoint, and those of [77] for Mentimeter;
• Flexibility in the creation of questionnaires (C3). Ease in the creation of questionnaires was assessed, as well as the options for editing, duplicating, and downloading questionnaires in widely used formats such as pdf, or importing questionnaires and developing a questionnaire from the questions of others. Furthermore, the flexibility of the applications to include different types of questions (multiple choice, true/false, short questions), including mathematical equations in the questions, number of answers, and correct answers associated with each question, the possibility of including questions with images or video, or feedback to student questions, or providing teachers’ explanations of the correct answers, was also assessed;
• Students’ perceptions (C4). The perception students have of the application with respect to motivation, engagement, concentration, perceived learning, attention, enjoyment, satisfaction, interest, enthusiasm, curiosity, and confidence was explored. The studies of Wang and Tahir [50] and Zainuddin et al. [48], among others, were used to assess the alternatives. The motivation provided by an app can be considered to be correlated with the quantity and quality of the gamification elements in the games, including memes, designing an avatar or choosing between those available, the possibility of adding images, getting rewards or bonuses, embedding YouTube videos, adding music to the questions or while completing the questionnaire, or showing the final ranking of participants;
• Results reports (C5). The capacity to have reports in Excel files with aggregated data, by student and by question, as well as showing participants’ results during the game. The option of hiding names of participants in real time was also assessed, since in some cases, students prefer results to be anonymous for their classmates. The possibility and ease of sending the scores to students’ parents was also analysed;
• Versatility in assessment of the questionnaire (C6). Versatility in assigning a score to each question was considered, as well as the option to count or not count the time used in answering, or just counting the number of right answers. The more options an app has for scoring the questionnaire, the more versatile the questionnaire is held to be, and the worst case is when it only counts the number of right answers;
• Capacity for group competition (C7). The option of interacting by teams in different modes in the development of gamification experiences such as team or blackboard mode, as well as allowing random or predefined team set-up, was analysed;
• Ease of use (C8). Our study analysed the need for students to install the app or to register to access the game, as well as the versatility of the application in class on a range of devices, and the need for auxiliary devices, such as overhead projectors. It also considered the consumption of Internet resources, since some applications might consume more resources than others, slowing the game down;
• Support (C9). The existence and quality of office support from the app, the number of publicly available questionnaires on the platform, and the number of active forums to exchange experience, doubts about solutions, and information about the app;
• Control of learning rate (C10). Each question on the questionnaire may take a different time to complete, which might change even from year to year, and so it is useful for the teacher to control the rate of activity, and so, of learning. This criterion assesses the capacity of the teacher and/or student to control the rate according to a predetermined time limit, unlimited time, and repeating the task as often as necessary.

The hierarchy of the model is shown in Figure 3.

4.2. Weighting

4.2.1. Subjective Weights

The subjective weights are generated from the judgements of decision makers to which mathematical methods such as the eigenvector method, weighted least squares method, Delphi method, mathematical programming models, etc., are applied [103].

The MACBETH approach [104] is a complete multicriteria methodology that only requires qualitative judgements provided by a decision maker or group to obtain a quantitative evaluation of the alternatives. The theoretical foundations can be seen in [105,106]; examples of real-world applications may be consulted in [107,108,109,110,111,112,113,114,115,116].

MACBETH is an additive value aggregation model due to the advantages of this type of model [117]: it is simple to apply and well known, the technical parameters must be clear and easily open to explanation, and it facilitates precise analysis of a complex problem and allows difficulties presented by ordinal aggregation to be avoided.

The MACBETH approach consists of an interactive methodology facilitating objective decision-making, with an exhaustive procedure, which other techniques do not have, such as the definition of indicators associated with each criterion, the assigning of reference levels for the scale levels of the descriptor, the construction of value functions that measure attractiveness in the range 100 and 0, and ensures a comparison of the criteria on a common scale, checking of the assigned values and results in each alternative and consistency in the judgements given.

The application first requires assessment criteria to be defined and structured into a value tree. For each criterion or fundamental point of view, a descriptor must be defined which identifies two reference levels of the scale. The decision maker makes pairwise comparisons between the scale levels of each descriptor, and between the criteria, based on difference of attractiveness using the semantic scales shown in

Table 2. MACBETH semantic scale.

Semantic Scale	Equivalent Numerical Scale	Description
Null	0	Indifference between the alternatives
Very weak	1	An alternative is very weakly attractive over another
Weak	2	An alternative is weakly attractive over another
Moderate	3	An alternative is moderately attractive over another
Strong	4	An alternative is strongly attractive over another
Very strong	5	An alternative is very strongly attractive over another
Extreme	6	An alternative is extremely attractive over another

.

The judgements of the decision maker obtained by pairwise comparisons are transformed into a MACBETH scale by linear programming. Let $v\left(x\right)$ be the score assigned to option $X$ and $x^{+}$ is at least as attractive as another option of $X$ and $x^{-}$ is at most equally as attractive as another option of X [117], the linear programming applied is:

$$Min \left[v\left(x^{+}\right)-v\left(x^{-}\right)\right]$$

$$\mathrm{Subject}\mathrm{to}v\left(x^{-}\right)=0\left(\mathrm{arbitrarily}\mathrm{assigned}\right)$$

$$\forall \left(x,y\right)\in C_0:v\left(x\right)-v\left(y\right)=0$$

$$\forall \left(x,y\right)\in C_i\cup \dots \cup C_s with i,s \in \left\{1,2,3,4,5,6\right\} and i\le s:v\left(x\right)-v\left(y\right)\ge i,$$

$$\forall \left(x,y\right)\in C_i\cup \dots \cup C_s and \forall \left(w,z\right)\in i,s\in C_{i^{\prime }}\cup \dots \cup C_s,$$

$$\begin{array}{c}with i,s, i^{\prime }, s^{\prime }\in \left\{1,2,3,4,5,6\right\} i\le s,i^{\prime }\le s^{\prime },and i>s^{\prime }:v\left(x\right)-v\left(y\right)\\ \ge v\left(w\right)-v\left(z\right)+i-s^{\prime }\end{array}$$

If this linear program is unfeasible, the judgements are considered inconsistent. If it is feasible, multiple optimal solutions may exist. In this case, the mean is given as the MACBETH scale [118].

The M-MACBETH software, which supports the MACBETH approach, is described in Bana e Costa et al. [119] (a demo and a user’s guide can be downloaded in http://m-macbeth.com/demo/, accessed on 4 April 2021) [120]. M-MACBETH performs a consistency check on the judgements given by the decision maker, and may suggest improvements in the judgements to guarantee consistency. Therefore, unlike other multicriteria methods, MACBETH does not allow any inconsistency [30].

MACBETH requires a descriptor to be defined for each criterion to be assessed. A descriptor is an ordered set of possible impact levels associated with a criterion, to objectively describe the impact of the alternatives with respect to that criterion [105]. The greater the objectivity with which the descriptor is created, the lower the ambiguity, and the better the model will be understood and accepted. Two of the levels of the descriptor are considered for reference and are called Good, considered by the decision maker to be undoubtedly satisfactory, and Neutral, if the decision maker considers a level neither satisfactory nor unsatisfactory. This has been checked by experiment, which significantly adds to the intelligibility of the criterion [106]. In the decision-making problem analysed in this study, almost all the descriptors were built by combining various basic interrelated qualitative features, making multi-dimensional descriptors [106]. As an example,

Table 3. Descriptor associated with the Academic performance criterion.

Scale Levels	Description
L21	A considerable improvement (>10%) can be seen in academic results from the use of continuous formative applications over the year via the app (Good).
L22	Some improvement (5–10%) can be seen in academic results from the use of continuous formative activities over the year via the app.
L23	A small improvement (up to 5%) can be seen in academic results from the use of continuous formative activities over the year via the app.
L24	No improvement can be seen in academic results from the use of continuous activities over the year via the app (Neutral).
L25	Results are worse after using continuous activities over the year via the app.

shows the descriptor created for the Academic performance criterion with the identified reference levels Good and Neutral. Other descriptors have been built for the other criteria.

To compute the subjective weights with the MACBETH approach, it is first necessary to generate the value functions for each criterion. The lecturer provided judgements between the scale levels of each descriptor using the MACBETH semantic categories or a range of two or more adjacent categories, which are shown in Table 2 [30]. When the difference in attractiveness between scale levels cannot be determined exactly, a positive category can be used. This feature of MACBETH is very useful for reflecting uncertainty by the decision maker in giving the judgements, and strengthens the fuzzy logic within fuzzy TOPSIS. The MACBETH questioning procedure should be used to complete the judgement matrix; this is done firstly by comparing the most attractive level of each descriptor with the least attractive, followed by the second most attractive with the least attractive, and so on. The most attractive level was next compared with the other options in decreasing order of attractiveness, and then the judgements making up the diagonal border of the upper triangular portion of the matrix are completed; finally, the remaining judgements from the upper diagonal are given [121]. For example, in the Academic performance criterion, the decision maker gave the judgements shown in Figure 3. The reference level Good is shown in green (L21) and the Neutral in blue (L24). The Figure shows that, when level L21 is compared with level L22, the decision maker hesitates between assigning very weak or weak, and so the range very weak–weak is assigned; it also shows the range of judgements when comparing L21 with L23 (weak–moderate) or L21 with L24 (moderate–strong). All the judgements given are consistent.

By linear programming, the M-MACBETH software creates a value function that associates a value 100 to the level Good and the value 0 to the Neutral level. As an example, Figure 4 shows the value function obtained for the Academic performance criterion. A similar process is applied to the other criteria, giving, in all cases, consistent judgement matrices and their respective value functions. The resulting value functions should be checked by the decision maker, to ensure that they properly represent the relative magnitude of the decision maker’s judgements [121].

To complete the weighting process between the criteria, an additional alternative must be created that includes all the criteria at the Neutral level in all the descriptors. The decision maker should give the judgements using the MACBETH semantic categories which evaluate the increase in attractiveness due to a change from the Neutral level to the Good level in one of its descriptors. This allows the criteria to be ranked from greatest to least attractiveness. Then, the most attractive swing will be compared to the second most attractive swing, and the most attractive swing with the third most attractive swing, and so on. This process continues row by row until the matrix is complete [121]. Figure 5 shows the MACBETH judgement matrix with the judgements given by the teacher of the subject. It can be seen that all the judgements are consistent.

Using the judgements, M-MACBETH computes the weightings associated with each criterion, giving values with the percentages shown in the bar graph in Figure 6. The red vertical line shows the range of weighting values compatible with the judgements of the decision maker [106]. These ranges are those used as thresholds (maximum and minimum values) of the fuzzy numbers, using as a modal value the value assigned and checked by the decision maker. In this way, the weightings obtained by MACBETH, converted into per units as TFN, are shown in

Table 4. Weightings of the criteria obtained via the MACBETH approach in the form of triangular fuzzy numbers.

Criteria	l	m	u
Capacity to combine with other methodologies or novel teaching tools	0.037	0.067	0.079
Academic performance	0.138	0.167	0.193
Flexibility in the creation of questionnaires	0.123	0.133	0.151
Students’ perceptions	0.123	0.133	0.151
Results reports	0.123	0.133	0.151
Versatility in assessment of the questionnaire	0.086	0.100	0.113
Capacity for group competition	0.003	0.033	0.064
Ease of use	0.037	0.067	0.079
Support	0.037	0.067	0.079
Control of learning rate	0.086	0.100	0.113

.

The lecturer justified the judgements given to obtain the weightings by stating that the Capacity for team competition, though useful, especially in the early years of the degree, would be used less often than individual competition. With regard to Support, although it is important to have questionnaires to copy or edit, or to have information to assist in creating questionnaires or making the most of the utilities or combining them with the rest of the teaching in the course, the teacher felt that as it was very specific material, he would prefer to produce his own questionnaires rather than copy or adapt others.

On the other hand, Academic performance was felt to be the most important criterion, since the final goal of gamification is to improve academic results; he also felt that Students’ perceptions in respect of student motivation was very important, as it could provide a significant incentive to study difficult or dull material.

The lecturer also remarked that if another course or degree programme were to be assessed, even within the field of Engineering, the weighting would change.

4.2.2. Objective Weights

Objective weights are obtained from mathematical models, for example, the entropy method, the CRiteria Importance Through Intercriteria Correlation (CRITIC) method, statistical variance, principal element analysis, multiple objective programming, etc., without any consideration of the decision maker’s judgements. The objective weights are especially applicable in decision problems where reliable subjective weights cannot be obtained [122].

The concept of information entropy was introduced by Shannon [123]. Information entropy is the measurement of the level of disorder of a system, but it can also measure the amount of useful information contained in the data. When the difference in the values between alternatives in the same criterion is high, the entropy is small, indicating that this criterion provides a lot of useful information and, therefore, the weight of this criterion should be high. However, if the difference is small and the entropy is therefore high, the weighting of that criterion should be small. That is, a broad distribution includes more uncertainty than a more sharply spiked one [122]. Therefore, the entropy theory is an objective method of weight determination [124] because the criteria weights are obtained directly from the performance matrix using an unbiased procedure.

Shannon developed the following three properties for the entropy measure H, for all $p_i$ within the estimated joint probability distribution P [103]:

• H is a continuous positive function;
• If all $p_i$ are equal, $p_i=1/n$, then H should be a monotonic increasing function of n;
• For all $n⩾2,H\left(p_1,p_2,\dots ,p_n\right)=H\left(p_1+p_2, p_3, \dots ,p_n\right)+\left(p_1+p_2\right)H\left(\frac{p_1}{p_1+p_2}, \frac{p_2}{p_1+p_2}\right)$.

Shannon entropy showed that the only function to satisfy these properties is:

$$H\left(x\right)=-k{\displaystyle \sum }_{i=1}^{n}p\left(x_i\right)logp\left(x_i\right)$$

(21)

where $k={\left(\ln \left(m\right)\right)}^{-1}$ and $x=\left(x_1, x_2, \dots , x_n\right)$ is a discrete random variable with values in a finite set, which occur with probability $p\left(x_i\right)$.

If there is a fuzzy decision matrix $\tilde{X}$ resulting from evaluating $m$ alternatives in $n$ criteria, and whose elements are ${\tilde{x}}_{ij}=\left(l_{ij},m_{ij},u_{ij}\right)$ the rating of the ith alternative with respect to the jth criterion, as shown in Equation (22):

$$\tilde{X}=\left(\begin{array}{cccc}{\tilde{x}}_{11}& {\tilde{x}}_{12}& \cdots & {\tilde{x}}_{1n}\\ {\tilde{x}}_{21}& {\tilde{x}}_{22}& \cdots & {\tilde{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{x}}_{m1}& {\tilde{x}}_{m2}& \cdots & {\tilde{x}}_{mn}\end{array}\right)$$

(22)

The objective criteria weights were computed using the procedure described in [125]:

• Calculate the normalised fuzzy decision matrix $\tilde{Z}=\left({\tilde{z}}_{ij}\right)$ via:

  $${\tilde{z}}_{ij}=\left(\frac{l_{ij}}{{\sum }_{i=1}^m{l}_{ij}}, \frac{m_{ij}}{{\sum }_{i=1}^m{m}_{ij}}, \frac{u_{ij}}{{\sum }_{i=1}^m{u}_{ij}}\right)$$

  (23)
• Calculate the Shannon entropy vector $\tilde{e}=\left({\tilde{e}}_1,{\tilde{e}}_2, \dots , {\tilde{e}}_n\right)$ from Equation (24):

  $${\tilde{e}}_j=\left(-\frac{1}{lnm}{\displaystyle \sum }_{i=1}^m{l}_{ij}ln{l}_{ij},-\frac{1}{lnm}{\displaystyle \sum }_{i=1}^m{m}_{ij}ln{m}_{ij},-\frac{1}{lnm}{\displaystyle \sum }_{i=1}^m{u}_{ij}ln{u}_{ij}\right)$$

  (24)

  where $l_{ij}ln{l}_{ij}$ or $m_{ij}ln{m}_{ij}$ or $u_{ij}ln{u}_{ij}$ are defined as 0 if $l_{ij}$, $m_{ij}$, or $u_{ij}$ are 0, respectively.
• Obtain the degree of divergence ${\tilde{d}}_j$ of the intrinsic information of each criterion $C_j$:

  $${\tilde{d}}_j=\left(1-\frac{1}{lnm}{\displaystyle \sum }_{i=1}^m{l}_{ij}ln{l}_{ij}, 1-\frac{1}{lnm}{\displaystyle \sum }_{i=1}^m{m}_{ij}ln{m}_{ij}, 1-\frac{1}{lnm}{\displaystyle \sum }_{i=1}^m{u}_{ij}ln{u}_{ij}\right)$$

  (25)
• Calculate the fuzzy weight vector $\tilde{w}=\left({\tilde{w}}_1,{\tilde{w}}_2, \dots , {\tilde{w}}_n\right)$ from Equation (26).

  $${\tilde{w}}_j=\left(\frac{1-\frac{1}{lnm}{\sum }_{i=1}^m{l}_{ij}ln{l}_{ij}}{{\sum }_{j=1}^{n}1-\frac{1}{lnm}{\sum }_{i=1}^m{l}_{ij}ln{l}_{ij}},\frac{ 1-\frac{1}{lnm}{\sum }_{i=1}^m{m}_{ij}ln{m}_{ij}}{{\sum }_{j=1}^{n}1-\frac{1}{lnm}{\sum }_{i=1}^m{l}_{ij}ln{l}_{ij}}, \frac{1-\frac{1}{lnm}{\sum }_{i=1}^m{u}_{ij}ln{u}_{ij}}{{\sum }_{j=1}^{n}1-\frac{1}{lnm}{\sum }_{i=1}^m{l}_{ij}ln{l}_{ij}}\right)$$

  (26)
• Normalise the fuzzy criteria weights.

Additionally, De Luca and Termini [126] defined fuzzy entropy as a measure of fuzziness using the Equation (27):

$$H\left(x\right)=-{\displaystyle \sum }_{i=1}^n({\mu }_A\left(x_i\right)log\left({\mu }_A\left(x_i\right)\right)+\left(1-{\mu }_A\left(x_i\right)\right)log\left(1-{\mu }_A\left(x_i\right)\right))$$

(27)

where ${\mu }_A\left(x_i\right)\in \left[0,1\right]$ is the membership of $x_i$ in the fuzzy set A.

Pal and Pal [127,128] proposed the entropy function based on the exponential gain function described in Equation (28):

$$H\left(x\right)=k{\displaystyle \sum }_{i=1}^n({\mu }_A\left(x_i\right)e^{1-{\mu }_A\left(x_i\right)}+\left(1-{\mu }_A\left(x_i\right)e^{{\mu }_A\left(x_i\right)}\right)$$

(28)

where $k$ is a normalising constant.

The crisp objectives weights obtained from fuzzy Shannon entropy, fuzzy De Luca and Termini entropy, and exponential entropy are shown in

Table 5. Crisp objective weights from fuzzy Shannon entropy, De Luca and Termini entropy, and exponential entropy errors $MAD$ and $CFE$.

Criteria	Fuzzy Shannon Entropy	De Luca and Termini Entropy	Exponential Entropy	Error Shannon-De Luca and Termini	Error Shannon-Exponential
Capacity to combine with other methodologies or novel teaching tools	0.033	0.179	0.107	−0.146	−0.074
Academic performance	0.014	0.348	0.099	−0.334	−0.085
Flexibility in the creation of questionnaires	0.012	0.369	0.105	−0.357	−0.093
Students’ perceptions	0.094	0.014	0.098	0.080	−0.004
Results reports	0.096	0.015	0.100	0.081	−0.004
Versatility in assessment of the questionnaire	0.131	0.001	0.096	0.130	0.035
Capacity for group competition	0.114	0.015	0.099	0.099	0.015
Ease of use	0.073	0.055	0.103	0.018	−0.030
Support	0.175	0.000	0.090	0.175	0.085
Control of learning rate	0.258	0.003	0.104	0.255	0.154
$MAD=$				0.168	0.058
$CFE=$				0.001	−0.001

. The criteria with the highest weights in Shannon entropy are: Control of learning rate, Support, and Versatility in assessment of the questionnaire. However, for De Luca and Termini entropy they are: Flexibility in the creation of questionnaires, Academic performance, and Capacity to combine with other methodologies or novel teaching tools. In exponential entropy, the most important criteria are: Capacity to combine with other methodologies or novel teaching tools, Flexibility in the creation of questionnaires, and Control of learning rate. Therefore, a certain agreement can be seen between the different techniques when identifying the most important criteria. Error assessments Median Absolute Deviation ($MAD$) and Cumulative sum of Forecast Errors ($CFE$) were jointly applied to assess the error in each entropy measure with respect to those obtained by fuzzy Shannon entropy; in this way, both systematic and random errors could be analysed. It can be seen that the errors in the weightings obtained from De Luca and Termini entropy are much greater (including inverse values, that is, higher weights in Shannon entropy are associated with lower weights in De Luca and Termini entropy and vice versa). The errors calculated from exponential entropy, on the other hand, are much lower, with values both above and below those generated from Shannon entropy. It is also shown that in both cases, $MADs$ are small, although exponential entropy returns an error 65.48% lower, with respect to those obtained from De Luca and Termini entropy. For $CFE$, random errors are practically non-existent in both cases.

The normalised decision matrix obtained by applying Equation (23) is shown in

Table 6. The normalised decision matrix.

ALTERNATIVES	C1	C2	C3	C4	C5
KAHOOT!	(0.030, 0.075, 0.114)	(0.280, 0.257, 0.233)	(0.097, 0.125, 0.152)	(0.219, 0.237 0.244)	(0.167, 0.194, 0.225)
QUIZIZZ	(0.152, 0.175, 0.205)	(0.120, 0.143, 0.163)	(0.161, 0.175, 0.196)	(0.281, 0.263, 0.244)	(0.233, 0.250, 0.250)
SOCRATIVE	(0.273, 0.250, 0.227)	(0.200, 0.200, 0.209)	(0.226, 0.225, 0.217)	(0.219, 0.237, 0.244)	(0.300, 0.278, 0.250)
TURNINGPOINT	(0.273, 0.250, 0.227)	(0.280, 0.257, 0.233)	(0.226, 0.225, 0.217)	(0.000, 0.000, 0.024)	(0.300, 0.278, 0.250)
MENTIMETER	(0.273, 0.250, 0.227)	(0.120, 0.143, 0.163)	(0.290, 0.250, 0.217)	(0.28°, 0.263, 0.244)	(0.000, 0.000, 0.025)
ALTERNATIVES	C6	C7	C8	C9	C10
KAHOOT!	(0.292, 0.290, 0.278)	(0.167, 0.200, 0.219)	(0.107, 0.143, 0.175)	(0.529, 0.435, 0.333)	(0.045, 0.103, 0.143)
QUIZIZZ	(0.389, 0.290, 0.278)	(0.500, 0.400, 0.313)	(0.321, 0.286, 0.250)	(0.294, 0.304, 0.300)	(0.227, 0.241, 0.257)
SOCRATIVE	(0.038, 0.097, 0.139)	(0.167, 0.200, 0.219)	(0.250, 0.257, 0.250)	(0.176, 0.217, 0.233)	(0.409, 0.345, 0.286)
TURNINGPOINT	(0.529, 0.323, 0.278)	(0.000, 0.000, 0.031)	(0.321, 0.286, 0.250)	(0.000, 0.000, 0.033)	(0.000, 0.000, 0.029)
MENTIMETER	(0.000, 0.000, 0.028)	(0.167, 0.200, 0.219)	(0.000, 0.029, 0.075)	(0.000, 0.043, 0.100)	(0.318, 0.310, 0.286)

. The fuzzy Shannon entropy vector, the fuzzy diversification vector, and the fuzzy criteria weights obtained by applying Equations (24)–(26), after normalising the fuzzy criteria weights, respectively, are shown in

Table 7. The fuzzy Shannon entropy vector, the fuzzy diversification vector, and the fuzzy criteria weights.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10
	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$
${\tilde{\mathit{e}}}_{\mathit{j}}$	(0.904, 0.956, 0.983)	(0.959, 0.980, 0.993)	(0.964, 0.983, 0.994)	(0.857, 0.861, 0.911)	(0.845, 0.855, 0.912)	(0.738, 0.814, 0.896)	(0.772, 0.828, 0.913)	(0.817, 0.898, 0.956)	(0.623, 0.740, 0.876)	(0.749, 0.000, 0.898)
${\tilde{\mathit{d}}}_{\mathit{j}}$	(0.096, 0.044, 0.017)	(0.041, 0.020, 0.007)	(0.036, 0.017, 0.006)	(0.143, 0.139, 0.089)	(0.155, 0.145, 0.088)	(0.262, 0.186, 0.104)	(0.228, 0.172, 0.087)	(0.183, 0.102, 0.044)	(0.377, 0.260, 0.124)	(0.251, 1.000, 0.102)
${\tilde{\mathit{w}}}_{\mathit{j}}$	(0.054, 0.021, 0.025)	(0.023, 0.010, 0.010)	(0.020, 0.008, 0.009)	(0.081, 0.067, 0.133)	(0.087, 0.070, 0.132)	(0.148, 0.089, 0.156)	(0.129, 0.082, 0.130)	(0.103, 0.049, 0.066)	(0.213, 0.125, 0.186)	(0.142, 0.480, 0.153)

.

4.2.3. Resulting Weights

Subjective weights ${\tilde{w}}_j^S$ and objective weights ${\tilde{w}}_j^O$ of each criterion $C_j$ were aggregated using Equation (29). $W^S$ and $W^O$ are the weightings associated with the objective and subjective weights, respectively, and have values between 0 and 1. The ranking of alternatives is calculated by assuming that objective and subjective weights are of similar importance, that is, $W^S=0.5$ and $W^O=0.5$.

$${\tilde{w}}_j=W^S\otimes {\tilde{w}}_j^S+W^O\otimes {\tilde{w}}_j^O\mathrm{with}{W}^S+W^O=1$$

(29)

The objective weights considered in the model are those obtained from fuzzy Shannon entropy, but those derived from De Luca and Termini entropy, and those given by Equation (28) from Pal and Pal [127,128], were also computed. This allows rankings to be compared among different techniques for obtaining objective weights (see Section 5, Results and Discussion)

5. Results and Discussion

The detailed characteristics of each app included in the research are described on the official website of each application (https://account.turningtechnologies.com/account/, accessed on 4 April 2021 [129], accessed on 4 April 2021; https://www.socrative.com/, accessed on 4 April 2021 [130]; https://quizizz.com/, accessed on 4 April 2021 [131]; https://www.mentimeter.com/, accessed on 4 April 2021 [132] and https://kahoot.com/, accessed on 4 April 2021 [133]). TurningPoint and Quizizz are free applications, while Socrative has a number of versions (free, Socrative PRO for K–12 teachers, and Socrative PRO for Higher Ed & Corporate), which is also the case with Kahoot! (free, Standard, Pro, Kahoot! 360, and Kahoot! 360Pro) and Mentimeter (free, Basic, Pro, and Enterprise). This analysis used the free version of each app.

Once the weightings and their means of integration are obtained, fuzzy TOPSIS is applied to obtain the ranking of the apps. The fuzzy weighted normalised decision matrix that results from combining the objective and subjective weights of Table 4 and Table 7, respectively, and applying $W^S=0.5$ and $W^O=0.5,$ is shown in

Table 8. Fuzzy weighted normalised decision matrix with $W^S=0.5$ and $W^O=0.5$, in the case of objective weights from fuzzy Shannon entropy.

Criteria	Alternatives	$({\mathit{l}}_{\mathit{i}\mathit{j}}, {\mathit{m}}_{\mathit{i}\mathit{j}}, {\mathit{u}}_{\mathit{i}\mathit{j}})$
Capacity to combine with other methodologies or novel teaching tools	KAHOOT!	(0.005, 0.013, 0.026)
	QUIZIZZ	(0.023, 0.031, 0.047)
	SOCRATIVE	(0.041, 0.044, 0.052)
	TURNINGPOINT	(0.041, 0.044, 0.052)
	MENTIMETER	(0.041, 0.044, 0.052)
Academic performance	KAHOOT!	(0.057, 0.080, 0.102)
	QUIZIZZ	(0.024, 0.045, 0.071)
	SOCRATIVE	(0.041, 0.062, 0.092)
	TURNINGPOINT	(0.057, 0.080, 0.102)
	MENTIMETER	(0.024, 0.045, 0.071)
Flexibility in the creation of questionnaires	KAHOOT!	(0.022, 0.036, 0.056)
	QUIZIZZ	(0.036, 0.050, 0.072)
	SOCRATIVE	(0.050, 0.064, 0.080)
	TURNINGPOINT	(0.050, 0.064, 0.080)
	MENTIMETER	(0.065, 0.071, 0.080)
Students’ perceptions	KAHOOT!	(0.071, 0.090, 0.142)
	QUIZIZZ	(0.092, 0.100, 0.142)
	SOCRATIVE	(0.071, 0.090, 0.142)
	TURNINGPOINT	(0.000, 0.000, 0.014)
	MENTIMETER	(0.092, 0.100, 0.142)
Results reports	KAHOOT!	(0.053, 0.071, 0.128)
	QUIZIZZ	(0.074, 0.092, 0.142)
	SOCRATIVE	(0.095, 0.102, 0.142)
	TURNINGPOINT	(0.095, 0.102, 0.142)
	MENTIMETER	(0.000, 0.000, 0.014)
Versatility in assessment of the questionnaire	KAHOOT!	(0.082, 0.086, 0.135)
	QUIZIZZ	(0.082, 0.086, 0.135)
	SOCRATIVE	(0.012, 0.029, 0.068)
	TURNINGPOINT	(0.105, 0.095, 0.135)
	MENTIMETER	(0.000, 0.000, 0.014)
Capacity for group competition	KAHOOT!	(0.020, 0.029, 0.068)
	QUIZIZZ	(0.059, 0.058, 0.097)
	SOCRATIVE	(0.020, 0.029, 0.068)
	TURNINGPOINT	(0.000, 0.000, 0.010)
	MENTIMETER	(0.020, 0.029, 0.068)
Ease of use	KAHOOT!	(0.021, 0.029, 0.051)
	QUIZIZZ	(0.063, 0.058, 0.073)
	SOCRATIVE	(0.049, 0.052, 0.073)
	TURNINGPOINT	(0.063, 0.058, 0.073)
	MENTIMETER	(0.000, 0.006, 0.022)
Support	KAHOOT!	(0.113, 0.096, 0.133)
	QUIZIZZ	(0.063, 0.067, 0.120)
	SOCRATIVE	(0.038, 0.048, 0.093)
	TURNINGPOINT	(0.000, 0.000, 0.013)
	MENTIMETER	(0.000, 0.010, 0.040)
Control of learning rate	KAHOOT!	(0.011, 0.087, 0.067)
	QUIZIZZ	(0.057, 0.202, 0.120)
	SOCRATIVE	(0.103, 0.290, 0.133)
	TURNINGPOINT	(0.000, 0.000, 0.013)
	MENTIMETER	(0.080, 0.261, 0.133)

. These are the values considered most appropriate and which give similar importance to objective and subjective weightings.

Since all the criteria are of the benefit type, the positive ideal point is defined as and the negative ideal point from Equations (16) and (17). The Euclidean distances $d_i^{+}$ and $d_i^{-}$ of each alternative from the $A^{+}$ and $A^{-}$ and the closeness coefficient $CC$ in the case $W^S=0.5$ and $W^O=0.5$ are shown in

Table 9. The distances, normalised closeness coefficient, and ranking of alternatives in the case of $W^S=0.5$ and $W^O=0.5$, using objective weights from fuzzy Shannon entropy.

Alternatives	${\mathit{d}}_{\mathit{i}}^{+}$	${\mathit{d}}_{\mathit{i}}^{-}$	$\mathbf{Normalised}\mathit{C}\mathit{C}$	Ranking
KAHOOT!	17.3427	0.6973	0.2052	3rd
QUIZIZZ	17.2100	0.8302	0.2439	1st
SOCRATIVE	17.2483	0.8045	0.2365	2nd
TURNINGPOINT	17.5048	0.5151	0.1516	5th
MENTIMETER	17.4964	0.5548	0.1628	4th

. It can be seen that Quizizz, Socrative, and Kahoot! are chosen in first, second, and third place, respectively.

Table 10. The distances, normalised closeness coefficient, and ranking of alternatives in the case of $W^S=0.5$ and $W^O=0.5$, using objective weights from fuzzy De Luca and Termini entropy.

Alternatives	${\mathit{d}}_{\mathit{i}}^{+}$	${\mathit{d}}_{\mathit{i}}^{-}$	$\mathbf{Normalised}\mathit{C}\mathit{C}$	Ranking
KAHOOT!	17.3549	0.6924	0.1843	4th
QUIZIZZ	17.2916	0.7609	0.2020	3rd
SOCRATIVE	17.2017	0.8487	0.2255	1st
TURNINGPOINT	17.2623	0.7753	0.2063	2nd
MENTIMETER	17.3602	0.6834	0.1819	5th

shows the distances, normalised closeness coefficient, and ranking of alternatives in the case of $W^S=0.5$ and $W^O=0.5$, using objective weights from fuzzy Luca and Termini entropy, and

Table 11. The distances, normalised closeness coefficient, and ranking of alternatives in the case of $W^S=0.5$ and $W^O=0.5$, using objective weights from exponential entropy.

Alternatives	${\mathit{d}}_{\mathit{i}}^{+}$	${\mathit{d}}_{\mathit{i}}^{-}$	$\mathbf{Normalised}\mathit{C}\mathit{C}$	Ranking
KAHOOT!	17.3427	0.6905	0.1980	3rd
QUIZIZZ	17.2152	0.8104	0.2327	1st
SOCRATIVE	17.2274	0.7986	0.2291	2nd
TURNINGPOINT	17.3949	0.6232	0.1789	4th
MENTIMETER	17.4654	0.5630	0.1613	5th

includes the same parameters but applying the objective weights from exponential entropy. The same ranking in the first three positions as for Shannon entropy is obtained from exponential entropy but, in the case of De Luca and Termini entropy, Socrative is in first place in the ranking, followed by TurningPoint and Quizizz. This is quite surprising, as TurningPoint is in a lower position in the ranking with the other objective weights and MCDA techniques used to validate the method (see the Validity of the proposed method section following).

5.1. Validity of the Proposed Method

The feasibility and validity of the proposed method is tested through PROMETHEE II, ELECTRE III, and fuzzy VIKOR (some of the methods proposed by the application that recommend the most suitable MCDA method carried out by Wątróbski et al. [15]). Objective weights from fuzzy Shannon entropy and subjective weights from MACBETH and $W^S=0.5$ and $W^O=0.5$ were used in all the MCDA applied.

In PROMETHEE II, the type I or strict immediate preference function was used in all criteria. The result was to obtain the positive ${\mathsf{\varphi }}^{+}\left(\mathrm{A}\right)$ and negative ${\mathsf{\varphi }}^{-}\left(\mathrm{A}\right)$ outranking flows and the net outranking flow $\mathsf{\varphi }\left(\mathrm{A}\right)={\mathsf{\varphi }}^{+}\left(\mathrm{A}\right)-{\mathsf{\varphi }}^{-}\left(\mathrm{A}\right)$ of alternative A, as shown in

Table 12. Positive, negative, and net outranking flows in PROMETHEE II.

Alternatives	KAHOOT!	QUIZIZZ	SOCRATIVE	TURNINGPOINT	MENTIMETER
${\mathsf{\varphi }}^{+}\left(A\right)$	1.4400	1.9630	1.8110	1.5280	1.2000
${\mathsf{\varphi }}^{-}\left(A\right)$	1.7260	1.2840	1.2780	1.6660	1.9880
$\mathsf{\varphi }\left(A\right)$	−0.2860	0.6790	0.5330	−0.1380	−0.7880
Ranking	4th	1st	2nd	3rd	5th

.

ELECTRE III performs the ranking from antagonistic classifications (ascending and descending distillation), and orders the alternatives from best to least good, and from worst to least bad. This is done using fuzzy overclassification logic. The data for the alternatives were normalised to a scale of 0 to 10. Therefore, for each criterion $j$, the indifference $q_j$ and preference coefficients $p_j$ must be the same for all criteria [134]; the veto threshold is not considered since for normalisation of the values of the alternatives with respect to the criteria, the differences between these values are very small, and the introduction of high values for the parameter makes no sense in this case, since in some criteria the preference threshold $p_j$ plays this role.

Table 13. Rankings in the ascending and descending distillation and final ranking in ELECTRE III.

Alternatives	Ranking in the Ascending Distillation	Ranking in the Descending Distillation	Ranking in the Median Preorder
KAHOOT!	2nd	3rd	3rd
QUIZIZZ	1st	1st	1st
SOCRATIVE	2nd	2nd	2nd
TURNINGPOINT	2nd	3rd	3rd
MENTIMETER	3rd	3rd	4th

shows the ascending ranking (from the worst alternative to the best), descending ranking (from the best alternative to the worst), and average ranking (to obtain a complete ranking, the final ranking is held to be an average of the ascending and descending ranking).

Table 14. Dominance Matrix in ELECTRE III. P+ means an alternative $A_i$ that is better than alternative $A_j$. I means that an altenative $A_i$ is equivalent to alternative $A_j$. P- means that $A_i$ is as good as alternative $A_j$.

Alternatives	KAHOOT!	QUIZIZZ	SOCRATIVE	TURNINGPOINT	MENTIMETER
KAHOOT!	0	P−	P−	I	P+
QUIZIZZ	P+	0	P+	P+	P+
SOCRATIVE	P+	P−	0	P+	P+
TURNINGPOINT	I	P−	P−	0	P+
MENTIMETER	P−	P−	P−	P−	0

shows the dominance matrix.

In the fuzzy VIKOR method, $v=n+1/2n=0.6$, where $n$ is the number of alternatives. The ${\tilde{S}}_j$ and ${\tilde{R}}_j$ are respectively the fuzzy separation of alternative $A_j$ from the fuzzy best value $f_i^{\ast }$ and the separation of alternative $A_j$ from the fuzzy worst value $f_i^0$. ${\tilde{Q}}_j$ gives the fuzzy separation measure of an alternative from the best alternative. ${\tilde{S}}_j$, ${\tilde{R}}_j$, and ${\tilde{Q}}_j$ are defuzzified using the Centre of Area (COA) method. $Q_j$ The resulting crisp $S_j$, $R_j$, and $Q_j$ and the corresponding associated rankings asociados are shown in

Table 15. Comparison of ranking with different MCDA techniques using objective weights from fuzzy Shannon entropy and subjective weights from MACBETH and $W^S=0.5$ and $W^O=0.5$.

Alternatives	${\mathit{S}}_{\mathit{j}}$		${\mathit{R}}_{\mathit{j}}$		${\mathit{Q}}_{\mathit{j}}$
	Value	Ranking	Value	Ranking	Value	Ranking
KAHOOT!	0.3483	4th	0.1266	5th	0.3281	5th
QUIZIZZ	0.2177	2nd	0.0636	1st	0.0594	1st
SOCRATIVE	0.2170	1st	0.0651	2nd	0.0632	2nd
TURNINGPOINT	0.3365	3rd	0.1247	4th	0.3144	4th
MENTIMETER	0.3924	5th	0.0954	3rd	0.2710	3rd

. The lower $Q_j$, the better the alternative.

Table 16. Comparison of ranking with different MCDA techniques using objective weights from fuzzy Shannon entropy and subjective weights from MACBETH and $W^S=0.5$ and $W^O=0.5$.

Alternatives	MACBETH+ Fuzzy TOPSIS	Fuzzy VIKOR	PROMETHEE II	ELECTRE III
KAHOOT!	3rd	5th	4th	3rd
QUIZIZZ	1st	1st	1st	1st
SOCRATIVE	2nd	2nd	2nd	2nd
TURNINGPOINT	5th	4th	3rd	3rd
MENTIMETER	4th	3rd	5th	4th

summarises the rankings obtained with MACBETH+TOPSIS, fuzzy VIKOR, PROMETHEE II, and ELECTRE III. It can be seen that all the techniques give Quizizz as the best solution, followed by Socrative.

In order to validate the proposed method, the similarity of the rankings obtained with all the MCDA techniques used was assessed using the Value of Similarity ($WS$) coefficient developed by Salabun and Urganiak [135]. This coefficient is strongly correlated with the difference between two rankings at particular positions, and the top of the ranking has a more significant influence on similarity than the bottom. The $WS$ coefficient is calculated using Equation (30):

$$WS=1-{\displaystyle \sum }_{i=1}^n(2^{-R_{xi}}\ast \frac{\left|R_{xi}-R_{yi}\right|}{max\left\{\left|1-R_{xi}\right|, \left|n-R_{xi}\right|\right\}})$$

(30)

where $n$ is the length of ranking and $R_{xi}$ and $R_{yi}$ are defined as the place in the ranking for the ith element in ranking x and ranking y, respectively. If the $WS$ coefficient is less than 0.234, then the similarity is low, and if it is higher than 0.808, then the similarity is high [135].

Table 17. $WS$ coefficients.

	FUZZY VIKOR	PROMETHEE II	ELECTRE III
$WS$ coefficient	0.846	0.901	0.984

shows the $WS$ coefficients of the ranking of the method described in this research with respect to those used to validate the method. Therefore, in all cases the similarity is high, but it is slightly higher for the ranking obtained from ELECTRE III.

5.2. Sensitivity Analysis

The sensitivity analysis performed by modifying the values of $W^S$ and $W^O$ can be seen in

Table 18. Sensitivity analysis with objective weights from fuzzy Shannon entropy.

Alternatives	Normalised CC/Ranking
	${\mathit{W}}^{\mathit{S}}=0$ ${\mathit{W}}^{\mathit{O}}=1$		${\mathit{W}}^{\mathit{S}}=0.2$ ${\mathit{W}}^{\mathit{O}}=0.8$		${\mathit{W}}^{\mathit{S}}=0.4$ ${\mathit{W}}^{\mathit{O}}=0.6$		${\mathit{W}}^{\mathit{S}}=0.5$ ${\mathit{W}}^{\mathit{O}}=0.5$		${\mathit{W}}^{\mathit{S}}=0.6$ ${\mathit{W}}^{\mathit{O}}=0.4$		${\mathit{W}}^{\mathit{S}}=0.8$ ${\mathit{W}}^{\mathit{O}}=0.2$		${\mathit{W}}^{\mathit{S}}=1$ ${\mathit{W}}^{\mathit{O}}=0$
KAHOOT!	0.2063	/3rd	0.2054	/3rd	0.2056	/3rd	0.2052	/3rd	0.2047	/3rd	0.2035	/3rd	0.2024	/3rd
QUIZIZZ	0.2637	/1st	0.2556	/1st	0.2480	/1st	0.2439	/1st	0.2400	/1st	0.2333	/1st	0.2273	/2nd
SOCRATIVE	0.2454	/2nd	0.2420	/2nd	0.2383	/2nd	0.2365	/2nd	0.2347	/2nd	0.2312	/2nd	0.2283	/1st
TURNINGPOINT	0.1191	/5th	0.1324	/5th	0.1449	/5th	0.1516	/5th	0.1579	/5th	0.1701	/4th	0.1805	/4th
MENTIMETER	0.1655	/4th	0.1646	/4th	0.1632	/4th	0.1628	/4th	0.1626	/4th	0.1619	/5th	0.1615	/5th

,

Table 19. Sensitivity analysis with objective weights from De Luca and Termini entropy.

Alternatives	Normalised CC/Ranking
	${\mathit{W}}^{\mathit{S}}=0$ ${\mathit{W}}^{\mathit{O}}=1$		${\mathit{W}}^{\mathit{S}}=0.2$ ${\mathit{W}}^{\mathit{O}}=0.8$		${\mathit{W}}^{\mathit{S}}=0.4$ ${\mathit{W}}^{\mathit{O}}=0.6$		${\mathit{W}}^{\mathit{S}}=0.5$ ${\mathit{W}}^{\mathit{O}}=0.5$		${\mathit{W}}^{\mathit{S}}=0.6$ ${\mathit{W}}^{\mathit{O}}=0.4$		${\mathit{W}}^{\mathit{S}}=0.8$ ${\mathit{W}}^{\mathit{O}}=0.2$		${\mathit{W}}^{\mathit{S}}=1$ ${\mathit{W}}^{\mathit{O}}=0$
KAHOOT!	0.1672	/5th	0.1733	/5th	0.1805	/5th	0.1843	/4th	0.1874	/4th	0.1950	/3rd	0.2024	/3rd
QUIZIZZ	0.1811	/4th	0.1887	/4th	0.1976	/3rd	0.2020	/3rd	0.2073	/2nd	0.2172	/2nd	0.2273	/2nd
SOCRATIVE	0.2238	/2nd	0.2244	/1st	0.2252	/1st	0.2255	/1st	0.2262	/1st	0.2270	/1st	0.2283	/1st
TURNINGPOINT	0.2297	/1st	0.2212	/2nd	0.2110	/2nd	0.2063	/2nd	0.2015	/3rd	0.1910	/4th	0.1805	/4th
MENTIMETER	0.1982	/3rd	0.1924	/3rd	0.1857	/4th	0.1819	/5th	0.1777	/5th	0.1698	/5th	0.1615	/5th

and

Table 20. Sensitivity analysis with objective weights from Pal and Pal entropy or exponential entropy.

Alternatives	Normalised CC/Ranking
	${\mathit{W}}^{\mathit{S}}=0$ ${\mathit{W}}^{\mathit{O}}=1$		${\mathit{W}}^{\mathit{S}}=0.2$ ${\mathit{W}}^{\mathit{O}}=0.8$		${\mathit{W}}^{\mathit{S}}=0.4$ ${\mathit{W}}^{\mathit{O}}=0.6$		${\mathit{W}}^{\mathit{S}}=0.5$ ${\mathit{W}}^{\mathit{O}}=0.5$		${\mathit{W}}^{\mathit{S}}=0.6$ ${\mathit{W}}^{\mathit{O}}=0.4$		${\mathit{W}}^{\mathit{S}}=0.8$ ${\mathit{W}}^{\mathit{O}}=0.2$		${\mathit{W}}^{\mathit{S}}=1$ ${\mathit{W}}^{\mathit{O}}=0$
KAHOOT!	0.1928	/3rd	0.1946	/3rd	0.1969	/3rd	0.1980	/3rd	0.1991	/3rd	0.2008	/3rd	0.2024	/3rd
QUIZIZZ	0.2400	/1st	0.2369	/1st	0.2339	/1st	0.2327	/1st	0.2315	/1st	0.2292	/1st	0.2273	/2nd
SOCRATIVE	0.2298	/2nd	0.2295	/2nd	0.2292	/2nd	0.2291	/2nd	0.2289	/2nd	0.2287	/2nd	0.2283	/1st
TURNINGPOINT	0.1762	/4th	0.1777	/4th	0.1786	/4th	0.1789	/4th	0.1790	/4th	0.1800	/4th	0.1805	/4th
MENTIMETER	0.1612	/5th	0.1613	/5th	0.1614	/5th	0.1613	/5th	0.1615	/5th	0.1613	/5th	0.1615	/5th

with the objective weights obtained from fuzzy Shannon entropy, fuzzy De Luca and Termini entropy, and exponential entropy, respectively. Table 16 shows that as the influence of the subjective weights increases, especially for very high values $W^S\ge 0.8$, a permutation in the ranking of the fourth and fifth positions takes place. If only the subjective weights are considered ($W^S=1$), Socrative is the alternative ranked first, but in all other cases, when the objective weights are taken into account, Quizizz is the alternative chosen. Therefore, it can be seen that the subjective weights have no influence on the ranking when $W^S<0.8$ and that Quizizz, Socrative, and Kahoot! are ranked in first, second, and third places, respectively, in these cases. The results demonstrate the need to combine subjective and objective weights to obtain more accurate results in the decision models, since, if only the subjective weights had been used, the results could have been misleading.

The sensitivity analysis performed by modifying the values of $W^S$ and $W^O$ using objective weights from fuzzy De Luca and Termini entropy is shown in Table 19. It can be seen that, as $W^S\ge 0.2$, Socrative is the first-placed alternative, followed by Quizizz. When only the objective weights are included, TurningPoint is the highest-valued alternative, followed by Socrative. The other alternatives also undergo changes in the ranking; for example, Kahoot! goes from last place, when only objective weights are considered, to fourth place when objective and subjective weights are given equal weight, and finally to third place when $W^S\ge 0.8$. TurningPoint goes from being the best alternative, when only objective weights are considered, to being in second place when $0.2\le W^S<0.6$, third place when $W^S=0.6$, and finally fourth place when $W^S\le 0.8$. It therefore seems that in this case, the results are unstable in the classification of alternatives, and the classification of an alternative may vary as the contributions of the objective or subjective weights are altered.

The sensitivity analysis performed by modifying the values of $W^S$ and $W^O$ using objective weights from Pal and Pal entropy is shown in Table 20. Quizziz and Socrative are the first and second alternatives, respectively, in all cases except when only subjective weights are considered. Kahoot!, TurningPoint, and Mentimeter are in third, fourth, and fifth place, respectively, in all cases; there is no change in the classification as the contribution of the objective and subjective weights is altered. These results show that the model is very stable and robust. Furthermore, these results are more in agreement with those obtained with fuzzy Shannon entropy.

A sensitivity analysis was also carried out, increasing and decreasing by 10% and 20% the weights of each criterion with respect to those obtained from MACBETH+Fuzzy Shannon entropy, while maintaining the weights assigned to the other criteria, to see whether this leads to any changes in the ranking of alternatives. Figure 7 shows the results of these variations. There is only one permutation in the ranking, between Mentimeter and TurningPoint, which move to the fifth and fourth places, respectively, when the weighting of the Control of learning criterion is decreased by 20%. The model is therefore seen to be stable.

The results were shown to the teacher, who was asked his opinion. He remarked that due to the characteristics of the course, subject, and student body, Quizizz was the alternative he considered most suitable, too.

Quizizz was therefore chosen as the application to do gamification in the Manufacturing Systems and Industrial Organisation course. Specifically, Quizizz was applied in the practical and problem classes as a way of remembering concepts and increasing student motivation. Students were divided into two groups (Group 1 and Group 2) to do these practical exercises and problems. These questionnaires include an extra question, about their assessment of what can be learnt with the tool used. The first year that Quizizz was used with students, 59.7% of students in Group 1 considered that the app was good or very good for learning, with 39% precision in giving correct answers; in Group 2, 90% of students valued the learning with Quizizz as good or very good, with a precision in the results of 44%. The following year, 73.17% of students in Group 1 valued it positively, with an academic result of 52% of correct answers; 72% of the students in Group 2 valued it positively, while the precision in the answers given was 61%. It was seen that Group 2 had better academic results than Group 1 in both years. The gamification activities were undertaken first in Group 1, and then a week later in Group 2. It seems that the students in Group 2, once they knew what Group 1 had done, performed better academically. It is also seen that the academic results have increased over the academic years, and so it is likely that the results will improve 10% in the next year.

6. Conclusions

There is ever stronger evidence of the favourable acceptance of gamification and its effectiveness in favouring highly engaging learning experiences. The many benefits described have led to a considerable increase in the number of applications aimed at gamification in teaching. Choosing the best one for a programme or year has thus become a complex decision. Nevertheless, the literature review carried out on different databases has shown that there are no studies using fuzzy multicriteria techniques to analyse the selection of gamification apps in university courses.

This study describes a model combining fuzzy TOPSIS with the MACBETH approach and fuzzy Shannon entropy, in order to choose the most suitable gamification application in the second-year degree programmes in Electrical Engineering and Industrial and Automatic Electronic Engineering at the Higher Technical School of Industrial Engineering at the Ciudad Real campus of the University of Castilla-La Mancha (Spain).

In the literature, fuzzy TOPSIS is usually combined with AHP or fuzzy AHP, despite the many criticisms directed at AHP. However, this study is the first in the literature to combine subjective weights obtained via MACBETH with objective weights computed using fuzzy Shannon entropy, and with the fuzzy TOPSIS methodology to obtain the ranking of alternatives. MACBETH provides a complete methodology for ensuring the accuracy of the weightings in the criteria, such as the reference levels and the definitions of the descriptors associated with each criterion; it also supplies a variety of tools to include doubts or incomplete knowledge of the decision maker, as well as the need to validate the results as they are obtained; furthermore, it avoids the many criticisms aimed at AHP. Additionally, weights derived from the data computed via fuzzy Shannon entropy are included in the study, giving greater reliability to the results. Objective weights from fuzzy De Luca and Termini entropy and exponential entropy computed with the Pal and Pal definition are compared with the obtained from fuzzy Shannon entropy, as well as the rankings obtained using these objective weights combined with the subjective weighs produced by MACBETH. The same ranking in the top three places as using Shannon entropy is obtained from exponential entropy but, in the case of De Luca and Termini entropy, Socrative is in first place in the ranking, followed by TurningPoint and Quizizz.

Objective and subjective weights are combined by assuming they are of equal importance. The results show that Quizizz, Socrative, and Kahoot! are to be found in first, second, and third place, respectively. The results of the proposed method are validated with PROMETHEE II, ELECTRE III, and fuzzy VIKOR. All the MCDA techniques used return Quizizz as the best solution, followed by Socrative. The similarity between the rankings of the various techniques was computed using the $WS$ coefficient, and values greater than 0.808 were obtained in all cases, and thus great similarity, although it was slightly greater for ELECTRE III.

The results obtained by the model were shown to the teacher of the subject, who also considered that Quizizz was the most suitable gamification tool. The solution was also contrasted with the real experience of the use of Quizizz over a number of academic years in a course. An average of 74.85% of the students considered that, in the first year that it was used, the learning experience was very good or good. In the second year, an average of 72.59% of students considered the learning experience to be very good or good. With respect to the learning results, the first year achieved a percentage of correct answers to the questionnaire of 41.5%, while in the second year the average of correct answers was 56.5%.

The models, criteria, and weightings of the criteria can be used as described in this study in other courses and programmes, or, indeed, adapted to the specifics of each course.

As future lines of development, the aim is to include, together with the apps assessed, other additional applications, to see whether Quizizz is still the first choice; the alternatives assessed in this study also continuously introduce new utilities, and so their valuation with respect to some of the criteria may change. Students’ achievements with different apps will also be tested over a number of years in the course or degree programme, as an increase in learning has been detected as they are used over successive academic years. It is also intended that a study of the most suitable apps in the area of master’s degrees be carried out. New methods to obtain the objective weights could be developed and compared. Additionally, group decision-making, considering all the teachers in the field the course belongs to, could be involved in the proposed method. This could be applied to the course analysed in this study, or to other courses. This might allow the most suitable gamification apps to be identified for each subject taught. Modern MCDA methods could also be used to validate the method proposed, provided they were adapted to the characteristics of the problem described in this research. One such proposal, for example, is the Characteristic Objects METhod (COMET), which is completely free from the rank reversal phenomenon.