Stochastic Comparisons of Some Distances between Random Variables

Abstract

The aim of this paper is twofold. First, we show that the expectation of the absolute value of the difference between two copies, not necessarily independent, of a random variable is a measure of its variability in the sense of Bickel and Lehmann (1979). Moreover, if the two copies are negatively dependent through stochastic ordering, this measure is subadditive. The second purpose of this paper is to provide sufficient conditions for comparing several distances between pairs of random variables (with possibly different distribution functions) in terms of various stochastic orderings. Applications in actuarial and financial risk management are given.

1. Introduction

Given a bivariate random vector $\mathit{X}=(X_1,X_2)$ with joint distribution function $K_X(x_1,x_2)=P\left(X_1\le x_1,X_2\le x_2\right)$ and marginal distribution functions $F_1\left(x\right)=P[X_1\le x]$ and $F_2\left(x\right)=P[X_2\le x],$ the random variable $|X_1-X_2|$ describes the distance between $X_1$ and $X_2$ in a sense that depends on the dependence structure of the vector. Different structures assign different meanings to this random variable and lead, obviously, to different ways of computing the expectation $E\left(|X_1-X_2|\right).$ The distance can be applied to random variables with identical and non-identical distribution functions, and we consider both cases. If $F_1=F_2=F,$ then $X_1$ and $X_2$ are copies of the same random variable X with distribution function $F\left(x\right)$, and $E\left(|X_1-X_2|\right)$ reveals information about $X.$ An example is the case of independent and identically distributed random variables, in which $E\left(|X_1-X_2|\right)$ is the Gini’s mean difference of $X_1,$ a well-known measure of variability (see, for example, [1]). We show in this work that, when $X_1$ and $X_2$ are dependent copies of the same random variable $X,$ $E\left(|X_1-X_2|\right)$ is still a measure of variability of X. A purpose of this paper is to study the properties of this functional in a general setting, where $X_1$ and $X_2$ are not necessarily independent.

If $X_1$ and $X_2$ are independent (or, more generally, if they are linked by a symmetric dependence structure), $|X_1-X_2|$ treats symmetrically the events $X_1<X_2$ and $X_2<X_1.$ However, sometimes, it is convenient to use a characteristic of proximity by treating them differently (in finance, for example, an investor evaluates differently gains and losses). The random excess of $X_1$ over $X_2,$ ${(X_1-X_2)}^{+},$ where $x^{+}=max\{x,0\}$ denotes the positive part of $x,$ is useful if we are interested in measuring the extent to which one random variable exceeds the other, rather than the distance between them in a bidirectional sense. Note that the absolute value $|X_1-X_2|$ can be split into two terms, each describing the excess of one random variable over the other, as follows:

$$|X_1-X_2|={(X_1-X_2)}^{+}+{(X_2-X_1)}^{+}.$$

If $X_1$ and $X_2$ are copies of the same variable $X,$ then $E({(X_1-X_2)}^{+})$ also reveals information about $X.$ For example, if $X_1$ and $X_2$ are independent, $E({(X_1-X_2)}^{+})$ is Gini’s mean semidifference.

In general, the functional $E\left(\varphi \left(\left|X_1-X_2\right|\right)\right),$ where $\varphi$ is a non-negative real function, has been largely studied in mathematics literature, mainly in the context of the Monge–Kantorovich problem (see [2], and references therein). The interest on this and other functionals used to measure the degree of difference between two random quantities goes back at least to the 1930s and the important contributions by Gini (see [3]) and Hoeffding [4]. Given two random vectors $\mathit{X}=(X_1,X_2)$ and $\mathit{Y}=(Y_1,Y_2),$ another purpose of this paper is to find conditions under which

$$E\left(\mathsf{\Phi }\left(\right|X_1-X_2\left|\right)\right)\le E\left(\mathsf{\Phi }\left(\right|Y_1-Y_2\left|\right)\right),\mathrm{for}\mathrm{all}\mathsf{\Phi }\in \mathsf{\Omega },$$

(1)

where $\mathsf{\Omega }$ is a subset of increasing real functions. Different choices of $\mathsf{\Omega }$ give rise to different stochastic orderings between $|X_1-X_2|$ and $|Y_1-Y_2|.$ This problem was addressed in [5,6,7] for the case where $\mathit{X}$ and $\mathit{Y}$ have independent components with the same marginal distribution functions (see Section 2 below for details). Here, we are concerned with two random vectors $\mathit{X}=(X_1,X_2)$ and $\mathit{Y}=(Y_1,Y_2),$ whose components are not necessarily independent nor are they required to have identical distribution functions. In this case, we explore conditions under which

$$|X_1-X_2|{\le }_{st,icx}|Y_1-Y_2|\mathrm{and}{(X_1-X_2)}^{+}{\le }_{st,icx}{(Y_1-Y_2)}^{+},$$

(2)

where ${\le }_{st}$ and ${\le }_{icx}$ are the usual stochastic order and the increasing convex order, respectively (these orders will be defined in Section 2 below).

This work is organized as follows. Section 2 contains preliminaries, such as definitions and background for the stochastic orders and dependence notions used in this paper, as well as a review of the properties that a variability measure should satisfy. In Section 3, given a random variable X with distribution function F, we show that any functional of the form $\nu \left(X\right)=E\left(\left|X_1-X_2\right|\right),$ where $X_1$ and $X_2$ are two copies of X with any type of dependence structure, is a measure of variability of $X.$ More generally, the distribution function $F_1$ of $X_1$ is allowed to be a distortion of F (we will explain the meaning of this below). In Section 4, given two random vectors $\mathit{X}=(X_1,X_2)$ and $\mathit{Y}=(Y_1,Y_2),$ we obtain conditions (both in terms of the marginals and the copulas) to make comparisons of the form (2). Section 5 contains two applications. In Section 5.1, we define a general class of premium principles based on the class of variability measures studied in Section 3. In Section 5.2, in the context of portfolio risk management, we assess the inclusion of a new asset in a portfolio by using the results obtained in Section 4. Finally, Section 6 contains conclusions.

Throughout this paper, given two random vectors $\mathit{X}=(X_1,X_2)$ and $\mathit{Y}=(Y_1,Y_2),$ we denote by $F_1,F_2$ and $G_1,G_2$ the respective marginal distribution functions. Given any other random variable $Z,$ we denote by $F_Z$ its distribution function.

2. Preliminaries

Let $\mathit{X}=(X_1,X_2)$ be a random vector with joint distribution function $K_X$ and marginal distribution functions $F_1$ and $F_2,$ respectively. According to the Sklar theorem, the joint distribution $K_X$ can be written as

$$K_X\left(x,y\right)=C\left(F_1\left(x\right),F_2\left(y\right)\right),$$

where C is the copula of the random vector $(X_1,X_2),$ that is, the joint distribution function of the vector-copula $\left(F_1\left(X_1\right),F_2\left(X_2\right)\right)$ (see [8]). If $F_1$ and $F_2$ are continuous, then C is unique. The copula contains the information about the structure of dependency of the random vector $\left(X_1,X_2\right).$ For every copula C and every $(u,v)$ on ${[0,1]}^2,$ it is well-known that

$$W(u,v)\le C(u,v)\le M(u,v),$$

(3)

where the copulas $W(u,v)=max(u+v-1,0)$ and $M(u,v)=min(u,v)$ are the Fréchet–Hoeffding bounds. Random variables with copula M are called comonotonic and random variables with copula W are called countermonotonic.

The motivation for the study of the properties of $E\left(\left|X_1-X_2\right|\right),$ where $X_1$ and $X_2$ are not necessarily independent, comes from the fact that some probability metrics and measures of variability that are sometimes better known under other expressions, take this form for different copulas between $X_1$ and $X_2.$ To give some examples, note that

$$E\left(\left|X_1-X_2\right|\right)={\int }_{-\infty }^{\infty }\left(F_1\left(x\right)+F_2\left(x\right)-2C(F_1\left(x\right),F_2\left(x\right))\right)dx.$$

(4)

If $X_1$ and $X_2$ are two copies of a random variable X with distribution function $F\left(x\right),$ (4) becomes

$$E\left(\left|X_1-X_2\right|\right)=2{\int }_{-\infty }^{\infty }\left(F\left(x\right)-C\left(F\right(x),F(x\left)\right)\right)dx.$$

(5)

If $X_1$ and $X_2$ are two independent copies of $X,$ then

$$E\left(\left|X_1-X_2\right|\right)=2\left(E\left(max(X_1,X_2)\right)-E\left(X\right)\right)$$

is the Gini’s mean difference (GMD) of $X,$ a well-known index of variability (see, for example, [1]). If $X_1$ and $X_2$ are comonotonic, then (see [9] or [10])

$$E\left(\left|X_1-X_2\right|\right)={\int }_0^1|F_1^{-1}\left(u\right)-F_2^{-1}\left(u\right)|du={\int }_{-\infty }^{\infty }\left|F_1\left(x\right)-F_2\left(x\right)\right|dx,$$

(6)

which is the Wasserstein distance, a well-known characteristic of proximity of two random variables (see [11]). If $X_1$ and $X_2$ are countermonotonic, then

$$E\left(\left|X_1-X_2\right|\right)={\int }_0^1|F_1^{-1}\left(u\right)-F_2^{-1}(1-u)|du$$

(7)

(see, for example, [2]). It is easy to see that, if $X_1$ and $X_2$ are two copies of $X,$ (7) can be rewritten as

$$E\left(\left|X_1-X_2\right|\right)=2E\left(\left|X-m_X\right|\right),$$

where $m_X$ is the median of $X.$ This measure is twice the median absolute deviation (MAD), another popular measure of variability.

In view of the above examples, it is natural to ask whether $E\left(\left|X_1-X_2\right|\right),$ where $X_1$ and $X_2$ are two copies of X with a copula $C,$ fulfills the requirements to be considered as a measure of variability of $X.$ Recall that a measure of variability $\nu$ is a map from the set of random variables to $\mathbf{R}$, such that given a random variable $X,$ $\nu \left(X\right)$ quantifies the variability of $X.$ Next, we list a set of properties that a measure of variability should reasonably satisfy (see, for example, [12] and references therein):

(P0)

Law invariance: if X and Y have the same distribution, then $\nu \left(X\right)=\nu \left(Y\right).$

(P1)

Translation invariance: $\nu (X+k)=\nu \left(X\right)$ for all X and all constant k.

(P2)

Positive homogeneity: $\nu \left(0\right)=0$ and $\nu \left(\lambda X\right)=\lambda \nu \left(X\right)$ for all X and all $\lambda >0$.

(P3)

Non-negativity: $\nu \left(X\right)\ge 0$ for all $X,$ with $\nu \left(X\right)=0$ if X is degenerated at $c\in \mathbf{R}$.

Bickel and Lehmann [13] also require $\nu \left(X\right)$ to be consistent with the dispersive order. Recall that two random variables X and Y are ordered in the dispersive order if the difference between any two quantiles of X is smaller than the corresponding quantiles of Y, where the quantile function of a random variable X with distribution function F is defined by $F^{-1}\left(\alpha \right)=inf\left\{x:F\left(x\right)\ge \alpha \right\},\alpha \in (0,1).$ The formal definition is as follows.

Definition 1.

Given two random variables X and Y with distribution functions F and G, respectively, we say that X is smaller than Y in the dispersive order (denoted by $X{\le }_{disp}Y)$ if $F^{-1}\left(p\right)-F^{-1}\left(q\right)$ $\le G^{-1}\left(p\right)-G^{-1}\left(q\right)$ for all $0\le q<p\le 1.$

A functional $\nu$ satisfying properties (P0) to (P3) is said to be a measure of variability or spread in the sense of Bickel and Lehmann if it satisfies in addition (see [13]):

(P4)

Consistency with dispersive order: if $X{\le }_{disp}Y$, then $\nu \left(X\right)\le \nu \left(Y\right)$.

A measure of variability in the sense of Bickel and Lehmann considers the variability or spread of a random variable throughout its distribution. Sometimes, however, there is an interest in measuring only the variability of X along the right tail of its distribution (in risk theory, for example, some popular measures focus on the variability of a risk X beyond the value at risk). When this is the case, the requirement on $\nu$ to be consistent with the dispersive order is too strong. A natural weaker requirement is to be consistent with the excess wealth order (see [14]), which is defined as follows.

Definition 2.

Given two random variables X and Y with distribution functions F and G, respectively, we say that X is smaller than Y in the excess wealth order (denoted by $X{\le }_{ew}Y)$ if ${\int }_{F^{-1}\left(p\right)}^{\infty }\overline{F}\left(x\right)dx$ $\le {\int }_{G^{-1}\left(p\right)}^{\infty }\overline{G}\left(x\right)dx,\forall p\in (0,1),$ where $\overline{F}=1-F$ and $\overline{G}=1-G$ are the tail (or survival) functions of X and $Y,$ respectively.

This allows us to consider the following property.

(P5)

Consistency with excess wealth order: if $X{\le }_{ew}Y$, then $\nu \left(X\right)\le \nu \left(Y\right)$.

Measures of variability have received great attention in the actuarial and financial literature (see [12,15,16,17,18], among others). In actuarial science, for example, a variability measure sometimes is combined with a location measure to build a premium principle (see [19]). For particular applications in this context, we may wish $\nu$ to satisfy the following properties:

(P6)

Comonotonic additivity: if X and Y are comonotonic, then $\nu (X+Y)=\nu \left(X\right)+\nu \left(Y\right).$

(P7)

Subadditivity: $\nu (X+Y)\le \nu \left(X\right)+\nu \left(Y\right)$ for all X and $Y.$

Furman et al. [12] say that $\nu$ is a coherent measure of variability if it satisfies (P0)–(P3) and (P7).

Next, we recall some other notions used in this paper. The sequence of inequalities (3) induces the following definition (see [8]).

Definition 3.

Given two copulas C and $C^{\prime },$ we say that C is smaller than $C^{\prime }$ in the concordance order (and write $C\prec C^{\prime }$) if $C(u,v)\le$ $C^{\prime }(u,v)$ for all $u,v\in (0,1)$.

Obviously, $W\prec C\prec M$ for every copula $C.$ The name of this order is due to the fact that some measures of concordance, such as Kendall’s tau and Spearman’s rho, are increasing with respect to $\prec .$

In Section 4 and Section 5, we will make use of the following stochastic orders. The reader may consult the books [20,21,22] for properties and applications.

Definition 4.

Let X and Y be two random variables with distribution functions F and G and finite expectations ${\mu }_X$ and ${\mu }_Y,$ respectively. Then, X is said to be smaller than $Y:$

(i) 

in the usual stochastic order (denoted by $X{\le }_{st}Y)$ if $\overline{F}\left(t\right)\le \overline{G}\left(t\right),$ for all $t,$

(ii) 

in the increasing convex order (denoted by $X{\le }_{icx}Y)$ if ${\int }_t^{\infty }\overline{F}\left(x\right)dx$ $\le {\int }_t^{\infty }\overline{G}\left(x\right)dx,\forall t,$

(iii) 

in the convex order (denoted by $X{\le }_{cx}Y)$ if $E\left(X\right)=E\left(Y\right)$ and $X{\le }_{icx}Y,$

(iv) 

in the increasing concave order (denoted by $X{\le }_{icv}Y)$) if ${\int }_{-\infty }^{t}F\left(x\right)dx$ $\ge {\int }_{-\infty }^{t}G\left(x\right)dx,\forall t.$

It can be shown that $X{\le }_{st}Y$ (respectively ${\le }_{cx},{\le }_{icx},{\le }_{icv}$) if and only if $E\left(\varphi \right(X\left)\right)$ $\le E\left(\varphi \right(Y\left)\right)$ for all increasing (respectively convex, increasing convex, increasing concave) functions $\varphi$ for which the expectations exist. When $X_2$ and $Y_2$ are independent copies of $X_1$ and $Y_1,$ respectively, it is well-known (see [5] and [6]) that

• $X_1{\le }_{disp}{Y}_1$ implies $|X_1-X_2|{\le }_{st}|Y_1-Y_2|,$
• $X_1{\le }_{ew,cx}{Y}_1$ implies $|X_1-X_2|{\le }_{icx}|Y_1-Y_2|.$

The result for the convex order was extended to the so-called s-convex order in [7]. In Section 3 and Section 4, we extend these results to the case where $X_2$ and $Y_2$ are not necessarily independent from (nor are they required to have identical distribution functions as) $X_1$ and $Y_1,$ respectively. For this, we need the following notions (see [23,24]).

Definition 5.

Let $\mathit{X}=(X_1,X_2)$ be a random vector.

(i) 

We say that $X_1$ is stochastically increasing in $X_2,$ denoted by $X_1{\uparrow }_{SI}{X}_2$, if $P[X_1>x_1\mid X_2=x_2]$ is a nondecreasing function of $x_2$ for all $x_1.$

(ii) 

We say that $\mathit{X}=(X_1,X_2)$ is positively dependent through stochastic ordering (PDS) if $X_1{\uparrow }_{SI}{X}_2$ and $X_2{\uparrow }_{SI}{X}_1.$

Intuitively, if $\mathit{X}=(X_1,X_2)$ is PDS, then its components are more likely simultaneously to have large values, compared with a vector of independent random variables with the same marginal distributions. For relationships between this and other dependence notions see, for example, Table 2 in [25]. The negative dependence analog of Definition 5 is as follows (see [24]).

Definition 6.

Let $\mathit{X}=(X_1,X_2)$ be a random vector.

(i) 

We say that $X_1$ is stochastically decreasing in $X_2,$ denoted by $X_1{\downarrow }_{SD}{X}_2$, if $P[X_1>x_1\mid X_2=x_2]$ is a nonincreasing function of $x_2$ for all $x_1.$

(ii) 

We say that $\mathit{X}=(X_1,X_2)$ is negatively dependent through stochastic ordering (NDS) if $X_1{\downarrow }_{SD}{X}_2$ and $X_2{\downarrow }_{SD}{X}_1.$

Intuitively, if $\mathit{X}=(X_1,X_2)$ is NDS, one component of the vector will tend to be large when the other component is small. It is easy to see that a random vector $\mathit{X}$ with continuous marginals is PDS (respectively, NDS) if and only if $C(u,v)$ is componentwise concave (respectively, convex). It is also well-known (see [26]) that a continuous random vector $\mathit{X}$ with copula C has the property PDS (resp. NDS) if and only if its copula C is PDS (resp. NDS).

3. A Family of Measures of Variability

Let $X_1$ and $X_2$ be two random variables with respective continuous distribution functions $F_1$ and $F_2$ and finite expectations. If $X_1$ and $X_2$ are two independent copies of $X,$ it is well-known (see [13]) that $\nu \left(X\right)=E\left(\left|X_1-X_2\right|\right)$ is a measure of variability in the sense of Bickel and Lehmann (that is, it satisfies properties (P0) to (P4)). Let h be a distortion function, that is, a non-decreasing function from $[0,1]$ to $[0,1]$ such that $h\left(0\right)=0$ and $h\left(1\right)=1$ (given two distribution functions F and $G,$ if $G=h\circ F$ we say that G is a distortion of F via h). In this section, we show that any functional of the form $E\left(\left|X_1-X_2\right|\right),$ where $F_2=F$ and $F_1=h\circ F,$ is a measure of variability of $X.$ In particular, if h is the identity function ($h\left(t\right)=t,$ for all $t\in [0,1]$) and $X_1$ and $X_2$ have a NDS copula, this measure satisfies all the properties (P1 to P7) listed above.

The following theorem extends a result of [5], stated as Theorem 3.B.42 in the book [20], in two directions: first, we consider two random vectors with the same copula instead of two random vectors with independent components; and, second, we allow the first marginal of each vector to be a distortion of the other (via the same h) instead of taking two copies of the same random variable.

Theorem 7.

Let X and Y be two random variables with distribution functions F and $G,$ respectively and let h be a distortion function. Let $\mathit{X}=\left(X_1,X_2\right)$ be a random vector with respective marginal distribution functions $F_1=h\circ F$ and $F_2=F.$ Similarly, let $\mathit{Y}=\left(Y_1,Y_2\right)$ be a random vector with marginal distribution functions $G_1=h\circ G$ and $G_2=G,$ respectively. Suppose that $\mathit{X}$ and $\mathit{Y}$ have the same copula $C.$ If $X{\le }_{disp}Y$, then $\left|X_2-X_1\right|{\le }_{st}\left|Y_2-Y_1\right|.$

Proof. 

Since the dispersive order is preserved by distortion functions (Theorem 13 in [27]), we have $X_1{\le }_{disp}{Y}_1$ and $X_2{\le }_{disp}{Y}_2.$ Since $\mathit{X}$ and $\mathit{Y}$ have the same copula, it follows from Definition 2.1 in [28] and Theorem 1 in [29] that there exists a function $\mathsf{\Phi }$ that maps stochastically $(X_1,X_2)$ into $(Y_1,Y_2)$, i.e., $\mathsf{\Phi }(X_1,X_2){=}_{st}(Y_1,Y_2)$, defined as

$$\mathsf{\Phi }(x_1,x_2)=({\mathsf{\Phi }}_1\left(x_1\right),{\mathsf{\Phi }}_2\left(x_2\right))=(G_1^{-1}\left(F_1\left(x_1\right)\right),G_2^{-1}\left(F_2\left(x_2\right)\right)),$$

where ${\mathsf{\Phi }}_i(·)$, $i=1,2$, is an increasing function that satisfies

$$\left|{\mathsf{\Phi }}_i\left(x\right)-{\mathsf{\Phi }}_i\left(x^{\prime }\right)\right|\ge \left|x-x^{\prime }\right|,\forall x,x^{\prime }\in \mathbb{R}.$$

(8)

It follows from the assumptions that ${\mathsf{\Phi }}_2\left(x\right)={\mathsf{\Phi }}_1\left(x\right)=G^{-1}F\left(x\right)$ for all x. Therefore,

$$\begin{array}{ccc}\hfill \left|Y_2-Y_1\right|& {=}_{st}& \left|{\mathsf{\Phi }}_2\left(X_2\right)-{\mathsf{\Phi }}_1\left(X_1\right)\right|,\hfill \\ & {=}_{st}& \left|{\mathsf{\Phi }}_1\left(X_2\right)-{\mathsf{\Phi }}_1\left(X_1\right)\right|,\hfill \\ & {\ge }_{st}& \left|X_2-X_1\right|,\hfill \end{array}$$

(9)

where the first and second equality in (9) follow from the fact that $\mathsf{\Phi }(X_1,X_2){=}_{st}(Y_1,Y_2)$ and ${\mathsf{\Phi }}_2(·)={\mathsf{\Phi }}_1(·)$, respectively. The inequality follows from (8) by using Theorem 1.A.1 in [20]. □

By taking $h\left(x\right)=x$ in Theorem 7, we have the following corollary.

Corollary 8.

Let $X_2$ and $Y_2$ be two copies of $X_1$ and $Y_1,$ respectively, such that $\mathit{X}=(X_1,X_2)$ and $\mathit{Y}=(Y_1,Y_2)$ have the same copula. If $X_1{\le }_{disp}{Y}_1$, then $|X_1-X_2|{\le }_{st}|Y_1-Y_2|.$

Remark 9.

Given two random vectors $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ with the same copula, the condition $X_i{\le }_{disp}{Y}_i,i=1,2$ is equivalent to say that the bivariate random vectors $\mathit{X}$ and $\mathit{Y}$ are ordered in a multivariate dispersion sense, see [30].

Now, we can prove the following result.

Theorem 10.

Let X be a random variable with strictly increasing distribution function F and let h be a strictly increasing distortion function. Let $X_1$ and $X_2$ be two random variables with copula C and marginal distribution functions $F_1$ and $F_2,$ respectively. Let ${\nu }_C\left(X\right)=E\left(\left|X_1-X_2\right|\right).$

(i) 

If $F_1=h\circ F$ and $F_2=F,$ then ${\nu }_C\left(X\right)$ is a comonotonic additive measure of variability in the sense of Bickel and Lehmann, that is, it satisfies properties (P0)–(P4) and (P6).

(ii) 

If $F_1=F_2=F$ and the copula C is NDS, then ${\nu }_C\left(X\right)$ satisfies all the properties (P0) to (P7).

Proof. 

We first prove (i). Let C be the copula of $X_1$ and $X_2$. From (4), we have

$$\begin{array}{ccc}\hfill {\nu }_C\left(X\right)& =& {\int }_{-\infty }^{\infty }\left(h\left(F\right(x)\right)+F\left(x\right)-2C(h\left(F\left(x\right)\right),F\left(x\right))dx\hfill \\ & =& {\int }_0^1\left(h\left(u\right)+u-2C\left(h\right(u),u)\right)d{F}^{-1}\left(u\right).\hfill \end{array}$$

(10)

Clearly, ${\nu }_C\left(X\right)=0$ if X is degenerated at $c\in \mathbf{R}$. This, together with the fact that $F^{-1}$ is non-decreasing, $F_{X+k}^{-1}\left(x\right)=F_X^{-1}\left(x\right)+k,$ for all k and $F_{\lambda X}^{-1}\left(x\right)=\lambda F_X^{-1}\left(x\right),$ for all $\lambda >0$ (see [31]), ensures that ${\nu }_C\left(X\right)$ satisfies properties (P0) to (P3). Since, given two random variables $Z_1$ and $Z_2,$ the condition $Z_1{\le }_{st}{Z}_2$ implies that $E\left(Z_1\right)\le E\left(Z_2\right),$ property (P4) (consistency of ${\nu }_C\left(X\right)$ with respect to the dispersive order) is a direct consequence of Theorem 7. Property (P6) follows from the fact that, if $Z_1$ and $Z_2$ are comonotonic, then $F_{Z_1+Z_2}^{-1}\left(u\right)=F_{Z_1}^{-1}\left(u\right)+F_{Z_2}^{-1}\left(u\right),$ for all $u\in (0,1)$ (see [32]). Under the assumptions in (ii), we have

$${\nu }_C\left(X\right)=2{\int }_0^1\left(u-C(u,u)\right)d{F}^{-1}\left(u\right).$$

(11)

Standard arguments show that

$$\underset{u\to i}{lim}{F}^{-1}\left(u\right)\left(u-C(u,u)\right)=0,i=0,1.$$

Therefore, integrating (11) by parts, we get

$${\nu }_C\left(X\right)=2{\int }_0^1{F}^{-1}\left(u\right)d\left(C(u,u)-u\right).$$

Since C is componentwise convex, (P5) follows from Theorem 8. (ii) in [33] and (P7) follows from Theorem 2.1 in [12]. □

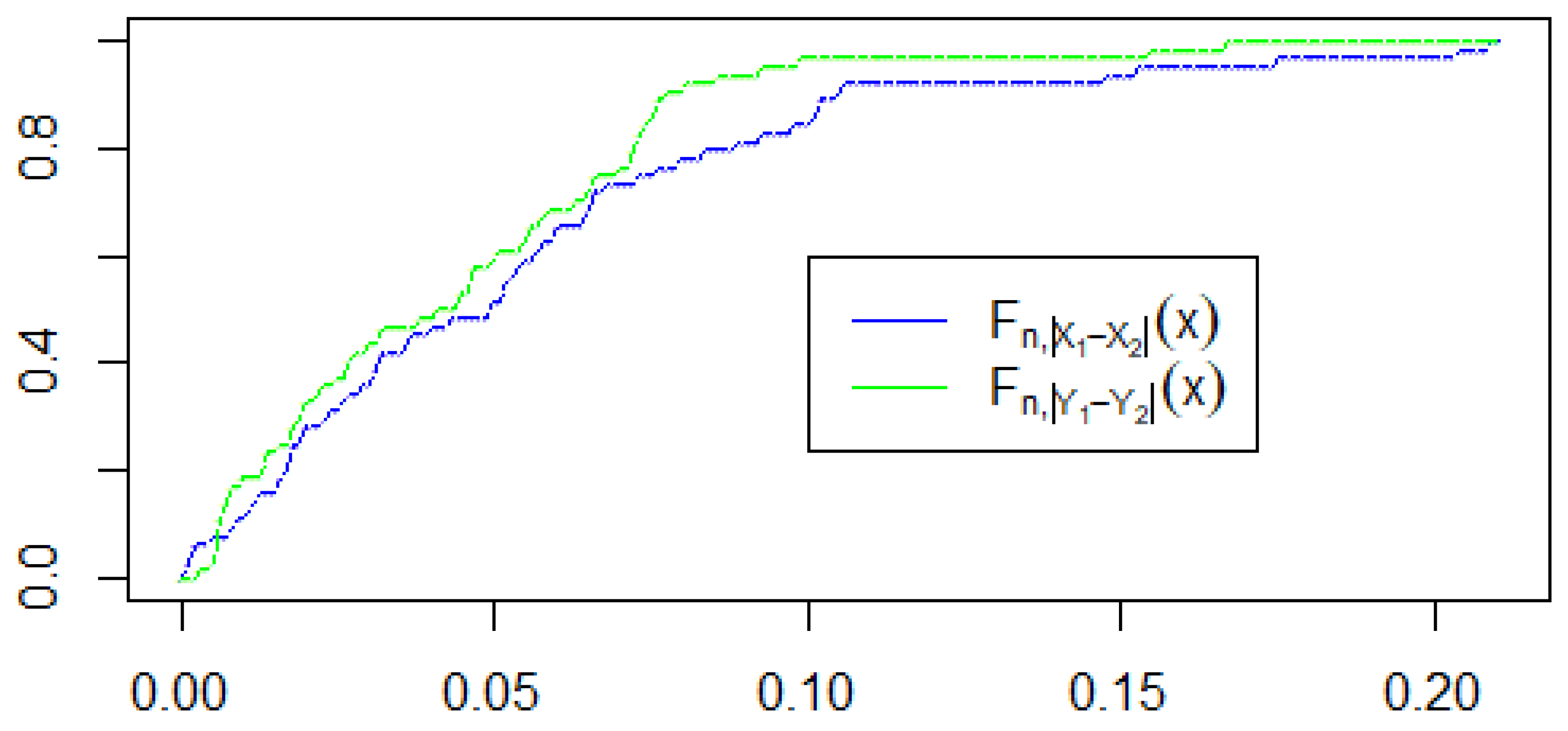
Example 11.

Two functionals satisfying the assumptions of part (i) are ${\nu }_{C_1}\left(X\right)=GMD\left(X\right)$ and ${\nu }_{C_2}\left(X\right)={\int }_{-\infty }^{\infty }\left|F_h\left(x\right)-F\left(x\right)\right|dx,$ which is the Wasserstein distance between F and its distortion $F_h=h\circ F,$ a variability measure introduced by [34]. Note that ${\nu }_{C_2}\left(X\right)=E\left(\left|X_1-X_2\right|\right),$ where $F_1=h\circ F,$ $F_2=F$ and $C_2$ is the Fréchet–Hoeffding upper bound copula (see (6)).

Example 12.

Using (7), it follows from Theorem 10 (ii) that ${\nu }_C\left(X\right)=E\left(\left|X-m_X\right|\right),$ where $m_X$ is the median of $X,$ satisfies all the properties (P0) to (P7) listed above. This measure can be written in the form $\frac{1}{2}E\left(\left|X_1-X_2\right|\right)$ where $F_1=F_2=F$ and where C is the Fréchet–Hoeffding lower bound copula (see (7) and the paragraph below it), which is an example of NDS copula (see [35] for this and other examples of NDS copulas).

4. Other Stochastic Comparisons

To begin this section, we consider two random vectors $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ with the same marginals. Denote by $\mathcal{R}(F_1,F_2)$ the space of bidimensional random vectors with marginal distribution functions $F_1$ and $F_2.$

Theorem 13.

Let $\mathit{X}=(X_1,X_2)\in \mathcal{R}(F_1,F_2)$ and $\mathit{Y}=(Y_1,Y_2)\in \mathcal{R}(F_1,F_2)$ be two random vectors with copulas C and $C^{\prime },$ respectively. If $C^{\prime }\prec C$, then:

(i) 

$|X_1-X_2|{\le }_{icx}|Y_1-Y_2|.$

(ii) 

${(X_1-X_2)}^{+}{\le }_{icx}{(Y_1-Y_2)}^{+}.$

Proof. 

Under the assumptions, it follows from Theorem 4 of [36] that $X_1-X_2{\le }_{icx}{Y}_1-Y_2.$ This means that $E\left(\mathsf{\Phi }(X_1-X_2)\right)\le E\left(\mathsf{\Phi }(Y_1-Y_2)\right)$ for all increasing convex $\mathsf{\Phi }$. Since $\mathsf{\Phi }\left(t\right)=\mathsf{\Psi }\left(\right|t\left|\right)$ is increasing and convex for any increasing convex function $\mathsf{\Psi },$ it follows that $E\left(\mathsf{\Psi }|X_1-X_2|\right)\le E\left(\mathsf{\Psi }|Y_1-Y_2|\right)$ for all increasing and convex $\mathsf{\Psi },$ which proves (i). The proof of (ii) is similar using the function $\mathsf{\Phi }\left(t\right)=\mathsf{\Psi }\left({\left(t\right)}^{+}\right).$ □

Remark 14.

An alternative proof of Theorem 13 can be given by using Theorem 1 in [37], which provides conditions to ensure, under the above assumptions, that $E\left(k(X_1,Y_2)\right)\ge E\left(k(Y_1,Y_2)\right)$ for certain classes of functions k. The proof is based on proving that the functions $k(x,y)=\varphi |x-y|$ and $k(x,y)=\varphi {(x-y)}^{+},$ with ϕ increasing and convex, satisfy those conditions.

A more general type of comparison can be made between two random vectors with possibly different (but stochastically ordered) marginals. The following two results provide conditions to compare two random excesses. The first result is given in terms of the usual stochastic order and the second result in terms of the increasing convex order.

Theorem 15.

Let $\mathit{X}=\left(X_1,X_2\right)$ be a random vector with respective marginal distribution functions $F_1$ and $F_2.$ Similarly, let $\mathit{Y}=\left(Y_1,Y_2\right)$ be a random vector with marginal distribution functions $G_1$ and $G_2,$ respectively. If $\mathit{X}$ and $\mathit{Y}$ have the same copula $C,$ $X_1{\le }_{st}{Y}_1$ and $X_2{\ge }_{st}{Y}_2$, then ${\left(X_1-X_2\right)}^{+}{\le }_{st}{\left(Y_1-Y_2\right)}^{+}.$

Proof. 

For $x\ge 0$,

$$\begin{array}{ccc}\hfill {\overline{F}}_{{\left(X_1-X_2\right)}^{+}}\left(x\right)& =& 1-{\int }_{-\infty }^{+\infty }P[X_1\le F_2^{-1}\left(p\right)+x|X_2=F_2^{-1}\left(p\right)]dp\hfill \\ & =& 1-{\int }_0^1{\partial }_{2}C(F_1(F_2^{-1}\left(p\right)+x),p)dp,x>0.\hfill \end{array}$$

Therefore, given $x\ge 0$,

$$\begin{array}{ccc}& & {\overline{G}}_{{(Y_1-Y_2)}^{+}}\left(x\right)-{\overline{F}}_{{(X_1-X_2)}^{+}}\left(x\right)\hfill \\ & =& {\int }_0^1({\partial }_{2}C(F_1(F_2^{-1}\left(p\right)+x),p)-{\partial }_{2}C(G_1(G_2^{-1}\left(p\right)+x),p))dp\ge 0,\hfill \end{array}$$

Since $G_1\left(x\right)\le F_1\left(x\right)$ for all $x,$ $G_2^{-1}\left(p\right)\le F_2^{-1}\left(p\right)$ for all $p\in (0,1)$ and ${\partial }_{2}C$ increases in the first argument (since ${\partial }_{2}C(u,p)$ is the distribution function of the random variable ($U|V=p$)). Therefore, ${\overline{F}}_{{(X_1-X_2)}^{+}}\left(x\right)\le {\overline{G}}_{{(Y_1-Y_2)}^{+}}\left(x\right)$ for all $x\ge 0,$ which ends the proof. □

Theorem 16.

Let $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ be two random vectors with copulas C and $C^{\prime }$, and marginal distribution functions $F_1,F_2$ and $G_1,G_2,$ respectively. If C is NDS, $C^{\prime }\prec C$, $X_1{\le }_{icx}{Y}_1$ and $X_2{\ge }_{icv}{Y}_2,$ then ${\left(X_1-X_2\right)}^{+}{\le }_{icx}{\left(Y_1-Y_2\right)}^{+}.$

Proof. 

Let us consider a vector ${\mathit{Y}}^{\mathbf{\ast }}=(Y_1^{\ast },Y_2^{\ast })$ with copula C and such that $Y_i^{\ast }{=}_{st}{Y}_i$ for $i=1,2$. From the assumptions, it follows that $X_2{\ge }_{icv}{Y}_2^{\ast },$ which is equivalent to say that $-X_2{\le }_{icx}-Y_2^{\ast }$ (Theorem 4.A.1 in [20]). Since $\mathit{X}$ and ${\mathit{Y}}^{\mathbf{\ast }}$ have the same copula $C,$ the random vectors $\widehat{\mathit{X}}=(X_1,-X_2)$ and $\widehat{\mathit{Y}}=(Y_1^{\ast },-Y_2^{\ast })$ have the same copula $\widehat{C}(u,v)=u-C(u,1-v)$. Moreover, since C is NDS (that is, componentwise convex), then $\widehat{C}(u,v)$ is PDS (that is, componentwise concave). It follows from Corollary 2.7 in [38] that $X_1-X_2{\le }_{icx}{Y}_1^{\ast }-Y_2^{\ast }.$ Since $C^{\prime }\prec C,$ it follows from Theorem 13 that $Y_1^{\ast }-Y_2^{\ast }{\le }_{icx}{Y}_1-Y_2.$ The result follows by using the fact that the increasing convex order is transitive and is preserved by the increasing convex transformation $\varphi \left(t\right)=t^{+}$ (see Theorem 4.A.8(a) in [20]). □

Remark 17.

In particular, Theorem 16 holds when $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ have the same NDS copula $C.$ In this case, $X_1{\le }_{icx}{Y}_1$ and $X_2{\ge }_{icv}{Y}_2$ imply ${\left(X_1-X_2\right)}^{+}{\le }_{icx}{\left(Y_1-Y_2\right)}^{+}.$

Lemma 18.

Let X and Y be two random variables that are symmetric about 0. Then:

(i) 

If $X^{+}{\le }_{st}{Y}^{+}$, then $\left|X\right|{\le }_{st}\left|Y\right|.$

(ii) 

If $X^{+}{\le }_{icx}{Y}^{+}$, then $\left|X\right|{\le }_{icx}\left|Y\right|.$

Proof. 

Let ${\overline{F}}_{X^{+}}$ and ${\overline{F}}_{\left|X\right|}$ be the tail functions of $X^{+}$ and $\left|X\right|,$ respectively. If X and Y are symmetric about 0, it is easy to see that ${\overline{F}}_{\left|X\right|}\left(t\right)=h\left({\overline{F}}_{X^{+}}\left(t\right)\right)$ for all $t,$ where h is the concave distortion function

$$h\left(t\right)=\left\{\begin{array}{ccc}2t\hfill & \mathrm{if}& 0\le t\le 1/2\\ 1\hfill & \mathrm{if}& 1<2t\le 1.\end{array}\right.$$

Now (i) and (ii) follow, respectively, from Theorem 2.6 (i) and Theorem 2.6 (v) in [39]. □

The following result follows immediately from Theorem 15 and Lemma 18.

Corollary 19.

Let $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ be two random vectors with the same copula C and with marginal distribution functions $F_1,F_2$ and $G_1,G_2,$ respectively. If $X_1{\le }_{st}{Y}_1$ and $X_2{\ge }_{st}{Y}_2,$ then $\left|X_1-X_2\right|{\le }_{st}\left|Y_1-Y_2\right|.$

The following result is also an immediate corollary of Theorem 16 and Lemma 18.

Corollary 20.

Let $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ be two random vectors with symmetric copulas C and $C^{\prime }$, and marginal distribution functions $F_1,F_2$ and $G_1,G_2,$ respectively. If C is NDS, $C^{\prime }\prec C$, $X_1{\le }_{icx}{Y}_1$ and $X_2{\ge }_{icv}{Y}_2,$ then $\left|X_1-X_2\right|{\le }_{icx}\left|Y_1-Y_2\right|.$

Remark 21.

In particular, Corollary 20 holds when $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ have the same symmetric NDS copula $C.$ When this is the case, $X_1{\le }_{icx}{Y}_1$ and $X_2{\ge }_{icv}{Y}_2$ imply $\left|X_1-X_2\right|{\le }_{icx}\left|Y_1-Y_2\right|.$

Since the independence copula is both NDS and PDS, a particular case of Corollaries 19 and 20 is the following.

Corollary 22.

Let $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ be two random vectors with independent components and with marginal distribution functions $F_1,F_2$ and $G_1,G_2,$ respectively.

(i) 

If $X_1{\le }_{st}{Y}_1$ and $X_2{\ge }_{st}{Y}_2,$ then $\left|X_1-X_2\right|{\le }_{st}\left|Y_1-Y_2\right|.$

(ii) 

If $X_1{\le }_{icx}{Y}_1$ and $X_2{\ge }_{icv}{Y}_2,$ then $\left|X_1-X_2\right|{\le }_{icx}\left|Y_1-Y_2\right|.$

The following corollaries extend Lemma 2.2 in [6] from the case of two random vectors with independent components to the case of two random vectors with the same symmetric NDS copula.

Corollary 23.

Let $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ be two random vectors with the same symmetric NDS copula C and with marginal distribution functions $F_1,F_2$ and $G_1,G_2,$ respectively. If $X_1{\le }_{cx}{Y}_1$ and $X_2{\le }_{cx}{Y}_2,$ then $\left|X_1-X_2\right|{\le }_{icx}\left|Y_1-Y_2\right|.$

Proof. 

The assumption $X_1{\le }_{cx}{Y}_1$ implies $X_1{\le }_{icx}{Y}_1.$ Since $X_2{\le }_{cx}{Y}_2$ holds if and only if $-X_2{\le }_{cx}-Y_2$ (Theorem 3.A.12 in [20]), it follows $-X_2{\le }_{icx}-Y_2.$ This is equivalent to write $X_2{\ge }_{icv}{Y}_2;$ therefore, the result follows from Corollary 20. □

Corollary 24.

Let $\mathit{X}=\left(X_1,X_2\right)$ and $\mathit{Y}=\left(Y_1,Y_2\right)$ be two random vectors with the same symmetric NDS copula, such that $X_2{=}_{st}{X}_1$ and $Y_1{=}_{st}{Y}_2$, all variables having finite means. If $X_1{\le }_{ew}{Y}_1$, then $\left|X_1-X_2\right|{\le }_{icx}\left|Y_1-Y_2\right|.$

Proof. 

It is well-known (see (3.C.7) in [20]) that $X_1{\le }_{ew}{Y}_1$ implies $X_1-E\left(X_1\right){\le }_{cx}{Y}_1-E\left(Y_1\right)$. The result follows from Corollary 23. □

5. Applications

5.1. An Application in Actuarial Science

In actuarial theory, a premium principle is a decision rule used by the insurer in order to determine the price for a risk to be insured. More formally, given a random variable X describing an insurance risk, a premium principle T assigns to X a number $T\left(X\right)$ which is the premium to be charged for accepting the risk X (see [19] for an overview). The simplest premium principle is the net premium $T\left(X\right)=E\left(X\right),$ which does not load for risk. More general premium principles are obtained by adding a load to the net premium that reflects the danger associated with the risk. Since the danger is often interpreted in terms of variability, a number of premium principles are obtained by adding to the net premium a risk load proportional to a specific measure of variability. Examples include the following:

• $T_1\left(X\right)=E\left(X\right)+\lambda \sqrt{Var\left[X\right]}$, with $\lambda >0$ (standard deviation premium principle)
• $T_2\left(X\right)=E\left(X\right)+\lambda GMD\left(X\right),$ with $\lambda >0$ (Gini’s premium principle)
• $T_3\left(X\right)=E\left(X\right)+\lambda E\left(\left|X-m_X\right|\right),$ with $\lambda >0$ (Denneberg’s premium principle)
• $T_4\left(X\right)=E\left(X\right)+{\int }_{-\infty }^{\infty }{\left|F_h\left(x\right)-F\left(x\right)\right|}^{p}dx,$ where $p\ge 0$ and h is a distortion function (see [34,40]).

Other examples can be found in [41]. Following this schema, we define a general class of premium principles based on distances between random variables.

Definition 25.

Given a risk X with distribution function $F,$ let $\mathfrak{F}$ be the family of premium principles of the form

$$T_C\left(X\right)=E\left(X\right)+\lambda E\left(\left|X_1-X_2\right|\right),\mathit{for}\mathit{some}\lambda >0,$$

where $X_1$ and $X_2$ are two copies of X such that $X_1$ and $X_2$ have copula $C.$

From the results in Section 2, we see that $T_2,T_3$ and $T_4$ (for $p=1$) are premium principles that belong to the family $\mathfrak{F}$ for different choices of the copula $C.$ Moreover, it follows from Theorem 10 that a premium principle $T_C\in \mathfrak{F}$ satisfies the following properties:

(a)

Risk loading: $T_C\left(X\right)\ge E\left(X\right)$.

(b)

Non unjustified risk loading: If $X=k\ge 0$ (k constant), then $T_C\left(X\right)=k.$

(c)

Translation invariance: $T_C(X+k)=T\left(X\right)+k$ for all constant k.

(d)

Scale invariance: $T_C\left(bX\right)=b{T}_C\left(X\right)$ for all constant $b>0$.

(e)

Comonotonic additivity: if X and Y are comonotonic, then $T_C(X+Y)=T_C\left(X\right)+T_C\left(Y\right).$

(f)

Subadditivity: if C is NDS, then $T_C(X+Y)\le T_C\left(X\right)+T_C\left(Y\right)$ for all X and $Y.$

A premium principle satisfying the above properties that does not follow the schema $T\left(X\right)=E\left(X\right)+\lambda D\left(X\right),$ where D is a measure of variability of $X,$ is the distortion premium principle [32], defined by

$$T_h\left(X\right)=-{\int }_{-\infty }^0(1-h\left[\overline{F}\left(x\right)\right])\mathrm{d}x+{\int }_0^{\infty }h\left[\overline{F}\left(x\right)\right]\mathrm{d}x,$$

where h is a concave distortion function. Our next result is related to a property of $T_h.$ Recall that, given a random variable Z with distribution function $F_Z,$ the family

$${\mathsf{\Pi }}_Z\equiv \left\{X=\mu +\sigma Z:\mu \in \mathbb{R},\sigma >0\right\}$$

is called a location-scale family of random variables. It is shown in [42] that the distortion premium principle $T_h$ reduces to $T_1$ (the standard deviation premium principle) for location-scale families of distributions. Next, we give a similar result involving the premium principle $T_C$ given in Definition 25.

Theorem 26.

Consider a location scale family ${\mathsf{\Pi }}_Z$ and let $T_C\in \mathfrak{F}.$ Then, $T_C$ reduces to $T_1$ (standard deviation premium principle) or, equivalently, to $T_h$ (ditortion premium principle) on ${\mathsf{\Pi }}_Z.$

Proof. 

Since $T_1$ is a special case of $T_h$ on location-scale families of distributions [42], it suffices to prove that $T_C$ reduces to $T_h$ on ${\mathsf{\Pi }}_Z.$ Let $X\in {\mathsf{\Pi }}_Z.$ Since $F_X\left(x\right)=F_Z\left(\frac{x-\mu }{\sigma }\right)$ for all $x,$ if $X_1$ and $X_2$ are two copies of X with copula $C,$ we have

$$\begin{array}{ccc}\hfill T_C\left(X\right)& =& E\left(X\right)+\lambda E\left[\left|X_1-X_2\right|\right]\hfill \\ & =& \mu +\sigma E\left(Z\right)+2\lambda {\int }_{-\infty }^{\infty }\left(F_X\left(x\right)-C(F_X\left(x\right),F_X\left(x\right))\right)dx\hfill \\ & =& \mu +\sigma E\left(Z\right)+2\lambda {\int }_{-\infty }^{\infty }\left(F_Z\left(z\right)-C(F_Z\left(z\right),F_Z\left(z\right))\right)\sigma dz\hfill \\ & =& \mu +\sigma E\left(Z\right)+2\lambda \sigma E\left[\left|Z_1-Z_2\right|\right],\hfill \end{array}$$

where $Z_1$ and $Z_2$ are two copies of Z with copula C (here, we have used that copulas are invariant for strictly monotone transformations of the random variables). Now, we equate this expression with $T_h\left(X\right)$ to obtain

$$\lambda =\frac{T_h\left(Z\right)-E\left(Z\right)}{E\left[\left|Z_1-Z_2\right|\right]}$$

where we have used that $T_h\left(X\right)=\mu +\sigma T_h\left(Z\right),$ because $T_h$ is scale and translation invariant. Observe that $\lambda$ is independent of $\mu$ and $\sigma$; therefore, we conclude that $T_C$ reduces to $T_h$ on C. □

5.2. An Application in Portfolio Risk Management

In portfolio risk management, investors diversify portfolios to reduce market risk. On average, a portfolio with several assets exhibits, unless they are perfectly correlated, less variability in returns than a portfolio with only one asset. To illustrate the results in Section 4, let us consider an investor whose portfolio has only one asset A with log-return $X_2.$ During the diversification process, the investor is concerned with the risk of two assets B and C with log-returns $X_1$ and $Y_1,$ respectively, that might be included in her/his portfolio. Here, the risk of these two assets B and C must be considered in relation to the asset A, which acts as a hedge. One way to assess the impact of each of these two assets is by comparing the distances $\left|X_1-X_2\right|$ and $|Y_1-X_2|$ in some stochastic sense. A smaller distance suggests a higher degree of similarity between the log-returns of the assets when evaluated jointly. If the assets B and C move in the opposite direction as the hedge A, a higher degree of similarity with A intuitively reduces the risk of the diversified portfolio. An alternative method to asses the impact of B and C on the portfolio is by using measures of contagious (see Section 4 in [43]).

Recall that the log return of an asset at week t is defined by $r_t=log(p_t/p_{t-1})$, where $p_t$ is the price of the asset at week t. For our empirical example, we work with log-returns of three stocks included in Nasdaq Composite index: Zoom Video Communications ($X_1$), Moderna ($Y_1$) and Booking Holdings Inc ($X_2=Y_2$) (we have selected three companies that were affected differently at the beginning of the financial crisis of COVID-19). The study is based on samples of size n = 64 for each financial institution ($\left\{x_{1i}\right\}$, $\left\{y_{1i}\right\}$ and $\{x_{2i}=y_{2i}\},$ for $i=1,\dots ,64$), measuring the share value from 23 December 2019 until 15 March 2021. Data were gathered from the public website http://es.finance.yahoo.com, accessed on 22 March 2021, and are related to the weekly close of trading to eliminate the time dependent effect. Suppose that, initially, the whole portfolio of our investor consists of stocks in only one company: Booking Holdings, Inc. To reduce risk, the investor plans to invest either in Zoom or Moderna and faces the problem of which of them should be chosen. A method that helps to make a decision, as explained above, is to compare the distances between the components of the random vectors $\mathit{X}=(X_1,X_2)$ and $\mathit{Y}=(Y_1,Y_2).$

Figure 1 plots the empirical distribution function of sample absolute differences $|x_{1i}-x_{2i}|$ between Zoom and Booking (green curve) and $|y_{1i}-y_{2i}|$ between Moderna and Booking (blue curve), for $i=1,\dots ,64$. The blue curve starts above; at some point around $x=0.005$, it crosses from above to below the green curve and, after that point, it seems to be everywhere below. The graphic is consistent with a model where $|X_1-X_2|$ and $|Y_1-Y_2|$ are ordered in the increasing convex order. Next, we give statistical significance to this conclusion.

We first perform some tests to study the marginal distributions of $X_1,X_2$ and $Y_1$. In order to check randomness, the classical runs test is performed with p-values 0.6143, 0.3134 and 0.2077, respectively. Symmetry is tested using the symmetry test by [44], obtaining p-values 0.388, 0.81, and 0.174, respectively. The Kolmogorov–Smirnov test for normality gives, respectively, the p-values 0.5424, 0.9154, and 0.3486. Therefore, there is not significant evidence to reject the hypothesis that the three log return distributions are random, symmetric, and normal.

A unilateral F-test for paired data, performed for testing the hypothesis of equality of variances against ${\sigma }_{X_1}<{\sigma }_{Y_1},$ gives a p-value of 0.000493, showing significant evidence that ${\sigma }_{X_1}<{\sigma }_{Y_1}$. The p-value of the t-test for testing ${\mu }_{X_1}={\mu }_{Y_1}$ against ${\mu }_{X_1}\ne {\mu }_{Y_1}$ is 0.7124, so we can not reject the equality of means. From the assumptions of normality, ${\mu }_{X_1}={\mu }_{Y_1}$ and ${\sigma }_{X_1}<{\sigma }_{Y_1}$, it follows $X_1{\le }_{icx}{Y}_1$ (see Table 2.2 in [22]).

The copulas C and $C^{\prime }$ are adjusted by using the goodness of fit test based on Kendall’s process [45,46]. Considering a bivariate normal (BN) copula, we obtain p-values 0.74 and 0.79, respectively; therefore, there is not statistical evidence to reject that C and $C^{\prime }$ are BN. Since the bivariate normal copula parameter is the Pearson correlation coefficient ${\rho }_{\mathbf{X}}$, we perform the Williams’s Test (bilateral) [47,48] for testing the hypothesis ${\rho }_{\mathbf{X}}={\rho }_{\mathbf{Y}}$ against ${\rho }_{\mathbf{X}}\ne {\rho }_{\mathbf{Y}}$ when the vectors share one component ($X_2=Y_2$). The p-value, 0.4622, indicates that we cannot reject the equality, which leads us to admit that $C=C^{\prime }\sim BN\left(\rho \right)$. Since the sample estimate of the Pearson’s correlation coefficient is negative, we test $\rho =0$ against $\rho <0$ by running the test for association between paired samples using Pearson’s correlation coefficient for the vector $\mathbf{X}$. The p-value, 0.0442, suggests that $\rho <0$, which means that the copulas are NDS (see Example 4.1 in [24]).

To conclude: the assumptions (1) $X_1{\le }_{icx}{Y}_1$ and that (2) the copulas C and $C^{\prime }$ are equal and are NDS, are supported by statistical significance. It follows from Corollary 20 that $|X_1-X_2|{\le }_{icx}|Y_1-Y_2|,$ which indicates that Zoom leads to a less risky portfolio than Moderna.

6. Conclusions

Given two random variables $X_1$ and $X_2$ that are not necessarily independent, we have provided several results concerning the distances $|X_1-X_2|,$ ${(X_1-X_2)}^{+}$ and their expectations. The most remarkable results of this study can be summarized as follows:

(a)

If X is a random variable with strictly increasing distribution function F and $X_1$ and $X_2$ are two random variables with a NDS (negative dependent through stochastic ordering) copula C and with marginal distribution functions $F_1=F_2=F,$ then $\nu \left(X\right)=E\left(\left|X_1-X_2\right|\right)$ is a variability measure satisfying the following properties: law invariance, translation invariance, positive homogeneity, non-negativity, consistency with the dispersive order, consistency with the excess wealth order, comonotonic additivity, and subadditivity. An example is the median absolute deviation $\nu \left(X\right)=E\left(\left|X-m_X\right|\right),$ where $m_X$ is the median of $X,$ which can be written in the form $\frac{1}{2}E\left(\left|X_1-X_2\right|\right),$ where C is the Fréchet–Hoeffding lower bound copula.

(b)

Given two random vectors $(X_1,X_2)$ and $(Y_1,Y_2)$ with possibly different marginals and copulas, we have given conditions, in terms of several stochastic orders, under which $|X_1-X_2|{\le }_{st,icx}|Y_1-Y_2|$ and ${(X_1-X_2)}^{+}{\le }_{st,icx}{(Y_1-Y_2)}^{+}.$

Two applications have been provided. In actuarial science, given a risk $X,$ we have proposed a general class of premium principles of the form $T_C\left(X\right)=E\left(X\right)+\lambda E\left(\left|X_1-X_2\right|\right),$ for some $\lambda >0,$ where $X_1$ and $X_2$ are two copies of X with copula $C.$ In portfolio risk management, we have assessed the inclusion of a new asset in a portfolio by comparing absolute values of differences. It is a question of future research to determine the circumstances under which the criterion used in Section 5.2 to include a new asset in a portfolio gives rise to a portfolio with smaller realized variance.

Finally, it is interesting to note that the random excess ${(X_1-X_2)}^{+}$ also has an appealing role in the context of risk management and quantitative finance. If $X_1\left(t\right)$ and $X_2\left(t\right)$ are the prices of two risky assets at time $t,$ the payoff of the option that gives the buyer the right to exchange the second asset for the first at the expiry time t (called exchange option) is ${(X_1\left(t\right)-X_2\left(t\right))}^{+}.$ In this context, the results in this paper can be used to compare different payoffs in a similar manner as in Section 5.2.