Parameters Identification of PV Triple-Diode Model Using Improved Generalized Normal Distribution Algorithm
Abstract
:1. Introduction
- ❖
- Relating its exploitation capability with the average of the current mean position of the population, the best-so-far solution, and the position of the current individual, and that may cause low convergence toward the best-so-far solution for reaching better solutions quickly whether the best-so-far solution is not a local minimum one.
- ❖
- Relating its exploration capability with three solutions selected randomly from the population and may make the algorithm explore regions that may already have been explored.
- ❖
- A novel ranking-based position updating method (RUM) to help the algorithm in exploring as many regions as possible; and
- ❖
- A premature convergence method (PCM) to help accelerate its convergence speed toward the near-optimal solution.
- Improving the GNDO by the novel RUM and the premature convergence method (PCM) to produce a new variant called RGNDO for tackling the parameter estimation of the TDM.
- Comparing the performance of RGNDO with some well-established parameter estimation techniques, in addition to the standard GNDO, on five well-known commercial PV modules confirms the superiority of RGNDO over these compared algorithms in terms of convergence speed and final accuracy, in addition to its competitivity for the computational cost.
2. Mathematical Descriptions of the Triple-Diode Model
3. The Standard Algorithm: Generalized Normal Distribution Optimization
3.1. Local Exploitation
3.2. Global Exploration
4. The Proposed Algorithm: RGDNO
4.1. Initialization
4.2. The Objective Function
4.3. Ranking-Based Novel Updating Method (RUM)
4.4. Premature Convergence Method (PCM)
- Utilizing each individual in the population through the optimization process by the RUM to help in exploring more regions within the search space as possible. The RUM here aids the standard GNDO to improve the exploration operator at the start of the optimization process as an attempt to prevent stuck into local minima, while, with increasing the current function evaluation, the exploration operator is gradually converted into exploitation to search around the best-so-far solution to promote the convergence speed.
- Highly stable due to using the PCM that helps in steering the convergence speed in the right direction of the best-so-far solution to explore the promising regions that appear within the optimization process.
5. Experimental Results
5.1. Parameter Settings
5.2. Dataset Descriptions
6. Results and Discussion
6.1. Test Case 1: RTC France Cell
6.2. Test Case 2: Kyocera KC200GT—204.6 W Module
6.3. Test Case 3: Ultra 85-P
6.4. Test Case 4: STP6-120/36 Module
6.5. Comparison between GNDO and RGNDO
6.6. CPU Time
6.7. Wilcoxon Rank Sum Test
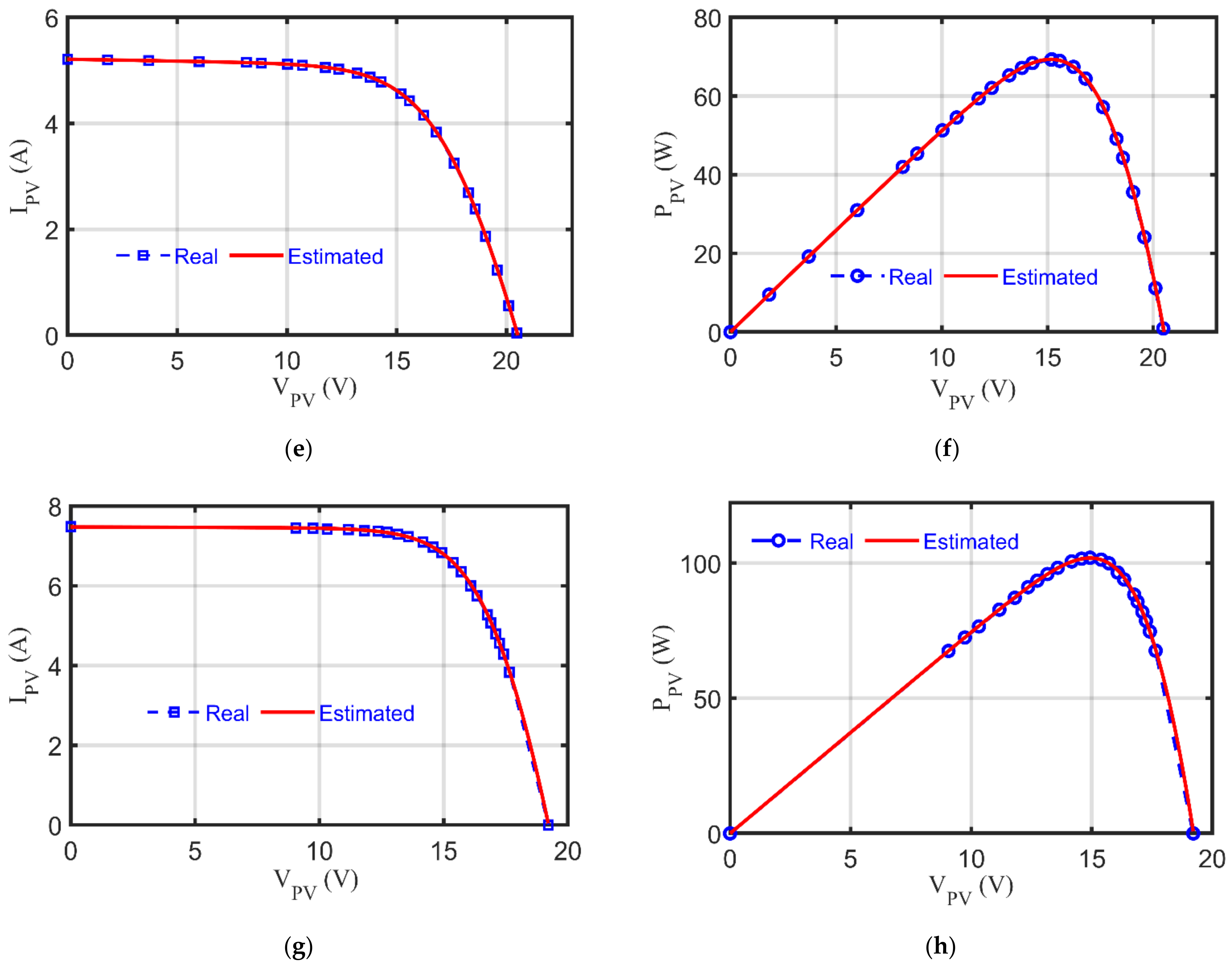
6.8. Various Steady-State Characteristics under Varied Operating Conditions
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alam, D.; Yousri, D.; Eteiba, M. Flower pollination algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.K.; Ryan, M.J. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 2020, 209, 694–708. [Google Scholar] [CrossRef]
- Selem, S.I.; El-Fergany, A.A.; Hasanien, H.M. Artificial electric field algorithm to extract nine parameters of triple-diode photovoltaic model. Int. J. Energy Res. 2020, 45, 590–604. [Google Scholar] [CrossRef]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Mekhilef, S.; Shamsudin, A. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution. Appl. Energy 2012, 99, 297–308. [Google Scholar] [CrossRef]
- El-Hameed, M.A.; Elkholy, M.M.; El-Fergany, A.A. Three-diode model for characterization of industrial solar generating units using Manta-rays foraging optimizer: Analysis and validations. Energy Convers. Manag. 2020, 219, 113048. [Google Scholar] [CrossRef]
- Long, W.; Cai, S.; Jiao, J.; Xu, M.; Wu, T. A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Convers. Manag. 2020, 203, 112243. [Google Scholar] [CrossRef]
- Li, S.; Gu, Q.; Gong, W.; Ning, B. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 205, 112443. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S.; Nouh, A.S. Coyote optimization algorithm for parameters extraction of three-diode photovoltaic models of photovoltaic modules. Energy 2019, 187, 116001. [Google Scholar] [CrossRef]
- Allam, D.; Yousri, D.; Eteiba, M. Parameters extraction of the three diode model for the multi-crystalline solar cell/module using Moth-Flame Optimization Algorithm. Energy Convers. Manag. 2016, 123, 535–548. [Google Scholar] [CrossRef]
- Ahmad, T.; Sobhan, S.; Nayan, M.F. Comparative analysis between single diode and double diode model of PV cell: Concentrate different parameters effect on its efficiency. J. Power Energy Eng. 2016, 4, 31–46. [Google Scholar] [CrossRef] [Green Version]
- Khanna, V.; Das, B.; Bisht, D.; Singh, P. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew. Energy 2015, 78, 105–113. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Mohamed, R. HSMA_WOA: A hybrid novel Slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest X-ray images. Appl. Soft Comput. 2020, 106642. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Basset, M.; El-shahat, D.; Elhoseny, M.; Song, H. Energy-Aware Metaheuristic algorithm for Industrial Internet of Things task scheduling problems in fog computing applications. IEEE Internet Things J. 2020, 1. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elhoseny, M.; Bashir, A.K.; Jolfaei, A.; Kumar, N. Energy-Aware Marine Predators Algorithm for Task Scheduling in IoT-based Fog Computing Applications. IEEE Trans. Ind. Inform. 2020, 17, 5068–5076. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Pillay, V.; Hirasen, D.; Sivanarain, K.; Govender, M. A Comparative study of meta-heuristic optimization algorithms for 0–1 knapsack problem: Some initial results. IEEE Access 2019, 7, 43979–44001. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Robust electrical parameter extraction methodology based on Interior Search Optimization Algorithm applied to supercapacitor. ISA Trans. 2020, 105, 86–97. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S. Parameter estimation of three diode photovoltaic model using grasshopper optimization algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef] [Green Version]
- Yousri, D.; Thanikanti, S.B.; Allam, D.; Ramachandaramurthy, V.K.; Eteiba, M. Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 2020, 195, 116979. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Do, T.D.; Kamel, O.M.; Mossa, M.A. Coyote optimization algorithm for parameters estimation of various models of solar cells and PV modules. IEEE Access 2020, 8, 111102–111140. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.; Duck, B.C.; Nadarajah, M. An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model. Energy Convers. Manag. 2020, 213, 112872. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Parameters extraction of three-diode photovoltaic model using computation and Harris Hawks optimization. Energy 2020, 195, 117040. [Google Scholar] [CrossRef]
- Chenouard, R.; El-Sehiemy, R.A. An interval branch and bound global optimization algorithm for parameter estimation of three photovoltaic models. Energy Convers. Manag. 2020, 205, 112400. [Google Scholar] [CrossRef]
- Liang, J.; Ge, S.; Qu, B.; Yu, K.; Liu, F.; Yang, H.; Wei, P.; Li, Z. Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models. Energy Convers. Manag. 2020, 203, 112138. [Google Scholar] [CrossRef]
- Long, W.; Wu, T.; Jiao, J.; Tang, M.; Xu, M. Refraction-learning-based whale optimization algorithm for high-dimensional problems and parameter estimation of PV model. Eng. Appl. Artif. Intell. 2020, 89, 103457. [Google Scholar] [CrossRef]
- Ridha, H.M.; Gomes, C.; Hizam, H. Estimation of photovoltaic module model’s parameters using an improved electromagnetic-like algorithm. Neural Comput. Appl. 2020, 32, 12627–12642. [Google Scholar] [CrossRef]
- Ridha, H.M.; Heidari, A.A.; Wang, M.; Chen, H. Boosted mutation-based Harris hawks optimizer for parameters identification of single-diode solar cell models. Energy Convers. Manag. 2020, 209, 112660. [Google Scholar] [CrossRef]
- Ram, J.P.; Pillai, D.S.; Rajasekar, N.; Chinnaiyan, V.K. Flower Pollination Based Solar PV Parameter Extraction for Double Diode Model. In Intelligent Computing Techniques for Smart Energy Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 303–312. [Google Scholar]
- Hassan, K.H.; Rashid, A.T.; Jasim, B.H. Parameters estimation of solar photovoltaic module using camel behavior search algorithm. Int. J. Electr. Comp. Eng. 2021, 11, 788–793. [Google Scholar] [CrossRef]
- Kashefi, H.; Sadegheih, A.; Mostafaeipour, A.; Omran, M.M. Parameter identification of solar cells and fuel cell using improved social spider algorithm. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2020. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L.; Gao, L. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization. Energy Convers. Manag. 2019, 186, 293–305. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Elavarasan, R.M.; Kumar, B.S. Enhanced chaotic JAYA algorithm for parameter estimation of photovoltaic cell/modules. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Ismaeel, A.A.; Houssein, E.H.; Oliva, D.; Said, M. Gradient-based optimizer for parameter extraction in photovoltaic models. IEEE Access 2021, 9, 13403–13416. [Google Scholar] [CrossRef]
- Mokeddem, D. Parameter Extraction of Solar Photovoltaic Models Using Enhanced Levy Flight Based Grasshopper Optimization Algorithm. J. Electr. Eng. Technol. 2021, 16, 171–179. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Korashy, A.; Yu, J. Photovoltaic cells parameter estimation using an enhanced teaching–learning-based optimization algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 767–779. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.D.; Premkumar, M.; Raj, T.D. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Huynh, D.C.; Ho, L.D.; Dunnigan, M.W. Parameter Estimation of Solar Photovoltaic Cells Using an Improved Artificial Bee Colony Algorithm. In Proceedings of the International Conference on Green Technology and Sustainable Development, Ho Chi Minh City, Vietnam, 27–28 November 2020; pp. 281–292. [Google Scholar]
- Ćalasan, M.; Jovanović, D.; Rubežić, V.; Mujović, S.; Đukanović, S. Estimation of single-diode and two-diode solar cell parameters by using a chaotic optimization approach. Energies 2019, 12, 4209. [Google Scholar] [CrossRef] [Green Version]
- Nayak, B.; Mohapatra, A.; Mohanty, K.B. Parameter estimation of single diode PV module based on GWO algorithm. Renew. Energy Focus 2019, 30, 1–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Mirjalili, S. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 224, 113301. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Parameter identification for solar cell models using harmony search-based algorithms. Sol. Energy 2012, 86, 3241–3249. [Google Scholar] [CrossRef]
- Fossum, J.G.; Lindholm, F.A. Theory of grain-boundary and intragrain recombination currents in polysilicon pn-junction solar cells. IEEE Trans. Electron Devices 1980, 27, 692–700. [Google Scholar] [CrossRef]
- Koohi-Kamali, S.; Rahim, N.; Mokhlis, H.; Tyagi, V. Photovoltaic electricity generator dynamic modeling methods for smart grid applications: A review. Renew. Sustain. Energy Rev. 2016, 57, 131–172. [Google Scholar] [CrossRef]
- Nunes, H.; Pombo, J.; Mariano, S.; Calado, M.; De Souza, J.F. A new high performance method for determining the parameters of PV cells and modules based on guaranteed convergence particle swarm optimization. Appl. Energy 2018, 211, 774–791. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elhoseny, M.; Chakrabortty, R.K.; Ryan, M. A Hybrid COVID-19 Detection Model Using an Improved Marine Predators Algorithm and a Ranking-Based Diversity Reduction Strategy. IEEE Access 2020, 8, 79521–79540. [Google Scholar] [CrossRef]
- Yousri, D.; Rezk, H.; Fathy, A. Identifying the parameters of different configurations of photovoltaic models based on recent artificial ecosystem-based optimization approach. Int. J. Energy Res. 2020, 44, 11302–11322. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Elgendy, M.A.; Abdeen, A.M. Parameters estimation of single-and multiple-diode photovoltaic model using whale optimisation algorithm. IET Renew. Power Gener. 2018, 12, 1755–1761. [Google Scholar] [CrossRef]
- Shell PowerMax Solar Modules for Off-Grids Markets. Available online: http://www.effectivesolar.com/PDF/shell/SQ-80-85-P.pdf (accessed on 5 March 2021).
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Haynes, W. Wilcoxon rank sum test. In Encyclopedia of Systems Biology; Springer: New York, NY, USA, 2013; pp. 2354–2355. [Google Scholar]













| Algorithm | Year | PV Model | Contributions and Limitations. |
|---|---|---|---|
| Classified Perturbation Mutation Based PSO Algorithm (CPMPSO) [24] | 2020 | SDM, and DDM |
|
| Enhanced Adaptive Differential Evolution [8] | 2020 | SDM, and DDM |
|
| GOA [18] | 2020 | TDM |
|
| Whale Optimization Algorithm (WOA) based Reflecting Learning (RLWOA) [25] | 2020 | SDM |
|
| Improved equilibrium optimizer (IEO) [2]. | 2020 | SDM, and DDM |
|
| Improved Electromagnetism-like algorithm [26] | 2020 | SDM |
|
| Grey Wolf Optimizer (GWO) And Cuckoo Search (CS): GWOCS [7] | 2020 | SDM, and DDM |
|
| Boosted Harris Hawk’s Optimization (BHHO) [27] | 2020 | SDM |
|
| FPA [28]. | 2020 | DDM |
|
| Camel behavior search algorithm (CBSA) [29]. | 2020 | SDM |
|
| Improved social spider algorithm [30] | 2020 | SDM, and DDM |
|
| Improved Teaching-Learning-Based Optimization (ITLBO) [31] | 2019 | SDM, and DDM |
|
| Chaotic JAYA (CJAYA) [32] | 2021 | SDM, and DDM |
|
| Gradient-baed optimizer (GBO) [33]. | 2021 | SDM, DDM, and TDM |
|
| Improved levy flight-based grasshopper optimization algorithm [34] | 2020 | SDM, and DDM |
|
| Enhanced teaching–learning-based optimization (ETLBO) [35]. | 2020 | SDM, and DDM |
|
| Slime mould algorithm (SMA) [36] | 2020 | SDM, and DDM |
|
| Improved Artificial Bee Colony Algorithm (IABC) [37] | 2020 | SDM |
|
| Chaotic optimization approach [38] | 2019 | SDM, and DDM |
|
| GWO [39] | 2019 | SDM |
|
| Parameter | L | U |
|---|---|---|
| 0.720205 | 3.87 × 10−7 | 9.43 × 10−9 | 1.49 × 10−8 | 0.03571 | 69.93044 | 1.90020 | 1.29812 | 1.68252 |
| Output: return 1. Input: N, , and NCG 2. 3. RK: a vector of size N and initialized with 0’s value. 4. Initialize a population of N individuals using Equation (12) 5. While 6. For 7. Create two random numbers , within [0, 1] 8. If 9. Calculate the mean of the population M using Equation (6) 10. Compute 11. Compute using Equation (4). 12. If 13. 14. 15. Else 16. 17. End 18. Else 19. // global exploration 20. Compute according to Equation (9). 21. If 22. 23. 24. Else 25. 26. End 27. Applying the ranking method depicted in Figure 2 28. End 29. ; 30. End 31. /// applying the premature convergence method. 32. Generate two random numbers and within [0, 1]. 33. If 34. For 35. Compute using Equation (16). 36. If 37. 38. 39. Else 40. 41. End 42. ; 43. End 44. End 45. End |
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [46] | 0.760205 | 3.87 × 10−7 | 9.43 × 10−9 | 4.49 × 10−8 | 0.0357 | 69.9304 | 1.5002 | 1.9981 | 1.8825 | 9.899220431 × 10−4 |
| ITLBO [31] | 0.760500 | 2.98 × 10−8 | 9.17 × 10−7 | 1.86 × 10−9 | 0.0381 | 59.7254 | 1.3101 | 1.7186 | 1.6611 | 7.618033553 × 10−4 |
| ISA [17] | 0.760500 | 1.21 × 10−7 | 1.00 × 10−9 | 1.68 × 10−6 | 0.0377 | 59.5672 | 1.3995 | 1.9936 | 2.0000 | 7.534445387 × 10−4 |
| HHO [22] | 0.759740 | 1.75 × 10−7 | 2.77 × 10−7 | 9.10 × 10−7 | 0.0342 | 127.1454 | 1.4533 | 1.7284 | 1.8222 | 1.546454764 × 10−3 |
| WOA [47] | 0.760010 | 2.86 × 10−9 | 6.62 × 10−7 | 6.64 × 10−7 | 0.0303 | 353.9084 | 1.5664 | 1.6037 | 1.6904 | 2.556963482 × 10−3 |
| CPMPSO [24] | 0.760500 | 9.62 × 10−8 | 3.73 × 10−7 | 1.67 × 10−6 | 0.0379 | 61.1542 | 1.3812 | 1.9995 | 1.9993 | 7.508298630 × 10−4 |
| GNDO [40] | 0.760499 | 1.02 × 10−6 | 4.43 × 10−7 | 1.40 × 10−7 | 0.0374 | 59.0192 | 1.9912 | 2.0000 | 1.4112 | 7.557191951 × 10−4 |
| RGNDO | 0.760500 | 9.08 × 10−8 | 1.96 × 10−6 | 1.58 × 10−7 | 0.0380 | 61.3221 | 1.3766 | 2.0000 | 2.0000 | 7.506838880 × 10−4 |
| Method | AEO [46] | ITLBO [31] | ISA [17] | HHO [22] | WOA [47] | CPMPSO [24] | GNDO [40] | RGNDO |
|---|---|---|---|---|---|---|---|---|
| Best | 9.899220 × 10−4 | 7.618033 × 10−4 | 7.534445 × 10−4 | 1.546454 × 10−3 | 2.556963 × 10−3 | 7.508298 × 10−4 | 7.557192 × 10−4 | 7.506838 × 10−4 |
| Worst | 4.845654 × 10−3 | 2.006802 × 10−3 | 3.193321 × 10−3 | 9.090638 × 10−3 | 1.140435 × 10−2 | 7.797626 × 10−4 | 1.457815 × 10−3 | 7.663392 × 10−4 |
| Avg | 2.480973 × 10−3 | 1.001097 × 10−3 | 1.568473 × 10−3 | 6.079471 × 10−3 | 8.282383 × 10−3 | 7.622312 × 10−4 | 8.259549 × 10−4 | 7.529015 × 10−4 |
| SD | 9.316490 × 10−4 | 3.767089 × 10−4 | 6.760342 × 10−4 | 2.146342 × 10−3 | 2.002442 × 10−3 | 8.744482 × 10−6 | 1.434043 × 10−4 | 3.933168 × 10−6 |
| Rank | 6 | 4 | 5 | 7 | 8 | 2 | 3 | 1 |
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [46] | 8.1614 | 1.13 × 10−9 | 2.42 × 10−8 | 2.67 × 10−9 | 0.0038 | 5.9997 | 1.7205 | 1.2159 | 1.7762 | 0.04384316 |
| ITLBO [31] | 8.1037 | 9.29 × 10−9 | 5.97 × 10−7 | 6.13 × 10−7 | 0.0040 | 352.8323 | 1.1612 | 1.9926 | 1.8737 | 0.04596226 |
| ISA [17] | 8.1797 | 1.00 × 10−9 | 1.19 × 10−9 | 2.50 × 10−9 | 0.0046 | 3.1251 | 1.0468 | 2.0000 | 1.6340 | 0.02897981 |
| HHO [22] | 8.1384 | 9.00 × 10−8 | 4.29 × 10−8 | 1.00 × 10−9 | 0.0033 | 23.2043 | 1.3046 | 1.5244 | 1.5825 | 0.05640261 |
| WOA [47] | 8.1265 | 1.02 × 10−9 | 3.47 × 10−6 | 1.02 × 10−9 | 0.0041 | 152.0232 | 1.0546 | 1.8552 | 1.4212 | 0.04680127 |
| CPMPSO [24] | 8.1888 | 1.65 × 10−9 | 1.49 × 10−9 | 9.70 × 10−9 | 0.0044 | 3.1390 | 1.0742 | 1.2009 | 1.9451 | 0.03042386 |
| GNDO [40] | 8.2002 | 1.00 × 10−9 | 1.00 × 10−9 | 1.04 × 10−9 | 0.0046 | 2.6505 | 1.0469 | 1.8270 | 1.6336 | 0.02822634 |
| RGNDO | 8.2011 | 1.00 × 10−9 | 1.00 × 10−9 | 1.00 × 10−9 | 0.0046 | 2.6410 | 1.0469 | 2.0000 | 2.0000 | 0.02821281 |
| Algorithms | AEO [46] | ITLBO [31] | ISA [17] | HHO [22] | WOA [47] | CPMPSO [24] | GNDO [40] | RGNDO |
|---|---|---|---|---|---|---|---|---|
| Best | 0.0438431608 | 0.0459622563 | 0.0289798147 | 0.0564026070 | 0.0468012666 | 0.0304238578 | 0.0282263443 | 0.0282128080 |
| Worst | 0.0934460402 | 0.1163438794 | 0.0867319890 | 0.1359284618 | 0.2418484379 | 0.0683562899 | 0.0683562899 | 0.0683562899 |
| Avg | 0.0654501748 | 0.0719622807 | 0.0581298639 | 0.1028267389 | 0.1369643198 | 0.0434628437 | 0.0422750429 | 0.0406449525 |
| SD | 0.0100639011 | 0.0163810072 | 0.0113337942 | 0.0229987194 | 0.0421336396 | 0.0100268403 | 0.0119265384 | 0.0145287520 |
| Rank | 5 | 6 | 4 | 7 | 8 | 3 | 2 | 1 |
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [46] | 5.226139 | 2.95 × 10−6 | 8.21 × 10−6 | 6.50 × 10−6 | 0.0112 | 3.9298 | 1.4669 | 1.7847 | 1.7682 | 2.455842651 × 10−3 |
| ITLBO [31] | 5.226022 | 8.88 × 10−6 | 2.50 × 10−6 | 1.00 × 10−5 | 0.0112 | 3.9630 | 1.9046 | 1.4497 | 1.7691 | 2.431633915 × 10−3 |
| ISA [17] | 5.226719 | 3.45 × 10−6 | 9.23 × 10−7 | 9.28 × 10−6 | 0.0111 | 3.8525 | 1.4903 | 1.6419 | 1.7129 | 2.497373210 × 10−3 |
| HHO [22] | 5.190855 | 5.21 × 10−6 | 4.44 × 10−6 | 3.45 × 10−6 | 0.0113 | 7.5484 | 1.5177 | 1.7167 | 1.7359 | 1.076041865 × 10−2 |
| WOA [47] | 5.198240 | 4.20 × 10−6 | 5.01 × 10−6 | 3.79 × 10−7 | 0.0116 | 5.9580 | 1.4955 | 1.6688 | 1.6537 | 1.032542474 × 10−2 |
| CPMPSO [24] | 5.225747 | 1.90 × 10−6 | 9.98 × 10−6 | 9.78 × 10−6 | 0.0113 | 3.9926 | 1.4273 | 1.7946 | 1.8201 | 2.423466909 × 10−3 |
| GNDO [40] | 5.226051 | 1.00 × 10−5 | 2.76 × 10−6 | 9.91 × 10−6 | 0.0112 | 3.9679 | 1.7967 | 1.4552 | 1.9194 | 2.428164856 × 10−3 |
| RGNDO | 5.225629 | 6.45 × 10−7 | 1.00 × 10−5 | 1.00 × 10−5 | 0.0113 | 4.0252 | 1.3519 | 1.7529 | 1.7439 | 2.417084253 × 10−3 |
| Algorithms | AEO [46] | ITLBO [31] | ISA [17] | HHO [22] | WOA [47] | CPMPSO [24] | GNDO [40] | RGNDO |
|---|---|---|---|---|---|---|---|---|
| Best | 0.002470471 | 0.002443520 | 0.002679316 | 0.019364346 | 0.010087377 | 0.002417985 | 0.002426150 | 0.002417084 |
| Worst | 0.018785517 | 0.017193050 | 0.017503896 | 0.039575676 | 0.049733913 | 0.005058644 | 0.011573784 | 0.002492268 |
| Avg | 0.004108074 | 0.003789465 | 0.007121044 | 0.027427524 | 0.027609976 | 0.002573152 | 0.002819667 | 0.002446177 |
| SD | 0.003918587 | 0.003717768 | 0.004665595 | 0.005092069 | 0.008970604 | 0.000482496 | 0.001656137 | 0.000025994 |
| Rank | 6 | 5 | 7 | 8 | 9 | 2 | 3 | 1 |
| Algorithms | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AEO [46] | 7.475257 | 6.02 × 10−9 | 1.85 × 10−6 | 2.26 × 10−6 | 0.004677 | 17.4376 | 1.9961 | 1.2418 | 1.7719 | 1.389396490646 × 10−2 |
| ITLBO [31] | 7.476115 | 1.90 × 10−6 | 1.77 × 10−8 | 1.00 × 10−9 | 0.004694 | 15.1633 | 1.2437 | 1.3065 | 1.4249 | 1.379885388914 × 10−2 |
| ISA [17] | 7.476936 | 1.00 × 10−9 | 1.88 × 10−6 | 1.00 × 10−9 | 0.004703 | 14.3643 | 1.9907 | 1.2424 | 1.5690 | 1.380086028210 × 10−2 |
| HHO [22] | 7.458183 | 2.18 × 10−6 | 3.64 × 10−9 | 2.56 × 10−9 | 0.004653 | 248.4131 | 1.2545 | 1.2125 | 1.4412 | 1.424187705506 × 10−2 |
| WOA [47] | 7.464125 | 1.82 × 10−6 | 1.62 × 10−6 | 9.32 × 10−6 | 0.004575 | 337.8192 | 1.9703 | 1.2357 | 1.7318 | 1.493293998738 × 10−2 |
| CPMPSO [24] | 7.476213 | 5.09 × 10−8 | 1.88 × 10−6 | 1.00 × 10−9 | 0.004692 | 15.1426 | 1.2443 | 1.2443 | 2.0000 | 1.379827332710 × 10−2 |
| GNDO [40] | 7.476214 | 1.93 × 10−6 | 1.01 × 10−9 | 1.00 × 10−9 | 0.004692 | 15.1424 | 1.2443 | 1.2442 | 2.0000 | 1.379827333205 × 10−2 |
| RGNDO | 7.476213 | 1.93 × 10−6 | 1.02 × 10−9 | 1.00 × 10−9 | 0.004692 | 15.1427 | 1.2443 | 1.2443 | 2.0000 | 1.379827332701 × 10−2 |
| Algorithms | AEO [46] | ITLBO [31] | ISA [17] | HHO [22] | WOA [47] | CPMPSO [24] | GNDO [40] | RGNDO |
|---|---|---|---|---|---|---|---|---|
| Best | 0.013893964 | 0.013798853 | 0.013800860 | 0.014241877 | 0.014932940 | 0.013798273 | 0.013798273 | 0.013798273 |
| Worst | 0.028970100 | 0.014295495 | 0.023508622 | 0.049436644 | 0.141388822 | 0.014659372 | 0.014863306 | 0.013799111 |
| Avg | 0.016038025 | 0.013925848 | 0.014629957 | 0.025279469 | 0.041237117 | 0.013899188 | 0.013882239 | 0.013798325 |
| SD | 0.003578909 | 0.000126236 | 0.001770716 | 0.009375668 | 0.026679451 | 0.000211721 | 0.000224301 | 0.000000149 |
| Rank | 6 | 4 | 5 | 7 | 8 | 3 | 2 | 1 |
| Algorithms | RTC France | KC200GT | Ultra 85-P | STP6-120/36 | ||||
|---|---|---|---|---|---|---|---|---|
| h | p-Value | h | p-Value | h | p-Value | h | p-Value | |
| RGNDO vs. AEO | 1 | 3.0199 × 10−11 | 1 | 2.5473 × 10−12 | 1 | 1.2057 × 10−10 | 1 | 3.0199 × 10−11 |
| RGNDO vs. ITLBO | 1 | 4.5043 × 10−11 | 1 | 2.6537 × 10−13 | 1 | 5.0922 × 10−8 | 1 | 3.3384 × 10−11 |
| RGNDO vs. ISA | 1 | 8.1527 × 10−11 | 1 | 1.1737 × 10−9 | 1 | 3.0199 × 10−11 | 1 | 3.0199 × 10−11 |
| RGNDO vs. HHO | 1 | 3.0199 × 10−11 | 1 | 1.6998 × 10−16 | 1 | 3.0199 × 10−11 | 1 | 3.0199 × 10−11 |
| RGNDO vs. WOA | 1 | 3.0199 × 10−11 | 1 | 3.5254 × 10−17 | 1 | 3.0199 × 10−11 | 1 | 3.0199 × 10−11 |
| RGNDO vs. CPMPSO | 1 | 4.1178 × 10−6 | 1 | 2.2893 × 10−4 | 1 | 5.5611 × 10−4 | 1 | 8.8411 × 10−7 |
| RGNDO vs. GNDO | 1 | 4.0772 × 10−11 | 1 | 4.1782 × 10−3 | 1 | 1.0907 × 10−5 | 1 | 1.8916 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Basset, M.; Mohamed, R.; El-Fergany, A.; Abouhawwash, M.; Askar, S.S. Parameters Identification of PV Triple-Diode Model Using Improved Generalized Normal Distribution Algorithm. Mathematics 2021, 9, 995. https://doi.org/10.3390/math9090995
Abdel-Basset M, Mohamed R, El-Fergany A, Abouhawwash M, Askar SS. Parameters Identification of PV Triple-Diode Model Using Improved Generalized Normal Distribution Algorithm. Mathematics. 2021; 9(9):995. https://doi.org/10.3390/math9090995
Chicago/Turabian StyleAbdel-Basset, Mohamed, Reda Mohamed, Attia El-Fergany, Mohamed Abouhawwash, and S. S. Askar. 2021. "Parameters Identification of PV Triple-Diode Model Using Improved Generalized Normal Distribution Algorithm" Mathematics 9, no. 9: 995. https://doi.org/10.3390/math9090995
APA StyleAbdel-Basset, M., Mohamed, R., El-Fergany, A., Abouhawwash, M., & Askar, S. S. (2021). Parameters Identification of PV Triple-Diode Model Using Improved Generalized Normal Distribution Algorithm. Mathematics, 9(9), 995. https://doi.org/10.3390/math9090995









